Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
Water SA
On-line version ISSN 1816-7950
Print version ISSN 0378-4738
Water SA vol.35 n.2 Pretoria Jan. 2009
Destratification induced by bubble plumes as a means to reduce evaporation from open impoundments
M van Dijk*; SJ van Vuuren
Department of Civil Engineering, University of Pretoria, Pretoria 0001, South Africa
ABSTRACT
The use of thermal mixing by means of compressed air appears to have important potential for evaporation suppression on deep reservoirs. Current methods used to reduce evaporation from open-water impoundments such as floating covers, modular covers, monolayers and shade structures have many disadvantages and negative impacts on the environment. These methods impact the natural/modified aquatic ecosystem established in the dam; alter aesthetic qualities; increase the risk of dam failure in times of flood; could potentially lead to an oxygen reduction in the water; and may compromise the natural water treatment functions and operations such as the reduction of harmful bacteria, exposure to sunlight (form of disinfection) and natural and mechanical aeration thereby increasing treatment costs.
The methodology proposed in this paper to help reduce evaporation losses from open-water impoundments, which indirectly addresses problems of water shortage and the associated economic impacts, involves the destratification of the water body using a bubble plume operated with minimal energy input to reduce surface water temperatures, with, a subsequent reduction in evaporation.
The literature, although limited, indicates that this proposed method has merit and requires further research to identify specific reservoirs (size, depth, usage) that could benefit from such a destratification system. Evaporation suppression of as high as 30 % was achieved in some case studies.
Keywords: bubble plume, destratification, evaporation reduction, evaporation suppression
Introduction
Due to South Africa's climate and geographical situation, South Africa experiences low rainfall and high evaporation rates leading to shortages of water and high losses of water from water storage facilities. Because of the sporadic, temporal and spatial distribution of precipitation, the only way that water supply can be controlled to meet demand is through storage. According to the National Water Resource Strategy (DWAF, 2004), South Africa depends mainly on surface water resources for most of its urban, industrial and irrigation requirements.
South African water authorities should therefore use the limited available resources effectively, efficiently and wisely for a sustainable future. The cost of evaporation losses is significant and has a major effect on the design and operation of reservoirs.
The water lost due to storage evaporation depends upon many factors including atmospheric evaporative demand, the size of the water storage and storage method (Craig, 2006). According to Craig (2006) there have been many attempts to reduce losses by altering how the water is stored, firstly by increasing the water depth and secondly by installing a good quality liner to prevent seepage. Current methods used to reduce evaporation from water resources such as floating covers, modular covers, monolayers and shade structures could have many disadvantages and negative impacts on the environment (Hughes et al., 1974). A scoping study done by Watts (2005) provides a number of commercially available products used in evaporation reduction such as shade cloth, polystyrene beads and foamed rubber. These are however mostly applicable to small dams.
These methods impact the natural/modified aquatic ecosystem established in the dam; alter aesthetic qualities; increase the risk of dam failure in times of flood; could potentially lead to an oxygen reduction in the water; and may compromise the natural water treatment functions and operations such as the reduction of harmful bacteria, exposure to sunlight (form of disinfection) and natural and mechanical aeration thereby increasing treatment costs.
The methodology proposed to reduce the effect of evaporation losses and indirectly solving the water shortage and increase the reliability of supply, involves the destratification of the water body using a bubble plume operated with minimal energy input to reduce surface water temperatures and subsequently reducing evaporation.
During summer, the surface water (epilimnion) of a reservoir heats and therefore becomes less dense. Below this surface layer, which is nominally 3 to 4 m deep, the water remains cold and more dense (hypolimnion). These layers are separated by a thermocline which acts somewhat as a barrier to normal convection circulation and prevents the hypolimnetic water from being circulated or mixed. This phenomenon is commonly termed stratification. By injecting a bubble plume in the cold hypolimnion layer artificial destratification will occur by means of diffusion, when this bubble rises to the surface through the different temperature layers.
In the summer months, water bodies stratify forming layers with different temperatures. The surface water reaches high temperatures, aiding evaporation. Artificial destratification, mixing to dissipate layers with the aim of uniform temperature gradients over the depth of the storage, is believed to reduce evaporation by bringing cold water from the lower layers to the surface, thereby reducing the surface water temperature. The air injection bubble plume system used for water quality applications has been observed to be one of the most cost effective, appropriate and viable solutions for artificial destratification. The application of this methodology for reducing open-water evaporation seems to have potential as first shown by Hughes et al. (1975) although very few references were found where this method is being used as a technique to reduce evaporation.
Objective of study
The main objective of this study was to investigate the potential reduction of evaporation from reservoirs by the destratification of the water system, thereby altering the temperature gradient. The bubbles released at a slow rate will disturb the stratified water layers as these move to the surface, bringing cooler water particles to the surface. Through a process of diffusion the cooler water will spread horizontally, as well as having a ripple effect from the source outwards. This will gradually lower the water surface temperature, increasing the energy needed for evaporation, thereby reducing evaporation from the reservoir.
The key objectives of the study were:
-
To investigate the potential of artificial destratification as a method for reducing the evaporation from reservoirs
-
To investigate the effectiveness of an air injection bubble plume system to destratify a water body (reservoir)
-
The quantification of the effect of the destratification on the surface water temperatures
-
The quantification of the reduction in evaporation loss from the reservoir.
The obtained results together with the information available from literature will be used in evaluating whether this proposed method is economically viable on a large scale and can be used in major reservoirs in South Africa.
Methodology
In order to meet the set key objectives a literature study was conducted to determine how a water body could be destratified. This included mechanical mixing and buoyant bubble plume releasing. Furthermore the evaporation process was explored to determine what the influence would be if the surface layer of the open-water impoundment was to be altered. The dominant components of the evaporation process needs to be identified in order to simplify the evaporation quantification process. Experimental and field work was conducted to get acquainted with the practical facets of the proposed method.
Evaporation
Evaporation constitutes the physical process by which water in the liquid phase becomes atmospheric water vapour. In South Africa the evaporation losses from our reservoirs are significant. As shown in Fig. 1, the evaporation rate is greater than 1 400 mm/a for most of the country. Evaporation has a significant influence on the yield of water supply reservoirs and on the economics of building reservoirs of various sizes.
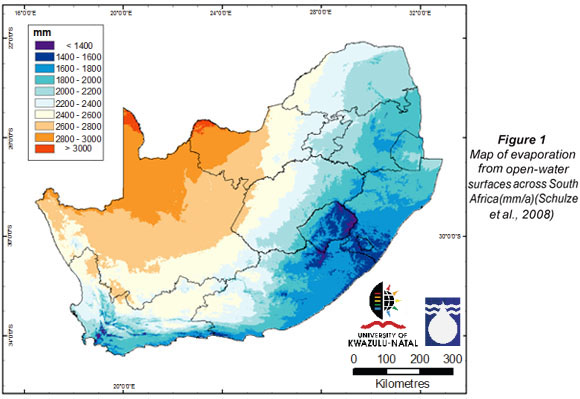
As described by Serrano (1997), the driving force in the evaporation process is solar radiation, which provides energy to the water molecules near the water body surface. The radiation causes an increase in the vibratory kinetic energy of the water molecules and when the amplitude of vibration overcomes the forces of molecular attraction, the molecules escape from the liquid mass into the air immediately above the surface. Absorption of energy is a prerequisite for the occurrence of evaporation.
The amount of energy required for the evaporation of one kilogram of water is called the latent heat of vaporisation, L (cal/kg). The required energy decreases as the temperature of the evaporating water increases or, in line with the objective of decreasing the evaporation, if the temperature of the evaporating water surface is decreased, this results in an additional energy requirement.
Evaporation is a diffusive process (transport mechanism) which is governed by Fick's law of diffusion. Water vapour will move from sections of air mass with high concentrations (just above the water surface) to sections of air with low concentrations (higher atmospheric regions of dryer air). The maximum number of molecules held by the air corresponds to the so called saturation vapour pressure which is a function of air temperature. The ratio of the actual vapour pressure to the saturated vapour pressure is defined as the relative humidity usually expressed as a percentage. High relative humidity values (>80%) indicate humid conditions with subsequent expected low evaporation rates.
The transport mechanism causes a vapour pressure gradient and thus the moist air immediately above the water surface is replaced with dryer air. This process is influenced by turbulent eddies resulting from the upward movement of moist air (seeing that moist air is lighter than dry air) as well as wind currents displacing moist air away from the surface. A general equation to express the evaporation rate that considers the above is Dalton's (1802) law in Serrano (1997).

where:
E = evaporation rate (mm/d)
es = saturated vapour pressure at the water surface temperature (mmHg)
ea = vapour pressure at a fixed distance above the evaporating surface (mmHg)
u = horizontal wind speed (km/h)
f (u) = function of the wind speed and other factors (h.mm / d.km. mmHg)
There is a strong correlation between evaporation and water surface temperature. This is clearly shown in the monotonic function relating water temperature to saturation vapour pressure.
There are various forms of Eq. (1), collectively called mass transfer equations, such as Harbeck (1962):

where:
A = reservoir surface area (km²)
W = wind speed at a point 2 m above the water surface (km/hour)
ea = vapour pressure at a point 2 m above the water surface (mmHg)
k = mass transfer coefficient equal to 0.054 (mm.h/ d.km0.9.mmHg)
Hughes et al. (1975) provided an evaporation suppression equation as a function of change in water surface temperature where es is a factor rather than an additive component of the equation as shown in Eqs. (1) and (2). This allowed for elimination of calculating the actual evaporation magnitudes and therefore the need to determine wind and other unchanged parameters combined into f (u). The basic evaporation suppression relationship is:

where:
f(T) = The function relating temperature to saturation vapour pressure
Tc = Temperature of the cooled system (thermally mixed) (°C)
Tn = Temperature during normal conditions in the reservoir (°C)
Another method which is commonly used is the water balance technique (Eq. (4). The application of this method requires an account of all streams, entering and leaving the reservoir, measured precipitation and estimates of net groundwater contributions.

where:
E = evaporation rate (m3/s)
Qi = average inflow rate (m3/s)
Qo = average outflow rate (m3/s)
ΔS = change in storage volume (m3)
Δt = period of analysis (s)
It is required to consider the heat addition and loss sources over time to enable integration of these effects on a reservoir and establish the potential suppression relationship. The energy budget technique is a valuable method for defining the heat flux. As mentioned before, evaporation requires the absorption of energy either supplied by solar radiation or the water body itself. As detailed in Serrano (1997), radiation is the emission of energy in the form of electromagnetic waves from all bodies above the absolute zero temperature, and thus it is possible to establish an energy balance (energy budget). The US Geological Survey researchers defined nine variables with units' cal/m².d, which constitute the energy budget (Harbeck, 1962 and Hughes et al., 1975) and illustrated in Fig. 2 (next page).
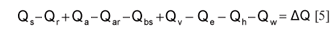
where:
Qs = incoming solar radiation
Qr = reflected solar radiation
Qa = incoming solar atmospheric long-wave radiation
Qar = reflected atmospheric long-wave solar radiation
Qbs = long wave radiation emitted by the body of water
Qv = energy advected into or from the reservoir (inflow and outflow)
Qe = energy used in evaporation
Qh = energy loss as sensible heat
Qw = energy advected by evaporated water
ΔQ = change in reservoir energy
From the analysis performed by Hughes et al. (1975) 2 of the 9 parameters emerged as being dominant; these are Qe (evaporation latent heat) and Qv (the outflow component).
Artificial destratification
To destratify a reservoir a bubble plume diffuser could be used. Bubbles released via the diffuser will rise through to the surface. The bubbles entrain cold and dense water in the cold hypolimnion layer and form a plume. This plume will rise through the layers until the mixture of air-water reaches its natural buoyancy where its density is equal to the density of the surrounding water (Moshfegi et al., 2005). At this point the plume stops and the entrained water is detrained and emitted horizontally. The heavy hypolimnetic water is carried up to the epilimnion and after mixing with the light epilimnetic water, it submerges down to the neutral buoyancy level in the thermocline where it forms an intermediate layer with relatively homogeneous density (Imteaz and Asaeda, 2000). This layer expands up and down until the entire depth is occupied by this layer. The replacement rates of the epilimnion and hypolimnion depend on the plume number (Asaeda and Imberger (1993) and Lemckert and Imberger (1993)). A high plume number indicates a rapid thickening of the intermediate layer.
There are usually 3 types of plumes which may form in a linearly stratified flow. The type of plume will depend on the relative strength of the stratification as well as the air flow rate (Asaeda and Imberger (1993). The optimum value of the air flow rate is the rate which produces one ejection at the water surface (Moshfegi et al., 2005). The diffuser is also designed to have a number of clusters where the individual bubble plumes have no interaction with each other since this will lower their efficiency. The diffuser is placed at a certain height above the bottom of the reservoir to prevent the disturbance of the bed sediments and the subsequent carrying of nutrients to the surface.
Lackey (1972) describes an aerator (Helixor) which consisted of a 46 cm diameter polyethylene tube containing a continuous coil which divides the tube into separate longitudinal sections. Air is released at the Helixor bottom through several small holes. The coiled design lengthens the air-water interface compared to a simple perforated pipe. The Parvin Lake in Colorado has a surface area of 19 ha and maximum depth of 10 m. The thermal stratification could effectively be eliminated by installing 2 aerators operating at 2.1 m3/min. In this set-up it was done to improve dissolved oxygen levels and to keep part of the lake ice-free during winter.
Kothandaram and Evans (1982) utilised a mechanical axial flow pump destratifier in conjunction with an aerator to eliminate the thermal layers and add oxygen to the reservoir for improvement of the water quality only, i.e. no mention of the additional benefit of reduced evaporation. Kirke and Gezawy (1997) designed and tested a mechanical circulator/aerator for lakes and reservoirs. Their designed system successfully destratified a reservoir and although it does not add oxygen directly, through natural processes of diffusion, wind, etc., the colder water is oxygenated.
An investigation by Henderson-Sellers to determine how destratification and re-aeration can be used as tools for in-lake management to prevent the lack of oxygen and the negative impact on water quality indicated that a spin-off to destratification is that the surface temperature is reduced in summer (Henderson-Sellers, 1981). This in turn has an influence on the energy budget and will result in a decrease in the rate of evaporation. According to Henderson-Sellers a first-order approximation suggests that a 2°C drop in surface temperature during the summer months is realistic which would result in a 10% saving.
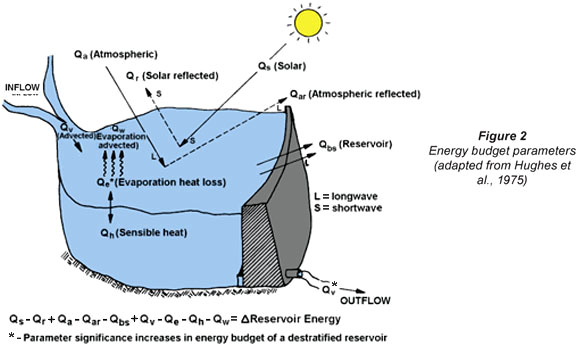
Destratification was proposed as one of the alternatives to increase the water temperature at the bottom outlet of a reservoir (Sherman, 2000) (see Fig. 3). The thermal mixing of the water would result in warmer water released into the river and in this way mitigate the effect of cold water pollution below dams. According to Sherman, Lorenzen and Fast (1977) proposed a rule of thumb of 150 ℓ/s of compressed air per 100 ha of reservoir surface area. The larger the destratification system the faster it can achieve the desired amount of destratification.
Sufficient destratification could result, depending on the month, in a reduced water surface temperature and the subsequent evaporation suppression. A suppression model for the thermal mixing was conceptualised by Hughes et al. (1975) and consisted of:
• Basic concept: Idealised suppression is calculated as a function of change in water surface temperature (ergo change in vapour pressure) caused by perfect mixing (isothermal temperature profile).
• Secondary effects: Sufficiently important secondary effects are included in the model such as:
- Extra heat due to the decrease in heat loss due to evaporation caused by suppression during the previous period, and
- Heat loss from the reservoir due to warmer than normal outflow from the mixed reservoir.
• Time resolution: Model parameters are determined on a monthly average basis. Heat flux is accumulated between months up to 6 months for reservoirs on which a seasonal analysis is appropriate and for annual or multi-year periods where carryover storage is important.
Results of destratification studies
A study by Koberg and Ford (1965) quantified the decrease in evaporation due to destratification of Lake Wohlford in California. The lake has a volume of 3.1 Mm3, its area is 53.1 ha and it has a maximum depth of only 15 m. A 15% reduction in evaporation was observed from May to June although the evaporation was 9% higher from September to November resulting in a net saving of 6%.
A research project undertaken in 1975 by the Utah Water Research Laboratory applied the suppression model as described above to 10 reservoirs in Utah in the United States. Table 1 shows the results of the seasonal model for reservoirs which had temperature profiles.

The flow index is computed from the monthly outflow /storage ratios; alternatively a seasonal index can be computed by weighting these ratios according to monthly evaporation factors which could provide a better indicator of the impact of outflow on seasonal suppression. Hughes et al. (1975) indicated that the suppression heat is the dominant secondary effect in large reservoirs.
According to Brown (1988) there are very few other references to destratification as a means to reduce evaporation. Hoy and Stephens (1979) in Brown (1988) analysed data from the Tarago Reservoir in Victoria (37.6 Mm3, surface area of 360 ha and maximum depth of 23 m). They estimated that lake evaporation was reduced by 25% over a 3-month period but the potential increase in evaporation in the following months was not determined.
Experimental set-up
One of the objectives of this research project was the quantification of the reduction in evaporation losses. An experimental set-up where the effect of destratifying the water body in a controlled environment and the subsequent reduction in evaporation could be determined was constructed at the hydraulic laboratories of the Department of Water Affairs and Forestry (DWAF) in Pretoria-West. Two reservoirs (Reservoir A and B) were constructed as shown in Fig. 4 (next page). Reservoir A was the benchmark reservoir with the destratification taking place in Reservoir B.

The reservoirs were insulated and roof covers were secured over the reservoirs to reduce the effect of precipitation, which would have a huge effect on reducing the water level temperatures and destratifying the layers. An onsite weather station was installed to record the exact weather conditions influencing the reservoirs. The station contained a rainfall meter, temperature sensors, anemometer to measure wind speed and wind direction. The change in water levels was determined using fixed point gauges. Based on the rate of change in water levels the evaporation rate could be determined.
Thermocouple sensors were used to measure the water temperatures of the different layers in the reservoirs to ensure that a stratified body of water was obtained. Thermocouples were placed 150, 250, 350, 450 and 1 150 mm below the surface. A data logger was used to record the data from the thermocouple sensors at a rate of a data set every 3 h. Both reservoirs formed thermal layers and after the bubble plume was introduced in Reservoir B the thermal layers were eliminated.
The bubble plume used to induce destratification was created with the use of an electronically controlled air regulator that regulated the induction of air into the system. The air induction box (AIB), shown in Fig. 5, was used to inject controlled volumes of air. The AIB is simply a regulator which can be set to release a specific volume of air at certain intervals. A small experimental set-up such as this does not require a large disturbance to create the destratification. The disturbance caused by simply removing the thermocouples from the water body would result in the thermal layers mixing. The air injected into Reservoir B was not optimised and it is believed that too much was injected.
The experimental work did underline the limitations of the set-up. The thermal effects on the sides of the reservoirs as well as the influence of the roof covers cannot be ignored. The focus was on trying to establish whether there is a difference in the rates of evaporation between a stratified reservoir and a thermally mixed reservoir. Although temperatures and all the other weather-related parameters were measured the difference in evaporation is only measured by means of the point gauges. During a period from March to April when the reservoirs were both allowed to stratify the 2 reservoirs had similar evaporation rates.
The results indicated that Reservoir B could be destratified using the bubble plume, and that there is a reduction in evaporation in this reservoir compared to the evaporation experienced in Reservoir A. The evaporation rate for a 2-month period (May and June), when Reservoir B was mixed with the aerator, indicated a reduction in evaporation of approximately 1%/month when comparing Reservoir B with that of A, although this was not an ideal period for this experiment. The measured evaporation in both reservoirs was less than the average monthly evaporation rate for Pretoria West which indicates that the roof covers played a significant role in the obtained values.
Field investigation
Destratification, where the colder bottom water is circulated, has been successfully applied to reservoirs which are deep (deeper than 20 m) but according to Craig (2006) it is less appropriate for most agricultural storages which are usually less than 7 m deep.
An experiment was also conducted at the Water Quality Resource Services' grounds at Roodeplaat Dam to determine the logistics involved in providing an aerator system for destratification. A 20 mm HDPE pipe 200 m in length was laid under the water into the dam. A diffuser was placed at the one end at a depth of approximately 16 m, activated by means of a solenoid valve. At the other end an air compressor with a timer control was connected. The compressor at 100 m pressure could discharge a specific volume bubble plume by opening the solenoid valve for a set period of time. A temperature probe and data logger were placed at the water surface within a 1 m radius above the diffuser to measure the change in temperature.
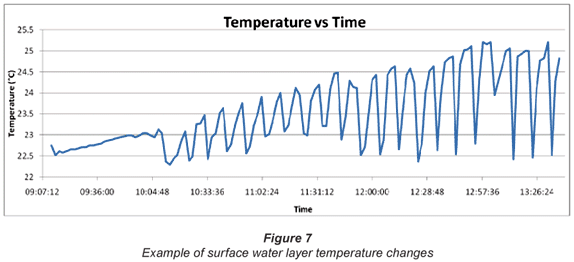
Various configurations were utilised, to alter the bubble plume volume and shape as well as the release times and intervals. The aim was to obtain an optimum set-up that would have the greatest effect on the water surface temperatures. In Fig. 6 the bubble plume reaching the surface can be seen.

As indicated in Fig. 7 a bubble plume was released every 10 min with logging taking place at 2 min intervals. The surface water temperature clearly drops by approximately 1 to 2.5ºC every time a bubble plume is released. The water surface temperature, however, returns to its original temperature again due to the mixing with the surrounding water. If a number of these release points were placed throughout the dam it is envisaged that the surface temperature could be reduced in this way.
By comparing the energy used by the bubble plume system, to that needed to reheat the water body a cost-benefit ratio can be determined and the economic viability of the proposed system determined.
There are some models available that could assist in designing the destratification system at a large scale. This is required to determine the number and position of release points, the volume and rate at which air should be released at each point and the anticipated mixed isothermal temperature of the body of water.
Models to determine the installation specifications and destratification evolution
There are various ways in which the full-scale artificial destratification system can be designed. The following 3 models/tools could be used to determine the optimum destratification system.
Destrat software
This software is used to calculate the specifications of the bubble plume. The model calculates the power requirements, the optimum flow, diffuser length and the number of clusters required (Moshfegi et al., 2005). The highest possible mixing efficiency will minimise the operating cost of the diffuser system. The model calculates the required air flow rate per diffuser port as well as the power required by each plume, the number of clusters, diffuser length as well as the pressure drop and head loss to determine the power required by each system.
Dynamic Reservoir Simulation Model (DYRESM)
DYRESM is a one-dimensional hydrodynamic model for predicting the vertical distribution of temperature, salinity and density in reservoirs satisfying the one-dimensional approximation. The one-dimensional approximation is valid when the forces that act in on a water body to destabilise it such as wind stress, surface cooling or rapid inflows do not act over prolonged periods of time.
The model provides quantifiably verifiable predictions of the thermal characteristics in such reservoir systems. The model parameterises the important physical processes leading to temporal changes in the temperature, salinity and density distributions in reservoirs.
The model divides a reservoir into a series of horizontal layers of variable size which can expand, contract, amalgamate, divide and move up and down according to the physical processes represented in the reservoir.
In DYRESM a simple single core plume is modelled with the movement of the plume determined from 3 differential equations of conservation of mass, momentum and buoyancy (Patterson and Imberger, 1989). The model can also be calibrated against field data using for instance thermistor chains and changing the major parameters.
Computational fluid dynamics (CFD)
Power efficiency in aeration devices for deep water bodies is essential due to the high injection pressure needed. Design optimisation with sound scientific tools is thus essential, and numerical modelling is without doubt one of the key tools in engineering. Buscaglia, Bombardelli and Garcia have developed a numerical model for large-scale bubble plumes accounting for mass transfer effects (Buscaglia et al., 2002).
Economic feasibility
There are a number of ways in which evaporation can be reduced as mentioned earlier. Watts (2005) developed a spreadsheet-based economic viability calculator to allow farmers to determine the circumstances under which an evaporation reduction system would be economical. The model includes:
-
Details of the dam (capacity, depth, surface area)
-
Local climatic data (rainfall, evaporation)
-
Estimates of operating conditions
-
Capital, operating and maintenance costs for the evaporation reduction system
-
Estimated life of the components of the system
-
Estimate of the evaporation reduction efficiency of the selected system
-
Current value of alternative water
-
Appropriate interest rates
-
Current gross margin for the crop grown.
In a study by Kothandaram et al. (1979) for the Illinois Institute of Natural Resources a pilot lake restoration investigation utilising aeration and destratification in Lake Catherine in the United States was undertaken. The pilot study was in operation over the period 18 May to 4 October 1978 and during this time the aerator utilised 45 800 kWh. Lake Catherine has a volume of 3.03 Mm3, surface area of 0.59 km² and a mean depth of 5.1 m. The cost of operating a successful destratification system like the one in Lake Catherine, would be ±R2 000/month (based on a 20c/kWh unit cost for electricity, low-demand season and only taking the active energy charge into account). The energy requirement to destratify 1 Mℓ (1 000 m3) of water is 4.52 W.
Although the authors of the study at Lake Catherine did not determine the reduction in evaporation, assuming a conservatively low 2% reduction could save ±1 750 m3/month. A reduction of 5% and higher might make it feasible to invest in a destratification system.
Hughes et al. (1975) utilised cost functions developed by Symons (1971) to analyse the reservoirs in the State of Utah. Symons (1971) summarises the results of a survey of water suppliers who have used artificial destratification for water quality reasons. Symons (1971) developed 3 figures showing the energy capacity requirements, the capital investment costs and the operating and maintenance costs each as a function of reservoir volume. These same cost functions were used by Hughes et al. (1975) to determine the water salvage costs as shown in Table 2.
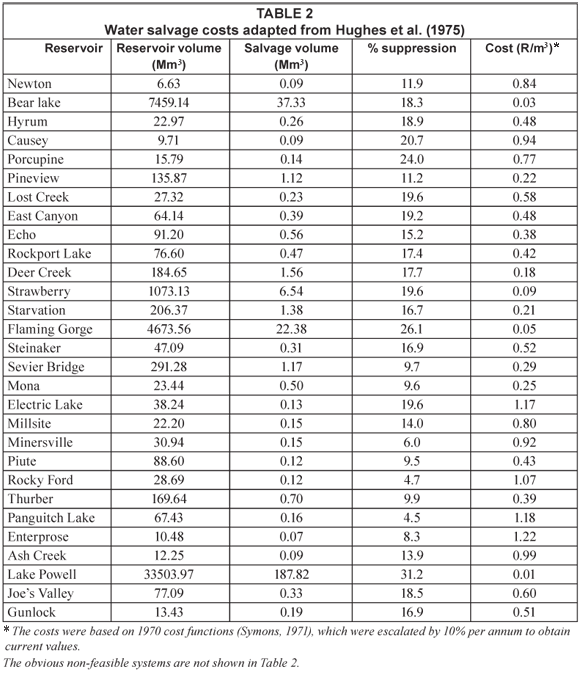
It is clear from Table 2 that the larger reservoirs have the greatest potential of being feasible.
An example for South Africa: There could be huge potential savings if the Sterkfontein Dam which is situated in the very upper reaches of the Vaal Dam catchment on the Nuwejaarspruit could be equipped with a destratification system.. The Sterkfontein Dam has a very small catchment area with negligible natural inflow receiving most of its water via the Tugela-Vaal Project. This is a pumped-storage scheme involving the net transfer of up to 630 x 106 m3 of water from KwaZulu-Natal. The water from KwaZulu-Natal is stored in Sterkfontein Dam and released to Vaal Dam via the Wilge River. Due to the favourable storage and climatic characteristics of Sterkfontein Dam, it is beneficial to store water in the deep cool Sterkfontein Dam and only release water to the shallow Vaal Dam when needed. The evaporation losses from Sterkfontein Dam, which is a highly efficient storage unit with an annual evaporation of 1 300 mm, are approximately 35 x 106 m3/a, which represents approximately 10% of the losses that would be experienced from Vaal Dam for a similar volume. Even a small 1% reduction in evaporation in Sterkfontein Dam could save up to 350 000 m3/a of expensive pumped water.
Conclusion
The total monetary cost of evaporation loss is significant and restricts development in South Africa. This research is still in its early stages but it is hoped that the method could be further developed and implemented on a pilot scheme in South Africa to demonstrate the benefits. The use of thermal mixing by compressed air appears to have important potential for evaporation suppression in deep reservoirs. The necessary conditions to achieve significant evaporation suppression according to Hughes et al. (1975) are as follows:
-
The reservoir should have sufficient depth (greater than ±18 m) to produce a marked natural thermocline and provide a relatively large volume of cold water for mixing.
-
An outlet/abstraction that is below the thermocline with sufficient outflow in relation to storage to transport a significant amount of excess heat from the reservoir.
The proposed system could have additional benefits such as:
-
Improving the overall water quality;
-
Reducing operating budget for raw water treatment;
-
Increasing the dissolved oxygen (DO) levels throughout the reservoir;
-
Increasing the fish habitat;
-
Reduction in algal growth by mixing of algae deeper into the water column and starving them of light, therefore reducing the sediment phosphorus load available to the water column and so starving the algae of nutrients (Auer et al., 1993). In other words phosphorus management through hypolimnetic aeration; and
-
Potentially improved habitat downstream of the reservoir (DO levels and temperature).
However, on the negative side, according to Henderson-Sellers (1981) there are some water users who require the abstracted water for potable use to be below a specified maximum and some fish species habitats in the thermocline layer could be destroyed when the lake is destratified.
During the field investigation it became clear that a number of bubble plume release points would be required to have an effect on the entire surface area. The design of the artificial destratification system still needs some further investigation and the models/tools described earlier would certainly assist in this regard.
Recommendations
Because of the major potential for water conservation in general as well as water for energy production additional research on destratification of deep reservoirs should be undertaken.
-
The experimental tests could be conducted on a larger scale to determine the extent and area of influence of the destratification system.
-
The suppression model as proposed by Hughes et al (1975) could be implemented on a number of South Africa's deep reservoirs and the potential suppression determined.
-
Experimental tests should be conducted in the summer months when evaporation rates are at a peak and over a few seasons to incorporate resulting weather and water temperature fluctuations and turnovers. Results from similar seasons could be compared to evaluate the accuracy and interpretation of results.
-
An alternative energy source for the air injection system could be investigated. Wind or solar energy would be ideal for application of the evaporation reduction system on dams where electrical energy would be difficult to supply and maintain.
References
ASAEDA T and IMBERGER J (1993) Structure of bubble plumes in linearly stratified environment. J. Fluid Mech. 249 35-57. [ Links ]
AUER MT, JOHNSON NA, PENN MR and EFFLER SW (1993) Measurement and verification of rates of sediment phosphorus release for a hyper-eutrophic urban lake. Hydrobiol. 253 301-309. [ Links ]
BROWN JAH (1988) The potential for reducing open water evaporation losses: A review. Proc. Hydrology and Water Resources Symposium. 1-3 February, Canberra, Australia. 108-115. [ Links ]
BUSCAGLIA GC, BOMBARDELLI FA and GARCIA MH (2002) Numerical modeling of large-scale bubble plumes accounting for mass transfer effects. Int. J. Multiphase Flow 28 1763-1785. [ Links ]
CRAIG IP (2006) Loss of storage water through evaporation with particular reference to arid and semiarid zone pastoralism in Australia. NCEA Publication. No. 1001858. University of Southern Queensland, Australia. [ Links ]
DWAF (2004) National Water Resource Strategy (1st edn.) URL: http://www.dwaf.gov.za [Accessed on 4 September 2006] [ Links ].
HARBECK GE (1962) A Practical Field Technique for Measuring Reservoir Evaporation Utilizing Mass Transfer Theory. US Geological Survey. Professional Paper 272-E Washington, DC. [ Links ]
HENDERSON-SELLERS B (1981) Destratification and re-aeration as tools for in-lake management. Water SA 7 (3) 185-189. [ Links ]
HOY RD and STEPHENS SK (1979) Field Study of Lake Evaporation: Analysis of Data from Phase 2 Storages and Summary of Phase 1 and Phase 2. Technical Paper 41. Australian Water Resources Council, Canberra, Australia. [ Links ]
HUGHES TC, RICHARDSON EA and FRANCKIEWICZ JA (1974) Open water evaporation and monolayer suppression potential. Water Salvage Potentials in Utah. Volume I. Utah Water Research Laboratory, Utah State University, Logan, Utah, USA. [ Links ]
HUGHES TC, RICHARDSON EA and FRANCKIEWICZ JA (1975) Evaporation suppression by reservoir destratification. Water salvage potentials in Utah. Volume II. Utah Water Research Laboratory, Utah State University, Logan, Utah, USA. [ Links ]
IMTEAZ MA and ASAEDA T (2000) Artificial mixing of lake water by bubble plume and effects of bubbling operations on algal bloom. Water Resour. 34 (6) 1919-1929. [ Links ]
KIRKE B and GEZAWY AEL (1997) Design and model tests for an efficient mechanical circulator/aerator for lakes and reservoirs. Water Resour. 31 (6) 1283-1290. [ Links ]
KOBERG GE and FORD ME (1965) Elimination of Thermal Stratification in Reservoirs and Resulting Benefits. United States Geological Survey. Water Supply Paper 1809-M. [ Links ]
KOTHANDARAMAN V, ROSEBOOM D and EVANS RL (1979) Pilot Lake Restoration Investigation – Aeration and Destratification in Lake Catherine. Illinois Institute of Natural Resources. Illinois State Water Survey, Urbana, Illinois, USA. [ Links ]
KOTHANDARAMAN V and EVANS RL (1982) Aeration-destratification of lake Eureka using a low energy destratifier. State Water Survey Division. Report No 294, Illinois State Water Survey Contract.Peoria, Illinois, USA. [ Links ]
LACKEY RT (1972) A technique for eliminating thermal stratification in lakes. Water Resour. Bull. 8 (1) 46-49. [ Links ]
LEMCKERT CJ and IMBERGER J (1993) Energetic bubble plumes in arbitrary stratification. J. Hydraul. Eng. ASCE 119 (6) 680-703. [ Links ]
LEMCKERT CJ, SCHLADOW G and IMBERGER J (1993) Destratification, some rational design rules. Proc. Australian Water and Wastewater Association (15th Federal Convention). 18-23 April, Gold Coast, Perth, Australia. 275-281. [ Links ]
LORENZEN MW and FAST AW (1977) A Guide to Aeration/Circulation Techniques for Lake Management. US Environmental Protection Agency. Research Series, EPA-600/3-77-004. [ Links ]
MOSHFEGHI H, ETEMAD-SHAHIDI A, and IMBERGER J (2005) Modelling of bubble plume destratification using DYRESM. J. Water Supply: Res. Technol.-AQUA 54 (1) 37-46. [ Links ]
PATTERSON CJ and IMBERGER J (1989) Simulation of bubble plume destratification systems in reservoirs. Aquat. Sci. 51 3-18. [ Links ]
SCHULZE RE, MAHARAJ M, WARBURTON ML, GERS CJ, HORAN MJC, KUNZ RP and CLARK DJ (2008) South African Atlas of Climatology and Agrohydrology. WRC Report No 1489/1/08. Water Research Commission, Pretoria, South Africa. [ Links ]
SERRANO SE (1997) Hydrology for Engineers, Geologists and Environmental Professionals. Hydroscience Inc. Lexington, Kentucky, USA. [ Links ]
SHERMAN B (2000) Scoping options for Mitigating Cold Water Discharges from Dams. Report 00/21 NSW. CSIRO Land and Water, Canberra, Australia. [ Links ]
SYMONS JM (1971) Quality Control in Reservoirs for Municipal Water Supplies. A Committee Report. Quality Control in Reservoirs Committee. AWWA. USA. [ Links ]
WATTS PJ (2005) Scoping Study – Reduction of Evaporation from Farm Dams. Final Report to the National Program for Sustainable Irrigation. Feedlot Services Australia. Toowoomba, Australia. [ Links ]
This paper was originally presented at the 2008 Water Institute of Southern Africa (WISA) Biennial Conference, Sun City, South Africa, 18-22 May 2008.
* To whom all correspondence should be addressed.
+2712 420 3176; fax: +2712 362 5218;
e-mail: marco.vandijk@up.ac.za














