Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
Water SA
On-line version ISSN 1816-7950
Print version ISSN 0378-4738
Water SA vol.35 n.1 Pretoria Jan. 2009
Flow-gauging structures in South African rivers part 2: calibration
P WesselsI, *; A RooseboomII
IDepartment of Water Affairs and Forestry, Private Bag X313, Pretoria 0001, South Africa
IIUniversity of Stellenbosch, Dept of Civil Engineering, Private Bag X1, Matieland 7602, South Africa
ABSTRACT
Accurate hydrological information is of paramount importance in a dry country such as South Africa. Flow measurements in rivers are complicated by the high variability of flows as well as by sediment loads and debris. It has been found necessary to modify and even substitute certain internationally accepted gauging station designs to overcome practical problems and to improve accuracies.
Part 1 of this paper concentrated on the attributes of different types of gauging structures and provided guidance on the design criteria applicable for selected structures. Part 2 of this paper in 2 parts contains information required to rate or calibrate the gauging structures that are most likely to be selected in the foreseeable future:
• Crump weirs
• Sharp-crested weirs
• Sluicing flumes.
This paper and its linked predecessor reflect the lessons that have been learnt by DWAF and other South African organisations and should be of value to others who have to perform flow measurements under similar conditions. The problems associated with the use of compound weir structures to gauge discharge and techniques that may be used to overcome some of these problems are also discussed.
Keywords: gauging structures, Crump weir, sharp-crested weir, compound weirs, dividing walls, modular flows, sluicing flume, flow measurement, rating of structures, rivers
Introduction
Flows in South African rivers vary considerably with time and therefore it has been policy in the South African Directorate of Hydrological Services in DWAF to build measuring or gauging structures in streams, even though they are relatively expensive. The biggest advantage of a permanent structure is that it can be pre-calibrated. A gauging structure creates an artificial control in a river that stabilises a river section and provides a determinable relationship between stage and discharge.
The following gauging structure types are mainly selected today to gauge discharges in South African rivers:
- Crump weirs (horizontal and V-shape)
- Sharp-crested (thin plate) weirs
- Sluicing flumes.
Formulae to rate or calibrate the above mentioned structures are discussed in this paper. Sharp-crested and Crump weirs may be utilised as simple structures (structures with a single weir crest) or as compound weir structures (structures with weir crests at different levels). Compound gauging weirs are used in an attempt to ensure accurate gauging and sensitivity over a wide range of discharges in streams. This is necessary to accommodate the sudden and large variations in discharge that occur in South African rivers. The impact of the use of multiple-weir crests on gauging accuracy in compound sharp-crested and Crump-weir structures is also discussed in this document.
Calibration of Crump-weir structures
Rating of horizontal Crump weirs for modular conditions
Flow conditions may be classified as modular when discharge over a weir is not being influenced by any variations in water level (stage) downstream of the structure. The formulae to rate horizontal Crump weirs for modular flow conditions (BSI 3680, 1986) are:

where:


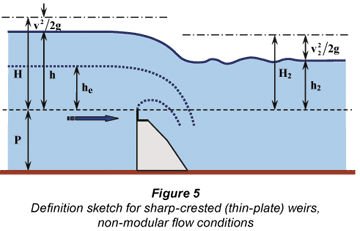
The parameters in the formulae and definition sketch are defined as follows:
Q = discharge (m3/s)
Cde = coefficient of discharge
P = pool depth below crest level (m)
b = width of crest perpendicular to flow direction (m)
g = acceleration due to gravity (m/s2)
h = gauged head (stage) relative to the weir crest (m)
H = total upstream energy head relative to the weir crest (m)
v = mean velocity in cross-section (m/s)
The following general limitations delineate the applicability of the formula:
h > 0.06 m for a crest section of fine concrete or equivalent
P > 0.06 m
b > 0.30 m
h/P < 3.5
b/h > 2.0
Within these limitations, the value of Cde can vary between 1.157, if h is equal to 0.06 m, and 1.163 for large values of h. This variation is less than 1% and the value of Cde may be taken at a constant value of 1.163 for practical purposes. The value of Cde is greater than unity due to convex flow lines and the formation of a separation pocket just downstream of the crest of the Crump weir.
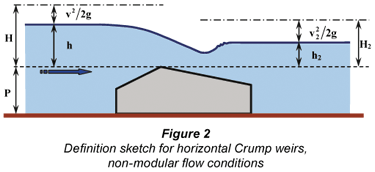
Rating of horizontal Crump weirs for non-modular conditions
In drowned or non-modular flow conditions the stage-discharge relationship for a Crump weir depends on both the upstream and downstream water levels. Provision was made in the original design of the Crump weir to gauge tail-water levels through small openings located (crest-tappings) in the downstream face of the weir, close to the crest. In South Africa, problems are experienced with sediment particles blocking these openings. Water levels recorded downstream of the hydraulic jump are thus used to correct for the influence of drowned flow conditions.
The discharge formulae to rate Crump weirs for drowned flow conditions (Ackers et al., 1978) are:

where:

f = drowned flow-reduction factor
The drowned flow-reduction factor (f) is a function of the submergence ratio  with H2 the total downstream energy head and H the total upstream energy head. The flow-reduction factor is determined by means of the following equations:
with H2 the total downstream energy head and H the total upstream energy head. The flow-reduction factor is determined by means of the following equations:

Rating of V-Crump weirs for modular conditions
The discharge formulae to rate V-Crump weirs (Ackers et al., 1978) are:

when H is within the V with a depth of Dv ; and

when H is above the top of the V (i.e. greater than Dv)
where:
CD = 0.633 for a V-Crump with a 1:2 upstream to 1:5 downstream profile
n = crest cross slope, normally 1:10 (n = 10)
Dv = vertical depth of the V
The following general limits define the use of the formulae:
h > 0.06 m for a crest section of fine concrete or equivalent
Dv/P < 2.5
H/P2 < 2.5 where P2 is the difference in height between the V-crest and the downstream channel bed
Rating of V-Crump weirs for non-modular conditions
The formulae to rate a V-Crump weir for non-modular flow conditions are:

when H is within the V with a depth of Dv and:
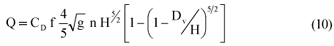
when H is above the V (i.e. greater than Dv) and where:
f = drowned flow-reduction factor
CD = 0.633 for a V-Crump with a 1:2/1:5 profile
n = crest cross slope, normally 1:10 (n = 10)
Dv = vertical depth of the V
The drowned flow-reduction factor (f) is determined as follows:


For submergence ratios exceeding 0.78, the flow-reduction factor (f) is determined as follows:

Calibration of sharp-crested (thin-plate) weir structures
Rating of sharp-crested (thin-plate) weirs for modular flow conditions
IMFT discharge formula (thin-plate weir)
The International Organisation for Standardisation document (ISO 1438/1, 1980) gives the following discharge formulae to rate a thin-plate weir for modular flow conditions:
- Kindsvater-Carter formula (Ackers et al., 1978)
- SIA formula (Society of Swiss Engineers and Architects) (Ackers et al., 1978)
- Rehbock formula (Ackers et al., 1978)
- IMFT formula (Institut de Mecanique des Fluides de Toulouse) (Ackers et al., 1978)
Uncertainties attributed to the discharge coefficient in these formulae, at the 95% confidence level, are less than 1.5% if h/P is lower than 1.0; less than 2% if h/P is between 1.0 and 1.5 and not greater than 3% if h/P is between 1.5 and 2.5. These accuracies are applicable only if additional restrictions on the values of h, b, P, h/P and (B-b)/2 are met (ISO 1438/1, 1980).
The IMFT formula is the only one of the above-mentioned formulae that is written directly in terms of the total head energy H, rather than the overflow depth h. The inclusion of the kinetic energy term 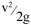 leads to a formula with a discharge coefficient that does not vary greatly, confirming the validity of the basic theory.
leads to a formula with a discharge coefficient that does not vary greatly, confirming the validity of the basic theory.

where:

The parameters used in the definition sketch and formulae are defined as follows:
Q = discharge (m3/s)
H = total energy head (=h +) in m
b = width of weir crest (m)
P = upstream pool depth (m)
Restrictions on the applicability of the IMFT formula are:
H/P < 2.5
h > 0.03 m
b > 0.20 m
P > 0.10 m

Within the restrictions set above, the value of the discharge coefficient (Cd) in the IMFT equation varies between 0.627 if H/P = 0 and 0.679 for H/P = 2.9, which is a variation of roughly 8%.
DWAF discharge formulae (thin-plate and sharp-crested weirs)
Due to the high sediment load of rivers in South Africa, the pools upstream of weirs tend to silt up. This reduces the pool depth (P) upstream of a weir and often creates H/P ratios of greater than 2.5. DWAF initiated research to address this problem and the equations presently in use to rate thin-plate and sharp-crested weirs were developed.
The DWAF equation to rate thin-plate weirs
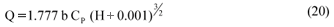
The coefficient Cp is included in order to cover a wider range of H/P values as set for the formulae in the publication of the International Organisation for Standardisation document (ISO 1438/1, 1980). Values for the coefficient CP are as follows:
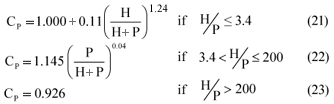
The DWAF equation to rate sharp-crested weirs

with
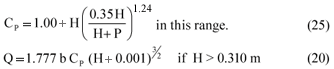
The values of the coefficient CP are the same as for the thin-plate weir equation when H > 0.310 m (Le Roux et al., 1990). The influence of the angle iron crest on the discharge over a sharp-crested weir requires an alternative equation to determine discharge accurately (Kriel, 1963).
Although it is possible to use these equations to rate thin-plate and sharp-crested weirs with a very shallow pool depth (P), caution is sounded when the Froude number (Fr) exceeds a value of 0.4 in the approach channel. The DWAF equations were evaluated (Hydraulics Research, 1986) as part of an assessment study of the potential water yield of the Lesotho Highlands Water Project. This evaluation revealed an inherent error in the equations of approximately ±2% for values of H/P < 3.4 increasing linearly to ±6% when H/P = 8.0. In this assessment it was recognised that the DWAF equations were designed to cover a wide range of upstream pool depths and describe these flow conditions better than alternative formulae.
Rating of sharp-crested (thin-plate) weirs for non-modular flow conditions
Thin-plate weirs are usually designed to operate only under modular flow conditions. In South Africa, sharp-crested weirs are widely used to gauge flow in natural streams. It happens quite often that downstream water levels are higher than the crest elevations of these weirs. In these circumstances, the weirs operate under drowned conditions and the rating of the weirs should be adjusted accordingly. Under drowned flow conditions the discharge over a weir depends on both the upstream and downstream water levels. The formulae mostly used in South Africa to correct for the impact of non-modular flow conditions in the calculation of discharge over drowned sharp-crested (thin-plate) weirs are:
The Villemont equation
The formula proposed by Villemont (1947) to compensate for non-modular flow conditions is:

where:
Q = actual discharge in the stream (m3/s)
Qd = discharge determined for modular flow conditions with an upstream head (h), as gauged under non- modular flow conditions (m3/s)
h2 = downstream water level, relative to crest elevation (m)
h = gauged upstream head in meter (drowned flow condition)
= submergence ratio
The DWAF equation
Different equations, including that of Villemont, were used by DWAF to correct for drowned flow conditions at sharp-crested weirs. Large discrepancies between the results of these equations led to a research project to determine the influence of submergence on discharge. This resulted in a new technique based on the momentum principle to calculate drowned discharges which is presently used by the Department. With this technique (Wessels, 1986) an equivalent theoretical modular flow condition, with the same discharge, is created for the gauged drowned flow condition at the weir. Once the equivalent modular flow situation is established, discharge can be calculated as if there is no submergence.
With this method, it is possible to determine discharge for submergence ratios up to 90% and higher. The equations to create an equivalent modular flow condition are as follows:

with:
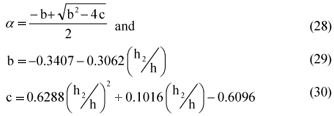
where:
he = equivalent modular upstream head (m)
h = gauged upstream head in drowned flow condition (m)
h2 = downstream gauged head relative to crest (m)
= submergence ratio
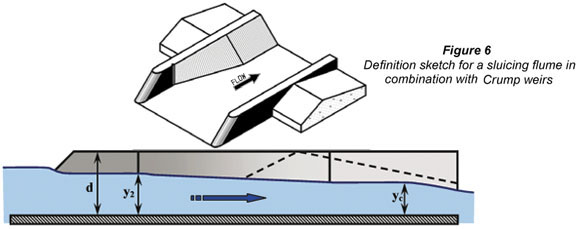
Calibration of sluicing flume structures
The University of Stellenbosch developed sluicing flumes with three standard depth-to-throat width ratios (d/b = 1; 0.5 and 0.25) as part of a Water Research Commission (WRC) project (Rossouw et al., 1998). All 3 flumes can be utilised in combination with either Crump or sharp-crested weirs. Each flume-weir combination has a unique formula to rate the structural combination. This resulted in 6 different sets of calibration theory. Only the sluicing flume mostly utilised (d/b = 0.5), in combination with Crump weirs will be briefly discussed in this paper. The different theories to rate all the different flume layouts and weir combinations are discussed and described in Rossouw et al., 1998 and Bruce et al., 2002.
Rating of a sluicing flume in combination with Crump weirs for modular flow conditions
Discharge confined inside the flume
Discharge is confined to the flume as long as the ratio y2/d is less than 0.9. In this ratio the stage measured at the gauging section in the flume is defined as y2 and the depth of the flume structure is denoted as d.
The discharge through a flume for a certain stage measurement (y2) in the flume is determined, as follows:
- Critical flow conditions are assumed at the flume outlet
- A theoretical discharge QT (m3/s) is determined for an estimated critical flow depth yc at the outlet of the flume

where:
g = gravitational acceleration (=9.81 m/s2)
Ac = cross-sectional area of flow in the outlet for a flow depth yc (m2)
Bc = water surface width in the flume outlet at flow depth of yc (m)
- The actual discharge is determined by applying a coefficient of discharge (Cd2)
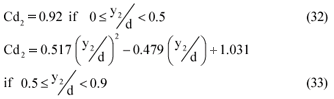
- By assuming no energy losses between the flume outlet and the stage measurement section, a theoretical value for y2 at the gauging section is determined
- If the theoretical determined value of y2 differs from the measured value, a new critical flow depth yc is estimated at the outlet
- The process is repeated until the difference between the measured value (y2) and the theoretically determined y2 value becomes negligible. The discharge that coincides with the final calculated y2 value is the corresponding true discharge through the flume for the measured stage.
Discharge through the flume and over the adjoining weir structures
The discharge through a flume and over the adjoining weir crest structures is determined, as follows:
- For a certain stage y2 measured at the gauging section, the corresponding energy head Es5 outside the abutment walls of the flume is determined by means of the following equation:
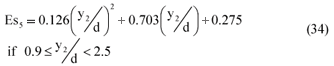
- Critical flow conditions are again assumed at the flume outlet
- A theoretical discharge QT (m3/s) through the flume is determined for an estimated critical flow depth yc at the outlet of the flume

- The energy head at the flume outlet is determined for the estimated critical flow depth
- By assuming no energy losses through the length of the flume the energy head at the outlet is adjusted until it corresponds with the energy head Es5 outside the flume, previously determined
- The true discharge through the flume is finally determined by applying a coefficient of discharge (Cd5). Cd5 is determined as follows for a certain y2 stage measurement:
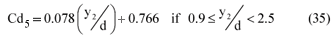
- The discharge (QW in m3/s) over the adjoining weir crests is determined using the appropriate discharge formula for the particular weir-crest type:

where:
CdW = discharge coefficient for the type of weir crest (m0.5/s)
b = width of weir crest (m)
d = depth of flume (m)
Rating of sluicing flumes for non-modular flow conditions
Non-modular flow conditions occur when a change in the water level downstream of the structure starts to influence the stage measurements inside the flume. The ratio of the downstream water level above the floor of the flume relative to the stage measured inside the flume indicates the degree of submergence of the structure. The maximum submergence ratio just before the stage measurements are influenced, is known as the modular limit. With discharge is restricted to the flume, the modular limit was found to be approximately 0.8 for all the flume layouts tested.
Methods to compensate for the impact of submergence on discharge calculations are very complex for the different flumes and flume-weir combinations. Theory and techniques to compensate for the impact of non-modular flow conditions on discharge are described in detail by Bruce et al. (2002).
Compound gauging weir structures
Almost without exception all the gauging structures built in South African rivers till the beginning of the 1980s were compound sharp-crested weirs. The first compound Crump weir was built in the Great Fish River in the Eastern Cape and came into operation during October 1977.
South African rivers are subject to large and sudden variations in discharge. Compound gauging weirs are used in an attempt to ensure accurate gauging and sensitivity over a wide range of discharges in streams. A compound gauging weir consists of a series of individual weirs, with the crest of each weir at a different level, across the width of a stream. Normally low discharges in a river flow only over the lowest crest of a compound weir (also called the low notch). As discharge increases more of the higher weir crests start to function. This ensures that discharge can be gauged accurately over a wide range of flows without causing an excessive increase in the water levels upstream of a weir.
Theory and coefficients to rate Crump and sharp-crested weirs are well established for two-dimensional flow conditions, which exist in weirs with only a single crest section (Ackers et al., 1978). To apply this theory to compound weirs, each crest should operate as a simple weir without influence from adjacent crest sections. Dividing walls should be constructed between the different weir crest sections or notches to minimise the possible influence of three-dimensional flow conditions. In this paper, three-dimentional flow conditions are defined as flow with three mutually perpendicular velocity components, and in two-dimentional flow conditions the horizontal velocity component parallel to the weir crest is absent.
The maximum difference in adjacent crest levels is also restricted to 0.5 m (BSI 3680, 1981). According to this British Standards Institution (BSI) Standard, the dividing walls should extend upstream past the section where the head is recorded and should also be high enough to separate the flow throughout the design range of the weir. Furthermore, the BSI requires a minimum thickness of 0.3 m for dividing walls to avoid sharp curvatures in flowlines at the entrances, which may be semi-circular or semi-elliptical.
A series of individual weirs operating in parallel is created across the river in this way. Discharge over the individual crests can be rated with the established discharge formulae for a single crest weir if stage is recorded between the dividing walls upstream of each weir section. With a compound weir, it is usually not economical to measure water levels upstream of each individual weir section (Ackers et al., 1978). If water levels are measured only at a single section of a compound weir, the total head is assumed constant over the full width of the weir. The total head across the compound structure is calculated at the individual weir section where the water level is recorded.
According to the BSI (BSI 3680, 1981) compound gauging weirs without dividing walls require in situ or model calibrations. From a South African perspective, this is probably the most important point in the Standard. Nearly all compound gauging weirs in South Africa have been constructed without dividing walls, thus deviating from the standards set by BSI 3680. This came about not only due to economic reasons, but also in order to reduce the risk of floating debris being trapped. Branches and trees entangled by dividing walls negatively affect the accuracy with which flows are gauged. These deviations from the BSI 3680 Standard, however, raised doubts about the gauging accuracy that can be achieved with compound weirs in South Africa.
Tests were undertaken in the hydraulics laboratories of DWAF in Pretoria and the Department of Civil Engineering at the University of Stellenbosch. Errors in gauging are expected to increase with an increase in three-dimensional flow conditions upstream of a compound weir. Parameters causing the highest degree of cross-flow will affect the gauging accuracy the most. These parameters are:
• Difference in adjacent weir crest levels
• Relative depth of flow over adjacent crests
• The proportional lengths of neighbouring notches
• The comparative flow velocities in the pool upstream of each crest.
Most of these parameters influence each other and the difference in adjacent crest levels will affect nearly all the other parameters. A systematic test programme was followed to determine the influence of all these parameters on the accuracy of flows gauged with compound weirs. In the tests, these parameters were varied to cover conditions that may be expected in practice. To establish the influence of the dividing walls on the accuracy of flow gauging, every model configuration was tested with and without walls. All tests were performed under modular flow conditions in a rectangular approach channel. Water levels were recorded at the prescribed positions for the different weir crest profiles by means of point gauges. In all the tests, the dividing walls projected a distance 6Hd upstream of the weir crest.
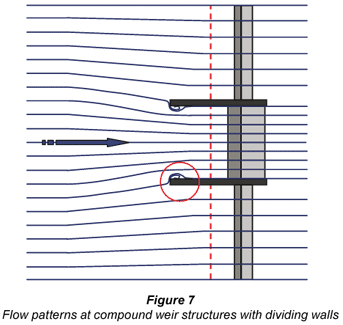
Compound weir structures with dividing walls
Discharge over the modelled compound weirs was calculated by assuming a constant total energy head across the full width of the weirs (BSI 3680, 1981). This head was obtained by adding the appropriate velocity head to the observed water level as measured between the dividing walls upstream of the lowest notch. Calculated discharges were compared with the actual discharges as tested in the models. In doing this, the effect of assuming a constant total energy head on the gauging accuracy could be investigated.
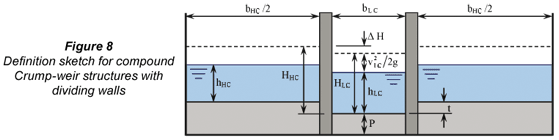
The test results revealed a general tendency to underestimate the actual discharge when all the crests were spilling. This is most prominent when the higher notches start to spill, indicating an inaccuracy in the assumption of a horizontal upstream energy head. This underestimation in discharge is caused by three-dimensional flow conditions that exist at the upstream ends of the dividing walls. These strongly curved flow conditions cause energy losses upstream of the section of stage measurement in front of the lowest notch, as shown in the sketch for a Crump structure with dividing walls.
At a structure with a very shallow upstream pool and relatively short low notch, the total energy head upstream of the higher notches (HHC) is ΔH more than the total energy head (HLC) calculated from the gauged water level upstream of the lowest notch of the weir. With increasing depth of flow over the higher notches, the accuracy of calculated discharges improves. This increase in accuracy may be attributed to flow lines becoming more parallel, as a result of the reducing influence of the step height on flow conditions in this region. When these energy losses (ΔH) are brought into account in the calculation of a total energy head in front of the higher notches, the underestimation in calculated discharge diminishes (Wessels, 1996).
Crump structures
With discharges confined only to the lowest weir crest between the dividing walls, the compound structure is rated as a simple Crump weir, using Eq. (1). Under these conditions the calculated discharges, for 42 tests executed, compare very well with the actual discharges modelled. On average the calculated discharges overestimated the actual discharges by 1.4 % with a standard deviation of 3.4%.
With discharges not only confined to the lowest weir crest, the total discharge (QT in m3/s) over a compound Crump weir with dividing walls is determined as follows (assuming a horizontal total energy head accross the entire weir and neglecting entrance losses):
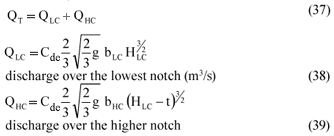
Providing for the effect of entrance losses (ΔH) caused by dividing walls in the calculation of discharge over compound Crump weirs, QHC is determined as follows in the final iteration process:
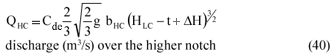
The energy losses (ΔH in m) at the entrance of the dividing walls for compound Crump weir structures are determined as follows:

where:
kCm = dimensionless correction coefficient for entrance losses
vLC = average calculated flow velocity in front of lowest weir crest (m/s)
The correction coefficient for the entrance losses is determined by the following equations:
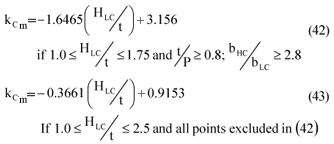

where:
HLC = total energy head upstream of the lowest weir crest (m)
t = height difference between lowest weir crest and adjacent weir crests (m)
bLC = width of lowest weir crest (m)
bHC = width of higher adjacent weir crest (m)
P = depth of pool upstream of lowest weir crest (m)
Based on the results of 88 tests executed independently in two different hydraulic laboratories, the calculated discharges (ignoring the entrance losses) underestimated the actual discharges by 4.3% on average with a standard deviation of 4.8%. Taking the effect of entrance losses into account in the calculation of discharges, the average error in the calculated discharges is 0% with a standard deviation of 2.9%.
Sharp-crested (thin-plate) structures
A similar series of tests as for the Crump structure was performed with sharp-crested structures. In this case, 61 tests were carried out and analysed with both the IMFT and DWAF formulae. Once again, if no corrections are applied to compensate for entrance losses caused by the dividing walls, the discharges calculated underestimate the actual discharges tested. Applying the IMFT formula, the actual discharges are underestimated on average by 4.9% with a standard deviation of 5.7%. The DWAF formula underestimated the actual discharges on average with 7.8%, with a standard deviation of 6.1%.
Compensating for the influence of the entrance losses caused by the dividing walls the average error in the calculated discharges using the IMFT formula was 0% with a standard deviation of 4.9%. The DWAF formula underestimated the actual discharge with 0.1% on average with a standard deviation of 4.1%. The formulae and methods to compensate for the impact of the entrance losses in combination with the IMFT and DWAF equations are discussed in detail by Wessels, 1996.
Compound weirs without dividing walls
In order to theoretically calculate the discharge over the compound weir structures not equiped with dividing walls, the following assumptions are made:
- The water surface level, as gauged upstream of the low notch, is horizontal across the width of the channel
- The total energy head upstream of the weir across the width of the river is horizontal
- The total cross-sectional area of discharge normal to the flow direction is used to determine the average approach velocity upstream of the weir.
Once again, the calculated discharges were compared with the actual discharges as tested in the models. In this case, the calculated discharges overestimate the flows tested in the models. The tendency to overestimate the calculated discharges is caused by energy losses in the proximity of the weir crests. Although flow conditions are nearly uniform with parallel flow lines at the section where the water levels are recorded, three-dimensional flow conditions exist just upstream of the weir crest. These three-dimensional flow conditions induce strongly curved flow lines at the point where the high and low notches meet. To compensate for these losses, the water level upstream of the weir crest increases.
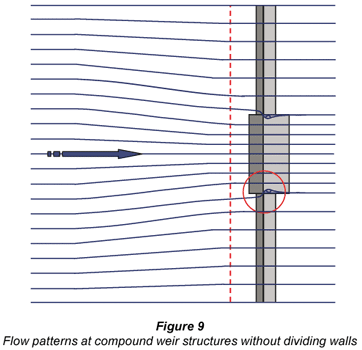
The measuring of stages upstream of these losses leads to an overestimation in calculated total energy head and results in too high calculated discharges. Applying a correction factor (ΔH) to the calculated total energy head (H) for the entire compound weir structure, reduces the overestimation in calculated discharge (Wessels, 1996). As the depth of flow over the structure increases the impact of the step height between the weir crests decreases. Flow lines become more parallel across the structure reducing the three-dimensional flow effect at the weir crest and also the overestimation in calculated discharges.
Crump structures
With discharges confined to the lowest weir crest calculated discharges in 41 tests overestimated the actual discharges modelled on average by 2.7% with a standard deviation of 2.4%. In 89 tests executed, with all the crests in operation (H/P > 1), the calculated discharges (ignoring the losses at the weir crest) overestimate the actual flows modelled on average by 2.8% with a standard deviation of 2.2%. When the higher weir crests just started to spill, the calculated discharges overestimate the actual discharges tested with more than 5%.
Discharge over a compound Crump weir without dividing walls, assuming a horizontal water surface and total energy head across the entire weir, is calculated as follows (ignoring the energy losses at the weir crest):
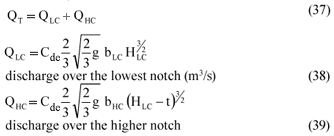
Providing for the effect of the energy losses (ΔH) caused by the three-dimentional flow conditions at the weir crests in the calculation of discharge over compound Crump weirs without dividing walls, QLC and QHC is determined as follows in the final iteration process:
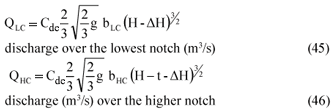
The energy losses (ΔH in m) near the weir crests of compound Crump-weir structures without dividing walls, are determined as follows:
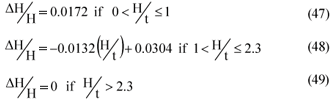
By subtracting the energy loss correction (ΔH) from the final calculated total energy head the calculated discharges overestimate the actual discharges with less than 0.1% with a standard deviation of 2.3% for flows confined to the lowest weir crest. With flow over all the crests of a compound Crump weir the calculated discharges and actual discharges underestimated the actual flows with less than 0.1% with a standard deviation of 1.5%.

The gauging accuracy obtainable with compound Crump-weir structures without dividing walls is the most significant result of the investigation, from a South African viewpoint. In fact, these structures yield greater accuracy in calculated discharge than compound structures with dividing walls, especially in combination with very shallow upstream pools and more than one crest spilling (Wessels, 1996).
Sharp-crested (thin-plate) structures
A similar series of tests as for the Crump structure was performed with sharp-crested structures. In this case, 60 tests were carried out and analysed with both the IMFT and DWAF formulae. Without correcting for the impact of the energy losses at the weir crests on the calculated total energy head, the IMFT formula overestimate the actual discharges tested on average with 1.5% with a standard deviation of 2.8%. Under the same conditions, the DWAF formula underestimates the actual discharges tested on average, by 0.3% with a standard deviation of 2.8%.
Applying the corrections to the total energy head the error in the calculated discharges for the IMFT formula is 0% with a standard deviation of 2.3%. For the DWAF formula the error, on average, is 0% with a standard deviation of 2.0%. The formulae and methods to compensate for the impact of the energy losses at the weir crests in combination with the IMFT and DWAF equations are discussed in detail in Wessels (1996).
Conclusions and recommendations
Clear preferences have developed in South Africa as far as flow-gauging structures in rivers are concerned. These preferences are due mainly to practical considerations and have led to the predominance of the following gauging structures:
- Crump weirs (horizontal and V-shape)
- Sharp-crested weirs
- Sluicing flumes.
The practical problems that have been encountered often involve sediments, submergence and debris.
On the small scale, sediments caused blockage of the crest tapping tubes on early Crump-weir structures. On a larger scale sediments have widely caused upstream pools to become too shallow to apply formulae within their limitations to rate gauging structures. This has been overcome partially by developing relationships for sharp-crested weirs allowing for very shallow upstream pool conditions. The sluicing flume has been developed especially to stimulate sediment through-flow in combination with weir structures.
The gauging accuracy obtained with sharp-crested weirs is very sensitive to non-modular (drowned) flow conditions. This impact can be neutralised at a high cost, by replacing sharp-crested weirs with other types of structures with high modular ratios, such as Crump weirs and sluicing flumes. A far more economical way to address gauging accuracy problems associated with non-modular flow conditions is to apply appropriate correction factors when the structure is rated. An improved formula has been developed to correct and quantify the impact caused by the additional damming caused by drowning of sharp-crested (thin-plate) weirs.
The gauging accuracy obtainable with compound weir structures not equipped with dividing walls in comparison to structures with dividing walls, is from a South African viewpoint most significant. Although the use of dividing walls between different weir crests is prescribed by international standards, these walls were omitted in the past in South Africa in attempts to reduce the risk of debris becoming entangled and also reducing construction costs. Techniques to calculate discharges over compound Crump and sharp-crested weirs more accurately were developed.
It is recommended that the theory and techniques described in this paper should be used to determine stage-discharge relationships (ratings) for the various structure types discussed. Structures and their upstream pools and should be surveyed on a regular basis (once every 5 years) and structures are to be re-calibrated accordingly.
Acknowledgements
The two papers on flow-gauging structures form the latest outcomes of extensive research which was undertaken in South Africa during the period 1975 to 2005. The research was undertaken and funded by the Department of Water Affairs and Forestry (DWAF), the Water Research Commission (WRC) and the University of Stellenbosch (US). Key role players in the research were P Wessels and AMM Muller (DWAF), DS van der Merwe (WRC) and A Rooseboom and J Rossouw (US).
The opinions expressed in this paper do not necessarily represent those of the listed organisations.
References
ACKERS P, WHITE WR, PERKINS JA and HARRISON AJM (1978) Weirs and Flumes for Flow Measurement. John Wiley & Sons, Chichester. [ Links ]
BRUCE H, ROSSOUW J and ROOSEBOOM A (2002) The Rating of Sluicing Flumes in combination with sharp-crested and Crump weirs under modular and non-modular flow conditions. WRC Report No. 980/2/00. Water Research Commission, Pretoria, South Africa. [ Links ]
BSI 3680: PART 4D (1981) Methods of Measurement of Liquid Flow in Open Channels Compound Gauging Structures. BSI, London. [ Links ]
BSI 3680: PART 4b (1986) Measurement of Liquid Flow in Open Channels Triangular Profile Weirs. BSI, London. [ Links ]
HYDRAULICS RESEARCH (1986) Lesotho Highland Water Project Assessment of Hydrometric Methods. Report No. EX 1424, Wallingford. [ Links ]
ISO 1438/1: Part 1 (1980) Water Flow Measurement in Open Channels using Weirs and Venturi Flumes Thin-plate Weirs. ISO, Geneva. [ Links ]
KRIEL JP (1963) Deurstromingskoëffisiënte vir hoekyster-meetdamkruine. The Civ. Eng. in S. Afr. 5 (10) 263-266. [ Links ]
LE ROUX FP and DELPORT A(1990) Handleidings vir Kalibrasieprogramme. Department of Water Affairs, Directorate of Hydrology, Pretoria, South Africa. [ Links ]
ROSSOUW J, LOUBSER C, ROOSEBOOM A and BESTER A (1998) Sluicing Flumes: A New Structure for Discharge Measurement in Sediment-Laden Rivers. WRC Report No. TT 103/95. Water Research Commission, Pretoria, South Africa. [ Links ]
VILLEMONT jr (1947) Submerged weir discharge studies. Eng. News-Record (25 December 1947) 54-57. [ Links ]
WESSELS P (1986) Korreksies vir die Effek van Versuiping op Skerpkruinmeetstrukture. M.Eng. dissertation, University of Pretoria, South Africa. [ Links ]
WESSELS P (1996) The Calibration of Compound Crump and Sharp-Crested Gauging Weirs in South Africa. Ph.D. dissertation, University of Stellenbosch, South Africa. [ Links ]
WESSELS P and ROOSEBOOM A (2009) Flow-gauging structures in South African rivers. Part 1: An overview. Water SA 35 (1) 1-10. [ Links ]
Received 16 October 2007; accepted in revised form 10 December 2008.
* To whom all correspondence should be addressed
+2712 3367922; fax: +2712 3261488;
e-mail: sfhserv@dwaf.gov.za














