Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
Water SA
On-line version ISSN 1816-7950
Print version ISSN 0378-4738
Water SA vol.34 n.5 Pretoria Oct. 2008
Clustering of groundwaters by Q-mode factor analysis according to their hydrogeochemical origin: a case study of the Cariri Valley (Northern Brazil) wells
Carlos José Freire MachadoI; Maria Marlúcia Freitas SantiagoII; Horst FrischkornIII, *; Josué Mendes FilhoII
IUniversidade Federal do Pará/Campus de Santarém, Física, Santarém-Pa/Brazil
IIUniversidade Federal do Ceará, Depto. de Física, Fortaleza-Ce/Brazil
IIIUniversidade Federal do Ceará, Depto. Engenharia Hidráulica e Ambiental, Fortaleza-Ce/Brazil
ABSTRACT
Factor analysis was applied to 56 groundwater samples collected from wells located in the Araripe Sedimentary Basin, in the north-east of Brazil. The parameters are a set of 9 physicochemical, chemical, and isotope data, constituted by electrical conductivity (EC), ionic concentrations of Ca2+, Mg2+, Na+, K+, Cl-, SO42-, alkalinity and δ18Oº/00. In R-mode factor analysis, the first 3 factors explain 62% of the variance, their loadings allowing the interpretation of hydrogeochemical processes that take place in the area. Q-mode factor analysis on the 56 water samples decreases space dimensionality to 6, explaining 93% of the total database information. With the aid of a scalar and angular measurement method, objects were clustered, resulting in 11 groups classified according to their inherent characteristics, related to their hydrogeological origin.
Keywords: hydrogeochemistry, R-mode factor analysis, Q-mode factor analysis, Araripe sedimentary basin, Cariri valley
Introduction
The ever-increasing demand for potable water requires knowledge of the quality of stored waters, as well as of the natural and anthropogenic processes that influence it. Waters stored in the same aquifer system can differ in their chemical composition due to internal and external processes, and suitable methodologies are needed for their identification.
A great manifold of parameters is used in water research for assessing water quality, pollution, evaporation, flow dynamics and chemical evolution through the water cycle. Thus, great amounts of data are generated. In order to gain insight into the relationships between the parameters associated with a given set of objects, multivariate techniques have been applied to reveal hidden affinities present in the database, and undetectable by other means. Mathematically, these methods reduce space dimensionality by a suitable choice of new dimensions constructed as linear combinations of the original ones, simplifying the representation of the data set and facilitating its interpretation.
Many multivariate analysis techniques have been applied in hydrological studies: R-mode analysis in groundwater quality studies (Grande et al., 1996; Liu et al., 2003; Panagopoulos et al., 2004; Garcia-Rodriguez et al., 2007); R-mode, Q-mode and cluster analysis to assess surface/groundwater interaction and groundwater mixing (Reghunath et al., 2002); R-mode and cluster analysis to study groundwater quality in the Blue Nile basin (Hussein 2004); principal component analysis (PCA), cluster, and discriminant analysis to evaluate spatial and temporal variations in river waters (Wunderlin et al., 2001; Singh et al., 2004); PCA and R-mode factor analysis to understand origin and variation of each solute in natural waters (Anazawa et al., 2005). Geochemical data were used to test the influence of different factor-analysis techniques on the results extracted (Reimann et al., 2002).
Material and methods
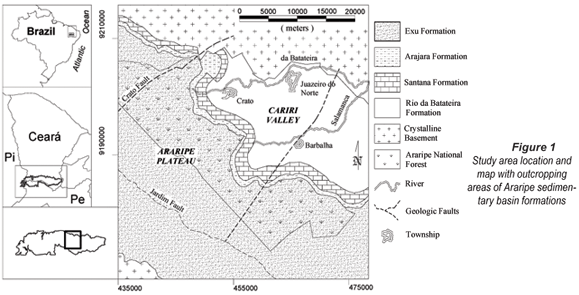
A set of 56 groundwater samples was analysed for 9 physical and chemical parameters comprising major ion concentrations (Ca2+, Mg2+, Na+, K+, Cl-, SO42-), alkalinity (alka), electrical conductivity (EC) and the isotope oxygen-18 (δ18Oº/00). The samples were taken from wells located in the Cariri valley, part of the Araripe sedimentary basin, Brazil, embedded in Precambrian basement rock. This basin is divided between the Federal States of Ceará, Pernambuco (Pe) and Piauí (Pi). The greatest part is in Ceará and comprises the Araripe plateau and the Cariri valley, containing the most important groundwater storage of the State. Figure 1 shows the region under study, enclosing the towns of Crato, Juazeiro do Norte, and Barbalha and the areas of the formations Exu, Arajara, Santana, and Rio da Batateira. Water samples were collected from the Rio da Batateira aquifer, from wells that provide water for industrial, rural and urban use.
Factor analysis
Factor analysis is a multivariate statistical method which, through a linear dependence model constructed in an abstract space called factor score space, searches for correlations among measured variables that characterise a set of objects/samples. Its main feature is to decrease space dimensionality through the construction of a new dimensional base that preserves the essential information contained in the original database. Linear dependencies of variables are measured in that new space, where new variables are defined by the column vectors of a so-called factor-loading matrix (A) in the space spanned by the column vectors of the factor score matrix (F).
R-mode factor analysis searches for interrelationships among variables. The mathematical model is:
YN x p = FN x kA'k x p + EN x p'
where:
Y is the data matrix in deviate form
yij =
xij - xj (with xij representing parameter j of object/sample i and xj the mean of variable j) or in standardised form, (sj being the standard deviation of variable j)
A' is A transposed and E the residual matrix.
The maximum likelihood estimation method was used to compute estimates for A by a numerical iterative procedure (Jöreskog 1967; 1977; Davis, 1986).
In R-mode factor analysis, to define the best dimensionality (k) of space, we have calculated chi-square (χk2) and the number of degrees of freedom (dk) for every factor space dimensionality. A measure of the relative importance in increasing the number of dimensions by one is defined by 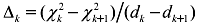 as the difference ratio between chi-square and degrees of freedom.
as the difference ratio between chi-square and degrees of freedom.
Q-mode factor analysis is a multivariate technique intended to classify objects according to interrelations among them, so that each object (row) in the data matrix is understood as a combination of hypothetical or real objects with specific parameter values. The technique consists of measuring the resemblance among objects (index of proportional similarity) normalising data matrix rows (objects) so that measured variables can be interpreted as proportions, 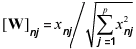 . Imbrie and Purdy (1962) defined the similarity coefficients as cos θnm = wn.w'm of the angle between any two data matrix row vectors (objects n and m), where wn = [wn1 wn2 .... wnp] is a row vector of matrix W. Then, the similarity matrix can be written as HN x N = WW'.
. Imbrie and Purdy (1962) defined the similarity coefficients as cos θnm = wn.w'm of the angle between any two data matrix row vectors (objects n and m), where wn = [wn1 wn2 .... wnp] is a row vector of matrix W. Then, the similarity matrix can be written as HN x N = WW'.
The model is expressed as the product of a factor- loading matrix (AN x k) and a factor score matrix (Fp x k), WN x p ≈ AN x k F'k x p , and the similarity matrix can be written as H = WW' = AF'FA'. This matrix can be factorised (Reyment et al., 1996) to find F and A.
To achieve simplicity (with the elements of factor-loading vectors approaching 0 or 1) varimax orthogonal rotation, designed by Kaiser (1958) so as to maximise the variance of the factors, was applied to the calculated factor-loading matrices.
Results and discussions
R-mode
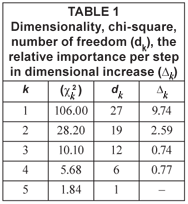
The parameters computed for our data set are listed in Table 1. Considerable information is gained when dimensionality increases from 1 to 2 (Δk = 9.74), from 2 to 3 (Δk = 2.59), but not from 3 to 4 (Δk = 0.74). So the best choice for dimensionality is 3, with 74% of accumulated information.
The varimax rotated factor-loading matrix is shown in Table 2 (where only factors with modulus greater than 0.24 are represented). The first factor explains 26% of total variance, the second, 20% and the third, 16%, total accumulated variance being 62%. This is the percentage of variance explained (in the entire database) without overestimating the amount of information available, according to the chi-square analysis. Space dimensionality decreased from the original 9 variables to only 3, so that, with the aid of multivariate statistical analysis, 3 main hydrogeochemical processes can explain the complexity of Cariri valley waters, as presented below.

Figure 2 is a bar diagram illustrating the relative importance of the variables in the factor-loading vectors from Table 2. All 3 factors have high EC loadings. The 1st factor, explaining 26% of the entire sample set variance, shows high correlation between Ca2+, Mg2+, SO42-, alkalinity and EC. As limestone and gypsum are common minerals in the Santana formation (Ponte and Appi, 1990), this factor proves that hydrogeochemical reactions relating precipitation/dissolution processes with calcite, dolomite, and gypsum minerals are important in water quality evolution in this area.
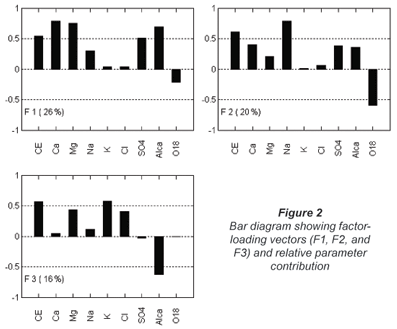
The 2nd factor, corresponding to 20% of total variance, is related to δ18Oº/00, Na+, Ca2+, SO42- and alkalinity. High correlation with Na+ and, to a lesser extent, with Ca2+, SO42-, and alkalinity can be associated with ion exchange by clay minerals, abundant in the Rio da Batateira formation.
The 3rd factor, responsible for 16% of the total variance, shows high correlations with EC, Mg2+, K+, Cl- and inverse correlation with alkalinity, and so it could represent contamination of waters by domestic sewage.
Q-mode
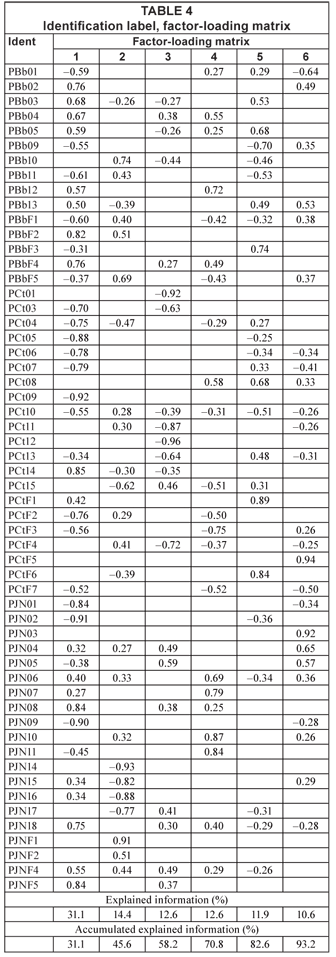
As in the R-mode case, Q-mode factor analysis also needs to define the dimensionality of factor score space. Table 3 defines space dimensionality and shows the information carried by each factor and total accumulated information as space dimensionality increases. When factors number 6, 93% of the information is accumulated; information is more uniformly distributed among factors from the second one on. The information for Factor 7, in 7 dimensions, and for Factors 7 and 8, in 8 dimensions, has low importance and can be discarded.
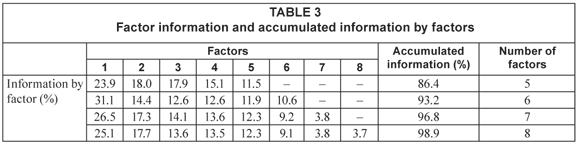
Results from varimax rotated factor-loading matrix calculation are given in Table 4 (next page) together with object (well) identification.
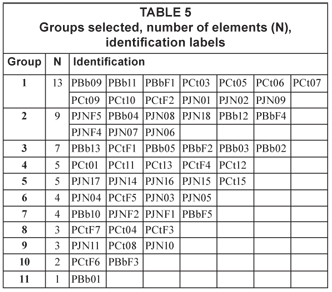
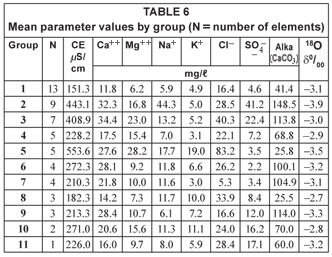
Application of the selection criteria (described above at the end of Q-mode factor analysis description) to the 56 elements in factor space resulted in 11 groups (Table 5 – next page). In order to interpret groups' characteristics, parameter means for each group were calculated (Table 6 – next page). As dimensionality is greater than 3, it is impossible to visualise the results from this procedure graphically in our three-dimensional visual space. Instead of grouping objects by visual inspection, they were analysed with respect to their angular and scalar distance between each member of the set, represented by vectors in a six-dimensional space, and from the group's centroid (defined by the mean vector, with unitary modulus, calculated considering all the elements in the group). If the angular separation and scalar distance between a given vector (object) and the group centroid in this factor score space is less than or equal to a respective predefined cut-off value, then the analysed element becomes an element of this group.
In our analysis, a cut off angle (θc) of 45º and a cut-off scalar distance (dc) equal to the equivalent distance between unitary vectors separated by the cut-off angle, i.e. dc = 2[1 – cos(qc)] were chosen.
Figure 3 shows bi-dimensional plots of elements' factor score space positions, marked by geometric symbols according to groups. All graphs have Factor 1 as abscissa. To avoid overloading the graphs, only group centroids are shown. Ordinates, representing the 2nd dimension, are Factors 2 to 6, respectively. Values approaching ±1 imply increasing importance.
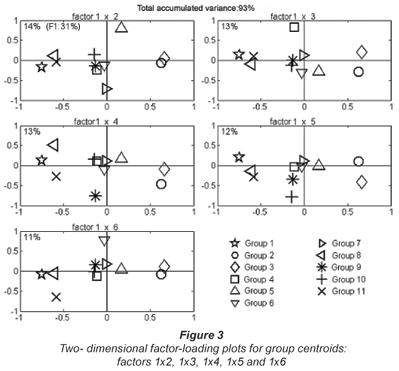
Table 6 shows that Group 1 (star) waters are only slightly saline and have a δ18O mean value of –3.1º/00, very close to the rainwater value (≈–3.2º/00; Santiago et al., 1997) . These waters represent recent recharge derived directly from rainfall. The fact that this group is the most numerous is not surprising, because its member wells exploit the uppermost unconfined aquifer in the Cariri valley. Factor 1 is the most important one to discriminate this group.
Group 2 water samples (circle) have high salinity and the lowest values of δ18O (–3.9º/00). High concentration values of Ca2+, SO42- and alkalinity imply that gypsum and limestone dissolution/precipitation processes are involved. These minerals are characteristic of the Santana formation lithology. Thus, this group was interpreted as recharge waters from the top of the Araripe plateau that percolated the Santana formation, and the low δ18O could be due to altitude effect on rainfall and/or to the presence of palaeo-waters because of the long transit time through that aquitard.
Water samples in Group 3 (diamond) show high EC combined with very high Ca2+ and high Mg2+ and SO42- concentrations as well as high alkalinity. Major ions' mean values are similar to those of Group 2, indicating the same geochemical environment. δ18O, however, is slightly higher (–3.0º/00), pointing to an origin from rainfall in lower altitude and/or slightly enriched by evaporation during runoff. We interpret these waters as recharge that leached Araripe plateau cliff matter.
Group 4 (square) waters have as principal characteristics high δ18O values (–2.9º/00) and low Ca2+, Na+, K+ concentrations and EC, implying fast infiltration to the aquifer. The elevated δ18O indicates slightly evaporated water. Factor 3 is important in discriminating this group.
Group 5 (triangle) waters are characterised by very high EC and Cl-, high K+ but low Ca2+ and SO42- concentrations. As Cariri valley natural waters have low Cl- concentration, these waters, from urban areas, are associated with chlorine pollution through residential wastewater, which is a major source of Cl-. δ18O = –3.5º/00 shows that these waters are mixed with palaeo-waters (uprising due to a reduction of hydraulic heads in the superior aquifer, caused by excessive pumping in well-fields for public supply). Factor 2 is of high importance in this group's discrimination.
The water samples in Group 6 (triangle) have mean parameter values near the universal mean. However, SO42- concentrations are the smallest of all groups. δ18O = –3.2º/00 indicates recent, fast recharge without evaporation. Factor 6 better discriminates this water type.
Group 7 waters (arrows to the right) show very low concentration of K+ and the lowest one for Cl-. The mean value of δ18O = –3.1º/00 indicates rainfall-derived recent recharge waters. Like Group 5, Factor 2 discriminates this group, but with negative values near –1. In this sense, it is the opposite of Group 5.
Water samples in Group 8 (arrows to the right) have very low alkalinity, low Ca2+, Mg2+ concentrations, and EC. The high δ18O value (–2.7º/00) reveals recent recharge waters that suffer evaporation before infiltration. Factors 1 and 4 (with positive correlation) best discriminate this group.
Group 9 waters (asterisk) have high alkalinity and close to rainfall δ18O (–3.3º/00). Factor 4 (with negative correlation) best discriminates this group.
Group 10, with 2 elements, and Group 11, with only 1, could not be interpreted hydrogeologically, but one can see that Group 9 is near Group 10, and Group 11 is near Groups 1 and 8. If a larger cut-off angle had been adopted and the 'discrimination power' reduced that way, these groups would have been integrated into their respective groups.
Conclusions
Multivariate statistical methods of factor analysis are shown to be an important tool for characterising hydrogeochemical processes and clustering groundwaters according to their shared hydrochemical characteristics. The 3 principal factors identified by R-mode factor analysis correspond to 3 principal processes taking place in the study area: precipitation/dissolution processes of calcium carbonate and gypsum, cation exchange processes occurring in clay layers, and processes related to anthropogenic contamination with chlorine. Q-modal analysis grouped all 56 samples collected in the study area into 11 groups, detecting similarities.
The relatively high number of groups found shows the wide variety of these groundwaters. In spite of it the methodology applied was efficient enough to permit association of factors and groups with hydrogeological environmental features of the research area.
Acknowledgments
The authors thank COGERH (Companhia de Gestão dos Recursos Hídricos do Estado do Ceará) and FUNCAP (Fundação de Amparo à Pesquisa do Estado do Ceará) for logistical and financial support, CAPES (Coordenação de Aperfeiçoamento de Pessoal de Nível Superior–Ministério da Educação–Brazil) for a fellowship for one of the authors (Machado) during postgraduate studies.
References
ANAZAWA K and OHMORI H (2005) The hydrochemistry of surface waters in andesitic volcanic area, Norikura volcano, central Japan. Chemosphere 59 605-615. [ Links ]
DAVIS JC (1986) Statistical and Data Analysis in Geology. John Wiley & Sons, New York. 656 pp. [ Links ]
GARCIA-RODRIGUEZ F, BATE GC, SMAILES P, ADAMS JB and METZELTIN D (2007) Multivariate analysis of the dominant and sub-dominant epipelic diatoms and water quality data from South African rivers. Water SA 44 (5) 653-658. http://www.wrc.org.za/downloads/watersa/2007/Oct%2007/2083.pdf [ Links ]
GRANDE JA, GONZÁLEZ A, BELTRÁN R and SÁNCHEZ-RODAS D (1996) Application of factor analysis to the study of contamination in the aquifer system of Ayamonte-Huelva (Spain). Ground Water 34 155-161. [ Links ]
HUSSEIN MT (2004) Hydrochemical evaluation of groundwater in the Blue Nile Basin, eastern Sudan, using conventional and multivariate techniques. Hydrogeol. J. 12 144-158. [ Links ]
IMBRIE J and PURDY E (1962) Classification of modern Bahamian carbonate sediments. Mem. Am. Assoc. Petrol. Geol. 7 253-272. [ Links ]
JÖRESKOG KG (1967) Some contributions to maximum-likelihood factor analysis. Psychometrika 32 443-482. [ Links ]
JÖRESKOG KG (1977) Factor analysis by least squares and maximum likelihood. In: Enslein K, Ralston A and Wilf HS (eds.) Statistical Methods for Digital Computers. John Wiley & Sons, New York. 454 pp. [ Links ]
KAISER HF (1958) The varimax criterion for analytic rotation in factor analysis. Psychometrika 23 187-200. [ Links ]
LIU, CHEN-WUING, LIN, KAO-HUNG, KUO and YI-MING (2003) Application of factor analysis in the assessment of groundwater quality in a blackfoot disease area in Taiwan. Sci. Total Environ. 313 77-89. [ Links ]
PANAGOPOULOS G, LAMBRAKIS N, TSOLIS-KATAGAS P and PAPOULIS D (2004) Cation exchange processes and human activities in unconfined aquifers. Environ. Geol. 46 542-552. [ Links ]
PONTE FC and APPI CJ (1990) Proposta de revisão da Coluna Estratigráfica da Bacia do Araripe. Proc. XXXVI Brazilian Congress of Geology (XXXVI Congresso Brasileiro de Geologia).Associação Brasileira de Geologia de Engenharia e Ambiental-ABGE; Natal/Brazil, Oct 1990. 1 211-226. [ Links ]
REGHUNATH R, SREEDHARA MURTHY TR and RAGHAVAN BR (2002) The utility of multivariate statistical techniques in hydrogeochemical studies: an example from Karnataka, India. Water Res. 36 2437-2442. [ Links ]
REIMANN C, FILZMOSER P and GARRETT RG (2002) Factor analysis applied to regional geochemical data: problems and possibilities. Appl. Geochem. 17 185-206. [ Links ]
REYMENT R and JÖRESKOG KG (1996) Applied Factor Analysis in the Natural Sciences (2nd edn.) Cambridge University Press, Cambridge. 371 pp. [ Links ]
SANTIAGO MMF, SILVA, CMSV, MENDES FILHO J and FRISCHKORN H (1997) Characterization of groundwater in the Cariri (Ceará, Brazil) by environmental isotopes and electric conductivity. Radiocarbon 39 (1) 49-59. [ Links ]
SINGH KP, MALIK A, MOHAN D and SINHA S (2004) Multivariate statistical techniques for the evaluation of spatial and temporal variations in water quality of Gomti River (India) – A case study. Water Res. 38 3980-3992. [ Links ]
SUBBARAO C, SUBBARAO NV and CHANDU SN (1996) Characterization of groundwater contamination using factor analysis. Environ. Geol. 28 175-180. [ Links ]
WUNDERLIN DA, DIÁZ MP, AMÉ MV, PESCE SF, HUED AC and BISTONI MA (2001) Pattern recognition techniques for the evaluation of spatial and temporal variations in water quality. A case study: Suqui'a River Basin (Córdoba-Argentina) Water Res. 35 (12) 2881-2894. [ Links ]
* To whom all correspondence should be addressed.
+55 85 3366 9775; fax: +55 85 3366 9627;
e-mail: cariri@ufc.br














