Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
Water SA
On-line version ISSN 1816-7950
Print version ISSN 0378-4738
Water SA vol.34 n.5 Pretoria Oct. 2008
Merged rainfall fields for continuous simulation modelling (CSM)
MS Frezghi*; JC Smithers
School of Bioresources Engineering and Environmental Hydrology, University of KwaZulu-Natal, Pietermaritzburg, Private Bag X01, Scottsville 3209, South Africa
ABSTRACT
Long sequences of rainfall at fine spatial and temporal detail are increasingly required, not only for hydrological studies, but also to provide inputs for models of crop growth, landfills, tailings dams, liquid waste disposal on land and other environmentally sensitive projects. Rainfall information derived from rain gauges, radar or satellites may not individually be adequate to meet the detail required by hydrological models or other water resource studies. Therefore, a suitable technique is required to estimate rainfall at finer spatial and temporal resolutions. Different techniques have been developed to merge rainfall information from rain gauges, radar and satellites in order to obtain the 'best' estimate of the 'true' rainfall field. However, the length of the radar and satellite estimated rainfall records is currently limited. In this study, the mean areal merged rainfall, derived from rain gauges and radar, was estimated for 26 subcatchments in the Liebenbergsvlei catchment, which is a research catchment, in South Africa for the period when radar data were available. By using the relationships derived between the merged rainfall and rain-gauge data, improved subcatchment rainfall may be estimated using the historical data from rain gauges located in and around the subcatchments. In most of the subcatchments the relationship between the daily mean areal merged rainfall of the subcatchment and the daily rainfall data from rain gauges is strong (R2 >=0.5). The relationship between the daily rain gauges and mean areal merged rainfall of the subcatchments is used to adjust the historical rainfall data from the daily rain gauges in order to estimate long sequences of subcatchment rainfall for input to continuous simulation models (CSMs).
Keywords: rain gauges, radar, rainfall, merged rainfall fields, catchment rainfall
Introduction
In the application of information derived from rainfall data in the fields of hydrology, engineering and agriculture, it is becoming increasingly important to know, or at least to have a reasonable estimate, of rainfall both in space as well as time, and in more detail than it is possible to deduce from the data collected at rain gauges in a sparse network (Pegram and Seed, 1998). Traditionally, mathematical techniques have been used to interpolate rainfall data from a rain-gauge network to estimate the rainfall at ungauged sites. However, a rain field estimated using mathematical interpolation does not necessarily represent an accurate estimate of the 'true rainfall' field. Therefore, other techniques have been developed to improve the estimation of the spatial distribution of rainfall. Some of these methods generate synthetic rainfall values using statistical models (e.g. Pegram and Seed, 1998; Pegram and Clothier, 2001), or are models based on the physical properties of a rain cell or cloud (Gupta and Waymire, 1993), or are techniques that derive a sound relationship between the radar field and the rain-gauge data based on prior knowledge of radar values and rain-gauge data relationships (Todini, 2001; Ehret 2002). Merged rainfall fields, derived from radar and rain gauges, are currently the best estimate of the 'true' rainfall field.
The reliable estimation of design floods provides safety in the design of hydraulic structures and improved risk assessment for water resource management. Design floods may be estimated from long records of observed streamflow data. However, the spatial distribution and record length of flow records are generally less than required for design flood estimation in most parts of the world, including South Africa. Design floods are frequently estimated from design rainfall derived from rainfall event using event-based approaches models (Schmidt and Schulze, 1987). Recently, continuous simulation models (CSMs) have been successfully used to improve the reliability of design flood estimates (e.g. Smithers et al., 1997, Cameron et al., 1999, Smithers et al., 2001). Rainfall is the most important input into CSMs and, therefore, CSMs require the best possible estimate of rainfall, both in space and time.
Rain gauges measure rainfall directly and rainfall depth accumulated over the period of interest is measured with a high degree of accuracy at the points where the gauges are located. However, rain-gauge networks are too sparse to capture the spatial variability of rainfall and with higher temporal scale the spatial variability of rainfall is averaged (Wilson and Brandes, 1979). Radar, on the other hand, measures a volume-averaged returned signal power which is converted to rainfall in two steps: first to reflectivity factor (Z), and then to instantaneous rainfall rate (R). Although indirect, radar estimates of rainfall provide a detailed sampling pattern in space and provide valuable information on the spatial variability of rainfall. However, rainfall estimated using radar lacks the accuracy at a point which rain gauges provide (Wilson and Brandes, 1979; Todini 2001).
Merging of radar and rain-gauge data using a suitable merging technique enables the best estimate of the spatial distribution of rainfall to be made. However, the length of available radar records in South Africa is currently limited and most hydrological models, and particularly CSM, require a long input sequence of rainfall records. Therefore, the objective of the study reported in this paper is to improve the estimation of catchment rainfall, for the period of available rain-gauge data, by using both the short records of available radar data and the long records of rain-gauge data. This study was focused on the Liebenbergsvlei catchment in the Free State Province, South Africa, where the required information was readily available.
Study area
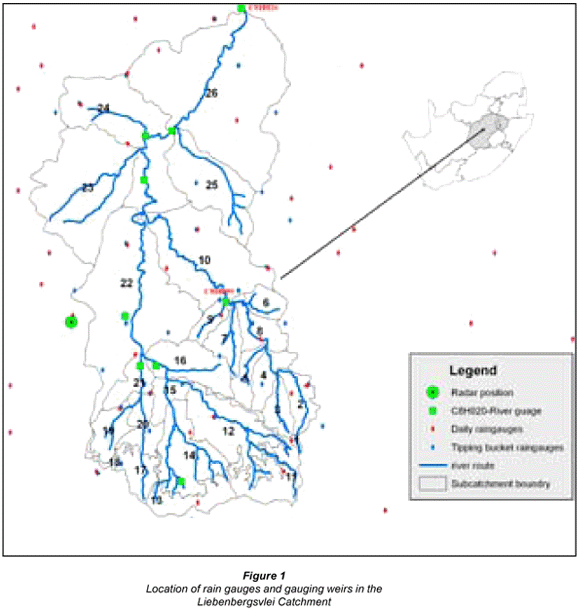
The Liebenbergsvlei catchment is a subcatchment of the Vaal River catchment and is located near Bethlehem in the Free State Province of South Africa, as shown in Fig. 1. The Liebenbergsvlei catchment is in a relatively dry region of South Africa and has an area of 4 694 km2 which receives an average annual rainfall total of 650 mm (Pegram and Sinclair, 2002). Most of this precipitation falls during the summer season, which ranges from October to February. The mean annual runoff depth from the catchment for the 21-year period from 1978 up to and including 1998 was 38 mm (Midgley et al., 1994). Rainfall has been intensively monitored in the Liebenbergsvlei catchment both by rain gauges (daily and recording tipping bucket gauges) and by radar. Therefore, the Liebenbergsvlei catchment was selected as a test site for this study. The delimitation of subcatchments in the study area was performed by Jewitt et al. (1997).
Merged rainfall fields
The merging of rainfall values from rain gauges and radar exploits the complementary characteristics of the techniques. Several methods have been developed for merging rain-gauge and radar data and the merged values have generally produced good results in terms of bias reduction, although little attention has been given to the reduction of variance because it requires prior knowledge of the variance structure, which is difficult to measure (Todini, 2001). The different nature of the errors, which implies their independence (Seo and Krajewski, 1990), can be exploited to produce unbiased and more reliable estimates of rainfall. Following this idea, Todini (2001) proposed a Bayesian combination technique, based on the use of block Kriging and a Kalman filter, which seeks to eliminate the bias in meteorological radar estimates of precipitation and to produce precipitation estimates which have a minimum variance on pixels of variable sizes.
Conditional merging
As documented by Sinclair and Pegram (2005) 'radar produces an image of the unknown true rainfall field which is subject to several well-known but poorly characterized sources of error (e.g. as detailed by Wilson and Brandes, 1979; Habib and Krajewski, 2002). However, the estimate retains the general covariance structure of the true precipitation field. The information from the radar can be conditioned using the spatially limited information obtained by interpolating between rain gauges to produce an estimate of the rainfall field that contains the correct spatial structure, while being constrained to the rain-gauge data. This process is illustrated in Fig. 2. The conditional merging technique of Ehret (2002) makes use of ordinary kriging to derive information from the observed gauged rainfall data.'
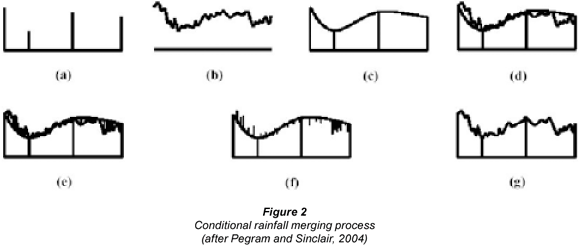
With reference to Fig. 2, the conditional merging process described by Pegram and Sinclair (2004), and utilised in this study, is as follows:
-
The rainfall field is observed at discrete points by rain gauges
-
The rainfall field is also observed by radar on a regular, volume-integrated grid
-
Kriging of the rain-gauge observations is used to obtain the best linear unbiased estimate of rainfall on the radar grid
-
The radar pixel values at the rain-gauge locations are interpolated onto the radar grid using kriging
-
At each grid point, the deviation between the observed and interpolated radar value is computed
-
The field of deviations obtained from (e) is applied to the interpolated rainfall field obtained from kriging the rain-gauge observations
- A rainfall field that follows the mean field of the interpolated rain-gauge data, while preserving the mean field deviations and the spatial structure of the radar field, is obtained.
Relationship between the daily rainfall data and merged rainfall data
Many hydrological studies require a long temporal sequence of spatially detailed and accurate rainfall data. However, the available rainfall data in South Africa are either long series of point rainfall, with no spatial information (rain-gauge rainfall data), or detailed spatial and temporal rainfall information, but with a limited period of record (radar and satellite rainfall values). Therefore, a relationship between the best estimate of the average daily rainfall depth in a subcatchment, obtained from merging the rain-gauge data with rainfall derived from a radar, and independent daily rainfall data from rain gauges, is developed in this section.
The merging procedure was assessed in two stages. Firstly, the merging process developed by Sinclair (2004), which is based on the conditional merging technique proposed by Ehret (2002), was validated using rainfall data from the tipping bucket rain gauges used in the conditioning of the radar rainfall values and, secondly, the merging procedure was verified using daily rainfall data from rain gauges which were independent and not used in the calibration of the merging process. Thereafter the reliability of the relationship between the averaged merged rainfall values for the subcatchments, obtained by combining the radar and rain-gauge data, and the rain-gauge data selected to represent the areal rainfall of the subcatchment, is investigated.
Validation of the merging software
In application of the merging process, kriging of the rain-gauge observations is used to obtain the best unbiased estimate of rainfall on the radar pixels and the observed rainfall values, at the pixel where the rain gauges are located, and fixed in the merged rainfall fields without adjustment. Therefore, the average merged rainfall values at the same location as the conditioning rain gauges, in this case the tipping bucket rain gauges, should be equal to the measured rainfall at the conditioning gauge. At the pixels where the conditioning rain gauges are located, the merging algorithm has 'exact' knowledge of the measured rainfall, and a 1:1 linear relationship (best fit straight line, Y = x; R2 = 1) between the average merged and conditioning gauge values was expected. Anywhere else in the merged field it was expected that some error would be present between the true rainfall field and the merged estimate (Y = ax + b; R2 < 1) at locations of rain gauges not used during the merging process. However, the closer a rain gauge is to a location of a rain gauge used in the merging procedure, the more accurate the merged value was expected to be.
The validation was performed by comparing each of the tipping bucket gauges to the co-located pixel in the merged rainfall field. This was done for all of the days where radar images were available to this study (2 October 1998 to 31 March 1999) and the results shown in Fig. 3, where a linear regression of y = 0.94x - 0.23 (R2 = 0.92) was obtained. According to the merging process developed by Sinclair (2004), radar pixels with no rain are masked (i.e. excluded) and hence in regions where the radar registered no rain, the merged value is assigned zero rainfall, even though a rain gauge in the region may have registered rainfall. This is a trade-off between being wrong at the rain gauge in a few cases and having rainfall over the entire data domain which means many 'false rainfall readings' elsewhere in the region of interest (Sinclair, 2004). When the merged values with masked zero values, resulting from no rain registered by the radar, are removed from the relationship, a near-perfect regression relationship of y = 1.001x - 0.036 (R2 = 1.0) was obtained, as shown in Fig. 4.
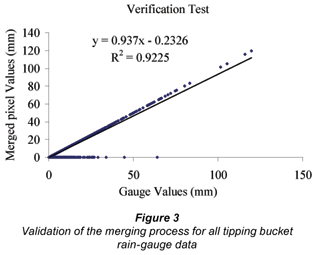
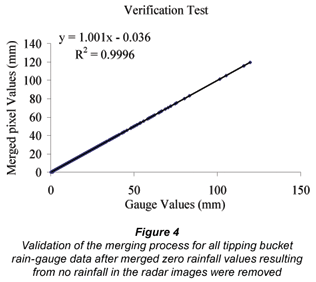
From the validation of the merged rainfall with the tipping bucket rain gauges used in the conditioning of the radar images, it is evident that the merging algorithm and software developed by Pegram and Sinclair (2004) successfully assigns rainfall values to the merged pixels from the respective rain-gauge values used in the conditioning of the radar images. This results in a combined gauge and radar field which matches the gauges at the gauge location as intuitively expected by hydrological practitioners.
Verification of the merging process at rain gauges not used in the conditioning of radar images
Average merged pixel values at daily rain gauges, which were not used in the conditioning of the radar field, were compared to the gauged values. Rain Gauge 0331607W, located in Subcatchment 22 as shown in Fig. 5, is used as an example of the verification, where a relationship of y = 1.04x - 0.07 (R2 = 0.70) was obtained from the linear regression between rainfall from the daily rain gauge (x) and the merged pixel values (y) at the rain-gauge location (Fig. 6). However, as explained above, some of the merged pixels are assigned zero values at pixels where the radar registered no rainfall and when these pixel values were excluded from the analysis, the relationship improved to y = 1.18x + 0.12 (R2 = 0.82) , as shown in Fig. 7.
Figure 8 shows the relationship between rainfall recorded at tipping bucket Rain Gauge L015, which was used in the conditioning of the radar rainfall images, and the average merged pixel rainfall values at the location of Rain Gauge 0331607W, which is located close to Rain Gauge L015 as shown in Fig. 5. The relationship between the point rainfall from the daily rain gauge (0331607W), not used in conditioning of the radar rainfall images, and the average merged rainfall values of a pixel at the location of the daily rain gauge, is a function of the radar rainfall values, the point rainfall from the conditioning tipping bucket rain gauges which are close to the daily rain gauges, and the distance between the tipping bucket rain gauges and daily rain gauge. Therefore, Fig. 8 shows the characteristic rainfall pattern between the point rainfall from the tipping bucket rain gauge and average merged rainfall values and it demonstrates the influence of the tipping bucket Rain Gauge L015, which is used to condition radar rainfall values to produce merged rainfall values, on the relationship between the point rainfall from daily rain gauges and averaged merged rainfall values of pixels at the location of the daily rain gauges.
Estimation of subcatchment rainfall from daily rainfall
Relationships between the mean merged areal rainfall in the subcatchments of the Liebenbergsvlei catchment, and daily and tipping bucket rain gauges selected to represent rainfall in the subcatchments, were developed using data for the period when the merged rainfall values were available. These relationships could then be used to improve the estimation of catchment rainfall using historical data from the selected rain gauges.
The downstream part of the Liebenbergsvlei catchment is relatively flat compared to the upstream part of the catchment. As a result the size of the subcatchments delineated by Jewitt et al. (1997) is bigger in the downstream portion than in the upstream part. As shown in Fig. 1, Subcatchment 26 is situated in the lower portion of the study area and it is a relatively flat area with an area of 827.34 km2. The location of Station 0367601W in Subcatchment 26 is shown in Fig. 9. Figure 10 shows the relationship between the average merged rainfall depth for Subcatchment 26, obtained by averaging all the merged daily rainfall values at each pixel within the subcatchment, and the daily rain gauge (W0367601) values. The linear relationship obtained y = 0.81x; R2 = 0.72) indicates that the daily rain gauge generally overestimates the areal rainfall for the subcatchment. Similar results were obtained for the other catchments, with typical R2 values ranging from 0.5 to 0.8.

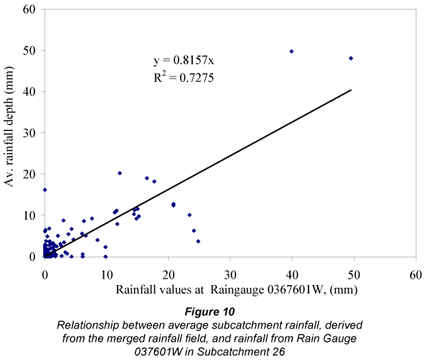
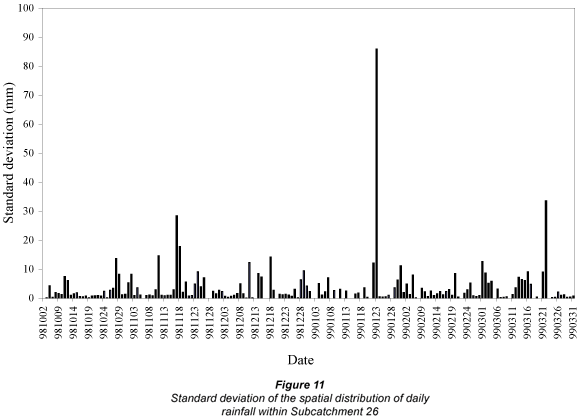
The spatial distribution of rainfall within the Subcatchment 26 is relatively uniform for the period shown in Fig. 11, where the standard deviation of merged daily rainfall over the subcatchment is shown, and where the majority of days have a standard deviation of less than 10 mm. The spatial uniformity of the rainfall over the subcatchment implies that there is little or no orographic effect on the spatial distribution of the rainfall. Although the area of Subcatchment 26 is relatively large, the spatial rainfall distribution of the subcatchment is relatively uniform as shown in Fig. 11. Therefore, the reason that rainfall at Rain Gauge 0367601W overestimates the average merged values for Subcatchment 26 could be attributed to the size of the catchment.
The correlation between selected daily rain gauges and the average merged rainfall depth for the subcatchments in Liebenbergsvlei catchment was found to be generally good, with correlation coefficients greater than 0.5 for most subcatchments. However, in most of the cases the use of a daily rain gauge to represent the rainfall for a subcatchment overestimates the average areal rainfall depth of the subcatchment by between 5% and 50%. The relationships obtained are largely dependent on the spatial variation of rainfall over the subcatchments and the location and altitude of the daily rain gauges. An ideal perfect relationship Y = x; R2 = 1) between the daily rain gauges and average rainfall depths of the subcatchments would only be obtained under a condition of perfect spatial uniformity of daily rainfall over the subcatchments.
Discussion and conclusions
Rainfall is highly variable in space and time. The reliable estimation of design floods from rainfall using CSM and other hydrological studies requires detailed information of the rainfall distribution in both space and time and for a long period of record. Traditional mathematical interpolation techniques have been used to determine the spatial distribution of rainfall over an ungauged area from rain-gauge networks. However, the rainfall fields from these techniques fall short of describing the 'true rainfall fields'. Since the introduction of weather radar as a rainfall-measuring technique, researchers have been working to develop a meaningful link between the radar estimated and rain-gauge measured rainfall data. As a result, models have been developed which combine the rainfall fields from the radar and rain-gauge networks and these rainfall fields represent the highly variable rainfall fields reasonably well.
Merged rainfall fields for the Liebenbergsvlei catchment were generated using an algorithm developed by Sinclair (2004) and Sinclair and Pegram (2005), which is based on the conditional merging technique of Ehret (2002). In this study, the merging technique was validated against data from tipping bucket rain gauges used in conditioning of the radar images. The conditional merging technique is intended to retain the rainfall depths used in the conditioning of the radar images in the merged rainfall field. The results obtained indicated that gauged rainfalls at the conditioning rain gauges were not always retained as the merging technique developed by Sinclair (2004) masks the pixels where the radar did not register any rain, even though rain gauges in this area may have reported rainfall. This was done to avoid false rainfall in other parts of the catchment. When the masked values were removed from the comparison, a nearly perfect relationship was obtained between the conditioning rain-gauge data and the merged pixel rainfall values located at the conditioning rain gauge, thus indicating that the merging algorithms performed as designed.
The merging technique was further verified using independent daily rain gauges which were not used in the conditioning of the radar images. For most subcatchments reasonably good verifications were obtained with the slope of the regression line ranging between 0.8 to 1.2 and correlation coefficients of greater than 0.5. However, the relationship depends on the distance between the tipping bucket rain gauge used in conditioning of the radar image and the daily rain gauge under consideration, as well as the accumulation timescale. Therefore extrapolation to different (particularly shorter) accumulation periods must be made with care.
The average merged rainfall values for each subcatchment of the Liebenbergsvlei catchment were related to rainfall from rain gauges selected to represent rainfall in the subcatchments. The relationships were generally found to be good, with correlation coefficients of greater than 0.5 for most of the subcatchments. However, the rain gauges selected to represent the areal rainfall of the subcatchments were generally found to overestimate the mean areal merged rainfall values of the subcatchments by between 5% and 50%. The relationship developed and the historical rainfall data from the rain gauges can be used to provide improved estimates of average catchment rainfall for use in CSM and other hydrological studies. The errors in estimating rainfall for a catchment using a rain gauge have been highlighted as a consequence of this study and the need to improve the estimation of catchment rainfall using the merging process where radar data are available is evident.
Acknowledgement
The Water Research Commission (WRC) is gratefully acknowledged for funding this research and the South African Weather Service (SAWS) for kindly sharing radar data from the Bethlehem radar.
References
CAMERON DS, BEVEN KJ, TAWN J, BLAZKOVA S and NADEN P (1999) Flood frequency estimation by continuous simulation for a gauged upland catchment (with uncertainty). J. Hydrol. 219 169-187. [ Links ]
EHRET U (2002) Rainfall and Flood Nowcasting in Small Catchments Using Weather Radar. Ph.D. Thesis. University of Stuttgart, Germany. [ Links ]
GUPTA VK and WAYMIRE EC (1993) A statistical analysis of mesoscale rainfall as a random cascade. J. Appl. Meteorol. 32 251-267. [ Links ]
HABIB E and KRAJEWSKI WF (2002) Uncertainty analysis of the TRMM ground validation radar-rainfall products: application to the TEFLUN-B field campaign. J. Appl. Meteorol. 41 558-572. [ Links ]
JEWITT GPW, TERBLANCHE D, MITTERMAIER M and GÖRGENS AHM (1997) Radar measured precipitation as input to a distributed hydrological model: An example from the Liebenbergsvlei. In: Proc. 8th S. Afr. Natl. Hydrol. Symp. 17-19 Nov. 1997, Water Research Commission, Pretoria, RSA. [ Links ]
KROESE NJ, MITTERMAIER MP and TERBLANCHE DE (1996) The February 1996 flood event: A radar, rain gauge and stream flow perspective. Proc. 13th Annu. SASAS Conf. Oct. 1996, city? [ Links ]
MIDGLEY DC, PITMAN WV and MIDDLETON BJ (1994) Surface Water Resources of South Africa 1990. WRC Report No. 298/2.1/94. Water Research Commission, Pretoria. South Africa. [ Links ]
PEGRAM GGS and CLOTHIER AN (2001) Downscaling rainfields in space and time, using the string of beads models in causal mode. Hydrol. Earth Syst. Sci. 5 175-186. [ Links ]
PEGRAM GGS and SEED AW (1998) The Feasibility of Stochastically Modelling the Spatial and Temporal Distribution of Rainfields. WRC Report No 550/1/98. Water Research Commission, Pretoria, RSA. [ Links ]
PEGRAM GGS and SINCLAIR DS (2004) A Flood Nowcasting System for the eThekwini Metro: Umgeni Nowcasting Using Radar - An Integrated Pilot Study. WRC Report No. 1217/2/04. Water Research Commission, Pretoria, South Africa. [ Links ]
PEGRAM GGS and SINCLAIR DS (2002) A Linear Catchment Model for Real Time Flood Forecasting. WRC Report No 1005/1/02. Water Research Commission, Pretoria, South Africa. [ Links ]
SEO DONG-JUN and KRAJEWSKI FK (1990) Stochastic interpolation of rainfall data from rain gauges and radar using co-kriging. Water Resour. Res. 26 915-924. [ Links ]
SCHMIDT EJ and SCHULZE RE (1987) Flood Volume and Peak Discharge from Small Catchments in Southern Africa, Based on the SCS Technique. WRC Report TT 31/87. Water Research Commission, South Africa. [ Links ]
SINCLAIR DS (2004) Personal communication. Department of Civil Engineering, Surveying and Construction, University of KwaZulu-Natal. Durban, RSA. [ Links ]
SINCLAIR DS and PEGRAM (2005) Combining radar and rain gauge estimate using conditional merging. Atmos. Sci. Lett. 6 19-22. [ Links ]
SMITHERS JC, SCHULZE RE and KIENZLE SW (1997) Design flood estimation using a modelling approach. In: D Rosbjerg, N Boutayeb, A Gustard, ZW Kundzewicz and PF Rasmussen (eds.) Sustainability of Water Resources Under Increasing Uncertainty. [ Links ] IAHS Publication 240 365-376. [ Links ]
SMITHERS JC, SCHULZE RE, PIKE A and JEWITT GPJ (2001) A hydrological perspective of the February 2000 floods: A case study in the Sabie River catchment. Water SA 27 (3) 325-332. http://www.wrc.org.za/archives/watersa%20archive/2001/July/1377.pdf [ Links ]
TERBLANCHE DE and MATHER GK (1992) The use of weather radars for precipitation research in South Africa. RCC/RSA Binational Symposium on remote sensing for environmental change, FRD, Pretoria, South Africa, June 1992. [ Links ]
TODINI E (2001) Bayesian conditioning of RADAR to rain gauges. Hydrol. Earth Syst. Sci. 5 225-232. [ Links ]
WILSON JW and BRANDES EA (1979) Radar measurement of rainfall: A summary. Bull. Am. Meteor. Soc. 60 1048-1058. [ Links ]
* To whom all correspondence should be addressed.
+2733 260 5487; fax: +2733 260 5818;
e-mail: 200282337@ukzn.ac.za














