Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
Phronimon
On-line version ISSN 2413-3086
Print version ISSN 1561-4018
Phronimon vol.19 n.1 Pretoria 2018
http://dx.doi.org/10.25159/2413-3086/4983
ARTICLE
The fall and original sin of set theory
Danie Strauss
North-West University dfms@cknet.co.za. https://orcid.org/0000-0002-2397-9181
ABSTRACT
Hermann Weyl published a brief survey as preface to a review of The Philosophy of BertrandRussell in 1946. In this survey he used the phrase, "The Fall and Original Sin of Set Theory." Investigating the background of this remark will require that we pay attention to a number of issues within the foundations of mathematics. For example: Did God make the integers-as Kronecker alleged? Is mathematics set theory? Attention will also be given to axiomatic set theory and relevant ontic pre-conditions, such as the difference between number and number symbols, to number as "an aspect of objective reality" (Gödel), integers and induction (Skolem) as well as to the question if infinity-as endlessness-could be completed. In 1831 Gauss objected to viewing the infinite as something completed, which is not allowed in mathematics. It will be argued that the actual infinite is rather connected to what is present "at once," as an infinite totality. By the year 1900 mathematicians believed that mathematics had reached absolute rigour, but unfortunately the rest of the twentieth century witnessed the opposite. The axiom of infinity ruined the expectations of logicism-mathematics cannot be reduced to logic. The intuitionism of Brouwer, Weyl and others launched a devastating attack on classical analysis, further inspired by the outcome of Gödel's famous proof of 1931, in which he has shown that a formal mathematical system is inconsistent or incomplete. Intuitionism created a whole new mathematics, which finds no counter-part in classical mathematics. Slater remarked that within this logical paradise of Russell lurked a serpent, hidden behind the unjustified employment of the at once infinite. According to Weyl, "This is the Fall and original sin of set theory for which it is justly punished by the antinomies." In conclusion, a few systematic distinctions are introduced.
Keywords: mathematics; logic; defining mathematics; integers; induction; successive infinite; at once infinite; completed infinite; intuitionism; logicism; axiomatic formalism; infinite totality; inconsistent; incomplete
The title of this article alludes to a statement made by Hermann Weyl in 1946 in a brief survey serving as preface to a review of The Philosophy of Bertrand Russell. In this Preface, Weyl discusses the relation of mathematics and logic. It was published in the journal American Mathematical Monthly. Our aim is to investigate the underlying issues behind this remark of Weyl. This will invite us to reflect on the nature of mathematics and some of the reasons why twentieth century mathematics gave rise to alternative trends of thought, such as neo-intuitionism (Brouwer, Weyl, Heyting, Dummett, Troelstra and others-differing from the school of Kronecker), logicism (Frege, Russell and Gödel) and axiomatic formalism (Hilbert and his followers). Paul Bernays, the younger co-worker of Hilbert, articulated a stance that provides an alternative view on the issues involved (see Bernays 1976, 74 ff. and 188).
Did God Make the Integers?
Since Georg Cantor erected what is today still known as Set Theory, in a time-span of 25 years, unexpected and surprising developments surfaced within the discipline of mathematics. Particularly during the 1880s, Cantor suffered under the criticism of Leopold Kronecker, who held the prestigious chair in mathematics at the University of Berlin. Kronecker is well-known for his statement that God made the integers and everything else is human handiwork. More recently Stephen Hawking edited a reader and chose as title for it: God Created the Integers (Hawking 2005).
However, upon closer reflection, it is clear that Kronecker and Hawking are mistaken. What God created is a multiplicity of natural and societal entities-which are not yet numbered. The given "pre-counted" multiplicity may call forth a counting reaction from human beings, but it is only then that numerals (number symbols) are invented. These numerals may initially refer to the natural numbers (1, 2, 3, 4, 5, ...) or the integers (0, 1, 2, 3, 4, ...). When there is a multitude of entities, they could be counted or even collected as members of what Cantor calls a set (Menge). Cantor's set concept contains two key elements (or, if one prefers to designate them in such a way, two primitive terms). In the first place a multiplicity of properly distinct objects of our intuition or thought, and secondly uniting this multiplicity into a whole (zu einem Ganzen) (Cantor 1932[1962], 282).
Set Theory and the Nature of Mathematics
How does this set concept link up with possible definitions of mathematics? Is mathematics the science offormal structures (Körner 1968, 72, Meschkowski 1972, 356) or is it the science of idealised structures (Bernays 1976, 176), or perhaps the science of the infinite (Weyl 1932, 7; 1966, 89)? Or should one straight-forwardly hold that mathematics is set theory (Maddy 1997, 36; see Hersh 1997, 27)?
If it is asserted that mathematics is Set Theory, "unsurmountable" problems immediately emerge because such a view cannot account for the history of mathematics. Whatever existed before the invention of Set Theory was not mathematics.
Hersh is sharply critical of the reductionist view that mathematics is set theory because one cannot say that those mathematicians who lived long before the invention of set theory, in fact, thought in terms of set theory. His categorical statement reads: "This claim obscures history, and obscures the present, which is rooted in history" (Hersh 1997, 27), adding the important remark: "An adequate philosophy of mathematics must be compatible with the history of mathematics. It should be capable of shedding light on that history" (Hersch 1997, 27).
Sets in Axiomatic Set Theory
Alternatively, we may start with the observation that any axiomatic set theory introduces at least one "primitive" term. It could be the membership relation (as in Zermelo-Fraenkel set theory) or even the concept of a set as such. However, Gödel once pointed out that, as yet, we do not even have a satisfactory non-circular definition of the term "set":
The operation "set of x's" (where the variable "x" ranges over some given kind of objects) cannot be defined satisfactorily (at least not in the present state of knowledge), but can only be paraphrased by other expressions involving again the concept of set, such as: "multitude of x's", "combination of any number of x's", "part of the totality of x's", where a "multitude" ("combination", "part") is conceived as something that exists in itself, no matter whether we can define it in a finite number of words (so that random sets are not excluded). (Gödel 1964, 262)
Any given definition of mathematics, therefore, presupposes a step backwards-assuming a position where one is no longer doing mathematics but is involved in reflecting on mathematics. This entails that any given definition will never be a part of mathematics. Just consider the statement that "mathematics is the science of formal structures/idealised structures/the infinite, and so on." Surely this "definition" is not a theorem, proof or derivation found in algebra, topology, set theory or any other part of mathematics.
One cannot define the discipline of mathematics exclusively with reference to any sub-discipline of mathematics either. What is required is a point of orientation that is not the creation of the working mathematician, since it must be given as something "out there" before special scientific mathematical work commences.
An Ontic Point of Connection
Hao Wang notes that Kurt Gödel is very "fond of an observation attributed to Bernays":
That the flower has five petals is as much part of objective reality as that its color is red. (quoted by Wang 1988, 202)
In spite of the fact that Gödel did not dispose over a theory in which the various modal aspects of reality are accounted for, he here unmistakably struggles with this aspectual dimension of reality (the meaning of the term aspectual will soon be clarified below).
Kattsoff argues that analogous to the nature of sensory objects, we may also recognise mathematical entities designated as intellectual objects-because they are observed by the intellect (Kattsoff 1973, 33). Later he calls this approach "quasi-empirical" (Kattsoff 1973, 40).
Number and number symbols
Gödel and Kattsoff wrestle with acknowledging that the numerical aspect of reality is not a mental construct. The only option is to explore this given functional trait of reality through an analysis of the meaning of given multiplicities. The first step is normally to "create" numerals-number symbols-such as "1", "2", "3", and so on). Simple acts of counting explore the primitive meaning of the arithmetical aspect of reality-in a twofold way:
(i) Every successive number symbol ("1", "2", "3" etc.) is correlated with ...
(ii) ... whatever is counted. Implicit in this account is the correlation of number symbols and the entities counted.
That is to say, there is a one-to-one relation which became a key feature of comparing sets. But before we pursue this avenue further, we have to say a bit more about the ontic status of modal aspects.
In opposition to Descartes, who claims that number and all universals are modes of thought (Descartes 1965a, 187, Principles of Philosophy, Part I, LVII), we have to recognise the ontic status both of the concrete, multi-aspectual entities and the modes of reality. When the word "factual" is used to designate what is given in an ontic sense prior to human cognition, then its meaning honours the epistemic side of what is factually at hand.
Gödel: Number as an "Aspect of Objective Reality"
Perhaps this plea for acknowledging the aspects of reality as truly existing (and not merely products of human thought) found its most impressive advocate in the thought of Gödel, with his abovementioned idea of "semiperceptions" when it concerns "mathematical objects." Next to a physical causal context within which something can be "given," Gödel refers to data of a second kind, which are open to "semiperceptions." Data of this second kind "cannot be associated with actions of certain things upon our sense organs" (Gödel quoted by Wang 1988, 304). These "semiperceptions" relate to the functional aspects of reality. Gödel says:
It by no means follows, however, [that they] are something purely subjective as Kant says. Rather they, too, may represent "an aspect of objective reality," but, as opposed to the sensations, their presence in us may be due to another kind of relationship between ourselves and reality. (Gödel quoted by Wang 1988, 304)
Once aspects of ontic reality are acknowledged, as noted earlier, it becomes understandable why Hersh is sharply critical of the reductionist view that mathematics is set theory, because one cannot say that mathematicians who preceded the invention of set theory in fact thought in set theoretic terms. According to him, an "adequate philosophy of mathematics must be compatible with the history of mathematics" and it "should be capable of shedding light on that history" (Hersch 1997, 27).
These ontic conditions not only make possible our concept of numbers but also explain why someone like Bernays (1976, 45) rejects the conception that an axiomatic system in its entirety is an arbitrary construction.
According to Bernays (1976), one cannot justifiably object to the axiomatic procedure by viewing it as arbitrary, since regarding the systematic foundation of arithmetic we are not concerned with "an axiom system configured at will for the need of it, but with a systematic extrapolation of elementary number theory conforming to the nature of the matter" (naturgemäß-I am italicising). The "nature of the matter" contains an implicit reference to the ontic status of the "multiplicity aspect" of reality-and it presupposes an awareness of the difference between the various (modal, functional) aspects of reality and the dimension of concrete entities and events functioning within these aspects.
Already in 1922, Skolem had a proper understanding of these issues. Yet, in spite of the objections of Kronecker and other intuitionists, Skolem had to concede that "the Cantorean theory completely won the day" ["daß die Cantorsche Theorie bald vollständig Siegte"] (Skolem 1929, 8). Hilbert was quite impressed with Cantor's set theory and even stated that no-one would drive us out of the paradise created for us by Cantor (Hilbert 1925, 170).
Integers and Induction
Skolem argues that arithmetic already has a sufficient foundation in inductive conclusions and recurrent definitions (Skolem 1922, 231). He points out that scholars working within the domain of set theory normally are convinced that the concept of an integer ought to be defined and that complete induction must be proved. He responds as follows:
Yet it is clear that one cannot define or provide an endless foundation; sooner or later one encounters what is indefinable or unprovable. Then the only option is to ensure that the first starting points are immediately clear, natural and beyond doubt. The concept of an integer and the inferences by induction meet this condition, but it is definitely not met by the set theoretic axioms such as those of Zermelo or similar ones. If one wishes to derive the former concepts from the latter, then the set theoretic concepts ought to be simpler and employing them then ought to be more certain than working with complete induction-but this contradicts the real state of affairs totally. (Skolem 1922, 230)
Restricting infinity to the successive infinite
His own approach still continues the classical prohibition formulated by Gauß in a letter to Schumacher in 1831: "So I protest against the use of an infinite magnitude as something completed, which is never allowed in mathematics" ["So protestiere ich gegen den Gebrauch einer unendlichen Große als einer vollendeten, welches in der Mathematik niemals erlaubt ist"] (Gauß quoted by Meschkowski 1972, 31).
The Completed Infinite?
However, when one explores the meaning of Cantor's definition of a set (mentioned earlier), it appears as if his set theory assumes that an uncompleted succession of numbers could be completed. One way of referring to what Aristotle designated as the actual infinite is, therefore, to speak of the completed infinite. But the contrast between the potential and actual infinite is for Cantor given in the difference between a variable and constancy. Variables point at successive values, whereas actual infinity is firm and determined while at once exceeding every finite magnitude (Größe) (Cantor 1932[1962], 401).
The fact that the initial Pythagorean claim, namely that everything is number, had to switch to space as mode of explanation, is still reflected in a spatially informed mode of speech, such as when the reference is to variable magnitudes, "veränderliche Größeri"-instead of simply referring to variables ["nicht veränderlich, sondern vielmehr in allen seinen Teilen fest und bestimmt, eine richtige Konstante"].
The feature of being a genuine constant, determined and fixed in all its parts, is clearly derived from our acquaintance with what is not subject to change, but what is certainly not intended is any succession that comes to an end, to completion. This highlights an unintended flaw in the just-mentioned restriction of Gauß: an infinite magnitude in mathematics as something completed is not allowed. Nowhere in Cantor's definition of actual infinity is anything said or implied about the "completion" of an infinite process. Therefore, the expression "completed infinitude"-"als einer vollendeten"-is literally self-contradictory: what is without an end cannot have an end. Fischer criticises the attempt to arrive at the square root of "2" with the aid of rational numbers as being an antinomic fiction, the fiction of the "vollendet-Unendlichen" ["the completed infinite"-Fischer 1933, 108].
From Variables to At Once
The concept of a variable is accompanied by the notion of change, which is intimately linked to the connection between the kinematic aspect (constancy, uniform flow) and the physical aspect of reality (dynamic changes, variability). In addition, everyday life is familiar with the fact that change can only be detected if something remains constant.
We have mentioned earlier that Skolem considers the concept of an integer and the inferences by induction to be simpler than the set theoretic ones. In 1929 he alludes to the antinomy of Russell who, independently from Zermelo, pointed out that if a set C has as elements all those sets A not having themselves as elements, then C is an element of C if and only if it is not an element of C. Skolem then mentions the attempt to avoid this antinomy by arguing that every set is not an element of itself. However, even within the axiomatisation of set theory the problems did not disappear, because the power-set axiom stipulates (within Zermelo-Fraenkel [ZF] set theory-Fraenkel, Bar-Hillel, Levy and Van Dalen [1973, 35]) that for any set a there exists the set whose members are just all the subsets of a:
In symbols:
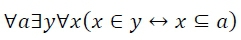
i.e., the initial set is then also a subset of itself-violating the proposed stipulation that every set is not an element of itself. Skolem adds the following problem: "Without general statements about 'all' sets one cannot build a set theory, and then, according to Cantor's definition, these should form part of the totality of the elements of a set" (Skolem 1929, 9).
Comparing natural numbers, integers, and fractions does not cause problems in arithmetic, but the comparison of sets does entail complications. The most important problem concerns the fact that also infinite sets, according to Cantor, are uniting a multiplicity of elements (members in ZF set theory) into a whole-and a whole or totality is not given in succession but at once. When we replace the expression potential infinity with the successive infinite and actual infinity with the at once infinite, it would not be so easy to employ the mistaken expression "completed infinity."
The Connection between "At Once" and "Actual Infinity"
Boyer (1959) points out that there is a vicious circle present in Cauchy's understanding of irrational numbers. The latter attempted to prove his theorem, namely "that for a sequence to converge to a limit it is necessary and sufficient that the difference between Sp and Sq, for any values ofp and q greater than n can be made less in absolute value than any assignable quantity by taking n sufficiently large" (Cauchy quoted in Boyer 1959). Although the necessity of the condition follows from the definition of convergence, the proof of the sufficiency of the condition requires a prior definition of the system of real numbers, of which the supposed limit S is one. However, without an initial definition of irrational numbers, this part of the proof begs the question.
His argument is that irrational numbers should be the limits of sequences of rational numbers. Boyer summarises the underlying petitio principii as follows:
But since a limit by definition is already defined as a number to which the terms of the sequence approach in such a way that ultimately the difference between this number and the terms of the sequence can be made less than any given number, the existence of the irrational number depends, in the definition of limit, upon the known existence, and hence the prior definition, of the very quantity whose definition is being attempted. (Boyer 1959, 232)
In other words, one cannot define the square root of the number 2 (λ/2) as the limit of the sequence 1, 1.4, 1.41, 1.414, ... In order to prove this the definitions of limit and convergence require that there must be, prior to this, a defined or demonstrated number in existence serving as limit.
Weierstrass, Dedekind and Cantor approached the circularity present in the idea that irrational numbers (real numbers) could be defined in terms of converging sequences of rational numbers (fractions), by taking recourse to the at once infinite.
The constructivist mathematician, Paul Lorenzen, explains the classical idea of the at once infinite in a neat way by linking it to the lasting influence of geometry.
This arithmetical concept of the set of all real numbers is apparently motivated by geometry. For this reason, one therefore still speaks about the arithmetical continuum ... One imagines ... the real numbers as being really present all at once-even every single real number as an infinite decimal fraction is presented as if the infinitely many digits all exist at once. [Dieser arithmetische Begriff der Menge aller reellen Zahlen ist augenscheinlich von der
Geometrie aus motiviert. Man spricht daher auch stets vom arithmetischen Kontinuum . Man stellt sich ... die reelen Zahlen als alle auf einmal wirklich vorhanden vor-es wird sogar jede reelle Zahl als unendlicher Dezimalbruch selbst schon so vorgestellt, als ob die unendlich vielen Ziffern alle auf einmal existierten.] (Lorenzen 1972, 162-163)
The discovery of the abovementioned antinomy regarding the set C having as elements those sets A not containing themselves as elements, contributed to the proliferation of diverging mathematical schools of thought during the previous century. At the Second International Congress of Mathematicians (Paris, 1900) Poincaré (quoted in Fraenkel et al. 1973) proudly announced:
Today there remain in analysis only integers and finite or infinite systems of integers ... Mathematics ... has been arithmetized ... We may say today that absolute rigor has been obtained. (Fraenkel et al. 1973, 14)
More than 70 years later, Fraenkel et al. conceded:
Ironically enough, at the very same time that Poincaré made his proud claim, it had already turned out that the theory of the "infinite systems of integers"-nothing else but a part of set theory-was very far from having obtained absolute security of foundations. More than the mere appearance of antinomies in the basis of set theory, and thereby of analysis, it is the fact that the various attempts to overcome these antinomies, to be dealt with in the subsequent chapters, revealed a far-going and surprising divergence of opinions and conceptions on the most fundamental mathematical notions, such as set and number themselves, which induces us to speak of the third foundational crisis that mathematics is still undergoing. (Fraenkel et al. 1973, 14)
The Impasse of Logicism
Frege, Dedekind, Russell and Gödel believed that mathematics could be based upon logic. Within this logicistic approach, Dedekind assumed an actual infinity of "objects" within my "Gedankenwelt" (Rucker 1982, 47 translates it with the term "mindscape").
The general aim of Russel's Principles of Mathematics is to show that "mathematics and logic are identical" (see Slater 1922[2010], xxxiii). Russell introduces a logical class concept to achieve this goal. The number "2" is defined in the following way: "1 + 1 is the number of a class w which is the logical sum of two classes u and v which have no common terms and have each only one term. The chief point to be observed is that logical addition of numbers is the fundamental notion, while arithmetical addition of numbers is wholly subsequent" (Russell 2010, 120). However, the meaning of number is clearly already used in order to distinguish between different ("logical") classes. To be sure, he speaks about the sum of "two classes" where each of them contains "one" element. This presupposes an insight into the numerical meaning of the numbers "1" and "2"! As an effect, the number "2", which was supposedly to be the outcome of logical addition, is presupposed by it!
On a more general level, another problem faces the logicist approach. It turned out that the Axiom of Infinity [InfAx] exceeds the realm of logic. Fraenkel et al. remark: "It seems, then, that the only really serious drawback in the Frege-Russell thesis is the doubtful status of InfAx, according to the interpretation intended by them" (Fraenkel et al. 1973, 186).
The Intuitionistic Reaction to the At Once Infinite
Already in his PhD of 1907, the Dutch mathematician L.E.J. Brouwer (also see Brouwer 1919; 1964) gave an indication of his own subsequent development. He follows in the footsteps of Leopold Kronecker who wanted to reduce every mathematical subdiscipline (geometry excepted) to the concept of ordinal numbers, with the aim to "arithmetise" "arithmetic" which he equated with the discipline of mathematics. But Brouwer took another important step by acknowledging a key feature of continuity, namely its infinite divisibility. This captured the critical mind of Hermann Weyl, a former student of Hilbert. Weyl presented a paper in 1921 on the New Foundational Crisis in Mathematics. He is critical of arithmeticism because it broke apart the continuum into a set of isolated points. In contrast to this, Weyl holds that it belongs to the essence of the continuum that it allows for an infinite divisibility: ". it belongs to the essence of the continuum that everyone of its parts allows for an unlimited continued division. ... In order to restore the continuous coherence of points contemporary analysis, because it has set apart the continuum into a set of isolated points, had to take refuge to the concept of an environment" (Weyl 1921, 77).
Laugwitz (1997) raised the same point in a related way by pointing out that classical analysis has resolved the continuum into a set of (isolated) points. Set theory then super-imposes upon it, with the auxiliary set theoretical construction of environments and open sets, a "topology" within which it is once again possible to speak of "continuity" ("Stetigkeit") (see Laugwitz 1997, 266).
Although modern (axiomatic) set theory (Cantor, Zermelo, Fraenkel, Hilbert, Ackermann, Von Neumann) pretends to be purely atomistic, it actually, in the undefined term "set," borrows the whole-parts relation from space (see below). This explains why Hao Wang informs us that Kurt Gödel speaks of sets as being "quasi-spatial"-and then adds the remark that he is not sure whether Gödel would have said the "same thing of numbers" (Wang 1988, 202).
Weyl also explains this point in a later context where he contrasts the element-set relation with the part-whole relation: "Not in the connection of element and set, but in that of part to whole Brouwer views, in harmony with intuition, the essence of the continuum" (Weyl 1966, 74).
Both Brouwer and Weyl had clarity about their own position regarding the notion of infinity. They rejected the at once infinite, and as a result, key elements of classical analysis cannot be upheld (see also Kaufmann 1930[1968]). The Bolzano-Weierstrass theorem is such an example. This theorem states that "every bounded infinite subset of Rp has a cluster point" (Bartle 1964, 76). Likewise, it is impossible, within intuitionistic mathematics, to show that there is a least lower bound or upper bound. Weyl (1921) mentions the case of a lower bound: "But of course the theorem of the lower bound of an arbitrary set of non-negative real numbers cannot be upheld."
A Distinct Kind of Mathematics
In order to appreciate what really happened within the intuitionistic school of mathematics, two quotations will be sufficient. Beth says: "It is clear that intuitionistic mathematics is not merely that part of classical mathematics which would remain if one removed certain methods not acceptable to the intuitionists. On the contrary, intuitionistic mathematics replaces those methods by other ones that lead to results which find no counterpart in classical mathematics" (Beth 1965, 89). Brouwer himself is quite clear:
As a matter of course also the languages of the two mathematical schools diverge. And even in those mathematical theories which are covered by a neutral language, i.e. by a language understandable on both sides, either school operates with mathematical entities not recognized by the other one: there are intuitionist structures which cannot be fitted into any classical logical frame, and there are classical arguments not applying to any introspective image. Likewise, in the theories mentioned, mathematical entities recognized by both parties on each side are found satisfying theorems which for the other school are either false, or senseless, or even in a way contradictory. In particular, theorems holding in intuitionism, but not in classical mathematics, often originate from the circumstance that for mathematical entities belonging to a certain species, the possession of a certain property imposes a special character on their way of development from the basic intuition, and that from this special character of their way of development from the basic intuition, properties ensue which for classical mathematics are false. A striking example is the intuitionist theorem that a full function of the unity continuum, i.e. a function assigning a real number to every nonnegative real number not exceeding unity, is necessarily uniformly continuous. (Brouwer 1964, 79)
The ultimate divergence is manifest in the fact that intuitionism rejects the at once infinite and with it the universal scope of the logical principle of the excluded middle. Weyl explains the situation: "Brouwer opened our eyes and made us see how far classical mathematics, nourished by a belief in the 'absolute' that transcends all human possibilities of realisation, goes beyond such statements as can claim real meaning and truth founded on evidence" (Weyl 1946, 9). In support of this statement, Weyl on the same page remarks that "Brouwer made it clear, as I think beyond any doubt, that there is no evidence supporting the belief in the existential character of the totality of all natural numbers, and hence the principle of the excluded middle ... is without foundation." The "there is" and "all" only makes "sense when applied to natural numbers," that is to say to the existence of these numbers combined with "the idea of iteration."
Nonetheless, during the first few decades of the previous century, there was an atmosphere of optimism regarding the possibility to prove that mathematics is consistent and complete. When Hilbert received honorary citizenship at Königsberg in 1930, he concluded his presentation with the hopeful exclamation: "We must know, we shall know!" (It is enshrined on his grave: "Wir müßen wissen; wir werden wissen"-see Hilbert 1970, 387). Unfortunately, Kurt Gödel has proven in 1931 that a formal mathematical system is inconsistent or incomplete (Roos summarises this outcome neatly: "Een formeel wiskundig systeem is niet consistent of niet volledig" [Roos 2010, 27]). In other words, no system of axioms is capable-merely by employing its own axioms-to demonstrate its own consistency. Yourgrau remarks: "Not only was truth not fully representable in a formal theory, consistency, too, could not be formally represented" (Yourgrau 2005, 68).
Grünfeld phrases the outcome of Gödel's proof in more detail:
Gödel proved that if any formal theory T that is adequate to include the theory of whole numbers is consistent, then T is incomplete. This means that there is a meaningful statement of number theory S, such that neither S nor not-S is provable within the theory. Now either S or not-S is true; there is then a true statement of number theory which is not provable and so not decidable. The price of consistency is incompleteness. (Grünfeld 1983, 45)
Given the bad personal relation between Brouwer and Hilbert, this discovery was devastating. According to Roos, Hilbert never recovered from this blow (he died in 1943) (Roos 2010, 27). Hilbert's proof theory wanted to show that all true mathematical statements could be incorporated in one system. However, Gödel demonstrated that no formal system can produce all true mathematical statements. In reality, Hilbert's predicament was even worse, for Gödel soon realised that his method also showed that something like arithmetic cannot prove its own consistency. With this, Hilbert's dogma was completely refuted. The expectation that there would be simple consistency proofs for complex theories faded completely (see Roos 2010, 27).
Hilbert's rival won the day on these issues and subsequently, Paul Bernays, the co-worker of Hilbert, had to revert to finitistic methods in their proof theory (contained in Hilbert and Bernays 1934[1939]).
Weyl declares: "It must have been hard on Hilbert, the axiomatist, to acknowledge that the insight of consistency is rather to be attained by intuitive reasoning which is based on evidence and not on axioms" (Weyl 1970, 269).
Anticipating the abovementioned positive assessment of Cantor's transfinite arithmetic by Hilbert as a paradise from which no one will drive us (Hilbert 1925, 170), Slater, in his Foreword to the 1922 edition of Principles of Mathematics, said: "But within this logical paradise lurked a serpent, and it revealed itself to Russell during the spring of 1901 when he was polishing his manuscript for publication" (Russell 1986[2010], xviii).
According to Brouwer's understanding of the history of mathematics, "classical logic was abstracted from the mathematics of finite sets and their subsets" (Weyl 1946, 9-10). The term "finite" is understood in the "precise sense that the members of such a set are explicitly exhibited one by one. Forgetful of this limited origin, one afterwards mistook that logic for something above and prior to all mathematics, and finally applied it, without justification, to the mathematics of infinite sets" (Weyl 1946, 10).
Against this background we can now appreciate why Slater discerned a serpent behind the logical paradise, characterised by Weyl in terms of the title of this article when he declared:
Concluding Remarks
The infinite divisibility of rational fractions follows from the part-whole relationship which is spatial in nature. The rational numbers imitate this feature, which is displayed in the fact that the numerical difference captured by rational intervals is also infinitely divisible. In the transition from integers ("whole" numbers) to fractions ("broken numbers") the original meaning of number is deepened ("disclosed") by pointing forwards (anticipating) an essential feature of space. But the infinite divisibility of a spatial continuum, in turn, points backward (retrocipates) to the primitive numerical meaning captured by mathematicians in terms of the successive infinite.
The rational numbers represent, therefore, an anticipation to a retrocipation. Phrased slightly different we may now say that the numerical difference between any two rational numbers clearly imitates or anticipates the totality-character of continuity (compare the interval as a starting point for the intuitionist continuum). Bernays emphatically states that it is the totality-character of the continuum that resists a complete arithmetisation of the continuum-keeping in mind that "the idea of the continuum is a geometrical idea expressed by Analysis in an arithmetical language" (Bernays 1976, 74).
But since the different sizes of intervals within the continuum are themselves "infinitely divisible" (the denseness of the rational numbers), the mentioned anticipation to the totality-character of continuity, due to the divisibility of such a whole and every one of its parts, immediately refers us back to the numerical aspect. This property of the rational numbers justifies us to speak about a semi-disclosed concept of number, guided by the infinite divisibility of a spatial continuum. It is only when the at once infinite is employed that we encounter the fully disclosed meaning of number, guided by the anticipatory hypothesis that we may work with infinite totalities in which all the parts are given as if they are present at once. The at once infinite is the first fully disclosed structural element of the numerical aspect, and it enables a disclosed handling of the real numbers.
However, intuitionism had to "borrow" the totality-character of continuity from the spatial aspect, but immediately tried to conceal this debt by over-emphasising the part-element of the spatial whole-part relationship which, due to its feature of infinite divisibility, "convinced" them that in fact they have developed a theory of real numbers and the continuum that precedes the notion of space.
Alas, exploring these alternative perspectives requires another article, exceeding the confines of the present one.
References
Bartle, R. G. 1964. The Elements of Real Analysis. London: John Wiley & Sons. [ Links ]
Benacerraf, P., and H. Putnam (Eds). 1964. Philosophy of Mathematics, Selected Readings. Oxford: Basil Blackwell. [ Links ]
Bernays, P. 1976. Gesammelte Abhandlungen, Darmstadt: Wissenschaftliche Buchgesellschaft. [ Links ]
Beth, E. W. 1965. Mathematical Thought. New York: D. Reidel Publishing Company. [ Links ]
Boyer, C. B. 1959. The History of the Calculus and its Conceptual History. New York: Dover Publications. [ Links ]
Brouwer, L. E. J. 1919. "Intuitionisme en Formalisme." In Wiskunde, Waarheid, Werkelijkheid. Groningen (quoted by Roos 2010). [ Links ]
Brouwer, L. E. J. 1964. "Consciousness, Philosophy, and Mathematics." In Philosophy of Mathematics, Selected Readings, edited by P. Benacerraf and H. Putnam. Oxford: Basil Blackwell, 78-84. [ Links ]
Cantor, G. 1932[1962]. Gesammelte Abhandlungen Mathematischen und Philosophischen Inhalts. Hildesheim: Oldenburg Verlag. [ Links ]
Descartes, R. 1965a. "The Principles of Philosophy." In A Discourse on Method, Meditations and Principles, Descartes, R. 1965b, translated by John Veitch, Introduced by A.D. Lindsay. London: Everyman's Library. [ Links ]
Descartes, R. 1965b. A Discourse on Method, Meditations and Principles, translated by John Veitch, Introduced by A.D. Lindsay. London: Everyman's Library. [ Links ]
Descartes, R. 1976. Descartes's Conversation with Burman, translated by J. Cottingham. Oxford: University Press. [ Links ]
Fischer, L. 1933. Die Grundlagen der Philosophie undderMathematik. Leipzig: Hamburg: Feliz Meiner Verlag. [ Links ]
Fraenkel, A., Y. Bar-Hillel, A. Levy, and D. van Dalen. 1973. Foundations of Set Theory, 2nd revised edition. Amsterdam: North Holland. [ Links ]
Gödel, K. 1964. "What is Cantor's Continuum Problem?" In Philosophy of Mathematics, Selected Readings, edited by P. Benacerraf and H. Putnam. Oxford: Basil Blackwell. [ Links ]
Grünfeld, J. 1983. "Euclidean Nostalgia." In International Logic Review (27) (June): 41-50. [ Links ]
Hawking, S. 2005. God Created the Integers. London: Penguin Books. [ Links ]
Hersh, R. 1997. What is Mathematics Really? Oxford: Oxford University Press. [ Links ]
Hilbert, D. 1925. "Über das Unendliche."Mathematische Annalen (95): 161-190. https://doi.org/10.1007/978-3-662-25726-5. [ Links ]
Hilbert, D. 1970. Gesammelte Abhandlungen, Vol. 3, Second Edition. Berlin: Verlag Springer. [ Links ]
Hilbert, D., and P. Bernays. 1934[1939]. Grundlagen der Mathematik. Vol. I, 1934; Vol. 11, 1939, Berlin: Springer. [ Links ]
Kattsoff, L. O. 1973. "On the Nature of Mathematical Entities." International Logic Review no. 7: 29-45. [ Links ]
Kaufmann, F. 1930[1968]. Das Unendliche in der Mathematik und seine Ausschaltung. Darmstadt: Wissenschaftliche Buchgesellscahft. Vienna: Franz Deuticke. [ Links ]
Körner, S. 1968. The Philosophy of Mathematics. London: Hutchinson & Co. [ Links ]
Laugwitz, D. 1997. "Mathematische Modelle zum Kontinuum und zur Kontinuität." Philosophia Naturalis (34): 265-313. [ Links ]
Lorenzen, P. 1972. "Das Aktual-Unendliche in der Mathematik." In Meschkowski 1972. Frankfurt am Main: Wissenschaftliche Buchgesellschaft, 157-165. [ Links ]
Maddy, P. 1997. Naturalism in Mathematics. Oxford: Clarendon Press. [ Links ]
Meschkowski, H. (Ed). 1972. Grundlagen der modernen Mathematik. Darmstadt: Wissenschaftliche Buchgesellschaft. [ Links ]
Reid, C. 1970. Hilbert. London: George Allen & Unwin. https://doi.org/10.1007/978-3-662-28615-9. [ Links ]
Roos, C. 2010. "Komt onvermoeide arbeid alles te boven?" Rede uitgesproken door prof.dr.ir. C. Roos bij het afscheid van de Faculteit Elektrotechniek, Wiskunde en Informatica aan de Technische Universiteit Delft, op vrijdag 10 december 2010. [ Links ]
Rucker, R. 1982. Infinity and the Mind: The Science and Philosophy of the Infinite. Boston: Birkhäuser. [ Links ]
Russell, B. 1956[2010]. The Principles of Mathematics. London: George Allen & Unwin. (First published in 1903, second edition 1937, seventh edition 1956). An unaltered edition appeared in 2010. [ Links ]
Skolem, Th. 1922. "Einige Bemerkungen zur axiomatischen Begründung der Mengenlehre." In Mengenlehre, by Felgner 1979, 57-72. Darmstadt: Wissenschaftiche Buchgesellschaft. [ Links ]
Skolem, Th. 1929. "Über die Grundlagendiskussionen in der Mathematik." Proceedings of the 7th Scandinavian Mathematical Congress, Oslo 1929, pp.3-21, In Mengenlehre, by Felgner 1979, 73-92. Darmstadt: Wissenschaftiche Buchgesellschaft. [ Links ]
Slater, J. G. 1903[2010]. Introduction to the 1992 edition of Russell's Principles of Mathematics. [ Links ]
Wang, H. 1988. Reflections on Gödel. Cambridge Massachusetts: MIT Press. [ Links ]
Weyl, H. 1921. "Ueber die neue Grundlagenkrise der Mathematik," Mathematische Zeitschrift Band 10: 39-79. https://doi.org/10.1007/BF02102305. [ Links ]
Weyl, H. 1932. "God and the Universe." In The Open World. New Haven: Yale University Press, 184. [ Links ]
Weyl, H. 1946. "Mathematics and Logic: A Brief Survey Serving as Preface to a Review of the Philosophy of Bertrand Russell." American Mathematical Monthly (53): 2-13. https://doi.org/10.1080/00029890.1946.11991619; https://doi.org/10.2307/2306078. [ Links ]
Weyl, H. 1966. Philosophie der Mathematik und Naturwissenschaft, 3rd revised and expanded edition. Vienna: R. Oldenburg. [ Links ]
Weyl, H. 1970. "David Hilbert and His Mathematical Work." In Hilbert, by Reid, 243-285. London: George Allen & Unwin. https://doi.org/10.1007/978-3-662-28615-9. [ Links ]
Yourgrau, P. 2005. A World without Time. The Forgotten Legacy of Gödel and Einstein. London: Penguin Books. [ Links ]














