Servicios Personalizados
Articulo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares en Google
Similares en Google
Compartir
Journal of Energy in Southern Africa
versión On-line ISSN 2413-3051
versión impresa ISSN 1021-447X
J. energy South. Afr. vol.32 no.4 Cape Town nov. 2021
http://dx.doi.org/10.17159/2413-3051/2021/v32ia8362
ARTICLES
Optimal sizing for a grid-connected hybrid renewable energy system: A case study of the residential sector in Durban, South Africa
Farzad Ghayoor; Andrew G. Swanson; Hudson Sibanda
Discipline of Electrical, Electronic and Computer Engineering, University of KwaZulu-Natal, Durban, South Africa
ABSTRACT
Many countries, including South Africa, have introduced policies and incentives to increase their renewable energy capacities in order to address environmental concerns and reduce pollutant emissions into the atmosphere. In addition, consumers in South Africa have faced the ever-increasing price of electricity and unreliability of the grid since 2007 due to the lack of sufficient electricity production. As a result, employing hybrid renewable energy systems (HRESs) have gained popularity. This research focuses on grid-connected HRESs based on solar photovoltaic (PV) panels and wind turbines as a potential way of reducing the dependency of residential sector consumers on the grid. It aims to identify the optimal sizing of renewable energy sources to be cost-effective for consumers over a certain period of time, using Durban as a case study. Two artificial intelligence methods have been used to obtain the optimal sizing for the available PV panels, wind turbines and inverters. The results shown that the combination of PV panels and battery storage can be a profitable option. A system using higher rated power PV panels can start to become profitable in a shorter lifetime, but employing batteries can only be cost-effective if a long enough lifetime is considered.
HIGHLIGHTS:
• Modelling the load and a HRES based on the residential consumer needs and available products.
• Defining the optimisation problem based on a cost evaluation indicator and identifying constraints.
• Determining the optimum combination of renewable energy sources.
• Assessing the cost of setting up a HRES for typical residential consumers.
Keywords: cost-effective HRES; genetic algorithm optimiser; particle swarm optimiser; wind and solar hybrid energy systems
1. Introduction
The availability of wind and solar in most areas and the maturity of the technology needed for generating electricity from such sources make them popular choices in hybrid renewable energy systems (HRESs). Wind and solar have complementary characteristics and so are suitable sources to be combined in a hybrid energy system. However, they both have intermittent natures and are highly dependent on environmental conditions.
Hybrid energy systems can be designed to work as stand-alone or grid-connected systems and can benefit from energy storage (ES) units. Regardless of the number and type of energy sources combined to form a hybrid energy system, optimisation is an important stage in designing such a system. Through optimisation, the best design with regard to certain criteria and constraints can be obtained. The design objectives used in optimising a hybrid energy system can be technical, financial, environmental, social, or a combination of these.
This research seeks to identify the optimal size of a grid-connected solar PV-wind-battery storage (BS) hybrid system that is cost-effective compared to a purely grid-connected system. In other words, it tries to identify the optimal size of each HRES component so that a consumer can recover an investment over a certain period of time through the reduced cost through purchasing less electricity from the grid's service provider. Solar and wind energy are location-based; this study has been based on the meteorological data of the coastal city of Durban, South Africa.
2. Literature review
Solar energy is random and intermittent, and usually ES systems are used to mitigate this characteristic. In solar-ES systems, the excess energy generated by PVs during the day can be stored to meet the load demand at night (Jacob et al., 2018; Hua et al., 2019). Wind turbines can also be combined with an ES unit in a wind-ES configuration. In such a configuration, the ES, which is in the form of a battery, is used to stabilise fluctuation associated with wind power (Xu et al., 2018), in addition to providing storage for the excessive generated power (García Clúa et al., 2018). The viability of consumer-based small-scale wind turbines for consumers in South Africa has been studied by Whelan and Muchapondwa (2011). A solar-BS configuration appears to be superior to the wind-BS system, according to Askari and Ameri (2012), because of possible sudden drops in wind speed. However, Maleki et al. (2016) presented contrasting results in another area. Likewise, Khare et al. (2017) obtained opposing conclusions in different regions based on the economy of the system. Therefore, it can be seen that design approaches will vary from one region to another because of meteorological and load characteristics, so it is important to reasonably select the energy resources for a specific area for which the hybrid system would be used.
Another possible configuration is wind-solar-BS (Atia and Yamada, 2016; Ahadi et al., 2016; Nnadi et al., 2014). The complementary nature of wind and solar in this configuration reduces the storage requirements and improves system availability. The optimum results for off-grid hybrid systems show that the wind-solar-BS systems require less battery storage capacity and so can be realised at a lower cost than wind-BS and solar-BS systems (Panayio-tou et al., 2012; Sanajaoba and Fernandez, 2016).
A wind and solar hybrid system can also be combined with non-renewable sources of energy. For example, a combination of wind, solar, and backup generators is very common in off-grid HRESs (Askarzadeh, 2017). To further reduce pollutant emissions, an ES is added to this configuration (Akram et al., 2018; Hove and Tazvinga, 2012) so that diesel fuel is only used when power generated by wind, solar and ES is insufficient (Mandal et al., 2018). Nevertheless, including batteries increases the maintenance cost of the system, as they have a short lifespan and must be replaced more often.
Grid-connected wind-solar HRESs have been considered by Alsayed et al. (2013) and Barakat et al. (2020). In this setup, the main source of power is from the renewable energy sources (RES), and the grid provides the deficit power only if RES cannot meet the load demand. It is also common to consider an ES for the wind-solar-grid configuration (Senjyu et al., 2006; Xu et al., 2013; Akram et al., 2017a; Akram et al., 2017b). In the wind-solar-ES-grid configuration, if the load is not satisfied by the wind-solar system, the deficit power is obtained from the ES. If the power from the ES is still insufficient, the required power will then be obtained from the grid. This combination utilises the complementary nature of solar and wind and the charge and discharge cycles of the BS to improve the system's reliability. The power from the grid would reduce energy storage requirements and improve system reliability. Senjyu et al. (2006) presented optimum configurations for hybrid systems for a residential building based on annual hourly data. The model was developed using the average electrical energy consumption of a single house in Okinawa in Japan. The aim was to minimise the total cost of the system, which is composed of the sum of initial, operational, and maintenance costs per year. Xu et al. (2013) presented an improved optimisation method for both stand-alone and grid-connected wind-solar-BS HRES to minimise the system's total cost, and showed that the grid-connected system could generate smoother power, with higher reliability and lower cost.
Optimal sizing is an essential aspect of designing HRESs, which helps to achieve a desired level of reliability at the least possible costs (Al Busaidi et al., 2014). To optimise an HRES, first, objective functions must be developed according to specific evaluation indicators. These indicators can cover the economic, reliability, social, and environmental aspects of the system. Optimisers will then be used to find the most suitable solution of the defined objective functions (Fadaee and Radzi, 2012). Optimisers that have been used in the sizing problem of the HRESs are generally classified as classical techniques, modern techniques and software tools. In classical techniques, objective functions are estimated by deterministic or probabilistic functions (Sinha and Chandel, 2015) and their optimum solutions are either found by differential calculus or through searching the whole design space with iterative methods (Siddaiah and Saini, 2016). However, the complexity of the HRESs' sizing problems increases as a result of the uncertainties related to RES and the technical factors associated with a system's location and its constructing components. This makes classical techniques less effective in solving such problems. As a result, there was a shift towards the use of modern techniques, which are based on meta-heuristics algorithms (Sinha and Chandel, 2015; Sharafi and Elmekkawy, 2014). Such algorithms, which are known as modern techniques, do not use differential calculus for finding descent directions. Instead, they use a large number of points throughout the design space looking for the optimal solution. In addition to mathematic al methods, there are different software tools, which are available for optimising HRES. Hybrid optimisation model for electric renewables (HOMER) and Improved hybrid optimisation by genetic algorithm (iHOGA) are the most widely used packages used for finding optimal sizing (Mahesh and Sandhu, 2015; Bahramara et al., 2016; Kimera et al., 2014).
Genetic algorithm (GA) is amongst the best artificial intelligence optimisation algorithms. It has been used by many researchers to determine the optimal size of HRESs (Zhao et al., 2014, Ogunjuyigbe et al., 2016, Rajanna and Saini, 2016, Elliston et al., 2013, Gan et al., 2016, Merei et al., 2013). Particle swarm optimisation (PSO) is another widely used heuristic algorithm, which boasts high efficiency and fast convergence speeds, and it is quite easy to implement (Paliwal et al., 2014; Sanchez et al., 2014). Nevertheless, the performance of PSO in optimising a system with four or more decision variables is low and, as a result, the optimised solutions become inadequate. Additionally, PSO may have a tendency of being stuck in local optima (Zahraee et al., 2016). GA, however, can avoid being trapped in local optima, but it requires a large number of iterations, which increases its computational time. Combining an exhaustive search algorithm with GA can overcome this limitation. The resulting hybrid algorithm can utilise GA's good convergence as well as its ability to avoid being stuck in local optima and advantage of lower computational time and effectiveness of an exhaustive search algorithm in finding optimal results (Tito et al., 2016). The long computational time of GA can also be overcome by using a stochastic model (for example, Markov) or chronology to forecast future state assumed from its current state. The high performance of GA can be combined with PSO to improve the accuracy of the solutions and global optimisation ability (Ma et al., 2016).
This research uses GA and PSO to find the optimum configurations for a grid-connected HRES for a residential building in Durban. The weather condition in Durban is such that the wind-solar combination cannot fully achieve its expected complementary characteristics, and so the obtained configuration can be different from other studies. We further improve the GA algorithm, compared with the work of Senjyu et al., 2006) work, which increases its speed without making a sacrifice on the optimiser performance. It is shown that the proposed GA has a faster convergence speed than the PSO.
3. Materials and methods
3.1 Materials
Meteorological data
The meteorological data used in this research are obtained from the Southern African Universities Radiometric Network (SAURAN, 2020) databas e (Brooks et al., 2015) for Durban station, with details given in Table 1 The average hourly data (8760 hours) was used, starting from January. The annual hourly data and histograms for Global Horizontal Ir-radiance (GHI), temperature and wind speed for this station is shown in Figure 1 (a)-(c). The statistics for the collected data are presented in Table 2
Load profile
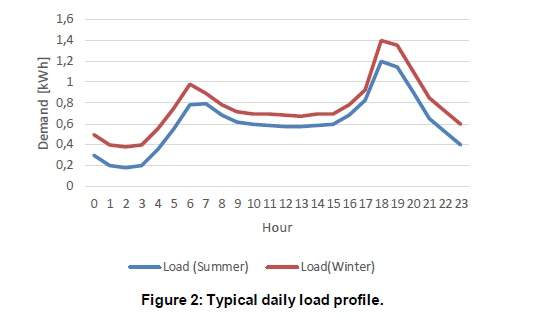
The data for the load profile was obtained from the study funded by the South African National Energy Development Initiative and done by Stellenbosch University and the University of Cape Town on profiling domestic electrical load (DELS, 2020). The data used was collected from an 80 m2 residential building in Durban. Figure 2shows the typical daily load profile for a high-consumption and a low-consumption month. The annual load profile of the given building is shown in Figure 3 and its corresponding statistics are recorded in Table 3 As is seen, the average hourly load consumption is 0.68 kWh with the peak value of 2.55 kWh. These are important pieces of information for selecting the correctly sized inverter.
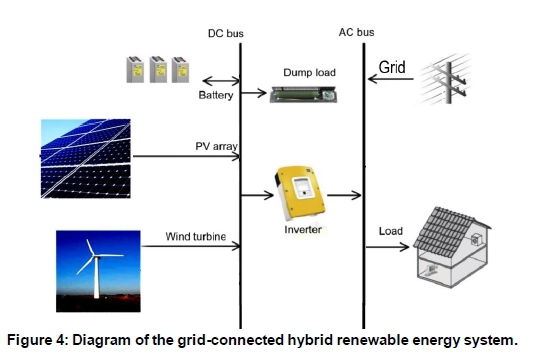
HRES model
The hybrid energy system considered in this study is shown in Figure 4 It consists of PV arrays, wind turbines and battery storage systems. The selected wind turbines are considered to be equipped with internal rectifiers and battery storage. As a result, the output of the wind turbine is in the form of DC power. The output of PV arrays, wind turbines and BS are all integrated into a DC bus. Although it is common that a grid-connected hybrid system injects its excessive generated power back to the grid, the eThekwini municipality has not finalized its small-scale embedded generation systems' tariffs. Therefore, this research, instead of injecting the excessive power generated by RES back to the grid, tries to find the best solution to store the energy within the system or dump it if necessary.
The power output of a wind turbine, PWT, can be calculated according to the wind speed at time t, v(t), as in Equation 1 (Arabali et al., 2013).
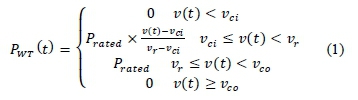
vci : cut in speed
vr : rated speed
vco : cut-out speed
Prated : rated power of the wind turbine
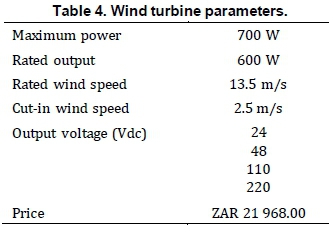
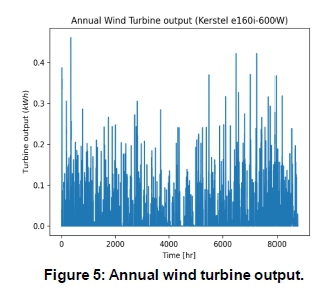
The selected wind turbine for this study is Kestrel e160i-600W, whose characteristics are given in Table 4 The rating is selected to be close to the average demand. The annual output power of this turbine based on the wind speed data given in Figure 1 is calculated by Equation 1 and is shown in Figure 5
Three PV panels were considered: Cinco 50W, Cinco 100W, and Cinco 200W. Their specifications, together with their current price on the market, are given in Table 5 The PV system's hourly output power can be calculated by Equation 2 (Chen et al., 2011).
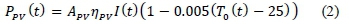
ApV : The panel area in m2
Npv : The panel efficiency
I : The solar irradiation in kW/m2
T0 : The atmospheric temperature in °C
However, according to the panel specifications, the generated power by these panels has a 90% yield in 10 years and 80% in 25 years . To reflect these in our simulation, a linear decline in the performance of PV panels in their lifetime is considered, so Equation 2 is modified to Equation 3.
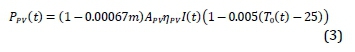
where m is the number of months in the system's lifetime. This means that, after 120 months (10 years), the coefficient value is equal to 1 - 0.00067 X 120 = 0.9 and after 300 months (25 years) it is equal to 0.8. The annual output power for each panel is shown in Figure 6 As is seen, the output power increases until it reaches its maximum power for each panel.
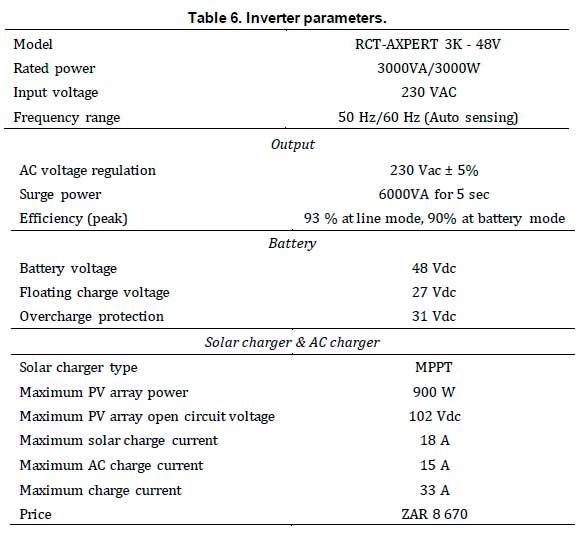
Based on the configuration of the proposed HRES and by considering the load profile, a 3kW hybrid inverter can provide sufficient power. The battery type used in this study is a SonX 100Ah 12V AGM, which were used in a bundle of four to be suitable for operating with the selected inverter. The inverter and battery parameters are given in Tables 6 and 7.
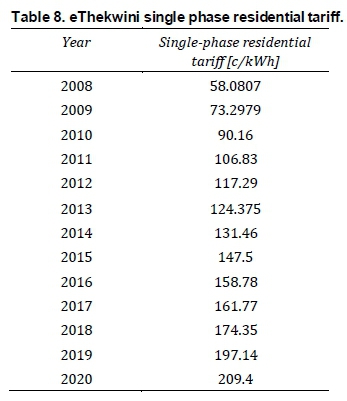
Tariff rates
The tariff rates used in this study were obtained from the eThekwini website (eThekwini Electricity Tariffs, 2020). Table 8shows the eThekwini tariffs structure from 2008 to 2020 for single-phase residential users. Figure 7shows the graphical representation of the tariff structure from 2008 to 2020 and the extrapolation for 2020 to 2030. Cubic (3rd order) polynomial trendline was used, as the best-fitted line, to fit the data from 2008 to 2020 and to predict the tariff till 2030. The prediction gives an annual increase of 11.8%, which is in-line with the historical 11.3% tariff increase from 2008 to 2020 (see Figure 7.
3.2 Methodology
System operation
Figure 8 shows the system operation flowchart. At any given time, a comparison between the load demand, PL, and energy produced by RES is made. If the demand is less than the energy produced by RES, the excess energy will be used to charge the BS, and upon the BS reaching its full capacity the excessive power will be dumped. On the condition that the load demand is greater than the energy produced by RES, the system uses the power stored in the BS to cover a part or all the power deficiency. If the BS does not contain sufficient energy, then the deficit energy should be purchased from the utility grid (UG). The BS can be discharged until its power reaches a minimum value of PBSmin. The inverter efficiency is denoted by N.
Proposed optimisation method
The optimisation objective in this research is to minimise the cost of the hybrid system such that the user would be able to pay back the cost of the system by the money saved over a period of time as a result of using RES for generating electricity. NPV was used for calculating the cost function (Equation 4).
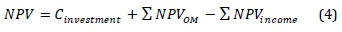
Cinvestment: The value of initial investment including installation.
NPV0M: The net present value of operation and maintenance cost
NPVincome: The net present value of the income generated by using the HRES
By considering an additional 20% of the component prices for installation, the investment costs (inclusive of installation) can be calculated by Equation 5.
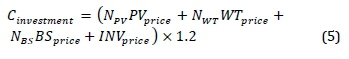
PVprice: The price of a single PV panel
WTprice: The price of a single wind turbine
BSprice: The price of a single bundle of battery storage
INVprice: The price of a single inverter
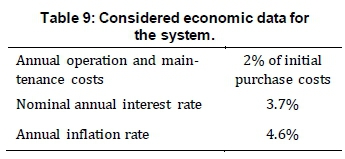
NPV, NWT, NBSare the number of installed PV panels, wind turbines and battery packs, respectively. Other assumed economic data are given in Table 9
The money saved as a result of using RES to generate electricity instead of purchasing it from the grid is considered as an income for the system. This income is used to recover the initial investments and operation and maintenance costs. The monthly power generated by the RES can be determined, and the income is therefore equal to the product of this amount and the tariff at a given time.
There are three constraints in this optimisation problem, which are on the number of PV panels, wind turbines and the BS units. These numbers should be positive integers. Also, the maximum number of PV panels should not exceed the available installation area of the proposed site. The PV panel dimensions considered in this study are given in Table 5
Optimisers
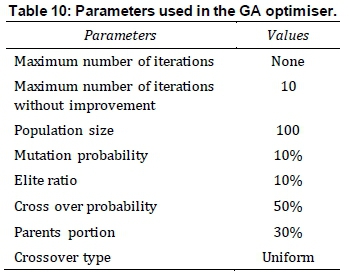
GA and PSO have been used to find the optimal solution of Equation 4 constrained by the maximum number of system components. Tables 10 and 11 give the parameters used for developing the GA and PSO optimisers.

4. Results and discussions
The cost function's value shows the amount of money spent on the HRES after a certain number of years. Therefore, a negative value shows a profitable system configuration. Python3 has been used on an Intel core 1.8 GHz i5 processor to simulate the system and obtain the optimal solutions. This section first provides a comparison between GA and PSO in identifying the optimal size of our considered HRES over 10 years of lifetime. The number of PV panels is constrained by the surface area of the selected building rooftop. All systems were allowed to have wind turbines and BS.
There is usually no restriction on the number of iterations for obtaining the optimal values in the GA algorithm. Instead, the algorithm will usually be set to stop when 95% of the genes converge. However, this takes a long time and, in this particular problem, it was realised that without making a sacrifice on the optimiser performance the optimisation could be stopped after 10 iterations with-no-fur-ther-improvement. Therefore, we considered this stopping criterion in addition to the GA parameters given in Table 10. PSO, on the other hand, is limited by the number of iterations. In PSO algorithms, the optimal solution is obtained by moving the particles through the search space until the algorithm reaches its maximum number of iterations, which is considered as 100 iterations.
As an example, the transition of the cost function with respect to iterations for optimising a hybrid system using 200W PV panels is shown in Figure 9 For this system, GA requires seven iterations to reach the optimal solution, and the algorithm stops after 17 iterations. However, the PSO algorithm could not obtain the optimal solutions and only stops as a result of reaching its iteration limit.
In Table 12 a comparison between the performance of GA and PSO optimisers in optimising systems with 10 years of lifetime is given. For a system using a 200 W PV panel, GA provides the optimal sizing as a system with 21 PV panels, no wind turbines and 2 battery storage units. The value of the cost function for this system is -R45 395.70. PSO, on the other hand, was only able to minimise the cost function to the value of -R45 299.40. This is achieved by a system containing 22 PV panels, no wind turbines and two battery storage units. The other interesting observation is that the GA not only has a better performance over PSO but also can achieve this over a shorter period. The total simulation time using GA was 528.9 seconds , while the same for the PSO was 1066.4 seconds. This is due to the modification made to the GA - to stop it after 10 iterations without improvement. Similar performance can be observed for a HRES using 100W and 50W PV panels.
In all three systems, GA can achieve a sizing that provides a lower-valued cost function in a shorter amount of time than the PSO algorithm. Moreover, in both methods, the required time for solving the optimisation problem is directly proportional to the size of the search space. This can be seen by comparing the required time for optimising the system components' size for different types of PV panels. The surface area of the 200 W PV panels is larger than the others, and so the maximum number of the 200 W PV panels that can be installed is less than the other two types. As a result, the search space for the 200 W is the smallest among the three, followed by the 100 W and 50 W panels. Due to the GA algorithm's superiority, that was to find the optimal size of the HRES's components for different system's lifetimes by setting the algorithm to stop after 10 iterations without improvements.
The optimal size and cost function value of systems using different types of PV panel and lifetime are shown in Table 13 All the values are obtained using the GA algorithm. It can be seen from the table that the system profitability increases by its lifetime. This means that the system can generate more income over a longer period of time as the income of the first few years would be used to cover the initial costs. Moreover, the profitability is increased by using PV panels with higher rated power. This is because the per Watt price of the PV panels decreases as the PV panel rated power increases. In other words, a 200 W PV panel cost is less than the fourfold price of a 50 W PV panel.
A HRES using the 100W and 200W can start becoming profitable after six years, while a user of a HRES based on the 50W panel should wait for at least seven years. The other finding is that, in the Durban area, employing wind turbines (based on the selected specification and price) would not be a cost-effective option. One reason can be because of the weather conditions in Durban, which, unlike many other locations, has a lesser wind speed during winter than in summer. So, the wind-solar combination cannot fully achieve its expected complementary characteristics. Moreover, employing BS can only become an economic decision if a long enough lifetime for a system is considered. This means that storing energy is not always an economical choice: sometimes dumping the excess power would become more cost-effective.
Table 14 gives the breakup of the cost function values given in Table 13based on their different components. By studying this table, it can be seen how much of the income would be spent to recover the initial investment and how much it costs to maintain the system over a given lifetime. In all cases, the income value is greater than the summation of the initial investment and the operation and maintenance costs, making the total cost a negative value.
Operation of the system with optimal configuration
This section considers the operation of an optimally configured HRES. The system is optimally sized over 10 years of lifetime. Figure 10shows the average annual consumption of the system from the grid and PV panels for different panel types. The horizontal axis shows the days over a period of one year, starting from the first day of January, and the vertical axis shows the consumption (in kWh).
As is seen, there is more power consumption from the grid during winter, where the demand is high, and the solar irradiation is low. However, during summer, where the solar irradiation is high, the PV panels generate more power. As a result of lower demand, the power generated by the PV panels on some summer days is sufficient to be the sole source of power for the system. Figure 11shows the average annual stored and dumped power for the optimally sized HRES using different types of PV panels.
The statistics for this figure are tabulated in Table 15 As is shown, the amount of stored power is increased by employing higher power PV panels. Moreover, as expected, more energy was dumped during summer as there is more excessive generated power due to high solar irradiation and low consumption. However, during wintertime, where the load demand is high, all the generated energy by the PV panels is either stored or used by the load.
5. Conclusion
The focus of this research was to identify the optimal sizing of a grid-connected HRES that is cost-effective for consumers over a period of time. By developing an optimal system, the consumers' dependency on the grid is reduced while the net cost of their electricity over a period of time is lowered. To achieve this, the system components and constraints were identified, and then a mathematical model of the system was developed and optimised. The case study for this research was a residential building in Durban. It was shown that a minimum of six years is required for the HRES to be profitable to the user. It was also shown that despite an increase in the initial investment and operation and maintenance costs of using higher rated power PV panels, the overall income generated by the HRES using higher rated panels would also increase. It became clear that using wind turbines would not be a feasible option, in the Durban area, which, unlike many locations, has lower wind speed during winter than summer. Consequently, the solar and wind combination is unable to fully achieve its expected complementary characteristics. Moreover, using BS is only cost-effective after eight years for the systems using the 200W and 100W PV panels, and after nine years for the systems using 50W PV panels. This means that for shorter system lifespans, it is more cost-effective to dump any excess power that is produced than to store it.
Author roles
Farzad Ghayoor conceptualised the idea and was involved in developing the algorithms and implementing the code in python. Andrew Swanson was involved with developing algorithm and reviewing the results against other results. Hudson Sibanda was involved with implementing the code and presenting the results. All were involved with writing the paper.
References
Ahadi, A., Kang, S.-K & Lee, J.-H. 2016. A novel approach for optimal combinations of wind, PV, and energy storage system in diesel-free isolated communities. Applied Energy, 170: 101-115. [ Links ]
Akram, U., Khalid, M. & Shafiq, S. 2017a. An innovative hybrid wind-solar and battery-supercapacitor microgrid system-development and optimization. IEEE Access, 5: 25897-25912. [ Links ]
Akram, U., Khalid, M. & Shafiq, S. 2017b. Optimal sizing of a wind/solar/battery hybrid grid-connected microgrid system. IET Renewable Power Generation, 12: 72-80. [ Links ]
Akram, U., Khalid, M. & Shafiq, S. 2018. An improved optimal sizing methodology for future autonomous residential smart power systems. IEEE Access, 6: 5986-6000. [ Links ]
Al Busaidi, A. S., Kazem, H. A. & Khan, M. F. 2014. A review of optimum sizing techniques for off-grid hybrid PV-wind renewable energy systems. International Journal of Students Research in Technology & Management, 2: 93-102. [ Links ]
Alsayed, M., Cacciato, M., Scarcella, G. & Scelba, G. 2013. multicriteria optimal sizing of photovoltaic-wind turbine grid connected systems. IEEE Transactions on Energy Conversion, 28: 370-379. [ Links ]
Arabali, A., Ghofrani, M., Etezadi-Amoli, M. & Fadali, M. S. 2013. Stochastic performance assessment and sizing for a hybrid power system of solar/wind/energy storage. IEEE Transactions on Sustainable Energy, 5: 363-371. [ Links ]
Askari, I. B. & Ameri, M. 2012. Techno-economic feasibility analysis of stand-alone renewable energy systems (pv/bat, wind/bat and hybrid pv/wind/bat) in Kerman, Iran. Energy Sources, PartB: Economics, Planning, and Policy, 7: 4560. [ Links ]
Askarzadeh, A. 2017. Solution for sizing a PV/diesel HPGS for isolated sites. IET Renewable Power Generation, 11: 143151. [ Links ]
Atia, R. & Yamada, N. 2016. Sizing and analysis of renewable energy and battery systems in residential microgrids. IEEE Transactions on Smart Grid, 7: 1204-1213. [ Links ]
Bahramara, S., Moghaddam, M. P. & Haghifam, M. R 2016. Optimal planning of hybrid renewable energy systems using HOMER: A review. Renewable and Sustainable Energy Reviews, 62: 609-620. [ Links ]
Barakat, S., Ibrahim, H. & Elbaset, A. A. 2020. Multi-objective optimization of grid-connected PV-wind hybrid system considering reliability, cost, and environmental aspects. Sustainable Cities and Society, 60: 102178. [ Links ]
Brooks, M. J., Du Clou, S., Van Niekerk, W. L., Gauché, P., Leonard, C., Mouzouris, M. J., Meyer, R., Van Der Westhuizen, N., Van Dyk, E. E. & Vorster, F. J. 2015. SAURAN: A new resource for solar radiometric data in Southern Africa. Journal of Energy in Southern Africa, 26: 2-10. [ Links ]
Chen, S. X., Gooi, H. B. & Wang, M. 2011. Sizing of energy storage for microgrids. IEEE Transactions on Smart Grid, 3: 142-151. [ Links ]
Domestic Electrical Load Study [Online]. Available: https://www.datafirst.uct.ac.za/dataportal/index.php/cata-log/DELS [Accessed 12-12-2020 2020]. [ Links ]
Elliston, B., Macgill, I. & Diesendorf, M. 2013. Least cost 100% renewable electricity scenarios in the Australian National Electricity Market. Energy Policy, 59: 270-282. [ Links ]
EThekwini Electricity Tariffs [Online]. Available: http://www.durban.gov.za/City_Services/electricity/Tariffs/Pages/default.aspx [Accessed 12-12-2020 2020]. [ Links ]
Fadaee, M. & Radzi, M. A. M. 2012. Multi-objective optimization of a stand-alone hybrid renewable energy system by using evolutionary algorithms: A review. Renewable and Sustainable Energy Reviews, 16: 3364-3369. [ Links ]
Gan, L. K., Shek, J. K. H. & Mueller, M. A. 2016. Optimised operation of an off-grid hybrid wind-diesel-battery system using genetic algorithm. Energy Conversion and Management, 126: 446-462. [ Links ]
García Clúa, J. G., Mantz, R J. & De Battista, H. 2018. Optimal sizing of a grid-assisted wind-hydrogen system. Energy Conversion and Management, 166: 402-408. [ Links ]
Hove, T. & Tazvinga, H. 2012. A techno-economic model for optimising component sizing and energy dispatch strategy for PV-diesel-battery hybrid power systems. Journal of Energy in Southern Africa, 23: 18-28. [ Links ]
Hua, Z., Ma, C., Lian, J., Pang, X. & Yang, W. 2019. Optimal capacity allocation of multiple solar trackers and storage capacity for utility-scale photovoltaic plants considering output characteristics and complementary demand. Applied Energy, 238: 721-733. [ Links ]
Jacob, A. S., Banerjee, R & Ghosh, P. C. 2018. Sizing of hybrid energy storage system for a PV based microgrid through design space approach. Applied Energy, 212: 640-653. [ Links ]
Khare, V., Nema, S. & Baredar, P. 2017. Optimisation of the hybrid renewable energy system by HOMER, PSO and CPSO for the study area. International Journal of Sustainable Energy, 36: 326-343. [ Links ]
Kimera, R., Okou, R., Sebitosi, A. B. & Awodele, K. O. 2014. Considerations for a sustainable hybrid mini-grid system: A case for Wanale village, Uganda. Journal of Energy in Southern Africa, 25: 33-43. [ Links ]
Ma, G., Xu, G., Chen, Y. & Ju, R 2016. Multi-objective optimal configuration method for a standalone wind-solar-battery hybrid power system. IET Renewable Power Generation, 11: 194-202. [ Links ]
Mahesh, A. & Sandhu, K. S. 2015. Hybrid wind/photovoltaic energy system developments: Critical review and findings. Renewable and Sustainable Energy Reviews, 52: 1135-1147. [ Links ]
Maleki, A., Khajeh, M. G. & Ameri, M. 2016. Optimal sizing of a grid independent hybrid renewable energy system incorporating resource uncertainty, and load uncertainty. International Journal of Electrical Power & Energy Systems, 83: 514-524. [ Links ]
Mandal, S., Das, B. K. & Hoque, N. 2018. Optimum sizing of a stand-alone hybrid energy system for rural electrification in Bangladesh. Journal of Cleaner Production, 200: 12-27. [ Links ]
Merei, G., Berger, C. & Sauer, D. U. 2013. Optimization of an off-grid hybrid PV-wind-diesel system with different battery technologies using genetic algorithm. Solar Energy, 97: 460-473. [ Links ]
Nnadi, D. B., Odeh, C. I. & Omeje, C. 2014. Use of hybrid solar-wind energy generation for remote area electrification in South-Eastern Nigeria. Journal of Energy in Southern Africa, 25: 61-69. [ Links ]
Ogunjuyigbe, A. S. O., Ayodele, T. R. & Akinola, O. A. 2016. Optimal allocation and sizing of PV/Wind/Split-diesel/Bat-tery hybrid energy system for minimizing life cycle cost, carbon emission and dump energy of remote residential building. Applied Energy, 171: 153-171. [ Links ]
Paliwal, P., Patidar, N. P. & Nema, R. K. 2014. Determination of reliability constrained optimal resource mix for an autonomous hybrid power system using Particle Swarm Optimization. Renewable Energy, 63: 194-204. [ Links ]
Panayiotou, G., Kalogirou, S. & Tassou, S. 2012. Design and simulation of a PV and a PV-wind standalone energy system to power a household application. Renewable Energy, 37: 355-363. [ Links ]
Rajanna, S. & Saini, R. P. 2016. Development of optimal integrated renewable energy model with battery storage for a remote Indian area. Energy, 111: 803-817. [ Links ]
Sanajaoba, S. & Fernandez, E. 2016. Maiden application of cuckoo search algorithm for optimal sizing of a remote hybrid renewable energy System. Renewable Energy, 96: 1-10. [ Links ]
Sanchez, V. M., Chavez-Ramirez, A. U., Duron-Torres, S. M., Hernandez, J., Arriaga, L. G. & Ramirez, J. M. 2014. Techno-economical optimization based on swarm intelligence algorithm for a stand-alone wind-photovoltaic-hydrogen power system at south-east region of Mexico. International Journal of Hydrogen Energy, 39: 16646-16655. [ Links ]
Senjyu, T., Hayashi, D., Urasaki, N. & Funabashi, T. 2006. Optimum configuration for renewable generating systems in residence using genetic algorithm. IEEE Transactions on Energy Conversion, 21: 459-466. [ Links ]
Sharafi, M. & Elmekkawy, T. Y. 2014. Multi-objective optimal design of hybrid renewable energy systems using PSO- simulation based approach. Renewable Energy, 68: 67-79. [ Links ]
Siddaiah, R. & Saini, R. P. 2016. A review on planning, configurations, modeling and optimization techniques of hybrid renewable energy systems for off grid applications. Renewable and Sustainable Energy Reviews, 58: 376-396. [ Links ]
Sinha, S. & Chandel, S. S. 2015. Review of recent trends in optimization techniques for solar photovoltaic-wind based hybrid energy systems. Renewable and Sustainable Energy Reviews, 50: 755-769. [ Links ]
Southern African Universities Radiometric Network [Online]. Available: https://sauran.ac.za/ [Accessed 12-12-2020 2020]. [ Links ]
Tito, S. R., Lie, T. T. & Anderson, T. N. 2016. Optimal sizing of a wind-photovoltaic-battery hybrid renewable energy system considering socio-demographic factors. Solar Energy, 136: 525-532. [ Links ]
Whelan, B. & Muchapondwa, E. 2011. Enhancing consumers' voluntary use of small-scale wind turbines to generate their own electricity in South Africa. Journal of Energy in Southern Africa, 22: 13-21. [ Links ]
Xu, F., Liu, J., Lin, S., Dai, Q. & Li, C. 2018. A multi-objective optimization model of hybrid energy storage system for non-grid-connected wind power: A case study in China. Energy, 163: 585-603. [ Links ]
Xu, L., Ruan, X., Mao, C., Zhang, B. & Luo, Y. 2013. An improved optimal sizing method for wind-solar-battery hybrid power system. IEEE transactions on Sustainable Energy, 4: 774-785. [ Links ]
Zahraee, S. M., Khalaji Assadi, M. & Saidur, R. 2016. Application of artificial intelligence methods for hybrid energy system optimization. Renewable and Sustainable Energy Reviews, 66: 617-630. [ Links ]
Zhao, B., Zhang, X., Li, P., Wang, K., Xue, M. & Wang, C. 2014. Optimal sizing, operating strategy and operational experience of a stand-alone microgrid on Dongfushan Island. Applied Energy, 113: 1656-1666. [ Links ]
Corresponding author: Tel.: +44 (0)1274383943














