Servicios Personalizados
Articulo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares en Google
Similares en Google
Compartir
Journal of Energy in Southern Africa
versión On-line ISSN 2413-3051
versión impresa ISSN 1021-447X
J. energy South. Afr. vol.29 no.4 Cape Town 2018
http://dx.doi.org/10.17159/2413-3051/2017/v29i4a2439
ARTICLE
Energy flow estimation-control of two interconnected microgrids
Diambomba H. TungadioI; Ramesh C. BansalII; Mukwanga W. SitiIII
IDepartment of Electrical, Electronics and Computer Engineering, University of Pretoria, Private Bag X20, Hatfield 0028, South Africa
IIDepartment of Electrical and Computer Engineering, University of Sharjah, Sharjah, P. O. Box 272 72, United Arab Emirates
IIIDepartment of Electrical Engineering, Tshwane University of Technology, Private Bag X680, Pretoria 0001 South Africa
ABSTRACT
Being dependent on weather, photovoltaic and wind system energy contributions fluctuate and are not continuously available, and sometimes not in the desired quantity. To avoid load shedding or blackout in this situation, the estimation-control of energy can be useful to ensure continuity of supply and assist the planning operation of the power system. This study proposes the estimation-control of the flow of energy between two microgrids interconnected via two alternating current tie-lines. Two sources of power generation depending on weather behaviours have been considered. The effectiveness of the proposed estimation-control model was shown using the Extended Kalman filter combined with the fmin-con algorithm.
Keywords: photovoltaic, wind energy, energy, power flow, tie-lines
1. Introduction
To ensure the balance of an interconnected system, it is first necessary that each area must be able to supply its own load without depending on the other networks. It can happen that, due to variations in the power system operation, one or more areas have deficit in electricity, at which moment electrical power can be transferred between the areas because the load change occurs continuously and randomly. As a result, the deviations of load frequency and the tie-line power flow from scheduled generation limits. Regulating the frequency to its nominal value and maintaining the flow of energy in the tie-lines between areas are the strategies adopted for daily management of the power system. The integration of the renewable energy sources into the power network makes the network complex, requiring advance control methods so that the system can be run safely and controlled effectively [1-3]. Active and reactive power controllers are needed to maintain quality of power supply under constant voltage and frequency. How to estimate and control this energy transfer between areas to ensure their balance is the question which is investigated in this paper.
Being dependant on weather, photovoltaic (PV) and wind energy contributions need to be estimated and controlled [4]. A great deal of research has been devoted to energy estimation [5-19]. A methodology for estimating the potential of rooftop solar photovoltaic was investigated [5]. Large-scale standalone wind turbine energy estimation was proposed [6], including the accurate energy production estimation. Mabel and Fernandez [7] developed the model for estimating energy yield from windfarms using artificial neural networks. The results showed that the model was an efficient energy yield estimation tool for windfarms. An investigation was made of the analytical model and algorithm for tracing active power flow based on an extended incidence matrix [8], which could be applied to any power network. The daily solar energy production estimation for minimising energy storage requirements in PV power plants was proposed [9], in an optimised energy management strategy for reliably exploiting PV power plants. A study proposed the wind distribution and capacity factor estimation for wind turbines in coastal region of South Africa, looking at current methods and advances in forecasting wind power generation [10-11]. Monteiro et al. [12] presented a model estimating PV power generation and carried out performance analysis using three artificial intelligence algorithms: a Kalman filter, artificial neural networks, and a support vector machine. The implementation of a new non-intrusive energy saving estimation has also been presented [13]. Wind resource estimation was conducted to estimate its annual energy contribution based on windspeed and power curve models [14]. Photovoltaic and wind power estimation and economic load dispatch using the firefly algorithm was presented [15], where four test cases were used to validate the approach experimentally. Active power deficit estimation in the presence of renewable energy sources was presented using DigSilent software simulator [16]. Bel-tran et al. [17] proposed daily solar energy estimation based on minimisation of energy storage needed for power plants. Active power estimation of PV generators for distribution network planning was proposed based on correlation models [18]. A wind estimation model was published based on a nonstandard extended Kalman filter (EKF) [19]. This Kalman filter was applied to estimate the maximum power extraction for variable speed wind turbines.
The energy storage system power output can, as a main component in the new power system (mi-crogrids), be estimated for its good management by increasing the power system reliability. Studies were made on battery state of charge estimation applying Kalman filter process [20 -25]. An online state of charge estimation for aerial lithium-ion battery packs based on the improved EKF was proposed [20] as an effective method estimating the state of the charge value for the lithium-ion-battery pack because of its capacity needs in high-power supply applications. The state of charge estimation of the battery pack using an improved extended Kalman filter is presented in [21]. The Kalman filter for state of charge estimation of lithium-ion battery based on a model uncertainty is analysed in [22]. The proposed model has better accuracy than with the unscented Kalman filter and adaptive unscented Kalman filter. State of charge estimation of lead acid batteries using an adaptive Kalman filter was applied in [23], where the model reduces the state of charge estimation error and makes it more reliable than using an a priori process and measurement noise covariance values. The state of charge estimation of two different commercial lithium-ion batteries was proposed in [24]. The state of energy and power capability estimation of a batteries using Kalman filter was proposed in [25], essentially introducing a novel modelbased joint estimation approach against uncertain external operating conditions and internal degradation status of battery cells. A Kalman filtering state of charge estimation for battery management system based on a stochastic fuzzy neural network battery model was introduced in [26], reducing the maximum error when compared with the real state of charge obtained from the discharging test.
Changing from one state to another, a power system requires for its management the use of more advanced techniques to ensure its development. The integration of renewable energy sources into the traditional network makes the power system management problem even more complex because of their irregularities and their dependence on weather.
Estimating the flow of energy, therefore, finds its place in the daily management of a new electricity grid. The system in the present study consists of two areas interconnected by two alternating current (AC) tie-lines to allow the flow of electrical energy. When the operation of the system is not disturbed, the energy transfer takes place from area one to area two to charge the battery. The production of electrical energy in the first area is provided by a hydroelectric plant and the windmill farm. The conventional thermal power station and solar panels and battery storage of an unused energy produces electrical energy in zone two. The configuration of the studied system is explained in Section 2. Problem formulation and modelling are detailed in Section 3, while Section 4 presents the system data, simulations results and discussions. Finally, Section 5 gives conclusions.
2. Configuration of the system studied
The analysed system consists of two interconnected micro-grids (a two-area system) as shown in Figure 1. Each area feeds its consumers and the tie-line allows electric energy to flow between the areas. Each power area has several generation sources, which are closely coupled to form a coherent group. All power sources respond in unison to the changes in the load demand. The control area 1 is made by one conventional thermal power plant (synchronous generator, SG1) and a windfarm. Conventional large hydro (SG2), PV array and energy storage system (ESS) are the energy source of area 2. The active power from SG1 and SG2 are known: P1 = 117 MW, P2 = 126 MW; wind power (from the windfarm in area 1) and solar power (from PV array area 2) are given under profile form which varies during the 24-hour period between the times [t0, tf], which was taken as the control horizon in this study.
3. Problem formulation and modelling
3.1 Problem definition
Microgrid interconnection presents many benefits, such as improved reliability in supplying the load, so that the total power generated can supply the peak load demand of the interconnected system. The bidirectional power flow via tie-lines allows the load demand to be met and well managed. The efficiency of the interconnected system is increased, and the generating units of each area cannot be overloaded by meeting the limits of the power reserve. The management of such interconnected system is more complex, despite its advantages. For stable operation, each area must be capable of feeding and totally absorbing its own load; and the power flow in the tie-line must be kept equal to zero (frequency deviation equal to zero).
A microgrid, while considering the varied production and the power demand, presents high non-linearities, changing dynamics and uncertainties that may require more advanced intelligent approach strategies, such as the optimal approach. Using more effective strategies would increase the performance of these find of systems. Wind and PV are sources of energy working in turbulent conditions and an unforeseeable environment. The microgrid control operation must be adjusted to improve the reliability and effectiveness of microgrids which strongly depend on the chosen and applied control operation strategies. This study proposes the control of active power and frequency in two tie-lines linking two microgrids. The active power output of the SG, PV, and the system constraints of the state of charge (SOC) of the battery are used as control variables. The power balance and the limits of the generation source should be met during the control horizon. Active power flowing in the tie-lines are considered as a state variable and the objective function is formulated as the minimisation of the difference of active power in both.
3.2 Mathematical modelling of the system
To maintain balanced power network operation, the total energy generated must be controlled and correctly dispatched to meet the total power demand. The total active power generated in Figure 1: Pg1and PG2for the respective microgrids 1 and 2 is given by Equations 1 and 2.
PGl = P (k) + P2 (k) + P (k) (1)
where, for microgrid 1, P1 (k) is the active power from the SG1 and P2 (k) the active power from the wind farm.
Pgt 2 = P5 (k)+Рб (k)+P7(k) (2)
where, for microgrid 2, P5 (k) is the power from the SG2, P6 (k )the active power from the PV array and P7 (k) the power of the ESS (charge and discharge mode). All these powers are taken as control variables.
The power P3(k) and P4(k) are considered as power flow in tie-lines and taken as state variables. The power deviations for each microgrid (or area) are given by Equations 3 and 4. The equations demonstrate the difference between the power generated and the demand of the system.
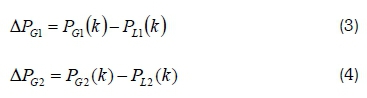
where PL1 (k) and PL2 (k) are respectively the load demand in microgrids 1 and 2.
The frequency deviation of the system is calculated using Equations 5 and 6 for each microgrid [27].

where 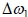 and
and 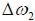 are the frequency difference for microgrids 1 and 2 respectively, and Ksys is the system frequency characteristic constant of the microgrid.
are the frequency difference for microgrids 1 and 2 respectively, and Ksys is the system frequency characteristic constant of the microgrid.
A tie-line is essentially used for energy exchange between control areas to provide inter-area support in severe conditions. If there is a mismatch between the power generated and demanded, a deviation in frequency for a particular area occurs. Since a tieline transports power in or out of an area, it must be accounted for in the incremental power balance equation of each area. The tie-line power deviation, 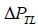 , using the microgrid's frequency deviation and synchronising power coefficient, (PS ), is calculated as follows [27]:
, using the microgrid's frequency deviation and synchronising power coefficient, (PS ), is calculated as follows [27]:
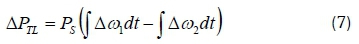
3.3 Proposed model
The problem is solved using seven control variables that are active power from all the sources. The power from the windfarm and PV array are modelled as a variable source, with a profile that varies from zero to its maximum for 24 hours. Each area feeds its own load: load 1 is supplied by power from the wind farm and SG1, and load 2 is fed by power from PV and SG2. For two interconnected networks, there always comes a time of energy exchange because of load variation on two sides and the impact of interconnection of energy sources that depend essentially on the weather. If power from the SG in either area 1 or 2 is insufficient and power from the windfarm and PV cannot meet the active power load demand, the power from the battery ESS can be used to feed the load and to keep the system balanced.
The estimation-control model applied in this study will help to estimate and control the energy flow from PV and wind sources, and the energy exchange between the two areas. The formulation of power system state estimation and generation of data can be found in the literature [28-31]. Estimation of energy (active power flowing) in the system is the first objective function. The optimal control approach is then applied by controlling active power flowing in the areas and power flow in the tie-lines as a second objective function and the maximisation of the use of renewable energy resources as a third objective function.
3.3.1 Estimation process
The EKF [26, 32-34] was chosen for the prediction of the tie-lines energy transfer and PV and wind energy flow output for the control purpose for 24 hours, considering the high nonlinearities characterising the power system and for control purpose that must be done in dynamic manner.
The power system can be defined using the discrete system given by Equation 8.
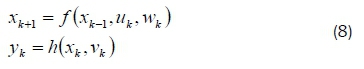
where Xk, uk, Wk, vk are state vector, input vector, vector of state noises and vector of measurement noises respectively. The function f is used to calculate the next state using the past estimated state. The function h is used to calculate the predicted measure using the predicted state. Using the Jaco-bian matrices (partial derivatives matrices), the co-variance matrix of errors is determined using Equation 9.

where Fkand Hkare partial derivatives matrices of the system.
The Jacobian matrix in Equation 9 is computed using the corrected and predicted states. These equations allow the system to be linearised around the estimated state values. Five steps were used to predict with the EKF [32-33]:
-
start process by updating equations
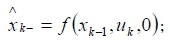
-
calculate the covariance matrix of the a priori
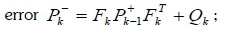
-
calculate the correction gain
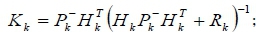
-
calculate the state vector a posteriori
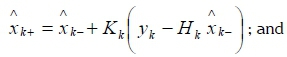
-
calculate the covariance matrix of a posteriori
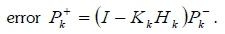
The 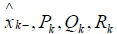 are a priori state estimate vector, a priori error covariance matrix, process noise covariance matrix and measurement noises covari-ance matrix respectively.
are a priori state estimate vector, a priori error covariance matrix, process noise covariance matrix and measurement noises covari-ance matrix respectively.
The first objective function is given by Equation 10.
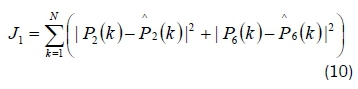
where 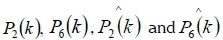 are the active power from PV and wind, and their estimated values respectively.
are the active power from PV and wind, and their estimated values respectively.
The second objective function is given by Equation 11.
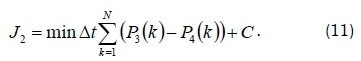
where At is the sampling time, P3 (k) and P4(k)are the power flow for tie-lines 1 and 2 respectively, and C = Bf x Δf is the frequency deviation constant, with Bf constant parameter depending to the frequency and Δf frequency variation.
The third objective function is given by Equation 12.

The problem is formulated as a multi-objective function given by Equation 13, considering the conflict of the three objective functions in the model.

3.2.2 Objective function
Considering Equations 6 and 9, the objective function can be expressed by Equation 14.
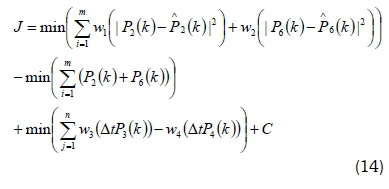
where wx, w2, w3, and W4are the weight factors.
This is subject to the equalities constraint given in Equation 15.
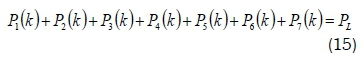
Equation 15 represents the power balance of the two microgrids, represented by Equation 16.

This is subject to the following inequalities constraint given in Equation 17.

Each energy source is constrained by minimum and maximum values as specified by Equation 17. The Pi (k) is the maximum power from each energy source during the normal network operation, expressed as Equation 18.
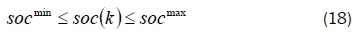
Equation 18 represents the boundary constraint of the BESS. The SOC value must be kept less than the full capacity of the BESS socmax and larger than its minimum capacity socmin as in Equation 19.

Equation 19 represents the power flow constraint for the safety of operations in the power network. The power flow from each area cannot be negative or less than its allowable maximum value, as presented by Equation 20.
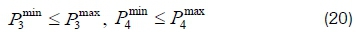
Equation 20 ensures that the tie-lines keep the net energy exchange out of the area at its schedule value, for the area to absorb its own load variations.
Equation 17 gives the power generation limits of P1(t), P2(t) , P5(t), P6(t) and P7(t) . Equation 18 represents the limit of the BESS.
The model has been applied using fmincon solver in Matlab because of the non-linearity of the power systems [28]. The canonical form is given by the basic conditions for the optimisation, as in Equation 21.
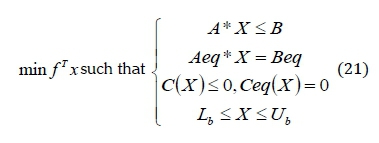
where f, X, B, Beq, C, Ceq, Lb, Ubare vectors; A , Aeq are matrices; Lb ≤ X ≤ Ub are lower and upper bounds; AX ≤ B is linear inequality constraint; AeqX = beq is linear equality constraint; C(X) ≤ 0 is nonlinear equality constraint; and Ceq(X) = 0 is a nonlinear equality constraint.
The vector X is a binary integer vector represented by the power flow from different components of the system.
The equality constraints given in Equation 12 can be converted into matrix form as in Equations 22 and 23.

The overall proposed estimation-control system is given in Figure 2. The main steps of the optimisation-control process are:
-
Input parameters for EKF process (active power under profile form, voltage measurements and angles generated for estimation process) [2831].
-
Start with estimation process.
-
Control and state variables definition.
-
Matrix A and vector B formulations (linear inequality constraint).
-
Determination of the linear equality constraint (matrix Aeq and vector Beq).
-
Formulation of lower and upper bounds vectors.
-
Formulation of the state of charge matrix (Aeql) and vector Beql.
-
Starting point choice.
-
Evaluations process: (1) Objective function; (2) Constraints.
-
Iterations and decision process.
-
End of process.
3.2.3 Battery storage system state of charge
The dynamic of the battery, charge and discharge gives its SOC. For the BESS in area 2 the SOC is given by Equation 24 [35]:
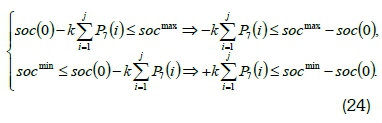
Using optimal control theory, Equation 22 can be translated into inequality constraints matrix for BESS as in Equation 25.

The linear vector constraint is represented by the vector in Equation 26.
4. Experimental analysis of the proposed model
System data: The main generator SG in each area has the following rating power: Pi(t) = 117MW and P5(t) = 126MW. Table 1 gives the variations on both during 24 hours because of power loss and other operating requirements. The rated frequency is 50Hz. The SG1 is a thermal power plant and SG2 is a large hydro. The characteristics of the windfarm and PV and a group of loads are given and used under profile form. The data for hydro-electric power plant and thermal plant (steam turbine) can found in the literature [27, 35-36]. The EKF and fmincon were implemented in Matlab 2016 in a H97M-D3H system with a processor: Intel(R) Core(TM) i5 CPU @ 3.30GHz,, 3301MHz, 4 Core(S), 4 Logical Processor(S) and a RAM of 8.00 GB.
5. Results and discussion
Three perturbations models (sudden increase of load demand) were introduced in microgrid 1 and microgrid 2 simultaneously and separately to observe the different deviations of active power in the tie-lines. Table 1 presents the optimal power flow of the system in MW, particularly the estimated and produced (or real values) active power form wind and PV systems: P2est and P2 for wind in area 1; P6est and P6 for PV in area 2. Energy transfer occurs when there is a disturbance in either area: from microgrid 1 to microgrid 2 at 12h00, 17h00, 18h00, 19h00, 20h00, 21h00, from microgrid 2 to microgrid 1 at 7h00, 13h00, 14h00, 16h00, and 17h00. The tielines, meanwhile, are solicited and stressed by the transfer of energy coming from the energy storage system to cover the power deficit.
Figure 3 represents the energy estimation simulations for wind 3(a) and for PV 3(b). Figure 4 gives in 4(a) and 4(b) the representation of load demand variation versus active power produced in areas 1 and 2 while the interconnected system goes under disturbance mode (regime). Active power from the windfarm can be produced during 24h daily and is dependent on the wind speed. This can be seen from Figure 3(a), which gives the variations of the active power production for 24 hours.
The production of active power using PV arrays is only possible from 6 am to 5 pm or 6 pm, whenever there is sunshine. The simulations results presented in Figure 3 (a) and (b) show the estimation of the wind and PV output during 24 hours. Based on the state estimation model using EKF, the predicted output values of wind and PV are well estimated except few errors. The estimation process was conducted with satisfactory results. One of the main goals of the proposed controller was to continuously supervise the interconnected system and the flow of energy from the windfarm and PV plant to the mi-crogrids and to do their estimations.
The energy storage system state of charge is given in Figure 5, which presents its dynamics for 24 hours (charge and discharging modes). Figures 6(a) and 6(b) present the active power deviation in tielines 1 and 2 with disturbance in areas 1 and 2. The active power variation in tie-lines 1 and 2 when mi-crogrid 2 (area 2) is perturbed is given in Figure 6(c) and 7(a). Figures 7(b) and 7(c) represent the active power variation in tie-lines 1 and 2 when microgrid 1 is disturbed.
Experimental observations: A classical perturbation system, for the first case, perturbation was introduced in area 1 and area 2. The objective was to test the robustness of the control strategy against a sudden active power demand variation (load) at the same time in both areas. Figure 6 (a) and 6 (b) indicates that, despite harsh conditions, the controller had a better performance. The active power control deviation was effectively damped to zero with small oscillations in a very short time: 3 s was enough to regulate the system.
Similar analyses (case 2 and case 3) were carried out using a disturbance model in area 1, Figures 6(c) and 7(a); and in area 2, Figures 7(b) and 7(c). Based on the three cases studied, the deviations of the active power in the tie-lines 1 and 2 are noted and controlled. For the case where both microgrids 1 and 2 are disturbed at the same time, the ripples showing the deviations in power in tie-line 1 goes to » -3.7MW and tie-line 2 goes to s» -5.1MW before starting stability process (Figure 6(a) and 6(b)). In the case where microgrid 1 is disturbed alone, the tie-lines 1 and 2 vary differently from 0s to 1s for tie-lines 1 and 2 from 2.5s to 3s (Figure 6(c) and 7(a)). When microgrid 2 is disturbed alone, the ripples showing the deviations of active power in tielines 1 and 2 are recorded between 0s and 1s (Figure 7(b) and 7(c)). The control process was performed in short time (3s for area 1 or microgrid 1 and 2s for area 2). The active power controller input in areas 1 and 2 was efficiently increased to match the load demand, without too much overshoots and oscillations. The active power deviation in tie-lines was driven to zero shortly after disturbance occurred, with less oscillations. The perturbed system was regulated after a short time.
6. Conclusion
This study has presented an energy flow estimation-control model of two interconnected microgrid systems, estimating the output power from wind and a photovoltaic array and minimising the difference in active power flow between two AC tie-lines. The robustness, reliability and nonlinearities associated with the control power system were ensured when solving the problem. The results graphically showed that the tie-lines power deviations due to the three disturbances introduced in areas 1 and 2 were controlled and limited. The response curves show the deviations in power system in the respective areas. It can be concluded from the analysis of these that the proposed optimal active power control regulator was effective in settling the change in the power system network to the required value in a reasonably short time. The controller model has led to the balance of the total active power generated and power demand of the studied system.
References
[1] Dubey, R., Joshi, D. and Bansal, R.C.2016. Optimization of solar photovoltaic plant and economic analysis. Electric Power Components and Systems, 44 (18), 2025-2035. [ Links ]
[2] Zobaa, A.F. and Bansal, R.C. (eds). 2011. Handbook of renewable energy technology. World Scientific Publishers, Singapore. [ Links ]
[3] Bansal, R.C. and Bhatti, T.S. 2008. Small signal analysis of isolated hybrid power systems: Reactive power and frequency control analysis. Alpha Science International, Oxford, U.K. [ Links ]
[4] Wan C., Song, Y., Xu, Z., Yang, G. and Nielsen, A.H. 2016. Probabilistic wind forecasting with hybrid artificial neural networks. Electrical Power Components and Systems, 44 (15), 1656-1668. [ Links ]
[5] Singh, R. and Banerjee, R. 2015. Estimation of rooftop photovoltaic potential of a city. Solar Energy, 115, 589-602. [ Links ]
[6] Cherif, H., and Belhadj, J. 2013. Energy estimation on large-scale time of stand-alone wind turbine. In Proc. of IEEE Electrical Engineering and Software Applications, Hammamet, Tunisia, 21-23 March, 2013: 1-6. [ Links ]
[7] Mabel, M.C. and Fernandez, E. 2009. Estimation of energy yield from wind farms using artificial neural networks. IEEE Transactions on Energy Conversion, 24 (2), 459-464. [ Links ]
[8] Xie, K., Zhou, J. and Li, W. 2009. Analytical model and algorithm for tracing active power flow based on extended incidence matrix. Electric Power System Research, 79, 399-405. [ Links ]
[9] Beltran, H., Perez, E., Aparicio, N. and Rodriguez, P. 2013. Daily solar energy estimation for minimising energy storage requirements in PV power plants. IEEE Transactions on Sustainable Energy, 4 (2), 474-481. [ Links ]
[10] Ayodele, T.R., Jimoh, A.A., Munda, J.L. and Agee, J.T., 2012. Wind distribution and capacity factor estimation for wind turbines in coastal region of South Africa. Energy Conversion and Management, 64, 614-625. [ Links ]
[11] Foley, A.M., Leahy, P.G., Marvuglia, A. and Mckeogh, E.J. 2012. Currents methods and advances in forecasting of wind power generation. Renewable Energy, 37, 1-8. [ Links ]
[12] Monteiro, R.V.A., Guimaraes, G.C., Moura, F.A.M., Albertini, M.R.M.C. and Albertini, M.K. 2017. Estimating photovoltaic power generation: performance analysis of artificial neural networks, support vector machine and Kalman filter. Electric Power Systems Research, 143, 643-656. [ Links ]
[13] Chanda, S., Shariatzadeh, F., Srivastava, A., Lee, E., Stone, W. and Ham, J. 2015. Implementation of non-intrusive energy saving estimation for Volt/Var control of smart distribution system. Electric Power Systems Research, 120, 39-46. [ Links ]
[14] Lydia, M., Kumar, S.S., Selvakumar, A.I. and Kumar, G.E.P. 2015. Wind resource estimation using wind speed and power curve models. Renewable Energy, 83, 425-434. [ Links ]
[15] Saxena, N. and Ganuli, S. 2015. Solar and wind power estimation and economic load dispatch using firefly algorithm. Procedia Computer Sciences, 70, 699-700. [ Links ]
[16] Hoseinzadeh, B., Da Silva, F.F. and Bak, C.L. 2015. Active power deficit estimation in presence of renewable energy sources. In Proc. IEEE Power and Energy Society General Meeting, Denver, Colorado, 26-30 July, 2015: 1-5. [ Links ]
[17] Beltran, H., Perez, E., Aparicio, N. and Rodriguez, P. 2013. Daily solar energy estimation for minimising energy storage requirements in PV power plants. IEEE Trans. Sustainable Energy, 4 (2), 474481. [ Links ]
[18] Marin, M.R., Sumper, A., Robles, A.V. and Jane, J.B. 2014. Active power estimation of photovoltaic generators for distribution network planning based on correlation models. Energy, 64, 758-770. [ Links ]
[19] Song, D., Yang, J., Cai, Z., Dong, M., Su, M. and Wang, Y. 2017. Wind estimation with a non-standard extended Kalman filter and its application on maximum power extraction for variable speed wind turbines. Applied Energy, 190, 670-685. [ Links ]
[20] Wang, S., Fernandez, C., Shang, L., Li, Z. and Li, J. 2017. On-line state of charge estimation for aerial lithium-ion battery packs based on the improved extended Kalman filter method. Journal of Energy Storage, 9, 69-83. [ Links ]
[21] Sepasi, S., Ghorbani, R. and Liaw, B.Y. 2014. Improved extended Kalman filter for state of charge estimation of battery pack. Journal of Power Sources, 255, 368-376. [ Links ]
[22] Li, Y., Wang, C. and Gong, J. 2016. A Combination Kalman filter approach for state of charge estimation of lithium ion battery considering model uncertainty. Energy, 109, 933-946. [ Links ]
[23] Han, J., Kim, D. and Sunwoo, M. 2009. State of charge estimation of lead acid batteries using an adaptive extended Kalman filter. Journal of Power Sources, 188, 606-612. [ Links ]
[24] Mastali, M., Arenas, J.V., Fraser, R., Fowler, M., Afshar, S. and Stevens, M. .2013. Battery state of the charge estimation using Kalman faltering. Journal of Power Sources, 239, 294-307. [ Links ]
[25] Zhang, W., Shi, W. and Ma, Z. 2015. Adaptive un-scented Kalman filter based state of energy and power capability estimation approach for lithiumion battery. Journal of Power Sources, 289, 50-62. [ Links ]
[26] Long, X., Junping, W. and Quanshi, C. 2012. Kalman filtering state of charge estimation for battery management system based on a stochastic fuzzy neural network battery model. Energy Conversion Management, 53, 33-39. [ Links ]
[27] Tungadio, D.H., Bansal, R.C. and Siti, M.W. 2017. Optimal control of active power of two microgrids interconnected with two ac tie-lines. Electric Power Components and Systems, 45(19), 2188-2199. [ Links ]
[28] Tungadio, D.H., Numbi, B.P., Siti, M.W. and Jimoh, A.A. 2015. Particle swarm optimization for power system state estimation. Neurocomputing, 148, 175-180. [ Links ]
[29] Tungadio, D.H., Jordaan, J.A. and Siti, M.W. 2016). Power system state estimation solution using modified models of PSO algorithm: Comparative study. Measurement, 92, 508-523. [ Links ]
[30] Exposito, A.G., Quiles, C.G. and Dzafic, I. 2015. State estimation in two time scales for smart distribution systems. IEEE Transactions on Smart Grid, 6 (1), 421-430. [ Links ]
[31] Tungadio, D.H., Numbi, B.P., Siti, M.W. and Jordaan J.A. 2013. Weighted least squares and itera-tively reweighted least squares comparison using particle swarm optimization algorithm in solving power system state estimation. In Proc. IEEE Afri-con, Point-aux-Piments, Mauritius, 9-12 September, 2013: 1264-1269. [ Links ]
[32] Tebianian, H. and Jeyasurya, B. 2015. Dynamic state estimation in power systems: Modelling, and challenges. Electric Power System Research, 121, 109-114. [ Links ]
[33] Cao Z., Lu J., Zhang R. and Gao F. 2016. Iterative learning Kalman filter for repetitive processes. Journal of Process Control, 46, 92-104. [ Links ]
[34] Beides, H.M. and Heydt, G.T. 2017. A robust iterated extended Kalman filter for power system dynamic state estimation. IEEE Transactions on Power Systems, 32 (4), 3205-3216. [ Links ]
[35] Tungadio, D.H. and Bansal, R.C. 2017. Active power reserve estimation of two interconnected mi-crogrids. Energy Procedia, 105, 3909-3914. [ Links ]
[36] Tungadio, D.H., Bansal, R.C, Siti, M.W., and Mbungu, N.T. 2018. Predictive active power control of two interconnected microgrids. Technol Econ Smart Grids Sustain Energy, 3 (3), 1-15 [ Links ]
* Corresponding author: +971 65050909: email: rcbansal@ieee.org














