Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
Journal of Energy in Southern Africa
On-line version ISSN 2413-3051
Print version ISSN 1021-447X
J. energy South. Afr. vol.27 n.2 Cape Town Mar./May. 2016
Incorporating a three dimensional photovoltaic structure for optimum solar power generation - the effect of height
Olufunmilayo Alice Mafimidiwo; Akshay Kumar Saha*
School of Electrical, Electronic and Computer Engineering, University of KwaZulu-Natal, Durban
ABSTRACT
In a renewable energy system, incorporating three-dimensional technology in solar power generation takes advantage of the three-dimensional nature of the biosphere so that energy collection occurs in a volume, contrary to what is commonly obtained in planar or flat photovoltaic panel. Three-dimensional photovoltaic technologies are capable of generating more power from the same base area when compared to the conventional flat solar panels. This investigation examines methodologies for computation and analyses the effect of height per unit volume compared with a plain surface arrangement. The results show remarkable increase in the energy generated by the three-dimensional photovoltaic structure over the two-dimensional planar structures.
Keywords: Three-dimensional technology, solar energy, height per unit volume, power output
1. Introduction
Solar power is a major energy source, capable of making a substantial contribution to fulfilling the world's future energy requirements. According to literature, the average cost of commercial photovoltaic (PV) modules stands at an average of about USD 1.89-2.50 /Wp (Sahay et al., 2013; Candelise et al., 2013, May 2012; Bernardi et al., 2012; Gaudiana, 2010). A photovoltaic system is a method of converting solar energy or irradiation directly into useful energy with the use of an electronic device called a semiconductor (Usama et al., 2012). At present, PV energy costs less than 1% of what it used to be in the past. In spite of a substantial decline in PV system costs, however, the levelised cost of electricity (LCOE) of PV remains high. As at 2011, the LCOE for residential systems without storage and with assumption of a 10% cost of capital was in the range USD 0.25-0.65 /kWh. With the addition of electricity storage added, the cost range increases to USD 0.36-0.71/kWh. In 2011, for thin-film systems, the LCOE of current utility-scale was estimated to be between USD 0.26 and USD 0.59/kWh. The cost for the crystalline solar PV system is higher (Candelise et al., 2013). For the PV solar energy conversion technology to be affordable and for building-integrated photovoltaics (BiPV) technology to become economically attractive for building applications, this cost can be brought down to at most USD 1/Wp (Shaari, 1998). This can only be made possible if the appropriate solar energy conversion technology were employed (Suto and Yachi, 2011) and a solar incentive programme and net metering were implemented (United States Department of Energy [DoE], 2008). Different types of solar cells are available for use for energy conversion technology. However, crystalline silicon (Si) dominates around 90% of the current PV market (Ismail et al., 2013).
Convectional PV modules have relatively low energy density and this is worsened by the fact that the output of the devices is dependent on the latitude of the installation and the weather conditions of the location; besides, the peak insolation hours available in most locations is limited (Bernardi, 2012; Aglietti et al., 2008), In achieving the energy conversion target, the use of low-cost base material, optimal device design and affordable device processing technology are vital (Gharghi et al., 2006b). Conventionally, for low-scale solar energy generation, flat PV panels are installed in residential and commercial rooftop installations. In cases where the rooftop is not adequate for use or the plants are too large for roof-mounting, solar modules can also be placed on the ground, either as a fixed mount or a tracking mount that follows the sun to orient the PV modules. Other options include mounting as structures that create covered parking or provide shade as window awnings. This is often used in multifamily or commercial applications (DoE, 2008). There is the need for establishing improved technology in order to optimise power generation per installation area. For more effective use of the sunlight energy, the number of hours the solar cells are in trajectory with the sun for peak power generation can be lengthened by incorporating sun-trackers (Mousazadeh et al., 2009; Moradi & Reisi, 2011), although the tracking has the disadvantage of introducing additional costs. It also requires larger space for operation thereby causing interference with other panels and possible shading and is also subject to occasional maintenance and disruptions. Furthermore, it is not suitable for residential or commercial installations due to its bulky moving parts (Yahyavi et al., 2010; Mafimidiwo & Saha, 2014). However, it is still being used for the fact that its price has reduced considerably (Philipps et al., 2015). A tracking system can be more cost efficient if the cost of its tracker is less than total costs of that system by a factor of (Tc - 1)/Tc where Tcis the tracking factor, which tends to unity as it improves the output power generated and this varies from location to location (Yahyavi et al., 2010). In addition to this, it can generate more energy with fewer solar panels, lower electrical device ratings and a smaller structure on about the same land area (Yahyavi et al., 2010; Philipps et al., 2015). Nevertheless, there is a need for improved technology for solar energy optimisation.
2. Three-dimensional photovoltaic structure
Three-dimensional photovoltaic (3DPV) technology is a new technology in PV energy generation that mimics the pattern found in nature of structures that collect sunlight in three dimensions (Suto & Yachi, 2011; Gharghi et al., 2006b; Yuji & Yachi, 2010). Three main physical reasons underlying the advantages of collecting light in 3D are the multiple orientations of the absorbers that allow for the effective capturing of off-peak sunlight, the avoidance of inter-cell shading, and the re-absorption of light reflected within the 3D structure (Suto & Yachi, 2011; Yahyavi et al., 2010; Bernardi et al., 2012).
These benefits enable the measured generated energy densities (energy per base area) to be higher by a factor of 2-20 than the stationary flat PV panels. The 3DPV is a new approach for achieving optimum solar energy that will yield a cost-effective, more reliable and most economically friendly alternative energy source (Aglietti et al., 2009; Bernardi et al., 2012q; Yuji & Yachi, 2010).
The 3DPV technology utilises the 3D nature of the dimensional structures such as the spherical or cubic system to absorb power in the entire volume of that material. Hence, power is measured in Watts per unit volume as against per area measurement as in the planar or two-dimensional system. Furthermore, the impact of height in system efficiency for the 3DPV is remarkable (Aglietti et al., 2009; Yahyavi et al., 2010; Yuji & Yachi, 2010). Some of the research carried out on this technology is briefly discussed in this paper.
2.1 Solar energy generation in three dimensions
According to the Massachusetts Institute of Technology (Myers et al., 2010), it has been established that 3DPV structures can increase the generated energy density in a linear proportion to the structure height, for a given day and location. The optimum shape of the 3D structures was derived using computer simulations such as genetic algorithms for optimising the generated output energy. These 3D structures include a cubic box open at the top, a funnel-shaped cubic box, a sphere, a parallelepiped, or any other 3D shape that in principle is found capable of doubling the daily energy density. The 3DPV structures were found to lessen some of the variability inherent in solar PV as they provide a more regular source of solar energy generation at all latitudes. They are found capable of doubling the number of peak power generation hours as they intensely reduce the seasonal, latitude and weather variations of solar energy generation when compared to a flat panel design (Bernardi et al., 2012; Yahyavi et al., 2010; Myers et al., 2010).
2.2 The 3DPV module assembly by Fibonacci number
The 3DPV technology by Fibonacci number method involves the arrangement of the individual solar cells of the three-dimensional PV module in a leaf-like manner. The arrangement revealed that such a modular design has the benefits of having each solar cell receive the reflected light from the other cells, thereby maximising power generation per installation area (Myers et al., 2010) It also enables solar cells to be stacked in a vertical configuration, which enhances the doubling of daily energy density (Yuji & Yachi, 2010; Yahyavi et al., 2010).
2.3 Fibonacci number composition for output power characteristics of a 3DPV module
Another research group carried out a test on a 3DPV module whose configuration was based on Fibonacci numbers (Suzumoto et al., 2012; Yuji & Yachi, 2010; Suto & Yachi, 2011). The simulation results revealed that the power generation characteristics of the solar cells depend on the shape and spacing of the solar cells for the most effective use of sunlight energy.
2.4 Spherical silicon solar technology
Accurate 3D technology was found to enable innovative and improved device design, which can result in overall cost effectiveness, improved material processing and system utilisation (Gharghi et al., 2006b, Szlufcik et al., 1997). Of particular interest is the spherical silicon solar technology, which was found to be attractive, ideal and quite inexpensive. It utilises low-cost silicon feedstock for its fabrication process, which is found to be simple and inexpensive (Gharghi et al., 2006a). In addition, self-supporting 3D shapes are discovered to create new schemes for PV installation and increase energy density that can facilitate the use of inexpensive thin film materials in area-limited applications. Hence, harnessing solar energy in three dimensions can open new avenues towards Terawatt-scale generation (Bernardi et al., 2012).
2.5 3D nanopillar-based cell modules
In recent years, much progress has been made in developing PV that can potentially be mass deployed (Fan et al., 2009). An example is 3D nanopillar-based cell modules which were used for the purpose of reducing solar cell cost by utilising novel device structures and materials processing to yield acceptable efficiencies. In this regard, the highly regular, single-crystalline nanopillar arrays of optically active semiconductors are directly grown on aluminium substrates, which are configured as solar modules. An example is the CdTe/CdS PV structure that incorporates 3D, single-crystalline nCdS nanopillars, which is embedded in polycrystalline thin films of p-CdTe, to enable high absorption of light and efficient collection of the carriers. The cadmium sulphide cell (CdS) and cadmium telluride cell (CdTe) are chemically different semiconductors with different bandgaps and doping or conductivity type. They form a good pair CdTe/CdS as one of the topmost successful heterojunction for PV applications to overcome the problem of poor junction formation. The prefix n or p attached to each semiconductor indicates the type of doping that is given to it, or it indicates its conductivity type (Green, 2015). Various experiments and modelling exercises proved the potency arising from the geometric configuration of this approach to enable enhanced carrier collection efficiency on both rigid and flexible substrates of the highly versatile nanopillars solar modules (Fan et al., 2009).
3. Effect of height in the Fibonacci method of 3DPV generation
The Fibonacci method of PV module (FPM) installation utilises numbers to attain the height spacing for volumetric adsorption of solar irradiation to optimise solar power generation in an area (Suto and Yachi, 2011, Yuji and Yachi, 2010, Seiji Suzumoto1, 2012). The manifestations of the Fibonacci numbers and the golden ratio are apparently endless and can be found throughout nature in the form and designs of many plants and animals (Grigas, 2013; Koshy, 2011). The Fibonacci sequence can be perceived in nature in the spirals of a sunflower's seeds and the shape of a snail's shell (Grigas, 2013). These numbers have also long been used in various manners in architecture, art and music as well as medicine, science and engineering. In particular, the numbers are widely used in engineering applications including computer data structures and sorting algorithms, financial engineering, audio compression, architectural engineering and solar energy application (Zou et al., 2004; Belegundu & Chandrupatla, 2011; Stakhov, 2005; Koshy, 2011). The numbers highlight the order and mathematical complexity of the natural world (Grigas, 2013). They are present in the leaf or petal arrangement of most plants as shown in Figure 1, frequently in order to maximise the amount of light received on the space allotted for each leaf or petal on the plant (Mafimidiwo & Saha, 2014; Gharghi et al., 2006b; Yuji & Yachi, 2010).
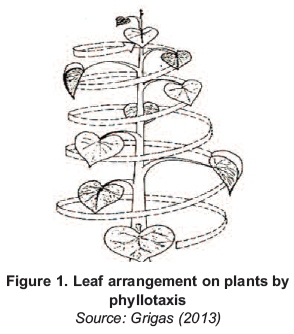
In a similar fashion, a mass of silicon with an expanded surface can absorb the solar radiation in layers of its crystallised molecules (Grigas, 2013). Conversely, the leaves are not usually arranged on a flat surface, but spread through the whole volume of a plant. This is analogous to the reason why trees tend to grow vertically - to access most of the solar rays in a given volume. Solar panels can be arranged in a similar fashion and the solar energy considered in terms of Watt-hours per unit volume. To install PV panels on a tall structure is, however more time-consuming and costly than laying them on the ground (Yahyavi et al., 2010). However, depending on the price of land, arranging the solar equipment on a raised structure could be more cost-effective. Another advantage of a vertical arrangement is the possibility of rotating Fibonacci solar panels in order to track the sun for a higher efficiency (Aglietti et al., 2009; Suto & Yachi, 2011: Gharghi et al., 2006b).
Although 3DPV solar power installations are not common, one such installation, using a FPM approach, exists in Ontario, Canada as shown in Figure 2. The solar-powered tree of about 0.5 kW is installed at Tourism London, Wellington Rd, Ontario Canada and it is funded by the Ontario Power Authority (City of London, 2014). It is 7 m tall and has 27 leaves, each producing power.

4. 3DPV structure effect on solar radiation intensity
The generated solar energy density is a function of the solar intensity called irradiance, which is measured in W/m2 (Boyd, 2013). Many parameters determine the intensity of solar radiation, including latitude, season, altitude, geographical conditions, atmospheric pressure, humidity, time of day, and some other extra-terrestrial effects such as solar storms. On a clear day, the intensity of solar radiation is at its maximum around noon and decreases towards dusk (Bernardi et al., 2012). However, the 3DPV structure was found to nearly double the number of peak hours available for solar energy generation and provide a measured increase in the energy density by a factor of about 2-20 without the use of sun-tracking in cloudy weather (Myers et al., 2010). The structure is also found to be able to reduce the large variability in solar energy generation with latitude and season, contrary to what is obtained in the case of planar solar configuration (Suto & Yachi, 2011; Yahyavi et al., 2010; Yuji & Yachi, 2010; Grigas, 2013). The solar radiation received on the surface of the material is proportional to the power absorbed in the entire volume of the 3DPV structure.
4.1 Energy per unit volume
Generally, some level of physical mass is required for energy of any sort to be absorbed and this energy is found to be proportional to the volume and density of that material (Suto & Yachi, 2011; Yahyavi et al., 2010; Bernardi et al., 2012).
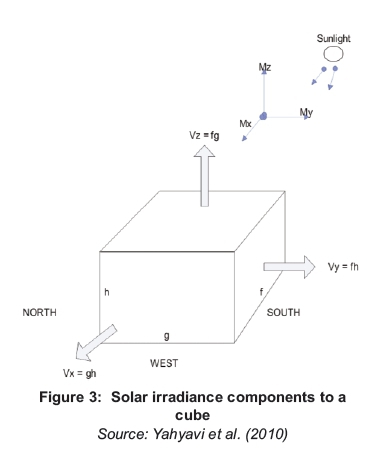
Mathematically, the material surface is two-dimensional, while the physical objects are three-dimensional (Yahyavi et al., 2010). It is proper to consider energy in the volume, as well as energy on the surface, in the context of solar energy (Yuji & Yachi, 2010). For energy per unit volume consideration, it is assumed that some solar collectors are effectively arranged within any three dimensional structure such as a cube with arbitrary dimensions f, g, h facing northerly with the x, y, z-axes (Myers et al., 2010). Hence, the cube volume, V, is also considered as a vector V with three assigned components, as in Equation 1:

These components are assumed to be proportional to the cube's three faces on which the solar beams radiate on the top, front and east or west at any given time.
The solar irradiance is considered a vector with variable components proportional to the absolute values of x, y, z components. Hence, solar power, P, going into the cube as indicated earlier can be extended and interpreted as the scalar product of the volume and irradiance vectors.
5. Methodology
In order to analyse the energy absorbed by the cube, this investigation considered the cube volume and the vector components of the surfaces as shown in Figure 3, with dimensions f, g, h standing northwest with the x, y, z - axes. As stated in section 4, the cube volume, V, was considered a vector V, with three components as given in Equation 1. These components of the volume vector were exposed to the solar beam radiation. It was also considered that the solar irradiance is also a vector, with variable components proportional to the absolute values of x, y, z given by Equation 1. The implication of this would be that the solar power going into the cube of a solar tree can be expressed as a scalar product.
Hence,

where:
Px = ghl [Cos(β)(θ)]
Py = fhl[Sin(α)Sin(β)Cos(θ) - Cos(α)Sin(θ)],
and Pz is given by Equation 3
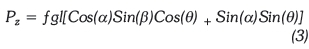
Total power is the vectorial sum of the components as shown by Equation 4:
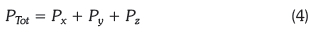
The value of irradiance and the angles β and θ are functions of time as described by (Kenny et al., 2006, Yahyavi et al., 2010). The module of irradiance M, which is defined as the average irradiance in any location at a certain latitude α, is introduced in Equation 5. For the purpose of computation, the M value applied here is taken as 62% for location latitude of -29.8833 (South).
Then,
Avg[Cos(β)Cos(θ)] = Avg[Sin(β)Cos(θ) = 0.62
Avg[Sin(β)] = 0 and f, g, h = 1
The module of irradiance for Durban is assumed here as 0.62 for the month of January and it is utilised here as a parameter of average irradiance at the latitude (α) -29.8833 (South). This is specified by the three components, including Equation 5.
Mx = 0.621
My = 0.621Sin(α)
Mz = 0.621Cos(α)
and
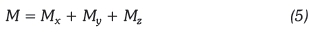
The average value of available solar power obtained within the volume is the scalar product of volume vector V and module of irradiance, M as indicated in Equation 6:

Hence, Equation 7 with its associated components and Equation 8 are derived.
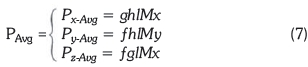
and
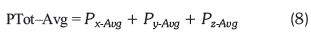
Dimensions f, g, h in these equations are the effective dimensions where 100% of the solar energy is absorbed. However, real dimensions of the occupied space are 'n' times larger; and n relates to the efficiency η of the collectors. The efficiency of the PV panels is assumed to be 16%, therefore, n is 2.5 in this case. This was found useful in the optimisation computations carried out on these two different solar panels installation configurations.
A solar power system can be more efficient depending on how it collects solar energy. In order to determine the solar irradiance in volume, it was assumed the solar panel was effectively arranged within a cube as shown in Figure 4. From Equation 4, more energy could enter a volume as compared with entering through a surface such that:

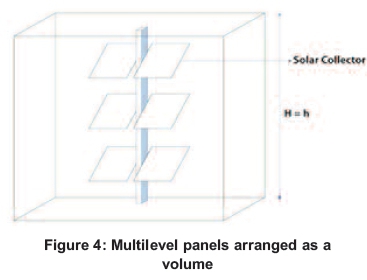
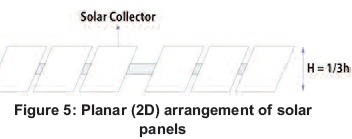
The main concept of measuring energy per unit volume is that solar collectors get more irradiance when elevated from the horizontal position as shown in Figure 5 to the vertical position as shown in Figure 4.
The solar cell efficiency depends on the collectivity factor c, defined as the ratio of the collected solar energy to the maximum solar energy available in an effective volume occupied by the solar system installed in an area and at a certain height. The amount of solar energy generated is a function of the collectivity factor and this was found to be in direct proportion with height.
5.1 Computation of solar energy in 3D and 2D
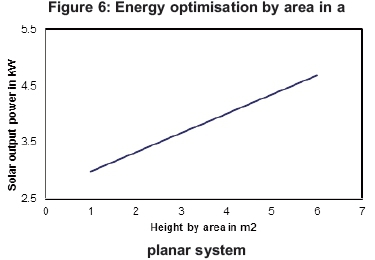
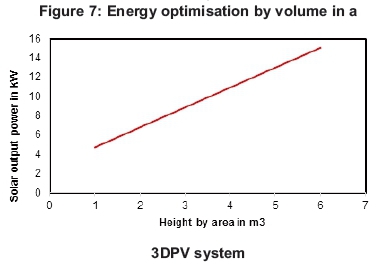
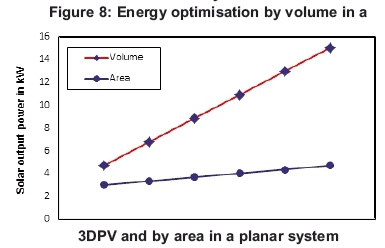
In this investigation, computation of solar energy in 2D and 3D was made with comparison between the results obtained on the power (Watts) generated with the tree-level arrangement (3D) in Figure 4 and power (Watts) generated by its equivalent coplaner arrangement (2D) in Figure 5 and the data was made using Matlab program, version R2012b. Analysis of results is presented according to Figures 6, 7 and 8.
5.2 The 3D configuration of the solar panel
In order to estimate the effect of height, the solar panel was configured in 3D and a 10 kW solar array was assumed for the multilevel fixed structure as shown in Figure 4. The effective volume dimensions occupied by the tree-level system were assumed to be f = 3.5; g = 2.5; and h = 3 m. The index of the real dimensions of the occupied space by the PV panel n was assumed to be 2.5, the assumed irradiation I, was 678 W/m2 for the solar panels installed at a tilted angle of towards South.
From Equation 5, the modules of irradiance of the solar radiation for the 3D and 2D structures were determined for this location and expressed as Equation 10:
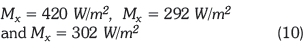
These values were used for modules of irradiance in the Matlab computations as in Equation 11 and associated components.

5.3 The 2D configuration of the solar panel
It was assumed that the elevation, for the 2D arrangement is one-third of the height h, for the 3D structure. In the 2D arrangement, not all the sides were present (as shown in Figure 5), hence only the front and the pop would receive the solar radiation. Consequently, for the 2D arrangement the average total power in Watts was estimated as according to Equation 12:
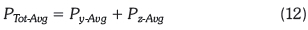
where:
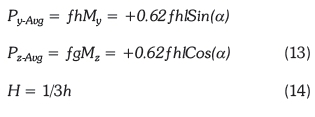
6. Results and discussion
The variables derived for the solar power in equations 4, 7 and 11 were used to determine generated powers for the 2D and 3D solar structures for height variation of 1 to 6 m. The values are presented in Table 1. The linear appearance of results in Figures 6-7, obtained in 2D and 3D cases was caused by the effects of other factors such as weather, while seasonal variations such as cloud and rain and temperature were not considered, for simplification.
Table 1 shows that, at the height of 1 m, the 2D and 3D solar structures generated output power of 2.983 kW and 4.714 kW respectively, corroborated by Figures 6 and 7, while at the height of 6 m, the 2D and 3D generated output power of 4.686 kW and 15.08 kW respectively, as supported by Figure 8. The percentage increase in the output power between the 2D and 3D solar structures was from 37% to 69% from the minimum height of 1 m to the maximum height of 6 m, respectively. Consequently, power generation in 3D installation got improved with increasing height.
The existence of a linear relationship between solar generated energy and the generated output power substantiated an increase in solar energy generated with increasing height. A solar farm with multiple trees may, however, give different results because of the shading effect from adjacent trees hindering the absorption of the reflected rays by the PV cells, causing a reduction in the generated output power. In order to avoid excessive partial shading of the elements, the solar trees would need to be installed with a relatively large spacing. A new set of equations would therefore be required to accommodate these changes (Sampatakos, 2014).
7. Conclusions
In this investigation, the effects of height on solar generated energy and power were analysed and discussed. All other variable parameters, such as weather conditions and time of the day, were not considered. The concept of energy-per-unit volume for solar energy for solar installation with consideration for height was corroborated by the results. The Module of Irradiance was found to be a simple and useful tool for establishing the per-unit component for the top, front, and the side surfaces of the irradiance into a unit volume. There was an enhanced power output with the use of the Module of Irradiance. The relationship between generated power by volume for the 3DPV system and the generated power by area for the planar system was found to be linear. The power generated by the 3DPV structure over the planar structure increased by 16%. Consequently, the introduction of height to solar power installation increases the performance of the solar device. However, in situations where more than one tree is used, different results might be obtained because of the tendency to experience uneven illumination of solar panels caused by overlapping shades of solar cells. This is a different possible scenario outside this study.
References
Aglietti, G. S., Redi, S., Tatnall, A. R. and Markvart, T., 2008. High altitude electrical power generation. WSEAS Transactions on Environment and Development 4:1067-1077. [ Links ]
Aglietti, G. S., Redi, S., Tatnall, A. R. and Markvart, T. 2009. Harnessing high-altitude solar power. IEEE Transactions on Energy Conversion, , 24(2):442-451. [ Links ]
Belegundu, A. D., Chandrupatla, T. R. 2011. Optimization concepts and applications in engineering. Cambridge: Cambridge University Press. [ Links ]
Bernardi, M., Ferralis, N., Wan, J. H., Villalon, R. and Grossman, J. C., 2012. Solar energy generation in three dimensions. Energy and EnvironmentalSscience 5(5):6880-6884. [ Links ]
Boyd, M. 2013. Analytical model for solar irradiance near a planar vertical diffuse reflector: Formulation, validation, and simulations. Solar Energy 91:79-92. [ Links ]
Candelise, C., Winskel, M. and Gross, R.J., 2013. The dynamics of solar PV costs and prices as a challenge for technology forecasting. Renewable and Sustainable Energy Reviews 26: 96-107. [ Links ]
City of London. 2014. Corporate energy conservation and demand management (CDM) Plan. Available: http://www.london.ca/residents/Environment/Energy/Documents/2014%20CDM%20Plan%20final.pdf [19 April 2016]. [ Links ]
Fan, Z., Razavi, H., Do, J.-W., Moriwaki, A., Ergen, O., Chueh, Y.-L., Leu, P W., Ho, J. C., Takahashi, T., Reichertz, L. A., Neale, S., Yu, K., Wu, M., Ager, J. W. and Javey, A. 2009. Three-dimensional nanopillar-array photovoltaics on low-cost and flexible substrates. Nature Materials 8:648-653. [ Links ]
Gharghi, M., Bai, H., Stevens, G. & Sivoththaman, S. 2006. Three-dimensional modeling and simulation of pn junction spherical silicon solar cells. IEEE Transactions on Electron Devices, 53(6) :1355-1363. [ Links ]
Green, M. A. and Archer, D. A., 2015. Clean electricity from photovoltaics. London: Imperial College Press. [ Links ]
Grigas, A., 2013. The Fibonacci Sequence: Its history, significance, and manifestations in nature. Senior Honours thesis, Liberty University, Virginia, USA. [ Links ]
Ismail, H., Mathew, S., Aloka, S., Narayanaswamy, B., Ming, L.C. and Hussain, S.A., 2013. Comparative performance of grid integrated solar photovoltaic systems under the tropical environment. In Innovative Smart Grid Technologies-Asia (ISGT Asia), 2013 IEEE:1-6. [ Links ]
Kenny, R. P, Huld, T. A. and Iglesias, S. 2006. Energy rating of PV modules based on PVGIS irradiance and temperature database. Proceedings of 21st European Photovoltaic Solar Energy Conference and Exhibition, 2006:4-8. [ Links ]
Koshy, T., 2011. Fibonacci and Lucas numbers with applications, John Wiley & Sons. [ Links ]
Mafimidiwo, O. A. and Saha, A. K. 2014. Improving solar energy generation through the use of three dimensional photovoltaics technology. Proceedings of the Southern African Universities Power Engineering Conference. University of KwaZulu-Natal, Howard Campus, Durban South Africa: 294-300. [ Links ]
Moradi, M. H. and Reisi, A. R. 2011. A hybrid maximum power point tracking method for photovoltaic systems. Solar Energy, 85(11):2965-2976. [ Links ]
Mousazadeh, H., Keyhani, A., Javadi, A., Mobli, H., Abrinia, K. and Sharifi, A., 2009. A review of principle and sun-tracking methods for maximizing solar systems output. Renewable and sustainable energy reviews 13(8):1800-1818. [ Links ]
Myers, B., Bernardi, M. and Grossman, J. C., 2010. Three-dimensional photovoltaics. Applied Physics Letters, 96(7):071902. [ Links ]
Philipps, S., Bett, A., Horowitz, K. and Kurtz, S. 2015. Current status of concentrator photovoltaic (CPV) technology. National Renewable Energy Laboratory, Golden, Colorado, USA. [ Links ]
Russell, G. 2010. Third-generation photovoltaic technology - The potential for low-cost solar energy conversion. Letter to Journal of physical chemistry 2010(1):1288-1289. [ Links ]
Sahay, A., Sethi, V. and Tiwari, A., 2013. A comparative study of attributes of thin film and crystalline photovoltaic cells. International Journal of Mechanical, Civil, Automobile and Production Engineering 3(7):267-270. [ Links ]
Sampatakos, D. 2014. Development of three dimensional PV structures as shading devices for a decentralized facade unit of the future. TU Delft, Delft University of Technology. [ Links ]
Suzumoto, S., Tayo, L. and Yachi, T., 2012. Output power characteristics of a three-dimensional photovoltaic module using fibonacci number composition. In IEEE 34th International Telecommunications Energy Conference:1-7. [ Links ]
Shaari, S. 1998. Photovoltaics in the built environment: an application for Malaysia. Dissertation for De Montfort University, Leicester. Available: https://www.dora.dmu.ac.uk/handle/2086/4157. [ Links ]
Stakhov, A. 2005. The generalized principle of the golden section and its applications in mathematics, science, and engineering. Chaos, Solitons & Fractals 26:263-289. [ Links ]
Suto, T., Yachi, T. 2011. Power-generation characteristics of an FPM by simulation with shadow-effect analysis. 37th IEEE Photovoltaic Specialists Conference, 19-24 June 2011. [ Links ]
Szlufcik, J., Sivoththaman, S., Nlis, J., Mertens, R. P. and Van Overstraeten, R. 1997. Low-cost industrial technologies of crystalline silicon solar cells. Proceedings of the IEEE 85:711-730. [ Links ]
United States Department of Energy. 2008. Energy efficiency and renewable energy. Available: www.fueleconomy.gov/feg/byfueltype.htm. [ Links ]
Usama, S. M., Arif, A. F. M., Kelley, L. and Dubowsky, S. 2012. Three-dimensional thermal modeling of a photovoltaic module under varying conditions. Solar energy 86: 2620-2631. [ Links ]
Yahyavi, M., Vaziri, M. and Vadhva, S. Solar energy in a volume and efficiency in solar power generation. In IEEE International Conference on Information Reuse and Integration:394-399. [ Links ]
Yahyavi, M., Vaziri, M. and Vadhva, S., 2010. Solar energy in a volume and efficiency in solar power generation. Available: http://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=5558900. [ Links ]
Yuji, A. and Yachi, T. 2010. A novel photovoltaic module assembled three-dimensional. 35th IEEE Photovoltaic Specialists Conference, 20-25 June 2010. [ Links ]
Zou, J., Ward, R. K. and Qi, D. 2004. A new digital image scrambling method based on Fibonacci numbers. Proceedings of the 2004 International Symposium on Circuits and Systems (Vol. 3). DOI: 10.1109/ISCAS.2004.1328909 [ Links ]
* Corresponding author. Tel: (+27) 031-260-2725; Email: saha@ukzn.ac.za














