Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
Journal of Energy in Southern Africa
On-line version ISSN 2413-3051
Print version ISSN 1021-447X
J. energy South. Afr. vol.27 n.1 Cape Town Feb. 2016
RESEARCH ARTICLES
Performance analysis of thermosyphon hybrid photovoltaic thermal collector
N. Marc-Alain Mutombo; Freddie Inambao*; Glen Bright
Discipline of Mechanical Engineering, University of KwaZulu-Natal, South Africa
ABSTRACT
The conversion of solar irradiance into electricity by a photovoltaic module (PV) is 6-17% of the incoming energy from the sun depending on the type of technology and the environmental parameters. More than 80% of incoming energy from the sun is reflected or absorbed by the solar module. The fraction of energy absorbed increases with solar cell temperature and the cells' efficiency drops as a consequence. The efficiency of a PV module is improved by combining a PV module and a thermal collector in one unit, resulting in a hybrid photovoltaic and thermal collector (PV/T). The purpose of this paper is to present the behavior a ther-mosyphon hybrid PV/T when exposed to variations of environmental parameters and to demonstrate the advantage of cooling photovoltaic modules with water using a rectangular channel profile for the thermal collector. A single glazed flat-box absorber PV/T module was designed, its behavior for different environmental parameters tested, the numerical model developed, and the simulation for particular days for Durban weather run. The simulation result showed that the overall efficiency of the PV/T module was 38.7% against 14.6% for a standard PV module while the water temperature in the storage tank reached 37.1 °C. This is a great encouragement to the marketing of the PV/T technology in South Africa particularly during summer, and specifically in areas where the average annual solar irradiance is more than 4.70 kWh/m2/day.
Key words: photovoltaic, thermal collector, storage tank, temperature, power output, efficiency, simulation
Nomenclature Roman
A area (m2)
b height of the channel (m)
D diffuse component of solar irradiance (kWh/m2day)
G global insolation on the horizontal (kWh/m2day)
H useful thermal energy [W]
H convective heat transfer coefficient (W/m2K)
I current (A)
L module length (m)
m mass flow rate [kg/s]
m simplification coefficient ()
P power (W)
S direct component of solar irradiance on the
horizontal (kWh/m2day)
S simplification coefficient ()
U overall heat transfer coefficient (W/m2K)
V voltage (V)
w channel water velocity (m/s)
x-y coordinates axis
z direction of water in channels
Greek symbols
A altitude (°)
B tilt angle (°)
Δ difference
H efficiency (%)
μ dynamic viscosity (kg/ms)
ξ dimensionless coefficient
ρ density (kg/m3)
τ transmittivity (-)
Subscripts
a ambient
c cells
e electrical
eff effective
f fluid
lcw lower channel wall
i inlet
o outlet
oc open voltage
r reference
sc short circuit
T total
th thermal
u upper, useful
ucw upper channel wall
Abbreviations
Cp specific heat (J/kgK)
GRADRAD greater radiometric
HMDE highest minimum daily energy
HYE highest year energy
NOCT normal operating cell temperature (°C)
PV photovoltaic
PV/T photovoltaic and thermal
1. Introduction
High electrical output can be obtained from a PV panel receiving high incidence solar irradiance. However, with high incidence irradiance the temperature of the solar cells increases and this reduces their efficiency.
Photovoltaic cells must be cooled by removing the heat in some way for better efficiency. This has led many researchers to develop hybrid photovoltaic and thermal collectors (PV/T) which generate electric power and simultaneously produce hot water or hot air (Mattei et al., 2006).
Using water in cooling systems is more efficient than using air. Photovoltaic cells are cooled by water convection with the water circulating in a closed circuit. The heat from PV cooling water is extracted into a storage tank and can be used in heating systems. The design of this technology uses rectangular profile thermal collector channels using natural convection fluid flow.
Theoretical and experimental studies of PV/T were conducted from as early as the mid-1970s (Chow, 2010). In 1976, Wolf M. analyzed the performance of a silicon solar array mounted inside a stationary flat plate collector using a lead-acid battery as the storage element (Wolf, 1976).
In 1979, Florschuetz presented a simple model for preliminary assessment of cooling system requirements for heat rejection from solar cells subjected to concentrated solar irradiation levels. Analysis of flat plate collectors from a Hottel-Whillier model for thermal collector was extended to the assessment of combined photovoltaic/thermal collectors and their efficiencies. Based on the extended model, examples of both thermal and electrical performance of a combined collector as a function of collector design parameters were presented and discussed. (Florschuetz, 1979).
In 1981, two separate one-dimensional analyses were developed for the prediction of the thermal and electrical performance of both liquid and air flat-plate photovoltaic/thermal (PVT) collectors (Raghuraman, 1981). Four years later, several potentially useful features in the design of photovoltaic/thermal (PVT) collectors were explored in order to determine their effectiveness and interaction (Cox III and Raghuraman, 1981).
In 1994, a hybrid photovoltaic thermal system based on natural convection of water in a thermal absorber fitted with circular channel tubes was studied and experiments were conducted for several days on a thermal collector alone. The finite difference method (FDM) was used to model and simulate the performance of the thermal collector (Agarwal and Garg, 1994). In order to understand and evaluate the solar hybrid systems, an experimental study was performed (Garg et al., 1994).
One year later, Garg and Agarwal (1995) performed the study of a hybrid forced circulation photovoltaic and thermal system and a developed a mathematical model for the system using the finite difference method. The algorithms for making quantitative predictions on the performance of the system were established by Bergene and Lovvik (1995) after proposing a detailed physical model of a hybrid photovoltaic thermal system.
In 2001, Huang et al. (2001) studied the performance of an integrated photovoltaic and thermal solar system (IPVTS) compared with a conventional solar water heater and demonstrated the idea of an IPVTS design.
In 2002, a hybrid PV/T unit that simultaneously produced low temperature heat and electricity was made from the combination of mono crystalline silicon photovoltaic cells with a polymer solar heat collector (Sandnes and Rekstad, 2002). Four 4 numerical models were built for the simulation of the thermal yield of a combined PV/T collector (Zondag et al., 2002).
In 2003, Zondag et al. (2003) evaluated nine different designs of combined PV thermal collectors in order to obtain a clearer view of the projected efficiency of the different concepts. In the same year, Chow (2003) established an explicit dynamic model for a single-glazed flat plate water heating PVT collector based on the control volume finite difference approach, and Coventry and Lovegrove (2003) presented the methods used to develop a ratio between electrical and thermal output energy for a domestic style PVT system.
The rectangular channels used with PV/T collectors are more efficient due to the fact that they provide a large surface area for heat exchange between the PV module and the thermal collector. This study is a particular case in which a simulation was run with Durban meteorological conditions for two particular days with a single glazed hybrid PV/T based on thermosyphon principle for water flow.
2. Solar irradiance on tilted surface
The flux of energy produced by the solar source reaching a surface per unit surface of an area is the insolation or solar irradiance. It is expressed in units of kWh/m2day for the average daily or monthly conditions at a given location. This quantity defines the maximum energy produced by a photovoltaic system for that particular location (Florida Solar Energy Center, 2010).
The photovoltaic panels are commonly tilted at a certain angle from the horizontal to receive the maximum amount of insolation. The insolation on the panels at the corresponding tilt angle is evaluated by separating the insolation into two components, the direct and the diffuse. Where solar irradi-ance data is available in the form of direct and diffuse components, the approach discussed in the next paragraph can be used to obtain the global insolation reaching the panels tilted at a certain angle β from the horizontal (Wenham et al., 2007).
Firstly, it is assumed that the diffuse component of insolation D is independent of the tilt angle approximately right for tilt angles of about or less than 45 °C. Secondly, the direct component of insolation on the horizontal surface S is to be converted into the direct component Sß that reaches the PV module tilted at angle β to the horizontal (Wenham et al., 2007), as shown in Figure 1

Consequently, Equation (1) is obtained:

where α is the altitude of the sun and β is the tilt angle.
The global insolation on array is the sum of the direct component Sßincident on a plane tilted at angle β to the horizontal and the diffuse component D independent parameter of the tilt angle, given by Equation (2):

3. Temperature influence on PV panel
Two important parameters of the I-V curve for a PV module are short-circuit current Iscand open-circuit voltage Voc. Iscand Vocchange with the incident solar irradiance G and the ambient air temperature Ta. as illustrated in Figure 2.
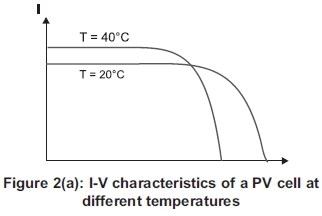
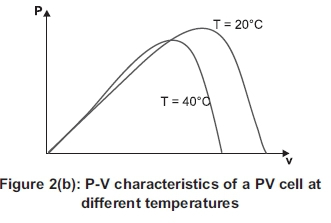
It is important to note that Vocdecreases with increasing module temperature, which leads to a noticeable decrease in the available maximum electrical power, in spite of a small increase in short-circuit current Isc, as illustrated in Figures 2(a) and 2(b).
These effects must be considered in any model for photovoltaic module efficiency. By definition, the efficiency of the PV system neis the ratio of electrical output energy P and the solar energy on the panels A*G and expressed in Equation 3.

where G is the insolation per unit of area and A the area of the panel.
The best known model is given by the Evans-Florschuetz correlation according to Equation 4:
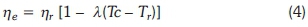
where nris the reference module efficiency at a PV cell temperature Trof 25 °C and at a solar irradiance G on the moudle of 1000 Wm-2. The Tcis the PV cell temperature, which depends on the environmental conditions and λ is the volume expansion coefficient 1/K.
The PV module power output is given by:

4. Conventional PV module
The conventional PV module is constituted of PV encapsulation protected on top by a front glazing and at the back by the back glazing and frame as illustrated in Figure 3
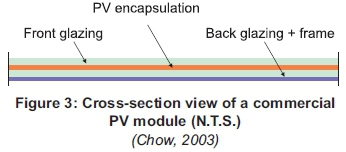
The electrical energy output from the PV module increases with the irradiance. At high irradiance the temperature of the solar module increases and its efficiency decreases as we can see from Equations 4) and 5. The temperature of the PV module is given by the empirical Equation 6:
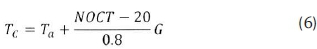
where NOCT is the normal operating cell temperature.
Therefore to increase the efficiency, particularly at high irradiance, the PV module must be cooled.
5. The PV/T module design and temperature modelling
The cooling system is constituted with a thermal collector plate, a storage tank and inlet and outlet pipes as illustrated in Figure 4
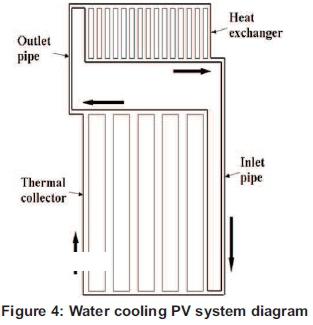
The heat of PV cells is removed from the module by water convection in thermal collector channels. Water is heated as the sun shines on the PV module, expands slightly, becomes lighter and is pushed through the collector outlet to the top of the tank by cold water from the tank that enters the bottom of the collector by gravity and rises again to the top of the tank by means of the thermosyphon principle as it warms up.
The collector plate comprises a front glazing PV encapsulation, a thermal absorber with rectangular flow channels, a thermal insulation and a back cover. The cross section view of the module is illustrated in Figure 5
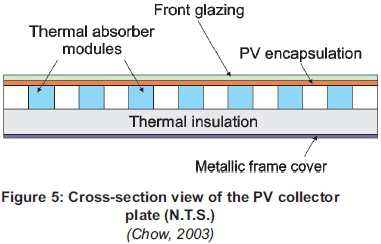
The thermal absorber is relied to the storage tank by inlet and outlet pipes. The outlet pipe routes hot water from the thermal absorber to the storage tank by buoyancy. The cold water from the tank is routed back to the thermal absorber through the inlet pipe. The bottom of storage tank is at least a foot higher than the top of the collector to avoid reverse flow during the night (Arunchala, 2011).
The temperature of solar cells is defined by the rate of water flowing in the thermal absorber channels.
Applying the energy balance on the thermal absorber gives Equation 7 for fluid temperature in channels:

where:
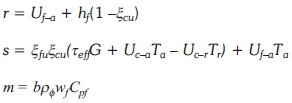
The average fluid temperature is given by Equation 8:

and the cell temperature is obtained from Equation 9:
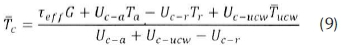
where
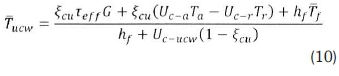
is the temperature of the upper channel wall.
The velocity of water in a rectangular channel due to the thermosyphon principle is obtained from Equation 11:
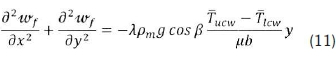
where g is the gravity, λ is the volume expansion coefficient, Tucwis the temperature of the upper surface of the channel, TJcw is the temperature of the lower surface of the channel, μ is the dynamic viscosity, β is the tilt angle of the module and b is the height of the channel.
The total or overall efficiency of the system is the ratio of the sum of electrical energy and useful thermal energy over the solar energy and is given by Equation 12:

in which ηεis the electrical efficiency of the PV/T system that can be obtained from Equation 3 and is the thermal efficiency of the thermal absorber given by Equation 13:

where Huis the useful thermal energy obtained from Equation 14:

6. The PV/T system behaviour against variation of environmental parameters
The important environmental parameters that influence the performance of a PV system are solar irra-diance, ambient temperature and wind velocity. The most important of them is solar irradiance because of the fact that the PV panel converts the light from the sun into electrical and thermal energies.
Figure 6 shows the impact of PV module behaviour compared with that of PV/T for solar irradiance varying from 0 to 1200 W/m2 at a constant ambient temperature of 25 °C and a constant wind speed of 1 m/s for eight hours. In Figure 6(a), the temperature of the cells for the PV/T module in the four first hours is observed. Temperature rises faster in the PV/T module than the PV module temperature for the first two 2 hours, then remains nearly constant after half of total time. The tank temperature rises following a positive exponential as shown in Figure 6(b). The maximum electrical energy and the overall efficiency are represented by Figures 6(c) and 6(d). As the solar irradiance rises, the maximum power point moves to the left for the conventional PV module, while the PV/T module remains at a constant voltage at the right of the PV module MPP as the solar irradiance increases. This behaviour is a great advantage for the electrical output of PV/T module as shown in Figure 7
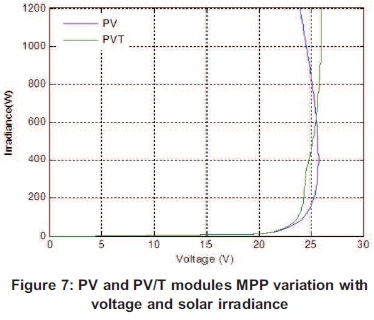
Figures 8(a)-(d) and Figures 9(a)-(d) represent the respective behaviours of PV and PV/T modules exposed to 1000 W/m2 for variable ambient temperature at wind velocity of 1 m/s and variable wind velocity at an ambient temperature of 25 °C.
In both cases, due to sudden exposition of PV/T module to high solar irradiance, the solution of Equation (6) is under-damped, which explains the oscillation behaviour of temperature of the cells due to a natural response of fluid temperature in the channels to thermal shock, as seen in Figures 8(a) and 9(a).
For an ambient temperature varying from 25 °C to 35 °C and wind velocity of 1 m/s, both PV and PV/T module temperatures rise linearly. The gradient of cell temperature against the time curve for PV module is greater than the gradient for cell temperature against time curve or PV/T module. This leads to a rapid increase of temperature in the case of the PV module. The maximum electrical energy of both systems decrease, while the efficiency is constant as seen in Figures 8(c) and 8(d). The storage tank temperature rises linearly as shown in Figure 8(b).
For a wind velocity varying from 0 to 12 m/s at ambient temperature of 25 °C. The temperature of the PV cells is constant. The temperature of the PV/T cells, which is less than that of the PV cells, decreases after half of the total time, while the maximum electrical energy output, which is greater than the constant PV maximum electrical energy output, increases as seen in Figures 9(a) and 9(c) respectively. The PV/T total efficiency decreases and stabilizes at a constant efficiency value of the PV module as shown in Figure 9(d). The temperature of the storage tank rises following a negative exponential as seen in Figure 9(b).
7. Durban flat-plate collector tilt angle
The sun's daily position in the sky differs over the course of the year. As a result, objects looking to maximize the use of solar energy, such as building thermal mass, photovoltaic panels and solar water heaters, should be orientated at an optimum angle for intended yearly time of use (Bellingham et al., 2009).
In South Africa the optimum tilt angle does not follow latitudinal gradient. It increases from about 24° in the northern part of the country towards the south-east, where it reaches values of up to 35° (Suri et al., 2012).
For Durban, Chris Bellingham et al. (2009) proposed the best angle for overall annual solar energy harvesting to be 35° to the horizontal.
Fixed PV arrays (i.e. panels that are fixed into position for the whole year) are typically installed with one of two requirements in mind: either to deliver the highest yearly energy (HYE), e.g. grid-connected PV arrays, or to deliver the highest minimum daily energy (HMDE) through the year, e.g. for battery-charging purposes. For Durban, Bekker (2007) proposed an optimal elevation tilt angle of 30° HYE optimal elevation.
Zawilska and Brooks (2011) recorded and analyzed solar radiometry and selected meteorological parameters for Durban, South Africa, over a full one-year period from January to December 2007 and found a 13% increase in energy availability, confirming the value of tilting flat-plate collectors in Durban at an angle equal to the latitude of 29.867° south.
8. Simulation and energy output
Two monocrystalline Q.PEAK 260 PV modules were used for simulation with Durban meteorological data. The first module was used as a conventional PV module, while the second was connected to a 150 liters tank. The two collectors were tilted at 29.867° south.
Weather data for two particular days were used. The environmental parameters were obtained from the Greater Durban Radiometric network (GRADRAD) for solar irradiance, and Weather Analytics for ambient temperature and wind velocity.
For the summer period, environmental parameters for the day of 22/12/2012 are represented in Figure 10
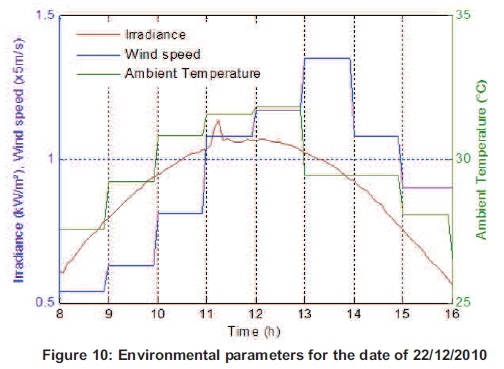
Simulation results for the PV and PVT modules behaviour for the particular day of 22/12/2010 with Durban weather conditions are given in Table 1
The behaviours of both systems are represented in Figure 11(a)-(d).
For the winter period, environmental parameters for the day of 27/06/2011 are represented in Figure 12
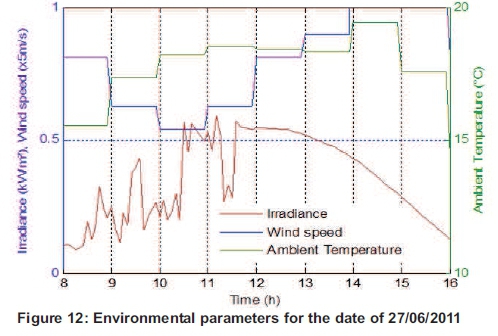
Simulation results for the PV and PV/T modules behaviours for the particular day of 27/06/2011 with Durban weather conditions are given in Table 2 The behaviours of both systems are represented in Figure 13
9. Conclusions
The simulation of two monocrystalline Q.PEAK 260 PV modules was conducted with one module on top of a thermal collector and connected to a 150 liters storage tank to constitute a PV/T module and both modules were exposed for eight hours to varying environmental conditions. It was found that no matter which environmental parameter is varied, the maximum electrical power output of PV/T module was always higher than of the PV module. The higher efficiency was obtained from the PV/T module because of cooling of the solar cells (decrease in cells temperature), with the heat removed from cells being used to heat water in the storage tank. For the typical summer day of 22/12/2010, the efficiency of the PVT module was 24.1% higher than the conventional PV module for the same dimensions and characteristics and the tank water temperature reached 37.1 °C. These results are encouraging regarding the use of PVT systems particularly in areas where hot water is also needed. This system provides both high electrical power output and hot water.
References
Agarwal R.K. and Garg, H.P (1994). Study of a photo voltaic-thermal system thermosyphonic solar water heater combined with solar cells. Energy Conversion and Management, 35, 605-620. [ Links ]
Arunchala U.C. (2011). Performance deterioration of thermosiphon solar flat plate water heater due to scaling. IIUM Engineering Journal, Special Issue, Mechanical Engineering. [ Links ]
Bekker, B. (2007). Irradiation and PV array energy out put, cost, and optimal positioning estimation for South Africa, Journal of Energy in South Africa, 18(2), 16-25. [ Links ]
Bellingham, B., Davies, G. and Human, A. (2009). Greening Durban 2010. eThekwini Municipality, KwaZulu-Natal, South Africa. [ Links ]
Bergene, T. and Lovvik, O.M. (1995). Model calculations on a flat-plate solar heat collector with integrated solar cells. Solar Energy 1995;55(6), 453-462. DOI:10.1016/0038-092X(95)00072-Y. [ Links ]
Chow T.T. (2003). Performance analysis of photovoltaic- thermal collector by explicit dynamic model. Solar Energy, 75(2), 143-152. DOI:10.1016/j.solen-er.2003.07.001. [ Links ]
Chow, T.T. (2010). A review on photovoltaic/thermal hybrid solar technology. Applied Energy, 87, 365 379. A review on photovoltaic/thermal hybrid solar technology. DOI:10.1016/j.apenergy.2009.06.037. [ Links ]
Coventry J.S. and Lovegrove K. (2003). Development of an approach to compare the 'value' of electric and thermal output from a domestic PV/thermal system. Solar Energy, 75(1), 63-72. DOI:10.1016/S0038-092X(03)00231-7. [ Links ]
Cox III, C.H. and Raghuraman P (1985).Design considerations for flat-plate-photovoltaic/thermal collectors. Solar Energy, 35(3), 227-421. DOI: 10.1155/2012/957847 [ Links ]
Florida Solar Energy Center (FESC). (2010). FSEC Standard 203-10: Procedures for photovoltaic system design review and approval. University of Central Florida, Cocoa, Florida. [ Links ]
Florschuetz L.W. (1979). Extension of the Hottel-Whillier model to the analysis of combined photovoltaic/thermal flat plate collectors. Solar Energy, 22, 361-366. DOI:10.4028/www.scientific.net/AMM.401-403.146 [ Links ]
Garg H.P and Agarwal PK. (1995). Some aspects of a PV/T collector/forced circulation flat plate solar water heater with solar cells. Energy Conversion and Management, 36, 87-99. [ Links ]
Garg, H.P., Agarwal, R.K. and Joshi, J.C. (1994). Experimental study on a hybrid photovoltaic-thermal solar water heater and its performance predictions. Energy Conversion and Management, 35, 621-633. [ Links ]
Huang, B.J., Lin, T.H., Hung, W.C, and Sun FS. (2001). Performance evaluation of solar photovoltaic/thermal systems. Solar Energy 70(5), 443-448. DOI:10.1016/S0038-092X(00)00153-5. [ Links ]
Mattei, M. Notton, G., Cristofari, C., Muselli, M. and Poggiand P. (2006). Calculation of the polycrystalline PV module temperature using a simple method of energy balance. Journal of Renewable Energy, 31(4), 553-567. DOI:10.1016/j.renene.2005.03.010. [ Links ]
Raghuraman P (1981). Analytical predictions of liquid and air photovoltaic/thermal, flat-plate collector performance. Journal of Solar Energy Engineering, 103, 291-298. DOI:10.1115/1.3266256 [ Links ]
Sandnes, B, Rekstad J. (2002). A photovoltaic/thermal (PV/T) collector with a polymer absorber plate- experimental study and analytical model. Solar Energy, 72(1), 63-73. DOI:10.1016/S0038-092X(01)00091-3. [ Links ]
Suri M., Cebecauer T., Skoczek A. and Betak, J. (2012). Solar electricity production from fixed-inclined and sun-tracking c-Si photovoltaic modules in South Africa. 1st Southern African Solar Energy Conference (SASEC), 21-23 May, Stellenbosch. [ Links ]
Wolf M. (1976). Performance analysis of combined heating and photovoltaic power systems for residences. Energy Conversion and Management, 16, 79-90. [ Links ]
Wenham, S.R., Green, M.A., Watt, M.E. and Corkish, R. (2007). Applied photovoltaics. 2nd ed. Padstow, Cornwall, UK: TJ International Ltd. pp. 22-23; 128-129. [ Links ]
Zawilska E. and Brooks M.J. (2011). Solar energy measurement on the South Africa east coast. World Renewable Energy Congress, Linköping, Sweden. [ Links ]
Zondag H.A, De Vries D.W, Van Helden WGJ, Van Zolingen RJC, Van Steenhoven AA. (2003). The yield of different combined PV-thermal collector designs. Solar Energy, 74, 253-269. DOI:10.1016/S0038-092X(03)00121-X. [ Links ]
Zondag H.A., de Vries, D.W., van Helden, W.G.J., van Zolingen, R.J.C. and van Steenhoven, A.A. (2002). The thermal and electrical yield of a PV-thermal collector. Solar Energy, 72(2), 113-128. DOI:10.1016/S0038-092X(01)00094-9. [ Links ]
* Corresponding author
Tel: +27 31 260 8530 E-mail: inambaof@ukzn.ac.za














