Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
Journal of Energy in Southern Africa
On-line version ISSN 2413-3051
Print version ISSN 1021-447X
J. energy South. Afr. vol.26 n.2 Cape Town May. 2015
Differential power algorithm based maximum power point tracking for a standalone solar PV system
Dinesh K Sharma; Ghanshyam Purohit
School of Engineering, Sir Padampat Singhania University, Udaipur, India
ABSTRACT
We report on an improved maximum power point tracking (MPPT) system based on a differential power algorithm. In the proposed algorithm, which is a modified form of a perturb and observe (P&O) algorithm, differential powers, as well as voltages at different time, are compared. The proposed algorithm has been implemented with a highly efficient boost converter, in which duty cycle of a switch is varied in such a way, that the power reaches a maximum at any instant of the day, irrespective of the environmental conditions. The improved MPPT is able to reduce the number of oscillations and tracking time significantly before reaching the maximum power point (MPP). The simulated I-V and P-V characteristic curves (individual and combined) of a solar PV module were generated in MATLAB.
Keywords: solar PV system, MPPT, efficiency, control algorithm, boost converter
1. Introduction
Generation of power from renewable energy sources is an important way to reduce carbon footprints in our environment. Low efficiency and high cost are the main factors which impedes the global utilization of renewable energy resources for generation of electrical power. Power generation, using solar PV (Koutroulis et al., 2001), is not popular (especially in developing countries) due to the higher cost and lower efficiency (D'Souza et al., 2005) of solar PV modules. The efficiency of a solar PV system can be maximized using a maximum power point tracker (MPPT). The MPPT is a power electronic circuit of an efficient DC-DC converter, which is controlled by an algorithm. The function of the control algorithm is to minimize the deviations (Hua and, Lin, 2003) from a maximum power point so that the maximum possible power can be extracted from the PV module(s) under varying atmospheric conditions (Subudhi, and Pradhan, 2013)] with minimum possible wastage of power. Various MPPT techniques and control algorithms (Esram and Chapman, 2007; Hohm and Ropp, 2003; de Brito et al., 2013; Moacyr et al., 2007; Thounthong, et al., 2013) have been studied.
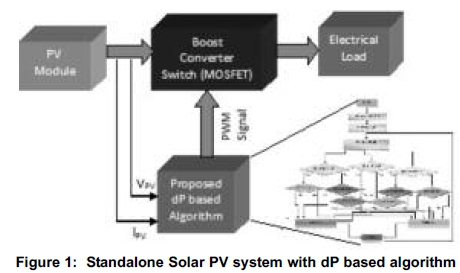
2. Standalone solar PV system modelling
Modelling of a standalone PV system is the basic requirement for obtaining the characteristic curve on which MPP is to be tracked. A standalone solar PV system (Amin et al., 2009; Xiao and Dunford, 2004) consists of a PV module, load, power electronic converters (DC-DC conversion or DC-AC conversion), charge controller (Xiao and Dunford, 2004) (to avoid undercharge and overcharge conditions of the battery) with battery (for storage) and Maximum Power Point Tracker (MPPT). The function of control algorithm is to decrease or increase the duty cycle of the switch (Subudhi and Pradhan, 2013; Koutroulis and Blaabjerg, 2012) power switch of DC-DC converter (Salam et al., 2010) by means of Pulse Width Modulation (PWM) in order to track the maximum power points on the characteristic curves of the PV module. Figure 1 represents a typical standalone solar PV system.
For implementing the proposed algorithm, it is required to model a solar PV system with maximum power points on the I-V and P-V characteristic curve of the PV module. The following section describes the electrical equivalent circuit and associated equation for the modelling of a solar PV module and to finally obtain the characteristic curves.
3
a) Electrical equivalent circuit of a solar PV module
An electrical equivalent circuit of a solar PV cell is shown in Figure 2. The circuit consists of a current source connected with a diode in parallel and two resistors RgHin parallel and Rg in series. The current produced by solar cell is given by equation (1).
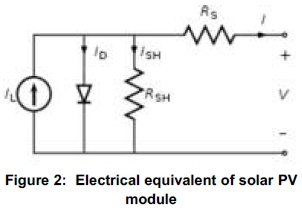
From the equivalent circuit it is evident that the current produced by the solar cell is equal to that produced by the current source, minus that which flows through the diode, minus that which flows through the shunt resistor (using Kirchhoff's current law) (Weidong et al., 2013:
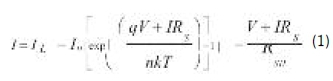
where,
IL= light generated current
I0 = reverse saturation current q = charge of electron
V = voltage across output terminals RS = series resistance
RSH= shunt resistance
n = ideality factor of diode k = Boltzmann's constant
T = room temperature
b) Simulated results of I-V and P-V characteristics of PV module
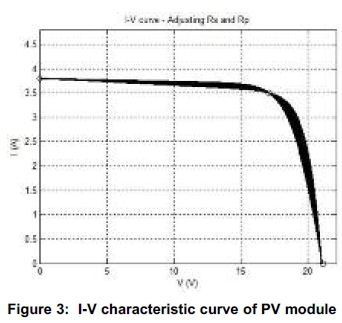
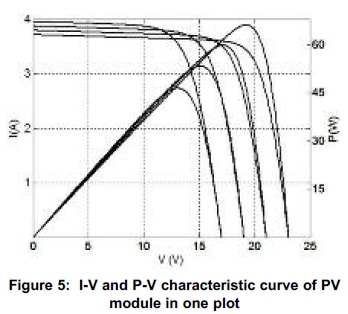
We obtained the simulated results for the I-V and P-V Characteristic curves of a PV module using MAT- LAB. The thick portion on these curves is due to continuous overlapping of different curves. The following I-V characteristic curves have been obtained by adjusting the series resistance (Rs=0.340000) and parallel resistance (RP=164.585828) of a two diode model (Femia et al., 2005) of a solar PV cell.
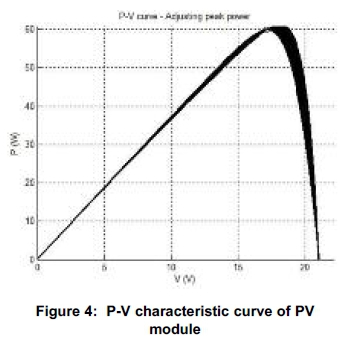
The following P-V characteristic curve was obtained in MATLAB by adjusting the peak power (Pmax= 59.85 W). This curve is the superposition of several curves, closely spaced in order to obtain its present form. This curve shows the shifting of maximum power point (MPP) for various solar irradiation levels. By adjusting the peak power, global MPP is obtained by different local MPPs on the P-V characteristic curves.
The following characteristic curve (I-V and P-V in one plot) has been obtained by superimposing the I-V and P-V at various values of voltage, current and power (in varying insolation) as shown in Figure 5.
4. Boost converter
A boost converter is required to vary the output voltage (as shown in characteristic curves) of the solar PV systems in order to obtain the MPP. The boost converter is a highly efficient power electronic converter which only raises voltage. The control algorithm is used to control the duty cycle of the switch of the boost converter. The duty cycle of the boost converter is formulated by:

where,
Ton= On period of switch of boost converter TOFF = Off period of switch of boost converter
The output voltage is related with the duty cycle of the boost converter as following:
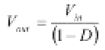
where,
Vin = input voltage to the boost converter, Vout = output voltage from the boost converter
D = duty cycle of the switch of boost converter.
The control algorithm is used to calculate the duty cycle (on and off time) of the switch of the boost converter. The proposed algorithm (based upon the difference of consecutive power and voltage levels) has been implemented to control the duty cycle of the switch of the boost converter.
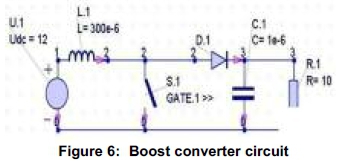
The boost converter circuit is described as follows:
1. DC voltage source (Vdc = 12 V), which is used for energizing the circuit
2. Inductor (L = 300e-6 H), which is used for storing and releasing the electrical energy
3. Power electronic switch, which is used for keeping ON and OFF of the switch
4. PN junction diode, which is used for blocking the reverse flow of current from load to source.
5. Capacitor (C = 1e-6 F) is used as voltage filter.
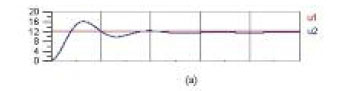
The results have been taken from Gecko Circuits simulation software (GeckoCIRCUITS). The results for various parameters [i.e. input voltage (u1), output voltage (u2), switch voltage (uS), inductor current (IL), capacitor current (Ic)] are obtained in Gecko Circuits and shown in Figure 7.The variation in output voltage (u2) along with the constant input voltage (u1) has been shown in Figure 7(a). This figure shows that the output voltage increases from 0 V to 16 V (peak value) after 170 e-6 sec. from the beginning. It further reduces from peak value to 8.5 V in the next 340 e-6 sec. Consequently, this waveform stabilizes at 408 e-6 sec. This waveform has been constant and almost overlapping with the input voltage.
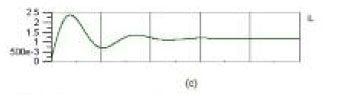
In Figure 7(b), the waveform of switch voltage (uS) is almost the same as that of output voltage (u2) with some oscillation before stabilization. Figure 7(c) represents the variation in inductor current (IL). In this figure, IL reaches to the peak value of 2.75 A in 136 e-6 sec. Further, IL goes down to the bottom value of 0.75 A at 280 e-6 sec. Subsequently, it goes up to the value of 1.25 A at 415 e-6 sec. Then after some minor oscillations, it stabilizes with the value of 1.15 A at 860 e-6.
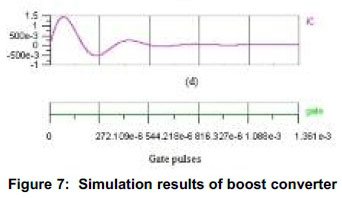
The variation of capacitor current (Ic) is depicted in Figure 7(d). The Ic increases from 0 A to the peak value of 1.5 A in 68 e-6 sec. Then it reduces slowly and reaches to the bottom value of -500 e-3 sec at 250 e-6 sec. Subsequently Ic further goes up from this value to 0.25 A at 410 e-6 sec. After some minor oscillations, Ic stabilizes at 0.9 e-3 sec. Sequence of gate pulses is represented in Figure 7.
5. Differential power (dP) algorithm
The control algorithm proposed in this paper is based upon the simple and widely used Perturb and Observe (P&O) algorithm (Amrouche et al., 2007; Villalva et al., 2009; Mohammed et al., 2012). In the proposed algorithm, the perturbation and observation steps are increased in order to closely track the maximum power point with minimum possible oscillations around the operating point on the characteristic curve of the solar PV module. In this algorithm, the different values of power are compared with each other at different instance of time. The presented algorithm is based upon the difference of old and new power values. Therefore, this algorithm may be called as differential power (dP) based algorithm.
In this algorithm, the difference of three consecutive power levels, as given in equations (1), (2) are calculated. Then the voltage differences of the corresponding power levels are calculated. Consequently, the voltage of the converter is increased and decreased accordingly. Due to this, the duty cycle (thereby pulse width) of the power switch is also modulated in order to efficiently track the MPPs.

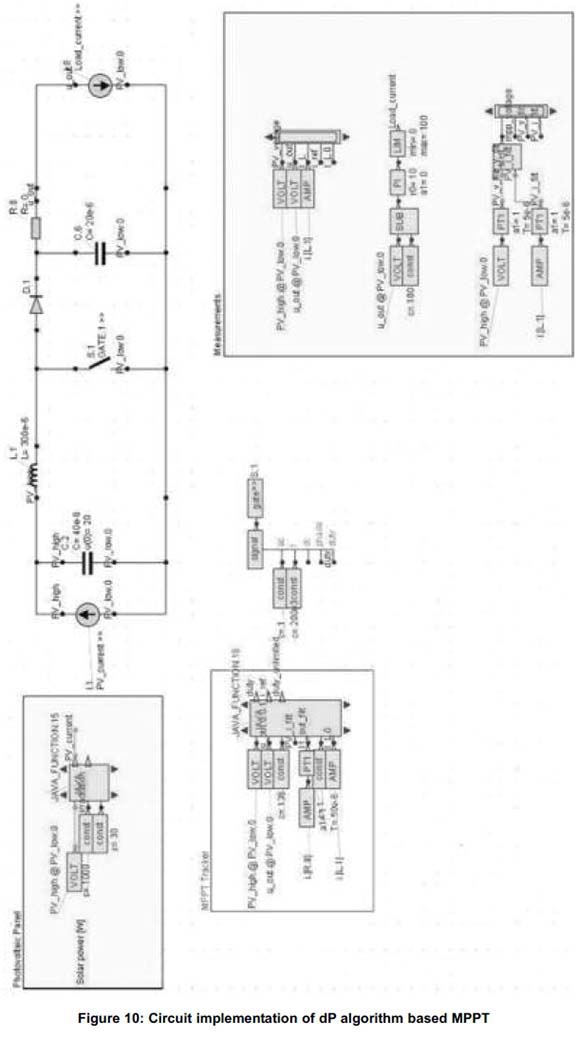
After comparing the differential power, from equations (1), (2) and (3), the corresponding voltages are also compared. Consequently, the duty cycle of the switch of the boost converter is modulated as shown in the dP algorithm (Figure 9). The main advantage of this method is that it works on the basis of calculation of power difference in consecutive instants throughout the day. Due to this, it provides the direct determination of maximum power from a solar PV system. The implementation circuit and simulation results are presented in the next section.
6. Results and discussion
The proposed algorithm has been implemented in Gecko Circuits as shown in the following circuit diagram in Figure 8. The simulation results of the MPPT with proposed algorithm are in Figure 8(a) and shows that the output voltage stabilizes rapidly, within a fraction of a second in comparison to the input PV voltage and inductor current (IL) which both stabilize at 4.975 seconds. In Figure 8(b), the voltage across the switch (sg.1) is also stabilized after 4.975 seconds. At the same time, the PV voltage (filter i.e. across C2) and PV current (filter i.e. through C2) decreases and increases respectively that follow the law of conservation of energy.
The results shown in Figures 8(a) and 8(b) indicate that the proposed algorithm is not only able to effectively reduce the stabilizing time (tracking time) of output (load) voltage but it also able to reduce the ripples and oscillations in the output. The result shows that the proposed method is able to track the MPP with a reduced number of oscillations and thereby higher stability of the solar PV system. At the same time, the efficiency of the solar PV system is increased due to lower amount of oscillations and the performance of the overall solar power system has been upgraded. The main disadvantage of this algorithm is that it has increased complexity.
7. Conclusion
In this paper, a differential power algorithm is presented and consequently implemented to control the operation of the boost converter. By the efficient control of the boost converter, the output power from the solar PV power generating system has been significantly increased for an optimal efficiency. The simulation results for characterization of the PV module (i.e. I-V and P-V characteristics) are presented. The simulation results of the realized circuit with the proposed algorithm are also presented, which shows the stable operating point for maximized constant output power from a solar PV system.
References
Amin, N.; Lam Zi Yi; and Sopian, K., (2009). Microcontroller based smart charge controller for standalone solar photovoltaic power systems, Photovoltaic Specialists Conference (PVSC), 2009 34th IEEE, Vol., No., pp.001094, 001097, 7-12 June 2009. [ Links ]
Amrouche, B. Belhamel, M. and. Guessoum A., (2007). Artificial intelligence based P&O MPPT method for photovoltaic systems, Revue des Energies Renouvelables ICRESD-07 Tlemcen (2007) 11- 16. [ Links ]
de Brito, M.A.G.; Galotto, L.; Sampaio, L.P; de Azevedo e Melo, G.; and Canesin, C.A., (2013). Evaluation of the Main MPPT Techniques for Photovoltaic Applications, IEEE Transactions on, Industrial Electronics, Volume: 60, Issue: 3, pp.1156 - 1167 March 2013. [ Links ]
D'Souza, N.S.; Lopes, L. A C; and Liu, X. (2005). An Intelligent Maximum Power Point Tracker Using Peak Current Control, Power Electronics Specialists Conference, 2005. PESC '05. IEEE 36th, Vol., No. pp.172, 16-16 June 2005. [ Links ]
Elgendy, M.A., Zahawi, B. and Atkinson D.J. (2012). Assessment of Perturb and Observe MPPT Algorithm Implementation Techniques for PV Pumping Applications, IEEE Transactions on Sustainable Energy, Vol. 3, no. 1, January 2012. [ Links ]
Esram, T., and Chapman PL., (2007). Comparison of Photovoltaic Array Maximum [ Links ]
Power Point Tracking Techniques, IEEE, Transactions on Energy Conversion, Vol. 22, No.2, June, 2007. [ Links ]
Femia, N., Petrone, G., Spagnuolo, G., and Vitelli, M., (2005). Optimization of perturb and observe maximum power point tracking method. IEEE Transactions on Power Electronics, 20, 963-973. [ Links ]
GeckoCIRCUITS. Power Electronic Simulation Software. [ Links ]
Green, M.A. (1992). Solar Cells - Operating Principles, Technology and System Application, University of NSW, Kensington, Australia. [ Links ]
Hohm, D.P, and Ropp, M.E., (2013). Comparative study of maximum power point tracking algorithms, Prog. Photovolt: Res. Appl., Vol. 11, pp. 47-62, 2003. [ Links ]
Hua, C., and Lin, J., (2003). An on-line MPPT algorithm for rapidly changing illuminations of solar arrays, Renew Energy 28, 1129-1142. [ Links ]
Koutroulis, E., Kalaitzakis, K., and Voulgaris, N.C., (2001). Development of a microcontroller-based. Photovoltaic maximum power point tracking control system. IEEE Trans. Power Electron, 16, 46-54. [ Links ]
Koutroulis, E., and Blaabjerg, F, (2012). A New Technique for Tracking the Global Maximum Power Point of PV Arrays Operating Under Partial-Shading Conditions, Photovoltaics, IEEE Journal, Vol.2, no.2, pp.184,190, April 2012. [ Links ]
Moacyr A. G. de B, Junior L.G., Sampaio L.P, Guilherme A. e Melo, G. A., and Canesin C.A., (2007). 'Main Maximum Power Point Tracking (MPPT) strategies intended for Photovoltaics, IEEE Transactions on Energy Conversion, Vol.22, No.2, June 2007. [ Links ]
Salam, Z.; Ishaque, K.; and Taheri, H.,(2010). An improved two-diode photovoltaic (PV) model for PV system, 2010 Joint International Conference on Power Electronics, Drives and Energy Systems (PEDES) & 2010 Power India, Vol., No., pp.1-5, 20-23 Dec. 2010. [ Links ]
Subudhi, B., and Pradhan, R., (2013). A Comparative Study on Maximum Power Point Tracking Techniques for Photovoltaic Power Systems, Sustainable Energy, IEEE Transactions, Vol. 4, No.1, pp.89 - 98, Jan. 2013. [ Links ]
Thounthong, P; Luksanasakul, A.; Koseeyaporn, P; and Davat, B., (2013). Intelligent Model-Based Control of a Standalone Photovoltaic/Fuel Cell Power Plant With Supercapacitor Energy Storage, IEEE Transactions on Sustainable Energy, Vol. 4, No.1, pp.240,249, Jan. 2013. [ Links ]
Villalva, M.G., Gazoli, J.R., and Filho, E.R. (2009). Analysis and simulation of the P&O MPPT algorithm using a linearized PV array model', Industrial Electronics, 2009. IECON '09. 35th Annual Conference of IEEE. [ Links ]
Weidong Xiao; Edwin, FF; Spagnuolo, G.; and Jatskevich, J. (2013). Efficient Approaches for Modelling and Simulating Photovoltaic Power Systems', Photovoltaics, IEEE Journal, page(s): 500 - 508 Volume: 3, Issue: 1, Jan. 2013 [ Links ]
Xiao, W., and Dunford, W.G., (2004). A modified adaptive hill climbing MPPT method for photovoltaic power systems. Proceedings of 35th Annual IEEE Power Electronics. Specialists Conference, Aachen, Germany. pp. 1957-1963. [ Links ]
Received 22 August 2014
Revised 24 February 2015