Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
Journal of Energy in Southern Africa
On-line version ISSN 2413-3051
Print version ISSN 1021-447X
J. energy South. Afr. vol.26 n.1 Cape Town Feb. 2015
Performance optimization of an air source heat pump water heater using mathematical modelling
Stephen TangweI; Michael SimonI; Edson L MeyerI; Sampson MwampheliI; Golden MakakaII
IFort Hare Institute of Technology, University of Fort Hare, Alice, Eastern Cape South Africa
IIDepartment of Physics, University of Fort Hare, Alice, Eastern Cape, South Africa
ABSTRACT
In South Africa, there is an ongoing constraint on the electricity supply at the national grid to meet the demand. Eskom is implementing various measures such as the Integrated Demand Management and the promotion and encouragement of the use of energy efficient devices like an Air Source Heat pump (ASHP) water heater to replace the high electrical energy consuming conventional geysers for sanitary hot water production. The ASHP water heater market is fast gaining maturity. A critical mathematical model can lead to performance optimization of the systems that will further result in the conservation of energy and significant reduction in global warming potential. The ASHP water heater comprises of an ASHP unit and a hot water storage tank. In this study, a data acquisition system (DAS) was designed and built which monitored the energy used by the geyser and the whole building, the temperature at the evaporator, condenser, tank outlet hot water, tank inlet cold water, the ambient temperature and relative humidity in the vicinity of the ASHP evaporator. It is also worthy to mention that the DAS also included to a flow meter and two additional temperature sensors that measured the volume of water heated and inlet and outlet water temperature of the ASHP. This work focused on using the mathematical equation for the Coefficient of Performance (COP) of an ideal Carnot's heat pump (CHP) water heater to develop basic computation in M-file of MATLAB software in order to model the system based on two reservoir temperatures: evaporator temperatures (Tevp) of 0°C to 40°C (approximated to ambient temperature, Ta) and condenser temperatures (TCon) set at 50°C, 55°C and 60°C (approximated to the hot water set temperature of 50°C, 55°C and 60°C) respectively. Finally, an analytical comparison of a CHP water heater to the practical ASHP water heater was conducted on a hot water set point temperature of 55°C. From the modelling results, it can be deduced that at 0°C Tevp, the COP was 5.96 and 2.63 for CHP and ASHP water heater respectively, at a hot water set temperature of 55°C. Above 20°C Tevp, the rate of change of COP increased exponentially for the ideal CHP system, but was constant at 0.01/°C for the practically modelled ASHP water heater.
Keywords: Air source heat pump; coefficient of performance; data acquisition system; mathematical model; Carnot's heat pump
1. Introduction
Hot water heating constitutes a significant percentage of energy consumption in the industrial, commercial and residential sectors worldwide. In South Africa, water heating is the largest residential use of energy, with up to 50% of monthly electricity consumption being used for this purpose (Meyer and Tshimankinda, 1998). The Eskom strategic plan outlook for 2010 to 2030 envisages over 20% reduction of electricity production from coal (Digest of SA Energy statistics, 2009) as shown in Figure 1. One way to achieve this energy conservation could be by the use of an energy efficient technology such as the implementation of a heat pump for sanitary hot water production. Figure 1 illustrates the statistical outlook for sources of electrical energy generation in South Africa.
In order to execute the afore-mentioned energy efficient technology, Eskom embarked in rolling out a rebate programme of approximately 65 580 units of residential ASHP to retrofit existing geysers until March 2013 (Eskom Report, 2010). Consequently, this strategy will go a long way to promote the use of this technology within the residential sector. Considering the fact that the ASHP technology has been recommended and accepted for demand and energy reduction, it is therefore imperative at this juncture to present a clear description of the ASHP The ASHP water heater is an electro-mechanical close circuit system comprising of a heat pump and a water storage tank. The key components of the heat pump unit are the evaporator coil, vapour compressor, heat rejection condenser and an expansion valve. The ASHP water heater operates on the principle of a vapour compression refrigerant cycle (VCRC). It can be categorized into integrated and retrofit types. In the integrated type both the ASHP unit and the storage tank exist as a single system; the ASHP lies on top of the tank while in the split type, the ASHP unit is situated below the storage tank and connected to it by pipes. Generally, both types can further be classified as one passed circulation system and recirculation system. Studies have documented that the ASHP water heater could provide hot water at 40 to 100 percent of the rate of electric resistance units and 30 to 50 percent of the rate of gas units, but required warm ambient temperatures and a large heat pump or storage tank so as to provide a constant flow of hot water (Bodzin, 1997; CBEEDAC, 2005). The characteristic of a heat pump that enables it to provide such a very high efficiency of 300% is called the coefficient of performance (De Swardt et al., 2000). The COP of an ASHP water heater is dependent on various parameters including component design, heating load cycle, thermo-physical properties of the working fluids, relative humidity and air speed through the duct space. The instantaneous, seasonal or annual COP can be calculated using simulation with the TRYSYN software package (Kline et al., 2000), and an analytic mathematical model that correlates COP and temperature for solar assisted ASHP water heater (Itoe et al., 1999).
2. Fundamental principles of ASHP water heater
The entire operational principle of an ASHP water heater is clearly illustrated in Figure 2. During a heating load cycle, the ASHP undergoes a VCRC. The cycle can only be achieved in the case of CHP by supplying electrical energy to the compressor and in a practical ASHP, energy is also needed to run the water circulation pump and fan as shown in Figure 2. The low pressure and temperature refrigerant extract aero-thermal energy from ambient air and the low pressure vapour flows to the compressor where it is compressed and discharged as superheated gas. The thermal energy absorbed by the gas is rejected at the condenser unit where incoming water from the ASHP inlet pipe is heated to hot water set point temperature. Finally, the refrigerant passes through an expansion valve where its pressure and temperature drops. The complete processes involved in the cycle are shown in the temperature versus entropy and pressure versus enthalpy graphs of Figures 3 and 4, respectively. From both figures, the saturated liquid and saturated vapour lines for the working fluid are distinguished by the critical temperature (Tc ) and the critical pressure (Pc).
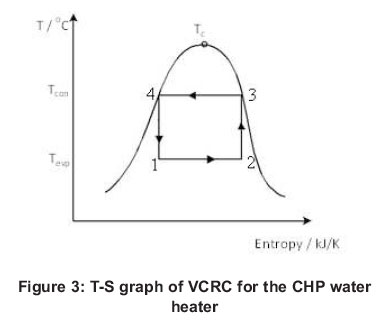
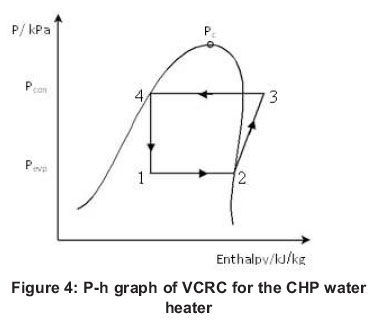
The COP of the heat pump could be determined by either using the pressure versus enthalpy graph or the temperature versus entropy graph and the essential parameters were obtained for the final COP calculation. The analysis of the processes involved in each section of the two figures is explained below: where h and s are specific enthalpy and specific entropy of the system, respectively, Ein is input electrical energy and Qout is the useful heat gain.
In order to understand and mathematically represent the processes taking place in the evaporator, compressor, condenser and expansion valve sections of the heat pump, a set of equations (1-8) were deduced. Analysing Figure 4, the process 1 to 2 occurred in the evaporator and the heat gain was calculated using equation 1.

Process 2 to 3 occurred at the compressor and heat gain was calculated as shown in equation 2

Process 3 to 4 occurred in the condenser and the heat rejected was calculated using equation 3

Process 4 to 1 occurred in the expansion valve and enthalpy change was calculated as shown in equation 4
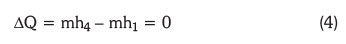
Using the definition of COP in terms of energy factor, equation 5 was obtained

From equation 5, both energies (Qout, output thermal energy and Ein, input electrical energy) can be expressed in terms of h to give equation 6.
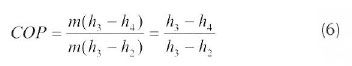
The COP could also be derived from Figure 3 and by using the first law of thermodynamics. The COP can be defined by equation 7
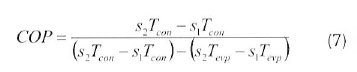
Simplifying equation 7 gives equation 8

Both the evaporator and condenser temperatures were expressed in Kelvin (K). Equation 8 was the COP formulation applied to the CHP water heater. Based on this equation, a computational programme which modelled the COP variation with temperature lift was generated from the M-file script of the MATLAB software.
3. Methodology
3. 1 Variations of the modelled COP of the CHP water heater with evaporator temperature
The modelled COP of CHP derived from equation 8 was used for ambient temperature ranging from 0oC to 40oC with the hot water set point temperature (condenser temperature) of 50oC, 55oC and 60oC. Figure 5 illustrates Carnot's COP variation in relation to ambient temperature, which is equal to the evaporator temperature. From Figure 5, it can be depicted that Carnot's COP increased linearly with ambient temperature from 0oC to 20oC at a rate of 0.15 / oC and above this range, the COP increased exponentially.
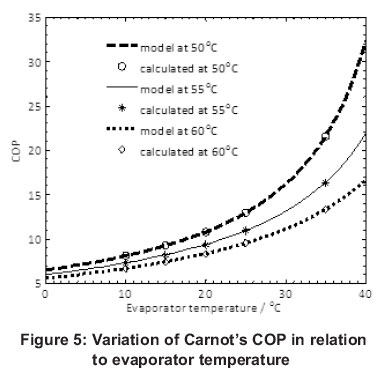
It was also observed that at the condenser temperature of 55oC, the COP increased with increase in evaporator temperature. The COP of 5.96 could be obtained at ambient temperature of 0oC, since the air contained waste heat at such a temperature provided there is no frost formation. At an ambient temperature of 40oC, a COP of 21.8 could be achieved as deduced from Figure 5 provided no parasitic heat losses occurred at the condenser. This indicates that all the rejected heat in the condenser is absorbed by the inflow water into the CHP unit.
3. 2 Mathematical modelling of practical ASHP water heater
The second aspect of this work, was to use the Marrison's COP correlation to mathematically model a practical ASHP water heater. Equation 9 illustrates the Marrison COP model while equation 10 shows the constraint COP equation used for the simulation.
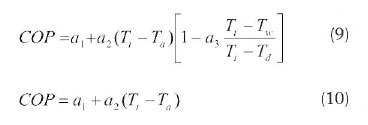
Equation 10 is a constraint equation to optimize the COP; where the constants a1 was the COP when Tt = Ta and a2 was the COP gradient determined for Tt = 50oC, 55oC and 60oC using the experimentally determined COP at an average ambient temperature of 10oC, 15oC, 20oC, 25oC and 35oC as shown in Table 1. The wet bulb temperature (Tw) was assumed to be equal to hot water set temperature (Tt) and (Td) was the dew point temperature.
Table 2 shows the predictors and scaling constants for the three different hot water set point temperatures derived from the linear regression model of the COP obtained from the data shown in Table 1.
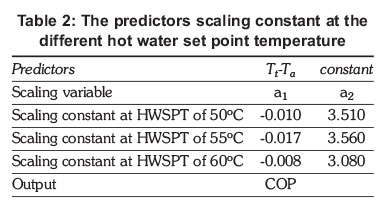
Figure 6 gives a presentation of measured and modelled COP at 50oC, 55oC and 60oC hot water set point temperatures. It can be delineated that if all other conditions affecting the COP remain constant, then the lower the hot water set point temperature the better the COP of the modelled ASHP water heater.
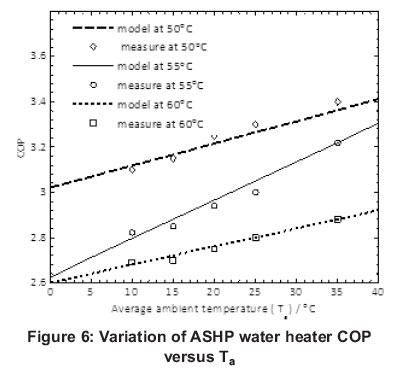
The dash dot, solid and dot lines are the optimized linear equations obtained for hot water set at 50oC, 55oC and 60oC. The average cold water temperature of 25oC at the bottom of the tank and average relative humidity of 75% were used. The solid line is for hot water set point temperature of 55oC. The modelled COP equation from equation 10 was used in the simulation designed in Simulink, which required both ambient temperature and electrical energy as its input parameters.
3. 3 Methodology for determination of input parameters
The computation of the COP using mathematical modelling was performed for a typical week baseline profile of a 4kW, 200 litres convectional geyser installed in a domestic residence (occupied by four adults and two children) of a middle class family at Fort Beaufort, South Africa. The geyser was allowed to operate without interruption for 24 hours on a daily basis. Figures 7 and 8 illustrate the DAS used to determine the hot water profiles and the analogous parameters appropriate to determine the system performance.
The U30-NRC data logger shown in Figure 7 is a Hobo no remote communication data logger logging various temperatures, counts from hot water drawn off and relative humidity per minute. The Power track analysers logged power, current, voltage and power factor per minute for geyser and the whole building. The Smart connectors at the connecting end of the sensors were connected to the logger via jack ports. The digital pulse input adapters were incorporated to all the sensors and they convert analogue signals to digital in order to reduce errors. Finally, the solar radiation shield was used to protect the temperature and relative humidity sensor. Figure 8 shows the built programme flow chart.
In the schematic diagram (Figure 8), the different metering transducers and sensors to measure the respective parameters are shown. The main electric power consumption and total current drawn to the building was measured by power track analyser 1. The device was installed on the main distribution board with the positive voltage cable (red) and the negative voltage cable (black) connected to the live and neutral lines of the mains. The current transformer of the power track analyser was placed on the live line of the mains. Power track analyser 2 was placed in the line supplying current to the geyser and it measured the current and the total power utilized by the 200 litres, 4kW high pressure geyser. These power meters were configured to log at every 1 minute interval. All the temperature sensors were thermistor resistance sensors. The temperature sensor 1 was well insulated and placed in the cold water inlet pipe to the geyser. Similarly, the temperature sensors 2, 3 and 4 measured the hot water temperatures to the outlet from the geyser, hot water to the bathrooms and kitchen respectively. Furthermore, a flow meter (T-Minol-130) was placed in close proximity to temperature sensor 1 on the hot water pipe and it measured the flow rate of hot water drawn in number of counts per minute. The relative humidity and temperature sensor measured the relative humidity and ambient temperature respectively. The hobo no remote communication (U30 /NRC) was used to log counts equivalent to the volume of water drawn, various temperatures, relative humidity and ambient temperature measurements.
3. 4 Simulation application using Simulink
In order to simulate the processes illustrated in Figure 8, the Simulink platform was used as shown in Figure 9. Figure 9 shows the simulation, architectural and programming sequence for system COP and energy consumption. The input parameters (electrical energy used by geyser and ambient temperature) for the practical ASHP and CHP over 30 minute interval were loaded to the two input sources using the interpolation sequence source from Simulink library. The multiplication block acted as a heat pump extracting aero-thermal energy from the vicinity around the evaporator and electrical energy via the compressor of CHP, while additional electrical energy was needed to drive the fan and water circulation pump of the practical ASHP. This combined energy was dumped into the storage tank as output thermal energy. Both the input and output energy profiles were displayed on the oscilloscope (energy profiles). The oscilloscope (COP profiles) displayed variation of the modelled COP of practical ASHP and of CHP water heaters versus time over 24 hours at 30 minutes interval. On the other hand, the oscilloscope (COP Vs Ta) also displayed variation of the modelled COP of practical ASHP water heater with the average ambient temperature within the duration of the simulation. After loading the respective input parameters into the discrete sources in the simulation model, the Simulink was set to start at time 0 and stop at time 23:30. Upon completion of the simulation, the three oscilloscopes would show the various desired output parameters. (thermal energy absorbed by hot water and COP). The performance of practical ASHP and CHP water heaters of the average weekday and average weekend from the 4-10th of June 2012 was used in the simulation application.
4. Results and discussion
4. 1 Analysis of the average weekday performance
The energy, the COP and temperature analysis of an average weekday (4-8 June 2012) over a 24 hour period are illustrated in Figures 10, 11, 12 and 13. Figure 10 shows the various energy profiles of an average weekday divided into three zones (zone A between 00:00 to 5:30, zone B between 5:30 to 12:00 and zone C between 12:00:23:30). Based on the energy consumed by a convectional geyser with an energy factor of 1, the electrical energy used is equal to thermal energy gained to heat water to set point temperature of 55oC. Hence, from Figure 10, the thermal output energy of practical ASHP water heater corresponded to the input electrical energy used by the geyser. Furthermore, the modelled output thermal energy of CHP water heater was also equal to the input electrical energy of the geyser. On the other hand, the CHP water heater input energy was displayed as Carnot heat pump water heater input energy (model CHPWH) using the ideal COP equation of heat pump. Similarly, the input electrical energy of practical ASHP water heater was achieved using the regression model for COP (model ASPHWH). This energy was much higher than the input energy of CHP water heater as justified by figure 11 (showing the variation of the modelled COP of practical ASHP water heater and COP of CHP water heater with the ambient temperature of an average weekday. From the temperature profiles (figure 12), the COP for both modelled practical ASHP and CHP water heaters depended on the ambient temperature.
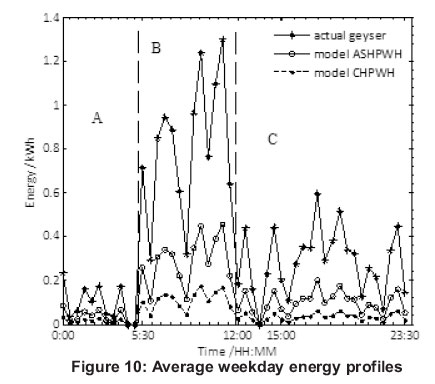
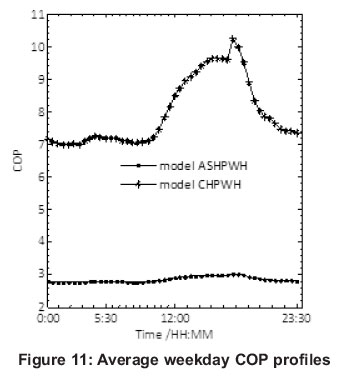
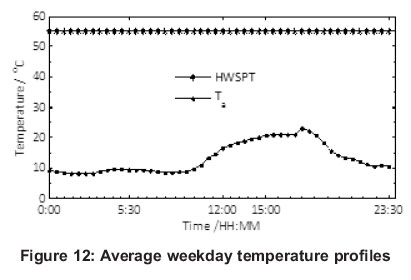
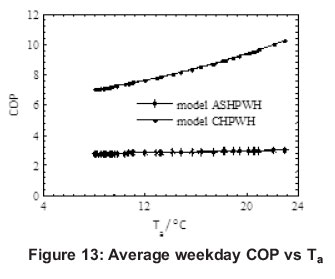
At the 18:00 hour, the maximum average ambient temperature of 23.13oC was measured and corresponded to a COP of 3.00 and 9.98 for both of the systems. Despite the average ASHPWH modelled COP of 2.78 in zone A, there was very little or no hot water drawn which meant that the energy used up compensated for standby losses. Consequently, the energy saved was minimal (1.11 kWh) and the amount of input electrical energy was 0.63 kWh. In zone B, more than 60% of the total average input energy was used by the modelled practical ASHPWH between 6:00 to 12:00 (3.60 kWh) and the thermal energy output of 10.09 kWh was produced, making a significant saving of 6.48 kWh but with an average COP of 2.80. Figure 12 shows the temperature profiles of the average weekday with the set point temperature for hot water at 55oC. However, in practice, there are instances where hot water (below the set point temperature) could be supplied by the geyser due to huge water drawn off just like in the case of a heat pump water heater - thus, indicating that the COP would be higher. Figure 13 illustrates the COP variation in relation to ambient temperature of the average weekday over a 24 hour period. Although the maximum temperature was 22.13oC at time 18:00, the energy saved was not maximum due to the low electrical input as depicted in Figure 10. Table 3 summarizes the comparative analysis of average values over 24 hours for the average weekday. It shows a modelled practical ASHP and CHP water heater's performance under the prevailing conditions using the mathematical modelling equations. The modelled ASHPWH is representing a practical heat pump water heater whose performance was determined from the mathematical model of COP while the CHP water heater represents a heat pump water heater whose performance was determined using the Carnot's equation of heat pump COP. It is also relevant to mention that the efficiency of the modelled ASHP water heater was the ratio of the modelled COP of ASHP water heater to the COP of CHP water heater. Table 3 summarizes the average weekday performance comparison analysis for the modelled ASHP and CHP water heater.
4. 2 Analysis of the average week-end performance
The energy, the COP and temperature analysis of the average weekend profiles over a 24 hour period are illustrated in Figures 14, 15, 16 and 17. From Figure 14, it can be depicted that the practical ASHP water heater used the least electrical input in zone A with a COP of 2.83 and an energy saving of 0.86 kWh. Comparing the COP of zone A to the COP of zone B (2.80), a larger energy saving of 7.93 kWh was achieved due to this significant level of input energy used during this period since the demand for hot water also increased. From Figure 15, the COP profile for both modelled ASHP and modelled CHP water heaters replicated a similar pattern to those profiles shown in Figure 11 (COP profiles of the average weekday).
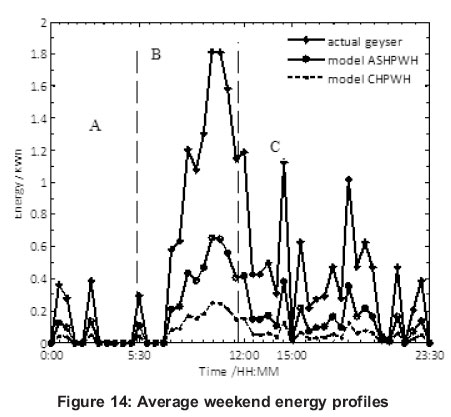
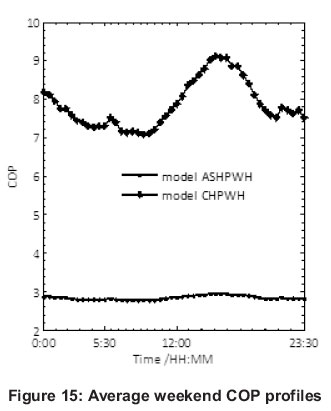
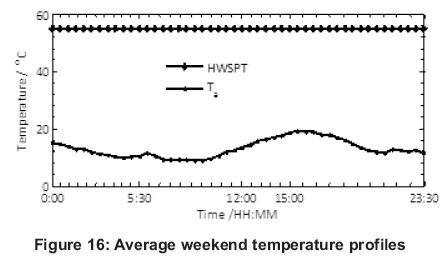
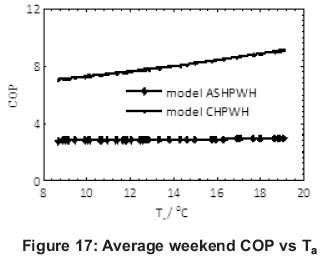
In zone C, there was an increase in the average COP but with a slightly lower electrical input energy as represented by the values 3.02 kWh and 1.08 kWh respectively, compared to Zone B. The temperature ranges (8oC to 23oC) were equal for both the average weekend and average weekday. This argument holds for both the temperature profiles in Figure 16 and the COP variation with average ambient temperature as shown in Figure 17. The maximum average COP of model ASHP water heater was 2.95 and was achieved at time 15:30, when ambient temperature was maximum (19.10oC). The complete analysis is as shown in Table 4.
Table 4 summarizes the average weekend performance comparison analysis for the model ASHP and CHP water heater.
5. Conclusion
The modelled COP of practical ASHP water heater depicted the real life performance of the ASHP water heater with a minimal deviation error due to the exclusion of the other factors that affect COP. Seasonal and annual COP can be accurately determined for the ASHP water heater provided transient evaporator temperature (which in practice differ from the ambient temperature of more than or equal to 4oC) and hot water set temperatures are known. The ASHP water heater is an energy efficient technology for sanitary hot water production, but when compared to the Carnot's heat pump water heater, which does not have auxiliary energy consuming components, the ASHP water heater is 37% to 40% efficient owing to the extra input energy required to run the water circulation pump and axial propeller fan. Mathematical modelling and simulation of COP can be determined without actually measuring the primary factors (load cycle, cold water temperature, etc.) but using theoretical values from the literature. Based on the modelled COP, energy savings and performance can be determined with some degree of confidence for any intending retrofit The ASHP water heater going to be installed provided ambient temperature and hot water set point temperatures are known in conjunction with the baseline profile for the geyser intended to be retrofitted, using the simulation application developed and built in the Simulink environment.
Acknowledgement
We are grateful for Eskom and the Institute of Technology, University of Fort Hare. for their financial supports that facilitated the acquisition of equipment for the research.
References
Bodzin, S. (1997), Air-to-Water Heat Pumps for the Home, Home Energy Magazine Online, July/August 1997. [ Links ]
Digest of South Africa Energy Statistics (2009). Department of Energy. [ Links ]
Domestic water heating and water heater energy consumption in Canada (CBEEDAC, 2005). [ Links ]
Energy Management and conservation handbook (2008). Nitin Goel, Thermo physical properties of refrigerants, CRC Press. [ Links ]
Eskom (2010). Integrated Demand Management www.eskom.co.za/home/about. [ Links ]
Ito S, Miura N and Wang K. (1999). Performance of a heat pump using direct expansion solar collectors. Solar Energy V65, 189-196. [ Links ]
Kline, S. A., et al. (2000). TRNSYS 15 A Transient system simulation program. University of Wisconsin Solar Energy. [ Links ]
MATLAB and Simulink software package (Math work corporation 2011b, version 7.12) [ Links ]
Meyer, J.P., and M. Tshimankinda (1998). Domestic Hot Water Consumption in South African Townhouses, Energy Conversion and Management, 39:7, 679-684. [ Links ]
Morrison, G.L., Anderson, T. and Behnia M. (2004). Seasonal performance rating of heat pump water heaters. Energy Conservation & Management. 76:147-152. [ Links ]
Received 5 March 2013
Revised 25 February 2015














