Optimization analysis of solar-powered average temperature Stirling heat engine

 

 

Khaled M Bataineh

Department of Mechanical Engineering, Jordan University of Science and Technology, Irbid, Jordan

 

 

---

ABSTRACT

This paper investigates the performance of the solar powered dish-Stirling engine using the non-linearized heat loss model of the solar dish collector and the irreversible cycle model of the Stirling engine. Finite time thermodynamic analysis is used to investigate the influence of the finite-rate heat transfer, operating temperatures, heat leak coefficient, and ratio of volume during regeneration processes, regenerator losses, thermal bridges losses on the maximum power output and the corresponding overall efficiency. The maximum overall system efficiency is 32% corresponding to absorber temperature and concentrating ratio of 850 K and 1300, respectively. The present analysis provides the basis for the design of a solar-powered mean temperature differential Stirling engine powered by solar dish system.

Keywords: Stirling engines, finite time thermodynamic, thermal losses, performance, regenerator effectiveness, numerical simulations.

---

 

 

1. Introduction

Solar energy is one of the most attractive renewable energy sources. Stirling heat engines convert heat energy into mechanical energy. Stirling engines work with an external heat supply. This makes them more reliable with lower maintenance requirements and their operation is relatively silent. Moreover, they can operate using low quality fuels and they can also use heat sources that do not depend on any combustion. The working gas can be maintained within the engine and need not be changed between the cycles. The fact that Stirling engines are driven by an external heat supply makes them appropriate for solar thermal applications. Furthermore, as they can combine different heat sources in one application, they are also appropriate for hybrid operations.

In a dish-Stirling system, a dish collector may be used to focus solar energy to supply power. The dish-Stirling system is comprised a parabolic dish collector and a Stirling heat engine. The resulting conversion unit is relatively small compared to other CSP systems. Among the three well- known and established concepts of CSP (Parabolic trough power plants, solar tower power plants, and dish-Stirling systems) the dish-Stirling system has achieved the highest efficiency (Mancini and Heller, 2003; Sahin, 2001).

The first solar application of the Stirling engine is attributed to the Swedish-American inventor and mechanical engineer John Ericsson, who built the dish -Stirling device in 1872 Ericsson invented a solar-powered hot air engine using a reflector to heat the displacer cylinder hot-end. The modern dish-Stirling technology was developed in the late 1970s and in the early 1980s. Eight different dish-Stirling systems, ranging in size from 2 to 50 kW, have been built during the last 20 years (Mancini and Heller, 2003). The dish - Stirling energy system has the highest efficiency for converting solar energy into electricity. A parabolic dish concentrates only the direct radiation that enters the system parallel to its optical axis. So, the solar dish has to be oriented always towards the Sun. As it is a point-concentrating system, it requires two-axes tracking. A point-concentrating system offers the possibility of having very high concentration ratios compared to line- concentration system. With these point-concentrating systems the high concentration ratios result in high receiver temperatures. Receiver temperatures above 800°C have been achieved. Such high operating temperatures allow for a high thermal-mechanical energy conversion efficiency and, consequently, high solar-to-electric efficiencies. Nevertheless, under typical conditions, they have an average solar-to-electric efficiency between 16 and 25% (Mohr et al., 1999).

Finite time finite temperature difference thermodynamics deals with the fact that there must be a finite temperature difference between the working fluid/substance and the source/sink heat reservoirs (with which it is in contact) in order to transfer a finite amount of heat in a finite time interval. It is a modern powerful tool used for performance analysis of practical engineering cycles. Finite time ther-modynamic originated with two independently published papers in 1957 (Chambadal, 1957; Novikov, 1957) and regained its popularity with another independent publication in 1975 by Curzon et al., (1975). Curzon et al. established a theoretical model of a real Carnot heat engine at maximum power output with a different efficiency expression from the well-known Carnot efficiency. Following that, several successful performance analyses and designs of dish - Stirling engine have been carried out during the past thirty years using finite time thermodynamic (Ladas and Ibraham, 1994; Popescu et al., 1996; Chen et al., 1998 Wu, 1998) to name a few. The results obtained by using finite time thermodynamic have even more realistic instructive significance for the optimal design of real solar-driven systems than those derived from traditional equilibrium thermodynamics. Analysing power, specific power and power density optimization of endoreversible and irreversible Stirling engine, and analysing the effect of heat transfer law and quantum characteristics of the working fluid on the Stirling engine performance have received significant attention be many researchers. Ibrahim et al. introduced the finite time analysis to the dynamic performance optimization of Stirling engines (Ladas and Ibrahim, 1994). They analyzed the Stirling engine cycle based on mass and energy balances with associated heat-transfer-rate equations. They concluded that there exists an optimum power output for a given engine design, based on engine speed and heat-transfer contact time. Radcenco and Popescu investigated the power optimization and the optimal distribution of heat transfer area of endoreversible and irreversible cycle with various laws (Popescu et al, 1996). Chen et al. investigated the performance of a solar-driven Stirling engine based on the linearized heat loss model of the solar collector and the irreversible cycle model of the Stirling engine (Chen et al, 1998). They pointed out that their method is valid for other heat loss models of solar collectors and the results obtained are also valid for a solar-driven Ericsson engine system using an ideal gas as its engine work substance .Wu et al. (1998) investigated the effects of heat transfer, regeneration time, and imperfect regeneration on the performance of the irreversible Stirling engine cycle. The results of their work provide a new theoretical basis for evaluating performance and improving Stirling engines. Kaushik and Kumar (2000) investigated the performance of an endoreversible Stirling heat engine using finite time thermodynamics. They found that an endoreversible Stirling heat engine with an ideal regenerator (εR=1.00) has an efficiency that is equal to the efficiency of an endoreversible Carnot heat engine. Yan and Chen (1997) studied the optimal performance of an endoreversible cycle operating between a finite heat source and sink. Sahin (2001) investigated the optimum operating conditions of endoreversible heat engines with radiation and convection heat transfer between the heat source and working fluid as well as convection heat transfer between the heat sink and the working fluid based on simultaneous processes. Senft (1998) studied the theoretical limitations on the performance of a Stirling engine subject to limited heat transfer, external thermal and mechanical losses. The performance analysis and optimization of low temperature differential Stirling heat engines powered by low concentrating solar collectors have been conducted (Chen et al., 1998; Costea et al., 1999; Kongtragool and Wongwises (2003); Kongtragool and Wongvises, (2005); Shahrir et al., 2005; Jose, 2007). Berchowitz et al. established several analyses and simulation methods of the engine (Costea et al., 1999). Kongtragool and Wongvises (2003) found a feasible solution which may lead to a preliminary conceptual design of a workable solar-powered low temperature differential Stirling engine. Results indicated that Stirling engines working with relatively low temperature air are potentially attractive engines of the future. Shahrir et al. (2005) presented a design of a low temperature differential double-acting Stirling engine for solar application. They concluded that there are optimal values of engine speed and swept volume and determined the critical engine parameters. Arenas (2007) described the design, manufacture and testing of a new portable solar kitchen with a large, parabolic solar reflector that folds up into a small volume. He found that the solar kitchen reaches an average power measurement of 175 W, with an energy efficiency of 26.6%. Li et al. (2011) developed a mathematical model of overall thermal efficiency of solar powered, high temperature differential dish-Stirling engine. When using the optimal parameters, their thermal efficiency reached 34%.

Previous studies have focused on high or low temperature Stirling engines, operating under mean temperature parameters, which have not received significant attention. Striling engines operating under mean temperatures do not require high grade expensive material selection nor do they require high-cost solar collectors because of their high concentration ratio. These advantages make Stirling engines very attractive and promising in terms of reliability and cost. The objective of this study is to investigate the optimal performance of solar-powered mean temperature differential dish-Stirling heat engines using finite-time thermodynamics. Thermal losses, imperfect regeneration, and both radiation and convective heat transfer modes are considered. The influence of major parameters such as operating temperatures, effectiveness of regenerator, heat leak coefficient, ratio of volume during regeneration processes, heat capacitance rate of heat source/sink external fluids, regenerator losses, thermal bridges losses on the maximum power output and the corresponding overall efficiency are investigated. Furthermore, this paper aims at providing the technical guidelines for the design of a solar-powered mean temperature differential Stirling engine powered by a solar dish system.

 

2. Solar - dish Stirling engine

The dish- Stirling engine system shown in Figure 1 uses a parabolic mirror to reflect and concentrate incoming direct insolation to receiver (focal point). Concentration of solar radiation is needed to achieve the temperatures required to effectively convert heat to work. The concentration ratio is one of the central parameters of the collector. To achieve adequate concentration of insolation the dish needs to track sun in two axes. The concentrated solar radiation is absorbed by the receiver (absorber) and transferred to the engine.

 

 

2.1 Stirling Engine cycle

The Stirling cycle is a thermodynamic cycle in which thermal energy is transformed into mechanical energy. The working gas is compressed at lower temperatures and is expanded at higher temperatures. The net result of these processes is converting heat into mechanical work. Besides the isothermal compression and expansion at different temperature levels, the Stirling cycle includes isochoric heating and cooling in order to change from one temperature level to the other. The P-V and T-S diagrams for the ideal cycle (all processes are reversible, i.e. there is no dissipation) are shown in Figure 2. The four ideal cycle processes shown in Figure 2 are:

• Process 1-2: Isothermal compression of the working gas under heat release at low temperature.
• Process 2-3: Isochoric heating of the working gas.
• Process 3-4: Isothermal expansion of the working gas under heat absorption at high temperature.
• Process 4-1: Isochoric cooling of the working gas.

The Stirling engines need efficient heat exchangers in order to transport thermal energy over the engine boundaries. A key component of Stirling engines is the regenerator, which stores and releases thermal energy periodically. An ideal regenerator will store the heat that is released by the working gas in the process 4-1 (isochoric cooling) and gives the same amount of heat back to the working gas in the process 2-3 (isochoric heating). An idea regenerator considerably raises the efficiency of the engine by maintaining heat within the system that otherwise would be exchanged with the environment. It thereby increases the heat flow from the high temperature reservoir to the low temperature reservoir without any additional mechanical work.

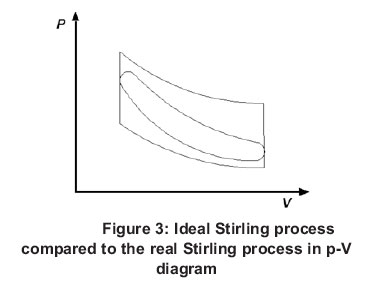
The real Stirling engine cycle deviates from an ideal Stirling cycle. The efficiency of the conversion of thermal energy to mechanical work in the real cycle is lower than that in the ideal process even with the same upper and lower temperature limits and the same gas volumes and masses. Figure 3 compares the p-V diagrams of a real cycle and the p-V diagrams of an ideal cycle. It can be seen that the area enclosed by the curve of the real process, which indicates the released work, is smaller than that enclosed by the ideal cycle curve. This difference might be attributed to the following:

• Dissipation losses due to mechanical friction losses, pressure losses in the working gas, or gas leakage.
• Permanent temperature changes.
• Actual regenerator efficiency cannot be 100%.
• Heat loss through the engine material.
• Adiabatic losses (pressure losses due to the expansion and compression processes).
• Clearance (dead) volume, which impedes that the whole working gas is subject to the heating and cooling processes and which reduces the compression ratio.

 

 

2.2 Efficiency parameters of a dish - engine system

The overall efficiency of a dish - Stirling system, i.e. the solar-to-mechanical efficiency, depends on the following parameters:

• Solar irradiance: The mechanical power output and the respective system efficiency of the dish -engine system depends on solar radiation conditions. A higher power output is expected with higher average irradiance values. However, higher irradiance results in a high receiver temperature and may cause high thermal losses.
• Radiation concentration: A higher concentration ratio results in a higher temperature in the absorber increasing the thermal-to mechanic efficiency of the system. However, higher concentration ratios require expensive manufacturing processes (of the absorber or possibly the whole system).
• Intercept factor: A reduced intercept factor will reduce the energy flow to the receiver, but it may increase the mean radiant flux density when only the central parts of the Sun image hit the receiver aperture.
• Thermal receiver efficiency: The radiative and convective heat losses affect the receiver efficiency.
• Engine efficiency.

 

3. Finite time Thermodynamics analysis of the system

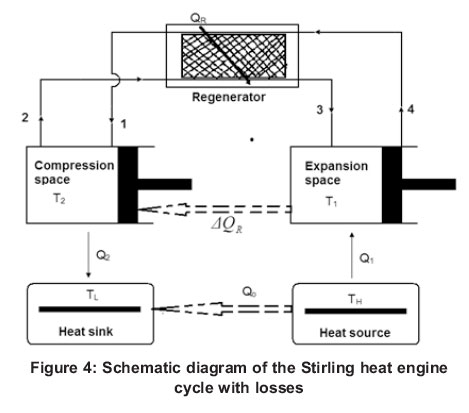
The objective of this paper is to develop a mathematical model for the dish solar collector, the Stirling engine, as well as the combination of the dish-Stirling engine system. Figure 4 is a schematic diagram of a Stirling heat engine cycle with finite-time heat transfer and regenerative heat losses as well as conductive thermal bridging losses from the absorber to the heat sink. We assumed finite heat exchanger areas, finite heat transfer coefficients and a finite rotation frequency, which induces speed-dependent fluid flows and time-dependent processes. The working substance in the Stirling cycle is assumed to be an ideal gas. Figure 5 is the Stirling heat engine T-S diagram. This cycle approximates the compression stroke of a real Stirling heat engine as an isothermal heat rejection process (1-2) to the low temperature sink. The heat addition to the working fluid from the regenerator is modelled as the constant volume process (2-3). Since this external heat transfer process occurs in finite time across finite temperature differences, it is an irreversible isothermal process. The expansion stroke producing work is modelled as an isothermal heat addition process (3-4) from a high temperature heat source. Finally the heat rejection to the regenerator is modelled as the constant volume process (4-1). Similar to process 2-3, it is also considered an irreversible isothermal process. If the regenerator is ideal, the heat absorbed during process 4-1 should be equal to the heat rejected during process 2-3, however, the ideal regenerator requires an infinite area or infinite regeneration time to transfer a finite heat amount, and this is impractical. Therefore, it is desirable to consider a real regenerator with heat losses ∆Q_R. In addition, we also consider conductive thermal bridging losses Qo from the absorber to the heat sink.

 

 

 

 

3.1 Dish analysis

The useful thermal power provided by the solar collector denoted as q_h, considering conduction, convection, and radiation losses are given by (Kongtragool and Wongvises, 2005):

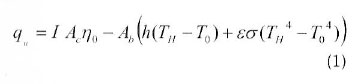
where I is the direct solar flux intensity, A_c is the collector projected area, η₀ is the collector optical efficiency. A_b is the absorber area, h is the overall convective heat transfer coefficient, T_H is the absorber temperature, T_o is the ambient temperature, ε is the emissivity factor of the collector, and σ is the Stefan's constant.

Thermal efficiency η_s of the dish collector is:

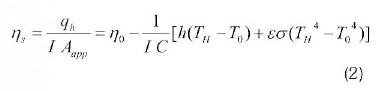
Where, C is the collector concentrating ratio.

3.2 Regenerative heat loss to the regenerator

It is important to consider the finite heat transfer through the regenerator. The regenerative processes are affected by internal thermal resistances to and from the thermal regenerator. Thus, regenerative losses are inevitable. Let DQ_R be the regenerative heat loss per cycle during the two regeneration processes, which is proportional to the temperature difference of the working fluid therefore the regenerative heat transfer is given by Kaushik and Kumar, (2001); Howell et al., (1977):

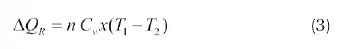
where C_v is the specific heat capacity of the working substance at constant volume in J/(kg K), and χ is the fractional deviation from ideal regeneration (i.e. χ = 1 for no- regeneration and χ = 0 for ideal regeneration), and n is the number of mole. Then:

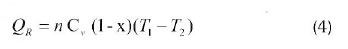
Due to the influence of irreversibility of the finite rate of heat transfer, the regenerative processes need a finite non-negligible time compared with the time of the two isothermal processes. In order to calculate the time of the regenerative processes, it is assumed that the temperature of the working substance in the regenerative processes is a function of time as given by Durmayaz et al, (2004) and is proportional to the temperature difference of the working fluid.

Where M is the proportionality constant and is independent of the temperature difference but depends on the property of regenerative material, called regenerative time constant and the ± sign belong to the heating and cooling processes, respectively. The time of two regenerative processes is:

Where, t₃ and t₄ are the time taken during two regenerative processes 2-3 and 4-1, respectively.

3.3 Heat transfer across the Stirling cycle

We need to consider radiation and convection modes of heat transfer between the absorber and the working fluid. Convection heat transfer is assumed to be the main mode of heat transfer between the heat sink and the working fluid. There are always thermal resistances between the working substance and the external heat reservoirs in the Stirling engine. In order to obtain a certain power output, the temperature of the working substance must therefore be different from that of the heat reservoirs. The amounts of heat Q₁ and Q₂ absorbed from the heat source at temperature Τ₁ and released to the heat sink at temperature T₂ by the working fluid during the two isothermal processes are:

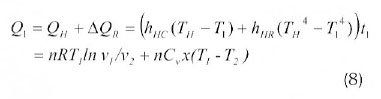
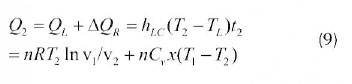
Where h_HC is the high temperature side convection heat transfer coefficient, h_HR is the high temperature side radiation heat transfer coefficient, h_LC is the low temperature side convection heat transfer coefficient, η is the mole number of the working gas, R is the universal gas constant, t₁, t₂ are the times spent on the two isothermal processes at temperatures T₁ and T₂, respectively (process 3-4 and 1-2)., χ is the fractional deviation from ideal regeneration (i.e. χ = 1 for no-regeneration and χ = 0 for ideal regeneration), and v₁ and v₂are specific volumes of the working fluid along the constant-volume heating and cooling processes, in m³/kg, and v₂/v₁is the volume compression ratio during the regenerative processes λ, i.e.

The conductive thermal bridging losses from the absorber at temperature T_H to the heat sink at temperature T_c is assumed to be proportional to the cycle time and is given by (Durmayaz et al., 2004):

where k_o is the heat leak coefficient between the absorber and the heat sink and τ is the cyclic period. Taking in account the major irreversibility mentioned, the net amount of heat released from the absorber Q_H at T_H and absorbed by the heat sink Q_L at T_L are given by:

Thus the total cycle time is given by:

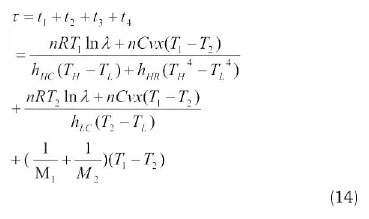
For the thermodynamic cycle 1-2-3-4-1, the magnitude of the network for this finite time cycle is:

The power output and thermal efficiency are given by:

Now from equations (3)-(17) the power output and thermal efficiency of Stirling engine are given by:

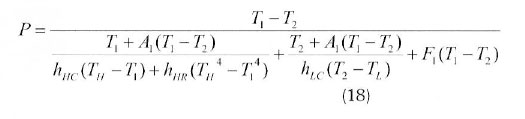
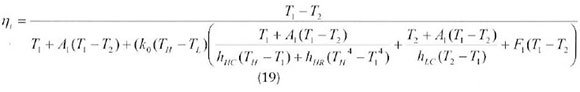
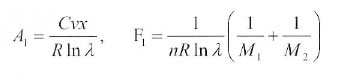
Where,

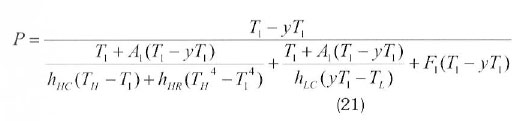
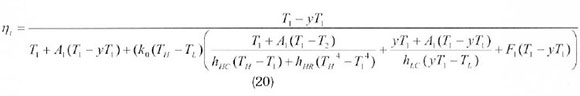
For the sake of convenience, a new parameter y = T₂/T₁ is introduced into eqs. (18) and (19), then we have:

To maximize the power output, take the derivative of eq. (18) with respect to the temperature T₁ and χ and equate it to zero, namely

the optimal working fluid temperature T_1opt and x_opt for this condition can be obtained from eq. (20) and (21), respectively:

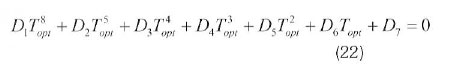
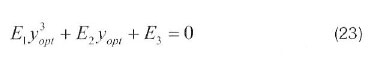
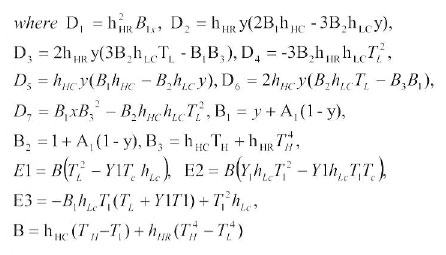
Solving eq. 22 for the optimal fluid working temperature, the maximum power output and the corresponding optimal thermal efficiency of the Stirling engine are:

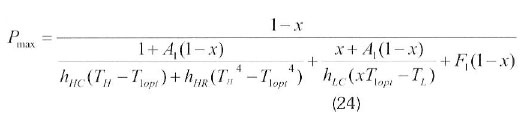
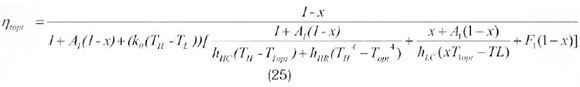
The maximum power thermal efficiency of the system is the product of the thermal efficiency of the collector and the optimal thermal efficiency of the Stirling engine (Kongtragool and Wongvises, 2005) namely:

 

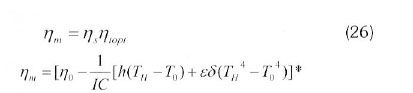
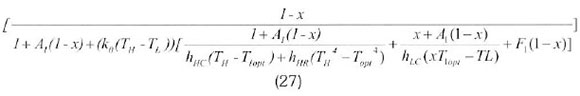
4. Numerical results and discussion

In order to evaluate the effect of the absorber temperature (TH), the concentrating ratio(C), the effectiveness of the regenerator x, temperature ratio y, and the heat leak coefficient (ko) on the solar-powered dish-Stirling heat engine system, all the other parameters will be kept constant at

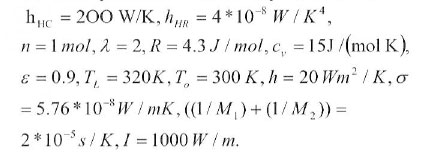
The above values are reasonable values corresponding to the typical operating condition of Stiring engines found in literature.

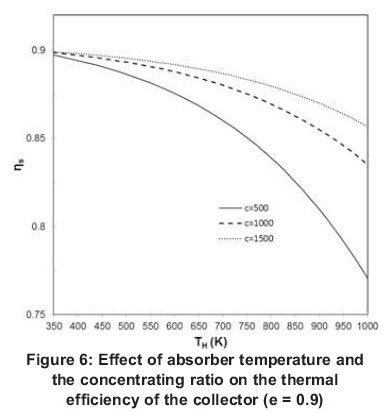
The effect of the absorber temperature T_Hand the concentrating ratio C on thermal efficiency of the collector is shown in Figure 6. It can be seen that the thermal efficiency of the collector decreases rapidly with increasing temperature of the absorber T_H. The rate of this decrease is inversely proportional to the concentration ratio C. The reduction in the thermal efficiency is due to increase in convective and radiative heat losses at higher absorber temperature. Finally, at low temperature, the maximum thermal efficiency is nearly equal to the optical efficiency of the concentrator.

 

 

The effect of absorber temperature and regenerator effectiveness on the optimal thermal Stirling efficiency is investigated and shown in Figure 7. It can be seen from Figure 7 that the thermal efficiency of the Stirling engine increases rapidly at the beginning until the absorber temperature reaches 750 K. The results of the model show that further increase in the absorber temperature will not improve the optimal efficiency of the engine significantly. The reason for this behaviour is due to the conductive thermal bridging losses, which increases with increasing absorber temperature. At high absorber temperature, the radiation losses start to dominate the heat transfer process. It is also found that the optimal thermal efficiency of the Stirling engine increases significantly along with regenerator efficiency.

 

 

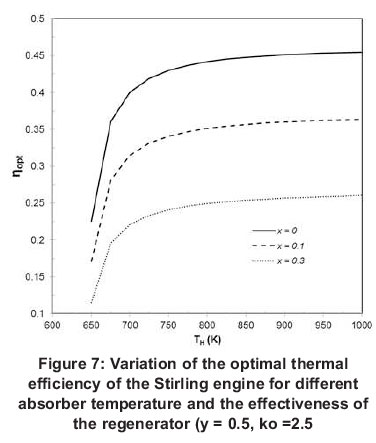
Figure 8 shows the effect of the absorber temperature (T_H) on the thermal efficiency of dish-Stirling engine system (ηm) for several values of concentrating ratio. It can be seen that for a given concentrating ratio, the maximum power thermal efficiency increases with the increase of the absorber temperature until it reaches the optimal value, and then decreases with increasing absorber temperature. The reason for this decrease is due to increasing thermal losses at the absorber due to high temperature differences. Furthermore, the thermal system efficiency increases with the increase of the concentrating ratio. The rate of reduction of the system's efficiency at higher absorber temperatures is slowed down by high values of concentration ratios C. The highest thermal system efficiency is 32% corresponding to an optimum absorber temperature of 850 K, while the Carnot efficiency reaches about 50%.

 

 

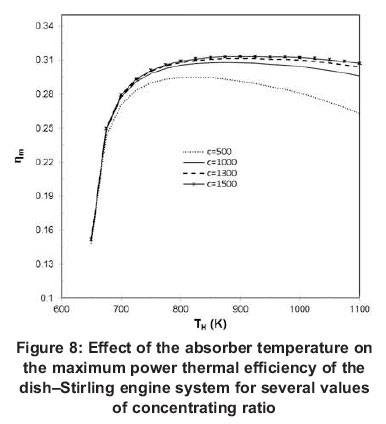
The effect of regenerator effectiveness on the maximum power thermal efficiency of the system is shown in Figure 9. It is seen that the maximum power efficiency increases with the increase of the effectiveness of the regenerator. It is also observed that when there is no heat loss through the regenerator (x = 0), the Stirling heat engine attains an efficiency almost equal to the Curzon-Ahlborn efficiency CA = 39.49 of an endoreversible Carnot heat engine at T_H = 850K. Nevertheless, an endoreversible Stirling heat engine with an ideal regenerator is as efficient as an endoreversible Carnot heat engine but it is not practical since an ideal regeneration requires infinite time or infinite regenerative area. Furthermore, we see that if the regenerator effectiveness drops from 100% to 90%, the thermal efficiency will drop to around 30% for T_H = 850 K. Finally, the regenerator effectiveness has smaller effect on system efficiency for low values of T_H compared to high values of T_H.

 

 

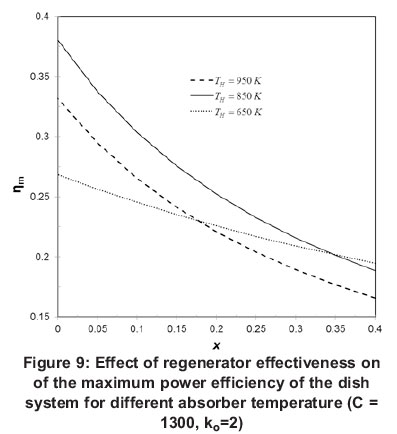
The effect of the heat leak coefficient k_o on the system thermal efficiency is shown in Figure 10. It is seen from Figure 10 that the heat leak coefficient reduces the maximum power efficiency of the system. It is also observed that rate of decrease is higher at lower absorber temperature.

 

 

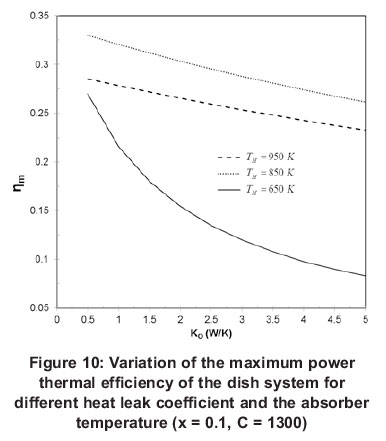
Figure 11 shows the variations of concentration ratio with maximum power efficiency of the dish-Stirling engine. According to this diagram, we can see that the system efficiency rises only slightly for concentration ratios over 1200. Taking the effect of a higher concentration ratio, the consequent higher receiver temperature and the higher thermal-to-mechanic efficiency isolated, we could suppose that the system efficiency should show a stronger dependence on the concentration ratio. However, higher thermal losses at higher temperatures reduce this dependence considerably. Taking this into consideration and taking into account the expected higher costs for the construction of dishes with a higher concentration ratio it may be not economical to aspire to concentration ratios higher than 1200.

 

 

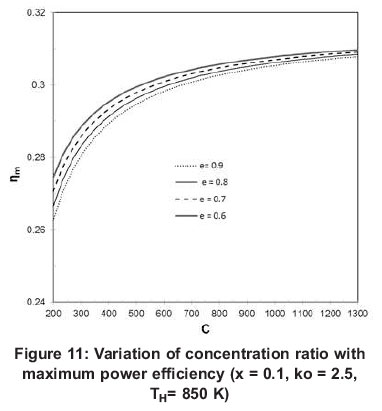
Figure 12 shows the variation of maximum power output of the system with respect to absorber temperature for different combination of temperature ratio and regenerator effectiveness. It can be seen from Figure 12 that the maximum power increases with increasing absorber temperature. The rate of power increase at T₁/T₂ = 0.5 is higher than that corresponding to T₁/T₂ = 0.7. The rate of power increase with absorber temperature increases with increasing regenerator effectiveness.

 

 

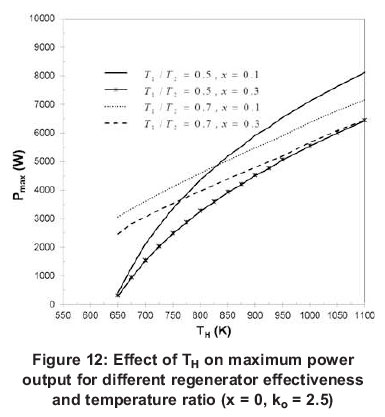
Figure 13 shows the variations of system efficiency with the temperature ratios y. This increases very rapidly with an increasing temperature ratio until it reaches a maximum value at T₁/T₂= 0.42. It is shown that the system efficiency increases very rapidly when the temperature ratio increases until an optimal value is reached. Past the optimal temperature ratio, the efficiency rapidly descends. The value of the optimal temperature ratio decreases with the increase in absorber temperature.

 

 

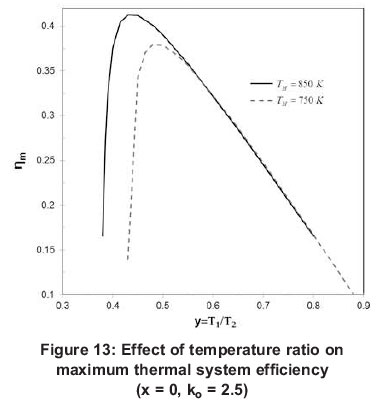
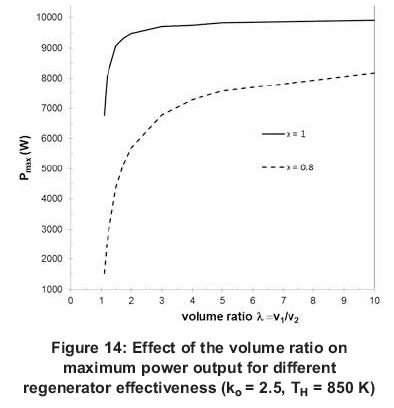
Figure 14 shows the effect of the volume ratio v₁/v₂on maximum power output. The power output increases very rapidly when the volume increases and starts to level off sharply when the volume ratio reaches 2 for ideal regeneration. However, when regeneration effectiveness equals 0.2, the power output increases rapidly at the beginning and the increase will start slowing down with the volume ratio. It can be observed that for ideal regeneration, the power output after a certain ratio is no longer a function of volume ratio. This is not the case for non- ideal regeneration. It can be seen that the effect of volume ratio is more notable for the non-ideal regeneration than that for an ideal regeneration. Finally, in order to have high power output, the constant cooling volume should be as high as possible compared to the constant heating volume.

 

 

5. Conclusion

Finite-time thermodynamics is used to optimize the power output and the thermal efficiency of the dish - Stirling engine when regenerative losses and thermal bridges losses are taken into account. The results show that the optimal thermal efficiency of the Stirling engine increases significantly with regenerator efficiency. It is also found that maximum power output increases with increasing absorber temperature. The highest thermal system efficiency is 32% when the corresponding optimum absorber temperature is equal to 850 K. For the non -ideal regenerator, maximum work output corresponds to high volume ratio values. The present analysis provides theoretical guidelines for the basis for the design, performance evaluation and system optimization of solar-powered mean temperature differential dish-Stirling engines powered by a solar dish system.

 

Nomenclature

A area, m²

C collector concentration ratio

C_v specific heat capacity, J mol^-1 k^-1

K_o heat leak coefficient, W K^-1

h heat transfer coefficient, WK^-1 or WK^-4

l direct solar flux intensity, Wm^-2

n the mole number of the working fluid, mol

M regenerative time constant, K s^-1

P power, W

Q heat transfer, J

q_u heat gain, W

R gas constant, J mol^-1 k^-1

t time, s

W work, W

λ ratio of volume during regenerative

τ cyclic period, s

η thermal efficiency

ε emissivity factor

σ Stefan's constant, W m^-2 K^-4

x effectiveness of the regenerator

Subscripts

b absorber

HC high temperature side convection

HR high temperature side radiation

L heat sink

LC low temperature side convection

m the system

R regenerator

t Stirling engine

o process ambient or optics

1-4 the processes

 

References

Arenas, José M. (2007). Design, development and testing of a portable parabolic solar kitchen. Renewable Energy 32, 257-266.         [ Links ]

Chambadal, P, (1957). Les Centrales Nucléaires, Armand Colin, Paris, 41-58.         [ Links ]

Chen Lingen, Yan Zijun, Chen Lixuan, and Andresen Biarne (1998). Efficiency Bound of a Solar-Driven Stirling Heat Engine System, Int. J. Energy Res., 22, 9, pp. 805-812.         [ Links ]

Costea, M., Petrescu, S., and Harman, C. (1999). The Effect of Irreversibilities on Solar Stirling engine Cycle Performance, Energy Convers Manage, 40, 15-16, pp. 1723-1731.         [ Links ]

Curzon, F L., and Ahlborn, B. (1975). Efficiency of Carnot Heat Engine at Maximum Power Output, Am. J. Phys, 43 (1975), 2, pp. 22-24.         [ Links ]

Durmayaz, A., et al., (2004). Optimization of Thermal Systems Based on Finite-Time Thermodynamics and Thermoeconomics, Prog Energy Combust Sci., 30, 2, pp. 175-271.         [ Links ]

Howell, J. R., and Bannerot, R. B. (1977). Optimum Solar Collector Operation for Maximizing Cycle Work Output, Solar Energy, 19, 2, pp. 149-153.         [ Links ]

Kaushik S.C. and Kumar S. (2000). Finite time thermodynamic analysis of endoreversible Stirling heat engine with regenerative losses. Energy 25: 989e1003.         [ Links ]

Kaushik S.C. and Kumar S. (2001). Finite time thermodynamic evaluation of irreversible Ericsson and Stirling heat engines. Energy Convers Manage; 42:295e312.         [ Links ]

Kodal Ali, and Sahin Bahri (2003). Finite size thermoeconomic optimization for irreversible heat engines. Int J Thermal Sci; 42:777e82.         [ Links ]

Kongtragool Bancha and Wongwises Somechai (2003). A review of solar-powered Stirling engines and low temperature differential Stirling engines [J]. Renew Sustain Energy Rev; 7: 131e54.

Kongtragool Bancha, and Wongwises Somehai (2005). Optimum absorber temperature of a once-reflecting full conical concentrator of a low-temperature differential Stirling engines. Renew Energy; 30:1671-87.         [ Links ]

Ladas H.G. and Ibrahim O.M. (1994). Finite-time view of the Stirling engine. Energy; 19(8):837-43.         [ Links ]

Li Yaqi, He Yaling, Wang Weiwei (2011). Optimization of solar-powered Stirling heat engine with finite-time Thermodynamics. Renewable Energy 36 421-427.         [ Links ]

Mancini, T., and Heller, P., (2003). Dish-Stirling Systems: An Overview of Development and Status [J], J. Solar Energy Eng., 125, 2, pp. 135-151.         [ Links ]

Mohr, M., Svoboda, P, and Unger, H. (1999). Praxis solarthermischer Kraftwerke. Berlin, Heidelberg: Springer.         [ Links ]

Novikov, H., 1957, Atomnaya Energiya, 3, 409-412.         [ Links ]

Popescu G, Radcenco V, Costea M, and Feidt M. (1996). Optimization of an endo-exo-irreversible Stirling motor. Rev. Gen. Therm. (35):656-661.         [ Links ]

Salah El-Din M.M. (1999). Thermodynamic optimization of irreversible solar heat engines. Renew Energy; 17:183-90.         [ Links ]

Sahin, A. Z., (2001). Finite-Time Thermodynamic Analysis of a Solar Driven Heat Engine, Exergy Int., 1, 2, pp. 122-126.         [ Links ]

Senft JR. (1998). Theoretical limits on the performance of Stirling engine. Int J Energy Res; 22:991-1000.         [ Links ]

Shahrir Abdullah, Belal F. Yousif, and Kamaruzzaman Sopian (2005). Design consideration of low temperature differential double-acting Stirling engine for solar application. Renewable Energy 30, 1923-1941.         [ Links ]

Thombarea D.G. and Verma S.K. (2008). Technological development in the Stirling cycle engines. Renewable and Sustainable Energy Reviews; 12:1-38.         [ Links ]

Wang J.T. and Chen J. (2002). Influence of several irreversible losses on the performance of a ferroelectric Stirling refrigeration-cycle. Appl Energy; 72: 495-511.         [ Links ]

Wu, F., et al., (1998). Performance and Optimization Criteria of Forward and Reverse Quantum Stirling Cycles, Energy Conversion and Management, 39, 8, pp. 733-739.         [ Links ]

Wu F, Chen LG, Sun FR, et al. (2008). Performance optimization of Stirling engine and cooler based on finite-time thermodynamic. Beijing: Chemical Industry Press p. 59.         [ Links ]

Yan Z, and Chen L. (1997). Optimal performance of an endoreversible cycle operating between a heat source and sink of finite capacities. J Phys A; 30: 8119-27.         [ Links ]

 

 

Received 19 February 2014
Revised 13 February 2015