Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
Journal of Energy in Southern Africa
On-line version ISSN 2413-3051
Print version ISSN 1021-447X
J. energy South. Afr. vol.25 n.4 Cape Town Nov. 2014
ANN-based evaluation of wind power generation: A case study in Kutahya, Turkey
Mustafa Arif Özgür
Department of Mechanical Engineering, Engineering Faculty, Dumlupinar University, Kutahya, Turkey
ABSTRACT
Wind energy is one of the most significant and rapidly developing renewable energy sources in the world and it provides a clean energy resource, which is a promising alternative in the short term in Turkey. The wind energy potential in various parts of Turkey is becoming economical due to reductions in wind turbine costs, and in fossil fuel atmospheric pollution. This paper is to present, in brief, wind potential in Turkey and to perform an investigation on the wind energy potential of the Kutahya region. A wind measurement station was established at Dumlupinar University Main Campus in order to □gure out the wind energy potential in the province. This study analyses the electricity generation capacity of the Kutahya region, Turkey, which uses the wind power system. In the study, the wind data collected from wind measurement stations between July 2001 and June 2004 (36 months) were evaluated to determine the energy potential of the region. Using this energy potential value, the power generation capacity of Kutahya was investigated for 17 different wind turbines. In this analysis, an ANN-based model and Weibull and Rayleigh distribution models were used to determine the power generation. In the ANN model, different feed-forward back propagation learning algorithms, namely Pola-Ribiere Conjugate Gradient, Levenberg-Marquardt and Scaled Conjugate Gradient were applied. The best appropriate model was determined as Levenberg-Marquardt with 15 neurons in a single hidden layer. Using the best ANN topology, it was determined that all the turbines were profitable except turbine type 1. The system with the turbine type 3 was decisively the most profitable case as determined at the end of the study according to Net Present Value concept.
Keywords: Levenberg-Marquardt; Net Present Value; Pola-Ribiere Conjugate Gradient; Rayleigh distribution; Scaled Conjugate Gradient; Weibull distribution
1. Introduction
The most important issue of today is to use natural energy sources in an efficient way which will not pollute the environment. The energy producers have an obligation to solve the environmental problems caused while producing energy for humanity's need today as well as tomorrow. There is a relation between energy and the environment. Environmental pollution increases with energy production and consumption; therefore, both the subjects must be handled together. In this regard, energy resources are necessary to be evaluated in terms of reserves, geographic distribution, production rates, pricing stability, business conditions, source credibility, and environmental interaction. Under these conditions, a sustainable and environmentally clean use of energy sources is urgently needed.
The wind potential assessment of a site requires the knowledge of the distribution law of the wind speed measured on the site. The statistical treatment of these measurements makes it possible to have a discrete distribution law. However, to obtain a more accurate analysis of the wind potential, a continuous distribution law is essential. For this purpose, the Weibull and Rayleigh models are often used (Thiaw, 2010). Previous studies have proven that the Weibull distribution function has its merits in wind resource assessment due to its great flexibility and simplicity, but particularly, it has been found to fit a wide collection of recorded wind data (Ulgen and Hepbasli, 2002; Dorvlo, 2002; Karsli and Gecit, 2003; Sulaiman et al., 2002; Celik, 2004; Keyhani et al., 2010; Arslan, 2010; Ouammi et al., 2010; Ozgur and Kose, 2006; Jaramillo and Borja, 2004; Chang et al., 2003 ).
Wind energy potential is not easily estimated because, contrary to solar energy, it depends on the site characteristics and topography to a large degree, as wind speeds are influenced strongly by local topographical features. The classification and characterization of an area as having high- or low-wind potential requires significant effort, as wind speed and direction present extreme transitions at most sites and demand a detailed study of spatial and temporal variations of wind speed values. Before determining the wind farm site, the hourly and monthly mean wind speed, wind speed distributions as well as the wind power densities should be analysed carefully (Keyhani et al., 2010).
In the literature, several studies dealing with artificial neural networks (ANNs) are available. One such example is the work of Dombayci and Gölcü (2009). They developed an ANN model to predict the ambient temperature for Denizli, another city in Turkey. The results show that the ANN approach is a reliable model for ambient temperature prediction. Kalogirou et al. (1999) programmed an ANN to learn to predict the performance of a thermosiphon solar domestic water heating system. An ANN was conditioned to use performance data for four types of systems, all employing the same collector panel under varying weather conditions. Li and Shi (2010) investigated three different ANNs namely adaptive linear element, back propagation, and radial basis function to predict wind speeds. The results show that even for the same wind data set, no single neural network model outperforms other universally in terms of all evaluation metrics. Moreover, the selection of the type of neural networks for best performance is also dependent upon the data sources. Mohandes et al. (1998) in their study used neural networks technique for wind speed prediction and compared its performance with that of an autoregressive model. Results on testing data indicate that the neural network approach outperforms the autoregressive model as indicated by the prediction graph and by the root mean square errors. Öztopal (2006) in his study presented the necessary weighting factors of surrounding stations to predict about a pivot using an ANN technique. The developed ANN model was found to predict the wind speeds for the winter season very accurately. Çam et al. (2005) in their study developed an ANN model to predict the average wind speed and wind energy values for the seven regions of Turkey. The network has successfully predicted the required output values for the test data; the mean error levels for the regions differed between 3% and 6%. Determining a distribution law for the speeds can be considered as a nonlinear regression problem, in which the distribution law (Weibull and Rayleigh) is identified so as to get nearer the discrete law. As regards function approximation, the techniques based on the ANN approach have, however, shown that they can deliver very good performances (Thiaw, 2010; Carolin and Fernandez, 2008; Jafarian and Ranjbar, 2010).
In this study, the wind data collected between July 2001 and June 2004 (36 months) was evaluated to determine the energy potential of the region. Using this potential, the power generation capacity of Kutahya was investigated for 17 different wind turbines. For this purpose, an ANN-based model was used besides Weibull and Rayleigh distribution models. In the ANN model, different feedforward back propagation learning algorithms, namely Pola-Ribiere Conjugate Gradient (CGP), Levenberg-Marquardt (LM) and Scaled Conjugate (SCG) Gradient, were applied. Finally, the models were evaluated using the net present value (NPV) analysis.
2. Materials and methods
2.1. Study area
2.1.1. Site description
The study area is the city of Kutahya, which is surrounded by mountains from the east and south, is located at an altitude of 969 m and has a population of 200 000. Situated at 39°42' latitude and 29°93' longitude, it lies on the Western Central part of the Aegean Region and therefore displays geographical properties similar to those of the Aegean, Marmara and Central Anatolia regions. The main campus of Dumlupinar University is the site of the study; it is situated at 39°29'6,34'' latitude and 29°54'4,04'' longitude and located at an altitude of 1094 m as shown in Figure 1 (Kose et al., 2004; Ozgur et al., 2009).
2.1.2. Wind characteristics of the region
According to data obtained between the years 1975 and 2010, average annual temperature, average sunshine duration time and average rainfall in the Kutahya province are measured as 10.8 °C, 5.8 hours and 45.4 kg/m2, respectively (DMI, 2011). Kutahya has a transition climate (otherwise known as a semi-continental climate). In general, Kutahya has low wind speeds and therefore, limited wind energy potential. However, there may be specific sites and applications where wind is a cost-effective option.
As seen in Figure.2a, average wind speed, blowing from the direction of North (N) and South-South-West (SSW) is 6.24 m/s and 6.00 m/s, respectively. In this study, the prevailing wind direction was determined as East (E) with a frequency distribution rate of 18.15% (see Figure.2b) (Ozgur, 2006).
The wind data used in the study was collected between July 2001 and June 2004 in 10 minute intervals and from various parts of the region (for detailed information see reference (Kose et al., 2004; Ozgur et al., 2009; Ozgur, 2006; Ozgur and Kose, 2006). The maximum monthly average wind speed was recorded as 5.3 m/s in February, when the minimum wind speed was recorded as 3.9 m/s in September. The wind data used in the study is as given in Figure 3.
2.2. Selected wind turbines
In the study, 17 different turbine models fabricated by four different manufacturers were selected to determine the power generation capacity of the study area. The installed capacities (IC) of these turbines range between 200 and 1650 kW, where the hub heights range between 36 and 85 m. The technical characteristics of related turbines are given in Table 1 (Ammonit, 2011).
2.3. Classical method for wind potential and energy generation
2.3.1. Weibull distribution function
Weibull probability density function (PDF) is a special case of the generalized two-parameter gamma distribution. The Weibull distribution can be characterized by f(V) of PDF and F(V) of cumulative distribution function (Bury, 1975; Fawzan, 2000). The PDF of the two-parameter Weibull distribution is given by the following equation:
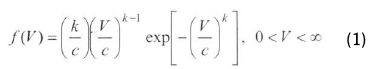
where c, k and V are the scale parameter, shape parameter, and wind speed, respectively. The cumulative distribution function is given by the equation (Hennesey, 1977; Stevens and Smulders, 1979; Garcia et al., 1997):

Here, the relation between c and k is as follows:

where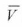 is the average wind speed. Γ(...) is the Gamma function, and is given as
is the average wind speed. Γ(...) is the Gamma function, and is given as

The standard deviation of the wind speed (σ) is determined by the following equation:
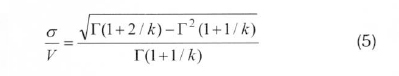
After calculating the parameters c and k, the most frequent wind speed and the maximum energetic wind speed are given by Eq. (6) and (7), respectively, which are as follows:
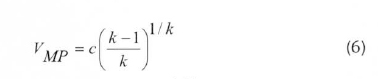
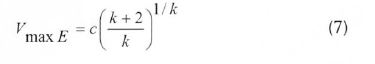
The shape parameter, k. commonly ranges between 1.5 and 3.0. When it assumes the value 2.0, it is called the Rayleigh distribution, and the PDF for the Rayleigh distribution can then be simplified as shown in Eq. (8).
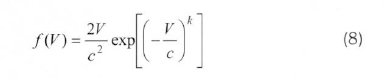
2.3.2. Power extracted from wind
The kinetic energy in air of mass 'm' moving with speed V is given by the following in SI units:
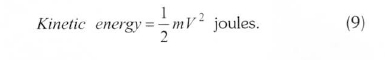
The volumetric flow rate is A∙V, the mass flow rate of the air in kilograms per second is ρAV , and the power is given by the following (Patel, 1942):
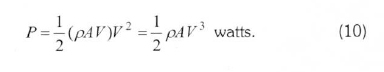
Here, ρ and A. respectively, define the density in kg/m3 and the area swept by the rotor in m2. Therefore, the wind-power density is given by the Eq. (11) in terms of the Weibull PDF, and the wind energy density is given by Eq. (12) for a period T.
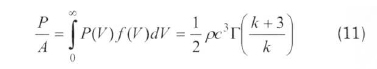
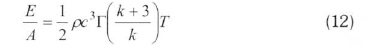
From the technological point of view, a wind turbine that converts the kinetic energy of the wind to electrical energy, starts to generate power at a cut-in wind speed (V1), and this process continues until a wind speed of VR, at which the nominal power generation PRis obtained. After this nominal point, the turbine starts to decelerate itself in a controlled manner until a speed of V0, called the cut-out wind speed, is reached. With reference to these benchmarks, the energy achieved from an ideal turbine is given as follows:
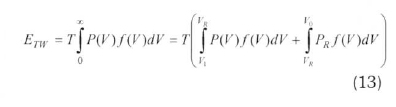
Substituting the Eq. (10) in Eq. (13). it can be rewritten as
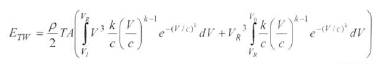 (14) *
(14) *
Because of the several losses occurring during the transmission mechanisms of the wind turbine, all the power carried by the wind can never be converted to electricity. In this regard, the actual power achieved from the turbine (PT) is calculated from the turbine-performance curve described by Eq. (15).
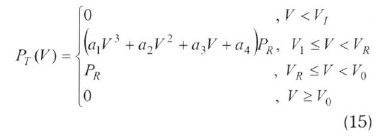
where a1, a2, a3, and a4 are the regression constants of the turbine-performance curves (Arslan, 2010; Wu, 2002). Combining the Eqs. (1), (10), and (15), Eq. (16) gives the actual energy released from a wind turbine.
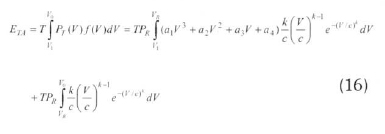
Therefore, the efficiency of the turbine (η) is the ratio of the real to the ideal energy-generation processes and is given by the following equation:

As observed from Eqs. (15)-(17), the turbine efficiency is a function of not only the wind characteristics but also wind distribution. In 1926. Betz first discovered that the wind power theoretically decreased with the wind speed. According to Betz. neglecting the transmission losses, the obtainable power from wind is approximately 59% of the total carried by it. In other words, the turbine efficiency cannot exceed the value of 59% (Golding, 1955: Considine, 1977).
For the period T, the generated nominal wind snergy from a turbine operating with full capacity is given by Eq. (18).

After this classification, two important parameters - capacity and availability factor - should oe defined for the estimation of power generated from a wind turbine. The capacity factor is defined as the ratio of the real-energy generation to nominal-energy generation and is given as follows (Ozgur, 2006: Decher, 1994):
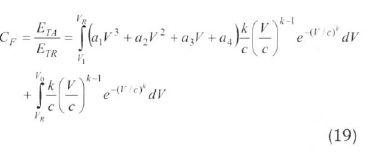
The availability factor is the operating percentage of a turbine and is given by the following equation:
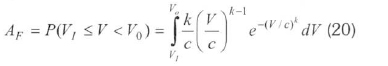
If the wind speed measurement has been made from a height of H1 above the ground, it is possible to assess the wind speeds at a height H2 by the relation:

vhere a is a parameter that depends on the soil roughness (Thiaw, 2010; Ozgur et al., 2009; Ozgur, 2006: Patel, 1942).
2.4. ANN modelling of wind power generation
Artificial neural networks are examples of the way that the biological neural system works. Nerve cells contain neurons. Neurons are interconnected in various ways and create a network. Likewise, ANN is a network applied successfully in a number of application areas such as medicine, economics, engineering, neurology, meteorology, etc. The ANN modelling is carried out in two steps: the first step is to train the network whereas the second is to test the network with data, which are not used for training. The unit element of an ANN is the neuron. As in nature, the network function is determined largely by the connections between the elements (Fu, 1994; Tsoukalas and Uhrig, 1997; Oztemel, 2003).
In an ANN, each unit is a basic unit of information process. Units are interconnected via links that contain weight values. Weight values help the neural network to express knowledge. There are several neural architectures. One of these architectures, widely used in engineering applications, is multilayer neural network (MLNN).
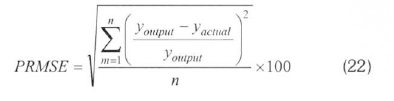
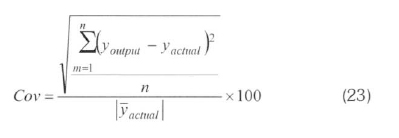
The MLNN consists of three layers at least: an input layer, an output layer and one hidden layer. The input and output layers represent the input and output variables of the model and the hidden layers hold the network's ability to learn the non-linear relationships between the input and output (Oztemel, 2003; Kalogirou, 2000). To obtain these relationships, several learning algorithms are available, one of which can be used. The most widely used algorithm is the feed-forward back propagation learning algorithm. It is a gradient descent algorithm. The most widely used algorithms are Levenberg-Marguardt (LM), Pola-Ribiere Conjugate Gradient (CGP) and Scaled Conjugate Gradient (SCG) in the field of energy. LM algorithm appears to be the fastest method for feed forward neural networks. CGP and SCG algorithms are a version of the Conjugate Gradient algorithm. Each of the conjugate gradient algorithms that have been discussed so far requires a line search. This line search is computationally expensive, since it requires that the network response to all training inputs be computed several times for each search (Hagan and Menjah, 1994; Fletcher and Reeves, 1964; Moller, 1993). ANN with a feed-forward back propagation algorithm learns by changing the connection weights, and these changes are stored as knowledge. The performance of the configured model is determined using some statistical methods such as the percent root mean square error (PRMSE), covariance (Cov) and the coefficient of multiple determinations (R2). These statistical parameters are formulated in terms of output value (youtput), target value (yactual), average of target (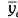 actual) and pattern (n) as follows (Arslan, 2011):
actual) and pattern (n) as follows (Arslan, 2011):
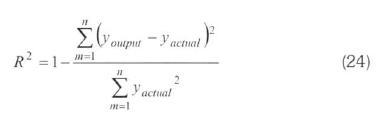
In this study, different feed-forward back propagation learning algorithms, namely Pola-Ribiere Conjugate Gradient (CGP), Levenberg-Marquardt (LM) and Scaled Conjugate Gradient (SCG) were applied. Inputs and outputs were normalized in the (0-1) range depending on the non-linear transfer function; logarithmic sigmoid (logsig). was used as given:

where z is the weighted sum, and given in terms of bias (b), weight (w) and output (y).

2.5 Economic analysis
The wind power plants handled herein have been evaluated economically using net present value (NPV) analysis. NPV is a powerful tool for the feasibility studies and can be determined with the following equation (Ozerdem et al., 2006; Zheng, 2009):

Where Btand Ctare the benefit and cost in the tth year respectively during the program, r represents the discount rate and N is the timescale of the plant.
To this end, the cost parameters selected for the on-grid configuration were the wind turbine (CWT) including installation and commissioning, and salvage (Csal) where the benefits were greenhouse gases (CCO2), repair and maintenance (CO&M), and the electricity sale (Ce). Accordingly, the general cost (C) and the benefit (B) of the system are as given in Equations (28) and (29).

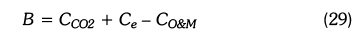
In this study, the unit costs used in the study were taken as 88 US$/MWh for electricity sale (Ce), 1250 US$/kW for wind turbine including installation and commissioning (CWT), %5 of cWT (Csal), 17.5 US$/MWh for operating and maintenance (CO&M) and 93.2 US$/MWh for greenhouse gases (CCO2) (Arslan, 2010; Green Economy, 2010; Blanco, 2009).
3. Results and discussion
In the ANN modelling of a wind power plant, the values of three inputs, turbine type, hub height and wind speed, were used. Generated power of the system was obtained as output. Different models were performed by using the software MATLAB. These models were built up using a dataset including 314 patterns. In the training step, 220 of these patterns (70% of total) were used. The remaining patterns, randomly selected from a number of 94, were used for testing. An increased number of neurons (from 6 to 16) were used to define the output accurately in a single hidden layer for 2000 epochs in the training algorithms. According to statistical performance evaluation, the summarized results are given in Table 2.
According to Table 2, all the studied ANN models are very satisfactory and can be used for the prefeasibility of a wind power plant with an acceptable accuracy. The LM training algorithm with 15 neurons in a single hidden layer was determined as the best model. Different models with more hidden layers were also tested but none was as much accurate as LM 15. The architecture of LM 15 is shown in Figure 4.
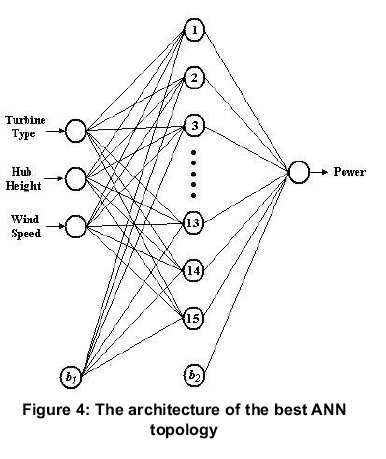
In the training step of this topology, PRMSE was determined as 0.4908% when the values of Cov and R2obtained were 0.5074 and 0.9995. These values were respectively 0.6475, 0.9606 and 0.9991 in the testing step. The statistical evaluation shows that the trained ANN model can be used for the designing of a wind power plant considered suitable for Kutahya, since it has high accuracy. The comparisons of the actual and ANN outputs are shown in Figure 5.
In this study, the wind data, appropriate to World Meteorology Organization (WMO) standards, collected between July 2001 and June 2004 in 10-minute intervals were evaluated to determine the energy potential of the region. This data was used to determine the power generation capacity taking 17 different turbine models into consideration in Weibull and Rayleigh distribution models. Besides these, technical characteristics of these turbines were also modelled using ANN to give the power generation capacity. The results are given in
Figures 6-8. According to these figures, the results of the ANN model are more accurate than those of Weibull and Rayleigh (Arslan, 2010; Ozgur et al., 2009; Ozgur, 2006; Ozgur and Kose, 2006).
For the economic evaluation of cost and benefit, the NPV concept was used, which included the greenhouse gas emission criteria. The calculations were based on the average energy generation of three years. The NPV results ratified for a discount rate of 0.14 (TCMB, 2010) are given in Table 3.
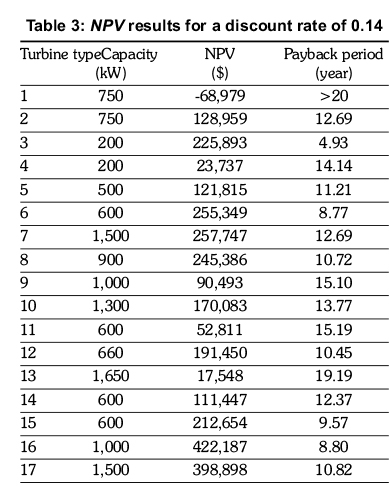
According to Table 3, the wind power generation is profitable for the existing turbine type 1. NPV values oscillate between US$ -68,979 and 422,187. Since the greater NPV means the more profitable, the most appropriate case seems to be the system with the turbine type 16. However, the least payback period is obtained for type 3 with an NPV value of US$ 225,893. So, this means that the most appropriate case is actually the system with the turbine type 3, when the capacities of the turbines are taken into consideration.
4. Conclusion
A highly unique flexible ANN algorithm was proposed to evaluate the wind power generation systems because of nonlinearity of the neural networks. The results analytically obtained were used to train the several ANN algorithms such as CGP LM and SCG. The trained algorithms were then tested and evaluated by the statistical methods such as Cov, RMS and R2. These statistical values showed that the best algorithm was LM. The degree of accuracy, between the real data and training data, is 99.95% for ANN algorithms, whereas the degree of accuracy, between the real data and testing data, is 99.91% for LM 15.
In this paper, the trained algorithms also show that the predicted values can be used to install a wind system with less data and high accuracy. Besides these, the best ANN topology gives more sensitive results in comparison to Weibull and Rayleigh distribution models. So, the neural network topology can be used for the feasibility studies of wind power projects. In this study, the NPV analysis-based ANN topology shows that the wind power systems for different 16 turbine types are profitable in Kutahya.
Equations 14, 16 and 19 repeated
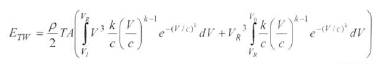 (14)
(14)
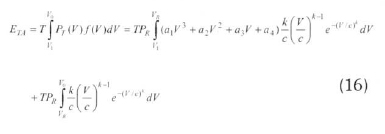
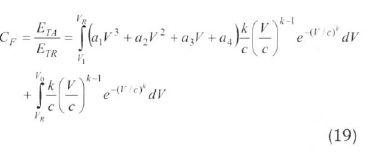
Nomenclature
A area swept by the rotor (m2)
ANN artificial neural network
AFavailability factor
B benefit (US$)
b bias number
C general cost (US$)
c scale parameter (m/s)
CF capacity factor
CGP Pola-Ribiere conjugate gradient
Cov covariance
Cco2cost of greenhouse gases (US$)
Cecost of electricity sale (US$)
Csal cost of salvage (US$)
CO&Mcost of operation and maintenance (US$)
CWTcost of wind turbine (US$)
CCO2unit cost of greenhouse gases (US$/MWh)
ceunit cost of electricity sale (US$/MWh)
csal unit cost of salvage (US$/MW)
CO&Munit cost of operation and maintenance (US$/MWh)
cWTunit cost of wind turbine (US$/MW)
ETAactual energy released from turbine (kWh)
ETWenergy achieved from an ideal turbine (kWh)
F(V) cumulative distribution function
f(V) Weibull distribution function
IC installed capacity (kW)
k shape parameter
LM Levenberg-Marquardt
m air of mass (kg)
MLNN multi-layer neural network
N lifetime of the plant (year)
NPV net present value (US$) n pattern
PDF probability density function
PRMSE percent root mean square error
PRnominal power generation (kW)
PTactual power achieved from the turbine (kW)
r discount rate (%)
SCG scaled conjugate gradient
V wind speed (m/s)
Vewind speed estimated at height H2 (m/s)
VMPmost frequent wind speed (m/s)
VmaxEthe maximum energetic wind speed (m/s)
Vmwind speed measured at the reference height H1 (m/s)
VRrated wind speed (m/s)
VIcut-in wind speed (m/s)
V0cut-out wind speed (m/s)
y output
Voutput output value
yactual target value
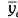 actual average of target
actual average of target
z weighted sum
Γ(...) gamma function
σ standard deviation of wind speed
η efficiency of turbine (%)
a ground surface friction coefficient
ρ air density (kg/m3)
References
Ammonit. (2011). Alwin software; WEC-Catalog. <http://www.ammonit.com/images/stories/software/AmmonitALWIN/alwin_zip.zip> (access January 2011). [ Links ]
Arslan, O. (2010). Technoeconomic analysis of electricity generation from wind energy in Kutahya, Turkey. Energy 35:120-131. [ Links ]
Arslan, O. (2011). Power generation from medium temperature geothermal resources: ANN-based optimization of Kalina cycle system-34. Energy 36:2528-2534. [ Links ]
Blanco, M.I. (2009). The economics of wind energy. Renewable and Sustainable Energy Reviews 13:1372-1382. [ Links ]
Bury, K.V. (1975). Statistical models in applied science. John -Wiley Science. pp.405-437. [ Links ]
Çam, E., Arcaklioğlu, E., Çavuşoğlu, A., and Akbiyik, B. (2005). A classification mechanism for determining average wind speed and power in several regions of Turkey using artificial neural networks. Renewable Energy 30:227-239.
Carolin, M., and Fernandez, E. 2008. Analysis of wind power generation and prediction using ANN: A case study. Renewable Energy 33:986-992. [ Links ]
Celik, A.N. (2004). A statistical analysis of wind power density based on the Weibull and Rayleigh models at the southern region of Turkey. Renewable Energy 29:593-604. [ Links ]
Chang, T.J., Wu, Y.T., Hsu, H.Y., Chu, C.R., and Liao, C.M. (2003). Assessment of wind characteristics and wind turbine characteristics in Taiwan. Renewable Energy 28:851-871. [ Links ]
Considine, D.M. (1977). Energy technology handbook. New York: McGraw Hill. [ Links ]
Decher, R. (1994). Energy conversion. New York: Oxford University Press. pp.454-475. [ Links ]
Dombayci, Ö.A., and Gölcü, M. (2009). Daily means ambient temperature prediction using artificial neural network method: A case study of Turkey. Renewable Energy 34:1158-1161. [ Links ]
Dorvlo, A.S. (2002). Estimating wind speed distribution. Energy Conversion and Management 43:2311-2318. [ Links ]
Fawzan, M.A. (2000). Methods for estimating the parameters of the Weibull distribution. Saudi Arabia: King Abdul-Aziz City for Science and Technology. p.1-11. [ Links ]
Fletcher, R., and Reeves, C.M. (1993). Function minimization by conjugate gradients. Computer Journal 7:149-154. [ Links ]
Fu, L M. (1994). Neural network in computer intelligence. Int. ed. New York: McGraw-Hill. [ Links ]
Garcia, A., Torres, J.L, Prieto, E., and Francisco, A. (1997). Fitting wind speed distributions: a case study. Solar Energy 62:139-144. [ Links ]
Golding, E.W. (1955). The generation of electricity by wind power. New York: Philosophical Library. p.318. [ Links ]
Green Economy. (2010). Objection to the draft renewable energy law from wind investors. <http://www.yesilekonomi.com/haberdetay.asp?id=NDI3> (access June 2010). [ Links ]
Hagan, M.T., and Menhaj, M. (1994). Training feedforward networks with the Marquardt algorithm, IEEE Transactions on Neural Networks 5:989-993. [ Links ]
Hennesey, J.P (1977). Some aspects of wind power statistics. Journal of Applied Meteorology 16(2):119-128. [ Links ]
Jafarian, M., and Ranjbar, A.M. (2010). Fuzzy modelling techniques and artificial neural networks to estimate annual energy output of a wind turbine. Renewable Energy 35:2008-2014. [ Links ]
Jaramillo, A.O., and Borja, M.A. (2004). Wind speed analysis in La Ventosa, Mexico: a bimodal probability case. Renewable Energy 29:1613-1630. [ Links ]
Kalogirou, S.A. (2000). Applications of artificial neural networks for energy systems. Applied Energy 67;17-35. [ Links ]
Kalogirou, S.A., Panteliou, S., and Dentsoras, A. (1999). Artificial neural networks used for the performance prediction of a thermosiphon solar water heater. Renewable Energy 18:87-99. [ Links ]
Karsli, V.M., and Gecit, C. (2003). An investigation on wind power potential of Nurdagi-Gaziantep, Turkey. Renewable Energy 28:823-830. [ Links ]
Keyhani, A., Ghasemi, M.G., Khanali, M., and Abbaszadeh, R. (2010). An assessment of wind energy potential as a power generation source in the capital of Iran, Tehran. Energy 35:188-201. [ Links ]
Kose, R., Ozgur, M.A., Erbas, O., and Tugcu, A. (2004). The analysis of wind data and wind energy potential in Kutahya, Turkey. Renewable and Sustainable Energy Reviews 8:277-288. [ Links ]
Li, G., and Shi, J. (2010). On comparing three artificial neural networks for wind speed forecasting. Applied Energy 87: 2312-2320. [ Links ]
Mohandes, M.A., Rehman, S., and Halawani, T.O. (1998). A neural networks approach for wind speed prediction. Renewable Energy 13(3):345-354. [ Links ]
Moller, M.F. (1993). A scaled conjugate gradient algorithm for fast supervised learning. Neural Networks 6:525-533. [ Links ]
Öztopal, A. (2006). Artificial neural network approach to spatial estimation of wind velocity data. Energy Conversion and Management 47:395-406. [ Links ]
Ozgur, M.A. (2006). Statistical analysis of wind characteristics of Kutahya and electricity production applicability. Ph.D. Thesis. Osmangazi University, Institute of Applied Science (in Turkish). [ Links ]
Ozgur, M.A., and Kose, R. (2006). Assessment of the wind energy potential of Kutahya, Turkey. Energy Exploration and Exploitation 24:113-130. [ Links ]
Ozgur, M.A., Arslan, O., Kose, R., and Peker, K.O. (2009). Statistical evaluation of wind characteristics in Kutahya, Turkey. Energy Sources Part A: Recovery, Utilization and Environmental Effects 31:1450-1463. [ Links ]
Ozerdem, B., Ozer, S., Tosun, M. 2006. Feasibility study of wind farms: A case study for Izmir, Turkey. Journal of Wind Engineering and Industrial Aerodynamics 94:725-743. [ Links ]
Oztemel, E. (2003). Artificial neural networks. Istanbul: Papatya Publications (in Turkish). [ Links ]
Patel, M.R. (1942). Wind and solar power systems. CRC Press: Chapter 4, ISBN 0-8493-1605-7. p.35. [ Links ]
Ouammi, A., Sacile, R., Zejli, D., Mimet, A., and Benchrifa, R. (2010). Sustainability of a wind power plant: Application to different Moroccan sites. Energy 35:4226-4236. [ Links ]
Stevens, M.J.M., and Smulders. P.T. (1979). The estimation of parameters of the Weibull wind speed distribution for wind energy utilization purposes. Wind Engineering 3(2):132-145. [ Links ]
Sulaiman, M.Y., Akaak, A.M., Wahab, M.A., Zakaria, A., Sulaiman, Z.A., and Suradi, J. (2002). Wind characteristics of Oman. Energy 27:35-46. [ Links ]
TCMB (Central bank of the republic of Turkey) (2011). The discount rate in 2010. <http://www.tcmb.gov.tr/yeni/reeskont/rediscount.html> (access May 2011). [ Links ]
Thiaw, L. A. (2010). Neural network based approach for wind resource and wind generators production assessment. Applied Energy 87:1744-1748. [ Links ]
Tsoukalas, L.H,, and Uhrig, R,E. (1997). Fuzzy and neural approaches in engineering. New York: Wiley. [ Links ]
Turkish State Meteorological Service (DMI) (2011). Data and evaluation of Kutahya. < http://www.dmi.gov.tr/veridegerlendirme/il-ve-ilceleristatistik.aspx?m=KUTAHYA> (access May 2011) [ Links ]
Ulgen, K., and Hepbasli, A. (2002). Determination of Weibull parameters for wind energy analysis of Izmir, Turkey. International Journal of Energy Research 26:494-506. [ Links ]
Wu, S,J. (2002). Estimating of the parameters of the Weibull with progressively censored data. 32. Japan Statistic Society p.155-163. [ Links ]
Zheng, W., Shi, H., Chen, S., and Zhu, M. (2009). Benefit and cost analysis of mariculture based on ecosystem services. Ecology Economics 68:1626-1632. [ Links ]
Received 11 November 2013
Revised 4 September 2014
* Equations 14, 16 and 19 have been shrunk in order to fit the column. They are given in their full size at the end of the paper














