Serviços Personalizados
Artigo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em Google
Similares em Google
Compartilhar
Journal of Energy in Southern Africa
versão On-line ISSN 2413-3051
versão impressa ISSN 1021-447X
J. energy South. Afr. vol.25 no.4 Cape Town Nov. 2014
The sensitivity of the South African industrial sector's electricity consumption to electricity price fluctuations
Roula Inglesi-Lotz
Department of Economics, University of Pretoria, Pretoria, South Africa
ABSTRACT
Numerous studies assume that the price elasticity of electricity demand remains constant through the years. This, in turn, means that these studies assume that industrial consumers react in the same way to price fluctuations regardless of the actual price level. This paper proposes that the price elasticity of industrial electricity demand varies over time. The Kalman filter methodology is employed in an effort to provide policy-makers with more information on the behaviour of the industrial sector with regards to electricity price changes, focusing on the period 1970 to 2007. Other factors affecting electricity consumption, such as real output and employment, are also captured. The findings of this paper show that price sensitivity has changed since the 1970s. It has decreased in absolute values from -1 in 1980 to -0.953 in 1990 and then stabilised at approximately -0.95 which indicates that the industrial sector has experienced an inelastic demand. In other words, the behaviour of industrial consumers did not vary significantly during the 2000s. In the long run and as the prices increase, probably reaching the levels of the 1970s or even before, the industrial sector's behaviour might change and the elasticity might end up at levels higher than one (elastic).
Keywords: electricity consumption; Kalman filter; price elasticity; industrial sector
1. Introduction
In South Africa, choosing the correct and appropriate electricity price regime has been under discussion during the last decade. During March 2012, the National Energy Regulator South Africa (NERSA) re-evaluated and reduced the agreed rate of increase of the electricity price for 2012. Eskom has also expressed its intentions for further application on price rises for two main reasons: first, Eskom argues that the current prices are not cost-reflective, and second, its capacity expansion plans include investing in two new power plants that will increase the company's operating costs. Before the next electricity price restructure, it is imperative for policy-makers to understand, and in a way, 'predict' the reactions of consumers to price changes. Even more important, the national electricity consumption trends do not necessarily represent each sector's individual behaviour. Different price structures as well as different electricity profiles are the main reasons why different economic sectors should be examined separately and treated accordingly.
Energy (and more specifically electricity) plays an essential role in the production capacity of a country. It is a crucial role, specifically for the manufacturing sector where energy is considered an irreplaceable input. In South Africa, the industrial sector is responsible for an average of 47% of the total electricity consumption (DoE, 2009), which makes this sector one of the most important ones from an energy consumption point of view. Ziramba (2009) studied the energy consumption of the industrial sector in South Africa and its interaction with other variables such as industrial output and employment (but not electricity prices). More recently, Inglesi-Lotz and Blignaut (2011a) found that, among various economic sectors such as agriculture and transport, the industrial sector was the only one whose electricity consumption behaviour is sensitive to price fluctuations during the period 1993 to 2006.
Following Inglesi-Lotz (2011), this paper proposes that the sensitivity of the industrial sector's electricity consumption to price fluctuations (price elasticity) has been changing through the years. As Inglesi-Lotz (2011) also points out, 'focus on variation is more important than only examining the level of change' - especially for the South African case after the price restructuring of 2009/10. The fluctuations are so drastic that one has to take into account changes in behaviour. Thus, the purpose of this paper is to estimate the time-varying sensitivity of the industrial sector's electricity consumption to price changes, using the Kalman filter econometric methodology for the period 1970 to 2007. (See Section 3 for a discussion on the reasons for the selection of the time period).
This paper combines and extends the results by Inglesi-Lotz (2011) and Inglesi-Lotz and Blignaut (2011a) in an effort to provide policy-makers with more information on the behaviour of the industrial sector with regards to electricity price changes. The findings will assist regulators and policy-makers in future decisions on price changes, a topic extremely relevant and crucial to the current South African case.
This paper is structured as follows: Section 2 provides a brief overview of studies that deal with the industrial sector's energy or electricity consumption, as well as a summary of the South African studies that deal with electricity prices and their effect on the economy either in its entirety or specific sectors. Section 3 presents the methodology and the data used. Section 4 presents the empirical results, and Section 5 summarises the findings and concludes by discussing some possible policy implications.
2. Literature review
During the last few decades, literature has paid special attention to price elasticities of energy demand. A possible reason for this is concerns regarding the environmental effects of the rising energy demand internationally, and the ever-increasing need to find appropriate instruments (if existing) to control it. The industrial sector, specifically, attracted more attention since it currently consumes approximately 37% of the world's total delivered energy (Abdelaziz et al., 2011).
Many studies have been conducted on the energy (electricity) demand of the industrial sectors in various countries within different geographical regions and with different economic backgrounds. These studies also use numerous methods. Different variables are used as factors other than prices affecting the demand depending on the specific region and the time period. But all-in-all, the major determinants of the industrial sector's energy (electricity) demand in the majority of the studies are output, price of electricity and employment (Al-Ghandoor et al., 2008; Jamil & Ahmad, 2011).
Table 1 presents a summary of international and local studies and their findings (in chronological order) that deal with the industrial energy (electricity) demand. This collection of studies, although by no means exhaustive of the literature, is indicative of the focus on a variety of countries (developed and developing) for different time periods. A variety of numerical estimations of the price elasticity, depending on the country and more importantly the period of the sample, is also observed.
For South Africa, only one study that sheds some light on the reaction of the industrial sector (among others) to the changes of prices is identified (Inglesi-Lotz & Blignaut, 2011a). Ziramba (2009) also studies the industrial sector's electricity demand reactions but excluded price from the factors affecting it. Another recent study by Inglesi-Lotz and Blignaut (2011b) looks at the different economic sectors and the factors that affect their increasing electricity consumption. However, due the nature of the method used (decomposition techniques), the effects of price fluctuations were not studied. Other studies also look at electricity demand trends in South Africa (Odhiambo, 2009; Amusa et al., 2010; Inglesi, 2010; Inglesi-Lotz, 2011) but focus on the aggregate demand of the economy. Furthermore, Ziramba (2009) finds that price was an insignificant factor for the residential demand of electricity in South Africa for the period 1978-2005.
3. Methodology and data
3.1 Econometric method
Econometric methods used in the analysis of energy vary in complexity from simple to relatively complicated and have been applied to temporal, spatial and sectoral data (Greening et al., 2007). More specifically, co-integration techniques have been used internationally (Engle & Granger, 1987; Johansen, 1991; Hendry and Juselius, 2000; Hendry and Juselius, 2001) and locally (Inglesi, 2010) to estimate the determinants of energy and electricity consumption. However, the common constraint in all these studies is the assumption that the relationship between electricity prices and consumption has remained constant through the years. Consequently, to take this a step further, Inglesi-Lotz (2011) employs the Kalman filter technique and proposes that price elasticity has evolved during the years and should not be treated as stable. Therefore, an average elasticity through the years is not assumed and different behaviour from electricity consumers under various price regimes and during various time periods is shown with this method.
It is therefore important to test for the general stability of parameters before selecting the Kalman filter as the method of preference. To test the stability of parameters, Hansen (1992) proposes a version of past approaches to cover general models with stochastic and deterministic trends. In this paper, this test is used to statistically confirm or reject the assumption of time-varying price elasticity before proceeding with the estimation.
There are two main types of models that can be represented by the Kalman filter: a) unobservable components models; and b) time-varying parameter models (Cuthbertson et al., 1992). In this study, the state-space model is applied with stochastically time-varying parameters to a linear regression in which coefficients representing elasticities are allowed to change over time.
Firstly,1 the formal representation of a dynamic system written in state-space form suitable for the Kalman filter should be described. The following system of equations presents the state-space model of the dynamics of a n x 1 vector, yt.
Observation (or measurement) equation:

State (or transition) equation:

where A, H and F are matrices of parameters of dimension (n x k), (n x r), (r x r), respectively, and xt is a (k x 1) vector of exogenous or predetermined variables. ξ is a (r x 1) vector of possibly unobserved state variables, known as the state vector.
In the observation equation, the factor xt is considered to be predetermined or exogenous which does not provide information about ξt+sor wt+s for s = 0,1,2,... beyond what is given by the sequence yt-1, yt-2,...,y1. Thus, xt could include lagged values of y or variables which are uncorrelated with ξT and wT for all T.
The overall system of equations is used to explain a finite series of observations {y1, y2,...,yT} for which assumptions about the initial value of the state vector ξtare needed. With the assumption that the parameter matrices (F Q, A, H or R) are functions of time, then the state-space representation (equations (1) and (2)) become:
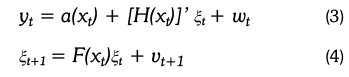
Where F(xt) is a (r x r) matrix whose elements are functions of xt; a(xt) is a (n x 1) vector-valued function; and H(xt) is a (r x n) matrix -valued function.
Equations (3) and (4) allow for stochastically varying parameters, but are more restrictive in the sense that a Gaussian distribution is assumed.
With regards to the specific application to the electricity model of this paper, the dependent variable is the electricity consumption of the industrial sector (cons) while standard variables used in the international and local literature (Ziramba, 2009; Inglesi, 2010; Nakajima & Hamori, 2010; Dilaver & Hunt, 2010) are considered as independent: price of electricity (p), real output of the industrial sector (y) and employment (n). All the variables are in natural log denoted by l.

In equation (5), all the parameters a are considered constant over time. However, after using the Hansen (1992) test, they will either be identified as time-varying or remain constant. An indication of this will be given even before the statistical test by the graphical representation of the data. The time-varying parameters will then also have a suffix t to denote the fluctuations over time to be estimated.
3.2 Data
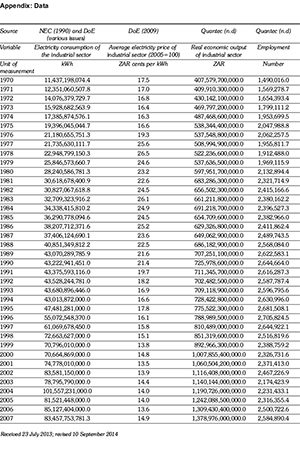
Local sources of data were primarily used for this exercise. Average electricity consumption is derived from the following different sources: South African Energy Statistics 1950-1989 by the National Energy Council (NEC, 1990) for 1970-1989 and the Aggregate Energy Balances by the Department of Energy (DoE, various issues). The series for average nominal prices of electricity for the industrial sector is obtained from the Energy Price Report 2009 also by the Department of Energy (DoE, 2009). Finally, the data series for the real economic output and employment of the industrial sector is obtained from the Quantec databases (Quantec, n.d.). The economic output figures are presented in real terms with 2005 being the base year. In order to transform, the nominal prices of electricity into constant with 2005 base year, the Consumer Price Index (CPI) figures from StatsSA is employed.
The electricity consumption was measured in kWh; the electricity prices (after the transformation) in South African Rand (ZAR) cents/ kWh (constant prices 2005); the economic output of the industrial sector in ZAR (constant prices 2005) and the employment in absolute number of employees.
Table 2 summarises the descriptive statistics of all the variables (in their linearised version) used in the analysis. These primary statistics are only presented as an indication of the nature of the raw data.
Figure 1 illustrates electricity consumption and prices as well as the real economic output and employment of the South African industrial sector for the period 1970-2008. The industrial economic output and its electricity consumption showed an upward trend for the entire period examined. This trend became more intense during the 1990s, when the sanctions against South Africa were lifted and the country's trade opened to the rest of the world. Since then the real economic production of the country rose with increasing rates to match the rising electricity consumption of the sector.
Employment showed a general upward trend until the end of approximately the 1980s and then its variation relatively stabilised until the end of the sample. This can be attributed to the industrialisation of the economy. It can be argued that the growth of the industrial sector during this period led to the substitution of labour with capital, especially after opening to international markets and gaining opportunities to import capital infrastructure and know-how. Although this was indeed a reality, the labour market also opened to all previously disadvantaged South Africans and, consequently, more employment opportunities were available. The lower labour costs of unskilled or semi-skilled workers also played a role in the higher number of people employed. From the graphical representation of employment in the industrial sector, it can be assumed that these two factors drove employment in opposite directions and, especially for the period 1985 to the beginning of 2000s, the range of employment change was relatively marginal (2.4-2.8 million). Overall, the increasing trend matches the trend of the output of the industrial sector and the electricity consumed.
Electricity prices increased drastically during the first half of the 1970s, reaching a peak in the beginning of the 1980s. However, prices started declining rapidly from the 1980s until the 2000s. Looking at the steep increase in prices from 1975 to 1976, it was decided to proceed with an estimation excluding the first five years of the sample and only start from 1976. Also, data for most of the variables is available until 2010/11; however, the latest information on sectoral electricity consumption from the Energy Balances was released in 2009 and on prices for 2008/09. Usually, the latest reports of energy data are re-evaluated as soon as more information becomes available and hence, the latest most accurate year of energy data is 2007. Also, the international crisis affected the output of the economy after 2008/09 and the decision was made to exclude the years after 2008 from the estimated sample. In the future, when information becomes available for the years after the crisis, this period can be treated as a structural break in any economic analysis of data.
From Figure 1, it can also be observed that the overall real output and employment both had a constant positive correlation with electricity consumption; while the price variation is more intense over the years and might show a more changeable relationship with electricity consumption on an annual basis. These observations might be an indication of the a priori expectations of the Hansen test results.
4. Empirical results
As discussed in Section 3, before proceeding with the estimation using the Kalman filter, the Hansen test is performed to either confirm or reject the parameter instability. From the graphical representation of the data, a more stable coefficient is expected for output and employment while the relationship between price and consumption of electricity is expected to vary over the years, represented in an unstable parameter. The null hypothesis of the Hansen test is parameter stability and an Lc statistic is used (Lagrange Multiplier tests family). If even one of the coefficients is confirmed statistically to be unstable, the Kalman filter will produce better results than a least squares estimation.
Table 3 presents the results of the Hansen test. The test statistic for output and employment is 0.192 with p-value higher than 0.2. Because the p-value is greater than the 10% level of significance, the null hypothesis of parameter stability cannot be rejected. Hence, the parameters for output and employment are found to be constant. The results of the Hansen test for the price coefficient indicated the test statistic is 0.4 and its p-value is 0.077. Since the p-value is less than the 10% level of significance, the null hypothesis of the test can be rejected. The conclusion is that the price coefficient is not constant through the years. Overall, based on the Hansen test results, the coefficients for output and employment should be considered as constant while the coefficient for price should be considered as time-varying in the Kalman filter estimation.
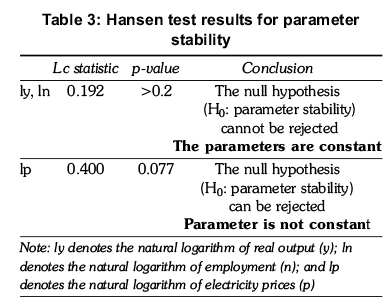
Table 4 presents the Kalman filter estimation results, and c(1) and c(2) (constant coefficients) show the output and employment coefficients respectively, while c(3) is the constant parameter of the equation. The coefficients are both positive and statistically significant: any positive change in the output or employment will result in an increase in electricity consumption.
Sv1 is the average of the price elasticity over the period 1976-2007 and it is negative as expected. (Law of demand: the higher the price of a good, the lower the quantity consumed of the good). Overall it is statistically significant with a p-value of zero. Both output and price coefficients are very close to the average coefficients reported in Inglesi-Lotz and Blignaut (2011) for the industrial sector. The price coefficient for the examined period (1993-2006) was -0.869 (here, -0.952) and the output elasticity was 0.712 (here, 0.690).
Figure 2 illustrates the evolution of price elasticity. In the beginning of 1980s, price elasticity of electricity demand was close to unit elastic. Since then, it has decreased in absolute values from -1 in 1980 to -0.953 in 1990. Thereafter, the elasticity stabilised at approximately -0.95 indicating that the industrial sector has experienced an inelastic demand. In other words, the behaviour of the industrial consumers did not vary significantly during the 2000s. That might explain why, in some studies, researchers assume that price has not played a significant role in the fluctuations of electricity consumption in the industrial sector and therefore not include prices in the estimations, for example, Ziramba (2009).
This result also confirms the main conclusion of Inglesi-Lotz (2011) that the sensitivity of consumers to price fluctuations became smaller in absolute terms, while the real prices of electricity declined over the last half of the sample examined. It can be seen in Figure 3 that, from 1977 until the beginning of 1990s, the electricity prices decreased in real terms and the price elasticity became lower in absolute terms. However, from the 1990s until the end of the sample period, prices stabilised at much lower rates than in the 1970s and 1980s, and the sensitivity of the consumers did not change drastically.
5. Conclusion
As the main electricity user, the industrial sector of South African plays an important role in the path of electricity consumption. Knowing and understanding the behaviour of this sector regarding electricity consumption will assist policy-makers in implementing appropriate policies. The sector's electricity performance has recently attracted attention. Ziramba (2009) studied the energy consumption of the industrial sector in South Africa and its interaction with other variables such as industrial output and employment (but not electricity prices). Later, Inglesi-Lotz and Blignaut (2011a) using panel data techniques, found that the industrial sector's electricity consumption was sensitive to price and output fluctuations on average during the period 1993 to 2006.
Most studies assume that the price elasticity of electricity demand remains constant through the years, that is industrial consumers behave the same way to price fluctuations regardless the economy's conditions or the actual level of prices. In South Africa, electricity prices have been low for a long period of time, which means that the economy as a whole did not react to price changes (Inglesi-Lotz, 2011). This paper follows Inglesi-Lotz (2011), who did an analysis for economy-wide electricity consumption, and uses the Kalman filter methodology to allow the price elasticity of industrial electricity demand to be time-varying. To capture other factors affecting electricity consumption, real output and employment are also included in the specification.
The findings show that price sensitivity has indeed changed since the 1970s: it has decreased in absolute values from -1 in 1980 to -0.953 in 1990. The elasticity stabilised at approximately -0.95 showing that the industrial sector has experienced an inelastic demand. In other words, the behaviour of industrial consumers did not vary significantly during the 2000s. This also confirms the main conclusion of Inglesi-Lotz (2011) that sensitivity of consumers to price fluctuations becomes smaller in absolute terms, while the real prices of electricity declined over the last half of the sample period. In addition, both papers show that the price elasticity of the electricity demand in the industrial sector or the economy as a whole has remained relatively constant, while prices were not fluctuating significantly. In other words, the sensitivity and behaviour of the consumers had remained unchanged; however, as soon as prices start varying it should be expected that the consumer's reaction to these changes will also alter.
These results also enable policy-makers to speculate about the effect of further electricity price increases planned by Eskom and NERSA for the next couple of years. An immediate change in the industrial sector's behaviour with the increase of prices should not be expected. However, in the long run and as the prices increase, probably reaching the levels of the 1970s or even before, the industrial sector's behaviour might change and the elasticity might end up at levels higher than one (elastic).
Acknowledgements
The author wishes to extend her gratitude to participants of the South African Energy Regulators Conference for their valuable comments and suggestions.
References
Abdelaziz, E.A., Saidur, R. and Mekhilef, S. (2011). A review of energy saving strategies in industrial sector. Renewable and Sustainable Energy Reviews, 15, 150-168. [ Links ]
Agnolucci, P. (2007). Non-transport energy consumption in the UK: a comparison of alternative approaches, mimeo. Cambridge: University of Cambridge. [ Links ]
Agnolucci, P. (2009). The energy demand in the British and German industrial sectors: Heterogeneity and common factors. Energy Economics, 31, 175-187. [ Links ]
Al-Ghandoor, A., Al-Hinti, I. and Sawalha, S.A. (2008). Electricity consumption and associated GHG emissions of the Jordanian industrial sector: empirical analysis and future projection. Energy Policy, 36, 258-267. [ Links ]
Amusa, H., Amusa, K. and Mabugu, R. (2009). Aggregate demand for electricity in South Africa: an analysis using the bounds testing approach to cointegration. Energy Policy, 37, 4167-4175. [ Links ]
Beenstock, M., Goldin, E. and Nabot, D. (1999). The demand for electricity in Israel. Energy Economics, 21, 168-183. [ Links ]
Caloghirou, Y.D., Mourelatos, A.G. and Thompson, H. (1997). Industrial energy substitution during the 1980s in the Greek economy. Energy economics, 19, 476-491. [ Links ]
Cuthbertson, K., Hall, S. and Taylor, M.P. (1992). Applied Econometric Techniques. New York: Harvester Wheatsheaf. [ Links ]
Department of Energy (DoE) (2009). Energy Price Report 2009. Pretoria: Department of Energy. [ Links ]
Department of Energy (DoE). Various issues. Aggregate energy balances. Pretoria: Department of Energy. [ Links ]
Dilaver, Z. and Hunt, L.C. (2010). Industrial electricity demand for Turkey: a structural time series analysis. Energy Economics, 33, 426-436. [ Links ]
Dimitropoulos, J., Hunt, L.C. and Judge, G. (2005). Estimating underlying energy demand trends using UK annual data. Applied Economic Letters, 12, 239-244. [ Links ]
Enevoldsen, M.K., Ryelund, A.V. and Andersen, M.S. (2007). Decoupling of industrial energy consumption and CO2 emissions in energy intensive industries in Scandinavia. Energy Economics, 29, 665-692. [ Links ]
Engle, R.F and Granger, C.W.J. (1987). Co-integration and error correction: representation estimation and testing. Econometrica, 55, 251-267. [ Links ]
Greening, L.A., Boyd, G. and Roop, J.M. (2007). Modelling of industrial energy consumption: An introduction and context. Energy Economics, 29, 599-608. [ Links ]
Hansen, B.E. (1992). Tests for parameter instability in regressions with processes. Journal of Business and Economic Statistics, 10, 321-335. [ Links ]
He, Y.X., Yang, L.F, He, H.Y., Luo, T. and Wang, Y.J. (2011). Electricity demand price elasticity in China based on computable general equilibrium model analysis. Energy, 36, 1115-1123. [ Links ]
Hendry, D. and Juselius, K. (2000). Explaining cointegration analysis: part I. Energy Journal, 21, 1-42. [ Links ]
Hendry, D. and Juselius, K. (2001). Explaining cointegration analysis: part II. Energy Journal, 22, 75-120. [ Links ]
Hunt, L.C., Judge, G. and Ninomiya, Y (2003). Underlying trends and seasonality in UK energy demand: a sectoral analysis. Energy Economics, 25, 93-118. [ Links ]
Inglesi, R. (2010). Aggregate electricity demand in South Africa: conditional forecasts to 2030. Applied Energy, 87, 197-204. [ Links ]
Inglesi-Lotz, R. (2011). The evolution of price elasticity of electricity demand in South Africa: A Kalman filter application. Energy Policy, 39, 3690-3696. [ Links ]
Inglesi-Lotz, R. and Blignaut, J.N. (2011a). Estimating the price elasticity of demand for electricity by sector in South Africa. South African Journal of Economic and Management Sciences, 14, 449-465. [ Links ]
Inglesi-Lotz, R. and Blignaut, J.N. (2011b). South Africa's electricity consumption: A sectoral decomposition analysis. Applied Energy, 88, 4779-4784. [ Links ]
Jamil, FF and Ahmad, E. (2011). Income and price elasticities of electricity demand: Aggregate and sector-wise analyses. Energy Policy, 39, 5519-5527. [ Links ]
Johansen, S. (1991). Estimation and hypothesis testing of cointegration vectors in gaussian vector autoregressive models. Econometrica, 59, 1551-1580. [ Links ]
Kamerschen, D.R. and Porter, D.V. (2004). The demand for residential, industrial and total electricity, 19731998. Energy Economics, 26, 87-100. [ Links ]
Lynk, E.L. (1989). The demand for energy by UK manufacturing industry. Manchester School of Economic and Social studies, 57, 1-16. [ Links ]
Nakajima, T. and Hamori, S. (2010). Change in consumer sensitivity to electricity prices in response to retail deregulation: a panel empirical analysis of the residential demand for electricity in the United States. Energy Policy, 38, 2470-2476. [ Links ]
National Energy Council (NEC). (1990). South African Energy Statistics 1950-1989. Pretoria: National Energy Council. [ Links ]
Odhiambo, N.M. (2009). Electricity consumption and economic growth in South Africa: A trivariate causality test. Energy Economics, 31, 635-640. [ Links ]
Pindcyck, R. (1979). Interfuel Substitution and the Industrial Demand for Energy: An International Comparison. Review of Economics & Statistics, 61, 169-179. [ Links ]
Quantec. n.d. Quantec databases. Pretoria: Quantec. [ Links ]
Roy, J., Sanstad, A.H., Sathaye, J.A. and Khadariia, R. (2006). Substitution and price elasticity estimates using inter pooled data in a translog cost model. Energy economics, 28, 706-719. [ Links ]
Ziramba, E. (2009). Disaggregate energy consumption and industrial production in South Africa. Energy Policy, 37, 2214-2220. [ Links ]
1. The detailed discussion on the Kalman filter methodology is adopted directly from Inglesi-Lotz (2011).
Appendix