Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
Journal of Energy in Southern Africa
On-line version ISSN 2413-3051
Print version ISSN 1021-447X
J. energy South. Afr. vol.25 n.2 Cape Town May. 2014
Voltage stability enhancement using an adaptive hysteresis controlled variable speed wind turbine driven EESG with MPPT
R Jeevajothi; D Devaraj
Department of Electrical & Electronics Engineering, Kalasalingam University, Virudhunagar, India
ABSTRACT
This paper investigates the enhancement in voltage stability achieved while connecting a variable speed wind turbine (VSWT) driven electrically excited synchronous generator (EESG) into power systems. The wind energy conversion system (WECS) uses an AC-DC-AC converter system with an uncontrolled rectifier, maximum power point tracking (MPPT) controlled dc-dc boost converter and adaptive hysteresis controlled voltage source converter (VSC). The MPPT controller senses the rectified voltage (VDC) and traces the maximum power point to effectively maximize the output power. With MPPT and adaptive hysteresis band current control in VSC, the DC link voltage is maintained constant under variable wind speeds and transient grid currents.The effectiveness of the proposed WECS in enhancing voltage stability is analysed on a standard IEEE 5 bus system, which includes examining the voltage magnitude, voltage collapse and reactive power injected by the systems. Simulation results show that the proposed WECS has the potential to improve the long-term voltage stability of the grid by injecting reactive power. The performance of this scheme is compared with a fixed speed squirrel cage induction generator (SCIG), a variable speed doubly-fed induction generator (DFIG) and a variable speed permanent magnet synchronous generator (PMSG).
Keywords: variable speed wind turbine, EESG, MPPT, adaptive hysteresis band current control, SCIG, DFIG, PMSG, voltage stability
1. Introduction
Wind power generation has received considerable attention worldwide in recent years (Hansen et al. , 2007) and the effective utilization of wind energy has been an important issue. As a result, VSWT systems with power electronics interfaces have attracted much interest.
The VSWT systems are usually based on DFIGs or PMSGs (Akie Uehara et al. , Heng Nian et al., Itsaso Martinez et al., Alejandro Rol'an et al., Si Zhe Chen et al., Manuel Pinilla et al., 2011). For the same power rating, the PMSG's cost is more than that of induction generator (IG) cost. But PMSG's have higher efficiency and so the higher material cost will be somewhat compensated by the extra electricity generated. Also IG's require capacitors for power factor correction and may increase the overall cost.
EESG is the regular synchronous generator equipped with field winding which is excited by a DC source. ENERCON of Germany introduced variable speed, direct drive (no gearbox) EESG as an alternative to a conventional wind technology solution. It is widely accepted as a mature technology, but the direct drive's global market share has never exceeded roughly 10%-15%, but the number of new entrants is growing rapidly (Aarti Gupta et al. ,2012). In EESG, the excitation can be varied and hence the output voltage of the wind-driven EESG can be controlled in terms of amplitude and frequency during fluctuating wind. Moreover, permanent magnets are not required reducing the cost of the system drastically. Thus, to increase the global market share of EESG, a new controllable power inverter strategy is implemented.
The DC link voltage is the most representative and relevant measurement because it shows the robustness of the converter system during voltage reduction on the mains. The capability to continue stable supply during line disturbances will strongly depend on the dynamics of the DC link. This paper focuses mainly on maintaining constant DC link voltage.
MPPT extracts maximum possible power from the available wind power (Jogendra Singh Thongam, et al., 2011). The amount of power output from a WECS depends upon the accuracy with which the peak power points are tracked by the MPPT controller of the WECS control system irrespective of the type of generator used. The MPPT algorithm proposed in Kesraoui, et al., (2011) senses the rectified voltage (VDC) alone and controls the same used here to control the dc-dc boost converter. The DC link voltage is maintained constant under varied wind speeds with this control.
Current control in VSC forces and the IGBT's to switch only when it is necessary to keep on tracking the reference of the current. The adaptive hysteresis current control in (Murat Kale et al., 2005) is applied to control the VSC in this system and the DC link voltage is maintained constant under transient grid currents with this control.
Under fault condition, the DC-link circuit of the WECS with AC-DC-AC converter system experiences over-voltage. Thus, stable operation of the grid and WECS is important. During a grid side fault, depending on the severity of the voltage sag, the grid side VSC injects an appropriate voltage to compensate for any balanced or unbalanced sag and establishes a stable operating point for the generator. The capability of the WECS in enhancing voltage stability is analysed by connecting it to an IEEE 5 bus system.
2. Wind energy conversion system
2.1 System configuration
Figure 1 shows the block diagram representation of the adaptive hysteresis controlled VSWT driven EESG with MPPT. The WECS consists of a pitchable wind turbine, an EESG, a passive rectifier, a MPPT controlled dc-to-dc boost converter and an adaptive hysteresis current controlled VSC.
The details of each component of the proposed WECS are given.
2.2 Wind turbine model
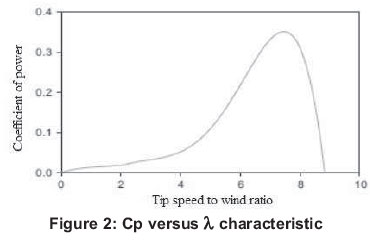
The performance of wind turbine is characterized by the non-dimensional curve of coefficient of performance (Cp), as a function of tip-speed ratio X. Cp as a function of X is expressed by equation (1) and it is shown in Figure 2.
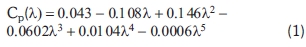
The tip-speed ratio is given by the expression:

where R is the radius of the wind turbine rotor in m, rom is the angular velocity of the rotor in rad/sec. and Vw is the velocity of the wind in m/s.
The output power of the wind turbine Pt is calculated using equation (3) as:

where A is the swept area of wind turbine rotor. It can be observed from Figure 2 that Cp is maximum when λ is equal to 7.5. In general,

Combining equations 1, 3 and 4, the expression for torque Tt developed by the wind turbine is written as:
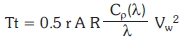
The power extracted from the wind is maximized when the power coefficient Cp is at its maximum. This occurs at a defined value of the tip speed ratio. Hence, for each wind speed; there is an optimum rotor speed where maximum power is extracted from the wind. Therefore, if the wind speed is assumed to be constant, the value of Cp depends on the wind turbine rotor speed. Thus, by controlling the rotor speed, the power output of the turbine is controlled.
2.3 EESG and rectifier
The electric power generated by EESG is given by:

where V is the generator voltage and Ia is the generator current.
For an ideal system, equations (4) and (6) can be equated.

where E is the induced voltage in the armature and Ra is the stator resistance.
Using equations (1) to (8), Pe is expressed as:
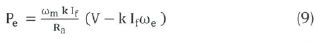
where If is the field current, coe is the electrical angular speed and V is the generator phase voltage.
The output voltage of EESG is rectified using a three-phase passive bridge rectifier. For a diode rectifier, the dc output voltage VDC is proportional to the generator phase voltage V. Therefore, equation (9) becomes
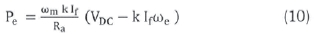
Figures 3a, 3b and 3c are the circuit diagrams provided to illustrate all the parameters of EESG given in Table 2 with respect to d-axis and q-axis.
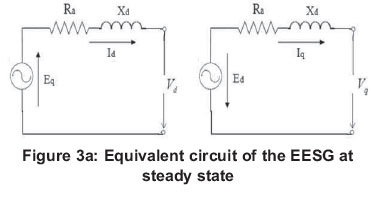
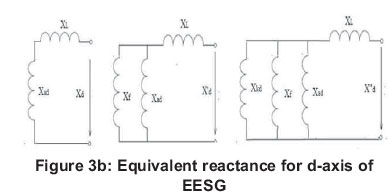
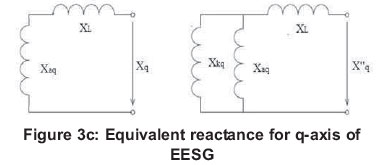

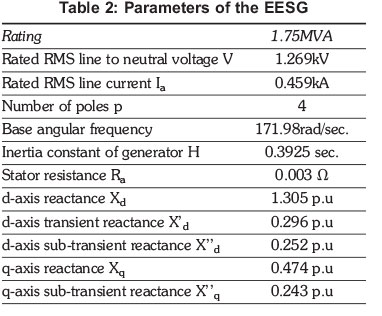
Figure 3a shows the equivalent circuit of the EESG at steady state. From this circuit, V and Ia can be represented with respect to d-axis and q -axis as:
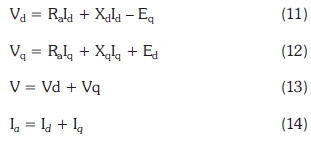
where Vd is the equivalent d-axis stator voltages, Vq is the equivalent q-axis stator voltages, Ra is stator phase resistance, Id is the d-axis equivalent stator currents, Iq is the q-axis equivalent stator currents, Ia is the rated rms line current, Xd is the synchronous reactance for the d-axis, Xq is the synchronous reactance for the q-axis, Ed is the induced voltage by d-axis flux and Eq is the induced voltage by q-axis flux. Figure 3(b) shows the equivalent reactance for d-axis of EESG.

where X'd is the d-axis transient reactance, X"d is the d-axis sub-transient reactance, Xad is the fictitious reactance, XL is the true reactance associated with flux leakage around the stator winding, Xf is the leakage reactance of the field winding and Xkd is the d-axis leakage reactance of damper winding(s).
Figure 3(c) shows the equivalent reactance for q-axis of EESG. If the armature MMF is aligned along quadrature axis, the only currents preventing the armature reaction flux from passing through the rotor iron are currents induced in q-axis part of the damper winding, because field winding is placed in the direct axis only. Due to this fact, it may be assumed, that q-axis transient reactance equals magnetizing reactance and only two equivalent reactances are defined as:
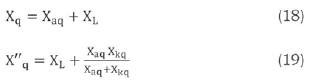
where X''q is the q-axis sub-transient reactance, Xaq is the fictitious reactance for the q-axis and Xkq is the q-axis leakage reactance of damper winding(s).
2.4 DC-DC Boost converter
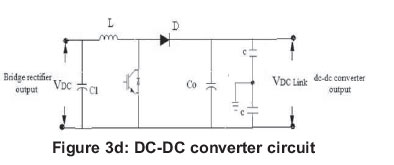
The EESG is not capable of generating a constant high voltage at low speed. Therefore, a dc-dc boost converter must be used to raise the voltage of the diode rectifier. A capacitor C1 is connected across the rectifier to lessen the variation in the rectified AC output voltage waveform from the bridge.
Figure 3(d) is an accompanying figure of Table 3, which shows the arrangement of the converter circuit, and items such as C1, capacitors, and L.

2.5 Voltage source converter
The VSC can act both as an inverter and as a rectifier. The VSC requires a minimum dc link voltage in order to operate, and here a DC-DC boost converter is introduced to increase the voltage level for the VSC. Variable voltage and frequency supply is invariably obtained from the three-phase VSC. Adaptive hysteresis type modulation is used to obtain variable voltage and frequency supply. Adaptive hysteresis current control in VSC forces and the IGBT's to switch only when it is necessary to keep on tracking the reference of the current.
3. Proposed control strategies
3.1 MPPT Control in DC-DC Boost converter
Maximum power occurs when

The control system makes use of the fact that the generated voltage and Vdc depend upon the speed of the turbine. Therefore, instead of sensing the turbine speed, it senses the Vdc and tries to control the same. The set point for this voltage is not constant. This is because the wind speed is varying every now and then which causes the optimum turbine speed to vary frequently. The set point is floating and has to be decided by a trial and error method. The method is called Peak seeking. Figure 4 shows the step and search control strategy to track maximum power.
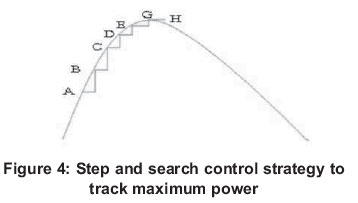
The strategy is to start with any arbitrary set point (A) i.e. reference dc voltage and check the output dc power. Then give a small increment to the set point. Again check the output at point B. If the output has increased, give an additional increment and check the output once again. Incrementing the set point through small steps should be continued till the stage (H) when the increment does not yield a favourable result. At this stage, a small decrement to the set point should be given. The set point will be moving back and forth around the optimum value. Thus, the power output could be maximized. In this method, after giving increment to the set point, both the power output as well as the voltage level has to be checked. Four possibilities arise:
- Power increased - voltage increased
- Power increased - voltage decreased
- Power decreased - voltage increased
- Power decreased - voltage decreased
Only when power output and the voltage are increased (case 1), the set point has to be incremented. If the wind speed changes from one value to another, the turbine is not being operated at the maximum power point at the new value. The MPPT controller has to search for the new maximum power point for the new wind speed.
Thus, depending upon the MPPT controller output, the dc-dc boost converter switch operates and maintains a constant Vdc link across the capacitor Co.
3.2 Adaptive hysteresis current control of VSC
Figure 5 illustrates the concept of adaptive hysteresis current control. The adaptive hysteresis band current control of three phase grid connected VSC and its working as explained in Murat Kale, et al., (2005) and is considered here.
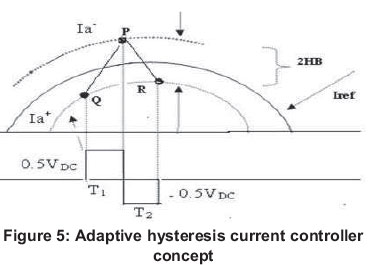
The adaptive hysteresis band current controller adjusts the hysteresis band width, according to the measured line current of the grid connected inverter. Let Iref be the reference line current and Iactual be the actual line current of the grid connected inverter. The error signal E can be written in equation (12) as:

When the measured current Ia of phase A tends to cross the lower hysteresis band at point 1, then switch S1 is switched ON. When this touches the upper band at point P, switch S4 is switched ON. The expression for adaptive hysteresis bandwidth is derived as:
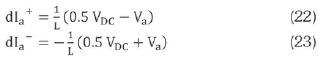
Aíhere L is the line inductance, Va is the grid voltage per phase and VDC be the DC link voltage.
From Figure 4 we obtain:
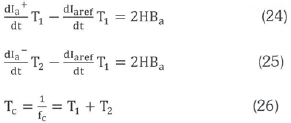
where T1 and T2 are the respective switching ntervals and fc is the switching frequency. Simplifying the equations, the hysteresis bandwidth (HB) is obtained as:

where fc is modulation frequency, m = dIaref /dt is the slope of command current wave. The profile of HBb and HBc are the same as HBa but have phase difference. According to (dIaref/dt) and Vdc voltage, the hysteresis bandwidth is changed to minimize the influence of current distortion on the modulated waveform. Thus, the switching signals for the VSC are generated by the adaptive hysteresis band current controller.
4. Simulation results
Simulation of the proposed utility scale variable speed WECS with EESG and VSC with adaptive hysteresis band current control technique in tracking maximum power has been carried out using Matlab/Simulink. A wind turbine of 1.5 MW rating has been connected to the 1.75MVA, 2.2kV EESG. The rating of the inverter is 1.3 MVA.
4.1 Parameters of proposed system
Table 1 shows the parameters of the simulated wind turbine.
Inertia constant of the wind turbine mentioned in Table 1 is defined as the kinetic energy stored in the rotor at rated speed divided by the VA base. The most significant component in wind turbine dynamics is the turbine inertia Hturb, due to the blade length and weight. It is given as:

where E is the energy stored in rotor mass, S is the VA base, J is rotating objective inertia and ωm is the mechanical angular velocity of rotor. The performance of wind turbines during transient situations is strongly influenced by this inertia constant.
Basic parameters used for the direct-drive generator model are given in Table 2.
Table 3 shows data used for the dc-dc converter of the VSWT.
4.2 Effect of pitch control
Simulation results are taken for two wind speeds 12 and 14 m/sec. At t = 10 sec., wind speed is changed from 12 to 14 m/sec and in step is shown in Figure 6.
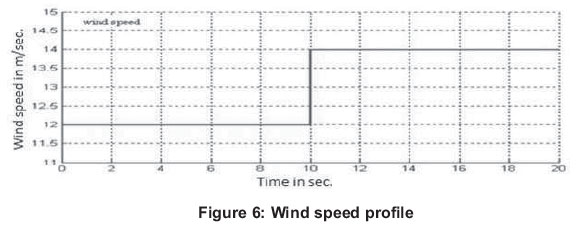
In this work, since 12.4 m/sec. is the rated wind speed, at 12m/sec., the pitch angle need not be activated. During this period, Cp.max is obtained as 0.44. At t=10 sec., as the wind speed is 14m/sec., which is above the rated wind speed of 12.4 m/sec., pitch control is activated. As the wind speed increases, the power generated by the wind turbine also increases. Once the maximum rating of the power converter is reached, the pitch angle is increased (directed to feather) to shed the aerodynamic power.
Here the pitch rate is chosen to be 4/0.7 degree/s. That is, the pitch angle can be ramped up at 4 degrees per second and it can be ramped down at 0.7 degrees per second.
The hysteresis rpm is chosen to be 2% of the maximum rpm. Small changes in the pitch angle can have a dramatic effect on the power output. Cp has changed to 0.39 at 14m/sec. as shown in Figure 7.
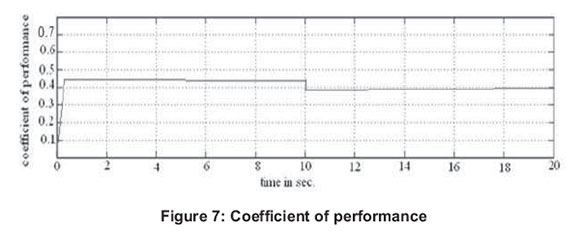
Figure 8 shows the variation of tip speed ratio with time. From this figure, it is observed that the turbine speed is well controlled to maintain an optimum tip speed ratio of 7 from 0 to 10 sec. at wind speed of 12m/sec. When wind speed is increased to 14m/sec., the optimum TSR is normally higher than the value at 12m/sec., but due to pitch control, it is kept at 7 itself. In general, three bladed wind turbines operate at a TSR of between 6 and 8, with 7 being the most widely reported value (Magdi Raghe.et.al., 2011).
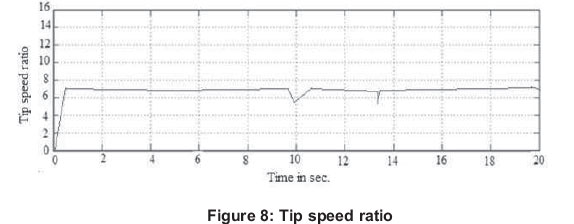
This indicates that the turbine speed is well controlled to maintain an optimum tip speed ratio to capture maximum energy. It shows that the MPPT controller is able to track maximum power and keep Cp of the wind turbine very close to maximum Betz' coefficient of 0.593. It is the maximum fraction of the power in a wind stream that can be extracted.
4.3 Maintaining constant DC link voltage with MPPT at wind speeds of 12 m/sec. and at 14 m/sec.
Simulation results of generator phase voltage and generator phase current at 12 m/sec with zooming between 0.2 to 0.4 sec. are shown in Figure 9 (a) and Figure 9(b). Figure 9(c) and Figure 9(d) show the generator phase voltage and generator phase current at 14 m/sec.
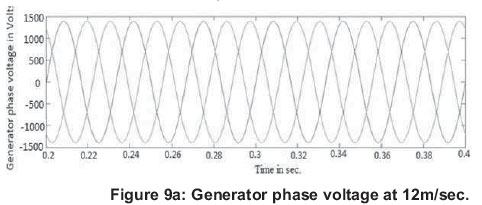
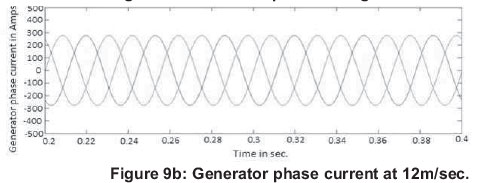
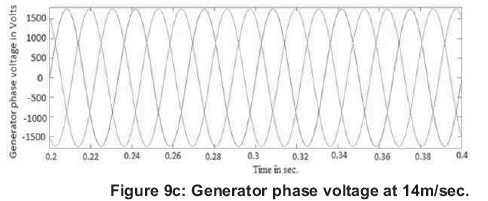
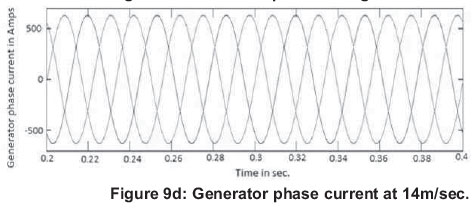
At 12m/sec, the generator rms phase voltage is 1.03kV and generator rms phase current is 210.49 A. At 14m/sec, the generator rms phase voltage is 1.27kV and generator rms phase current is 459.25 A. The power output at 14m/sec. is higher than that at 12m/sec. So, with increase in wind speed, the power output of the wind generator also increases.
Under both wind speed conditions, the switching signals to boost the converter are controlled with MPPT control and DC link voltage across Co is maintained constant which is shown in Figure 10.
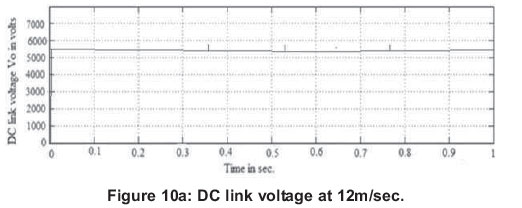
Figure 10(a) and Figure 10(c) show the DC link voltage from t= 0 to 1 sec. at 12m/sec. and 14m/sec. respectively. The simulation result of DC link voltage with zooming between 0.2 to 0.4 sec. is shown in Figure 10(b) and Figure 10(d). In the WECS with MPPT control proposed in this paper, it is possible to maintain a DC link voltage of 5.369 kV under both the wind speeds of 12m/sec. and 14m/sec.

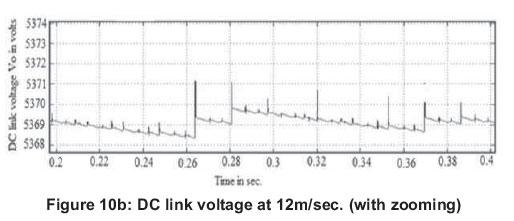
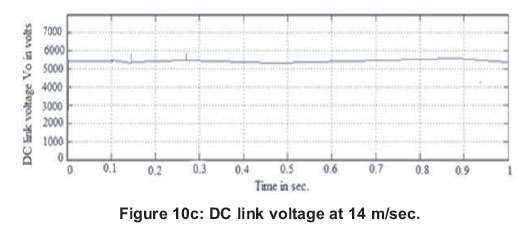
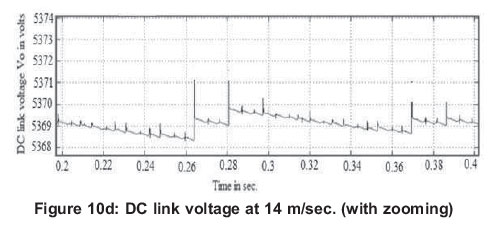
4.4 Maintaining constant DC link voltage control with adaptive hysteresis band current controller at load currents of 50A and 130A
To analyse the dynamic response of an adaptive hysteresis current controller, the grid current is increased from 50A to 130A by applying load. The adaptive hysteresis current controller acts under this condition and made the load current to track the reference current command at a faster rate and prevented the grid waveforms getting distorted. Figure 11 shows the grid voltage at the point of common coupling.
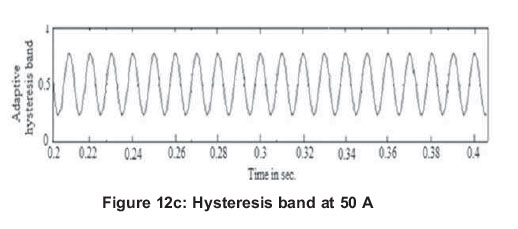
Figures 12 (a, b and c) show the grid current of 50A, inverter output phase current and corresponding hysteresis band at 50A of grid current.
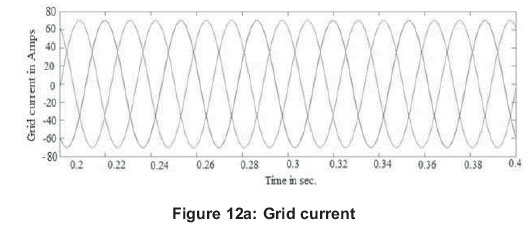
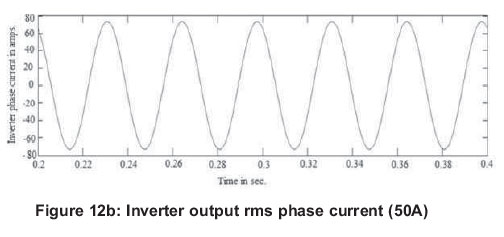
Figures 13 (a, b and c) show the grid current of 130 A, inverter output phase current and corresponding hysteresis band at 130 A of grid current.
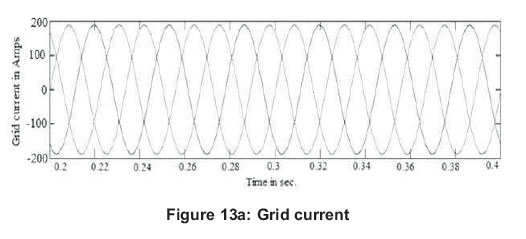
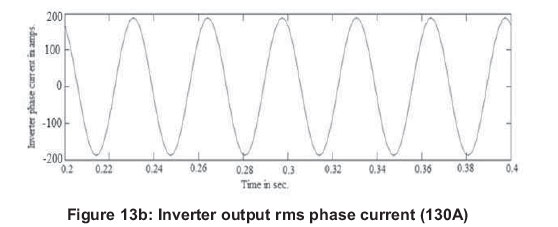
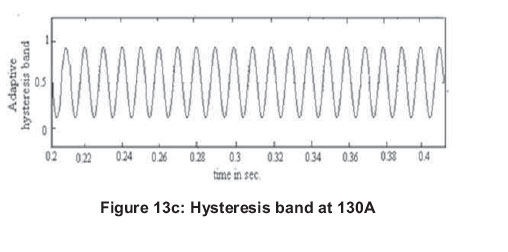
As indicated in Figures 12(c) and 13(c), the adaptive hysteresis band varied according to the variation in load in order to maintain the constant switching frequency of operation.
Figure 14(a) and Figure 14(c) show the DC link voltage from t= 0 to 1 sec. at load conditions of 50 A and 130 A respectively. The simulation result of DC link voltage with zooming between 0.2 to 0.4 sec. is shown in Figure 14(b) and Figure 14(d). The WECS with adaptive hysteresis current control in VSC proposed in this paper is able to maintain DC link voltage at 5.369 kV under both the load conditions of 50 A and 130 A.
4.5 Results of voltage stability enhancement
The performance of the proposed EESG system in enhancing the voltage stability is analysed using IEEE 5 bus system. The wind generators are connected one by one and their capability to inject reactive power to enhance voltage level is analysed.
In the IEEE 5 bus system, Bus 3 is considered as the load bus, and Bus 4 as the generator bus. The IEEE 5 bus system is simulated using MATLAB software and the in-built models of SCIG, DFIG and PMSG are connected and tested.
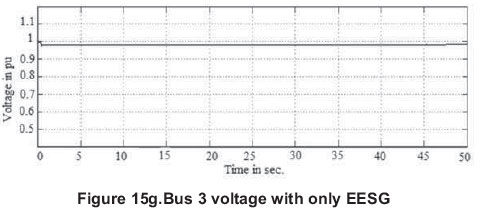
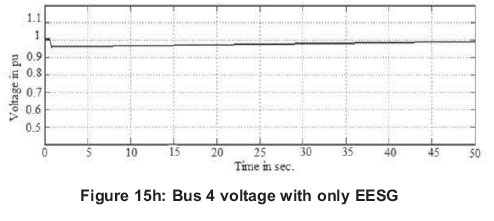
A situation where one high-voltage transmission line gets disconnected is considered first. The changes in voltage levels in the system when connected with SCIG, DFIG, PMSG and proposed EESG are presented in Figures 15 (a, b, c, d, e, f, g and h). The voltage and reactive power control is necessary in order to keep a stable output voltage to maintain the power system voltage balance.
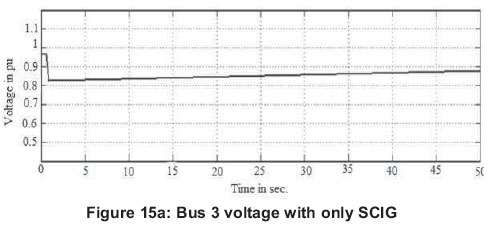
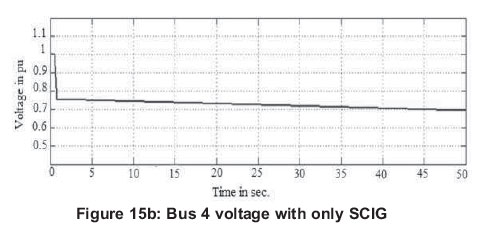
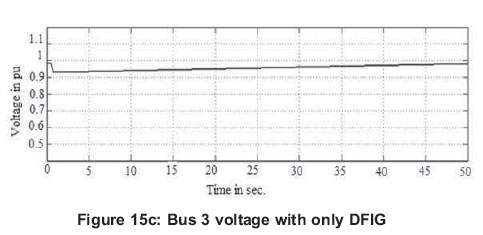
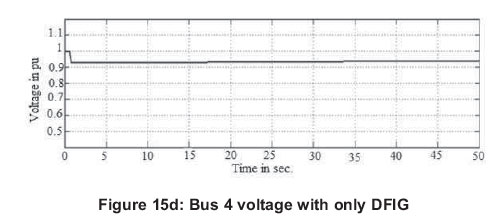
With SCIG connected into the power system, transmission level voltage dropped and initiated a voltage collapse event as shown in Figures 15 (a) and 15 (b). SCIG always consumes reactive power. The reactive power consumption of the SCIG is nearly always partly or fully compensated by a capacitor bank to achieve a power factor close to one in the steady state.
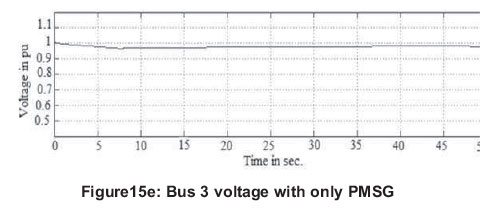
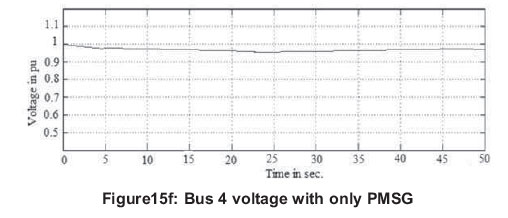
When connected with DFIG, PMSG and proposed EESG, a possible voltage collapse event is avoided. The DFIG, PMSG and EESG have complete control of reactive and active power. They utilized their reactive power injection capability to maintain transmission level voltage within limits after the grid disturbance.
The PMSG and EESG differ from DFIG in that the magnetization is provided by a permanent magnet pole system or a dc supply on the rotor, providing self-excitation property. Self-excitation allows operation at high power factors and high efficiencies. Voltage fluctuation in a PMSG is very low. Comparing the voltage levels in generator and load buses of DFIG and PMSG from Figures 15 (c), (d), (e) and (f), it is observed that, voltage fluctuation in PMSG is lesser.
Similarly, when comparing the performance of PMSG and proposed EESG from Figures 15(e), (f), (g) and (h) with respect to voltage levels during disturbance, they produced similar results. PMSG needs no power converter for field. Normally PMSG gives higher efficiency and energy yield due to very small energy losses in rotor and produce superior results than EESG. Here with proposed efficient, modified converter control in the EESG system, a substantial amount of reactive support is injected and the voltage collapse event is completely avoided, voltage dips are much mitigated and maintained the performance similar to PMSG.
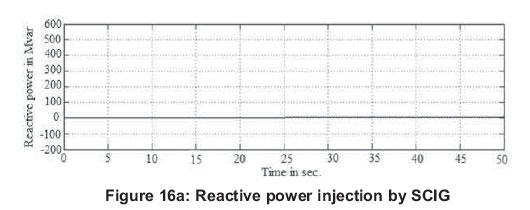
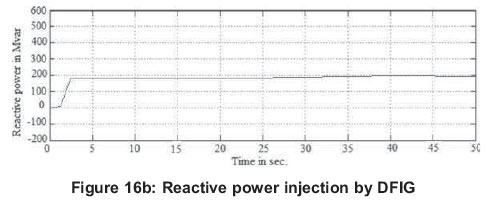
Figures 16(a)-(d) show the reactive power injection capability of the 4 systems. From Figure 16(a), it is seen that the wind turbine system with SCIG is not capable of injecting reactive power. DFIG, PMSG and EESG are having the reactive-power injection capability which can be seen from Figures 16 (b), 16(c) and (d). Compared to DFIG and PMSG, the proposed EESG has much better reactive power injection capability.
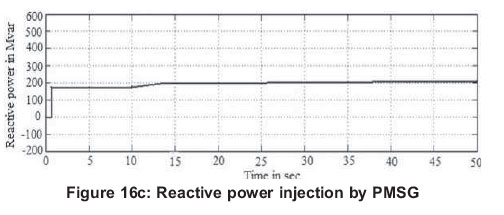
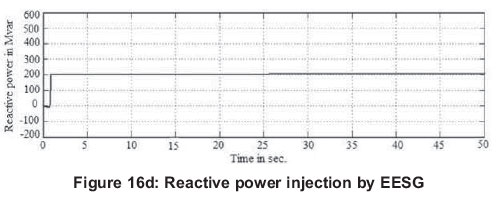
5. Conclusion
In this paper, adaptive hysteresis controlled VSWT driven EESG with MPPT is integrated into power systems and its impact on voltage stability is analysed.
It is found that with the proposed control, DC link voltage is maintained constant under varying wind speeds and different load conditions. The steady-state power transfer capacity of the transmission line is also increased.
Compared to the fixed speed SCIG, standard variable speed systems namely DFIG, PMSG and proposed EESG have more capability to improve long-term voltage stability by reactive power compensation. Among the variable speed systems, EESG with the proposed control strategy is found to assist the grid to delay or prevent a voltage collapse event more effectively and voltage dips are also mitigated.
References
Gupta A., Jain D.K. &, Dahiya S. (2012). Some Investigations on Recent Advances in Wind Energy Conversion Systems. IPCSIT Vol. 28. [ Links ]
Hansen, A.D. & Hansen, L. H. (2007). Wind turbine concept market penetration over 10 years (1994-2004). Wind Energy, 10(1), pp. 81-97. [ Links ]
Kale M. & Ozdemir E. (2005). An adaptive hysteresis band current controller for shunt active power filters, Electric Power Systems Research, 73(2), pp.113-119. [ Links ]
Kesraoui, M., Korichi, N., & Belkadi, A. (2011). Maximum power point tracker of wind energy conversion system, Renewable Energy: Generation & Application, 36(10), pp.2655-2662. [ Links ]
Martinez I. M., Tapia G., Susperregui A, & Camblong H. (2011). DFIG Power Generation Capability and Feasibility Regions under Unbalanced Grid Voltage Conditions. IEEE Trans. Energy Conversion, 26(4), pp. 1051 - 1062. [ Links ]
Nian H., Song Y., Zhou P, & He Y. (2011). Improved Direct Power Control of a Wind Turbine Driven Doubly Fed Induction Generator During Transient Grid Voltage Unbalance. IEEE Trans. Energy Conversion, 26(3), pp. 976 - 986. [ Links ]
Pinilla M & Martinez S. (2011). Selection of Main [ Links ]
Design Variables for Low-Speed Permanent Magnet Machines Devoted to Renewable Energy Conversion. IEEE Trans. Energy Conversion, 26(3), pp. 940 - 945. [ Links ]
Raghe M. & Ragheb A.M. (2011). Wind Turbines Theory - The Betz Equation and Optimal Rotor Tip Speed Ratio. In: Dr. Rupp Carriveau, editor. Fundamental and Advanced 20 Topics in Wind Power, University of Illinois at Urbana-Champaign. 216 Talbot Laboratory. USA, pp.19-38. [ Links ]
Rolan A., Corcoles F, & Pedra J. (2011). Doubly Fed Induction Generator Subject to Symmetrical Voltage Sags. IEEE Trans. Energy Conversion, 26(4), pp. 1219 - 1229. [ Links ]
Thongam J.S, & Ouhrouche M. (2011) MPPT Control Methods in Wind Energy Conversion Systems. In: Dr. Rupp Carriveau, editor. Fundamental and Advanced 20 Topics in Wind Power, University of Illinois at Urbana-Champaign. 216 Talbot Laboratory. USA pp.339-360. [ Links ]
Uehara A. Pratap A., Goya T., Senjyu T., Yona A., Urasaki N., & Funabashi T. (2011). A Coordinated Control Method to Smooth Wind Power Fluctuations of a PMSG-Based WECS. IEEE Trans. Energy Conversion, 26(2), pp. 550 - 558. [ Links ]
Zhe Chen S, Cheung N.C., Zhang Y, Zhang, M & Min Tang X. (2011). Improved Grid Synchronization Control of Doubly Fed Induction Generator Under Unbalanced Grid Voltage. IEEE Trans. Energy Conversion, 26(3), pp. 799 - 810. [ Links ]
Received 19 August 2012
Revised 13 April 2014














