Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
Journal of Energy in Southern Africa
On-line version ISSN 2413-3051
Print version ISSN 1021-447X
J. energy South. Afr. vol.25 n.1 Cape Town Jan. 2014
Solar water heater contribution to energy savings in higher education institutions: Impact analysis
Olawale M PopoolaI; Clément BurnierII
ICentre for Energy and Electric Power, Tshwane University of Technology, Pretoria
IIESIEE, Amiens, and French South Africa Institute of Technology
ABSTRACT
This paper focuses on the impact of Solar Water Heaters (SWH) at a higher institution of learning. An energy audit was conducted for the evaluation of the energy conservation measure: energy conoduction Energy is a key element in the development of any country or institution; as a result any shortage in energy will have a serious effect on the economy and social aspect of such country or institution. South Africa has, in recent years, experienced high economic growth as well as a rapid expansion in the elsumption analysis, correlation of consumption with weather; financial criteria, payback period and needed solar heater system (SWH) to determine the energy that may be termed as wastage or can be saved. The method of investigation includes assessment of the hot water usage within the institution campus and residencies, analysis of bills, metering and development of a software model for the analysis of energy use, system needed and environmental variables. This renewable measure (SWH) showed a high potential of energy and financial savings for higher education institutions especially those with residences.
Keywords: energy, solar water heater, software development and validation
1. Introduction
Energy is a key element in the development of any country or institution; as a result any shortage in energy will have a serious effect on the economy and social aspect of such country or institution. South Africa has, in recent years, experienced high economic growth as well as a rapid expansion in the eectric power consumer base (Ijumba & Sebitosi, 2001). As a result, the demand for electricity has escalated but has not been matched by corresponding investment in generation (Ijumba & Sebitosi, 2001). The South Africa White paper on Renewable energy and Clean Development, 2003 set a target of 10 000 GWh as its contribution to final energy consumption, and this is expected to be achieved through partnerships and will, overcome market barriers and promote widespread use of sustainable energy solutions (Department of Energy, 2012).
Investment in renewable energy and energy efficiency is important so as to reduce the negative economic, social and environmental impacts of energy production and consumption in South Africa. Currently, renewable energy contributes relatively little to primary energy and even less to the consumption of commercial energy (Winkler, 2005). There are various sources of renewable energy e.g. from biomass, wind, solar and small-scale hydro, however in this part of the world solar is readily available. The Southern African region, and in fact the whole of Africa, has sunshine all year round. The annual 24-hour global solar radiation average is about 220 W/m2 for South Africa. Most areas in South Africa average more than 2 500 hours of sunshine per year, and average solar-radiation levels range between 4.5 and 6.5kWh/m2 in one day (www.energy.gov.za). Solar energy, like all other renewable energies, is very safe and environmentally friendly. There are no emissions; the source of fuel is the sun, unlike coal-powered stations (Department of Energy, 2012). There are various technologies hinged on solar usage, such as solar-photovoltaic, solar water heaters etc.
Water-heating accounts for a third to half of the energy consumption in the average household (www.energy.gov.za; Department of Mineral Resources, 2007). In South Africa, water heating is derived mainly from electricity, being the most common energy-carrier employed. The equivalent of a large coal-fired power station (2 000 MW+) is used to provide hot water within the domestic sector alone (www.energy.gov.za; Department of Mineral Resources, 2007).
Since the inception of the accelerated domestic electrification programme through grid extension in South Africa, a major distortion of the national load curve has emerged, with the early evening load peak growing significantly. Modelling indicates that the introduction of solar water-heating can ameliorate the situation substantially. As a result of such deduction, according to the Department of Energy resource on water heating made available for solar water heating, switching from electrical to solar water-heating can, therefore, have significant economic and environmental benefits (www.energy.gov.za).
The South Africa country's utility and policy makers have proposed domestic solar water heating as one of the most viable complimentary solutions to the country's energy and environmental crises (Ijumba & Sebitosi, 2011). Economic benefits may include reduction of energy bills, reduction on peak load at the power utility, greenhouse gas (GHG) emissions reduction, and release of scare capital to other pressing needs.
On the other hand, there are some issues negating the use of SHW, this includes high up-front-capital cost of the system and limited funding for SWH installation by government, banks and other private partnerships. Others include savings impact analysis as well as good economic and financial investigations in terms of investment- payback period.
To alleviate the issues centred around funding and investment, the South African government brought on board a Standard Offer Incentive Scheme that will fund Energy Efficiency and Demand Side Management (EEDSM) interventions. This scheme is aimed at creating an expanded opportunity for attracting the much-needed sustainable financial stimulus into the energy efficient and renewable programme. SWH is amongst the allowable technologies (Department of Energy, 2012).
Commercial buildings and residential home owners' have not shown much interest due to the negating issues raised earlier. In order to assist and give a good perspective of SWH contribution, there is the need to investigate both the savings impact and cost with respect of the high upfront capital involved in the implementation of SHW.
2. Problem description
As a result of electricity shortage and outages in South Africa, coupled with ambiguous tariffs increases within short intervals by the power utilities, this has resulted in high maintenance costs (e.g. generator running and fuel cost) and reduced capital expenditure for the higher education institutions. There is the need to find ways of reducing energy consumption and energy bills.
This project aims at evaluating the impact of SWH usage at an institution of higher learning which will inevitably reduce its energy consumption. The case study is Tshwane University of Technology (TUT), Pretoria Campus.
3. Objectives
The main objective of this study is to demonstrate to management of higher education institution, TUT, that renewable energy (Solar Water Heaters) implementation can yield significant benefits and improve competitiveness of the institution within the limited financial resources available to it. Others objectives include:
• The need to explore the usage of renewable energy sources and its integration to the existing electrical sources at the campus.
• Pollution levels and the energy prices are increasing on a daily basis. Consequently, there is the need to find ways to reduce such issues.
4. Method of investigation
The method of investigation includes audit of hot water usage within the campus, analysis of bills, metering and development of a software model for the analysis/evaluation of the energy impact and solar system design. To achieve the steps outlined, the following were applied in the evaluation of energy savings measures.
4.1 Solar water heating solution
For the model development, Matlab software environment Matlab 7.10. (R2010) was employed. The developed model is expected to give an ample view of investment and payback period, energy and cost saving effects etc. With this evaluation, the usage of SWH may or not be justifiable. The synoptic schematic of the working steps of the software using Matlab is shown in Figure 1.
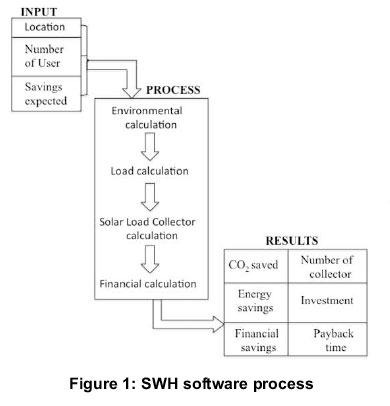
The model development and software analysis was undertaken in steps (see Appendix 1). Firstly, consideration of the environmental values (latitude, declination, solar radiation, slope of the collectors, cold-water temperature and etc.). Secondly, water heating load in KWh per year. Thirdly, energy savings due to the use of the collectors taking into consideration the fraction of saving the user needs. Lastly, makes a synthesis about the financial part and gives the energy saved, the money saved, the initial investment, the number of collector needed and the payback period.
For the investigation, several inputs are needed. However, for this model or software application analysis, the following were taking into consideration: collector and tank model, electricity price, the outside temperature and days of the year. To achieve the outputs as shown in Figure 1, the following calculations were undertaken.
(a) Estimated load calculation
Load calculation is necessary for determining the water heating energy consumption without the solar system as a baseline reference point. This is used for evaluating how much energy and funds (money) will be saved.
From the sampling survey conducted in terms of human behaviour and usage within the campus hostel, findings showed that consumption of hot water during a day is around 7.5 Litres per individual using the number of beds at the hostel as occupants. The total hot water consumption is therefore is the number of people in a building multiplied by the consumption (Duffie & Beckman, 1991).
At TUT University, most of the hot water consumption is at the hostels, hence the number of people is assumed to be the number of beds in each hostel. The energy required can be express as (Redpath, 2012):
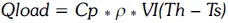
Where Cp is the heat capacitance of water (4 200 (J/kg)/ °C); ρ its density (1 kg/L); and Ts is the cold water temperature afterwards; Qload is calculated for a year period; "Th" is the hot water temperature in the tanks in most cases, the average value is 60 oC.
Yearly load took into consideration the type of buildings as well as the purpose and activities in such buildings. For instance, at the hostels, investigation showed that buildings were fully occupied during the week. However, as a result of the rest periods and holiday of between 2-3 months (no other activities took place during this period at the audited residences), the yearly average occupation per year is ~ 75 %.
(b) Calculation of environmental variables
The variables outlined here were applied in the SWH model analysis.
Cold water temperature
To determine the cold water temperature, the following formula was applied:
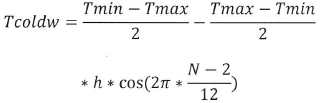
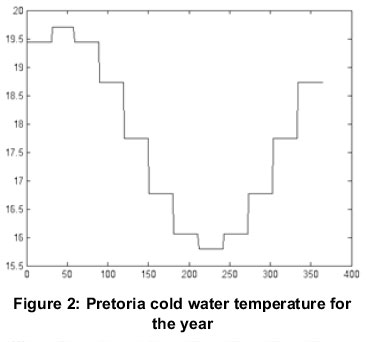
Tmin and Tmax are the value of maximal and minimal cold water (corresponding to the soil temperature from 2m deep), in Pretoria these values are around 19.7 and 15.7 Celsius degrees; h indicates the location of the project, if it is in south or north hemisphere (1 if north or -1 if south hemisphere); and N is the number of the month (between 1 and 12). From the formula, it is possible to have the average value of cold water for each month of the year. Figure 2 shows the estimates cold water temperatures for Pretoria according to number of days.
Sky irradiance
The sky irradiance variable is an indispensable parameter used for calculating the energy collected by the solar panels. In order to calculate the sky irradiance value, the basic concept of energy engineering was applied as shown by the evaluation.
Declination
Declination: is the angular position of the sun at solar noon (corresponds to the moment when the sun is at its highest point in the sky).
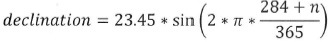
The declination for each day of the year (n is the day number) was calculated using Matlab software and the result obtained is from 23.45 at June 21th to -23.45 as at December 21th.
Sunset hour angle
The sunset hour angle 'ws' is the solar hour angle corresponding to the time when the sun goes down. It is given by the following equation:
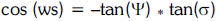
It takes 15 degrees per hours (positive in afternoon and negative in the morning) correspond for 360 degrees per day.
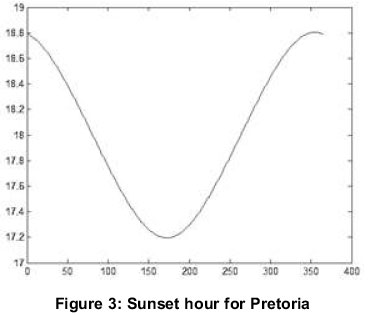
Figure 3 shows the sun set hour for Pretoria (lat- itude = 25.732 S) according to days. For example, on 14th July, the sun set at 17h16 (note: this value is an average considering the sun at noon (12h00).
Extra-terrestrial radiation
The extra-terrestrial radiation is the solar radiation before it reaches the atmospheric land layer. The extra-terrestrial radiation in a horizontal plane 'H0' can be evaluated for days of the year with the following equation:
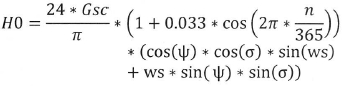
Where Ψ is the latitude, σ the declination, ws the sunset hour angle, and n the number of the day. Gsc corresponds to the solar constant equal to 1367 W/m2. The value of H0 with this formula is dimensioned in Wh\m2.
Solar radiation for an inclined plane
The solar radiation for an inclined plane has to be known so as to be able to evaluate the load of the solar panels and the amount of solar energy that can be accumulated. The formula for solar radiation in an inclined plane is given by the equation:
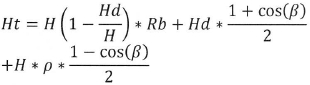
ρ is the ground reflectivity supposed to be equal to 0.2 if the yearly temperature is higher than 0 °C; and 0.7 if the temperature is lower than -5°C. In this case, the value for Pretoria is 0.2 as a result of the average yearly temperature being equal to 20°C.
Hb is the product of monthly average beam radiation: Hb = H-Hd; Rb is a geometric factor depending on the slope of the collector (β), the latitude (Ψ), the declination ( σ) and days:
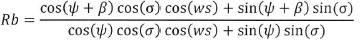
The formula is used for the southern hemisphere. As for the northern hemisphere, the sign before β in the cosine and sine function needs to be changed. ws is the sunset hour angle which is dependent on Ψ and σ previous. Hd is the monthly average daily diffuse radiation calculated in two different cases using the global irradiation (H) and the clearness index (Kt).
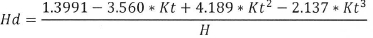
If ws>81.4 degrees
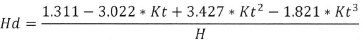
If ws>81.4 degrees
And β is the slope of panels. The slope of the surface will be fixed for each day and will be:
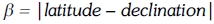
Two cases were considered using the software, the collector as a tracking collector which can be programmed to the value above; or consider as a fixed collector using the mean value of 'beta'. For Pretoria TUT campus, a test fixed collector was considered because tracking collectors are rarely in use nowadays apart from the difficulty in estimating the initials.
Sky radiation
The value of the sky irradiance is needed to quantify radiative transfer exchanges between a body (solar collector) and the sky. The actual sky radiation falls somewhere in-between the clear and the cloudy values. If c is the fraction of the sky covered by clouds, sky radiation may be approximated by:
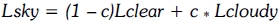
Where clear sky long-wave radiation (in the absence of clouds) is:
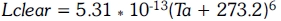
Ta is the ambient temperature in °C. For cloudy skies, the average temperature is assumed to be Ta-5°C and emit long wave radiation with an emittance of 0.96, that is, the irradiance of a sky cloudy is computed as:
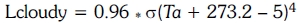
Where σ is the Stefan-Boltzmann constant assumed to be equal to 5,669x10-8 (W/m2)/K4.
To find an approximate monthly value of 'c' the formula below may be applied:

Kd is calculated by using the average clearness index ('Kt') and the Collares-Pereira and Rabl correlation:
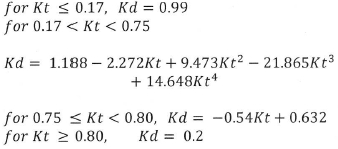
Load collected
The energy collected per unit collector area per year is described by the following equation:
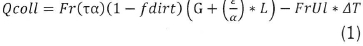
Where Fr(τα) and FrUl are collector characteristics explained in due course, G is the global incident solar radiation of the collector (taking the yearly average irradiation in an optimally inclined plane from the Joint Research Centre-European Commission website, the ratio ε/α is set to 0.96 (ε is the long wave emissivity of the absorber), ΔT is the temperature differential between the working fluid entering the collectors and outside ambient temperature that is Ts-Ta. L is the relative long wave sky irradiance. It is defined as:
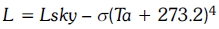
Where Lsky is the long wave sky irradiance previously calculated and Ta the ambient temperature expressed in °C.
This model includes also the losses due to snow, dirt and piping. The dirt value is the losses due to snow; dirt can affect the irradiance level experienced by the collector. Therefore, Fr(τα) is mul- tiplied by (1- f dirt), typical values range from zero to a few percent. In the project location study (Pretoria, South Africa) it rarely snows, hence the value depends only on the dirt. This value is around 5%.
Hot water is stored in tanks and run through imperfectly insulated pipes giving rise to heat being lost to the environment. The load collected value is affected by these losses as shown in the equation:
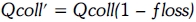
The value loss is the losses in the pipes and the tank (if needed). This value varies between 1 to 12 %; hard to estimate due to its dependency on several factors such as length of the pipes and water usage in the tank.
Collector panels
Three types of solar collector are considered in equation 1; these are glazed collectors, evacuated collectors and unglazed collector. The needed changes in the applicable equation are the collectors characteristics, namely FrUl and Fr(τα). There are generic values for these characteristics if not provided by the manufacturers.
Water pump load
To direct the heated water in the collector to the water tank or the existing water heating process, one or more water pumps is needed. The energy value of the water pump is based on this formula:
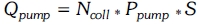
Where Qpump is the energy needed to pump the water in a year. Ppump is the power by surface unity of the collector (this value is generally between 8 and 22 W/m2). S is the area taken by the collectors in m2. And Ncoll the number of working hours the solar collector is used.
The value of Ncoll can be approximated as:
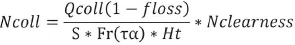
This value is given by the energy collected by the solar system taking into account the losses divided by the energy without losses and multiplied by the number of daytime hours of days in the years Nclearness. Nclearness is the factor of the clearness index (computed in "Extra-terrestrial radiation" part) number of hours in the days.
(c) Financial evaluation
Using the various calculations as previously mentioned, the energy and cost savings will be justified as shown by the graph in terms of payback period and profitability. The energy saved is attributed to the use of the solar water heating system/process.
The money saved in relation to years is shown in Figure 4.
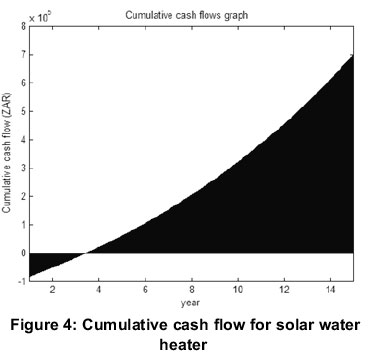
Figure 4 is the result of the eco formula below using inputs such as the initial investment, the inflation and the electricity price.
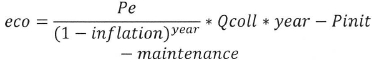
Pe is the electricity price; Qcoll is the energy calculated earlier; Pinit is the initial price which corresponds to the price of collectors and the tank (if needed). Solar collector lifetime is around 25-30 years; however, for the software analysis the value of 20 years was (will be) used. This is to take care of the possible maintenance cost according to the piping or the tanks. The maintenance is estimated by the initial price of the items divided by the lifetime per year (in a lower value), however, the value of the initial price is based on this formula:
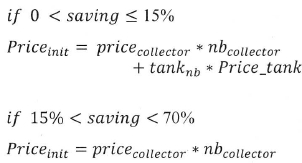
The price of the water pump is included in the price of the solar collector. Only the power consumption of the water pump is considered in the financial part. That is the cost of power consumption by the water pump will be subtracted from the money saved as a result of the installed SWH. For estimation of the inflation rate, the mean value (5.47%) for the last 10 years in South Africa was (will be) applied (see http://www.global-rates.co for the last ten-year inflation rate).
5. Model validation and application
The goal of this software is to give an ample view of investment, energy and money saving, payback, baseline energy of the building, environmental variable-cold water temperature profile, solar irradiation on an inclined plane, number and slope of collector for better efficiency, energy required by the water pump etc.
To evaluate and validate the developed model applications, the proposed energy saving measure was evaluated using the following procedures:
5.1 Solar water heating - process
The SHW process in Figure 1 was applied in the application development (Appendix 1). In order to substantiate the implementation of the solar water heating process using the developed application, the following parameters were inputted (Duffie & Beckman, 1991; Redpath, 2012; Retscreen):
• Location of installation: 25°43'56" South, 28°9'42" East; Elevation: 1310 m a.s.l.
• Type and size of solar collector: 12 Pipe Evacuated Solar Collector (Xtreme solar company) with a surface area of 2.2256 m2 (total cost ZAR 7439.28)
• Type, size and cost of water storage tank: JoJo; 10000 litres capacity; ZAR 8366.00
The number of the tanks in the project is dependent on the number of people using hot water and the fraction of energy/money saving expected.
Other needed inputs for the MATLAB SWH application include:
5.2 Water consumption
From the audit exercise carried out at the campus, the total number of beds at the six residences is 1 250. The average daily hot water usage per day was estimated to be 9 500 litres (average of 7.6 litres).
5.3 Hot water electricity consumption per year
The use of hot water corresponds to electrical consumption, however, in order to quantify the yearly water consumption, the holiday period in South Africa needed to be taken into account. Using the South Africa school calendar (www.kwathabeng.co.za/travel/south-africa/destinations.html?cal=school, 2011), there is around 94 days of vacation in a year which is about 25% of the number of days in year. As a result, the use of residences is consequently around 75% in a year with an estimated annual water heating consumption of around 1 279MWh/year.
5.4 Energy consumption and energy saved
The fraction of energy saving is set to 70% (maximum) so as to be able to reduce most of energy thereby cumulating into financial savings consump- tion; while the remaining will be supplied by electric resistance heating (electric geysers).
5.5 Lifetime of project
The lifetime of the existing project is fixed to 10 years.
5.6 Result obtained
Using the SWH model, the energy required to heat water is 1 535 MWh/year while the energy produced by the solar water process is 1 074 MWh/year. This shows that the amount of energy consumed without the solar water heating system is 461 MWh/year according to software application. This is expected to be saved using SWH.
According to the cumulative cash flow graph in Figure 5, the intended project implementation or solution shows a payback time of 3 years and 10 months. The slope of the collectors needs to be inclined at an around 25.2 degrees for maximum irridance utilization.

The number of collector needed to achieve the expected energy from SHW is 329, with an area of 732 m2. This means that 54 collectors of 120m2 area need to be implanted on each residential building roof. The SHW impact is expected to bring about 938 ton of CO2 emission reduction. In summary, the impact of SHW will translate into around 7.1 million rand financial savings over a 10 year period.
6. Conclusion and recommendation
In order to assist policy makers in the areas of energy management, the impact of SWH in a learning institution was investigated. In the course of the investigation, study of the existing usage pattern, development of simulation techniques for analyses and evaluation was carried out. The highlights of this study were the introduction of environmental variables which are very crucial to SHW implementation, operation and justification. This was mathe- matically modelled and very much differs from the existing models currently available.
Results obtained show that financial, operational and environmental benefits will arise as a result of solar water heating implementation at learning institutions. These benefits include maintenance cost reduction (geyser repairs, generator repairs/ maintenance. fuel cost etc.) and, more importantly the electricity consumption reduction thereby cumulating into financial savings for the institutions.
Acknowledgements
This work was supported by Eskom, South Africa, and the Centre for Energy and Electric Power, Tshwane University of Technology. Special mention must be made to the Julien Masson (ESIEE, Amiens, and French South Africa Institute of Technology that participated in the research work, as well as Prof J. Munda.
References
Department of Energy, (2012). White paper of Renewable energy: solar power (www.energy.gov.za/files/renewables_frame.html). [ Links ]
Department of Mineral Resources. Resources Year book, 2007. Minerals, energy and geology. www.gcis.gov.za/sites/default/files/docs/resourcecentre/year-book/2007/chapter16.pdf. [ Links ]
Duffie, J.A. and Beckman, W.A., (1991). Solar Engineering of Thermal Processes, 2nd Edition, John Wiley & Sons. [ Links ]
Electric Power Research Institute, (1993). Engineering Methods for estimating the impacts of Demand -Side Management Programs: Volume 2: Fundamental equations for residential and commercial end uses. TR-100984, Vol. 2. [ Links ]
Eskom Power Conservation Programme. www.esko-midm.co.za/power-conservation-programme. [ Links ]
Fritz W.L.O. & Kallis, D.C. (2010). Domestic load-profile measurements and analysis across a disparate consumer base. 18th International conference on the Domestic Use of Energy Conference, 2010. [ Links ]
Holm. D, (2005). Market Survey of Solar Water Heating in South Africa for the Energy Development Corporation (EDC) of the Central Energy Fund (CEF). Solar sure.
Howard, G, (2005). The experience with Energy Efficiency policies and programmes in IEA Countries; Learning from the critics, IEA information paper, Colorado. [ Links ]
Ijumba, P & Sebitosi, A. B., (2010). Evaluating the Impact of Consumer Behaviour on the Performance of Domestic Solar Water Heating Systems in South Africa. Journal of Energy in Southern Africa, Vol. 21, No 1. [ Links ]
Meyer, J. & Tshimankinda, M., (1997). Domestic Hot Water Consumption in Southern Africa Houses for Developed Communities. International Journal of Energy Research, Vol. 21, Pg. 667-675. [ Links ]
National Solar Water-Heating Programme (www.energy.gov.za/files/esources/renewables/WaterHeating.pdf). [ Links ]
Redpath, D., (2012. Thermosyphon heat-pipe evacuated tube solar waters for northern maritime climates. Solar energy Vol. 86, Pg. 705-715, [ Links ]
Okoro, O., Chikuni, E. & Oluseyi, P, (2008). Introducing an Energy Efficiency Awareness Programme at the University Of Nigeria, Nsukka (Unn). Industrial & Commercial Use of Energy, 2008. [ Links ]
Popoola O.M., Jimoh, A.., & Nicolae, D. 2010. Automating Consumers' Connections to the Distribution Network for Enhanced Performance. International Review of Electrical Engineering, Vol.5. No. 5. [ Links ]
Renewable Energy. http://www.energy.gov.za/files/resources/renewables/r_solar.html. [ Links ]
Retscreen® International Solar Water Heating Project Analysis Chapter; retscreen.com and retscreen software. [ Links ]
Solar references for monthly radiation and outside temperature. Available at www.pa.eu.re.jrc.ec.euro [ Links ]
Winkler, H. (2005). Renewable energy policy in South Africa: policy options for renewable electricity. Energy Policy 33 (2005) 27-38. [ Links ]
Wright, A & Firth, S., (2007). The nature of domestic electricity-loads and effects of time averaging on statistics and on-site generation calculations. Applied Energy Vol. 84, Pg. 89-403. [ Links ]
Received 20 March 2012
Revised 18 February 2014














