Serviços Personalizados
Artigo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em Google
Similares em Google
Compartilhar
Journal of Energy in Southern Africa
versão On-line ISSN 2413-3051
versão impressa ISSN 1021-447X
J. energy South. Afr. vol.24 no.3 Cape Town Jan. 2013
RESEARCH ARTICLE
Solar radiation analysis and regression coefficients for the Vhembe Region, Limpopo Province, South Africa
Sophie T MulaudziI; Vaithianathaswami SankaranII; Meena D LyskoIII
IDepartment of Physics, University of Venda
IIDepartment of Physics, University of Venda
IIIOptronic Sensor Systems, Defence Peace Safety Security, Council for Scientific and Industrial Research
ABSTRACT
Given the limited observed and reliable data for solar irradiance in rural parts in South Africa, a correlation equation of the Angström-Prescott linear type has been used to estimate the regression coefficients in the Vhembe District, Limpopo Province, South Africa. Five stations were selected for the study, with the greatest distance between stations less than 180 km. Monthly regression coefficients were derived for each station based on an observation dataset of sunshine duration hours and global horizontal irradiance. The correlation coefficients appear to be above 0.9. The representative Angström-Prescott model for the Vhembe Region was found by collating the data for each station and then averaging the respective correlation coefficients. This paper presents the generated regression coefficients for each station and for the Vhembe Region.
Keywords: South Africa, global horizontal irradi-ance, Angstrom Prescott, linear regression, solar radiation
1. Introduction
Limpopo Province is situated in the north-eastern part of South Africa and it incorporates about 10% of South Africa's total land. Over 75% of households within this province rely on alternative fuel for cooking and heating (El-Sebaii et al., 2005) of which less than 1% is reliant on solar systems; even though the province has solar energy potential to support all of the province's energy demand. It is identified that the quantitative knowledge of solar surface irradiance would better help in initiatives such as the leveraging of financial support for solar energy projects, for designing of efficient solar energy systems and for the planning of cost effective maintenance solutions.
An attempt is now made for a quantitative knowledge of the solar resource. The limited in-situ observations for solar irradiance data across the province makes it necessary to consider model predictions. Modelling provides the means for generating global solar irradiation predictions at different sites where the measured data is unavailable. This paper reports on the regression coefficients of the Angström-Prescott linear regression model to predict average daily global solar radiation for one of the five regions in the Limpopo Province, namely the Vhembe Region.
2. Methodology
2.1 Regression model
The total solar irradiance (HT) on a horizontal surface at ground is the sum of the sun's direct beam () (BHorizontal) and sky diffuse (DHorizontal) solar irradiance. That is:

Moreover, with attenuation by traversing through the atmosphere, one may express equation (1) in a relative form with the extra-terrestrial irradiance Ho. The ratio H/Ho is referred to as the clearness index. In a similar manner, the sun's direct beam reaching the surface is the cloudless index given by the ratio of instantaneous actual sunshine hours (Na) to a predicted possible sunshine hours (Np). Equation (1) is then represented as:
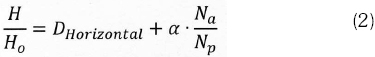
The factor α is introduced to account for atmospheric scattering and attenuation by air particles such as water, dust, aerosols and gases. In its simplest form, with DHorizontai and α as regression parameters, Equation (2) leads to the basic Angström-Prescott model to predict solar irradiance at any location. So, estimation of the monthly average daily global solar radiation (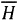 , MJ/m2) on a horizontal surface, at a particular site, is given by Angström-Prescott (Angstrom, 1924) and (Iqbal, 1983) as:
, MJ/m2) on a horizontal surface, at a particular site, is given by Angström-Prescott (Angstrom, 1924) and (Iqbal, 1983) as:

where α and b are now the regression coefficients to be determined,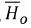 is the monthly average horizontal extra-terrestrial solar radiation.
is the monthly average horizontal extra-terrestrial solar radiation. 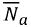 and
and 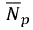 are daily average duration of the actual and predicted possible sunshine hours respectively. The parameters
are daily average duration of the actual and predicted possible sunshine hours respectively. The parameters 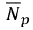 and
and 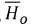 are computed according to the deterministic expressions given in, for example (Iqbal, 1983), (Garg et aí., 2002) and (Rai, 2009).
are computed according to the deterministic expressions given in, for example (Iqbal, 1983), (Garg et aí., 2002) and (Rai, 2009).
2.2 Data accessibility
It follows from equation (3) that a linear regression analysis between clearness index and cloudless index will directly lead to the estimation of the Angström-Prescott coefficients a and b. 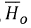 and
and 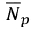 have fixed values for a geographic location, as shown.
have fixed values for a geographic location, as shown.  and
and 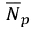 vary temporally and depend on the site specific climatic conditions. They are gotten from observation with pyranometers and sunshine recorders, respectively.
vary temporally and depend on the site specific climatic conditions. They are gotten from observation with pyranometers and sunshine recorders, respectively.
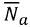 for the stations in this study was obtained from the South African Weather Services (SAWS). The SAWS network uses Campbell Stokes sunshine recorders to measure the actual sunshine hours,
for the stations in this study was obtained from the South African Weather Services (SAWS). The SAWS network uses Campbell Stokes sunshine recorders to measure the actual sunshine hours, 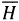 data is from the Agricultural Research Council (ARC). The ARC and SAWS networks do not overlap so 5 locations were selected such that the ARC/SAWS pairs are in close proximity to one another.
data is from the Agricultural Research Council (ARC). The ARC and SAWS networks do not overlap so 5 locations were selected such that the ARC/SAWS pairs are in close proximity to one another.
The data set considered is from 1 January to 31 December, 2010. This data set was quality checked to remove outliers, which included removing data points if the clearness index was greater than 1, as well as data points with little or no correlation between observed sunshine duration and global horizontal solar irradiance.
2.3 Statistical analysis
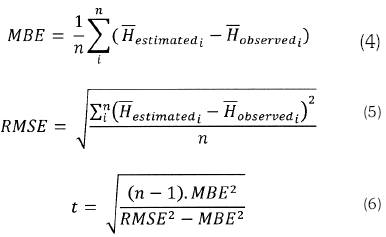
The generated regression equations for each site were used to calculate the monthly average daily global solar radiation. These values of global radiation were then compared against the measured data for the locations. The accuracy of the estimated horizontal global solar radiation data against the 'true data' is tested by calculating the mean bias error (MBE), root mean squared error (RMSE) and t-statistic. The formulas for the statistics indicators (Togrul, 1998) and (Stone, 1993) are given by equations (3), (4) and (5), where is the number of data pairs observed and the subscript i ranges from 1 to n. The use of the additional t-statistic is used to assess the reliability of the results. This is because it is possible to have a large RMSE value whilst at the same time a very small MBE. To determine whether the model's estimates are statistically significant, a critical t-vaíue at a = 95% confidence level is taken from the standard statistical tables. That is, tcriticaí = 1.96. In order to analyse the model's estimates at (1 - α) confidence level the calculated t must be such that -1.96 < t <1.96.
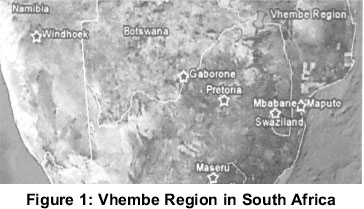
3. Study area
The Vhembe Region and selected study points are shown in Figures 1 and 2, respectively.

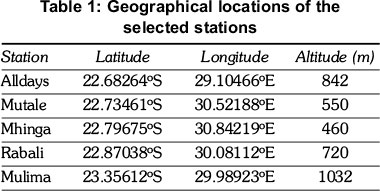
The study points are: Alldays, Rabali, Mutale, Mhinga and Mulima (see Table 1 for their geographical location). Alldays, which is just outside the Vhembe Region, is included for comparison.
4 Results and discussions
4.1 Actual versus possible sunshine hours
Figure 3 shows  and
and 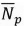 for the Vhembe Region. In the Vhembe region, we generally observe winter season during the months of May, June and July. During this period we normally expect lower actual sunshine hours than the other seasons. But the actual sunshine hours is rather more during the year under investigation in winter and this may be attributed to limited absolute clear sky days for that particular year. In addition to that it is always preferable to calibrate the measuring instruments on regular basis in order to get a reliable set of data. Unfortunately, the calibration records are not available for the area under study.
for the Vhembe Region. In the Vhembe region, we generally observe winter season during the months of May, June and July. During this period we normally expect lower actual sunshine hours than the other seasons. But the actual sunshine hours is rather more during the year under investigation in winter and this may be attributed to limited absolute clear sky days for that particular year. In addition to that it is always preferable to calibrate the measuring instruments on regular basis in order to get a reliable set of data. Unfortunately, the calibration records are not available for the area under study.
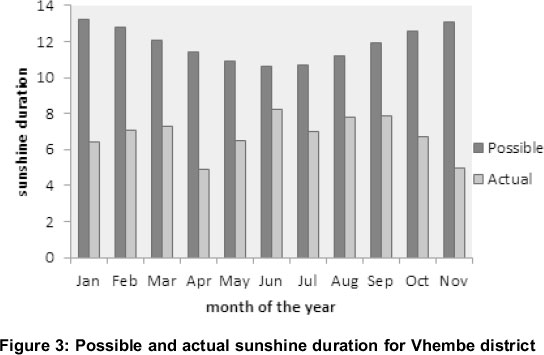
4.2 Station specific linear regressions
The ratios of clearness and cloudless indices for the accumulated data sets (that is, data for an annum) are plotted in Figure 4 for the five sites in this study. The figure also shows the coefficient of determination (R2) for the 1st order linear curve fits for each of the sites. R2 ≥ 0.9 for over 80 % of the linear regressions. One may assume R2 < 0.8 as an indication that the investigated data set is questionable in terms of reliability. The reliability of the data set will depend on the implementation of calibration of the pyranometers and general maintenance of the observing instruments. It is noted that only data with R2 < 0.5 have been excluded from the analysis in this work in an effort to investigate a larger data set.
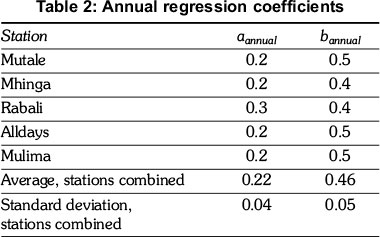
The annual regression coefficients for all the sites have been determined by the linear regression curves to the data sets for the respective sites. The derived annual regression coefficients are given in Table 2. The table also shows the calculated linear regression coefficients for all stations combined as well as the respective standard deviations. The standard deviations suggest a combined uncertainty of a ± 20% and b ± 11%, which may be acceptable given the uncertainties of raw data. It follows that the annual average linear regression coefficients may be considered representative coefficients for the Vhembe Region. That is, the Angström-Prescott linear regression model for the Vhembe Region in the Limpopo Province may be represented as:
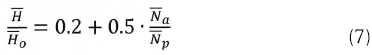
4.3 Validation of results
The developed model shown as equation (7) is used to estimate the horizontal global solar radiation for the five stations in this study. The respective estimated horizontal global solar radiation is then compared with the measured values. The 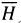 estimated,
estimated, 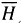 measured, MBE, RMSE and t-statistic for each of the stations is given in Table 3 (with tcritical at 5 % = 1.96). The comparison of observed to estimated horizontal global solar radiation for the five locations is given by the plots in Figure 5. It is assumed that the larger variations (see, for example, Mulima from September to November) may be due to discrepancies in the raw data sets and subsequent filtering process. Also, one may expect larger deviations between
measured, MBE, RMSE and t-statistic for each of the stations is given in Table 3 (with tcritical at 5 % = 1.96). The comparison of observed to estimated horizontal global solar radiation for the five locations is given by the plots in Figure 5. It is assumed that the larger variations (see, for example, Mulima from September to November) may be due to discrepancies in the raw data sets and subsequent filtering process. Also, one may expect larger deviations between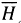 estimated and
estimated and 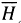 measured when the cloudless indices are very low.
measured when the cloudless indices are very low.
The goodness of fit statistics, shown in Table 3, demonstrates that the derived linear correlation coefficients may be used in the Angström-Prescott model to estimate monthly average daily global solar radiation on a horizontal surface, for the respective locations in this study. All regressions are within the range of tcriticai = 1.96.
Overall, the determined annual regression coefficients for the Vhembe Region appear consistent with the reports such as for the locations: Toledo (Almorox et al., 2004) (where a = 0.2170 and b = 0.5453), Lesotho (Safari et al, 2009) (where a = 0.266 and b = 0.512), and Bulawayo (Gopinathan, 1988) (where a = 0.304 and b = 0.440). Moreover, Pereira (Pereira, 1988) has recommended general values of a and b to be 0.250 and 0.50 respectively, for any location and climate.
5. Summary
It may be concluded from the presented work that the monthly average daily global solar radiation on a horizontal surface for any location in the Vhembe Region may be estimated using the re-parameterized Angström-Prescott linear regression model as given by equation (7). Further investigation on the quality of the raw data and consideration of a longer observation period is needed to improve the confidence of the model.
Acknowledgement
We thank the Agricultural Research Council (ARC) for the meteorological parameter data for the north-eastern region and the South African Weather Services (SAWS) for the actual sunshine data closest to the ARC sites.
References
Allen, R. G., Pereira, L. S., Raes, D., and Smith, M., (1988). Crop Evapotranspiration. Guidelines for computing crop water requirement. FAO Irrigation and drainage paper 56. Rome. [ Links ]
Almorox, J., and Hontoria, C., (2004). Global solar radiation estimation using sunshine duration in Spain. Energy conservation and management, Vol. 45: 1529 - 1535. Elsevier. [ Links ]
Angstrom, A., (1924). Solar and terrestrial radiation. Q.J.R.Meteorol. Soc, Vol. 50: 121-125. [ Links ]
El-Sebaii, A. A., and Trabea, A. A., (2005). Estimation of global solar radiation on horizontal surfaces over Egypt. J.Solids, Vol. 28 (1). [ Links ]
Garg, H. P and Prakash, J., (2002). Solar Energy fundamentals and applications. Tata McGraw-Hill Publishing Company Limited, New Delhi. [ Links ]
Gopinathan, K. K., (1988). A general formula for computing the coefficients of the correlation connecting global solar radiation to sunshine duration. Solar Energy, Vol. 41(6): 499-50 [ Links ]
Iqbal, M., (1983). Introduction to solar radiation. New York: Academic Press. [ Links ]
Rai, G. D., (2009). Solar Energy Utilization. Khanna Publishers [ Links ]
Safari, B., and Gasore, J., (2009). Estimation of global solar radiation in Rwanda using empirical models. Asian Journal of Scientific Research, Vol. 2 (2): 6875. [ Links ]
Statistics South Africa, (2001). Census 2001: Primary tables Limpopo: Census '96 and 2001 compared, Report No. 03-02-11. [ Links ]
Stone, R. J., (1993). Improved statistical procedure for the evaluation of solar radiation estimation models. Solar Energy Vol. 51: 289. [ Links ]
Togrul, I. T., (1998). Comparison of statistical performance of seven sunshine-based models for Elazig, Turkey, Chemica Acta Turuca, 26, 37. [ Links ]
Togrul, I. T., (1998). Comparison of statistical performance of seven sunshine-based models for Elazig, Turkey, Chemica Acta Turuca, 26, 37. [ Links ]
Received 9 January 2012
Revised 18 June 2013














