Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
Journal of Energy in Southern Africa
On-line version ISSN 2413-3051
Print version ISSN 1021-447X
J. energy South. Afr. vol.24 n.1 Cape Town Jan. 2013
Thermal modelling of low concentrator photovoltaic systems
JD Gerber; MA Benecke; FJ Vorster; EE van Dyk
Nelson Mandela Metropolitan University, Port Elizabeth
ABSTRACT
Efficient thermal management of low concentrator photovoltaic (LCPV) systems will allow maximizing of the power output and may also substantially prolong operating lifetime. For this reason, it is necessary to develop a thorough understanding of the thermal transfer and dissipation mechanisms associated with an LCPV system. The LCPV system under consideration uses a 7-facet reflector optical design, providing a geometric concentration ratio of approximately 4.85. The LCPV system succeeded in increasing the short circuit current from 1A to 5.6A, demonstrating an effective concentration ratio of approximately 4.75. LCPV system temperatures in excess of 80°C were recorded without a thermal management system. A basic thermal model was developed and assessed under various environmental conditions. The effectiveness of a heat-sink, which reduced the temperature difference between the LCPV receiver temperature and the ambient temperature by 37.5%, was also evaluated. The results discussed in this paper will assist the future development of techniques aimed at reducing the high temperatures associated with LCPV systems.
1. Introduction
Concentrator photovoltaic (CPV) systems use refractive or reflective optical elements to concentrate a large amount of solar energy onto a small area of PV material. CPV systems are therefore capable of substantially reducing the cost of electricity production. However, the increased temperature associated with these CPV systems places significant strain on the PV receiver which may lead to rapid degradation. The open circuit voltage of the PV receiver is also reduced during these high temperature conditions, which leads to a corresponding loss in power output.
For these reasons, it is essential to gain an understanding of the energy transfer mechanisms of LCPV systems. A basic thermal model was developed to mathematically illustrate the various thermal transfer and dissipation mechanisms which occur within a LCPV system. Once the energy transfer mechanisms are adequately understood a thermal management system may be developed to reduce the high cell temperatures associated with LCPV systems.
The purpose of this paper is to discuss the optical and thermal sub-systems of a designed LCPV system, whilst focussing on the thermal properties needed to design a thermal management system.
2. Optical model
Figure 1 shows the CPV system under investigation. The system consists of a 7-facet reflector system, providing a geometric concentration ratio (Xg) of 4.85. Owing to optical losses associated with the reflector material, an effective concentration ratio (Xe) of less than 4.85 is expected.
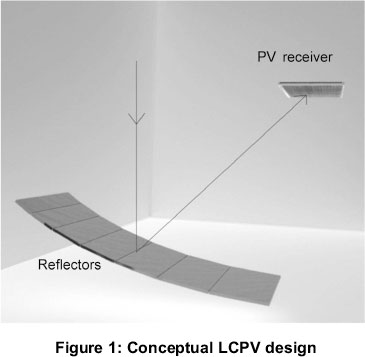
The PV receiver under investigation consists of 8 series connected poly-crystalline silicon cells. These cells are attached to an aluminium sheet using a thermally conductive and electrically insulating bonding material.
2.1 Thermal model
The thermal model developed is based on the conservation of energy with the following assumptions:
- The thickness of the receiver is much smaller than its lateral dimensions, therefore, the heat transfer model is assumed to be one-dimensional.
- Irradiance is the only source of incident energy.
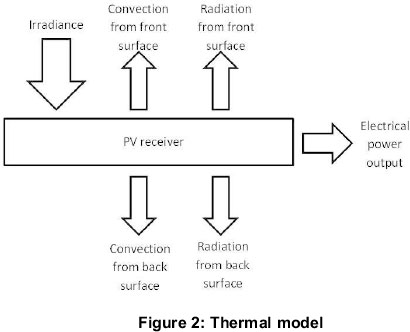
- Energy is dissipated by radiation, convection and through conversion into electrical energy. Figure 2 shows the energy transfer mechanisms associated with a LCPV system.
The thermal model can be used to quantify the energy dissipation and transfer under thermal equilibrium conditions when the temperature of the PV receiver is relatively constant. At thermal equilibrium:
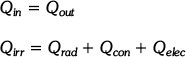
In order to avoid mechanical damage and shading of the PV cells, it is preferable to measure the temperature at the back of the PV receiver. Owing to the high thermal conductivity of the aluminium base and the thermal conductive materials used, the temperature of the front of the PV receiver is assumed to be equal to temperature of the back of the PV receiver.
Energy dissipation through convection (Qcon ) and radiation (Qrad ) may be determined by the following equations:
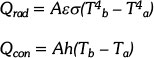
Where h is the convective energy transfer co-efficient and Ta and Tb are the ambient and PV receiver temperatures respectively.
It is straightforward to calculate the energy dissipated through convection by monitoring the air flow and temperatures within the LCPV system. However, owing to the complex geometry of the LCPV system, a complicated convective pattern develops and thus direct calculation of h is not possible. The energy dissipated through convection may be determined indirectly by considering the change in temperature of air and the mass flow rate over the PV receiver by the following equation:
![]()
where Tin is the ambient temperature, Tout is the average air temperature after convection and C is the specific heat capacity of the air.
2.2 Experimental
An experiment was conducted to evaluate the thermal model experimentally. The entire LCPV system was housed within an insulated wooden box, designed to restrict energy losses to the environment. Panel fans were used to simulate air flow across the PV receiver and two glass sheets were used to ensure parallel and direct air flow. K-type thermocouples were used to measure temperatures at various points within the LCPV system. Figure 3 shows a simplified illustration of the above mentioned experiment.
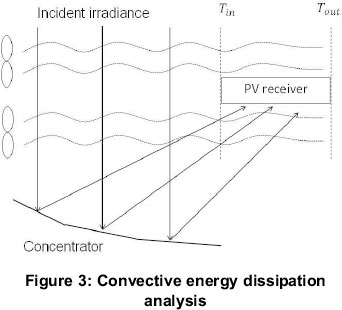
The PV receiver temperature was measured and used to quantify energy dissipation through radiation. Anodised aluminium has an emissivity of approximately 0.8, while the emissivity of the PV cells was assumed to be similar due to their anti-reflective properties. For this reason, the PV receiver is assumed to have an overall emissivity of 0.8.
The ambient temperature (Tin) and the average air temperature after convection (Tout) were measured at the positions as shown in Figure 3, and these temperatures were used to evaluate energy dissipation through convection. A constant air flow of 1.2m/s was supplied by the panel fans.
Owing to the inclusion of glass sheets in the experimental design, the amount of energy incident on the PV receiver was calculated using Fresnel equations for reflection and absorption. Also, the PV receiver was operated in open circuit, so Qelec = 0.
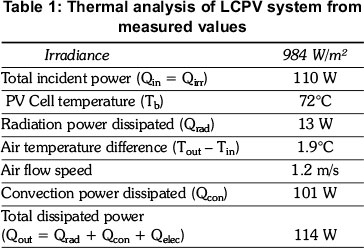
Table 1 shows the basic parameters involved in determining the validity of the thermal model. The values shown in Table 1 were averaged over a 20 minute period during which the PV receiver temperature was relatively constant. The observation of constant PV receiver temperature is a good indication that steady state conditions have been reached. The total dissipated power corresponds closely to the total incident power (less than 4% error). Table 1 thus effectively illustrates the validity of the developed thermal model. A representative convective transfer co-efficient (h) of 48W/m2.K was calculated using the data listed in Table 1. However, this convective transfer co-efficient is not applicable under all conditions and should be re-calculated using steady state data points at the beginning of each new experimental configuration due to its high dependence on environmental conditions and geometrical orientation. Fortunately, the thermal model allows convenient empirical calculation of the convective transfer co-efficient for subsequent experiments.
3. Modelling system temperatures
The most important consequence of an accurate thermal model is the ability to predict system temperatures under various environmental conditions. A program was written in Mathematica to calculate PV receiver temperature based on irradiance and ambient temperature. As stated earlier, it is important to use a small amount of data at the beginning of each experiment to calculate the convective transfer co-efficient. All of the following experiments were conducted using the same insulated enclosure as discussed in section 3.2.
3.1 Wind speed
Theoretically, the convective transfer co-efficient of a surface is dependent on the velocity of the air flowing over the surface. A higher wind speed should lead to a higher convective transfer co-efficient and subsequently a lower PV receiver temperature. Figure 4 shows the measured PV receiver temperature (blue line) at various wind speeds as well as the temperature predicted by the thermal model (purple data points).
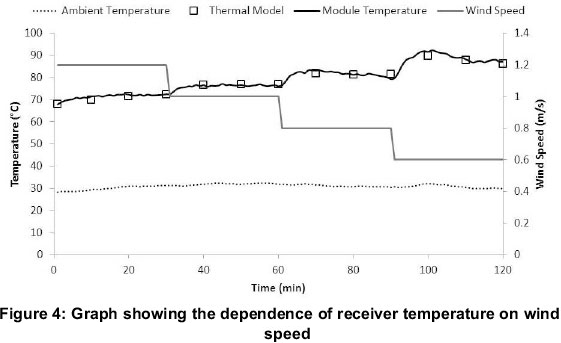
Figure 4 clearly illustrates the dependence of receiver temperature on air velocity. The PV receiver temperature is approximately 70°C when the air velocity is 1.2 m/s. However, the PV receiver temperature increases significantly to approximately 90°C when the air velocity is reduced to 0.6 m/s. As can be seen from Figure 4, the thermal model predicts temperatures that correspond closely to the measured temperatures. For each set of air velocity (V) a separate convective transfer co-efficient (h) was calculated and a parameter extraction was performed to quantify the dependence of PV receiver temperature on air velocity. Experimentally it was determined that h α V0.55, whereas the theory predicts a relationship of the form h α V05 for air flow over a horizontal plate. Although the experimental setup considered has a different (non-horizontal) geometrical alignment it still corresponds closely to the theoretical prediction.
3.2 Irradiance
Different irradiance conditions should not have any observable effect on the convective transfer co-efficient of the LCPV system. Varying irradiance only disrupts the energy balance described by the thermal model. An increase in irradiance should result in higher PV receiver temperatures, while a decrease in irradiance should result in lower PV receiver temperatures. Figure 5 shows the measured PV receiver temperature under varying irradiance conditions as well as the temperature predicted by the thermal model.
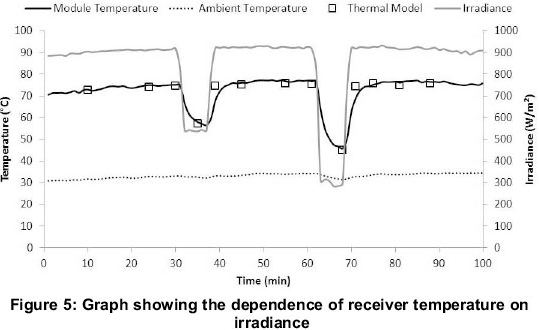
Figure 5 clearly illustrates the dependence of receiver temperature on irradiance. The PV receiver temperature is approximately 75°C when the irradiance is above 900 W/m2. However, the PV receiver temperature decreases significantly to approximately 45°C when the irradiance drops to below 300 W/m2. As can be seen from Figure 5, the thermal model predicts temperatures that correspond closely to the measured temperatures.
4. Heat sink
The primary function of a heat sink in a LCPV system is to decrease the temperature of the PV receiver. This is achieved by providing a larger area for convection to occur. Figure 6 shows a basic illustration of the heat sink used in this study. The heat sink is manufactured from aluminium and has 25 fins. The convective area for the heat sink configuration is approximately 0.125 m2, while the convective area for the configuration without the heat sink is 0.05 m2.
An experiment was conducted to assess the effectiveness of the heat sink shown in Figure 6 by measuring the operating temperature of the LCPV system with and without the heat sink attached. The LCPV system was housed within the same insulating enclose as discussed in section 3.2. The panel fans were used to simulate air flow of 1.2m/s across the PV receiver. Figure 7 shows the temperature difference between the PV receiver temperature and the ambient temperature.
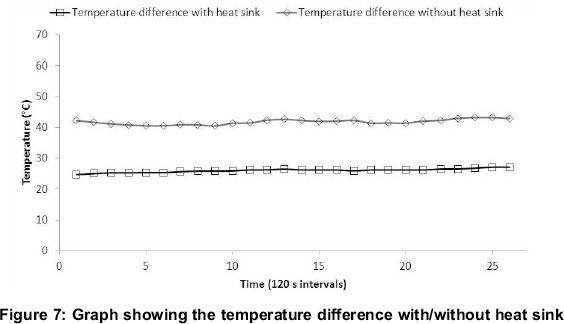
It is clearly illustrated in Figure 7 that the addition of the heat sink reduces the temperature difference. The temperature difference is approximately 40°C without a heat sink and approximately 25°C when a heat sink is included, which corresponds to a reduction of 37.5% in receiver temperature. Theoretically, it can be shown that a heat sink as shown in Figure 6 should reduce the temperature difference by more than 50% if the convective transfer co-efficient is unaffected by the addition of the heat sink. However, the inclusion of a heat sink in the LCPV system design may decrease the convective transfer co-efficient by obstructing air flow and subsequently limiting the air velocity through the fins.
6. Conclusions
The thermal model successfully predicted the PV receiver temperatures associated with various wind speeds and varying irradiance conditions. However, high operating temperatures (>80°C) associated with the LCPV system still limit the electrical power output. The addition of a heat sink reduced the temperature difference between the LCPV system temperature and the ambient temperature by 37.5%, but more research is necessary to design an optimal thermal management system.
References
Butler B.A., (2010). Investigation of Low Concentrator Photovoltaic Receivers and Systems, M Sc Dissertation, Nelson Mandela Metropolitan University. [ Links ]
Incropera FP, & De Witt D.P, (2001). Fundamentals of Heat and Mass Transfer, Fourth Edition, Wiley. [ Links ]
Luque A., & Hegedus S., (200)3. Handbook of Photovoltaic Science and Engineering, Wiley-VCH. [ Links ]