Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
Journal of the South African Institution of Civil Engineering
On-line version ISSN 2309-8775
Print version ISSN 1021-2019
J. S. Afr. Inst. Civ. Eng. vol.61 n.3 Midrand Sep. 2019
http://dx.doi.org/10.17159/2309-8775/2019/v61n3a5
TECHNICAL PAPER
Validating traffic models using large-scale Automatic Number Plate Recognition (ANPR) data
A Robinson; C Venter
ABSTRACT
The development of reliable strategic traffic models relies on comprehensive and accurate data, but traditional survey methods are time-consuming and expensive. Manual surveys often yield small samples that require estimated expansion factors to enable the data to represent the population. Modellers have turned to new data sourced from various electronic devices to improve the reliability of the data. Automatic Number Plate Recognition (ANPR) data is one such data source that can be used to extract travel time, speed and partial origin-destination (OD) information. This study assesses ANPR data in terms of its comprehensiveness and accuracy, and shows how it can be used for the validation of strategic traffic models. Data was obtained from the Gauteng freeway system's Open Road Tolling (ORT) gantries for a period of several months. A new methodology is developed to process traffic model outputs such that they are directly comparable to the partial origin-destination outputs derived from the ANPR data. It is shown that comparing the model distribution against observed ANPR data highlights potential trip distribution issues that are not detected using standard model validation techniques.
Keywords: ANPR, traffic models, origin-destination, validation
INTRODUCTION
Automatic Number Plate Recognition (ANPR) entails the automated recording of the number plate, date/time and location of each vehicle that passes a roadside camera, using vehicle number plate recognition software. Records of individual vehicles that pass multiple cameras can be matched to determine the path of the vehicle and calculate travel times between the survey locations. If cameras are in a closed cordon, the origin and destination of external trips passing through the cordon can be determined. A series of ANPR cameras along a route, or at strategic locations throughout a network, would not observe every vehicle upon entry and exit to the network, and constitutes an open format number plate survey. Both closed and open format ANPR data have the potential to provide information that can be useful during the development of strategic traffic models, in ways that are not possible with other sources of traffic data. Comprehensive traffic observations from loop detectors, like ANPR, provide link speed and volume information which is useful during the calibration and validation of traffic models. But the additional ability of ANPR to track individual vehicles from point to point also provides potentially useful data on the distribution of trips through the network. While this constitutes partial rather than comprehensive origin-destination (OD) data, it may still serve as an additional independent data set against which model outputs can be validated. ANPR data has rarely been used in this way.
The objective of this paper is to examine the use of ANPR data for traffic model validation in terms of its comprehensiveness and accuracy. ANPR data is provided by the South African National Roads Agency SOC Ltd (SANRAL) from the Open Road Tolling (ORT) system deployed on the Gauteng Freeway Improvement Project (GFIP). Selected link volumes and journey times are, for demonstration purposes, compared with the GFIP traffic model's 2015 forecasts. In addition, the trip distribution characteristics of the ANPR data are exploited by extracting partial OD and trip length distribution metrics for comparison with modelled quantities. This required the development of a new methodology to process traffic model outputs such that they are directly comparable to ANPR-derived partial OD data. This is a feature of model validation that has not been found in previous studies.
The paper first provides a brief overview of the literature regarding techniques for developing and validating strategic traffic models, and specifically matrix estimation. It then describes the study context in terms of the GFIP, and the extent and accuracy of the ANPR data that is collected. The development of a technique for extracting suitable data from strategic models for comparison against ANPR data is presented, and implemented using the GFIP data to reach conclusions regarding the validity of the GFIP model forecasts. Finally, drawing on this work, the potential strengths and pitfalls of using ANPR data for traffic model improvement are discussed.
DATA REQUIREMENTS FOR STRATEGIC TRAFFIC MODEL DEVELOPMENT
Traditional strategic traffic models are developed using the standard four-step process. For this, these models typically require the following data sets:
■ Road network geometric information to develop the core network
■ Land use data to determine the trip generation
■ Origin-destination (OD) data to derive the trip distribution
■ Generalised cost data to determine mode and route choice
■ Speed and traffic count data for the volume-delay relationships used in assignments
■ Journey time and traffic counts to calibrate and validate the model.
OD trip matrices are fundamental inputs into traffic studies and traffic models. As observed data only provides information to form partial matrices, the development or synthesis of full trip matrices has been the focus of many studies dating back to John Wootton in 1972 (Kirby 1979). Data is obtained through household, roadside or other interview survey techniques. A full "prior" trip matrix is then determined using distribution functions derived from the survey data, and estimated and calibrated from using other observed data such as traffic counts. Model validation must be undertaken using independent data not used in the model development and calibration. The validation of the trip distribution is based on the comparison of partial OD volumes (after calibration) with cordon and screen-line counts, and of modelled trip length frequency distributions (TLFD) with those observed in surveys and previous studies.
Given the difficulties of estimating base year OD matrices from incomplete information, some researchers (Willumsen 1981; Fisk 1989; Tamin & Willumsen 1989) have sought to maximise the use of additional information such as traffic counts to produce cost-effective trip matrix estimations. The problem remains that the number of independent traffic counts are typically insufficient to produce a unique OD matrix. To create a unique matrix with N zones one requires N fully balanced traffic counts, all taken at the same time with no other sinks and sources other than the zone connectors (Ortúzar & Willumsen 1998). This is an impossible task in large-scale models.
This is where Automated Number Plate Recognition holds promise, as it is possible to generate larger sets of data for use during matrix estimation, distribution function calibration, and validation. In a simple form, the concept of using ANPR data in OD matrix estimation is described by Ramirez et al (2013) where it was applied in a limited way at localised intersections. Castillo et al (2008), Minguez et al (2010), and Hadavi and Shafahi (2016) researched the optimisation of camera locations to maximise the potential coverage and usefulness of the data obtained. Asakura et al (2000), Dixon and Rilett (2005), and Van Vuren and Carey (2011) used ANPR to analyse trips on motorways to derive through-trips and interchange-to-interchange trips. They also derived methods to expand samples where the cameras did not cover all lanes. Sun et al (2014) developed metrics for tracing vehicles passing cameras while travelling on a city network, and Himayounfar et al (2011) assessed travel patterns to benchmark normal behaviour to highlight suspicious drivers for law enforcement. Carpenter et al (2012) used Bluetooth devices (having a similar application to ANPR) along a 15 mile section of the SR-23 in Jacksonville, Florida, and recognised that the data could be used as a model validation tool. These authors also suggested that further work is required in reviewing output from select link analysis from a traffic model, i.e. extracting a trip matrix of all trips that pass through as specified section of road (or link).
No examples have been found in the literature of the use of ANPR data collected over a large area - as opposed to a single corridor or small area - for the validation of traffic models. The ANPR data produced by the Open Road Tolling system in Gauteng provides an opportunity for testing the feasibility and usefulness of such an application of what is essentially by-product or "exhaust" data from the tolling infrastructure.
THE GAUTENG FREEWAY IMPROVEMENT PRoJECT (GFIP)
The GFIP comprised the upgrading and tolling of 201 km of urban freeways in Gauteng, South Africa, and included the addition of carriageway lanes and the upgrading of interchanges. The freeways are tolled using an Open Road Tolling (ORT) system incorporating 42 directional toll gantries at approximately 10 km spacing. The GFIP freeway network and the locations of the toll gantries on the freeway network are depicted in Figure 1.
Equipment on the toll gantries includes the following systems required for toll collection:
■ Cameras with ANPR capability
■ Volumetric vehicle classification systems.
As each vehicle passes under a toll gantry, the vehicle's number plate, its toll classification (SANRAL 2018), date/time stamp and gantry number are recorded. SANRAL provided the ANPR data used in this research.
The GFIP strategic traffic and toll revenue forecasting model was developed in 2007 to determine the impact of the freeway upgrades and tolling on freeway traffic volumes and the surrounding road network.
The traffic model was developed using the SATURN (Van Vliet 2015) traffic modelling software and used the provincial GTS200 (Gauteng Department of Roads and Public Works 2006) traffic model as a starting point. The model was updated and calibrated to 2006 base year traffic data including:
■ Journey time surveys from the freeways and major competing routes
■ Land use data, interpolated between the 2001 census data and the 2010 land use forecasts
■ Revised trip generation rates
■ Revised average trip lengths for light and heavy vehicles
■ Approximately 600 classified traffic counts from 2006.
The forecast years were 2010, 2015 and 2025.
REVIEW OF THE ANPR DATA
Extent of the ANPR data
Monthly ANPR data was provided in text files. Prior to receiving the data, the vehicle licence number (VLN) was replaced with a random number VLN ID to anonymise the data to comply with the Protection of Personal Information Act, 2013. Each vehicle's VLN ID remained constant within each month's data to ensure that vehicles could be tracked through the network over consecutive days.
Table 1 provides the total number of gantry entries per month between February 2014 and July 2015. Approximately 71 million ANPR records per month were obtained from all 42 gantry locations over this period.

ANPR data accuracy
The accuracy of the ANPR data was assessed in two ways. Firstly, the data was compared to equivalent electronic traffic counts obtained from permanent counting stations located along the freeway network, and secondly, based on an interrogation of the completeness of the data in terms of the ability to track vehicles through the network which would be affected by unreliable number plate records.
SANRAL has installed electronic traffic counters at freeway interchanges as part of its Comprehensive Traffic Observation (CTO) programme. The counters at the interchanges upstream of each toll gantry were used and compared to the gantry's ANPR data. The equivalent average hourly weekday and weekend traffic counts were extracted from each database for each gantry location and compared. The average hourly volumes were calculated by adding the hourly volumes for every weekday or weekend day and dividing by the number of weekdays and weekend days in the month. Any missing data was recorded as zero for the hours where the data was missing; therefore, including zero would reduce the averages. Figure 2 - comparison of ANPR (Gantry 19) and CTO (Station 1894) data - and Figure 3 are two typical examples of comparative hourly flows for the ANPR and CTO data. Figure 2 data is typical of most of the ANPR/CTO comparisons, where flow profiles reveal only minor differences, with the ANPR data reflecting marginally higher average volumes. Figure 3, however, shows significant differences, where the ANPR data shows noticeably higher volumes. Investigating the differences revealed that lower CTO hourly averages resulted from missing data (zero) in the CTO database for periods of time. The cause of the missing data is unknown, but could be due to system malfunction. Since the ANPR data has no such data gaps, it can be considered at least as comprehensive and reliable a source of traffic volume data as the CTO systems, and in many cases better. As the ORT system is used to allocate toll transactions to road users, a high degree of accuracy and reliability is essential.


Added usefulness of ANPR data also depends on the ability to track vehicles between camera locations through the recording and matching of number plates (VLN ID). The ANPR data from the gantries was processed to identify anomalies in terms of misread or otherwise unusable number plates. The information in Table 2 was provided by SANRAL's service provider for the electronic toll collection (ETC). These ANPR records were identified as either:
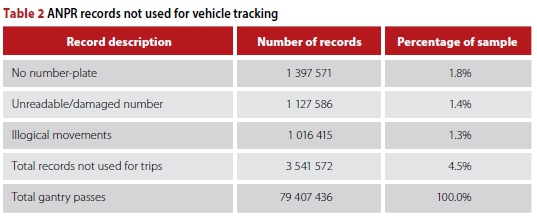
■ Vehicles without number plates
■ Unreadable number plates being obscured or damaged
■ Illogical gantry combinations, possibly from cloned number plates passing gantries in illogical order or in impossibly short time periods.
These records cannot be used for number plate tracking, and effectively reduce the sample of the ANPR data for vehicle tracking by approximately 5%. This error was considered small enough that no correction or expansion of the remaining data was needed prior to its use for model validation. It is clear that, with a number plate matching rate of over 95% from more than 79 million records, the ANPR data obtained from the GFIP's ORT system is a near-complete and continuous source of information on vehicle movements between gantry locations on the freeway network.
PROCESSING ANPR DATA AND OUTPUTS
Regarding the processing of the ANPR data, it must be noted that the ANPR cameras are on the toll gantries, and in this study reference to a gantry also means an ANPR camera location. Processing ANPR data for a selected time period required the development of a software program, which took the following into consideration:
■ The traffic counts were to include all vehicles passing a selected gantry.
■ All VLN anomalies (Table 2) were excluded from gantry-to-gantry (G2G) matrices.
■ A maximum time needed to be specified to pass between adjacent gantries, before it is assumed that the vehicle left the freeway and re-joined it later to perform a second trip.
■ A G2G distance matrix was derived from the gantry locations on the network.
Output from the software comprised traffic data relating to selected days of the week, times of the day and vehicle class.
The following traffic data was derived from the ANPR data:
■ Hourly traffic flow profiles at each gantry, i.e. accurate traffic counts for the average week day and average day including weekends
■ Average travel times between gantries for each hour of the day, which can be used to validate the modelled link volume delay curves on the freeway network
■ Average speeds between gantries, which were calculated using the above G2G travel times and the G2G distance matrix
■ Average G2G traffic counts, which are the numbers of vehicles that entered the freeway and were recorded passing a specified series of gantries within a specified time before leaving the freeway
■ The trip length frequency distribution obtained by relating the G2G traffic counts to the G2G distance matrix.
The G2G traffic counts are provided in matrix format, and Table 3 displays an example of the number of light vehicle trips between the first ten gantries (numbered in the first row and column) for the average weekday morning peak hour. Note that the full 42 gantry-matrix has been reduced for clarity and the gantry numbers correspond to the gantry locations depicted in Figure 1.

The traffic counts on the diagonals represent the number of vehicles that enter and exit the freeway and only pass under the one gantry. In this matrix, these amount to about 64% of all observed trips, indicating a high usage of Gauteng freeways for short distance trips. The 219 trips from gantry 4 to gantry 6 enter the freeway between gantries 2 and 4 and exit the freeway between gantries 6 and 8. The downward trend in trips from gantry 2 to gantry 10, which are southbound trips on the N1, indicates a decreasing proportion of trips as the trip length increases. These G2G counts provide an independent data source to validate the distribution of trips that use the freeways in the traffic model. However, a methodology is required to extract comparative information from the traffic model.
METHODOLOGY TO EXTRACT EQUIVALENT G2G TRAFFIC VOLUMES FROM A STRATEGIC TRAFFIC MODEL
Select link (SL) analysis is a standard process incorporated in traffic modelling software that identifies the origins and destinations of all trips that use a certain link (Van Vliet 2015). Following the work of Carpenter et al (2012), select link (SL) analysis was used to derive an OD matrix for the trips that pass under each gantry.
Figure 4 depicts the possible trips that can be recorded through a notional freeway section with gantries (ANPR sites) A, B and C. The entry/exit points are numbered 1 to 14; these could be freeway, on-ramp or off-ramp nodes and represent the traffic model zones.

Let a denote the number of vehicle trips counted at gantry A. In model matrix format, the cells that contain trips through gantry A would include trips with origin zones 1, 2 and 3 and destination zones 4 to 14. Therefore, this includes trips that pass under gantry A only, under gantries A and B, and gantries A, B and C, and result in Select Link A (SLA) matrix as shown in Matrix 1.

Similarly, the cells that contain trips included in a select link matrix through gantry B, will include vehicle trips (b) with origin zones 1 to 7 and destination zones 8 to 14, resulting in Select Link B (SLB). Cells that contain trips that are included in a select link matrix through gantry C comprise trips (c) entering through zones 1 to 11 and exiting through zones 12 to 14. These trips include trips that pass under gantries A&B&C, B&C, and C only, resulting in Select Link C (SLC). A combined select link analysis through gantry A, B or C results in SLabc as shown in Matrix 2.

Examining the matrices for SLA, SLB, SLCand SLABC for a single cell, a trip that passes through gantries A, B and C in the three individual matrices, and the combined matrix is the same. Therefore:

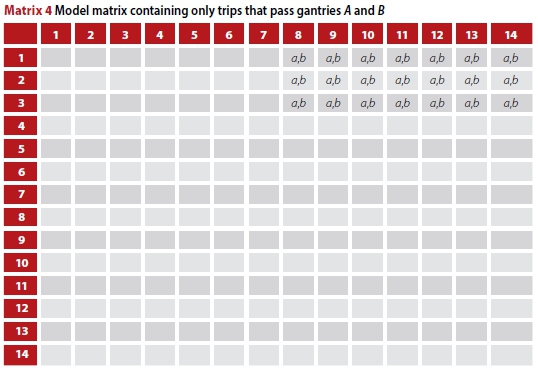
As a first step, to isolate the cells of an OD matrix which only relate to trips that pass through one "start" and one "end" location, A and B, and ignoring other gantries at this time, consider the combination of two of the select link matrices SLAand SLB (Matrix 3). The cells of interest are only those that contain the trips a,b.

The next operation uses the Hadamard product (Horn & Johnson 2012), which simply multiplies the corresponding cells of two matrices of equal dimensions, i.e. (X · Y) ij = (X)ij (Y) ij. The Hadamard product of SLAand SLBwill produce a zero where there is only a or b, and ab = a2 = b2 in the cells containing a,b. The square root of the resulting cell elements will produce the matrix with all the cells that contain a,b as shown in Matrix 4.
The sum of the model matrix trips that pass under gantry locations A and B can therefore be expressed as:

Where:
Tqab= the trips through gantry location A and B
SLa = Select Link matrix through gantry location A
SLB= Select Link matrix through gantry location B
However, including gantry C, some trips that pass under gantries A and B also pass under gantry C, and Matrix 4 would include a c in the cells representing origin zones 1, 2 and 3 and destination zones 12, 13 and 14. These trips should not be included in the desired result if only the trips between A and B and not through C, are required.
Subtracting SLCfrom Matrix 4 results in Matrix 5, since c = a = b. The desired trip matrix containing only those trips that pass under gantries A and B and not gantry C is obtained by removing the negative cells from Matrix 5, resulting in Matrix 6.

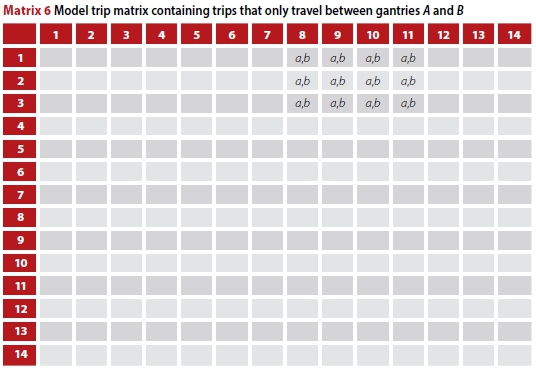
Summing the values in the resultant cells, which are the OD pairs of the trips that only pass under gantries A and B, produces the equivalent of the G2G count in the G2G matrix from A to B. This is given by Equation 3:
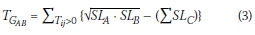
Similarly, if one were to isolate the cells containing the trips that only pass through gantry location B, one can show that both SLaand SLcshould be subtracted from the product. Equation 2 does not change, since both input matrices are SLB. However, the result includes trips through A (a,b), C (b,c) and A and C (a,b,c) as shown in Matrix 7.

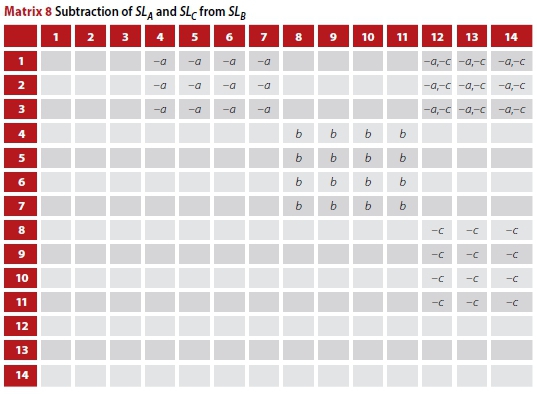
Subtracting SLAand SLCwill result in the cells containing a,b and b,c becoming zero, but with -a, -c, and -a, -c in the other overlapping cells, as shown in Matrix 8. Summing the positive values will result in only the trips in the modelled trip matrix that pass under gantry B without passing under gantry A or gantry C.
The process can, in general, be represented by the formula:

Where:
TGab= trips from gantry A to gantry B only
SLA= Select Link matrix through gantry A
SLB= Select Link matrix through gantry B
ΣSLt-1= Select Link matrix(ces) of gantry(ies) upstream of gantry A
ΣSLb+1= Select Link matrix(ces) of gantry(ies) downstream of gantry B
The upstream and downstream gantries provide a "plug" on the ends of the desired section of the route. If there were more than one external gantry along the freeway, this should be added to the second part of Equation 4 above, i.e. replacing SLb+1 with (SLb+11 + SLb+12)- It was also discovered, while testing the formula on the GFIP model, that any route that provided a bypass to the first or last gantry A or B would "leak" traffic into the system from beyond the first or last gantry. A gantry that can be used as another external "plug" can be added to the external gantry list. This would, however, make the process onerous in a detailed network where there are potentially multiple alternative routes.
The solution to this problem lies in the fact that only positive cell values of the model's SL matrices are added to derive the G2G equivalent value; therefore any number of other "plugs" can be added to the second part of Equation 3. It would also be easier to identify the ANPR camera (gantry) locations along a given route than identifying all possible alternative routes. Therefore, by summing all SL matrices (SLall) and subtracting the sum of the SL matrices along the desired route, including SLaand SLb(i.e. SLRt), the result would "plug" every possible "leak". Therefore, Equation 4 becomes:
Where:

TGab= trips from gantry A to gantry B only
SLa= Select Link matrix from the gantry A link
SLb= Select Link matrix from the gantry B link
SLall= sum of Select Link matrices of all gantry locations
SLrt= sum of Select Link matrices along the route inclusive of gantry A and gantry B
If trips between two gantries can choose two alternative routes, the ODs per route, or both routes, can be derived using:
SLrt1 = sum of SL matrices along route 1
SLrt2= sum of SL matrices along route 2
SLrt1,2 = sum of SL matrices along routes 1 and 2
VALIDATING A TRAFFIC MODEL USING ANPR DATA
Various data sets can be extracted from the ANPR data for use in validating a base year traffic model. As the ANPR data is not available for the base year itself (2006), the 2015 ANPR data from the ORT system was compared with the outputs of the 2015 forecasts from the GFIP traffic model. This serves to demonstrate the validation techniques described above.
Traffic counts
Figure 5 compares the modelled peak-period freeway traffic volumes at the gantry locations and the volumes derived from the ANPR data. These results show that, while the modelled and ANPR flows match quite well, the modelled light vehicle forecast is ±9% too low, while the heavy vehicle forecasts are ±20% too low. A standard measure for comparing modelled volumes (V) and actual traffic volumes (V2) in traffic modelling is the use of the GEH statistic represented by the following formula (Department for Transport 2014):
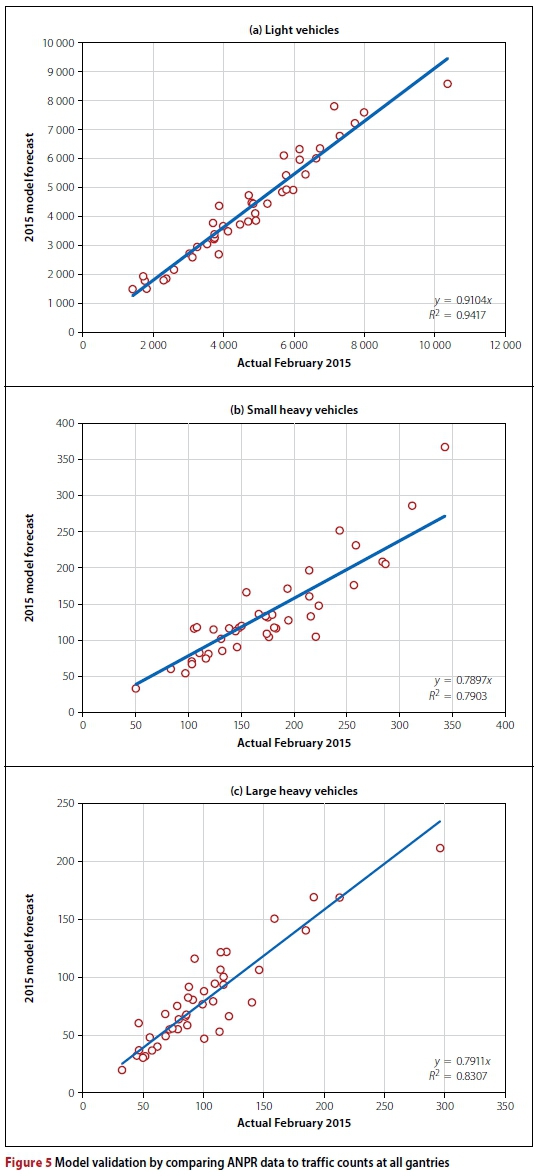
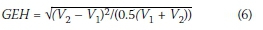
The average GEH statistic across gantry locations was 8.04 for light vehicles. Whilst not ideal (a validated model requires a GE of 5 or less for 85% of observations), it mus be noted that this is the comparison of a nine-year old forecast to measured counts and not the validation of a calibrated base year model; thus, some inaccuracy is to be expected. Under-forecasting in the model is most likely related to the high levels of toll non-payment experienced on the ORT network, as full toll compliance (assumed in the model) would have caused more deviation of trips from the tolled network to alternative roads.
Journey times
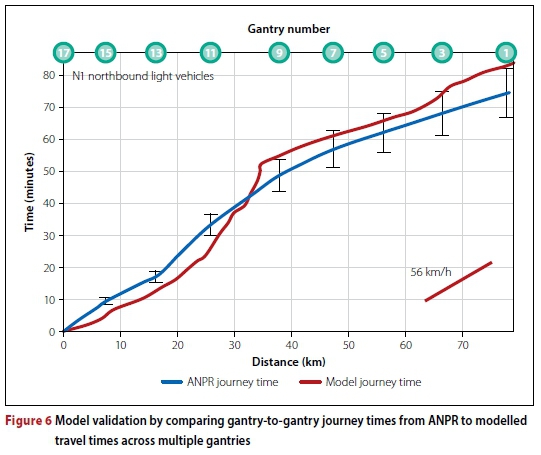
Journey times were extracted from the ANPR data, and checked for accuracy and consistency before being averaged for comparison to modelled journey times extracted from the traffic model. An example of the comparison for a section of the freeway spanning nine gantries is depicted in Figure 6. In this comparison, the modelled freeway journey time remain within the maximum recommended devia tion of 15% from the measured journey times (Department for Transport 2014) over most of the length of the freeway. It also highlights specific freeway sections where the volume delay functions may require adjustment.
Trip Length Frequency Distribution (TLFD)
Figure 7 shows the comparison between the TLFD of the modelled trips using the freeways and the TLFD derived from the ANPR data using the G2G counts and distances between the gantries. Only light vehicles are shown for illustration. This correlation appears to validate the model in terms of the TLFD of trips using the freeways. It serves as an indication that th structure of the origin-destination matrix of freeway trips is close to accurate. The modelled average trip length for light vehicles, 11.43 km, is very close to the ANPR average of 11.30 km. However, as freeway trips are only a portion of all trips on the network, the same cannot be concluded for the model as a whole - additional trip length data from the remainder of the network is required to validate the rest of the network.

Matrix trip distribution
The G2G ANPR count matrix disaggregates 42 gantry counts into over 350 independent point-to-point counts with associated distances. Deriving an equivalent G2G matrix from the traffic model, using Equation 5 and the methodology described above, enables the validation of the distribution of trips within the cells of the model's trip matrices. This comparison is shown in Figure 8. Whilst the TLFD from the ANPR data and the model correlate well, there is a greater variance in the disaggregated G2G counts, which in turn relates to the distribution of trips in the model trip matrices. On average, as can be expected, modelled values are slightly lower than actual ANPR values, the difference being about 6%.
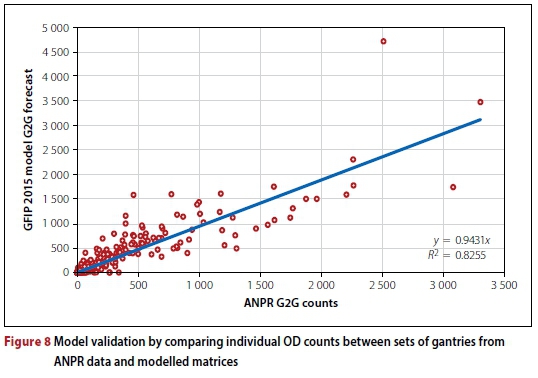
Apart from providing an overall sense of the accuracy of the model's OD matrix, the variances between individual cells can be examined to identify specific trends or problems. It was decided to focus only on the worst-performing gantry pairs as an illustration. No generally acceptable criterion exists for assessing OD volumes from a partial matrix, so the GEH statistic (Equation 6) was once again used to examine differences between the ANPR data and modelled values. The twelve gantry pairs with the highest (worst) GEH values are shown in Table 4.
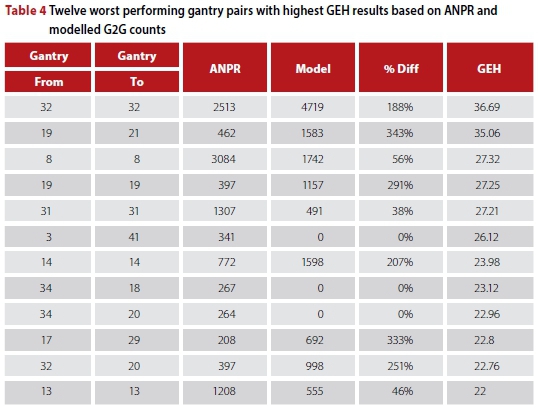
Gantry numbers 8 and 32 are critical locations (refer to Figure 1) in that they are the entry arms to two of the highest trafficked system-interchanges on the network. With the "from" and "to" gantries being the same, it implies that these counts refer to short distance trips. These results therefore show that:
■ Westbound on the N12 entering the Gillooly's Interchange the model has nearly twice the number of short distance trips as ANPR.
■ Southbound on the N1 entering the Buccleuch Interchange the model has approximately half the number of short distance trips as ANPR.
■ Between gantries 19 and 21, i.e. south bound on the N3 travelling between the Buccleuch and Gillooly's Interchanges, without using the N1 or N12, the model estimates over three times the number of actual trips.
This detailed comparison between the G2G counts and the model outputs highlights some significant localised discrepancies in the trip matrix distribution. This information can be very useful to pinpoint specific model improvements that may be needed, for instance where incorrect volume-delay curves were used in the freeway or (more likely) alternative route networks, leading to an incorrect assignment of trips onto the freeway. It is noted that this discrepancy could not have been picked up by only validating the model on the basis of the trip length frequency distribution, as the over- and under-assignments cancel each other out and leave the modelled TLFD close to the actual. It is the availability of large-scale ANPR data, and the partial OD matrix that results, which provide novel opportunities for matrix validation at levels of accuracy that were not possible before.
If a model is used to assess a scheme where a revenue stream or economic benefits are derived from distance-based costs and fares, the impact of these discrepancies may not be too significant if, as in the above case, the errors are averaged out in the TLFD. However, if no such averaging occurs, or if the model is to be used for a public transport scheme where the revenue is based on a boarding fare plus a distance-based fare, the number of short-and long-distance trips along the specific route can have a significant impact on the revenue stream. This revenue risk may have significant implications if the proposed scheme is part of a privately funded Public Private Partnership (PPP) concession (Bain 2009).
SUMMARY
When considering new large-data sources, one must identify the data's strengths and weaknesses. ANPR data also has strengths and weaknesses in terms of all the data requirements of traffic models. Table 5 provides a summary of the traffic model data needs and ANPR's strengths and weaknesses when compared to other large (electronically derived) data sources.

It is evident from the above that ANPR data is, like all other data sets, not the answer to all traffic model data needs. The major strength in the ANPR data is the ability to disaggregate the counts to independent counts over specific distances and enabling the validation of a model's trip distribution in the trip matrix. This has been enabled by the development of the methodology to extract equivalent count over distance (select link to select link) matrices from the model. The process of validating a traffic model using ANPR data has highlighted the fact that current methods of validating a traffic model may not uncover potentially critical problems in the distribution of trips in the matrix, even though the comparison to traffic counts and the TLFD show the model to be acceptable.
FURTHER RESEARCH
The extraction of the equivalent G2G counts from the model means that it is possible to produce a trip sub-matrix that only contains the trips that make up the G2G count. It is then possible to factor the cell values of the extracted sub-matrix so that the sub-matrix total equals the G2G count and re-inserting the sub-matrix values back into the original matrix. An iterative process of extraction, factoring and re-insertion would potentially improve the calibration of the traffic model's trip matrices, thus utilising the trip distribution characteristics of the ANPR data. This process is similar to current matrix estimation to traffic count techniques, except that there are more (N.(N-1)/2 counts from N ANPR sites) that are all independent - a desirable combination for matrix estimation (Ortúzar & Willumsen 1998).
CONCLUSIONS
The availability of ANPR data from the 201 km of the GFIP freeways utilising the 42 Open Road Tolling (ORT) gantries resulted in a significantly large data set, and an opportunity to assess this data for use in validating and improving traffic models. The processed data provided traffic counts, journey times along the freeway network and G2G (ANPR camera to camera) counts with related distances travelled on the freeways. Whilst the traffic counts and journey times provide dependable independent data, this information can be provided from other available means of data collection such as Comprehensive Traffic Observation (CTO) counting stations and journey time surveys from samples of probe vehicles.
The strength of the ANPR data lies in its ability to track large numbers of individual vehicles from point to point, thus producing counts over specific distances (G2G counts), which have the distribution of trips embedded in the data. The difficulty is that the G2G counts do not relate directly with the actual ODs in a model. The methodology developed to extract "G2G counts" from the traffic model has enabled the comparison of the ANPR data to the model outputs. From this work, the following can be concluded: ■ ANPR technology can provide large accurate data sets that can be used for the development and validation of strategic traffic models. Where, as in the GFIP case, the ANPR data is intended for use in toll transactions, the coverage is near-complete in terms of vehicle volumes. Provided all lanes on the links are covered by the camera, there is no need to estimate expansion factors to represent the population.
■ The location of the ANPR cameras can be either in a closed cordon or in an open layout, as in the GFIP freeway network. Optimising the location of the cameras would provide data sets with significant usefulness for both traffic modelling and traffic operation optimisation.
■ As the ANPR data used in this research was limited to the freeway network, the traffic count and journey time data was also limited to the freeways, and hence a limitation in the ANPR data is that it only relates to a limited number of routes. Probe data (e.g. from on-board GPS equipment) has a broader coverage, and is useful for journey time information, even if smaller samples with unknown sample sizes are used.
■ The major advantage of ANPR data is the ability to disaggregate the single point counts into accurate and independent counts associated to specific route distances, i.e. they can relate to the traffic model's trip distribution.
■ The method developed to isolate the trips in a traffic model's trip matrix that represents the G2G counts enables the direct comparison of the ANPR data with the modelled trip distribution, hence offers a means to validate the partial OD matrix.
■ The application of the above method to validate the GFIP model's partial matrix showed that, even though a model's journey times, TLFD and counts might be sufficiently accurate, there may still be irregularities in the trip matrices. The averaging of results may contribute to an acceptable validation outcome using standard validation procedures. The comparison of partial OD matrices, based on ANPR data, may help to identify localised discrepancies in the trip matrix that can be very useful to pinpoint specific model improvements that may be needed, and that might otherwise be missed.
ACKNOWLEDGEMENTS
The authors would like to acknowledge the South African National Roads Agency SOC Limited for access to the ANPR data and the use of the Gauteng Freeway Improvement Project traffic model, as well as Nicholas Robinson for the development of the software used to process the ANPR data.
REFERENCES
Asakura, Y, Hato, E & Kashiwadani, M 2000. Origin-destination matrices estimation model using automatic vehicle identification data and its application to the Han-Shin Expressway Network. Transportation : Planning - Policy - Research - Practice, 27(4): 419-438. DOI:10.1023/A:1005239823771. [ Links ]
Bain, R 2009. Credit Risk Analysis; Toll Road Traffic & Revenue Forecasts: An Interpreter's Guide. Seville, Spain: Publicaciones Digitales. [ Links ]
Carpenter, C, Fowler, M & Adler, T J 2012. Generating route specific origin-destination tables using Bluetooth technology. Transportation Research Board Circular No. 2308, 96-102. DOI:10.3141/2308-10 [ Links ]
Castillo, E, Menéndez, J M & Sánchez-Cambronero, S 2008 . Traffic estimation and optimal counting location without path enumeration using Bayesian networks. Computer-Aided Civil and Infrastructure Engineering, 23(3): 189-207. [ Links ]
Department for Transport (UK) 2014. TAG Unit M3.1 Highway Assignment Modelling. London: Department for Transport, Transport Appraisal and Strategies Modelling Division. [ Links ]
Dixon, M P & Rilett, L R 2005. Population origin-destination estimation using automatic vehicle identification and volume data. Journal of Transport Engineering, 131(2): 75-82 . DOI:10.1061/ ASCE 0733-947X 2005 131:2 75 . [ Links ]
Fisk, C 1989. Trip matrix estimation from link traffic counts: The congested network case. Transportation Research. Part B, 23B(5): 311-336. [ Links ]
Gauteng Department of Roads and Public Works 2006. Gauteng Transport Study 2000. Pretoria. [ Links ]
Hadavi, M & Shafahi, Y 2016. Vehicle identification sensor models for origin-destination estimation. Transportation Research. Part B, 89: 82-106. [ Links ]
Himayounfar, A, Ho, A, Zhu, N, Head, G & Palmer, P 2011. Multi-vehicle convoy analysis based on ANPR data. IET Conference, Stevenage UK. [ Links ]
Horn, R A & Johnson, C R 2012. Matrix Analysis. Cambridge, UK: Cambridge University Press. [ Links ]
Kirby, H 1979. Patrtial matrix techniques. Working Paper 111. University of Leeds, Institute of Transport Studies. Available at: http://www.eprints.whiterose.ac.uk/2413. [ Links ]
Minguez, R, Sanchez-Cambronero, S, Castillo, E & Jimenez, P 2010. Optimal traffic plate scanning location for od trip matrix and route estimation in road networks. Transportation Research. Part B, 44(2): 282-298. DOI:10.1016/j.trb.2009.07.008. [ Links ]
Ortúzar, J & Willumsen, L 1998. Modelling Transport, 2nd ed. New York: Wiley. [ Links ]
Ramirez, S, Kovacic, K & Ivanjko, E 2013. Origin-destination matrix estimation of traffic flow on highway network. Croatia: University of Zegrab, Department of Intelligent Transport Systems. [ Links ]
SANRAL (South African National Roads Agency Ltd) 2018. 29 January: GFIP Toll tariff and discount structure announcement. Available at: http://www.nra.co.za/live/content.php?Session_ID=fd97f3e5eef9aadbdfba1b146eb41448&Item_ID=4505. [ Links ]
Sun, Y, Zhu, H, Zhou, X & Sun, L 2014. VAPA: Vehicle activity patterns analysis based on automatic number plate recognition system data. Proceedings, 2nd International Conference on Information Technology and Quantitative Management (ITQM), Moscow, Russia. Elsevier Procedia Computer Science. [ Links ]
Tamin, O & Willumsen, L 1989. Transport demand model estimation from traffic counts. Transportation 1986-1998, 16(1): 3. [ Links ]
Van Vliet, D 2015. SATURN User Manual. University of Leeds, Institute for Transport Studies. [ Links ]
Van Vuren, T & Carey, C 2011. Building practical origin-destination od/trip from automatically collected GPS data. Proceedings, European Transport Conference, Glasgow, Scotland. [ Links ]
Willumsen, L 1981. Simplified transport models based on traffic counts. Transportation : Planning - Policy - Research - Practice, 10(3): 257-278. [ Links ]
 Correspondence:
Correspondence:
ALAN ROBINSON
Traffic Engineer/Transport Planner
South African National Roads Agency
Northern Region
38 Ida Street
Menlo Park
Pretoria 0040
South Africa
T: +27 12 426 6299
E: robinsona@nra.co.za
PROF CHRISTO VENTER
Associate Professor
Centre of Transport Development
Department of Civil Engineering
University of Pretoria
Pretoria
South Africa
T: +27 12 42 0 2184
E: christo.venter@up.ac.za

ALAN ROBINSON Pr Eng (MSAICE) is a Traffic Engineer and Transport Planner working for the South African National Roads Agency. His focus has been on the development of transport models to derive traffic forecasts for road infrastructure projects, including revenue predictions and financial feasibility for toll road projects.

PROF CHRISTO VENTER Pr Eng (MSAICE) is an Associate Professor of Transportation Engineering in the Department of Civil Engineering at the University of Pretoria. His teaching and research activities focus on public transport, transport policy and planning, travel demand modelling, and social aspects of mobility.














