Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
Journal of the South African Institution of Civil Engineering
On-line version ISSN 2309-8775
Print version ISSN 1021-2019
J. S. Afr. Inst. Civ. Eng. vol.60 n.3 Midrand Sep. 2018
http://dx.doi.org/10.17159/2309-8775/2018/v60n3a3
TECHNICAL PAPER
Reliability assessment of the South African wind load design formulation
J Botha; J V Retief; C Viljoen
ABSTRACT
The representation of the strong wind climate and the reliability calibration of wind loading are the main components of the provisions for local conditions in the South African wind load standard. The reliability implications of new probability models for wind load and an updated map of the characteristic wind speed are assessed in this paper. Wind load probability distributions are based on a combination of new models for free-field wind pressure, pressure coefficients and terrain factors with existing information. The results from both assessments show that the wind load partial factor of 1.3 does not result in adequate reliability performance for typical design situations. A partial factor of 1.6 is recommended. Where an increased partial factor for wind loading will result in a corresponding increase in the design wind load, the introduction of an updated map of the characteristic wind speed for South Africa is shown to result in an overall reduction of wind load. Regional analysis, however, indicates that there are regions in the Western and Eastern Cape that will have increased design wind loads. Combined with an updated partial factor of 1.6, the aggregate increase in design wind loads across South Africa is shown to be 11%.
Keywords: wind loading code, probabalistic models, reliability assessment, partial factor calibration
INTRODUCTION
Provisions for wind loading formed an important component of the advancement achieved by the introduction of the South African Loading Code SANS 10160:2010 to national structural design practice. The considerations for using the Eurocode standard EN 1991-1-4:2005 as the primary reference for SANS 10160-3:2010 for wind loading were recorded by Goliger et al (2009a; 2009b). Differences between the general strong wind climatic conditions for which EN 1991-1-4 is formulated and the conditions found in South Africa could, however, not be accounted for in SANS 10160-3. An extensive assessment of the South African strong wind climate was required to effect the adaptation of the Eurocode wind loading procedures to South African conditions.
The reliability assessment reported in this paper touches on two major considerations when the Eurocode was adapted to South African conditions and practice for the South African Loading Code. Although the need to adapt environmental loads to local conditions is obvious, substantial efforts are required to characterise these conditions properly in order to derive design measures that are calibrated to South African reliability requirements. The default safety levels on which Eurocode procedures are based are significantly more conservative than the levels on which South African standards are calibrated (Retief & Dunaiski 2009).
In the reliability assessment the geographical representation of the strong wind climate across South Africa, as expressed by the characteristic or basic wind speed (yb0). is considered, together with a probability model for wind loading that can be used to derive a partial wind load factor (yw) for the country as a whole. This paper firstly develops a set of wind load probability models that can be used to assess the reliability performance of wind loading based on revised SANS 10160-3 procedures. Changes in wind loading as a result of the combined effects of the revised specified wind speed and the adjusted load factor are then determined to assess the integral implications of the updated reliability information and wind load design specifications.
GENERALAPPROACH
The first step in the process of reliability assessment is to develop a probability model for wind load for South Africa. The model (Wsans) incorporates the probability distribution for the free-field wind pressure (Qref) to represent the complex strong wind climate of the country. This is combined with other structural wind loading components, as described by the Davenport wind loading chain (Davenport 1961, 1983). The probability models for pressure coefficients (cp) and terrain roughness (ct) provided by Botha et al (2018) are complemented by estimates of secondary wind load components from the literature. Various combinations of new and existing component models are used to derive ranges of reliability results, similar to the indicative models provided by the Joint Committee on Structural Safety (JCSS) Probabilistic Model Code (JCSS 2001).
Assessment of partial factors for wind loading (Yw) is done in two steps: a preliminary derivation of Yw from the wind load model on its own provides an indicative value directly, allowing easy comparison between alternative models. This is followed in the second step by reliability modelling in which structural resistance is parametrically represented and compared directly with design procedures.
The final step in the assessment is to provide an indication of the influence of the combined effect of changes to Yw and the specification of the geographical distribution of the characteristic or basic wind speed (yb0) proposed by Kruger et al (2017).
Related wind load probability models
Milford (1985) provided both a set of wind component models and an integral model (Wmil). An integral model reported by Kemp et al (1987) was used for reliability assessment of SANS 10160:2010. Gulvanessian and Holicky (2005) and Holicky (2009) provided component and integral models for the reliability assessment of wind loading for the Eurocode.
The JCSS Probabilistic Model Code (JCSS 2001) provides ranges for the distribution parameters of the Davenport components and also serves as a background to the wind load models used to assess the Eurocode. The probability distributions of the various models have been summarised by Botha et al (2018).
The wind load component and integral probability distributions provide useful information against which WSANS can be assessed. Updated versions of the Milford (WUp-Mil), Gulvanessian and Holicky (WUp-G&H) and Holicky (WUp-H) models are used to complement the reliability assessment based on WSANS. This approach leads to a range of results similar to those of the JCSS model, but incorporating the information on Qref for South Africa and for Cp and ct as reported by Botha et al (2018). The way in which WSANS and the updated models have been derived is outlined below.
The influence of changes in the basic wind speed as provided by Kruger et al (2017) (see also SANS 2017) in comparison with SANS 10160-3:2011 (SANS 2011b) is used to determine geographical changes in design wind loading, in addition to the influence of the modification of yw Goliger et al (2017) provide a review of changes in the representation of wind speed in South Africa in terms of both the updated information and the reliability basis of design.
Free-field wind pressure
The probability model for the free-field wind pressure (Qref) is based on the set of probability models provided by Kruger et al (2013) for the annual extreme wind speed (Va) for a set of 74 recording stations across the country. Numerous extreme value probability models were used to obtain appropriate distributions for the complex strong wind climate. These models were:
-
General Extreme Value (GEV) models, predominantly using the Type I distribution (Gumbel)
-
The Peak-Over-Threshold (POT) method, including the General Pareto Distribution (GPD) and Exponential Distribution (EXP)
-
Mixed climate models for regions where both synoptic and meso-scale strong winds are observed
Due to the diversity of the climate and the limited recording periods, no representative probability distribution for the country as a whole could be established. The observed shape parameters (k), however, varied between values of -0.4 and 0.5, indicating both bounded and unbounded distributions, with both cases having reliability as well as phenomenological implications. The selection of the Gumbel distribution (k = 0) may therefore be accepted as a reasonable generalised approximation for fitting the upper tails of the diverse distributions to the country for the purpose of developing a single representative reliability model. The dispersion of the single model incorporates both the inherent variability of strong wind occurrence and their geographical differences. Although Kruger et al (2013) accounted for uncertainties due to the selection of appropriate extreme value distributions and limited recording periods for individual positions, representation of all positions by a single model is the most important epistemic uncertainty (Botha et al 2018).
The use of the Gumbel distribution for wind load calibration is widely reported in the literature (see, for example, Baravalle & Köhler 2018; Hansen et al 2015; Xu et al (2014); Holicky 2009). Although Simiu et al (2001) report a better fit of the reverse weibull distribution than the Gumbel distribution for a set of 100 stations across the United States, it is noted that in many instances the differences were small. A similar survey by Hong and Ye (2014) for 235 stations across Canada concludes that the GEV distribution provides a better fit to the data than the Gumbel distribution. Unrealistically low values for the upper bound for certain regions raise concerns regarding the suitability of GEV models with variable k values for reliability assessment. Using the Gumbel models, good agreement is obtained between site and regional analysis.
The probability model for free-field wind pressure (Qref) is based on extreme value occurrences of wind storms and is therefore time variant. The reference time for Qref is 50 years (Botha et al 2018), which is consistent with the 50-year return period characteristic wind speed (yk) specified in SANS 10160-3 (Kruge+r et al 2017) and the target reliability index value (ßT) as applied in the basis of design (SANS 10160-1 2011a) for South Africa (Retief & Dunaiski 2009). This practice is also consistent with the practice followed by other wind load probability models invoked in this assessment.
The target level of reliability for a 50-year reference period is taken at ßT = 3.0, in accordance with the value introduced by Kemp et al (1987) for SABS 0160:1989 and maintained for SANS 10160:2010, as recorded by Retief and Dunaiski (2009). This is consistent with the practice followed in, for example, ASCE-7 (Ellingwood et al 1980), although a more conservative value of ßT = 3.8 is the default value for the Eurocode (ECCS 1996).
PROBABILISTC WIND LOAD MODELS
The set of four alternative probabilistic wind load models ( WSANS , WUp-Mil , WUp-G&H , WUp-H ) was developed on the basis of the way in which the underlying probability distributions for the Davenport wind load components were determined. A summary of the compilation of the wind load models from the load components is provided in Figure 1. The free-field wind pressure (Qref) applies to all models since it represents the South African strong wind climate. The distributions for the other two primary components (cp, ct) were applied directly to Wsans, and they were also used to update the distributions for the other three load models. Two secondary components for wind directionality (cd) and a general model uncertainty (cM) were estimated for Wsans and used without modification for the updated models. The models are discussed in greater detail in subsequent sections.
New SANS probability model WSANS
The new probability model for wind loading (Wsans) is based on the South African strong wind climate and SANS 10160-3 design models for pressure coefficient (Cp) and terrain roughness (ct) provisions, complemented by models that have been chosen to represent, conservatively, the influence of the additional factors on total wind load uncertainty. The wind directionality factor accounts for extreme wind load observations and probability models that neglect wind direction, resulting in a reduced probability of orthogonal wind loading.
Wind directionality effects were included in the model as a deterministic variable with a value of 0.85. This follows directly from the results obtained from the studies by Ellingwood and Tekie (1999) and Rigato et al (2001) regarding the effects of wind directionality on design wind loads on structures. Although wind directionality certainly has an inherent variability, not enough information was available to estimate the variability accurately with an acceptable degree of confidence. Judging from existing probabilistic models which include directionality effects, such as the Milford (1985) model, the variability is almost negligible in comparison with the variability of the other wind load components. The decision to include the factor as a deterministic variable was therefore deemed to be reasonable.
Other wind load uncertainties, such as the lack of both spatial and temporal correlation of wind pressures across the structure, topographical effects and "hidden safety factors" in the design wind load formulation (Holicky et al 2016), were included in the full model through the use of a model uncertainty factor. Although these factors reduce the systematic bias of wind loads, it is difficult to quantify this influence. An upper limit approximation based solely on engineering judgement was made by selecting a normal distribution with a bias value of 0.95 and a nominal standard deviation value of 0.10. The true influence of these factors will decrease the bias further. However, as this decision is primarily subjective, it was decided to err conservatively by not reducing the bias by more than a nominal 5%.
The Wsans model is summarised in Table 1 in terms of the distribution parameters for the various wind load components. It is, however, convenient to derive a single probability distribution for Wsans to be used in reliability assessment.
The combined exceedance probability for the set of wind load components can be obtained from a First Order Reliability Method (FORM) analysis (see, for example, Ang & Tang 1984; Holicky 2009). The multivariate expression for the product of the wind load components (c¿) can be set up in a reliability performance function as given by Equation (1), where wd is a deterministic design wind load which can be varied parametrically to obtain the relationship between wind load and exceedance probability.

Fitting of a Gumbel distribution to the upper tail of the distribution provides a convenient single probability model for Wsans. The same approach was followed by Milford (1985), Gulvanessian & Holicky (2005) and Holicky (2009) to derive single expressions for wind load probability. (Note that a direct calculation of the mean and standard deviation of Wsans from the mean and standard deviation of the components gives values of 0.65 and 0.48 respectively, as compared with the values of 0.71 and 0.39 given in Table 1.)
Bayesian updating of existing probabilistic models
As summarised in Figure 1, three additional probability models for wind load were derived by combining the new distributions for the primary wind load components with the distributions provided by Milford (1985), Gulvanessian and Holicky (2005), and Holicky (2009) respectively. The original distributions for the free-field wind pressure Qref were simply replaced with the model specifically developed for the south African climate. Original models for secondary wind load components were retained.
The pressure coefficient and terrain roughness factor indices in the existing models were updated using Bayesian updating. The updated probability distributions were calculated by taking linear combinations of the previous models and the new models using standard combination rules for normally distributed random variables (Holicky 2009). The existing models and new models were weighted equally, thereby assigning equal importance to both sources.
The three primary components have the greatest influence on the total uncertainty, and therefore the fact that those components are included in all models makes the models directly comparable. Furthermore, the comparison of these models provides an indication of the sensitivity of the total wind load uncertainty to the inclusion of secondary factors. The models are summarised in Tables 2 to 4. The same parametric FORM analysis used for the derivation of a single wind load model from the component distributions as applied to WSANS was applied to each updated model.
WIND LOADING RELIABILITY ASSESSMENT
The derivation of a probabilistic wind load model Wsans reported above reflects the incorporation of diverse uncertainties across a large design space, in terms of both geographical variance and structural configurations, into a single expression given by Equation (2) with the distribution parameters, the mean (p) and standard deviation (a), given in Table 1. Reliability assessment represents a continuation of the process of condensation, but with the inclusion of the pragmatic objective to assess (or derive) a suitable single partial wind load factor (yw) that could be used in design practice, such as that used in SANS 10160-1 & 3. The scope is, however, extended, also requiring the joint effects of uncertainties from the set of combined loads and the resistance of the full range of structures.
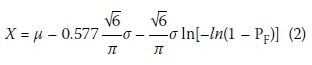
In this assessment the reliability implications of Wsans on its own is first explored and compared to the set of updated models (WUp-Mil , WUp-G&H, WUp-H ). Indicativevalues for yw are derived as the starting point for an extended assessment in which the combined effects of permanent load (G) and parametric representation of resistance (R) are included. Throughout the process a distinction should be made between the reliability models of the basic variables (W, G, R) and the selection of the design parameter (yw) which are directly related to standardised design.
Through the use of numerous probabilistic wind load models, the reliability assessment performed serves as a sensitivity study in which the influence of the wind load uncertainty on the reliability performance of the South African loading code's design functions is determined. A range of reliability requirements is obtained by using four models from different sources, similar to the range of values obtained when using the JCSS model (2001). The influence of the probabilistic models used can be clearly established, allowing a more informed decision regarding the choice of the wind load partial factor.
Comparison of wind load probability models
A direct comparison of the probability distributions for the four models as given in the final row of Tables 1 to 4 is provided in Figure 2. It is convenient to express the exceedance probability (Pf) in terms of a reliability index value ß = 0-1(1-Pf), where O is the cumulative normal distribution function. Since all the wind load components are normalised to the characteristic values, the parametric value of the wind load wd (see Equation 1) corresponding to ß represents the ratio of design to characteristic wind load (wd / Wk), which is the same as the load factor (yw) for the value of ß (and Pf).
Design standards allow the separation of the target reliability ß into values aEßT for loads and aR for resistance respectively, based on the respective sensitivity factors aE = 0.7 and aR βT= 0.8 (ISO 2394:2015 and Eurocode EN 1990:2002); in ASCE7-10: 2003 the sensitivity factors are reversed to aE = 0.8 and ar = 0.7. Once again, the simplification of sensitivity factors into fixed values, as opposed to variable values based on load ratios, is a requirement in order to develop a single representative model effectively. The effects of the sensitivity factors are, however, not ignored.
Partial factors for wind loading (yw) can then be read off directly from the graph at values of aE ßT = 0.7 x 3.0 = 2.1 (or PF = 0.018) for South Africa. with the corresponding value of 2.66 as obtained for the Eurocode target reliability of 3.8 (or PF = 0.0039). as shown in Figure 2. Values for yw. assuming these sensitivity factors and calculated from the Gumbel Equation (2). are listed in Table 5. However. values may also be obtained from the graph for other sensitivity factors as required.
The results in Figure 2 indicate the range of values for yw obtained from the alternative new probability models. The general increase of values in comparison with those based on the original models demonstrates the effect of underestimating wind load uncertainties. By considering all four models. an indicative range of the partial factor values required to provide adequate reliability performance is established. For the South African baseline target reliability level this range is between 1.45 and 1.72.
When a value of aE = 0.8 is used. in accordance with ASCE-7. the values of yw increase by 13%. When the adjustment also includes provision for resistance by taking är = 0.7 to determine yR. the combined effect reduces to 10% - 5% for the resistance coefficient of variation (wR) of 0.1 - 0.25. This should be compared with the 19% difference in the range of yw values obtained from the different models for W.
A comparison of the new model envelope with the JCSS envelope is shown in Figure 3. The new model envelope overlaps the JCSS envelope on the upper bound. where higher partial factors are required for a given target reliability level. Provision for the specific South African strong wind climate and improved estimates for the time-invariant components of the wind load model both contribute to the narrowing of the range of results. in comparison with the broad JCSS envelope. More refined estimates based on additional information on component uncertainties should lead to further narrowing of this range.
Reliability assessment considering combination of actions and resistance
The preliminary and indicative nature of deriving point estimate values of yW can be improved by extending the reliability performance function to include related basic variables. For this reason a more detailed assessment was performed using a combination of wind and permanent load structural resistance. Load combinations with other variable loads. such as imposed loads. were not considered. but the same method may be used to extend the assessment by including those load combinations.
The assessment was performed using the same method as used by Retief and Dunaiski (2009) in the previous reliability calibration of SANS 10160. The method consists of determining a single graph which represents the global safety factor (GSF) required to achieve a target level of reliability (ß). Wind load standard design functions are then assessed through comparison with the GSF to ensure acceptable reliability performance. The primary advantage of this method is that partial factors can be adjusted and the reliability performance assessed without recalculating the GSF.
The method is based on a reliability performance function g(X), as given in Equation (3), in which the limit state is expressed as a simple linear combination of the basic variables, namely the structural resistance (R), permanent loads (G) and wind loads (W). A summary of the probabilistic models for the basic variables is given in Table 6. The assessment was done using the four full models derived earlier in this paper, as well as the model used in the previous reliability assessment of SANS 10160 by Retief and Dunaiski (2009) for comparison. It should be noted that the coefficient of variation or structural resistance was parametrically varied in 5% increments in order to determine the reliability requirement for different construction materials.
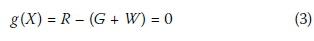
The reliability requirement against which design functions are assessed is found by obtaining an inverse FORM solution to Equation (3) for a given target reliability. From the results the GSF is obtained as the ratio of the characteristic values of the resistance (RK) and the combined permanent (Gk) and wind loads (WK), as shown in Equation (4). By parametrically varying the ratio of wind actions to total actions (x) as defined in Equation (5), the reliability requirement is obtained for the full range of combinations of permanent and wind loads.
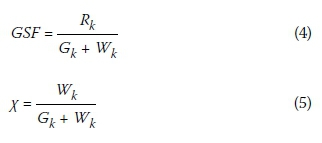
By using the general target reliability of ß = 3.0 for the South African loading standard, the reliability requirement GSFR may be determined. Figure 4 shows the reliability requirements obtained using the new wind load models, as well as the model used for the previous reliability assessment of the standard (Kemp et al 1987), denoted as the SABS model. A coefficient of variation of resistance of Wr = 0.15, which is representative of typical reinforced concrete structures, was used in the assessment.
A clear disparity is seen in the reliability requirements obtained using the new models and the SABS model. The low reliability requirement obtained using the SABS model led to the adequacy of the model being questioned. The inconsistency of the SABS model with general wind load probability models was confirmed and traced to an error in transferring results from background investigations (Botha 2016).
As the reliability requirements of the new wind load models are different, assessing the performance of a design function (f) against the reliability requirements (GSFR) obtained using the four models provides a good indication of how the uncertainty of the wind load affects the total reliability performance of the standard. The general equation for the design function for the combination of permanent and wind actions (f (x)) used in SANS 10160 (2011a) is given in Equation (6) in terms of the dimensionless load ratio x.
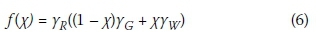
A noticeable feature of GSFRshown in Figure 4 is its convex shape, where GSFR is initially somewhat reduced due to the reduced probability that both the permanent and variable actions deviate substantially from the characteristic value. This well-known non-linearity of the performance function (Equation (3)) is the reason why dual linear design functions (Equation (6)) are often stipulated. In the case of SANS 10160-3, two sets of partial load factors (yG , yW) for permanent (G) and wind (W) loads are stipulated: the (STR) load case generally applies, with partial factors 1.2, 1.3, and for situations where permanent load dominates, i.e. for low values of x, the partial factors for the STR-P load case are 1.35, 1.0. Compliance is required for the most stringent load case. The sufficiency of the partial factor for wind loading Yw = 1.3 for the STR load case is considered here, based on the set of wind load probability models derived above.
A series of parametric reliability evaluations was done to consider the effects of load combination and structural resistance. Table 7 provides a summary of the representative parametric range of models for structural resistance, as expressed by the coefficient of variability (wR), and the partial factors for the STR and STR-P load cases. The resistance factor (yr) corresponds to a target level of reliability for resistance that is scaled by the sensitivity factor for resistance aR= 0.8, resulting in ßR= (0.8)(3.0) = 2.4 (or PF = 0.0082), and therefore the factor varies for different values of the coefficient of variation of resistance wR. The values for Yr will be reduced by 3% - 8% if aR= 0.7 in accordance with ASCE 7-10, with a proportional change tof(x) as provided by Equation (6). The sensitivity of the reliability performance to aRis clearly small in comparison with the difficulty of matching the nonlinear reliability requirement shown in Figure 4 with the linear design function f (x). This is confirmed by subsequent results.
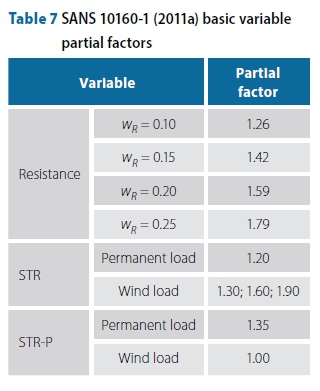
A reliability assessment using the method described above was performed using each of the four new probabilistic wind load models in turn. The reliability requirements obtained are shown in Figure 5 for parametrically varied values of the coefficient of variation of resistance. The SANS design functions were plotted over the reliability requirements obtained, with the STR partial factor for wind loads increased parametrically from the present value of 1.3 in increments of 0.3. This was done in order to assess the adequacy of the current partial factor value and, in the case that it is not sufficient, to determine what partial factor value would result in adequate reliability performance of the design functions.
It is immediately clear from Figure 5 that the existing partial factor for a wind load of Yw str = 1.3 is not acceptable for the required reliability performance of ß = 3.0 using any of the full wind load models. As the reliability performance is not measured against a single reliability requirement, but rather against a range of values, it is reasonable to assume that the appropriate reliability requirement lies somewhere between that of the Updated Eurocode (Gulvanessian & Holicky 2005) and the Updated Holicky curves. The STR-P function has sufficient reliability performance for values of x between 0.0 and 0.3, as expected. From the point where the STR function with Yw str = 1.3 crosses the STR-P function, the reliability performance is inadequate for all models across the entire range of resistance values considered. From this result it is clear that Yw str should be adjusted.
Holicky (2005) estimated that a realistic range of load ratios for most design situations is between 0.1 and 0.6, although the load ratio value will vary significantly for specific cases. This reliability assessment shows that an STR partial wind load factor value of Yw, STR. = 1.6 or higher would result in acceptable reliability performance of the SANS 10160 design functions across this range. This is based on a comparison with the average reliability requirement from the range of values obtained using the four new models. It is clear from the results, however, that for light, wind-sensitive structures with load ratios of x > 0.6, a partial factor of 1.6 would not be adequate for the average reliability requirement. Further investigation is required in order to develop the most efficient way to treat the reliability performance of these types of structure.
It is also noteworthy that the partial factor value of 1.6 corresponds well to the partial factor values obtained from the preliminary reliability assessment performed using direct FORM analysis of the wind load models as presented in the previous section and summarised in Table 5.
INFLUENCE ON DESIGN WIND LOADS
The influence of an adjustment of the partial factor for wind load (yw) on the resulting wind load values provides a direct measure of the practical implications of the reliability reassessment of SANS 10160-3: 2011b. However, the extensive revision of the South African strong wind climate and the pending introduction of a revised map for the fundamental free-field wind speed (yb0) should be included in determining changes in the design wind load. whereas an increase in Yw will result in a direct proportional increase in wind load, the underlying gust wind map reported by Kruger et al (2013b) indicates an overall reduction in characteristic wind speed (yk), but with complex geographical features that include regions where vkincreases. This section aims to quantify the influence of these changes on the total design wind load across the country.
The current SANS 10160 wind map and the new drafted map (SANS 2017) are shown in Figure 6. It should be noted that the wind speeds shown on the current wind map include the "gust conversion factor" of 1.4 as stipulated in the code. From inspection it is clear that the new wind map will lead to a significant reduction in wind loads across a large part of the country when compared with the current wind map.
In order to quantify the change in wind load due to the new wind map, it is necessary to convert the gust wind speeds to gust wind pressures. The equation for the calculation of design wind loads (wd) according to the stipulations of SANS 10160-3 is given in Equation 7. As the air density (p), terrain roughness factors (cr) and pressure coefficients (cp) are constant multiplication factors in this formulation, they are not affected by changing the wind map, and the influence of the ultimate wind loads on structures due to the change in the map may be calculated directly from the change in gust wind pressure.

The first step in the method was to establish a regional map of the country by overlaying the two maps shown in Figure 6 and defining regions by the resulting overlapping boundaries. Using constant multiplication factors of unity for the air density, terrain roughness factors and pressure coefficients, the gust wind speed values were then converted to design wind pressures. The design wind pressure was calculated for each region using the current wind map (w¡exist) and the new wind map (wi new). The systematic bias (b¡) was then calculated for each region (i) by taking the ratio of the design pressures from the two maps, as shown in Equation 8. By normalising the new wind pressure relative to the current wind pressure, a bias value of less than unity indicates a reduction in total wind load, whereas a bias value of greater than unity implies an increase in total wind load for the region. The regional bias values mapped across South Africa are shown in Figure 7. Finally, the averaged bias across multiple regions (bavg), such as the bias for each province or across the entire country, could be determined by calculating a weighted average of the bias values using the area of each region (A¡), as shown in Equation 9.
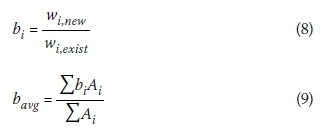
The area-averaged bias across the country was calculated to be 0.90. The incorporation of the new wind map into the South African wind load standard will therefore result in a total wind load reduction of 10% on average across the entire country. Figure 7 shows that this bias is not evenly distributed across the country. Certain areas, specifically
the Free State and large portions of the Northern Cape, Western Cape and Eastern Cape, show a slight increase in the total wind load of approximately 4%. Certain regions in the central Eastern Cape and Western Cape show a significant increase of up to 26%. However, this increase is offset by significant decreases in the average wind load across the remainder of the country, with reductions of between 15% and 35% in the northern parts of the country and a reduction of up to 49% in areas near Beaufort West, due to the anomalous high wind speed region stipulated in the current wind speed map.
In addition to quantifying the influence of the new wind speed map on the total wind load across the country, it is also possible to incorporate the influence of an updated partial factor for wind loads. In the previous section it was shown that the current SANS 10160 wind load partial factor for the STR design function does not meet the required reliability performance, based on a reliability assessment using four reliability models representing the possible range of uncertainties inherent in the SANS wind load formulation. To determine the influence of an updated partial factor, a factored systematic bias (bfactored) may be calculated by multiplying the area-averaged bias (bavg) by the ratio of the updated partial factor (ynew) to the current partial factor (1.3), as shown in Equation 10. A summary of the bfactored values for the provinces of South Africa and across the entire country for different partial factor values is presented in Table 8. It can be seen that an updated partial factor of 1.45 would result in a bias value of 1.01. effectively negating the average reduction in wind loads due to the new wind speed map. Using a partial factor of 1.6 or higher in order to ensure adequate reliability performance of the code. as calculated in the preceding reliability assessment. would result in average wind load increases of 11% or higher.
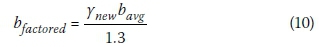
When considering yw= 1.30. which is representative of the case where the new wind speed map is used but the wind load partial factor remains unchanged. the bias values for the Gauteng. Limpopo. Mpumalanga. North West and Northern Cape Provinces indicate a significant decrease in total wind load. For the coastal provinces KwaZulu-Natal. and the Eastern and Western Cape. the bias is obtained from aggregation of a range of values. since some regions do experience a significant increase in the total wind load. but the majority of the regions (by area) experience a decrease.
SUMMARY, CONCLUSIONS AND RECOMMENDATIONS
The reliability assessment of wind load design needs to consider topics ranging from the random nature of extreme wind storms. through the uncertainties of the load models. to the reliability elements of the load design formulation. A distinction needs to be made between a reliability model (W) of the various sources of variability and uncertainty of the underlying load processes and the basic reliability elements of the characteristic wind speed (vk) and load factor (yw) of design procedures. While W remains the best estimate of the aggregate uncertainty of wind loading. vk and yw provide a design safety bias to ensure exceedance of the required reliability.
This paper provides a reassessment of reliability models for extreme wind conditions for South Africa and the design procedures implemented in the design standard SANS 10160-3. the sufficiency of the reliability representation in the standard. and the implications of the adjustment of yWtogether with (vb.0) for wind load on structures.
The reliability implications of two sets of information on wind loading on structures in South Africa. as provided for in SANS 10160-3. are considered in this paper. Mapping of the basic wind speed 0) to represent the geographical distribution of the strong wind climate of the country has been proposed by Kruger et al (2017). Probability models for wind loading that provide for both the time-dependent characteristics of wind storms for the country (Qref) and primary time-independent Davenport wind load components for pressure coefficients (cp) and terrain effects (ct). as specified in SANS 10160-3. are provided by Botha et al (2018).
The revised wind map for vb.0indicated a general reduction in the wind speed. with significant increases for specific regions. The new models for the primary wind load components indicate that a larger partial load factor for wind (yW) will be required to achieve the target reliability of ßT = 3.0 applicable to SANS 10160-3. This would result in a systematic increase in wind load on structures for the country as a whole.
The new probability model for wind load (WSANS) results in less conservative bias and dispersion as expressed by the mean and standard deviation (see Table 1) in comparison with the models presented by Kemp et al (1987) and Milford (1985) on which the present wind load factor yw= 1.3 is based. Figure 2 indicates that better agreement between the new and previous models is obtained when the Milford model is updated (WUp-Mil) to include the present information on the free-field wind pressure (Qref) (see Figure 1 and Table 2). Updated models applied to the assessment of the Eurocode (Wup-G&H. WUp-H) converge into an upper and lower range respectively for the wind load probability model. as shown in Figure 2. and interpreted in terms of first estimates of yW. ranging between values of 1.45 and 1.72. as indicated in Table 5. Figure 3 demonstrates that the range of distributions not only emulates the JCSS model. but also falls within its range of results. albeit close to the upper limit. The result is that the modelling of wind load probability is based on new information. although it is still anchored to the models used for both South Africa and the Eurocode. akin to rational sensitivity analysis. A consensus conclusion is that the present value of yW= 1.3 is clearly insufficient.
The complexity of providing an acceptable and consistent level of reliability through a single partial factor for wind loading is clearly demonstrated by the results given in Figure 5 for a parametric comparison between the required global safety factor (GSFr) given by Equation (4) and that provided by a design function (Equation (6)). However. a number of observations regarding the value of yWmay be made. It is clear that the current wind load partial factor of yw= 1.3 provides insufficient values for GSF to achieve the required reliability across the range of conditions represented by Figure 5. A value of yw= 1.6 generally achieves GSF values within the range indicated by the four probability models for wind load. within the mid-range of values for load ratios x for typical structures. and for the range of construction materials.
An exceptional situation is for light structures withx > 0.5 and a low coefficient of variation for resistance wR. such as for steel. These structures may be sensitive to both wind loading and achieving insufficient reliability. even for a relatively large value of yW. At the other extreme. structures with large values of Wr generally achieve sufficient reliability and may be expected not to be sensitive to wind loading. Provision for such diverse conditions should rather be considered in the materials-based standards. taking cognisance of the probabilistic nature of wind load provisions.
The map for vb.0indicates a general reduction of the characteristic wind speed over large parts of the country. but increases over several smaller regions (see Figure 6). with a geographical average reduction in wind load of 10% (see Figure 7 and Table 8). The most significant observation is that an implementation of yw= 1.6 will reverse the reducing effect of the updated wind map to result in an increase of 11% in the design wind load. A comparison of Figure 7 and Table 8 indicates that regional effects are not effectively captured by breaking down the effects into provinces. The exception is that Gauteng. as both the smallest province and the economic heartland of the country. will be neutrally affected.
The analysis and results presented here follow an engineering process in which information on uncertainties in the standardised design procedures of SANS 10160-3 are compiled. integrated and applied to derive pragmatic design parameters in accordance with the simplified format of characteristic wind speed Vb 0 and a partial factor yw to comply with reliability requirements for wind load design. The basic claim that can be made is that the results should represent an improvement on the present reliability provisions of the standard since they are based on a substantial body of information that has been systematically exploited to come to a conclusion. The outcome therefore represents background information to the process of reliability based on wind load standardisation, rather than on state-of-the-art models for the various Davenport wind loading components.
There are significant opportunities to improve the reliability model for wind loading for use in devising more effective reliability-based design procedures. The obvious topic is to update the information on the South African strong wind climate to include the accumulated records in terms of both the recording period and the geographical distribution, allowing for more extensive extreme value modelling. Significant uncertainties in the time-invariant wind load components are indicative of the potential for improving the design standard, for example as reflected by recent efforts related to the Eurocode (see, for example, Steenbergen and Vrouwenvelder 2015).
REFERENCES
ASCE7-10 2003. Minimum Design Loads for Buildings and Other Structures. American Society of Civil Engineers, Structural Engineering Institute. [ Links ]
Ang AH-S & Tang W H 1984. Probability concepts in engineering planning and design: Volume 2 Decision, risk and reliability. John Wiley & Sons, New York. [ Links ]
Baravalle, M & Köhler, J 2018. On the probabilistic representation of the wind climate for calibration of structural design standards. Structural Safety, 70: 115-127. [ Links ]
Botha, J 2016. Probabilistic models of design wind loads in South Africa. PhD thesis. Stellenbosch: Stellenbosch University. http://hdl.handle.net/10019.1/100058. [ Links ]
Botha, J, Retief, J V & Viljoen, C 2018. Uncertainties in the South African wind load design formulation. Journal of the South African Institution of Civil Engineering, 60(3): 16-29. [ Links ]
Davenport, A G 1961. The application of statistical concepts to the wind loading of structures. ICE Proceedings, 19(4): 449-472. [ Links ]
Davenport, A G 1983. The relationship of reliability to wind loading. Journal of Wind Engineering and Industrial Aerodynamics, 13(1): 3-27. [ Links ]
ECCS (European Convention for Constructional Steelwork) 1996. Background Documentation: Eurocode 1 (ENV1991) Part 1: Basis of Design. Report No 94. Joint Committee on Structural Safety, ECCS. [ Links ]
Ellingwood B, MacGregor J G, Galambos T V & Cornell C A 1980. Development of a probability-based load criterion for American National Standard A58: Building Code Requirements for Minimum Design Loads in Buildings and Other Structures. NBS Special Publication 577. US Department of Commerce/National Bureau of Standards. [ Links ]
Ellingwood, B R & Tekie, P B 1999. Wind load statistics for probability-based structural design. Journal of Structural Engineering, 125(4): 453-463. [ Links ]
EN (European Standard) 2002. EN 1990:2002 Eurocode. Basis of structural design. Brussels, European Committee for Standardisation (CEN). [ Links ]
Goliger, A M, Retief, J V, Dunaiski, P E 2009a. Review of codification of wind-loading for structural design. Chapter 3-1 in Retief, J V & Dunaiski P E (Eds) 2009. Background to SANS 10160. Stellenbosch: SUN MeDIA. [ Links ]
Goliger, A M, Retief, J V Dunaiski, P E & Kruger, A C 2009b. Revised wind-loading design procedures for SANS 10160. Chapter 3-2 in Retief, J V & Dunaiski P E (Eds) 2009. Background to SANS 10160 Stellenbosch: SUN MeDIA. [ Links ]
Goliger, A M, Retief, J V & Kruger, A C 2017. Review of climatic input data for wind load design in accordance with SANS 10160-3. Journal of the South African Institution of Civil Engineering, 59(4): 2-11. [ Links ]
Gulvanessian, H & Holicky, M 2005. Eurocodes: using reliability analysis to combine action effects. Structures and Buildings, 158(1): 243-252. [ Links ]
Hansen, S O, Pedersen, M L & Sorensen, J D 2015. Probability-based calibration of pressure coefficient. Proceedings, ICWE14 Conference, Porto Alegre, Brazil. [ Links ]
Holicky, M 2005. New load combinations for equal safety of structural members. Proceedings, ICOSSAR 2005, Rome, Italy, 19-23 June, Millpress, Rotterdam, 641-645. [ Links ]
Holicky, M 2009. Reliability Analysis for Structural Design. Stellenbosch: SUN MeDIA. [ Links ]
Holicky, M, Retief, J V & Viljoen, C 2016. Partial factors for wind actions considering hidden safety due to time-invariant components. Proceedings, 6th International Conference on Structural Engineering, Mechanics and Computation, 5-7 September, Cape Town. [ Links ]
Hong, H P & Ye, W 2014. Estimating extreme wind speed based on regional frequency analysis. Structural Safety, 47: 67-77. [ Links ]
ISO (International Standards Organization) 2015. ISO 2394:2015. General principles on reliability for structures. Geneva: ISO. [ Links ]
JCSS (Joint Committee on Structural Safety) 2001. Probabilistic Model Codes. http://www.jcss.byg.dtu.dk/Publications/Probalistic_Model_Code.aspx. [ Links ]
Kemp, A R, Milford, R V & Laurie, J 1987. Proposals for a comprehensive limit states formulation for South African structural codes. The Civil Engineer in South Africa, 29(9): 351-360. [ Links ]
Kruger, A C, Goliger, A M & Retief, J V 2013. Strong winds in South Africa. Part 1: Application of estimation methods. Journal of the South African Institution of Civil Engineering, 55(2): 29-45. [ Links ]
Kruger, A C, Retief, J V & Goliger, A M 2017. Development of an updated basic wind speed map for SANS 10160-3. Journal of the South African Institution of Civil Engineering, 59(4): 12-25. [ Links ]
Milford, R 1985. Extreme value analysis of South African gust speed data. CSIR unpublished Internal Report 85/4. [ Links ]
Retief, J V & Dunaiski, P 2009. Background to SANS 10160. Stellenbosch: SUN MeDIA. [ Links ]
Rigato, A, Chang, P & Simiu, E 2001. Database-assisted design, standardization, and wind direction effects. Journal of Structural Engineering, 127(8): 855-860. [ Links ]
SANS (South African National Standard) 2011a. SANS 10160-1. Basis of structural design and actions for buildings and industrial structures. Part 1. Basis of structural design. Pretoria: South African Bureau of Standards. [ Links ]
SANS (South African National Standard). 2011b. SANS 10160-3. Basis of structural design and actions for buildings and industrial structures. Part 3. Wind actions. Pretoria: South African Bureau of Standards. [ Links ]
SANS (South African National Standard) 2017. SANS CD 10160-3: Committee Draft of Part 3. Wind Actions. SABS TC98 SC1. Pretoria: South African Bureau of Standards. [ Links ]
Simiu, E, Heckert, N A, Filliben, J J & Johnson, S K 2001. Extreme wind load estimates based on the Gumbel distribution of dynamic pressures: an assessment. Structural Safety, 23: 221-229. [ Links ]
Steenbergen, R D J M & Vrouwenvelder, A C W M 2015. Reliability-based calibration of partial factors for the future evolution of EN 1990 for wind actions. JCSS and CEN/TC250/WG7 Workshop, February, Delft, Netherlands. [ Links ]
Xu, F, Cai, C & Zhang, Z 2014. Investigations on coefficients of variation of extreme wind speed. Wind and Structures, 18(6): 633-650. [ Links ]
 Correspondence:
Correspondence:
J Botha
2 Strasbourg Street, Kraaifontein, Cape Town 7570
South Africa
T: +27 72 948 1694
E: jacques.botha@safrica.com
J V Retief
Department of Civil Engineering, Stellenbosch University
Private Bag X1, Matieland, Stellenbosch 7602
South Africa
T: +27 21 808 4442
E: jvr@sun.ac.za
C Viljoen
Department of Civil Engineering, Stellenbosch University
Private Bag X1, Matieland, Stellenbosch 7602
South Africa
T: +27 21 808 4444
E: cbarnardo@sun.ac.za

DR JACQUES BOTHA obtained a BEng (Civil) degree in 2012 and a PhD (Structural Engineering) in 2016, both from Stellenbosch University. His research interests are in probabilistic modelling, wind loading and informatics. He is currently employed as a Software Engineer at 4C IT Software Solutions in Bellville, Cape Town.

PROF JOH AN RETIEF (Fellow) Is Emeritus Professor in Civil Engineering at Stellenbosch University. His interests are in the application of structural reliability in the various fields of structural design standards. Accordingly, he has made contributions to the development of design standards nationally and Internationally. He holds DEng degrees from Pretoria and Stellenbosch Universities and degrees from Imperial College, London, and Stanford University, California.

PROF CELESTE VILJOEN (PrEng, MSAICE) is a researcher on structural risk and reliability at Stellenbosch University. She is a member of SABS National Committee TC 98/02, the convenor of the working group developing SANS 10100-3, a member of the working group for the revision of ISO 13824 and a member of the International Joint Committee on Structural Safety.














