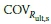Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
Journal of the South African Institution of Civil Engineering
On-line version ISSN 2309-8775
Print version ISSN 1021-2019
J. S. Afr. Inst. Civ. Eng. vol.60 n.2 Midrand Jun. 2018
http://dx.doi.org/10.17159/2309-8775/2018/v60n2a6
TECHNICAL PAPER
Determination of base and shaft resistance factors for reliability-based design of piles
X-Y Bian; X-Y Chen; H-L Lu; J-J Zheng
ABSTRACT
This paper aims to propose a procedure for calculating separately the resistance factors for ultimate base and shaft resistances for the reliability-based design of piles. The proposed procedure can clearly explain the different sources of uncertainties of the bearing capacity, including those from ultimate base and shaft resistances. The study evaluates the convergence of the proposed procedure, and the effects of relevant parameters on resistance factors. Finally, two examples are used for comparison and application of the presented method for determining ultimate base and shaft resistance factors. Convergence analysis proves that the final resistance factors can be rapidly obtained, and maintain good stability using the iteration algorithm included in the proposed procedure. A parametric study indicates that the ratio of dead load to live load and initial values of the ultimate shaft (or base) resistance factor, have a limited effect on the final convergence values of ultimate shaft (and base) resistance factors. However, the target reliability index has significant influence on the ultimate shaft and base resistance factors. The validation example shows that the ultimate shaft and base resistance factors, as calculated in this paper, are conservative compared to the results by Kim et al (2011), due to the consideration of more uncertainties. The recommended ultimate shaft and base resistance factors for the reliability-based design of piles can be obtained conveniently using the proposed procedure in the application example.
Keywords: pile, reliability, resistance factor, ultimate base resistance, ultimate shaft resistance
NOTATION
The following symbols are used in this paper:
b ratio of Rult,b to (LD + LL)
coefficient of variation for
coefficient of variation for
coefficient of variation for LD
coefficient of variation for LL
g limit state function
L load
LD dead load
LL live load
Pf failure probability
Rult ultimate resistance of pile
Rult,b ultimate base resistance of pile
Rult,s ultimate shaft resistance of pile
s ratio of Rult,s to (LD+LL)
βreliability index
βT target reliability index
YD load factor for dead load
YL load factor for live load
θlimit value of calculation accuracy
λD bias factor for LD
λL bias factor for LL
λult,b bias factor for Rult,b
Ault,s bias factor for Rult,s
ρratio of Ld to LL
Øult,b resistance factor for Rult,b
Øult,s resistance factor for Rult,s
initial value of Øult,s
INTRODUCTION
Load and resistance factor design (LRFD) is conceptually a more advanced design method than the existing working stress design (WSD). The key improvements of LRFD over the traditional WSD are the ability to provide a more consistent level of reliability and the possibility of accounting for load and resistance uncertainties separately (Foye et al 2006). Successful implementation of LRFD in geotechnical engineering contributes to an economical and safe design.
Many researchers and practitioners are now recognising the great advantages of LRFD in practice, and more and more relevant research is being incorporated into LRFD for driven piles based on reliability analysis (Zhang et al 2001; Paikowsky 2004; AASHTO 2007). Many countries and regions, such as the United States, Canada, South Africa, China mainland, Japan, Korea, Singapore, Europe and Hong Kong, are replacing or have already replaced WSD with LRFD for structural design. However, LRFD in geotech-nical engineering has not been fully developed yet (Kim et al 2011).
Against this background, a rational framework for LRFD development should be established for the replacement of resistance factors calculated based on factors of safety with those calculated based on reliability analysis. The LRFD framework is conducive to maintaining the same levels of load factors for all loads under different conditions. A number of studies have looked at calculating and calibrating resistance factors for geotechnical engineering. Zheng et al (2012) presented a Bayesian optimisation approach to determine the resistance factor of piles, and recommended values for the resistance factors of driven piles. Bian et al (2015) incorporated the serviceability limit state requirements into LRFD for the ultimate limit states of piles to determine the resistance factors for reliability-based design of piles. Phoon and Kulhawy (2002), and Phoon et al (2003) proposed a multiple resistance factor design concept for foundations and studied the uplift resistance factors for uplift side resistance, uplift tip resistance and dead weight of foundation against uplift force. Honjo et al (2002) established a procedure for the calculation of partial factors for dead load, seismic load, base resistance and shaft resistance of axially-loaded cast-in situ piles. Kim et al (2011) contributed to the development of LRFD for axially-loaded driven piles in sands, the evident feature of which is that the resistance factors for base and shaft resistances were calculated separately to account for their different uncertainty levels. Basu and Salgado (2012) developed resistance factors for drilled shafts for a design method based on soil parameters.
However, methods to determine the ultimate base and shaft resistance factors are not well developed. This paper will present a novel method to calculate the ultimate base and shaft resistance factors for the reliability-based design of piles. First, an iterative algorithm to estimate the ultimate base and shaft resistance factors will be presented using the reliability theory and LRFD criteria. Second, the convergence of the proposed procedure will be analysed. Third, the effects of relevant parameters - ratio of dead load to live load, initial value of base (or shaft) resistance factor, and target reliability index - on resistance factors will be evaluated. Finally, the validation and practical application of the presented method will be shown with two examples to illustrate the feasibility and availability of the presented method.
LOAD AND RESISTANCE FACTOR DESIGN
Design criterion
Considering an axially-loaded driven pile, the ultimate pile resistance (or bearing capacity) Rult is generally expressed as the summation of ultimate base resistance (or end resistance) Rult,b and ultimate shaft resistance (or shaft friction) Rult,ss(Poulos & Davis 1980):

The key advantage of the LRFD approach is that significant uncertainties (e.g. load and material resistance) can be incorporated quantitatively into the design process. If only dead load LD and live load Ll are considered, the LRFD design formula for an axially-loaded driven pile can be written as (AASHTO 2007):
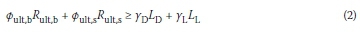
where Øult,b and Øult,s are the resistance factors for Rult,b and Rult,s respectively; and γD and γL are the specified load factors for dead and live loads respectively.
Resistance factors
Suppose resistance Rult and load L follow lognormal distribution and they are statistically independent (Ang & Tang 2007; Wang & Kulhawy 2008; Dithinde et al 2011). It should be pointed out here that the probability distribution for load L is certainly suitable to dead load LD and live load Ll, namely lognormal distribution. The limit state function (g) in accordance with LRFD framework is established:

The reliability index β, which is used to estimate the reliability of piles and reflect the safety status of piles, can be calculated using the following formula (Federal Highway Administration 2001; Bian et al 2016):
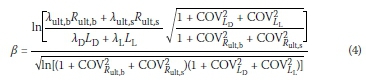
where λult,b, λult,s, λD and λL are the bias factors for Rult,b, Rult,s, Ld and LL respectively; and 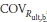 ,
, 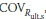 ,
, 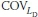 and
and  are the coefficients of variation (COVs) for Rult,b, Rult,s, LD, and LL respectively. Here the bias factor includes the net effect of various sources of errors, such as inherent soil variability, measurement error, and transformation uncertainty.
are the coefficients of variation (COVs) for Rult,b, Rult,s, LD, and LL respectively. Here the bias factor includes the net effect of various sources of errors, such as inherent soil variability, measurement error, and transformation uncertainty.
LRFD is the limit state design (mainly including ultimate limit state and serviceability limit state for piles), and only the ultimate limit state requirements are focused on in this paper. As the critical state of the design formula (Equation 2) is necessary for the study, replacing the inequality sign in Equation 2 with an equality sign gives:
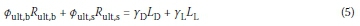
Then Rult,b and Rult,sscan be expressed respectively as:
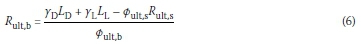
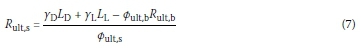
Substituting Rult,b and Rult,s, expressed respectively by Equations 6 and 7, into Equation 4, and replacing βin Equation 4 with target reliability index (βT), gives the following expressions for Øult,b and Øult,s
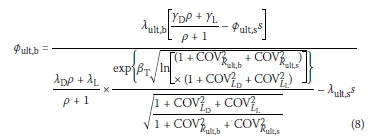

Equations 8 and 9 indicate that Øult,b and Øult,s are functions of many parameters, such as ρ, βT s, b and so on. Among these parameters ρ, βT, s and b are key factors influencing Øult,b and Øult,s due to great uncertainties for them. Here βT is a certain level of reliability, for which piles designed using the LRFD method will guarantee. In other words, the reliability index of a pile designed using LRFD is greater than or equal to the target reliability index.
Probabilistic parameters
Based on the foregoing discussion, there are two sets of information required to estimate resistance factors: load and resistance information (including load factor, bias factor, Cov). A review of literature (AASHTo 2007) suggests that the following probabilistic parameters can be used for LD and LL: λD = 1.08,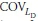 = 0.13, λL = 1.15,
= 0.13, λL = 1.15, 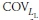 = 0.18, yD = 1.25 and yL = 1.75. ρ= LD/LL is structure-specific and changes with span length (Hansell et al 1971; Withiam et al 2001). Hansell et al (1971) also proposed an empirical formula, LD/LL = (1 + I)(0.0132l), to relate LD/LL with span length, where L is the dynamic load factor (taken as 0.33 for LRFD loads), and L is the span length in feet. ρ= LD/LL spreads over from 0.576 to 5.184 when L varies from 10 m to 90 m, and ρ= 3.0 is a frequently used value.
= 0.18, yD = 1.25 and yL = 1.75. ρ= LD/LL is structure-specific and changes with span length (Hansell et al 1971; Withiam et al 2001). Hansell et al (1971) also proposed an empirical formula, LD/LL = (1 + I)(0.0132l), to relate LD/LL with span length, where L is the dynamic load factor (taken as 0.33 for LRFD loads), and L is the span length in feet. ρ= LD/LL spreads over from 0.576 to 5.184 when L varies from 10 m to 90 m, and ρ= 3.0 is a frequently used value.
Formula pf= Φ(-β) expresses the relationship between failure probability (pf) and β(see Table 1). The acceptable βτis in essence the maximum acceptable failure probability. For example, determining acceptable βT = 3.0 means the acceptable maximum failure probability is 0.001.
Barker et al (1991) reduced the target reliability index for driven piles to a value between 2.0 and 2.5, especially for a group system effect. Paikowsky (2004) suggested an initial target reliability index between 2.0 and 2.5 for a pile group, and 3.0 for a single pile. Paikowsky (2004) also recommended target reliability indices of 2.33 (corresponding to 1% probability of failure) and 3.00 (corresponding to 0.1% probability of failure) for representing redundant and non-redundant pile groups, respectively. As suggested by Barker et al (1991) and Paikowsky (2004), five levels (2.0, 2.5, 3.0, 3.5 and 4.0) of target reliability index will be considered in this study and the corresponding resistance factors calculated.
Probabilistic parameters for Rult, Rult,b and Rult,s from literature are summarised in Table 2. Equations 8 and 9 demonstrate that b (= Rult,b/(LD + LL)) and s (= Rult,s/(LD + LL)) are two key parameters for evaluation of resistance factors. However, both b and s are difficult to determine, because Rult,band Rult,s depend largely on site conditions and pile types. For example, Rult,bof friction piles is generally very small and may be ignored with respect to Rult,s, which means that 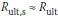 , resulting in
, resulting in 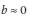 and
and 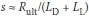 . Moreover, for a safe design
. Moreover, for a safe design 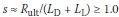 . For end-bearing piles Rult,s is generally very small, and may be ignored with respect to Rult,b, which means that
. For end-bearing piles Rult,s is generally very small, and may be ignored with respect to Rult,b, which means that 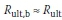 , resulting in
, resulting in 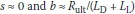 . Moreover, for a safe design
. Moreover, for a safe design 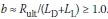 . For end-bearing friction piles and friction end-bearing piles, b and s are complex and need further study.
. For end-bearing friction piles and friction end-bearing piles, b and s are complex and need further study.
PROCEDURE TO CALCULATE RESISTANCE FACTORS
Procedure flow chart
Equations 8 and 9 indicate that Øult,b and Øult,s mainly depend on ρ, βT,s,b and other parameters. Especially, Øult,b computed using Equation 8 will be submitted into Equation 9 to compute Øult,s, and this Øult,s will be resubmitted into Equation 8 to compute Øult,b again. This computation process is in fact an iteration process, which contributes to build a procedure for resistance factors calculation, as shown in Figure 1 (Bian et al 2016). In Figure 1, 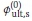 is the initial value of swhere θis the limit value of calculation accuracy.
is the initial value of swhere θis the limit value of calculation accuracy.
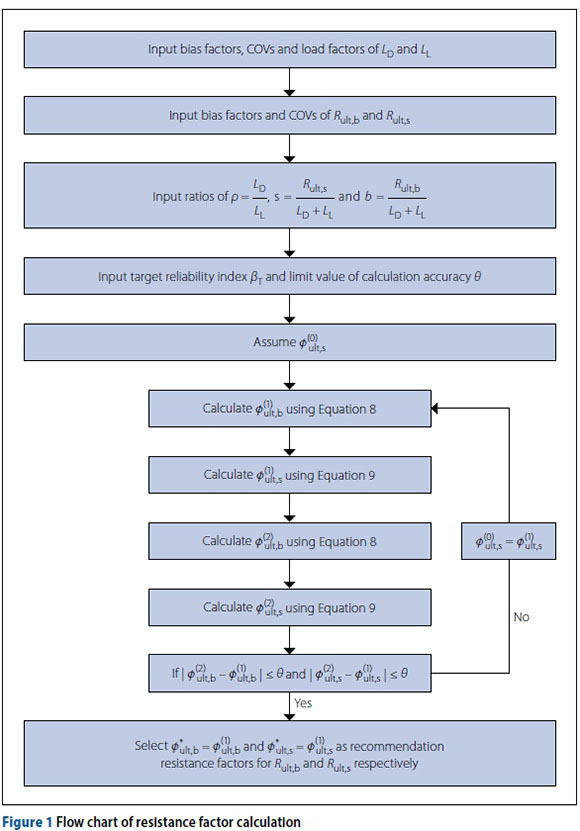
With reference to Figure 1, the proposed approach to determine resistance factors 0ult,b and 0ult,s for reliability-based design of piles is outlined in the following steps:
■ Step 1 Input statistical parameters of load and resistance. Bias factors, COVs and load factors Ld and Ll can be determined referring to the previous literature. Bias factors and COVs of Rult,b and Rult,ssare estimated using the load test database of piles.
■ Step 2 Input combination parameters p = LD/LL s= Rult,s / (LD+LL) and b = Rult,b / (LD+LL). For ρ, the commonly used values (such as 0.5, 1.0, 2.0, 3.0, 4.0 and 5.0) from the previously mentioned literature are welcome, while s and b need to be evaluated depending on site conditions and pile types.
■Step 3 Input βT and precision limit value θ. For βT the commonly used values (such as 2.0, 2.5, 3.0, 3.5 and 4.0) will be accepted for further study. θis set as 0.0001.
■ Step 4 Determine initial value
(or
). Six values, namely 0, 0.2, 0.4, 0.6, 0.8 and 1.0, will be suggested to study the influence of
(or
) on the final results.
■ Step 5 Calculate ∅ult,b and ∅ult,s Submit
into Equation 8 to compute ∅ult,b, and denote as
Submit
into Equation 9 to compute ∅ult,s, and denote as
. Repeat this process to obtain
and
■ Step 6 Examine convergence. If
,
,
and
satisfy
, and
are taken as the final resistance factors
, repeat Step 5.
Convergence analysis of calculation procedure
The validity and application conditions of the procedure are investigated in depth in this section. All related computation tasks will be completed using MS Excel. Convergence of the proposed procedure to calculate resistance factors was made using the following parameters: ρ= 3.0, imagemaqui = 0.5, βT= 3.0 and θ= 0.0001. Parameter s was set as 0.5, 1.0, 2.0 and 3.0. For each value of s, b was set as 0, 0.5, 1.0, 2.0, 3.0 and integer ≥ 4.0, respectively. Here statistics of LD and LL(namely λD = 1.08, 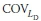 = 0.13, λL, = 1.15,
= 0.13, λL, = 1.15, 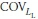 = 0.18, yD = 1.25 and yL = 1.75) presented by AASHTO (2007) are accepted to compute the resistance factors Øult,b and Øult,s,. Bias factors and COVs of Rult,b and Rult,spresented by Jardine et al (2005), and summarised in Table 2 by the authors, are also used in this section. Final resistance factors obtained for each combination and the number of iterations required to reach the set level of accuracy (θ = 0.0001) are summarised in Table 3.
= 0.18, yD = 1.25 and yL = 1.75) presented by AASHTO (2007) are accepted to compute the resistance factors Øult,b and Øult,s,. Bias factors and COVs of Rult,b and Rult,spresented by Jardine et al (2005), and summarised in Table 2 by the authors, are also used in this section. Final resistance factors obtained for each combination and the number of iterations required to reach the set level of accuracy (θ = 0.0001) are summarised in Table 3.
In Table 3, NM indicates that the combination (b = 0 and s = 0.5) is meaningless for the reliability-based design of piles, while NRC indicates that the iterative process could not reach convergence. Employing the information from Table 3, a bold judgement can be made that the iterative process proposed in this paper reached convergence only when the sum of s and b was less than 4. This requirement meets the demand for reliability-based design of piles satisfactorily. The LRFD criteria for piles, the most important limit state design method, has been expressed by Equation 2. For reliability-based design of piles, Rulttdoes not excessively exceed the load effects. Due to this, and given that safe designs are those with Rult/(Ld + LL) ≥ 1.0, b = Rult,b/(LD+ LL) and s = Rult,s/(LD+ LL)will be limited to between 0 and 3.0. It is also pointed out that runs with b = 0 are done purely for comparison, as b = 0 implies a pure friction pile which is not possible.
From Table 3, the following preliminary conclusions can be drawn: for a given s, the number of iterative steps increase with increasing b, as shown from columns 10 to 13. For example, with s = 0.5, the iterative steps are 4, 5, 7 and 20 corresponding to b with values of 0.5, 1.0, 2.0 and 3.0 respectively; with s = 2.0, the iterative steps are 3, 8 and 15 corresponding to b with values of 0, 0.5 and 1.0 respectively.
PARAMETER ANALYSIS AND DISCUSSION
In this section, load statistical parameters (including λD = 1.08, 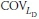 = 0.13, λL = 1.15,
= 0.13, λL = 1.15, 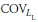 = 0.18, rD= 1.25 and YL= 1.75) presented by AASHTO (2007), and resistance statistical parameters (including Ault,b = 1.023, λult,s= 1.088,
= 0.18, rD= 1.25 and YL= 1.75) presented by AASHTO (2007), and resistance statistical parameters (including Ault,b = 1.023, λult,s= 1.088, 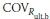 = 0.201 and
= 0.201 and 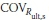 = 0.287) presented by Jardine et al (2005) are used to compute the resistance factors Øult,b and Øult,s
= 0.287) presented by Jardine et al (2005) are used to compute the resistance factors Øult,b and Øult,s
Effect of ρon resistance factors
To study the effect of ρon Øult,b and Øult,s, the following parameters were kept constant: 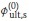 = 0.5, s = 1.0, b = 1.0, βτ= 3.0 and θ= 0.0001. It is also well reasoned to set ρas 0.5, 1.0, 2.0, 3.0, 4.0 and 5.0 respectively. Using these parameters, Øult,b and Øult,s were calculated using the proposed procedure and plotted against ρin Figure 2.
= 0.5, s = 1.0, b = 1.0, βτ= 3.0 and θ= 0.0001. It is also well reasoned to set ρas 0.5, 1.0, 2.0, 3.0, 4.0 and 5.0 respectively. Using these parameters, Øult,b and Øult,s were calculated using the proposed procedure and plotted against ρin Figure 2.
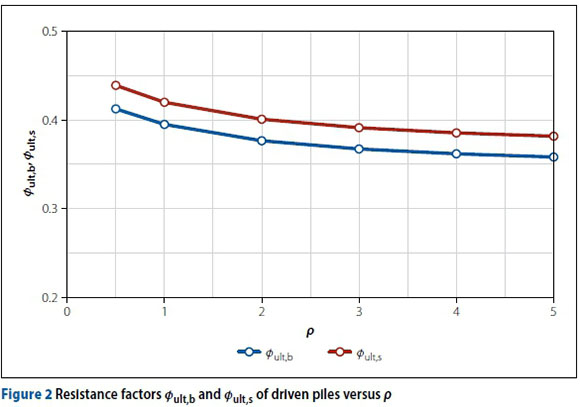
Varying ρdid not influence convergence, with convergence generally obtained within six iterative steps. It can be seen from Figure 2 that both Øult,b and Øult,s decrease slightly with increasing ρ. However, the difference between Øult,b and Øult,s is an approximate constant for all p. Under the given assumptions, Øult,s is larger than Øult,b, and the average difference between Øult,b and Øult,s is about 0.025.
Effect of  on resistance factors
on resistance factors
To study the effect of 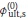 on final resistance factors (Øult,b and Øult,s), the following parameters were kept constant: ρ= 3.0, s = 1.0, b = 1.0, βT = 3.0 and θ= 0.0001. Parameter
on final resistance factors (Øult,b and Øult,s), the following parameters were kept constant: ρ= 3.0, s = 1.0, b = 1.0, βT = 3.0 and θ= 0.0001. Parameter 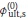 was set as 0, 0.2, 0.4, 0.6, 0.8 and 1.0 respectively, and the two resistance factors were calculated and plotted against
was set as 0, 0.2, 0.4, 0.6, 0.8 and 1.0 respectively, and the two resistance factors were calculated and plotted against 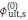 in Figure 3.
in Figure 3.
Varying  did not influence convergence significantly, with convergence reached within no more than seven iterative steps. It can be seen from Figure 3 that both Øult,b and Øult,s versus
did not influence convergence significantly, with convergence reached within no more than seven iterative steps. It can be seen from Figure 3 that both Øult,b and Øult,s versus 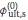 are approximate horizontal lines, which illustrate that convergence values Øult,b and Øult,s are both independent of
are approximate horizontal lines, which illustrate that convergence values Øult,b and Øult,s are both independent of  , as Øult,b and Øult,s are determined as 0.37 and 0.39 respectively. This conclusion provides support to the rationality of the proposed procedure for resistance factor calculation.
, as Øult,b and Øult,s are determined as 0.37 and 0.39 respectively. This conclusion provides support to the rationality of the proposed procedure for resistance factor calculation.
Effect of βτ on resistance factors
To study the effect of βT on Øult,b and Øult,s the following parameters were kept constant: ρ= 3.0, = 0.5, s = 1.0, b = 1.0 and θ= 0.0001. βT was set as 2.0, 2.5, 3.0, 3.5 and 4.0. Calculated values of Øult,b and Øult,s are plotted against βT in Figure 4.
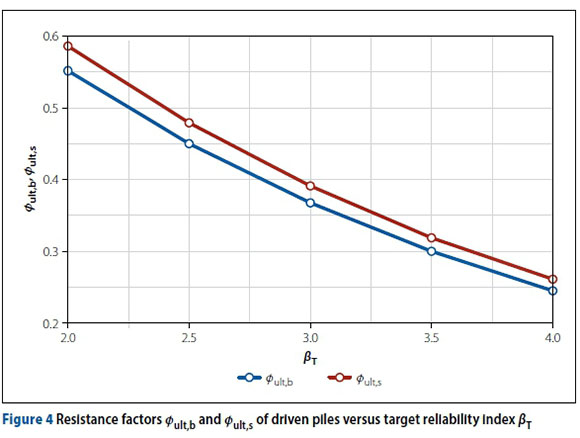
In Figure 4, both Øult,b and Øult,s decrease sharply with an increase of βT, which shows that both Øult,b and Øult,s are very sensitive to βT For example, when βT increases from 2.0 to 4.0, Øult,b decreases from 0.55 to 0.25, and Øult,s decreases from 0.59 to 0.26. Varying βT had a significant effect on iterative steps. For βT = 2.0, the iterative steps were 12; for βT = 2.5, 3.0 and 3.5 respectively, the iterative steps were all nearly 6; and for βT = 4.0, the iterative steps were only 4.
In summary, engineers should very seriously consider a suitable βT to conduct the reliability-based design of pile foundations. Selecting a small βT will leave the piles designed using LRFD methods at risk. Selecting a large βT will lessen the identified resistance factors, the design scheme will be conservative and the cost will be uneconomical. The analysis in this section indicates that the values of βT between 2.5 and 3.0 are suitable. βT between 2.5 and 3.0 indicates the acceptable maximum failure probability between 0.1% and 0.6%, which is low enough for general pile foundation engineering. Besides, the iterative steps are nearly 6 for βτ with values between 2.5 and 3.0, and the computational efficiency is good, too.
validation and application
Practical validation and application of the proposed method will be illustrated by the following two examples, respectively.
Validation example
According to Kim et al (2011), Øult,b and Øult,s values were calibrated using their proposed method for building and bridge structures, which are compatible with the ASCE/SEI 7-05 (ASCE 2005) load factors and the AASHTO (2007) load factors. For comparison and validation, the corresponding load statistical parameters are considered in this section (Kim et al 2011): in the case of ASCE/ SEI 7-05, λD = 1.05, COVL= 0.1, λL = 1.0 and 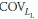 = 0.25; while in the case of AASHTO, λD = 1.05,
= 0.25; while in the case of AASHTO, λD = 1.05, 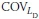 = 0.1, λL = 1.2 and
= 0.1, λL = 1.2 and 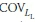 = 0.205. Also, yD= 1.25 and Yl= 1.75 are selected for both ASCE/SEI 7-05 and AASHTO cases. The process of estimating the resistance factors for building and bridge structures must satisfy the following conditions:
= 0.205. Also, yD= 1.25 and Yl= 1.75 are selected for both ASCE/SEI 7-05 and AASHTO cases. The process of estimating the resistance factors for building and bridge structures must satisfy the following conditions:
1. Utilise ρ= LD/LLwith four different values: 1.0, 2.0, 3.0 and 4.0
2. Utilise βT with four different values: 2.0, 2.5, 3.0 and 3.5
3. Determine both s = Rult,s/(Ld + Ll) and b = Rult,b/(LD + LL) as 1.0
4. Select resistance statistical parameters referring to Jardine et al (2005), namely λult,b= 1.023, λult,s= 1.088,
= 0.201 and
= 0.287.
Calculated results of Øult,b and Øult,s using the proposed method in this paper are shown in Table 4. For building structures with the ASCE/ SEI 7-05 (ASCE 2005) load factors, the calculated Øult,b and Øult,s values vary within the ranges 0.55-0.62 and 0.58-0.66 for βT = 2.0; 0.44-0.50 and 0.47-0.53 for βT = 2.5; 0.36-0.40 and 0.38-0.43 for βT = 3.0; and 0.29-0.32 and 0.31-0.34 for βT = 3.5, respectively, depending on the ratio ρ= LD/LL (ρ= LD/LL range of 1.0-4.0).
For bridge structures with the AASHTO (2007) load factors, the calculated Øult,b and Øult,s values vary within ranges 0.55-0.58 and 0.58-0.62 for βT = 2.0; 0.45-0.48 and 0.48-0.51 for βT = 2.5; 0.36-0.39 and 0.39-0.41 for βT = 3.0; and 0.30-0.32 and 0.32-0.34 for βT = 3.5, respectively, depending on the ratio ρ= LD/LL (ρ = LD/LL range of 1.0-4.0).
For ease of comparison, the results of Øult,b and Øult,s from Kim et al (2011) are also given in Table 4 (columns 11 to 16). Comparison shows that the results of Øult,b and Øult,s for building and bridge structures compatible with load factors from ASCE/ SEI 7-05 (ASCE 2005) and AASHTO (2007) computed in this paper, are smaller than the results from Kim et al (2011). These differences may be due to many probable reasons, but it should be pointed out here that some main uncertainty factors are not considered in Kim et al (2011), such as proportions of shaft (base) resistance to load (namely Rult,s/(LD + LL) and Rult,b / (LD+ LL)), the correlation between Øult,b and Øult,s and so on.
For example, in Kim et al (2011), Øult,b and Øult,s for building and bridge structures compatible with load factors from AASHTO (2007) vary within ranges of 0.82-0.87 and 0.70-0.75 for βT = 2.5; 0.76-0.79 and 0.63-0.66 for βT = 3.0; and 0.69-0.73 and 0.57-0.60 for βT = 3.5. These resistance factors in Kim et al (2011) seem to be very large for the reliability-based design of piles. The resistance factors proposed by AASHTO (2007) for strength limit state for shallow foundations are generally between 0.35-0.60, which perhaps more strongly support the results in this paper.
Application example
Luo (2004) compiled a database of pile load tests, including 151 driven pile load tests. From these databases only 128 driven pile load tests with sufficient information (measured ultimate bearing capacity, base resistance and shaft resistance) were analysed. The bias factors and COVs of pile resistances were calculated by authors referring to Luo (2004): λult,b = 1.18, λult,s= 1.21, 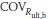 = 0.34, and
= 0.34, and 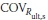 = 0.22, respectively. Computed resistance factors using the proposed procedure are summarised in Table 5 for the following conditions:
= 0.22, respectively. Computed resistance factors using the proposed procedure are summarised in Table 5 for the following conditions:
1. Set ρ= Ld/Ll at four different values: 1.0, 2.0, 3.0 and 4.0
2. Set βT at four different values: 2.0, 2.5, 3.0 and 3.5
3. Both sets s = Rult,s/(LD + LL) and b = Rult,b/(LD+ LL) at 1.0
4. Accepted load statistical parameters presented by AASHTO (2007), namely λD = 1.08,
= 0.13, λL = 1.15,
= 0.18, yD = 1.25 and yL= 1.75.
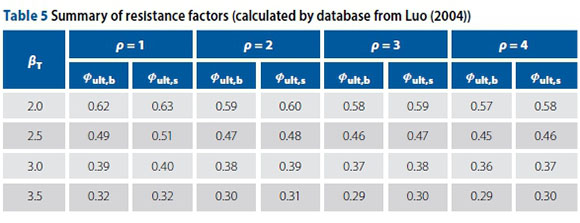
Based on the results shown in Table 5, one can see that the calculated Øult,b and Øult,s values vary within the ranges of 0.57-0.62 and 0.58-0.63 for βT = 2.0; 0.45-0.49 and 0.46-0.51 for βT = 2.5; 0.36-0.39 and 0.37-0.40 for βT = 3.0; and 0.29-0.32 and 0.30-0.32 for βT = 3.5, respectively, depending on the ratio ρ= LD/LL (ρ = LD/LL range of 1.0-4.0). The variations of Øult,b with the different ρvalues are very small; this is also the case for Øult,s. This further verifies the conclusion obtained in the section above titled "PARAMETER ANALYSIS AND DISCUSSION", that both Øult,b and Øult,s decrease slightly with increasing ρ. Therefore, the recommended resistance factors can be proposed with different target reliability levels by considering the influence of ρreferring to Table 5. For a target reliability level, the mean value of four resistance factor values, corresponding to ρ= 1, 2, 3 and 4, is determined as the recommended resistance factor. By this method, based on the calculated resistance factors shown in Table 5, this study presents the recommended resistance factors for 128 driven pile load test cases, coming from Luo (2004) and summarised in Table 6.
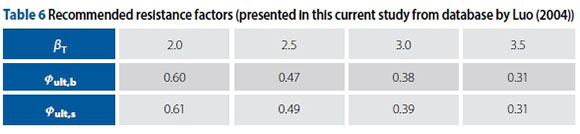
Table 6 shows that the recommended resistance factors are significantly different for different βT indices. This phenomenon is actually compatible with the conclusion, as obtained in the section above, titled "PARAMETER ANALYSIS AND DISCUSSION", that βT is an important factor for the determination of resistance factors, as it is essential to choose the appropriate target reliability index for the reliability-based design of piles using the proposed method in this paper. According to the presented values of βT between 2.5 and 3.0 mentioned earlier, the recommended values of the resistance factors are 0.38-0.47 for Øult,b and 0.39-0.49 for Øult,s.
CONCLUSIONS
Uncertainties regarding the bearing capacity of piles actually derives from the ultimate base and shaft resistances, and should be explained separately in the reliability-based design of piles. The way to solve this problem is by developing a method to evaluate and study the ultimate base and shaft resistance factors respectively. This is the major contribution achieved in this paper.
Convergence analysis demonstrates that the presented iteration algorithm to estimate ultimate base and shaft resistance factors converges rapidly and remains stable. The condition of convergence (i.e. b and s between 0 and 3.0) can meet the demand of the reliability-based design of piles satisfactorily.
In addition, parameter analysis indicates that the ratio of dead to live loads has a limited influence on calculated resistance factors. The overall consideration of dead and live loads in the determination of ultimate base and shaft resistance factors is reasonable. Similarly, the initial seed resistance factor also has little effect on convergence of the final resistance factors. Any initial seed resistance factor could be selected in the reliability-based design of piles. However, the target reliability index significantly influences computed resistance factors, and an appropriate target reliability index is required for the reliability-based design of piles.
In a nutshell, the ultimate base and shaft resistance factors for the reliability-based design of piles can easily be obtained using the proposed procedure with an appropriate target reliability index. The application example has illustrated this point.
ACKNOWLEDGEMENTS
The authors would like to express their gratitude to the National Key Research and Development Program of China (2016YFC0800208) and the National Natural Science Foundation of China (51708428, 51408444, 51378404).
REFERENCES
AASHTO (American Association of State Highway and Transportation Officials) 2007. AASHTO LRFD Bridge Design Specifications, 4th ed. Washington, DC: AASHTO. [ Links ]
Ang, A H-S & Tang, W H 2007. Probability Concepts in Engineering: Emphasis on Applications to Civil and Environmental Engineering, 2nd ed. New York: Wiley. [ Links ]
ASCE (American Society of Civil Engineers) 2005. Minimum design loads for buildings and other structures. Report ASCE/SEI 7-05. Reston, VA: ASCE. [ Links ]
Barker, R, Duncan, J, Rojiani, K, Ooi, P S K, Tan, C K & Kim, S G 1991. Manuals for the design of bridge foundations. National Cooperative Highway Research Program (NCHRP) Report 343. Washington, DC: Transportation Research Board, National Research Council. [ Links ]
Basu, D & Salgado, R 2012. Load and resistance factor design of drilled shafts in sand. Journal of Geotechnical and Geoenvironmental Engineering, 138(12): 1455-1469. [ Links ]
Bian, X Y, Zheng, J J, Xu, Z J & Zhang, R J 2016. A method to calculate resistance factors for LRFD of driven piles. Proceedings, 6th Asian-Pacific Symposium on Structural Reliability and its Applications, Shanghai, China, pp 157-163. [ Links ]
Bian, X Y, Zheng, J J & Xu, Z J 2015. Incorporating serviceability limit state requirements into reliability-based analysis and design of piles. KSCE Journal of Civil Engineering, 19(4): 904-910. [ Links ]
Dithinde, M, Phoon, K K, De Wet, M & Retief, J V 2011. Characterization of model uncertainty in the static pile design formula. Journal of Geotechnical and Geoenvironmental Engineering, 137(1): 70-85. [ Links ]
Federal Highway Administration 2001. Load and Resistance Factor Design (LRFD) for highway bridge substructures. Washington, DC: Department of Transportation. [ Links ]
Foye, K C, Salgado, R & Scott, B 2006. Resistance factors for use in shallow foundation LRFD. Journal of Geotechnical and Geoenvironmental Engineering, 132(9): 1208-1218. [ Links ]
Hansell, W C & Viest, I M 1971. Load factor design for steel highway bridges. AISC Engineering Journal, American Institute of Steel Construction, 8(4): 113-123. [ Links ]
Honjo, Y, Suzuki, M, Shirato, M & Fukui, J 2002. Determination of partial factors for a vertically loaded pile based on reliability analysis. Soils and Foundations, 42(5): 91-109. [ Links ]
Jardine, R J, Chow, F C, Overy, R & Standing, J 2005. ICP Design Methods for Driven Piles in Sand and Clays. London: Thomas Telford. [ Links ]
Kim, D, Chung, M & Kwak, K 2011. Resistance factor calculations for LRFD of axially loaded driven piles in sands. KSCE Journal of Civil Engineering, 15(7): 1185-1196. [ Links ]
Luo, S X 2004. Research and engineering application on probability limit states design method of pile foundations. [in Chinese] Chengdu, China: Southwest Jiaotong University, pp 65-70. [ Links ]
Michiyo, S & Minoru, M 1993. The control of steel pipe pile driving based on reliability analysis of bearing capacity estimation. Soils and Foundations, 33(3): 40-53. [ Links ]
Paikowsky, S G 2004. Load and resistance factor design (LRFD) for deep foundations. National Cooperative Highway Research Program (NCHRP) Report 507. Washington, DC: Transportation Research Board, National Research Council. [ Links ]
Phoon, K K & Kulhawy, F H 2002. Drilled shaft design for transmission line structure using LRFD and MRFD. Deep Foundations (GSP), 116: 1006-1017. [ Links ]
Phoon, K K, Kulhawy, F H & Grigoriu, M D 2003. Multiple Resistance Factor Design (MRFD) for spread foundations. Journal of Geotechnical and Geoenvironmental Engineering, 129(9): 807-818. [ Links ]
Poulos, H G & Davis, E H 1980. Pile Foundation Analysis and Design. New York: Wiley. [ Links ]
Wang, Y & Kulhawy, F H 2008. Reliability index for serviceability limit state of building foundations. Journal of Geotechnical and Geoenvironmental Engineering, 134(11): 1587-1594. [ Links ]
Withiam, J L, Voytko, E P, Barker, R M, Duncan, J M, Kelly, BC, Musser, S C et al 2001. Load and resistance factor design (LRFD) for highway bridge substructures. Federal Highway Administration (FHWA) Report HI-98-032, NHI Course No. 13068. Washington, DC: FHWA. [ Links ]
Zhang, L M, Tang, W H & Ng, C W W 2001. Reliability of axially loaded driven pile groups. Journal of Geotechnical and Geoenvironmental Engineering, 127(12): 1051-1060. [ Links ]
Zheng, J J, Xu, Z J & Liu, Y 2012. Optimised Bayesian method for resistance factor of piles. [in Chinese] Chinese Journal of Geotechnical Engineering, 34(9): 1716-1721. [ Links ]
 Correspondence:
Correspondence:
DR XIAO-YA BIAN
Wuhan Institute of Technology School of Civil Engineering and Architecture Wuchang Campus
Wuhan, Hubei, China
T: +86 27 8719 4698
E: bianxy@hust.edu.cn
PR0FXU-Y0NG CHEN
Wuhan Institute of Technology School of Civil Engineering and Architecture Wuchang Campus
Wuhan, Hubei, China
T: +86 27 8719 4698
E: cxy1314kl@126.com
PROF HAI-LIN LU
Wuhan Institute of Technology, School of Civil Engineering and Architecture, Wuchang Campus
Wuhan, Hubei, China
T: +86 27 8719 4698
E: hail_lu@yangtzeu.edu.cn
PROF JUN-JIE ZHENG
Huazhong University of Science and Technology School of Civil Engineering and Mechanic
Wuhan, Hubei, China
T: +86 27 8755 7024
E: zhengjj@hust.edu.cn

DR XIAO-YA BIAN is a lecturer in the School of Civil Engineering and Architecture at the Wuhan Institute of Technology, China. He obtained his PhD in Geotechnical Engineering from the School of Civil Engineering and Mechanics at the Huazhong University of Science and Technology, China. His special interests are risk and reliability of geotechnical engineering, and ground improvement.

PR0FXU-Y0NG CHEN Is an assistant professor In the School of Civil Engineering and Architecture at the Wuhan Institute of Technology, China. He obtained his PhD in Bridge Engineering from the School of Civil Engineering and Mechanics at the Huazhong University of Science and Technology, China. His special interests are bridge reinforcement and non-probabilistic reliability of bridges.

PROF HAI-LIN LU is a professor in the School of Civil Engineering and Architecture at the Wuhan Institute of Technology, China. He obtained his PhD in Structural Engineering from the School of Civil Engineering at the Tianjin University, China. His special interest is earthquake resistance ofengineering structures.

PROF JUN-JIE ZHENG is a professor in the School of Civil Engineering and Mechanics at the Huazhong University of Science and Technology, China. He obtained his PhD in Geotechnical Engineering from the Zhejiang University, China. His special interests are reliability in geotechnical engineering, ground improvement and tunnel engineering.