Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
Journal of the South African Institution of Civil Engineering
On-line version ISSN 2309-8775
Print version ISSN 1021-2019
J. S. Afr. Inst. Civ. Eng. vol.59 n.4 Midrand Dec. 2017
http://dx.doi.org/10.17159/2309-8775/2017/v59n4a7
TECHNICAL NOTE
An empirical preliminary prediction of heave
G A Jones
ABSTRACT
The method described in the paper titled "Prediction of heave from the plasticity index and percentage clay fraction of soils" by Van der Merwe (1964) has been in common use since then. It predicts the potential heave due to the moisture change from a relatively dry state to a near-saturated state under a covered area, i.e. a maximum state change. In reality this may not always be the case, and this Note proposes an adaptation to the method whereby the probable change in moisture content is utilised in the calculation. This is determined by the in-situ moisture and the estimated equilibrium moisture content (EMC) derived from the liquid limit.
Keywords: potential heave, equilibrium moisture, unit heave
INTRODUCTION
The Van der Merwe (1964) method, which is based on observations of heave of buildings on the Free State clays, has been extensively used for over 50 years in South Africa. It has the great advantage that it uses simple routine laboratory tests, Atterberg Limits and Gradings, a point emphasised by Van der Merwe in his paper. It was intended to give a preliminary estimate of potential heave, and, if this was significant, further testing such as the oedometer could be carried out.
Van der Merwe (1964) also stated that the "accuracy of this prediction will be governed by the actual moisture changes that occur in the soil".
To a large extent this important caveat has been ignored over the years, and the distinction between maximum potential heave (estimated by his method) and the realistic or probable heave (determined by the actual moisture changes) has been lost.
This technical note suggests a modification to his method, which depends on an estimate of moisture change based on the prediction of an equilibrium moisture content (EMC), derived from the liquid limit of the soil, and from measurement of the initial moisture content.
A summary of the Van der Merwe (1964) method is given in the next section, and the proposed modification is described in the following section.
THE VAN DER MERWE METHOD
The Van der Merwe method for the prediction of heave is summarised as follows:
i. The potential soil expansiveness is classified as Very High, High, Medium and Low from the Atterberg Limits and clay fraction using Figure 1.
ii. The potential expansiveness class is then related to unit heave using the Jennings and Kerrich (1962) correlation given in Table 1.
iii. A depth factor is introduced by which the potential expansiveness is reduced to take account of the in-situ stress "due to the increase in the weight of overlying soil and due to decreases in changes in moisture content and other factors" (Van der Merwe 1964). The depth factor is given in Table 2.
iv. Heave calculation: The calculation of potential heave for a hypothetical 3 m thick stratum comprising three layers of differing potential expansiveness is given in Table 3.
PROPOSED MODIFIED HEAVE PREDICTION
As proposed above, the Van der Merwe (1964) method should be modified to take account of the most probable increase in moisture content under a covered area.
It is suggested that the unit heave shown in Table 1, expressed as strain m/m, should be in the more rational unit of strain per percentage change in moisture content, i.e. m/m/w. The question is: What were the increases in moisture on which Jennings and Kerrich (1962) based their unit heaves?
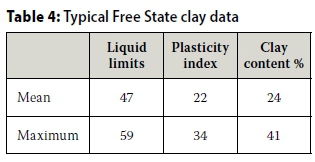
Based on their data on Atterberg Limits, gradings and clay content, and Van der Merwe's (1964) initial moisture content, together with equilibrium moisture content (EMC), an estimate can be made of the increase in moisture content of the typical Free State clay on which the original method of heave prediction is based, as shown in Table 4.
No data could be found on moisture content after heaving had taken place, but the EMC can be estimated using the equation quoted by Weston (1980):

From the data in Table 4 for Very High Potential Expansiveness material, the EMC is therefore 59/2 = 29%, and since the initial moisture is 14% (Van der Merwe 1964), the increase in moisture is then approximately 15%.
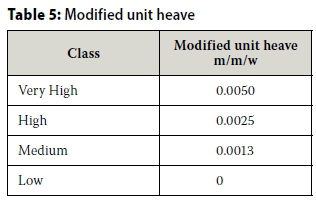
The Jennings and Kerrich (1962) unit heaves in Table 1 can therefore be modified by expressing them as m/m/w, as shown in Table 5.
These unit heaves can then be used to calculate probable heave, provided the initial moisture content is known, since an estimate of the final moisture, the EMC, can be derived from the liquid limits.
For the profile given in the original heave calculation in Table 3, the modified calculation is given in Table 6. If the initial moisture content is 20% for the hypothetical example, W is the increase in moisture, and the heave is the modified unit heave from Table 5 multiplied by the change in moisture W and by the Depth Factor.
The estimated heave in this hypothetical example is half that of the original calculation. Correspondingly, if the initial in-situ conditions are dry, i.e. similar to the original Free State clays, then the unmodified and modified methods will predict similar heaves. At a site recently reported by Jones et al (2016) the modified estimate was only one third of the unmodified estimate, because the initial moisture content in the low-lying area was high. At this site swell tests were carried out, and Figure 2 on page 66 summarises the results.
Figure 2 shows that for the Very High potentially expansive clay:
Swell % = 0.5 Moisture Increase (%)
and this corroborates the modified unit heave given in Table 5 for the Very High class material.
The proposed method suggests that the final moisture content is the EMC, but it is possible that an estimate of heave is required for an increase to saturated moisture, for example to simulate poor drainage or a leaking pipe. In such a case the EMC can be increased by say 3%, the assumed difference between the EMC and saturation; or alternatively the saturation moisture content can be calculated from measurements of the density and unit weight. In this way an indication of differential heave can be made.
CONCLUSION
The proposed modification requires only the additional measurement of the in-situ moisture content to the Atterberg limits and clay content, and this should in any case be necessary, particularly for investigations of clays, since an assessment of their state is essential. The modification could be seen as transforming an estimate of potential heave for a maximum moisture change, to that of an estimate of probable heave for a realistic or expected moisture change.
It is likely that in some cases the modified estimated heave will be lower than that using the Van der Merwe method and would result in a lower NHBRC (National Home Builders Registration Council) classification. In these cases, careful consideration should be given to the implications of allocating a lower classification. It would be prudent in all cases where the empirical approach, modified or unmodified, indicates significant heave, to carry out swell or other tests to confirm the potential heave.
REFERENCES
Jennings, J E & Kerrich, J E 1962. The heaving of buildings and the associated economic consequences with particular reference to the Orange Free State Goldfields. The Civil Engineer in South Africa, 4(11): 221-248. [ Links ]
Jones, G A, Meintjes, H A C, Aucamp, J P & Dutchman, J R 2016. A case study of heave due to flooding. Proceedings, 1st Southern African Geotechnical Conference, 4-6 May, Sun City, 221-228. [ Links ]
Van der Merwe, D M 1964. The prediction of heave from the plasticity index and percentage clay fraction of soils. The Civil Engineer in South Africa, 6(6): 103-107. [ Links ]
Weston, D J 1980. Expansive roadbed treatment for Southern Africa. Proceedings, 3rd International Research and Engineering Conference on Expansive Clays, Denver, CO, Vol. 1, 339-360. [ Links ]
 Correspondence:
Correspondence:
G A Jones
SRK Consulting
PO Box 55291
Northlands 2116
South Africa
T: +27 11 441 1128
E: gjones@srk.co.za

DR GARY JONES graduated from Cambridge University and received his PhD from the University of Natal. He worked as a road and geotechnical engineer in Zimbabwe, the United Kingdom and Uganda, and from 1965 in South Africa. After spells with various consultants and the Natal Roads Department, he moved to the CSIR (Council for Scientific and Industrial Research) and then to VKE in Pretoria. Whilst there he, together with (now) Prof Eben Rust of the University of Pretoria, invented and developed the piezocone for use in soft soils and tailings dams. From 1981 he has been at SRK Consulting where, after retiring, he became a Corporate Consultant and continues in this role.