Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
Journal of the South African Institution of Civil Engineering
On-line version ISSN 2309-8775
Print version ISSN 1021-2019
J. S. Afr. Inst. Civ. Eng. vol.59 n.2 Midrand Jun. 2017
http://dx.doi.org/10.17159/2309-8775/2017/v59n2a5
TECHNICAL PAPER
The two-points condensation technique (TPC) for detection of structural damage due to vibration
A N Al-Qayyim; B Ö Çağlayan
ABSTRACT
In recent years, damage detection, as determined by variations in the dynamic characteristics or response of structures, has received considerable attention in the literature. This paper proposes a new damage identification technique that identifies damage location. A methodology termed the Two-Points Condensation Technique (TPC) is presented. It uses identification of stiffness matrix terms to assess damage, based on the incomplete measurement of captured vibration test data. This study identifies damage using free vibration test data in the time domain. Most other techniques used at present are based on data in the frequency domain. The TPC method uses a set of matrices by reducing the structural system to a two-degrees-of-freedom system and then compares the identified coefficients of the stiffness matrices with the coefficients of the theoretically condensed stiffness matrices. The damage location is obtained by observing the change in value of the stiffness coefficients of the two-degrees-of-freedom systems. For the computation, an optimisation uses a program written in MATLAB code. The code can be executed both under the MATLAB and Octave environments. The TPC technique is applied to experimental data obtained from a steel beam model structure after introducing a thickness change in one element. Two case studies are considered. In both cases, the method accurately detects the damage, and determines its location. In addition, the results illustrate that observing changes in the stiffness matrix coefficients can be a useful tool for monitoring structural health. As the procedure proposed here is in a time domain, to eliminate time-consuming calculations this procedure is suitable for structures that are not continuously monitored, but are monitored within scheduled time periods.
Keywords: continuous surface wave test, CSW, soil stiffness, non.linear analysis, foundation settlement
INTRODUCTION
Changes in the material and/or geometric properties of a structural or mechanical system, including the changes in the boundary conditions and system connectivity, are defined as 'damage' that adversely affects the current or future performance of that system. Implicit in this definition is a comparison between two different states of the system (Farrar & Doebling 1999).
Structural health monitoring (SHM) is a procedure targeted at providing accurate and real-time information about the performance and health state of a structure. SHM includes an approach to the process of characterising and detecting damage of engineering structures. The objective of SHM is to monitor the in situ behaviour of a structure accurately and efficiently, to evaluate its performance under various service loads, to discover areas subject to damage or weakening, and to determine the health or condition of the structure (Czichos 2013). In the area of SHM, the term 'damage' in mechanical structures can be understood intuitively as denoting a defect or failing that impairs the functional behaviour and working conditions of engineering structures. The modification to material properties or structural physical parameters can also be considered as damage (Tadeusz et al 2013).
The main damage detection approaches may have some limitations. For example, the mode shape approach is only sensitive in the case where the measurement point is close to the node points (see Figure 4) for a particular mode (Liang & Chan 2009).
Salawu and Williams (1995) conducted modal tests of a full-scale bridge before and after rehabilitation, and determined that the variation in natural frequencies of the bridge was not only due to structural repairs, although both modal assurance criterion (MAC) and the coordinate modal assurance criterion (COMAC) performed well to indicate the location of the repairs.
Doebling and Farrar (1996) pointed out that the frequency shift method has considerable practical limitations for civil structures, because it is insensitive to damage unless when there is severe damage or an accurate measurement is applied. On the other hand, the frequency response function approach is insensitive to the damage unless severe damage has occurred or accurate measurement of vibration was done. The inverse method is at present still only being investigated theoretically (Friswell 2008).
For the curvature/strain modes approach, Pandey et al (1991) demonstrated that the damage to beam structures can be identified using mode shape curvature. Chance et al (1994) found the measured strain mode shape to be much more feasible for damage localisation. But recording strain over the whole structure is not yet feasible with current technology; therefore, a new methodology and equipment are needed.
Stubbs et al (1992) presented the pioneering work on using modal strain energy for damage localisation. However, when the damage is located in a structural element that is not sensitive to the modal parameter changes, the modal strain energy approach cannot detect the damage in such an element in a structure. On the other hand, for the dynamic flexibility approach based on higher vibration modes rather than lower modes, a large number of dynamic modes are needed to find a stiffness matrix estimation or its changes, and mainly the higher modes need to be measured. However, measuring the higher frequency response is very difficult to do because of practical limitations (Sinou 2009). From a testing standpoint, exciting the higher frequency response of a structure requires more energy to produce a measurable response at these higher frequencies than at the lower frequencies. Koh et al (2006) demonstrated a method called condensed model identification for identification of full stiffness matrices for damage assessment based on incomplete measurement. They used three types of reduction methods, namely static condensation, dynamic condensation, and System Equivalent Reduction Expansion Process (SEREP) methods.
Pokharkar and Shrikhande (2010) used the same Koh et al (2006) approach with the mass-invariant constraint for the identification of condensed models in different time windows. Both studies used the input and output data to develop mathematical models to characterise the input-output behaviour of an unknown system by means of experimental data, which was acceleration within their studies.
For all the above-mentioned methods, input and output data are needed to identify the location and severity of damage, while the present study indicates the damage and its location for incomplete measurement using the output data only. The present method requires fewer sensors than the above-mentioned methods. The method is also a useful tool in that it evaluates the structure using real-time acceleration measurements.
The two-points condensation (TPC) technique reduces the whole structure stiffness matrix to a set of two-degrees-of-freedom matrices. The identified stiffness matrices Kcare compared with the undamaged reduced stiffness matrices Kr By observing the changes in the stiffness matrix coefficients of the two-degree-of-freedom systems, the damage location can be obtained. In the TPC technique, the identified stiffness matrix Kccan be obtained by optimising the equation of motion using the measured test data. The stiffness matrix of the undamaged structure Kris obtained by reducing the theoretical stiffness matrix of the structure.
In this study, the theoretical stiffness matrix Kois generated using data from the design drawings of the structure. SEREP is used to condense the matrices required in the TPC technique. To verify the efficiency of the technique, two cases are studied:
■ For the first case, the influence of the position of the vibration sensors relative to the damage location is studied.
■ For the second case, the sensitivity of the technique to the size of the damage is studied.
TWO-POINTS CONDENSATION (TPC) TECHNIQUE
The TPC technique is an analytical method that detects structural damage by observing the value of changes in the stiffness matrix coefficients. The technique compares the reduced theoretical stiffness matrix Kr with the identified stiffness matrix Kc. For modelling the beam in the MATLAB/Octave environment, the consistent mass matrix and the Euler-Bernoulli beam element stiffness matrix are used (Reddy 2006).
The theoretical stiffness matrix Kois obtained using the as-built drawings of a structure. The reduced theoretical stiffness Kris generated by condensing the theoretical stiffness matrix Koto a two-degrees-of-freedom (2-DOF) stiffness matrix. The selection of these degrees of freedom corresponds to the vibration acceleration measurement sensor locations.
In this technique the SEREP method is used to reduce the stiffness and mass matrix to 2-DOFs. The SEREP condensation has the best computational performance and leads to smaller errors in the identification of stiffness values (Koh et al 2006).
The TPC technique calculates the identified stiffness matrix Kcby finding the optimal solution of the equations of motion, which should correspond to the real system properties (the mode shapes and frequencies).
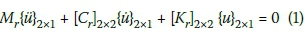
Where:
Kr= The stiffness matrix of the reduced system
Mr= The mass matrix of the reduced system Cr= The damping matrix of the reduced system
ü = The acceleration vector
ú = The velocity vector
u = The displacement vector.
In this technique, the input data includes the reduced mass matrix Mrand initial stiffness matrix Krin addition to the corresponding vectors of acceleration ü, velocity u, and displacement u. The first and second measured modal frequencies are part of the input data and are used to calculate the damping coefficients and control the solution of finding the identified (reduced) stiffness matrix.
The technique uses the theoretical mass matrix of the structure because it does not generally change (Pokharkar & Shrikhande 2010). The damping matrix C is calculated according to Rayleigh damping. The damping matrix is optimised due to the stiffness updating. The optimisation solver minimises the function given in Equation 2, which is based on the equation of motion.
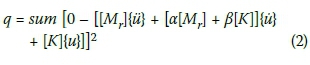
Where a and β are the damping coefficients (see "Damping matrix" section below). This technique uses the multi-objective function solver to find the optimal solution of the function given in Equation 2. MATLAB code was developed to analyse the beam based on the steps outlined in Figure 1.
The comparison of the identified stiffness matrices Kcand reduced theoretical stiffness
matrices Kris used to locate the damage. Large changes in the stiffness coefficients of the 2-DOF matrices indicate the location of the damage. The changes in the stiffness matrix are shown in Equation 3.
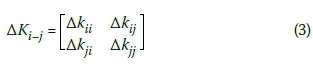
Where:
ΔK;_y = the change matrix of the set of nodes i and j
Δku= the difference in the coefficients of the Kcmatrix and the Krmatrix at position (i, i)
Δk„ = the difference in the coefficients of ij
the Kcmatrix and the Krmatrix at position (i, j)
Δk„ = the difference in the coefficients of ji the Kcmatrix and the Krmatrix at position (j, i)
Δkjj = the difference in the coefficients of the Kcmatrix and the Krmatrix at position (j, j).
When large changes are observed by comparing with Δkjj, the location of the damage can be determined. If Δkiiis greater than Δkjj, it means that the damage is located near to the node i.
Analytical reduction of system matrices using SEREP method
From an analytical approach standpoint, the finite element method assumes that a continuous structure can be discretised by describing it as an assembly of finite elements, each with a number of boundary points that are commonly referred to as nodes. The main problem to overcome in SHM and damage detection is the typical mismatch of the selected number of degrees of freedom of an analytical and an experimental representation of a structural dynamic system.
For damage detection, the concept of model reduction (or, alternatively, model expansion) plays an important role. Using condensation or expansion, it is possible to compare a large analytical set of DOFs to a relatively small set of experimental DOFs. Reduction and expansion also play a very important role with regard to model updating. Consequently, the set of the tested DOFs requires reducing the number of DOFs of a large model without losing any information or characteristics of the dynamic system in the modelling process.
The SEREP condensation method partitions the degrees of freedom into a set of slave DOFs and master DOFs. The DOFs are arranged to place the slave DOFs as the first s coordinates, while the remaining master DOFs are the last m coordinates (Friswell & Motiershead 1995). Here the coordinates represent the location of sub-matrices in the original matrix.
The reduction of the stiffness matrix is thus accomplished by identifying those degrees of freedom to be condensed or reduced as slave degrees of freedom, and to express them in terms of remaining master degrees-of-freedom.
The dynamic equations of equilibrium for an undamped n degree-of-freedom model may be written as:

Where: Ü(t) and U(t) are the acceleration and displacement response vectors. The displacement response vector U(t) in Equation 4 can be expressed as shown in Equation 5 using the mode superposition method:

in which Φ is the complete eigenvector matrix of the full model, and q(t) is the modal coordinate vector. It is well known that the computation of the complete eigenvector matrix is not required for a large model. Therefore, modal truncation is usually used in the mode superposition technique (Qu 2004). If p eigenvectors of the full model are used in the mode superposition, Equatioin 5 is rewritten as:

With the arrangement of the total degrees of freedom, Equation 6 may be partitioned as:
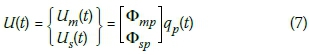
This is equivalent to two equations (8 and 9):
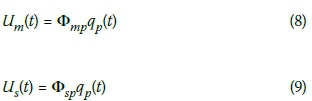
Equation 8 provides a description of the displacement responses at the master DOFs in terms of the eigenvector matrix at these DOFs. The sub-matrix <Dmp is generally not a square matrix. Since the number of knowns in Equation 8 are greater than the number of unknowns, Equation 8 can be put into a normal form by transforming this equation as:

Substituting Equation 8 into Equation 10 produces:
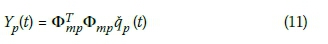
in which 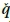 p(t) is an approximate solution of qp(t) (O'Callahan et al 1989). Although the square coefficient matrix of
p(t) is an approximate solution of qp(t) (O'Callahan et al 1989). Although the square coefficient matrix of 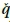 p(t) will in general be of full rank and possess an inverse, the determining of the inverse of this matrix using standard methods may encounter some numerical difficulty, and singular-value decomposition solution is usually required. Symbolically
p(t) will in general be of full rank and possess an inverse, the determining of the inverse of this matrix using standard methods may encounter some numerical difficulty, and singular-value decomposition solution is usually required. Symbolically 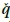 p(t) could be solved from Equation 11 as:
p(t) could be solved from Equation 11 as:
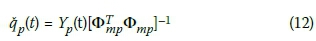
Substituting Equation 10 into Equation 12 produces the general form of the solution of the modal coordinates in terms of physical coordinates and modal matrix as:

Where 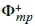 is the generalised inverse of matrix Φmp and is defined as:
is the generalised inverse of matrix Φmp and is defined as:
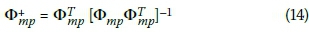
Equation 13 represents the "best" solution of the p variables given in Equation 8. For convenience, the solution qP(t) of Equation 8 can be approximated by qp(t), (Qu 2004):

Substituting Equation 15 into Equation 9 leads to:

When the dynamic condensation matrix is available (Equation 17), the coordinate transformation matrix T may be given by the following (Kammer 1987):

The coordinate transformation matrix is obtained by substituting Equation 15 into Equation 7:
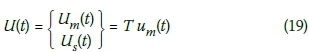
Where:
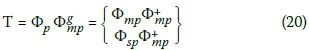
Using the coordinate transformation in Equation 20, the reduced system matrices are given by:

Due to its significant numerical computational advantages, the SEREP condensation method is often used in commercial FEM packages.
Damping matrix
Udwadia (2009) discusses non-proportional damping in linearly damped vibrating systems in which the stiffness and damping matrices are not restricted to being symmetric and positive-definite in simple systems with two-degrees-of-freedom; they conclude that if the system has an active element, as commonly arises in the active control of a structure, the stability is more difficult to physically interpret, and their approximation by damping matrices that commute with the stiffness matrices needs to be carried out with considerable care and caution. In this study, as there is no active element, proportional damping is taken into consideration.
The damping matrix is calculated using Rayleigh damping where the damping is defined as being proportional to the mass and the stiffness of the structure (Chopra 2012):

The damping ratio for the nth mode of such a system is:

The coefficients α and β can be determined from damping ratios of the ithandjh modes respectively: ξi; and ξj respectively. Expressing Equation 24 for these two modes in matrix form leads to:
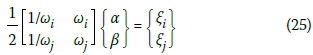
These two algebraic equations can be solved to determine the coefficients α and β. Seeing that the damping matrix is proportional to the mass and stiffness matrices, the change in the damping matrix due to the change in the stiffness is taken into account.
The damping ratios ξi and ξi for the first mode and second mode are calculated using the half-power bandwidth method using Equation 26 (Silva & Clarence 2000):

The angular frequency ωn for each mode is obtained by using a Fast Fourier Transform technique (FFT) (Monson 1996). By plotting the Fourier amplitude spectra of the signals recorded, the frequencies associated with the modes of vibration of the structure are located at the corresponding vibration amplitude peak values.
As shown in Figure 2, the angular frequencies ω2and ω1 are obtained by finding the corresponding angular frequencies for the amplitude that is equal to the amplitude at ωndivided by 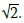 .
.
Signal integration
To obtain the velocity and displacement required for the equation of motion, the trapezoidal rule for numerical integration is applied to acceleration data, where: New area = area so far + increment of the area The increment of the area is the trapezoidal approximation, i.e. the half sum of the parallel sides times the perpendicular distance (Leis 2011), as illustrated in Figure 3.
Optimisation technique
Multi-objective optimisation is a mathematical optimisation technique used to optimise more than one objective function simultaneously. In this study, a multi-objective optimisation technique is used to optimise the equation of motion used in the TPC technique.
The problem of reducing a set of nonlinear functions Fi(x) subject to a set of goals 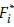 is addressed by the MATLAB/ Octave code developed. The maximum of
is addressed by the MATLAB/ Octave code developed. The maximum of 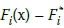 is minimised by the unscaled goal attainment problem. The algorithm coded is used to find x to minimise the maximum of
is minimised by the unscaled goal attainment problem. The algorithm coded is used to find x to minimise the maximum of 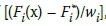 , where the weighting variables wtare a given positive value. The solution is controlled by the given lower and upper limits of the solution, where lower limit < x < upper limit (Edward et al 2011). The TPC technique finds the best stiffness value to satisfy the function given in Equation 2, as well as the corresponding frequencies. The initial inputs are as follows:
, where the weighting variables wtare a given positive value. The solution is controlled by the given lower and upper limits of the solution, where lower limit < x < upper limit (Edward et al 2011). The TPC technique finds the best stiffness value to satisfy the function given in Equation 2, as well as the corresponding frequencies. The initial inputs are as follows:
1. The reduced theoretical stiffness matrix.
2. The reduced mass matrix.
3. The acceleration, velocity and displacement vectors.
4. The first mode and second modal frequencies.
5. The damping ratios of the first two modal frequencies.
6. To determine the upper limit and lower limit of the solution, it is assumed for this study that the stiffness degradation is between 140% and 80%, respectively.
7. A goal function value of zero is used in order to get the optimal value of K in the function given in Equation 2.
8. Weighting function values of unity are used in this study.
The technique uses the reduced theoretical stiffness matrix as a starting point where the solver finds the best stiffness matrix values that satisfy the equation of motion and the associated modal frequencies.
The output of the solution process is the identified (optimised) stiffness matrix. Kcis then used for comparison purposes to locate the damage.
EXPERIMENTAL STUDY
The structural system used in this study is a simply-supported steel beam with a span of 2.3 m. The cross-section of the beam is a rectangular section of 100 mm by 21.9 mm. The material properties of the beam are as follows:
Mass density = 7 850 kg/m3
Young's modulus E = 205.9 GPa
The experimental setup is shown in Figure 4.
Damage in the form of stiffness degradation is introduced into the beam by welding a plate (100 mm x 500 mm) with a thickness of 3.8 mm at a distance of 450 mm from the left beam support. The material properties of the plates are the same as the material properties of the beam. The change in thickness leads to change in the stiffness of a part of the beam.
For modelling the beam in the MATLAB/ Octave environment, the consistent mass matrix and the Euler-Bernoulli beam element stiffness matrix are used (Reddy 2006). In order to apply the technique, the beam is divided into five segments, as shown in Figure 5(a). The damaged segment is located between points 2 and 3, as shown in Figure 5(b).
The DOFs considered in the model are vertical displacements and rotations at each node. The DOFs (θVθ2, θ3, θ4, θ5and θ6) refer to the rotations, where the DOFs (v2, V3, V4 and V5) refer to the vertical displacements.
For the damaged beam prototype, four accelerometers are placed at points 2, 3, 4 and 5 of the beam, as shown in Figure 5(c). The mass of each accelerometer including the clamping apparatus is 0.88 kg. These masses are added to the global mass matrix of the system as lumped masses at the nodes where the accelerometers are located. It is essential to collect sufficient data to establish the correct mass matrix by visual inspection of the model and to use the applicable shop drawings.
The motion of the beam is initiated by using a pullback-quick release method by tying a rope to the middle of the beam span and then cutting it after having pulled it downwards.
Figures 6(a) and 6(b) show the acceleration data captured during the test, as well as the velocity and displacement signals obtained by integrating the acceleration signals obtained from the four channels using the trapezoidal method. The acceleration data is collected at a sampling rate of 500 Hz.
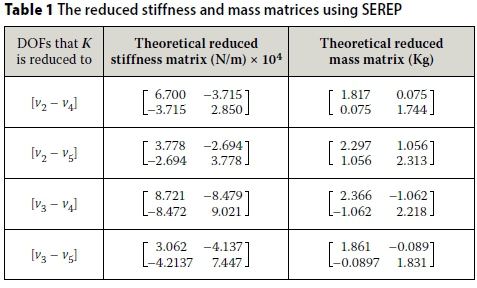
To apply the damage detection algorithm developed, as described in this paper, the theoretical stiffness matrix Koand mass matrix M of the system are reduced to two DOFs using the SEREP method. The DOFs are selected to cover all the possible combinations of vertical DOFs. The selected DOFs are v2- v4, v2- v5, v3- v4, and v3 - v5. The resultant matrices for the condensed structural system are given in Figure 7.
Using the SEREP condensation method, the reduced stiffness and mass matrices are produced for each set of two DOFs, as shown in Table 1.
By plotting the Fourier amplitude spectra and using Equations 23 through 26, the damping matrix, frequencies and damping ratios are calculated. Figure 8 shows the Fourier amplitude spectra for the first three frequencies for the measured values for the four channels of the five-segment beam model. The frequency of the first mode for all nodes is 9.4 Hz, while the damping ratio is 0.0185. The second mode has a frequency of 38 Hz, and the damping ratio is 0.0681.
The identified stiffness matrix Kc, which is obtained as output from the optimisation, is compared with the reduced theoretical stiffness matrices Kr. The comparison is based on Equation 3. The results of the comparison between (Kc) and (Kr) are provided in Table 2. The solution is checked by comparing the frequencies computed from the analytical model to that of the physical structural system (see Figure 1).
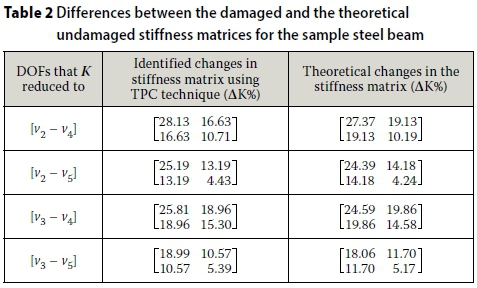
The results in Table 2 show that the large percentage changes in coefficients of the stiffness matrix occur at coefficients of nodes that are near to the location of the damage.
For the condensed stiffness matrix Kv2-v4 using DOFs (v2- v4), the percentage change in coefficient kV2V2 is larger than the change in coefficient kV4V4. This indicates that the damage is located near to node 2 rather than near to node 4. The same conclusion can be established from ΔK for DOFs v2 - v4, v2- v5, v3- v4, and v3- v5( see Table 2 column 1).
The effect of acceleration sensor positioning
For this first case study, the effect of the position of the sensors relative to the damage location is investigated. To determine the effect of sensor positioning, the same beam described above is divided into six segments of equal length (Figure 9).
Five accelerometers are placed at the intermediate points 2, 3, 4, 5 and 6. The damaged segment is located between points 2 and 4, as shown in Figure 9(a). The degrees of freedom θ1,θ2, θ3, θ4, θ5, θ6 and θ7refer to the rotations, while the degrees of freedom v2, v3, v4, v5and v6refer to the vertical displacements, as shown in Figure 9(b). The acceleration data is collected using a sampling rate of 500 Hz. Figure 10 shows the recorded vertical acceleration signals, velocity signals, and displacement signals. These signals are for the degrees of freedom v2, v3, v4, v5and v6 respectively.
In this test, the global stiffness matrix is reduced to the following DOFs: ([v2- v4], [v2- v5], [v3- v4], [v3- v5] and [v4- v5]). The initial value for the stiffness matrix used is the undamaged theoretical stiffness matrix. The damping parameters are calculated in the same way as that of the previous example. Table 3 shows a comparison of the results for the theoretical coefficients of the condensed stiffness matrices and the coefficients calculated using the TPC technique.
For the first result of DOFs [v2- v4], both the nodes (2, 4) are located outside the damaged area. Node 2 is closer than node 4 to the damage area, which explains the large change that occurs in the coefficient kv2v2 The result for [V3- V4] shows the large changes concentrated in k V3V3 rather thankV3V3 because node 3 is located at the damaged segment, while node 4 is outside the damaged segment.
The result of [V4- V5] indicates the damage at the left side of the segment; both nodes are, however, outside the damaged segment. The result of [v4- v5] provides a good indication of the location of damage.
sensitivity of the TPC technique for damage extent
The sensitivity of the technique to indicate the extent of damage is investigated by reducing the size of the damaged area. The same beam shown in Figure 5 is considered here. For this case, the damage size is reduced by cutting a piece off the plate. The width of the plate remains the same, but the length of the plate representing the damage is now reduced to 430 mm, 360 mm, 290 mm, 210 mm and 170 mm, as shown in Figure 11.
A 500 Hz sampling rate is used for all tests, and the global stiffness matrices are reduced to the following DOFs: ([v2 - v4], [v3 - v4] and [v3 - v5]. The recorded signals are pre-processed, and the results of five tests using the TPC technique are shown in Table 4.
The percentage differences of the values of the coefficients of the stiffness matrices indicate the stiffness degradation caused by the structural damage. The bigger difference between Kiiand Kjjfor any given i and j indicates the damage location.
The results shown in Table 4 demonstrate that the technique is successful to find the location of the damage in the beam, even if the damage is small. Investigating the results of all tests for one set of points can indicate the ability of the technique to reflect the degradation in stiffness.
CONCLUSIONS
This study investigated the changes in the stiffness due to the presence of structural damage. Experimental studies using the two-points condensation technique (TPC) were described. The approach using TPC represents a non-destructive test method that uses vibration signal records to identify the structural damage according to the measured changes in dynamic characteristics of the structure.
The experimental results obtained from a steel beam model structure demonstrate the usefulness of the TPC technique. This method has several advantages:
■ The concept is simple and easy to apply without using complex calculations.
■ Using the TPC technique, the structure is reduced to a 2-DOF structure; this decreases the volume of data to be captured and the volume of data to be dealt with at a time. Using more tests will help to obtain more precise values for the change in stiffness coefficients and improve damage location.
■ Accuracy is achieved in detecting the location of the damage where the TPC technique results have demonstrated good agreement with actual results.
The results indicate that the TPC technique is capable of indicating the damage location for different sizes of damage. According to the damage size sensitivity tests, the technique can show stiffness degradation. Additionally, experimental results demonstrate that the SEREP reduction method is suitable for use with the TPC technique. The damping effect has to be accounted for to ensure accurate results when applying this solution technique.
Finally, the TPC technique shows the location of damage regardless of the place of the acceleration sensors or the size of the damage. The technique finds the location of damage when the acceleration sensors are near to the damage, as well as when they are far from the damage.
LIST OF ACRONYMS
COMAC Coordinate Modal Assurance Criterion
DOF Degrees Of Freedom
FFT Fast Fourier Transform
FEM Finite Element Method
MAC Modal Assurance Criterion
SEREP System Equivalent Reduction Expansion Process
SHM Structural Health Monitoring
TPC Two-Points Condensation Technique
LIST OF SYMBOLS
α, β Damping coefficients
Φi The rotational degrees of freedom at node i
vtThe degrees of freedom of vertical displacements at node i
ξ η The damping ratio for the nth mode
ξι Damping ration of mode ith
ξ·: Damping ration of mode jth
Φ The complete eigenvector matrix of the full model
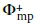 The generalised inverse of matrix ω η The angular frequency
The generalised inverse of matrix ω η The angular frequency
C Damping matrix
CrDamping matrix of the reduced system
K Globel stiffness matrix
KoTheoretical stiffness matrix
KcIdentified stiffness matrix
KrUndamaged reduced stiffness matrix
AK- The change matrix of the set of nodes and j
ΔküThe difference in the coefficients of the Kcmatrix and the Krmatrix at position (ι, ι)
Δk„ The difference in the coefficients of the Kcmatrix and the Krmatrix at position (i , j)
Δkji The difference in the coefficients of the Kcmatrix and the Krmatrix at position (j, ι)
Δkjj The difference in the coefficients of the Kcmatrix and the Krmatrix at position (j, j)
M Globel mass matrix
MrMass matrix of the reduced system
q(t) The modal coordinate vector
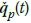 Approximate solution of δp(t)
Approximate solution of δp(t)
u Displacement vector
ü Velocity vector
ü Acceleration vector
Ü(t) Acceleration response vectors
U(t) Displacement response vectors
T The coordinate transformation matrix
REFERENCES
Chance, J E, Worden, K & Tomlinson G R 1994. Processing signals for damage detection in structures using neural networks. Proceedings, SPIE 2191, Smart Structures and Materials, 187. [ Links ]
Chopra, A K 2012. Dynamics ofStructures: Theory and Applications to Earthquake Engineering, 4th ed. Harlow, UK: Pearson Education. [ Links ]
Czichos, H 2013. Handbook of Technical Diagnostics Fundamentals and Application to Structures and Systems. Berlin, Heidelberg, Germany: Springer Verlag. [ Links ]
Doebling, S W & Farrar, C R 1996. Computation of structural flexibility for bridge health monitoring using ambient modal data. In: Lin, Y K & and Su, T C (Eds.), Proceedings, 11th ASCE Engineering Mechanics Conference held at Fort Lauderdale, FL, 20-22 May 1996. New York: ASCE Press, 1114-1117. [ Links ]
Edward, B M, Shapour, A & Balakumar, B 2011. An Engineer's Guide to MATLAB, 3rd ed. Upper Saddle River, NJ: Pearson Education. [ Links ]
Farrar, C R & Doebling, S W 1999. Damage detection and evaluation. II: Field applications to large structures. In: Silva, I M M & Maia, N M M (Eds.), Modal Analysis and Testing, NATO Science Series E, Vol. 363, London: Kluwer Academic Publishers, 345-378. [ Links ]
Friswell, M I & Motiershead, J E 1995. Finite Element Model Updating in Structural Dynamics. Dordrecht, Netherlands: Springer Science & Business Media. [ Links ]
Friswell, M I 2008. Damage Identification using Inverse Methods. Vol. 499 of the series CISM International Centre for Mechanical Sciences. Vienna, New York: Springer Verlag, 13-66. [ Links ]
Kammer, D C 1987. Test-analysis model development using an exact modal reduction. International Journal of Analytical and Experimental Modal Analysis, 2(4): 174-179. [ Links ]
Koh, C G, Tee, K F & Quek, S T 2006. Condensed model identification and recovery for structural damage assessment. Journal of Structural Engineering, ASCE, 132: 2018-2026. [ Links ]
Leis, J W 2011. Digital Signal Processing Using MATLAB for Student and Researchers, 1st ed. New York: Wiley. [ Links ]
Liang, W & Chan, T H T 2009. Review of vibration- based damage detection and condition assessment of bridge structures using structural health monitoring. Paper presented at the 2nd Infrastructure Theme Postgraduate Conference: Rethinking Sustainable Development: Planning, Engineering, Design and Managing Urban Infrastructure, 26 March 2009, Brisbane, Australia. [ Links ]
Monson, H H 1996. Statistical Digital Signal Processing and Modeling, 1st ed. New York: Wiley. [ Links ]
O'Callahan, J, Avitabile, P & Riemer, R 1989. System equivalent reduction expansion process (SEREP). Proceedings, 7th International Modal Analysis Conference, Las Vegas, NV, 30 January - 2 February 1989, 29-37. [ Links ]
Pandey, A K, Biswas, M & Samman, M M 1991. Damage detection from changes in curvature mode shapes. Journal of Sound and Vibration, 145(2): 321-332. [ Links ]
Pokharkar, P V & Shrikhande, M 2010. Structural health monitoring via stiffness update. ISET Journal of Earthquake Technology, 47(1): 47-60. [ Links ]
Qu, Z-Q 2004. Model Order Reduction Techniques with Applications in Finite Element Analysis, 1st ed. London: Springer Verlag. [ Links ]
Reddy, J N 2006. An Introduction to the Finite Element Method, 3rd ed. New York McGraw-Hill. [ Links ]
Salawu, O S & Williams, C 1995. Bridge assessment using forced-vibration testing. Journal of Structural Engineering, 121(2): 161-173. [ Links ]
Silva, D & Clarence, W 2000. Vibration Fundamentals and Practice. Boca Raton, FL: CRC Press. [ Links ]
Sinou, J J 2009. A Review of Damage Detection and Health Monitoring Mechanical Systems from Changes in the Measurement of Linear and Non linear Vibrations. Hauppauge, NY: Nova Science Publishers, 643-702. [ Links ]
Stubbs, N, Kim, J T & Topole, K 1992. An efficient and robust algorithm for damage location in offshore platforms. Proceedings, ASCE 10th Structures Congress, 13-15 April 1992, San Antonio, TX, 543-546. [ Links ]
Tadeusz, S, Tadeusz, U & Wieslaw, S 2013. Advanced Structural Damage Detection. New York: Wiley. [ Links ]
Udwadia, F E 2009. A note on nonproportional damping. Journal of Engineering Mechanics, 135(11): 1248-1256. [ Links ]
 Correspondence:
Correspondence:
A N Al-Qayyim
Engineering Affairs Department
University of Babylon Babylon Iraq
T: +964 780 041 8990
E: ahmed_alqayyim@yahoo.com
B Ö Çağlayan
Department of Civil Engineering
Istanbul Technical University Sariyer
Istanbul 34469 Turkey
T: +90 212 285 6561
E: caglayan@itu.edu.tr

DR AHMED AL-QAYYiM is a lecturer at the University of Babylon. He obtained his Bachelor's and Master's degrees in Civil Engineering from the University of Babylon in Iraq, and his PhD from Istanbul Technical University. His field of work includes structural health monitoring, signal processing, damage detection of structures, system identification, and nonlinear analysis of structures. His experience includes assessments for more than 40 railway bridges, as well as design, construction, and management of large structures for water and wastewater treatment plants, bridges and multi-storey buildings.

PROF BARLAS ÇAGLAYAN is Assistant Professor and senior lecturer and researcher at Istanbul Technical University (ITU). He obtained his BEng, MSc and PhD degrees in Civil Enginering from ITU. He gained experience in testing structures, system identification and structural fatigue through the NATO Science for Stability Programme research projects between 1990 and 1996. Since 1992 he has tested more than 200 railway bridges and building structures in Turkey and abroad. The focus areas of his work over the past decade include structural health monitoring, damage detection, earthquake engineering and post-earthquake structural damage evaluation.














