TECHNICAL PAPER

 

Numerical modelling of flexible pavement incorporating cross-anisotropic material properties. Part I: Surface circular loading

 

 

J W Maina; F Kawana; K Matsui

Correspondence

 

 

---

ABSTRACT

Accurate numerical modelling of the behaviour of road pavement layers is an important requirement for the design and evaluation of road pavements. This modelling includes the prediction of pavement performance under the action of traffic loading and environmental factors. Depending on the complexity of the models, properties of pavement layers that may be considered are wide-ranging - from linear or nonlinear elastic to cross-anisotropic through to linear visco-elasto-plastic. Some properties, such as cross-anisotropic, are not only related to placement and compaction of the pavement layers, but are also inherent to the materials used. Other properties, such as linear visco-elasto-plastic, are specific to asphalt concrete and depend on the speed and magnitude of traffic loading, as well as the environment (temperature) in which the road is located. This paper presents basic theoretical derivation of numerical modelling of a flexible pavement considering cross-anisotropic material properties (with isotropic properties as a special case). The solutions derived in this paper are based on Hankel transformation of Navier's equations. The accuracy and validity of the solutions are verified through comparisons with a proprietary finite element method (FEM) package. For this purpose, a pavement structure composed of five main layers constituted by isotropic and cross-anisotropic (also known as transversely isotropic) material properties is analysed. In order to vary some of the layer properties with depth, the main layers were sub-layered, resulting in a 17-layer pavement system.

Keywords: pavement, linear-elastic analysis, transversely isotropic, cross-anisotropy, isotropic, circular loading

---

 

 

BACKGROUND INFORMATION

To support the movement of people and goods, as well as access to education and training, employment and health care, a sound road network - which in South Africa is most often designed and evaluated using the South African Pavement Design Method (SAPDM) - plays a key role in the socio-economic development of a country. South Africa, in the recent past, has experienced considerable growth in both passenger and freight traffic volumes because of increased economic activities. The high level of truck traffic is causing premature failures, mostly on provincial and municipal road networks.

The South African National Roads Agency Ltd (SANRAL) teamed up with the roads industry, the Council for Scientific and Industrial Research (CSIR) and academia in an effort to improve the SAPDM and the design of roads in South Africa. The partnership called for skills development and the building of capacity to optimise design, maintenance and repair strategies against road (premature) failures. To achieve this, a better understanding of the properties of materials used in road constructions and modelling of structural behaviour of pavements was deemed necessary.

The SAPDM, which uses multilayer linear elastic (MLLE) theory to determine pavement structural responses, was introduced in the late 1960s and early 1970s. Since its introduction, developments in material characterisations and numerical modelling have taken place. In addition, advanced computer software and hardware make it possible now to determine the stress/strain/displacement distributions of pavements under surface loading in a matter of seconds.

This paper presents the outcome of the efforts to improve the standard pavement analysis for circular surface loading by introducing capability to consider cross-anisotropic material properties (with isotropic as a special case). This capability is not possible in the current SAPDM software. After rigorous validation and verification, software resulting from this development has now become the analysis engine of the new SAPDM, and it will be used when the loading on the surface of the road pavement is circular in shape.

 

MOTIVATION FOR INCORPORATING CROSS-ANISOTROPIC PROPERTIES

Cross-anisotropy is the most prevalent but less considered type of materials properties in pavement layers. In this regard, the elastic properties in the lateral and vertical directions are considered to be different. The road construction process involves directional rolling compaction of materials, which invariably results in different mechanistic properties in vertical and horizontal directions (Masad et al 2006). A cross-anisotropic material has a vertical axis of symmetry of rotation, i.e. the elastic properties are equivalent in all directions perpendicular to the axis of symmetry (horizontal or radial direction). In general, these properties are different from those in the direction parallel to the axis (vertical direction).

In engineering mechanics, cross-anisotropy of an elastic material is defined by five independent elastic constants - two elastic moduli in vertical and horizontal directions (E_vand E_h), two Poisson's ratios in vertical and horizontal directions (v_vhand v_hh) and one shear modulus (G_hv) as presented by Love (1944). Several experiments have also proven the existence of cross-anisotropic properties in pavement layers, and these properties have been measured in the laboratory (Correia 1999; Adu-Osei et al 2001; Tutumluer et al 2003; Masad et al 2006). Typically, the level of cross-anisotropy is characterised by the ratio of the horizontal to vertical modulus (E_h/E_v). In contrast, isotropic materials have the same elastic properties in both the vertical and horizontal directions, which are described by three independent elastic constants: E, v and G.

The importance of incorporating cross-anisotropic material property in the pavement analysis was demonstrated by Masad et al (2006), who showed how the accuracy of calculated pavement displacements improved when the aggregate base layer was considered to be cross-anisotropic. In their study, Masad et al (2006) used a Finite Element (FE) program to calculate pavement surface displacements, and compared their results with measured values from 246 different sections in the Association of American State Highway Officials (AASHO) road test. The study revealed that the displacements calculated using isotropic material properties tended to be smaller than measured displacements in the field. Further analysis showed that the errors between measured and calculated responses were minimised when the elastic modulus in the horizontal direction was assumed to be 30% of the elastic modulus in the vertical direction (E_h/E_v= 0.3). Also, the findings seem to be in agreement with results reported in another study on the level of anisotropy (E_h/E_V) of unbound and chemically stabilised aggregate systems (Salehi-Ashtiani et al 2008).

Other researchers such as Emeriault and Chang (1997), and Masad et al (2004) have also used the micromechanics theory to determine cross-anisotropic properties of granular base materials. Adu-Osei et al (2001) used the linear elastic theory coupled with system identification to develop a testing system, in a triaxial test setup, that could identify the five parameters that represent cross-anisotropic properties of unbound materials. This test was developed in a collaborative research between the universities of Illinois and Texas, whereas the field validation data was collected from a full-scale pavement test study conducted at Georgia Tech (Georgia Institute of Technology). The validation of the anisotropic modelling approach was accomplished by analysing conventional flexible pavement test sections, where the GT-PAVE finite element program was used to predict responses to loading in an unbound aggregate base layer, and compared these predicted responses to the measured values (Tutumluer et al 2003). Wang and Liao (1999) listed and meticulously summarised the numerous studies for cross-anisotropic half-space subjected to different types of loading, such as line loads, circular loads, parabolic loads, ring loads, and varying rectangular loads.

 

THEORETICAL DEVELOPMENT

Linear elasticity

Because of azimuthal symmetry for circular surface loading, responses present in axisym-metric elastic problems are displacements u = u(r,z),w = w(r,z) in horizontal, r- and vertical, z-directions respectively, normal stresses σ_r, σ_zand σ_θin the horizontal, r-and vertical, z- and circular, θ- directions respectively, as well as shear stress τ_rz on the r or z face in the respective z or r direction, as shown on Figure 1.

In this regard, the differential equilibrium equations in cylindrical coordinates may be expressed using modified Navier's Equations 1 and 2:

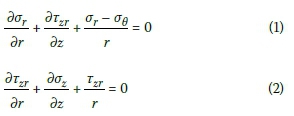
Corresponding axisymmetric strains may be expressed in terms of axisymmetric displacements as follows:

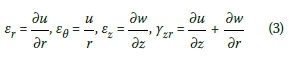
Generalised Hooke's law

In linear elasticity, if the stress is sufficiently small, Hooke's law is used to represent the material behaviour and to relate the unknown stresses and strains. The general equation for Hooke's law is given below:

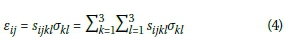
Where: i, j = 1, 2, 3

In this case S_ijkl is a fourth-rank tensor called elastic compliance of the material. Each subscript of s_ijkitakes on the values from 1 to 3, giving a total of 3⁴ = 81 independent components in s. However, due to the symmetry of both ε_ij and σ_kl, the elastic compliance s must satisfy the relation:

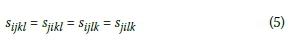
It follows from Equation 5, therefore, that the generalised Hooke's law presented in Equation 4 can be simplified to become:

Where: i, = 1,..,4

This relationship reduces the number of s components to 16, as seen in the following linear relation between the pseudovector forms of the strain and stress:

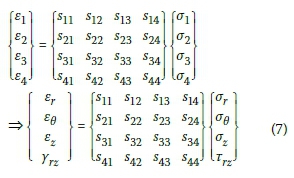
The s matrix in this form is also symmetric. It, therefore, contains only ten independent elements. The number of independent elements is obtained by counting elements in the upper right triangle of the matrix, including the diagonal elements (i.e. 1 + 2 + 3 + 4 = 10). Furthermore, if the material exhibits symmetry in its elastic response, the number of independent components in the compliance s matrix will be reduced even further.

For example, in the simplest case of isotrop-ic materials whose elastic moduli are the same in all directions, only three unique components (s₁₁, s₁₂, s₄₄) exist, as shown in Equation 8. In the elastic range, these three coefficients of the ordinary model require three parameters (elastic modulus E, Poisson's ratio v and shear modulus G) for their definitions as follows:

Where: s₁₁= 1/E, s₁₂= -v/E, s₄₄= 1/G, G = E/[2(1 + v)]

In cross-anisotropic materials, however, five unique components (s₁₁, s₁₂, s₁₃, s₃₃, s₄₄) exist, as shown in Equation 9. In the elastic range, these five components of the ordinary cross-anisotropic model require five parameters (E_v, E_h, v_hv, v_hh, G_hv) for their definitions (Love 1944).

Where: s₁₁ =1/Eh, s₁₂ =-vhh/Eh, s₁₃ =-vhv/Ev,

s₃₃ = 1/Ev, s₄₄ = 1/Ghv,

G_hv = E_v/[2(1 + v_hv)]

Writing the stresses in terms of the strains would require Equation 7 to be inverted, yielding:

Where: c_ij is a fourth-rank tensor called elastic stiffness of the material.

The stiffness and compliance matrices in Equation 10 are related in the following form:

Three components (c₁₁, c₁₂, c₄₄) exist for isotropic materials, whereas, in cross-ani-sotropic materials, five unique components (c₁₁, c₁₂, c₁₃, c₃₃, c₄₄) exist.

It should be noted that responses for a special cross-anisotropy case where E_v= E_hand v_vh= u_hhexist and will be similar to the isotropic case presented by Maina and Matsui (2004).

Equation 12 below shows the five components of the elastic stiffness c and Equations 13-17 define each of the five components:

Where:

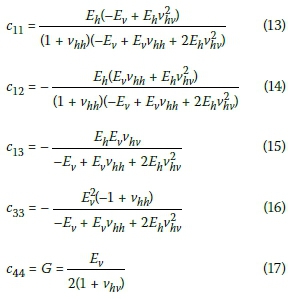
Substituting Equation 12 into 10 yields:

Expanding Equation 18 by expressing strains in terms of elastic displacement based on Equation 3 gives:

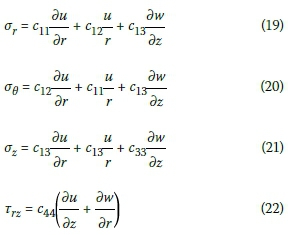
Substituting Equations 19-22 into Equations 1 and 2, with some rearrangement, will result in Equations 23 and 24:

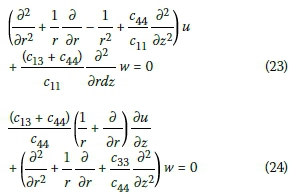
Derivation of displacement and stress solutions using Hankel transformation

One convenient way of deriving displacement and stress solutions is to use Hankel transformation (Miyamoto 1977; Sneddon 1951). In this regard, Hankel transformation of Equations 23 and 24 would yield, respectively:

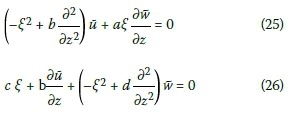
Where:

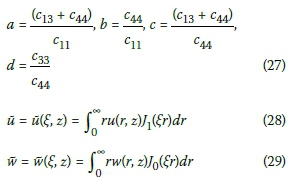
ū and 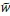are Hankel transformations of the displacements for u and w, whereas J₀(ξ_r) and J₀(ξ_r) are Bessel functions of first kind and order 0 and 1, respectively. ξ is the parameter of Hankel transformation corresponding to r. Equations 25 and 26 can be simplified by representing a differential function with respect to z as λ. The next step is to eliminate ü from the modified equations, and simplifying, resulting in:

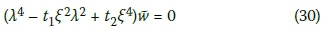
Where: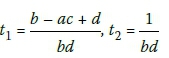

With the four roots, λ derived as:

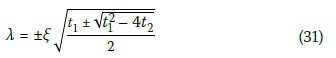
Putting back the differential function in Equation 30 yields:

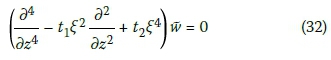
With reference to the roots in Equation 31, the solution form of Equation 32 depends on the sign of the coefficient: t₁² - 4t₂·

Furthermore, and this is very important, depending on the numerical integration methods used, it may be necessary to modify the solution for w to obtain stable and accurate responses of the pavement structure. The solutions presented hereunder were based on the numerical methods used in this research.

1. Solution 1: t₁² - 4t₂> 0, where E_h > E_v

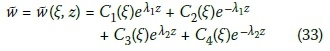
Where:

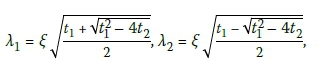
and C_l(ξ), C₂(ξ), C₃(ξ), and C₄(ξ) are coefficients of integration.

In order to obtain stable and accurate results of pavement responses, Equation 33 was modified to:

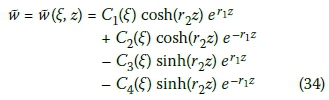
Where:

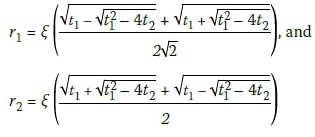
2. Solution 2: t₁²- 4t₂ = 0, where E_h = E_v

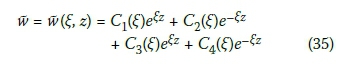
3. Solution 3: t² - 4t₂ < 0, where. E_h < E_v.

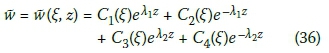
Where:

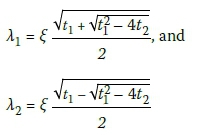
For stable and accurate results of pavement responses, it was necessary to modify Equation 36 to:

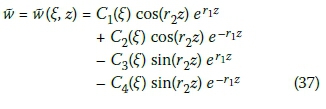
Where:

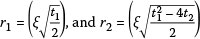
Boundary condition - vertical circular surface loading

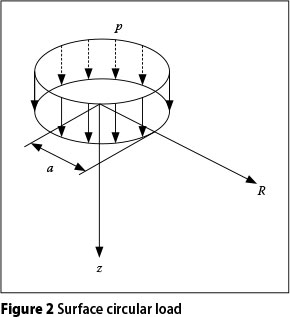
The boundary condition at the surface of the pavement considers an equilibrium between external and internal vertical and shear stresses. For the case shown in Figure 2, where there is only uniformly distributed vertical circular load P, whose radius is a on the road surface, the Hankel transformation of the equilibrium of internal and external stresses is given as:

 

 

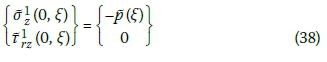
Where:

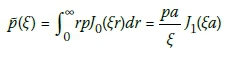
Pavement responses

By applying Hankel inverse transformation of all the Hankel transformed solutions, it is possible to determine solutions for pavement responses at any point in a pavement structure. However, when r = 0, the computation of σ_rand σ_θ using Equations 19 and 20 is not straightforward because of the term 1/r. The L'Hospital rule (Taylor 1952) is used to derive the solutions.

After Hankel transforms have been determined, it is possible to determine responses at any point (r, z) in the pavement structure through Hankel inverse transformation using the following equations:

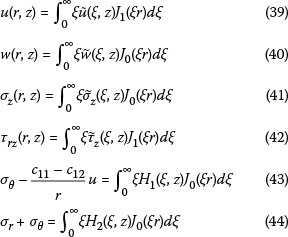
Where:

 

 

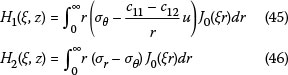
WORKED EXAMPLES

Solutions developed in this study were used to compute responses at different positions within a pavement structure. The pavement structure for which the simulation results are presented here are shown in Figure 3 on page 25. A vertical load of 21.5 kN and a diameter of 238 mm resulting in a 483 kPa contact stress was used in the analysis. All layers except the asphalt layer were modelled with isotropic, linear-elastic properties. The asphalt layer was modelled with cross-anisotropic, linear elastic properties. Information on all the layers, including sub-layers, is shown in Table 1. The sub-layering of each of the upper four main layers into four sub-layers resulted in a total of 17 layers, as shown in Table 1.

The vertical stiffness in the asphalt sub-layers shows a marginal increase close to the surface that is a function of the effect of temperature variations with depth for a specific time of the day used in the analysis. The top and bottom asphalt sub-layers show significant reduction in the effective horizontal stiffness resulting from cracking initiating from both the top and bottom of the main asphalt layer.

Discussion of results

Figures 4 and 5 show comparisons between the numerical method developed in this study and a proprietary FEM package for stresses (Szz) and (Sxx) as well as strains (Ezz) and (Exx) distributions with depth, z-direction, under the centre of a circular surface load of magnitude 21.5 kN load (483 kPa contact stress). From these results it is clear that the closed-form solutions developed in this study have achieved a very good level of accuracy, as their results compare very well with results from a proprietary FEM package.

It is also important to mention here that the software developed from this work has become the analysis engine for the new SAPDM.

 

CONCLUSIONS

1. A numerical tool for the analysis of an elastic multilayer system under the action of surface circular load, considering both cross-anisotropy and isotropy material properties, has successfully been developed.

2. The numerical tool developed in this study is capable of performing analyses for an unlimited number of points in an elastic multi-layered pavement system with an unlimited number of layers, and on the surface where an unlimited number of uniformly distributed circular loads act.

3. The results shown in this paper confirm the accuracy and reliability of the closed-form theoretical solutions developed.

A very good match of results was obtained between the numerical tool developed in this study and a proprietary FEM package. 4. The numerical tools developed can be used to improve the design, evaluation and analysis of road/runway pavement systems.

 

ACKNOWLEDGEMENTS

This research study was part of the revision of the SAPDM, a project sponsored by the South African National Roads Agency SOC Ltd (SANRAL) and the Council for Scientific and Industrial Research (CSIR). The incentive funding for rated researchers received from the National Research Foundation (NRF) is also gratefully acknowledged, as well as the support from Dr Hechter Theyse for setting up the numerical problem together with Prof Rudi Du Preez to run the proprietary FEM analyses for comparative purposes.

 

REFERENCES

Adu-Osei, A, Little, D N & Lytton R L 2001. Cross-anisotropic characterization of unbound granular materials. Transportation Research Record No. 1757, 82-91.         [ Links ]

Correia, A G (Ed.) 1999. Unbound granular materials. Laboratory testing, in-situ testing and modelling. Proceedings, International Workshop on Modelling and Advanced Testing for Unbound Granular Materials, Lisbon, Portugal, 21-22.         [ Links ]

Emeriault, F & Chang, C S 1997. Anisotropic elastic moduli of granular materials from a micromechanical approach. Journal of Engineering Mechanics, ASCE, 123(12): 1289-1293.         [ Links ]

Love, A 1944. A Treatise on the Mathematical Theory of Elasticity. New York: Dover Publications.         [ Links ]

Maina, J W & Matsui, K 2004. Developing software for elastic analysis of pavement structure responses to vertical and horizontal surface loadings. Transportation Research Record No. 1896, 107-118.         [ Links ]

Masad, S, Little, D & Masad, E 2006. Analysis of flexible pavement response and performance using isotropic and anisotropic material properties. Journal of Transportation Engineering, ASCE, 132(4): 342-349.         [ Links ]

Masad, S, Little, D & Lytton, R 2004. Modeling nonlinear anisotropic elastic properties of unbound granular bases using microstructure distributed tensor. International Journal of Geomechanics, ASCE, 4: 254-263.         [ Links ]

Miyamoto, H 1977. Three-Dimensional Problems in the Theory of Elasticity (in Japanese). Tokyo: Syokabo Publishers.         [ Links ]

Salehi-Ashtiani, R, Little, D N & Masad, E 2008. Anisotropy level prediction model of unbound aggregate systems. Proceedings, First International Conference on Transportation Geotechnics (ICTG-1), 25-27 August, Nottingham, UK, pp 253-262.         [ Links ]

Sneddon, I N 1951. Fourier Transforms. New York: McGraw-Hill.         [ Links ]

Taylor, A E 1952. L'Hospital's rule. American Mathematical Monthly, 59(1): 20-24.         [ Links ]

Tutumluer, E, Little, D N & Kim, S H 2003. Validated model for predicting field performance of aggregate base courses. Transportation Research Record No. 1837, 41-49.         [ Links ]

Wang, C D & Liao, J J 1999: Computing in transversely isotropic rocks using influence charts. Rock Mechanics and Rock Engineering, 32(1): 51-70.         [ Links ]

 

 

Correspondence:
Department of Civil Engineering
University of Pretoria
Private Bag X20
Hatfield 0028
South Africa
T: +27 12 420 6608
E: james.maina@up.ac.za

Department of Bioproduction and Environment Engineering
Faculty of Regional Environment Science
Tokyo University of Agriculture
1-1-1 Sakuragaoka
Setagaya-ku
Tokyo, 156-8505
Japan
T: +81 3 5477 2342
E: fk205262@nodai.ac.jp

Department of Civil and Environmental Engineering
Tokyo Denki University
Hatoyama
Hiki
Satama, 350-0394
Japan
T: +81 492 96 5703/2549
E: matsui@g.dendai.ac.jp

 

 

 

PROF JAMES MAINA (Pr Eng, MSAICE, FSAAE) is a professional pavement engineer, full-time professor of civil engineering at the University of Pretoria, and currently on secondment as a technical director of a QA/QC Project for roads in the State of Qatar. He obtained his PhD from Miyazaki University in Japan. His professional activities include QA/QC in road projects, pavement materials, and the development of advanced numerical analysis (modelling) tools for pavement engineering application. He also teaches both under- and post-graduate classes at the University of Pretoria.

 

 

PROF FUTOSHI KAWANA is an associate professor at the Tokyo University of Agriculture in Japan. His specialises in structural mechanics. He received his doctorate in engineering from the Science University of Tokyo in 2004. He is a member of the Japan Society of Civil Engineers, the Pavement Diagnosis Researchers Group (NPO) and the Japanese Society of Irrigation, Drainage and Rural Engineering.

 

 

PROF KUNIHITO MATSUI is emeritus professor of civil and environmental engineering at Tokyo Denki University in Japan. He obtained his PhD from the Department of Mechanics and Hydraulics at the University of Iowa, USA, in 1974. His areas of interest include structural analysis in pavement structures, static and dynamic back-calculation of pavement systems, non-destructive testing, thermal analysis of pavement systems, parameter identification, sensitivity analysis and structural optimisation.