Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
Journal of the South African Institution of Civil Engineering
On-line version ISSN 2309-8775
Print version ISSN 1021-2019
J. S. Afr. Inst. Civ. Eng. vol.58 n.4 Midrand Dec. 2016
http://dx.doi.org/10.17159/2309-8775/2016/v58n4a2
TECHNICAL PAPER
Experimental and analytical investigation into the stiffness of composite steel-reinforced timber beams with flexible shear connectors
W M G Burdzik; S Skorpen
ABSTRACT
Most of the current research on the design of timber composite beams involves either complex mathematical models which are not checked with experimental testing, or is purely based on experimental work with no attempt to model the behaviour. In a literature review the authors failed to find a practical way of designing composite timber beams, other than in the Eurocode 5. The equations in Eurocode 5 are unfortunately limited in their application. This paper looks at stiffening timber beams, with a known stiffness distribution, by screwing or nailing a steel strip to the underside of the beam. The modelled behaviour is compared with experimental test results and recommendations for the analysis and design of such members are given.
The experimental work involved determining the stiffness of twenty-four South African pine beams reinforced with metal strips. The spacing of the connectors was varied to ascertain the increase in stiffness of the composite with a reduction in the connector spacing. The analytical methods used were the Eurocode 5 method, as well as two finite element modelling methods, which may be used to determine the composite stiffness. The results of the three methods used show a remarkably good fit with the lower-bound experimental results.
Keywords: composite, timber, steel, beams, flexible connectors
INTRODUCTION
Timber design codes SANS 10163:2003 (SANS 2003) and BS EN 1995-1-1:2004 (EN 2004) call for beams to be designed for strength criteria, as well as serviceability criteria. The most important serviceability criterion is deflection, which is not only influenced by creep, but also by the modulus of elasticity of the beam. Sometimes beams that meet the strength criteria deflect too much under permanent loading only. To overcome a lack of stiffness, the second moment of area can be increased by either adding timber with a similar modulus of elasticity or by adding less material, such as steel, with a much higher modulus of elasticity.
Current research done on timber-steel composite beams is often either largely experimental work, with little attempt made to compare the results with the analytical design method given in Eurocode 5 (EN 2004), or complex mathematical modelling which is not checked with experimental results. The Euocode 5 design method is also very limited in its application, as it applies only to flexural members where the stiffening element stretches from support to support. Examples of current research include timber-steel-hybrid beams in high-rise buildings (Winter et al 2012), work on two-dimensional simply-supported composite beams (Xu et al 2006), the analysis of partial composite beams (Girhammer et al 2006) and a simplified analysis method for composite beams with interlayer slip (Girhammer 2009). The authors believe that, because of the highly varied nature of timber, experimental verification is a crucial part of all timber-related research. Practical methods for analysis are also important for design engineers who would not necessarily be designing composite timber structures on a regular basis.
With the above in mind the authors had a two-pronged approach to the problem. The initial approach was to see how well proposed finite element models and the Eurocode equations would be able to predict the stiffness of composite timber and steel flexural elements. This was done by measuring the stiffness of each piece of timber, the steel plate and the predicted stiffness of the connector (based on test values) prior to the assembly of the composite.
With the successful completion of the first set of tests, which showed remarkable correlation between the proposed finite element models, the Eurocode equations and the individual test results, the tests were expanded to include other connectors and thickness of steel plate.
Most design engineers would not have the facilities to measure the timber stiffness, the stiffness of the steel plate or the stiffness of the connectors, and would have to use published values. The authors felt it prudent to validate the theoretical values, based on the actual stiffness of the beams and steel plates, with test results. Predicted theoretical values agreed with the measured stiffness within acceptable experimental tolerances. The authors feel confident to recommend that design engineers use the theoretical design method, and base the stiffness on the published characteristic density and modulus of elasticity of the steel and timber.
COMPOSITE BEAM CONNECTORS
When adding steel to improve beam stiffness, the best solution is to glue the metal strip to the underside of the beam with some form of epoxy glue, although phenol resorcinol formaldehyde has been used before (Ebersohn 1994). The adhesive forms a very thin layer between the steel and the timber, and this layer has a very high stiffness. Very little or no slip occurs between the two materials. Practical problems, such as the proper cleaning of the steel and the clamping of steel to the timber, make this a fairly difficult and expensive option, especially on site. Furthermore, many engineers do not trust the bond between the steel and the timber, as even small impurities such as oil or milling scale cause de-bonding and subsequent stress peaks around the de-bonded areas, which can lead to complete de-bonding of the two materials. When the epoxy is subjected to elevated temperatures, such as would occur during a low-intensity fire, degradation of the epoxy layer takes place, which could cause failure (Mouritz 2002). High-temperature-resistant low-viscosity epoxies are available, but these would not necessarily be used in the construction industry.
Acceptable alternatives are mechanical fasteners, such as high-tensile screws or nails. Mechanical fasteners, however, need to undergo deformation before they are able to transfer loads (nails are preferable, as the pre-drilled holes in the steel plate can be much smaller than for screws). This relative movement between the materials leads to loss in stiffness and strength. The stiffness of the composite will lie somewhere between the sum of the individual stiffnesses and that of the fully composite element. Figure 1shows the strain distributions for three conditions, namely the idealised condition (no slip on the interface), no connection between the two materials, and limited slip on the interface.
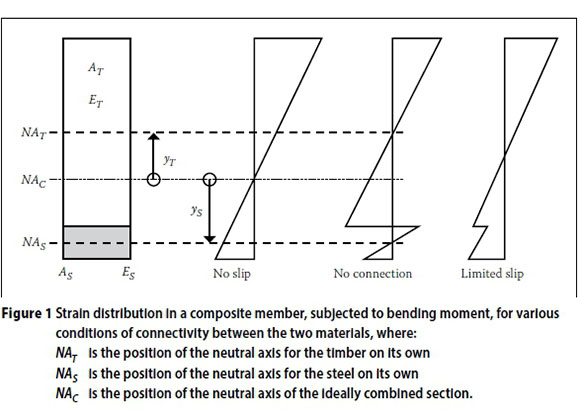
The fully connected, i.e. no slip, stiffness of the section can be given by the parallel axis theorem:
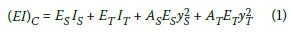
Where:
(EI)c is the combined stiffness of the section with no slip on the interface
Eg is the modulus of elasticity of the steel
Is is the second moment of area of the steel about its own axis
ysis the distance from the combined neutral axis to the neutral axis of the steel
ETis the modulus of elasticity of the timber
IT is the second moment of area of the timber about its own axis
yTis the distance from the combined neutral axis to the neutral axis of the timber
With no positive connection between the timber and the steel, the stiffness of the combined section is reduced to:
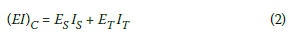
Many engineers who do not design timber structures on a regular basis would assume the idealised case, calculate the shear force on the interface and design the connection to transfer the load. This method ignores the deformation of the connector and the loss in stiffness as a result of that deformation. However, a simple beam or shell finite element model that can accurately predict the stiffness of the composite member, taking the stiffness of the connector into account, will make it easier for designers to assess the consequences of using steel and timber composites with flexible connectors.
EUROCODE 5 MODEL
Eurocode 5, BS EN 1995-1-1:2004 Appendix B contains an equation that can be used to determine the effective flexural stiffness of mechanically joined beams. This equation is based on a simply-supported beam with uniform distributed loading where the composite section stretches from support to support. The basic assumptions are given, and the equation offered to the designer is as follows:
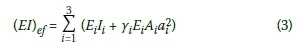
The two-element composite timber and steel beam that was used for this investigation is shown in Figure 2
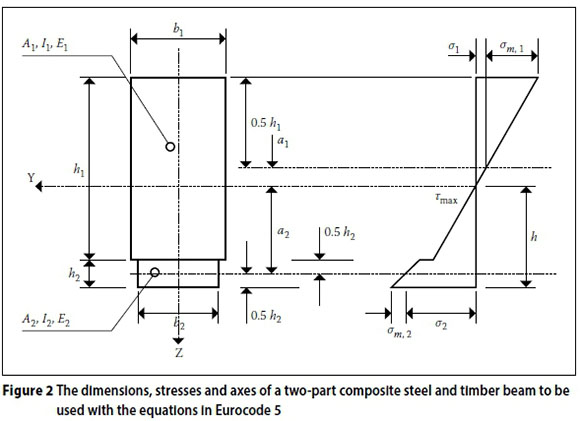
For a two-element composite member, as shown in Figure 2 the equation may be simplified with:
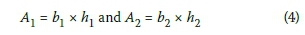
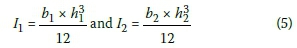
y2 = 1
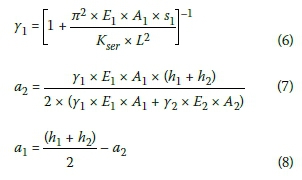
Where:
b is the width of the member in m
h is the height of the member in m
Ε is the modulus of elasticity of the member in kN/m2
Kseris the stiffness of the connector in kN/m
s is the spacing of the connectors in m γ is a connector stiffness parameter
Eurocode 5 also has equations that may be used to determine the stresses in the individual members, so that they may be checked for strength. From these equations it is possible to determine the bending moment and axial force components in each member.
The theoretical stiffness of the connector can be calculated by using the equations given in Table 7.1 of BS EN 1995-1-1:2004.
Screws and nails with pre-drilling:

Nails (without pre-drilling):

Where:
Kseris the stiffness of the screwed connection in kN/m
d is the screw diameter in mm
pmis the mean mass density in kg/m3
It should be noted that this equation is unit-dependent. Clause 3 of BS EN 1995 allows the stiffness for steel-to-timber connections
Kserto be multiplied by 2.0.
FINITE ELEMENT MODELS
The following two finite element methods can be used to predict the stiffness of the combined section:
■ Beam elements, where the centreline of the timber beam and the centreline of the steel strip or plate are connected by means of elements that have the same flexural stiffness as the shear stiffness of the connector.
■ Shell elements, where the timber beam that is divided into shell elements is connected to the steel elements by means of three-dimensional axial and moment springs that model the shear stiffness of the connector. The shell element method will give the stiffness as well as the stresses in the members, whereas the beam element method will give the axial forces as well as the bending moments in each element.
Beam element method
The composite beam can then be assembled as shown in Figure 4 The connecting elements between the centreline of the timber beam and the centreline of the steel plate are given a stiffness of K (as calculated in Equation 12), and are spaced at the required spacing of the nails or screws. They also need to have a high axial stiffness to simulate the contact pressure between the plate and the timber beam and ensure that the steel plate is forced to the same deflection as the underside of the timber beam. The authors propose that the Eurocode connection stiffness Kserbe used for K in this method where testing of the connector stiffness is not possible.
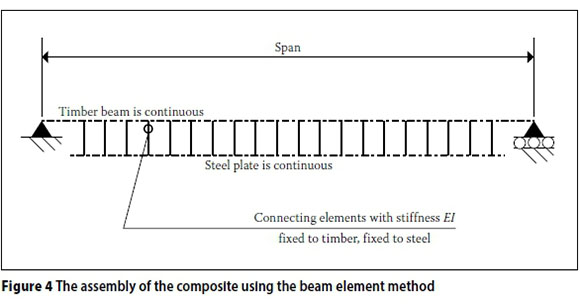
The method that is used to define the connector must take cognisance of the way in which the connection element is deformed. The connector may be placed through a pre-drilled hole in the thin steel plate and screwed or nailed into the timber beam. When screws are used, the top of the hole may be bevelled to accommodate the screw head. This bevel will allow for some rotation of the screw head to take place, whereas the shaft into the timber can be seen as fixed to the centreline of the timber beam. The stiffness of the connector can then be defined in terms of the stiffness of the connecting 'spring'. Figure 3 shows the assumed deflected shape of the connector. The assumption is made that the connector bends in double curvature.
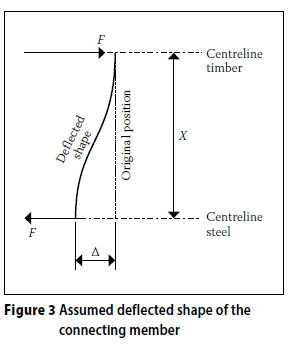
The stiffness of the connection K is given by E/A. Standard deflection tables in the Steel Designer's Manual (1983) may be used to calculate the deflection in terms of the stiffness of the connecting element AB. The deflection is given by:

The stiffness of the connecting element EI is then given by:
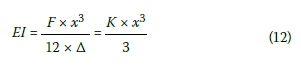
Where:
F is the longitudinal shear force at the interface between the two members in kN
x is the distance between the centrelines of the connected members in m
EI is the stiffness of the connector in kN.m2
K is the shear stiffness of the connector in kN/m
Δ is the displacement of the connector under the shear force in m
Shell elements
The composite beam can be assembled as shown in Figure 5 The timber beam is divided into shell elements, the dimensions keeping within the bounds of the standard element sizes as suggested by Brooker (2006). The width of the beam is the shell thickness. The steel plate is then also divided into the correct proportions. On the contact surface between the timber elements and the steel elements, springs are placed so that the shear stiffness of the springs K is the same as the expected stiffness of the screwed connection.
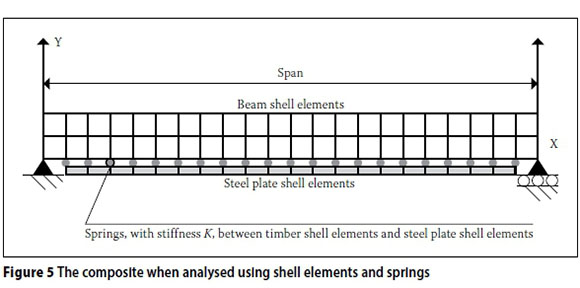
The connector shear stiffness of K is calculated in Equation 12 in the X direction, has a large stiffness in the Y direction and no moment stiffness. A high axial stiffness (Y direction) is required to simulate the contact pressure between the plate and the timber beam and ensure that the steel plate is forced to the same deflection as the underside of the timber beam. The authors propose that the Eurocode connection stiffness Kserbe used for K in this method where testing of the connector stiffness is not possible.
INITIAL EXPERIMENTAL VALIDATION
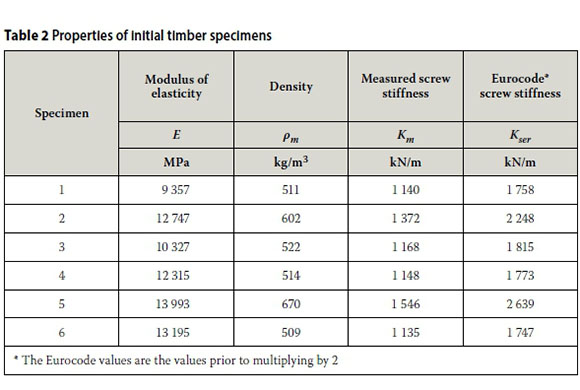
Six South African pine specimens (3.1 m long, 36 mm χ 149 mm), marked as Grade 5 but having a stiffness closer to Grade 7, as well as six 30 mm χ 5 mm thick steel plates were selected for the initial evaluation of the proposed finite element methods. The steel plates had screw holes drilled at a spacing of 50 mm and were to be screwed to the underside of the timber beams. The spacing of the connectors was varied between 400 mm and 50 mm to ascertain the increase in stiffness of the composite with a reduction in the connector spacing.
The stiffness and properties of all the components of the reinforced timber beam were measured:
■ The stiffness of the connectors was measured.
■ The equivalent modulus of elasticity of the steel reinforcement strips was determined.
■ The density and modulus of elasticity of each timber beam were measured.
Measured stiffness of connectors (screw joints)
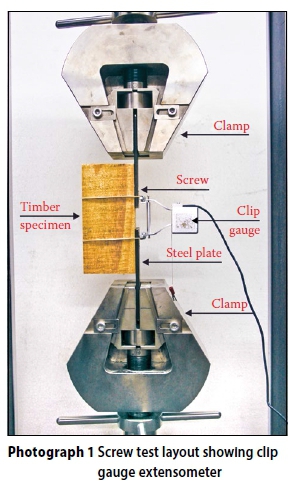
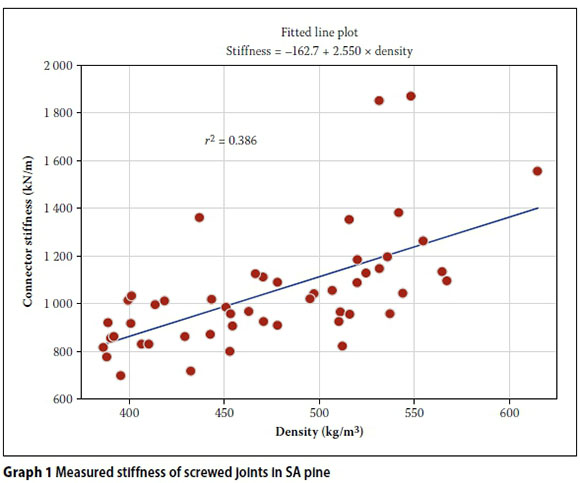
Fifty double-screw connections were constructed, as shown in Photograph 1 and these were tested for stiffness by measuring the relative displacement of the two lines on the steel plates under load with the help of clip extensometers. The results of the screw tests are given in Graph 1 The connector stiffness is calculated by determining the slope of the linear portion of the load-deflection curve. The linear portion is taken as the load divided by deflection between 10% and 40% of the ultimate strength of the connection. The density was calculated by accurately determining the dimensions and mass weight of each specimen and by dividing the mass by the volume.
Equivalent modulus of elasticity of steel reinforcement strip
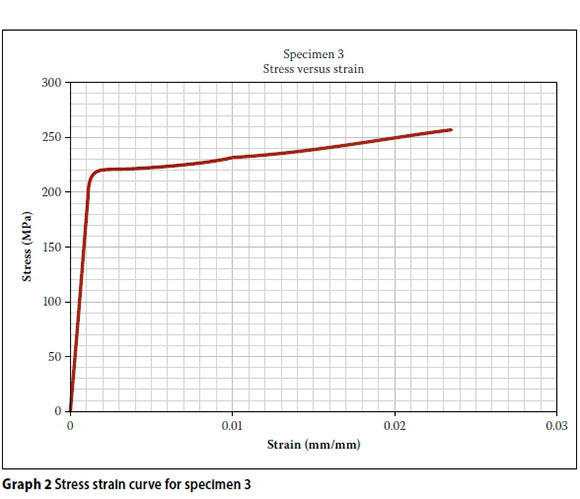
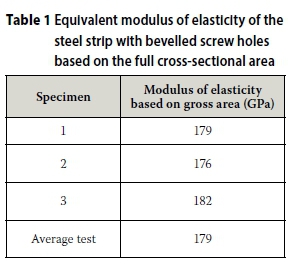
The equivalent modulus of elasticity of the steel reinforcement strip with pre-drilled connector holes was determined by obtaining the tensile load versus elongation of the strip. The equivalent modulus of elasticity was determined from the stress-strain graph (see Graph 2 and Table 1. The full cross-sectional area of 5 mm x 30 mm was used to determine the equivalent modulus of elasticity (shown in Table 2. Three strips were tested.
Photograph 2(a) shows the testing of a steel reinforcement strip, and Photograph 2(b) shows where the mill scale on the steel strip has come off the steel, as well as the distortion around the holes. It was noteworthy to observe how the mill scale popped off the strip as the loading was increased to the yield stress and beyond.


Density and modulus of elasticity of the timber beam
The timber pieces were weighed so that the average density could be determined. The stiffness of the connectors depends to a large extent on the density of the timber. Four-point loading was applied, and the deflection measured in the middle of the member so that the average modulus of elasticity could be calculated. The properties of the specimens are shown in Table 1
Once the modulus of elasticity and density of the timber beams were determined, the stiffness of the connectors was calculated using the following two methods:
■ The measured connector stiffness Km determined by experimental testing:
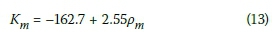
Where:
Kmis the experimentally determined stiffness of the connector in kN/m
pmis a mean density of the timber beam
■ Connector stiffness determined by Eurocode method (Table 7.1 of BS EN 1995):

Where:
Kser is the stiffness of the connector in kN/m
pmis the mean density of the timber beam in kg/m3
Table 2 shows the properties of the timber beams used, and the calculated connector stiffness using the two methods described above.
Test procedure of the composite beams
The testing for stiffness was done by means of four-point loading and the beams were loaded to the maximum service stress, i.e. about 45% of the characteristic stress of the timber alone. Test specimens were estimated to be of Grade 7, so the beams were loaded to a stress of about 7 MPa. This was well within the elastic stress range of the composite beam. The 3.1 m long beams spanned 3.0 m, with the steel having a length of 2.9 m so that it would not rest on the supports. The authors did not want the plates to rest on top of the end supports, as they were worried that the friction forces induced at the supports could lead to a slightly higher stiffness, and none of the analytical models take friction into account. Deflection was measured in the middle of the span and the load-deflection increases were measured at 10 Hz. Initial fixing of steel plates was with a screw spacing of 400 mm, and the tests were then repeated on each specimen with the screws at 200 mm, 100 mm and 50 mm. This was accomplished by halving the spacing after each test had been completed. A total of six beams were used, giving a total of 24 test results. The experimental setup is shown in Figure 6 and Photograph 3
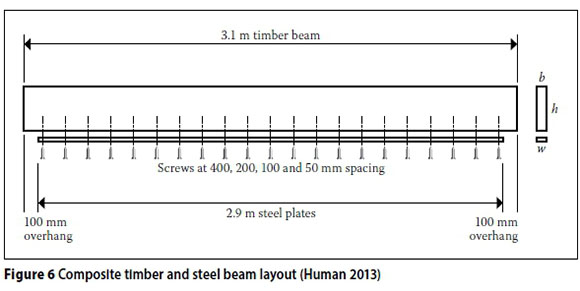

The screws were tightened fully and then loosened a little so that frictional forces between the steel and the timber would be minimised. In the actual construction of the steel-reinforced timber composite, one would expect the steel plates to initially be fixed tightly to the timber beam. Friction between the interfaces could increase the stiffness. Over time, the cross-sectional dimensional changes of the timber as a result of moisture variation will create a gap at the connection interface, thereby eliminating the friction.
Each specimen was then tested in the same way until all six specimens of each configuration had been tested. The composite beam stiffness was then calculated using Equation 6 from the standard stiffness tables in the Steel Construction Handbook.
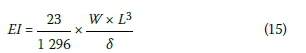
Where:
W = total point load, placed as W/2 at thirds of the span
δ = the deflection measured at midspan
L = the span of the beam
EI = the flexural stiffness of the composite beam
Comparison of test results with finite element analyses and Eurocode equations
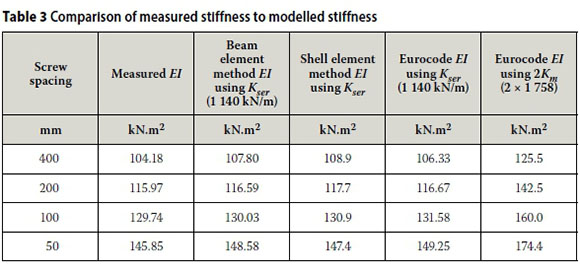
Only the flexural rigidity of Specimen 1 is shown to illustrate the good correlation between the measured results, the two finite element models where the connector stiffness is modelled, and the Eurocode equations (see Table 3. Both the calculated connector stiffness Kserand the measured connector stiffness Kmhave been used for the Eurocode method. PROKON (2014) software was used for all the finite element models.
The following properties were used for the anaylsis:
■ E = 9357 MPa
■ 30 mm x 5 mm steel plate with E = 179 GPa
■ Km= 1 140 kN/m (from Eq 13) with density of 511 kg/m3
■ Iconnector = 2.43 x 10-10 m4 (from Eq 12) with the element in double flexure
■ Kser= 1 758 kN/m (from Eq 14) and this may be multiplied by 2 (Section 7, 7.1 (3) of BS EN 1995-1-1;2004)
As can be seen from Table 3 there is very good correlation between the measured stiffness EI and the Eurocode method, as well as the proposed finite element methods. However, the Eurocode screw stiffness equation, where the stiffness using steel plates is two times the timber-to-timber stiffness, could overestimate the stiffness by 20%. The other methods, using the Eurocode stiffness for timber-to-timber (i.e. without multiplying by 2), are in the region of 2% of the tested value.
FURTHER EVALUATION OF PROPOSED FINITE ELEMENT MODELS
In order to further validate the three proposed design methods, tests on a further 18 timber beams, reinforced with steel plates, were performed. The timber beam size was kept the same as the initial tests, and the connector type and steel plate thickness were varied. (Human 2013; Huang 2014; Meintjies 2014; Abdul 2014).
Three variables play a part in the stiffness of the composite member, these being the stiffness of the steel plate, the stiffness or spring constant of the connection, and the stiffness of the timber member. The modulus of elasticity of the steel plate has little variability, which reduces the variables that would influence the stiffness of the composite to two, namely timber stiffness and connection stiffness. By reducing the variables to two, it was felt that a steel-reinforced timber beam would give a good indication of whether the proposed analysis methods have any merit.
Table 4 shows the specimens with the different steel plate thicknesses and the type of connectors used.
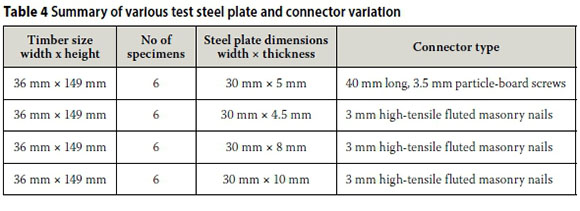
To increase the number of test values, the authors decided to gradually decrease the spacing of the screws from a spacing of 400 mm, to 200 mm, to 100 mm and finally to 50 mm. This would then give four test results for every specimen. A total of 24 beams were used with a total of 96 test results. The experimental setup was similar to the setup in Figure 6
Prior to assembly of the composites, the stiffness and density of each piece of timber were determined (see Table 5. This was done using the standard four-point loading test on edge. The stiffness that was obtained from each individual test, with each spacing of the connector, was compared to the stiffness that had been obtained by using the three proposed design methods - using the characteristic modulus of elasticity of the tested timber, the stiffness of the steel based on the full area of the section, and the stiffness of the nail or screw using the Eurocode dowel connector stiffness for dowels through steel. Characteristic values were used, as a practising engineer cannot be expected to measure the modulus of elasticity of each individual piece of timber, or the reduced modulus of elasticity of the steel.
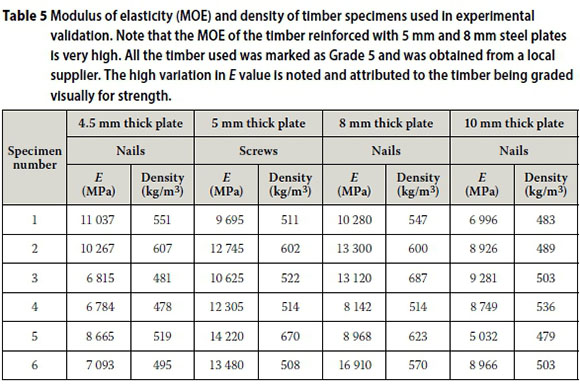
The method proposed by Leicester (1986) was used to determine the lower-bound characteristic value of the modulus of elasticity, as well as the density (see Table 6 from the experimental results. These values were used in the analytical Eurocode method and the two finite element methods to determine the characteristic stiffness of the composite beams. It is noted that the experimental E values differ from the values in SANS 10163 for a Grade 5 timber, as they are closer to a Grade 7.
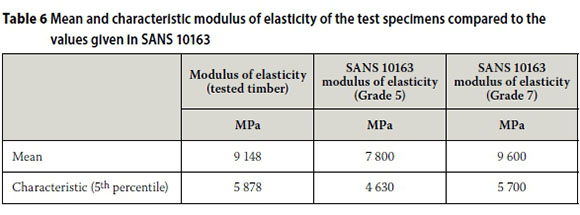
The mean density of the tested timber was 541 kg/m3 and the characteristic density was 444 kg/m3. SANS 10163 gives minimum densities for Grade 5 as 360 kg/m3 and Grade 7 as 425 kg/m3. More important is that the mean density for Grade 5 would be in the region of 425 kg/m3 and 500 kg/m3 for Grade 7.
The theoretical stiffness of the screws and nails can be calculated by using Equations (9) and (10) given in SANS 10163:Part 1 or Table 7.1 of BS EN 1995.
Clause (3) of BS EN 1995 allows the stiffness for steel-to-timber connections Kserto be multiplied by 2.0. However, using the initial test results it was decided to not multiply Kser by 2, as the stiffness of the initial tests was overestimated when this factor was applied.
For the 3.5 mm screw in mean density of timber = 516 kg/m3, the stiffness Kserwill be 1 784 kN/m, which is the value used in the analyses.
For the 3.0 mm nail, without pre-drilled holes, in mean density of timber = 516 kg/m3, the stiffness Kserwill be 941 kN/m, which is the value used in the analyses.
COMPARISON
Graphs 3, 4, 5 and 6 show the measured stiffnesses for the composite beams with various connectors, connector spacing and steel plate thicknesses. They also show the theoretical stiffnesses calculated using the three different proposed design methods, and the stiffnesses calculated assuming full fixity and no connection.
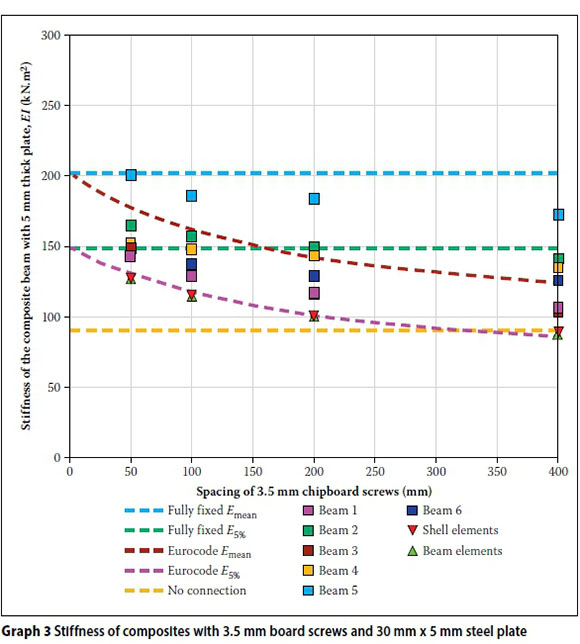
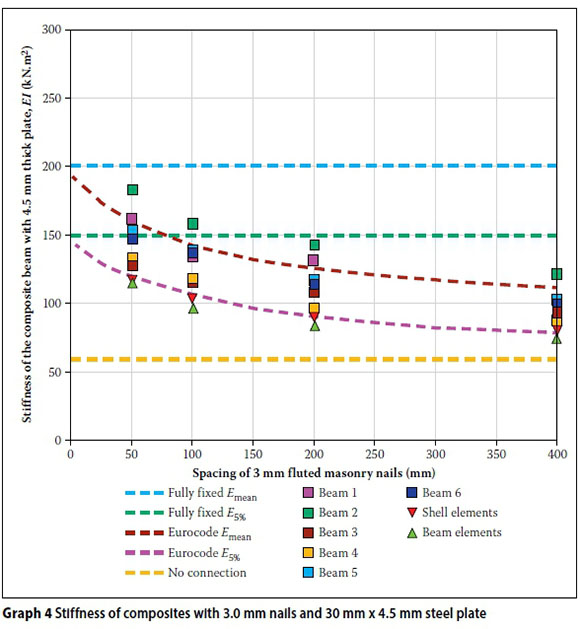
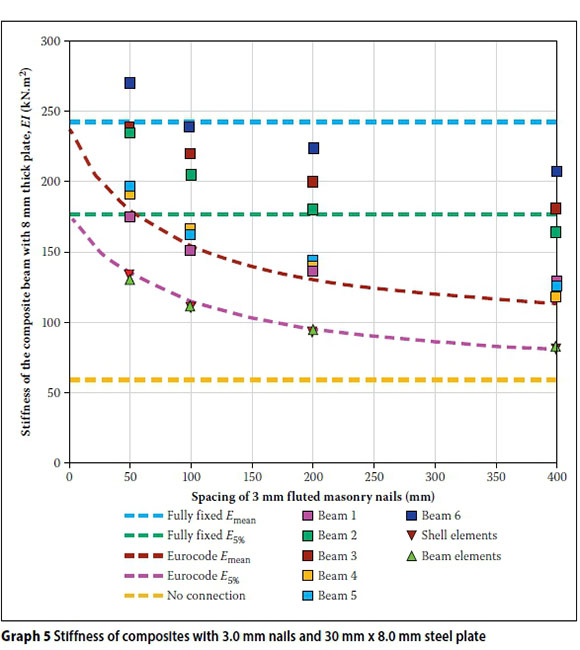
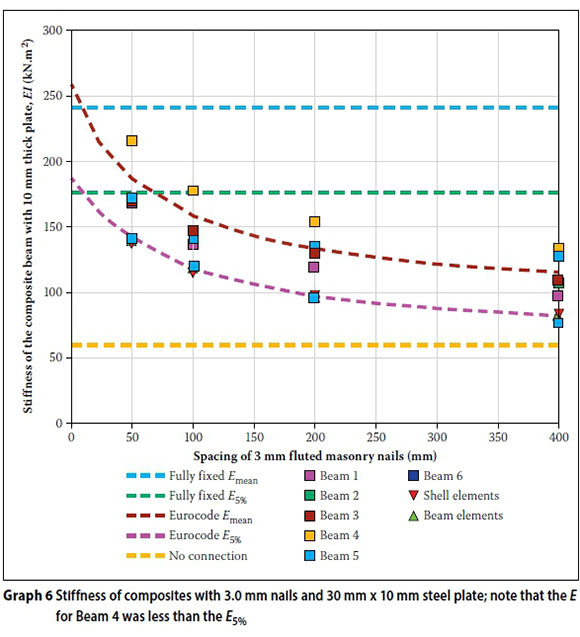
All the theoretical values have been calculated using the measured MOEmean and MOE5% for the tested timber. The SANS 10163 MOEmean and MOE5% values for Grade 5 timbers are not compared, as the intent of this work was to compare test values against the proposed modelling methods. For the shell and beam elements, only the fifth percentile MOE has been used to avoid confusion between the data and the theoretical.
Where the test results are higher than the stiffness based on Eurocode 5 equations using MOEmean, it is because the timber had a higher stiffness than the MOEmean of the sample. Beam 6 of the sample using 8 mm steel plates (Graph 5 had an exceptionally high MOE and tested above the fully-fixed case. Only one test specimen had a modulus of elasticity that was less than the MOE5% of the sample and that was beam 4 (Graph 6.)
Comparing the four graphs, the following can be noted:
■ The increase in stiffness of the composite beam as the spacing of the connectors decreases.
■ Full fixity can theoretically be achieved when connector spacing tends towards zero; however, this would not be practical.
■ There is a significant difference in predicted stiffnesses depending on whether MOEmean or MOE5% is used, and many of the test values fall below the predicted value for MOEmean and connector stiffness based on the mean density.
■ The MOE5% calculated stiffnesses correlate with the lower-bound curve from the experimental results, indicating a safe design.
■ There is a very good correlation between the two finite element models and the Eurocode spring model, as can be seen on the lower-bound curves of Graphs 1 to 4.
■ The MOE value of the timber has a significant effect on the stiffness of the composite beam. The timber used for the 8 mm plate beams had high Ε values, and thus were stiffer composite beams when compared to the composite beam with the 10 mm thick plate which used timber with a lower MOE.
CONCLUSION
The objective of this investigation was to find suitable analytical methods that could be used by structural engineers to obtain an acceptable effective cross-sectional stiffness of a composite timber-steel beam, when using flexible connectors.
Three design methods were used in this paper and these were compared to test values. The methods in order of complexity are:
■ A spring model as given in Eurocode 5
■ A finite element model using beam elements
■ A finite element model using shell elements.
Engineers or designers who do not have that much experience with timber design can easily understand the methods presented. The finite element methods have an added advantage in that it makes it possible for the designer to specify non-linear behaviour for the connectors when investigating failure of the composite element.
The three design methods all use the following properties, which are easily obtained from design codes or other literature without testing:
■ The 5th percentile modulus of elasticity of timber
■ The mean density for the grade of timber
■ The Eurocode connector stiffness equation which is based on the mean density
■ The full cross-section of the steel member may be used with no loss of area or second moment of area due to holes.
Note that the Eurocode 5, BS EN 1995-1-1:2004 method for the stiffness of screwed and nailed connections, which is given in Equations 9 and 10, should not be multiplied by 2 as recommended in the code when connecting a steel plate to timber, as the stiffness is then overestimated.
It was concluded that the stiffness, given by the Eurocode spring method and both the beam and the shell finite element methods, showed a remarkably good fit with the lower-bound experimental values if the characteristic modulus of elasticity is used. Using these methods for design would result in a conservative assessment of the stiffness of a composite timber and steel beam. It was also noted that the full fixity condition cannot be achieved in reality with a practical connector spacing.
The Eurocode 5 method for determining composite stiffness is specifically for a simply-supported member subjected to uniformly distributed loading, with the composite section stretching from support to support. The authors find it encouraging that it is possible to use the fairly simple finite element methods to obtain the composite stiffness with some measure of assurance. It gives the designer the option of designing for a specific loading case, as well as giving the designer the possibility of using the finite element methods to analyse continuous multiple-span members, and also members where the composite does not necessarily stretch from support to support.
LIST OF NOTATIONS
b = the width of the member in m
d = the screw diameter in m
E = the modulus of elasticity
EI = the flexural stiffness of the composite beam
EIC= the combined stiffness of the section with no slip on the interface
Eg = the modulus of elasticity of the steel
ET= the modulus of elasticity of the timber
F = longitudinal shear force at the interface between the two members (kN)
f = frequency (Hz)
h = the height of the member in m
I = the second moment of area of the board on flat
Is= the second moment of area of the steel about its own axis
It= the second moment of area of the timber about its own axis
K = the stiffness of the connector in kN/m
Kser= the stiffness of the connector in kN/m (using Eurocode)
Km= the stiffness of the connector in kN/m (determined experimentally)
L = the span of the beam
ys= the distance from the combined neutral axis to the neutral axis of the steel
yt= the distance from the combined neutral axis to the neutral axis of the timber
NAT= the position of the neutral axis for the timber on its own
NAs= the position of the neutral axis for the steel on its own
NAC= the position of the neutral axis of the ideally combined section
s = the spacing of the connectors in m
t = thickness of the board (m)
w = mass of the board (kg)
W = point load
x = distance between the centrelines of the connected members (m)
∆W = change in the point load
γ = a connector stiffness parameter
pm= the mass density in kg/m3
∆δ = the change in the deflection that matches the change in the point load, measured in the middle of the span
δ = the deflection at the middle of the span
Δ = the displacement of the connector under the shear force in m
REFERENCES
Abdul, J 2014. The prediction of the true effective stiffness of composite timber and steel beams. BEng Project Report, University of Pretoria, Department of Civil Engineering. [ Links ]
Brooker, O 2006. How to design reinforced concrete flat slabs using finite element analysis. Camberley, UK: The Concrete Centre. [ Links ]
Ebersohn, W 1994. gteel reinforced timber structures. MEng dissertation, University of Pretoria, Department of Civil Engineering. [ Links ]
EN (European Standard) 2004. EN 20041995-1-1 2004 + A1:2008. Eurocode 5: Design of Timber Structures - Part 1-1: General - Common Rules and Rules for Buildings. Brussels: European Committee for Standardization (EN). [ Links ]
Girhammer, U A, Pan, D H 2007. Exact static analysis of partially composite beams and beam-columns. International Journal of Mechanical Sciences, 49(2): 239-255. [ Links ]
Girhammer, U A 2009. A simplified analysis method for composite beams with interlayer slip. International Journal of Mechanical Sciences, 51(7): 515-530. [ Links ]
Huang, J 2014. The prediction of the true effective stiffness of composite timber and steel beams. BEng Project Report, University of Pretoria, Department of Civil Engineering. [ Links ]
Human, W 2013. The prediction of the true effective stiffness of composite timber and steel beams. BEng Project Report, University of Pretoria, Department of Civil Engineering. [ Links ]
Leicester, R H 1986. Confidence in estimates of characteristic values. Proceedings, 19th Conference of the CIB-W18, Florence, Italy, September. [ Links ]
Meintjies, J 2014. The prediction of the true effective stiffness of composite timber and steel beams. BEng Project Report, University of Pretoria, Department of Civil Engineering. [ Links ]
Mouritz, A P 2002. Post-fire flexural properties of fibre-reinforced polyester, epoxy and phenolic composites. Journal of Material Sciences, 37: 1377-1386. [ Links ]
PROKON 2014. PROKON Software Consultants Ltd. PROKON suite of structural analysis programs. Pretoria. [ Links ]
SANS (South African National Standard) 2004. gANg 10162-1. jhe gtructural Use of gteel. Part 1: Limit-gtates Design of Hot-rolled Steelwork. Pretoria: SABS Standards Division. [ Links ]
SANS (South African National Standard) 2003. gANg 10163-1. jhe gtructural Use of jimber. Part 1: Limit-states Design. Pretoria: SABS Standards Division. [ Links ]
SANS (South African National Standard) 2001. gANg 10163-2. jhe gtructural Use of jimber. Part 2: Allowable Stress Design. Pretoria: SABS Standards Division. [ Links ]
Steel Designers' Manual, 4th ed. 1983.Suffolk, UK: Constructional Steel Research and Development Organization. [ Links ]
Winter, W, Tavoussi, K, Pixner, T & Parada, F R 2012. jimber-steel-hybrid beams for multi-storey buildings. Paper presented at the World Conference on Timber Engineering, Auckland, New Zealand. [ Links ]
Xu, R & Wu, Y 2006. Two-dimensional analytical solutions of simply-supported composite beams with interlayer slips. International Journal of Solids and Structures, 44: 165-175. [ Links ]
 Correspondence:
Correspondence:
W M G Burdzik
Department of Civil Engineering University of Pretoria Pretoria 0002
South Africa
T: +27 12 420 2746
E: walter.burdzik@up.ac.za
S Skorpen
Department of Civil Engineering University of Pretoria Pretoria 0002
South Africa
T: +27 12 420 2196
E: sarah.skorpen@up.ac.za

PROF WALTER BURDZIK (Pr Eng) is Professor of Structural Engineering in the Department of Civil Engineering at the University of Pretoria, South Africa. He received his degrees from the University of Pretoria and has been involved in timber research and structural timber design for the past 40 years. He runs one of the few recognised timber-testing facilities in South Africa and is often involved in queries surrounding the importing of structural timber and wood-based products. He has also been involved in all the SANS committees charged with writing the South African timber design codes and specifications that have to do with wood-based structural products. His other fields of interest include analysis of structural systems, as well as steel, concrete and masonry design.

SARAH SKORPEN (Pr Eng, C Eng, MIStructE) is a lecturer in the Department of Civil Engineering at the University of Pretoria, South Africa, where she teaches strength of materials and steel design to undergraduates. Sarah spent nine years working for the Buildings and Structures Division of Royal HaskoningDHV, and joined the University of Pretoria fouryears ago. She obtained an MEng (Structural Eng) from the University of Pretoria, and is currently working on her PhD.














