Servicios Personalizados
Articulo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares en Google
Similares en Google
Compartir
Journal of the South African Institution of Civil Engineering
versión On-line ISSN 2309-8775
versión impresa ISSN 1021-2019
J. S. Afr. Inst. Civ. Eng. vol.57 no.2 Midrand abr./jun. 2015
http://dx.doi.org/10.17159/2309-8775/2015/v57n2a4
TECHNICAL PAPER
Using small-strain stiffness to predict the load-settlement behaviour of shallow foundations on sand
A Archer; G Heymann
ABSTRACT
Foundation settlement prediction is a challenging task due to the difficulties associated with the quantification of the soil stiffness and the abundance of available analysis methods. Of the different soil stiffness moduli that may be measured, the initial small-strain stiffness is important since it can be measured both in the field and the laboratory, and settlement prediction methods using this parameter are becoming more common. The objective of this paper is to present a settlement prediction method for shallow foundations that only uses small-strain stiffness as input parameter.
The method was developed by conducting physical modelling in the geotechnical centrifuge at the University of Pretoria to quantify the behaviour of shallow foundations on sand. Bender and extender elements were used to obtain the small-strain stiffness profile below the foundation before it was vertically loaded and the load-settlement curve determined. The tests were conducted on different density sands corresponding to loose, medium-dense and dense sand. A non-linear stepwise analysis approach was used in conjunction with a softening function, with variables calibrated to obtain the best fit solution for the different sand densities. Results indicate that the accuracy of the proposed method decreases as the sand density increases, but that load-settlement behaviour can be predicted with reasonable accuracy.
Keywords: small-strain stiffness, foundation settlement, centrifuge testing, softening function
INTRODUCTION
Settlement prediction of shallow foundations is essential for the design of a structure. This requires accurate input parameters and a reliable analysis method. Small-strain shear stiffness (G0) and small-strain Young's modulus (E0) are important soil parameters, because they can be measured in the field and the laboratory using seismic testing techniques. This paper describes a foundation settlement prediction method that only requires G0 or E0 as an input parameter. Centrifuge testing was done to obtain the load-settlement behaviour of a foundation on different density sands. Predicted and measured results were compared and predictions were limited to a maximum settlement of 10% of the foundation diameter (i.e. 0.1D).
LITERATURE REVIEW
Settlement of shallow foundations depends on various factors, including the magnitude of the applied load, foundation size and geometry, foundation stiffness, ground stiffness and the strength of the underlying material (Canadian Geotechnical Society 2006). All these factors may contribute to uncertainty, and as stated by Yongqing (2011), accurate estimation of foundation settlement remains a significant challenge in foundation design.
However, Das and Sivakugan (2007) argued that settlement prediction for shallow foundations is primarily dependent on the accuracy with which the stiffness of the soil can be quantified, as well as the choice of analysis methods. Numerous methods for estimating foundation settlement have been proposed, and Douglas (1986) reported the existence of more than forty methods for the estimation of foundation settlement on granular soils. A report by Lutenegger and DeGroot (1995) on settlement methods for granular soils found in excess of 50 different methods. Most of these methods rely on indirect correlations with in situ tests such as the standard penetration test (SPT) and the cone penetration test (CPT), with only nine of the methods based on elasticity theory which requires stiffness as input parameter. Archer (2014) summarised a representative sample of 16 elasticity-theory-based methods to predict load-settlement curves, illustrating the differences in approaches taken by various authors. It was shown that more recent methods incorporate the initial small-strain stiffness (either the shear- or Young's modulus), indicating the move towards using the initial small-strain stiffness for foundation settlement analysis. This move can be attributed to the fact that in situ and laboratory seismic testing are becoming increasingly popular, and that values obtained are reliable (Campanella 1994; Woods 1978).
Mayne and Poulos (2001) suggested that finite difference and finite element methods may be the most realistic way of incorporating soil non-linearity when analysing foundation settlement, but this is a time-consuming task and requires a skilled analyst. They suggested that, for a preliminary estimate, a method may be used where the initial small-strain modulus is degraded for an appropriate strain level, and then applying a linear elastic analysis method. The shortcoming of this approach is that, in order to apply the appropriate strain level, an estimation of the foundation settlement is required before the analysis is conducted.
Small-strain stiffness of soil
Soil stiffness is expressed in different forms, including: shear modulus (G), constrained modulus (M), bulk modulus (K) and Young's modulus (E). For the purpose of foundation design the values of shear- and Young's modulus are commonly used and these two parameters are interrelated by Poisson's ratio (v). Clayton (2011) stated that a comprehensive understanding of the stiffness parameters at small strains is essential if realistic ground movement predictions are to be made. Recently a better understanding of the non-linear stiffness behaviour of soil, also known as modulus degradation, has provided engineers with an efficient approach to produce more reliable stiffness values for design (Yongqing 2011). Conceptually the small-strain stiffness (G0 or E0) is considered to be constant for small-strain values up to a strain level of about 0.001% to 0.002%, and at strain levels below this value it is often assumed that the soil behaves elastically (Clayton & Heymann 2001). Above this strain level nonlinear behaviour of the soil is observed and the stiffness decreases as strain increases.
Softening functions
The high stiffness at very small strain is not necessarily relevant for a geotechnical problem. It is therefore important to reduce the small-strain stiffness to a value relevant to the strain level that occurs for a specific design problem. This is achieved with softening functions or modulus reduction curves. These can be divided into two categories: (1) curves based on stiffness and strength parameters, and (2) curves based only on stiffness parameters, with both categories including the current strain level as an input value. Softening curves which use stiffness parameters only do not require the strength of the soil to be quantified.
Many stiffness reduction curves have been proposed to describe the non-linear stress strain relationship observed for soils, including Vucetic & Dobry (1991), Rollins et al (1998), Clayton & Heymann (2001). These softening curves have been established from triaxial and resonant column tests conducted in the laboratory and, since the boundary conditions below a shallow foundation are different, the question remains as to whether these softening curves can be applied directly to settlement of shallow foundations.
Elkahim (2005) argued that modulus reduction curves should have a minimum number of parameters for defining the nonlinear relationship without compromising accuracy; the parameters should ideally have physical meaning and it should be easy to derive them. For this study a modified hyperbolic relationship presented by Oztoprak and Bolton (2013) was used as the softening function, as shown in Equation 1:
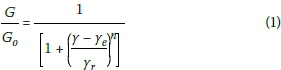
Where:
G = shear modulus
Go= small-strain shear modulus
γ = current shear strain
ye= elastic threshold shear strain; if γ < γe then G/Go = 1
γr = reference shear strain; if γ = γe+ γr then G/Go = 0.5
n = curvature parameter
This softening function is appealing for settlement prediction methods, as the only soil parameter required is small-strain shear stiffness.
Measurements of small-strain stiffness
Soil stiffness can be measured by laboratory tests, as well as by in situ tests. Different test methods can only determine stiffness values at certain strain levels, and therefore not all methods are applicable for small-strain stiffness determination. Seismic geophysical techniques are effective to determine the small-strain stiffness of geomaterials. These techniques measure the wave velocity which can then be used together with the bulk density (pbulk) to calculate the small-strain stiffness. The small-strain shear stiffness can be calculated from the shear wave velocity (Vs) using Equation 2:
Go= Pbulk X V2s (2)
Seismic techniques are attractive because they can be conducted in the field and in the laboratory, but Elhakim and Mayne (2003) suggested that in most cases results obtained from in situ tests are superior to laboratory tests. An advantage of in situ seismic testing is the fact that large volumes of soil can be tested, and that the test is conducted at the current stress condition with minimal disturbance of the material. Surface wave testing in particular is becoming increasingly popular, since these tests are non-invasive, nondestructive and cost-effective (Menzies 2000).
EXPERIMENTAL METHODOLOGY
Physical modelling was conducted to measure the load-settlement behaviour of a shallow foundation on sand. The modelling was done with the 150 G-ton geotechnical centrifuge of the University of Pretoria, and details of the centrifuge facility were given by Jacobsz et al (2014). The centrifuge tests were conducted at an acceleration of 50 g.
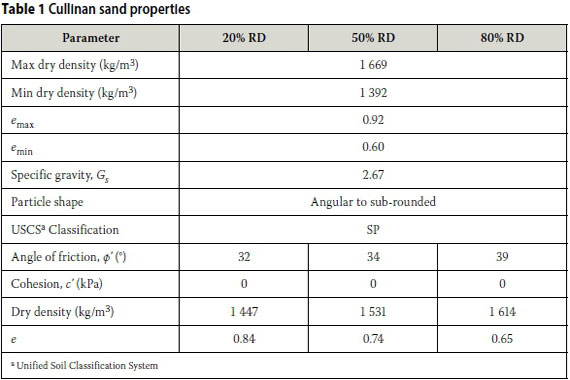
The soil used for the experimental work was a standard testing sand from the University of Pretoria, known as Cullinan sand. The sand was characterised through various laboratory tests, and for the experimental work relative densities of 20%, 50% and 80% were targeted. These relative densities correspond to loose, medium-dense and dense sand respectively. A summary of the relevant properties of the Cullinan sand is given in Table 1.
Centrifuge model
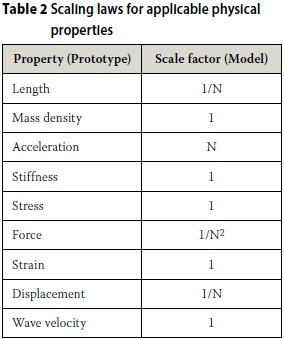
Centrifuge testing is used to test a reduced scale model of a large prototype and it is achieved in a centrifuge using centripetal acceleration. The model is reduced by a scale factor (N) equivalent to the acceleration of the centrifuge relative to 1 g, and since the acceleration is known, scaling laws can be used to convert the measured properties and values of the model to a full-scale prototype equivalent. Applicable scaling laws are shown in Table 2, and since the centrifuge tests were conducted at 50 g acceleration, N = 50.
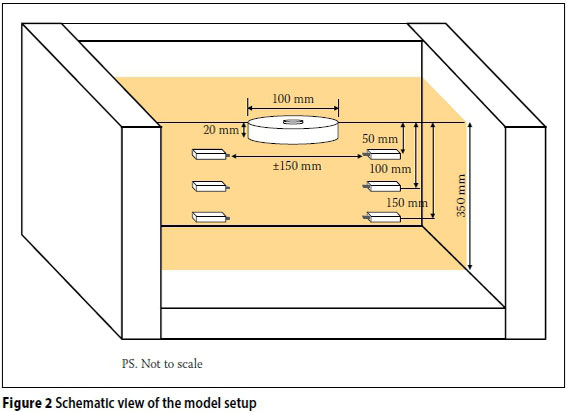
A model container, with inside dimensions of 600 mm x 400 mm x 400 mm (L x W x H) was used for the modelling, and the sand height in the model container was 350 mm. A circular aluminium model foundation of 100 mm diameter (D) and 20 mm thickness was used. The model foundation scales to an equivalent 5 m diameter and 1 m thick prototype foundation at 50 g, and the dimensions were chosen for the foundation to behave as a rigid foundation. Fine P100 grit sandpaper was glued to the bottom of the foundation to replicate a rough base.
A Pfaff-silberblau SHE3.1 Mechanical Ball Screw Jack was used to apply the load. An HBM U93 50 kN load cell and an HBM WA50 50 mm LVDT were attached to the jack to measure the applied load and corresponding settlement. The 50 kN load capacity of the system was adequate to achieve between 0.2D and 0.3D settlement for all relative densities. Solartron Metrology AS/15 S series 30 mm displacement sensors were used to measure the sand settlement during centrifuge spin-up in order to calculate the sand density at different levels of acceleration. The model setup is shown in Figure 1.

Standard quick-mount bender- and extender elements from Piezo Systems, Inc were used to measure the shear and compression wave velocities of the sand at different depths. Bender elements are two-layer piezoelectric crystals, and depending on the wiring, are made to bend, twist or elongate. When these elements bend, they are referred to as bender elements, and when they elongate they are referred to as extender elements. Due to their perceived simplicity, bender elements have become popular in laboratory and centrifuge tests (Clayton 2011). Bender elements are used in pairs consisting of a transmitter and receiver, and due to the bending of the elements, shear waves are produced. Extender elements work on the same principle as bender elements, but due to the elongation, compression waves are generated. If a voltage is applied to the transmitter element, a mechanical wave is generated that travels through the soil and is detected by the receiver element. If the tip-to-tip distance between elements (Ltt) is known, as well as the travel time (Δt) of the wave from the transmitter to the receiver element, the wave velocity can be calculated. If the shear wave velocity is known, Equation 2 is used to calculate the small-strain shear stiffness. For the experiments the bender and extender elements were placed a distance of approximately 150 mm apart. This value was chosen as it was close enough to obtain a good quality signal, but far enough not to influence the load-settlement behaviour of the foundation or be damaged during loading. Three sets of bender- and extender elements were placed at three depths below the foundation. Each set consisted of bender- and extender element transmitter and receiver pairs placed at depths of 50 mm, 100 mm and 150 mm, which correspond to prototype depths of 0.5D, 1.0D and 1.5D. Small-strain measurements were taken at different g-levels during centrifuge acceleration at 10 g, 20 g, 30 g, 40 g and 50 g, which gave prototype depths ranging between 0.5 m to 7.5 m. This allowed a detailed small-strain stiffness with depth profile to be obtained. Figure 2 shows a schematic view of the model indicating the placement of the bender elements.
Once 50 g was reached, the final small-strain measurements were taken, where after the foundation was loaded with the jack. Load-settlement measurements were taken until either the maximum capacity of the load cell was reached or at a maximum settlement of 30 mm (0.3D). For the experimental work a total of six tests were conducted, i.e. two tests at each relative density.
EXPERIMENTAL RESULTS
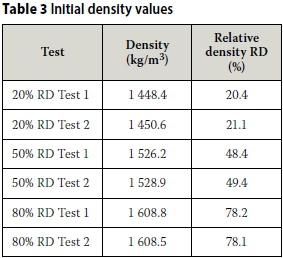
The initial densities obtained for the different tests are presented in Table 3, together with the corresponding relative density values. The values show that the initial values were within 2% of the target relative densities. The sand settlements measured at different acceleration levels during spin-up were used to calculate the in-flight densities in order to calculate the small-strain stiffness at each acceleration. The average relative density values obtained at 50 g for the 20% RD, 50°% RD and 80°% RD tests were 24.6%, 49.5% and 78.8% respectively.
Small-strain stiffness data
For the shear wave velocity measurements a ± 10 V continuous square wave with an input frequency of 25 Hz was used for the transmitting signal. The input frequency allowed the received signal to dissipate completely before the next signal was triggered to avoid interference occurring between two consecutive signals.
One of the difficulties with using bender elements in centrifuge modelling is the mechanical noise induced by the centrifuge itself. One of the methods used to mitigate this effect was to design a charge amplifier with electronic high- and low-pass filters to filter the unwanted mechanical noise. Although the filters gave enhanced in-flight received signals, the signal-to-noise ratio (SNR) was still low. To further increase the signal quality, signal stacking was used as a signal processing tool to increase the signal-to-noise ratio by summing successive signals. This increased the signal quality by reducing the effect of the mechanical noise induced by the centrifuge. Stacking is a common signal-processing tool which has been used with much success to improve the signal quality in noisy environments (Brandenberg et al 2006; Brandenberg et al 2008). A total of 60 stacks for each data set were found to be sufficient to reduce the background noise and obtain a clear signal.
Different methods are available for travel time determination. The most common techniques are measuring the time between the onset of the sender driving signal and detecting the first arrival at the receiver element (visual picking), travel time between two receivers some distance apart along the ray path detecting the same seismic event, as well as cross-correlation and cross-power spectrum methods (Leong et al 2005). For this project, the method of visual picking of the first arrival was used.
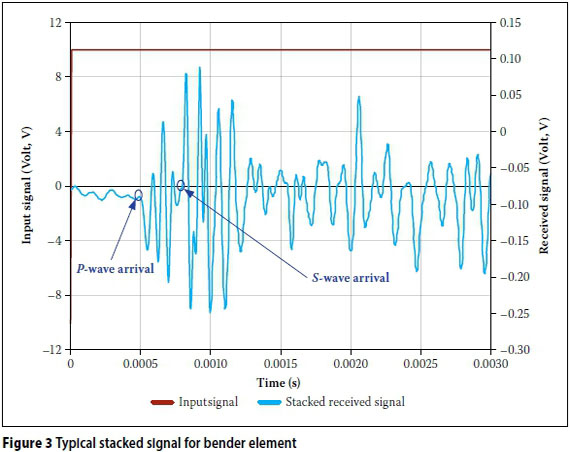
The stacking procedure was conducted for all the measurements, which amounted to a total of 90 bender- and extender-element measurements per soil profile. Compression (P) waves arrive before shear (S) waves since P-waves travel faster. After the stacking algorithm was run to process a data set, the first arrival was chosen. Figure 3 shows a typical bender element result after filtering and stacking. As shown in the figure, the first arrival is the P-wave, with the S-wave arriving some time later. The extender elements were used to detect the arrival time of the P-waves. The bender element tests also generated strong P-wave signals, and the comparison of the bender element and extender element time histories was used to identify the first arrivals of the P-waves and S-waves. Since the second wave set is the arrival of the S-wave, the first break of this set was taken as the first arrival for the S-wave velocity calculation. The analyses of all the signals were approached in this manner to obtain the first arrival times.
From the shear wave velocities and densities the small-strain shear modulus (G0) was determined at each depth. Figure 4 shows the G0vs depth results of the 20% RD tests. The depth values shown are the prototype depth scaled from the depths at which the bender elements were placed. Seed and Idriss (1970) suggested an empirical relationship between Goand mean effective stress (p'o) as Go = K (p'o)0.5where K = 8 000 for loose sand, and 12 000 for dense sand.
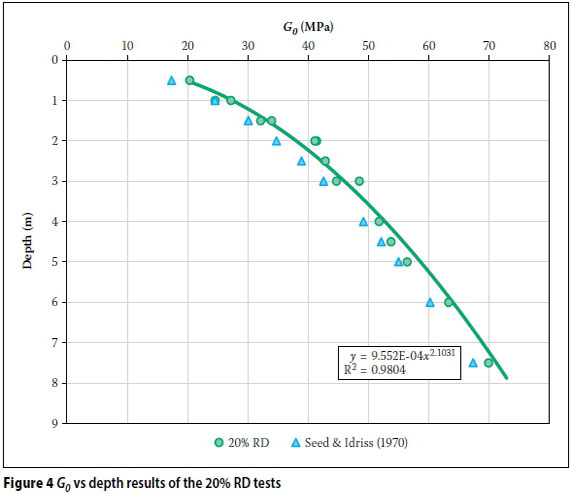
Also shown in Figure 4 is the values proposed by Seed and Idriss (1970) for loose sand, which can be seen to be in close proximity to the values obtained for the centrifuge tests.
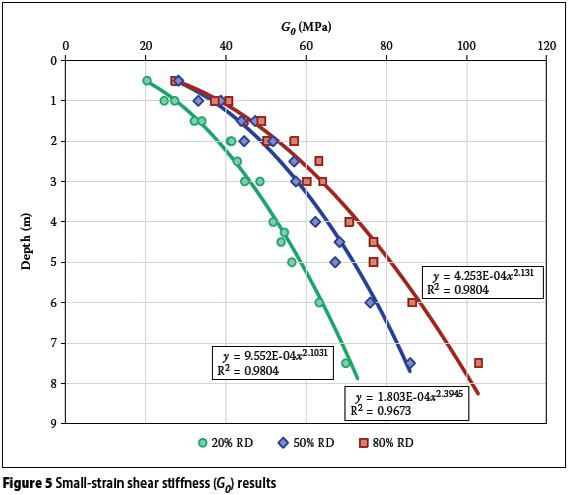
Figure 5 shows the small-strain stiffness results for the different density tests. Some scatter of the data is evident, but in general Go increased with depth and density as expected. The figure also shows the power function trend lines for the three different densities. The coefficient of correlation (R2) is also shown in the figure and the values indicate a good fit with the data for all three data sets. The power function equations were used to calculate the stiffness at the required depths below the foundation for the settlement analysis.
Load-settlement results
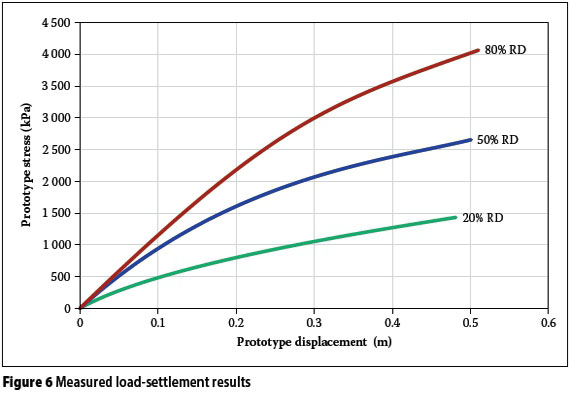
A total of six load-settlement tests were conducted, two tests for each density. The results were converted to the prototype scale, i.e. for a 5 m foundation. In practice, settlements larger than 10% of the diameter (D) are usually not tolerated (i.e. 0.1 D) and this study focused on the load-settlement behaviour up to a settlement of 0.1 D. The average load-settlement results for the two tests at each density were used, giving three data sets, one each for the 20°% RD, 50°% RD and 80% RD tests. The results are shown in Figure 6.
LOAD-SETTLEMENT ANALYSIS
The objective of this study was to assess whether the load-settlement curve for a shallow foundation on sand can be predicted using only small-strain stiffness data. This implies that no laboratory or in situ testing is required to obtain strength parameters or the ultimate bearing capacity. This is particularly useful for materials such as uncemented sands and gravels that are difficult to sample undisturbed.
A non-linear stepwise method was implemented to calculate foundation settlement, using the small-strain stiffness data and assuming axis-symmetrical conditions and uniform contact stress distribution for a circular footing. The methodology may be summarised as follows:
1. Determine the small-strain stiffness profile (Go or E'o) with depth from appropriate in situ or laboratory testing.
2. Subdivide the material below the foundation into layers to a depth below the influence zone of the foundation.
3. Assign E'o as initial drained Young's modulus for each layer. E'o may be calculated from Go and Poisson's ratio (v') as E'o = 2(1 + v')Go.
4. Quantify the maximum contact stress (q) between the foundation and the soil, as well as the number of load steps to be used.
5. Use Boussinesq's theory to calculate the vertical (Δσ'z) and horizontal (Δσ'r) effective stress increment at the centre of each layer beneath the centre of the foundation. For a circular foundation with radius (R) and uniform contact stress increment (Δq), the effective vertical and horizontal stress increments for a load step are calculated as follows:
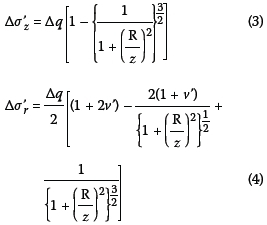
6. Calculate the vertical strain increment (Δεν) for the first load step for each layer using the appropriate E'o for each layer:
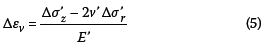
Calculate the shear strain increment assuming axis-symmetrical conditions:
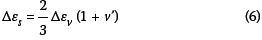
7. From the strain in each layer, and using an appropriate softening function, calculate the Young's modulus value at the end of the load step. This is the new Young's modulus for the next load step.
8. The process is repeated until the maximum applied contact stress is reached.
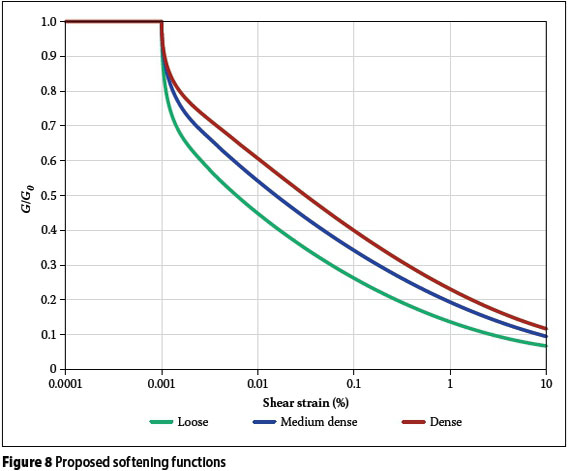
9. The change in thickness of each sub-layer is the layer thickness (Hi) multiplied by the total vertical strain (ενi) for the layer. And the total settlement is the sum of the change in thickness of all (i) sub-layers:
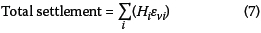
10. The load-settlement curve is constructed from the settlement for each load increment.
It should be noted that no specific stiffness degradation curve is associated with the method, and an appropriate stiffness degradation curve may be chosen by the analyst. For this study the hyperbolic softening function shown in Equation 1 was used. Since the load-settlement data was measured for different density sands, the variables for the softening function could be calibrated and the accuracy of the method assessed.
Load-settlement prediction
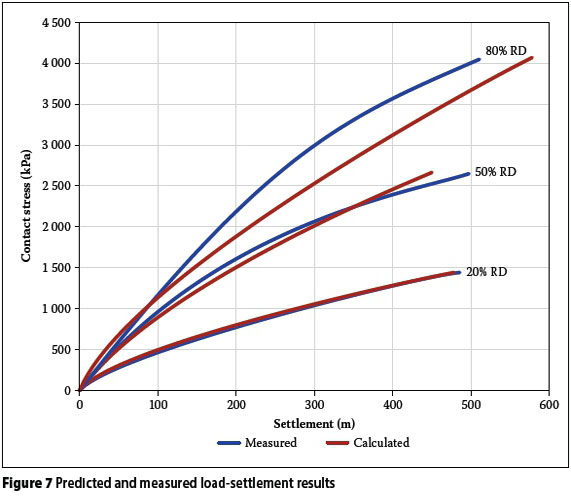
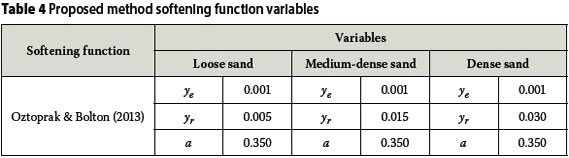
For each of the results shown in Figure 6, the proposed methodology was used to predict the stress-settlement curves. For the analyses presented in this paper, 1 000 load increment steps were used, with the maximum contact stress the same as the measured stress at a settlement of 0.1D. For the hyperbolic relationship shown in Equation 1 the elastic threshold strain (ye) was fixed at 0.001% strain, and the other two variables of the relationship (yrand n) were adjusted with the aim of finding the best fit between the measured and predicted curves. Figure 7 shows the results of the predicted and measured load-settlement curves. Table 4 shows the softening function variables for the different densities, and the softening functions are graphically represented in Figure 8. The measured and predicted curves agreed closely for the loose sand, and the level of agreement decreased as the density of the sand increased.
Prediction accuracy
It is clear from Figure 7 that there is good agreement between the 20% RD measured and predicted results. The accuracy does, however, decrease with increasing soil density. In order to assess the accuracy of the predicted results, the error between the measured and predicted settlement values was quantified with the following equation:

At small contact stresses the denominator in Equation 8 is small, and the equation becomes numerically unstable. Therefore only error values for applied contact stresses above 50 kPa were considered, since foundations are in most cases designed for loads above this value. The error values are shown in Figure 9. Positive errors indicate an over-estimation of the predicted settlement and negative errors indicate underestimation. As was seen from the load-settlement results shown in Figure 7, the maximum error increased with increasing soil density. The error ranged between -12% and 3% for loose sand, between -22% and 11% for medium-dense sand, and between -30% and 27% for dense sand.
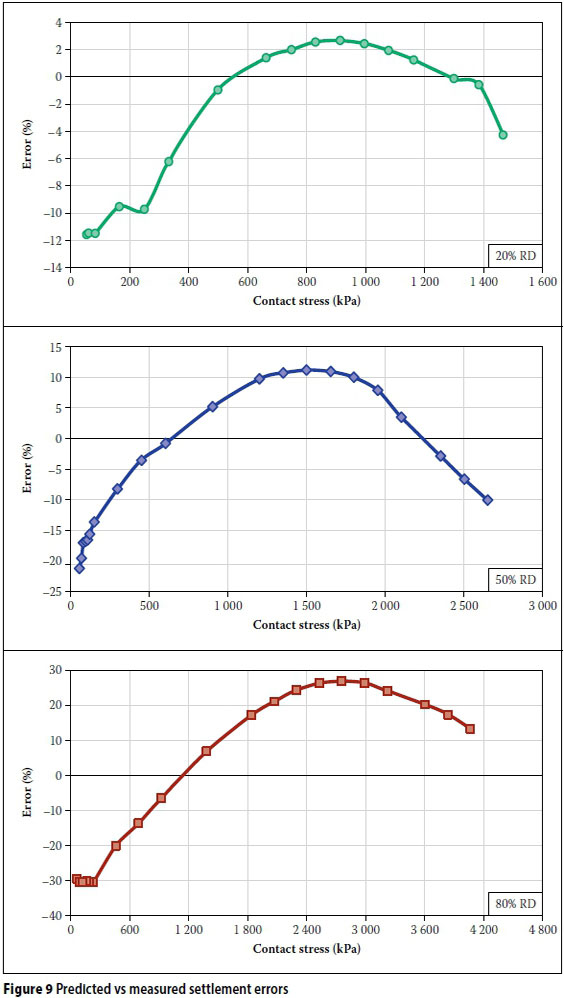
The differences in accuracy may be as a result of different mechanisms dominating when shallow foundations settle in loose and dense soils. It has been shown by numerous authors (e.g. Das 2009) that the settlement mechanisms below shallow foundations are significantly different for loose soils for which volumetric strains dominate (punching failure) and dense soils where shear strains are concentrated in shear bands, as assumed in classical bearing capacity plasticity analysis. The prediction model adopted in this paper is an elastic calculation that only requires stiffness as input parameter. This approach may be more applicable to a failure mechanism corresponding to loose soil, and therefore the increased accuracy. Due to the bearing capacity failure mechanism, settlement prediction on dense soil may require a strength component to be incorporated in the prediction model to increase the prediction accuracy. These are, however, only postulations and further research is required to fully understand the reason for the difference in accuracies.
CONCLUSIONS
Engineers continually strive to find methods which predict settlement of shallow foundations more accurately, because foundation settlement is often the governing aspect in design. With in situ and laboratory seismic testing becoming increasingly popular, settlement prediction methods utilising the initial small-strain stiffness are also becoming more common.
The objective of this study was to develop a foundation settlement prediction method that only requires the small-strain stiffness profile (Go or E0) as input soil parameters, and which may be applied to settlements of up to 10% of the foundation diameter (i.e. 0.1D). Centrifuge tests were conducted on an equivalent 5 m diameter circular shallow foundation using three different density sands to obtain measured load-settlement curves. The different density sands were loose, medium-dense and dense sands, and bender and extender elements were used to determine the small-strain stiffness profile below the foundation.
A non-linear stepwise method was proposed to predict the load-settlement behaviour of the foundation. The method requires a stiffness degradation curve, but is not bound by a specific stiffness degradation curve. Results were presented using a hyperbolic stiffness degradation curve for which the variables were calibrated to obtain the best fit for the different density sands.
From the results it is clear that the accuracy of the proposed method decreases as the density of the sand increases, and was found to be within 12% for loose sand, 22% for medium-dense sand and 30% for dense sand. The accuracy of the method should be judged in the context of the few input parameters required, the large range of settlement predictions up to 0.1D, as well as the large spectrum of soil densities for which it is applicable.
REFERENCES
Archer, A 2014. Using small-strain stiffness to predict the settlement of shallow foundations. MEng dissertation, Pretoria: University of Pretoria. [ Links ]
Brandenberg, S J, Choi, S, Kutter, B L, Wilson, D W & Santamarina, J C 2006. A bender element system for measuring shear wave velocities in centrifuge models. In: Ng, C, Wang, Y & Zang, L (Eds) Proceedings, 6th International Conference on Physical Modelling in Geotechnics, Hong Kong: Taylor and Francis. [ Links ]
Brandenberg, S, Kutter, B & Wilson, D 2008. Fast stacking and phase corrections of shear wave signals in a noisy environment. Journal of Geotechnical and Geoenvironmental Engineering, ASCE, 134(8): 1154-1165. [ Links ]
Campanella, R 1994. Field methods for dynamic geotechnical testing: An overview of capabilities and needs. In: Ebelhar, R, Drnevich, V & Kutter, B (Eds), Dynamic Geotechnical TestingII, ASTM STP1213. ASCE. [ Links ]
Canadian Geotechnical Society 2006. Canadian Foundation Engineering Manual, 4th ed. Canadian Geotechnical Society. [ Links ]
Clayton, C R I 2011. Stiffness at small strain: Research and practice. Géotechnique, 61(1): 5-37. [ Links ]
Clayton, C R I & Heymann, G 2001. The stiffness of geomaterials at very small strains. Géotechnique, 51(3): 245-256. [ Links ]
Das, B M & Sivakugan, N 2007. Settlements of shallow foundations on granular soil - An overview. International Journal of Geotechnical Engineering, 1(1): 19-29. [ Links ]
Das, B. 2009. Shallow foundations: Bearing capacity and settlement, 2nd ed. Boca Raton, FL, US: CRC Press. [ Links ]
Douglas, D J 1986. State-of-the-art. Ground Engineering, 19(2): 2-6. [ Links ]
Elhakim, A 2005. Evaluation of shallow foundation displacements using soil small-strain stiffness. PhD thesis, Atlanta, GA, US: Georgia Institute of Technology. [ Links ]
Elhakim, A & Mayne, P 2003. Derived stress-strain-strength of clays from seismic cone tests. In: Di Benedetto, H, Doanh, T, Geoffroy, H & Sauzéat, C (Eds), Deformation Characteristics of Geomaterials. Lyon, France: A A Balkema & Netherlands: Swets and Zeitlinger. [ Links ]
Jacobsz, S, Kearsley, E & Kock, J 2014. The geotechnical centrifuge facility at the University of Pretoria. In: Gaudin, C & White, D (Eds), Proceedings, 8th International Conference on Physical Modelling in Geotechnics, Perth, Austra lia: CRC Press. [ Links ]
Leong, E, Cahyadi, J & Rahardjo, H 2005. Measuring shear wave velocity using bender elements. Geotechnical Testing Journal, 28(5): 488-498. [ Links ]
Lutenegger, A & DeGroot, D 1995. Settlement of shallow foundations on granular soils. Research Report, Boston, MA, US: Massachusetts Highway Department. [ Links ]
Mayne, P & Poulos, H 2001. Approximate displacement influence factors for elastic shallow foundations - Closure. Journal of Geotechnical and Geoenvironmental Engineering, 127(1): 99-102. [ Links ]
Menzies, B 2000. Near-surface site characterisation by ground stiffness profiling using surface wave geophysics. In: Saxena, K & Sharma, V (Eds), Instrumentation in Geotechnical Engineering. H.C.Verma Commemorative Volume. New Delhi: Oxford and IBH Publishing Co. [ Links ]
Oztoprak, S & Bolton, M D 2013. Stiffness of sands through a laboratory test database. Géotechnique, 63(1): 54-70. [ Links ]
Rollins, K M, Evans, M D, Diehl, N B & Daily, W D III 1998. Shear modulus and damping relationships for gravels. Journal of Geotechnical and Geoenvironmental Engineering, ASCE, 124(5): 396-405. [ Links ]
Seed, H & Idriss, I 1970. Soil moduli and damping factors for dynamic response analyses. Research Report EERC70-10, Berkeley, CA, US: University of California. [ Links ]
Vucetic, M & Dobry, R 1991. The effect of soil plasticity on cyclic response. Journal of the Geotechnical Engineering Division, ASCE , 117(1): 89-107. [ Links ]
Woods, R D 1978. Measurement of dynamic soil properties. Proceedings, ASCE Geotechnical Engineering Division Specialty Conference -Earthquake Engineering and Soil Dynamics, Pasadena, CA, US: ASCE. [ Links ]
Yongqing, H 2011. Settlement of shallow foundation on cohesionless soil considering modulus degradation of soil. PhD thesis. Singapore: Nanyang Technological University. [ Links ]
 Correspondence:
Correspondence:
André Archer
Department of Civil Engineering
University of Pretoria
Pretoria 0002
South Africa
T: +27 (0)82 451 2195
E: andre.archer@up.ac.za
Prof Gerhard Heymann
Department of Civil Engineering
University of Pretoria
Pretoria 0002
South Africa
T: +27 (0)12 420 3627
E: gerhard.heymann@up.ac.za

ANDRÉ ARCHER completed his BEng degree in 2009 at the University of Pretoria, after which he joined Aurecon SA as a junior geotechnical engineer. He completed his BEng (Hons) degree during his time in the consulting industry and subsequently obtained his MEng degree. During his MEng studies he joined the academic environment as an assistant lecturer atthe University of Pretoria. His research interests include geotechnical laboratory testing and physical modelling in the geotechnical centrifuge. He is currently studying towards a PhD in Civil Engineering at the Hong Kong University of Science and Technology.

PROF GERHARD HEYMANN (Pr Eng, MSAICE) is a professor in the Department of Civil Engineering at the University of Pretoria. He holds BEng, BEng (Hons) and MEng degrees from the University of Pretoria, and a PhD from the University of Surrey. He has been involved with teaching and research in geotechnical engineering forthe past 24 years. His fields of interest include the characterisation of soil behaviour and its application in geotechnical engineering. He is a past chairman of the Geotechnical Division and is currently Editor-in-Chief of the Journal of the South Afrcan Institution of Civil Engineerng.














