Servicios Personalizados
Articulo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares en Google
Similares en Google
Compartir
Journal of the South African Institution of Civil Engineering
versión On-line ISSN 2309-8775
versión impresa ISSN 1021-2019
J. S. Afr. Inst. Civ. Eng. vol.57 no.2 Midrand abr./jun. 2015
http://dx.doi.org/10.17159/2309-8775/2015/v57n2a3
TECHNICAL PAPER
A proposal for the probabilistic sizing of rainwater tanks for constant demand
J E Allen; J Haarhoff
ABSTRACT
In recent years there has been an international trend towards installing rainwater tanks in an attempt to save water. This study investigates the possibility of simplifying the process of sizing a rainwater tank for optimal results under constant water demand. The required size of a rainwater tank is influenced by the Mean Annual Precipitation, the size of the roof which is being used for harvesting, the water demand, the desired certainty of supply and the rainfall patterns. The study investigates the use of a generalised equation of the form y = a(x - 1)b + c, where x is a runoff parameter, y is a storage parameter and a, b and c are constants which differ for each location, depending on rainfall characteristics. Results obtained using the generalised equation are compared to results obtained by simulating tank behaviour over a 16-year period (1994-2009) at three rainfall stations. The results suggest that such an equation can be used to estimate the storage capacity of a rainwater tank.
Keywords: Tank sizing, rainwater harvesting, probalistic sizing
INTRODUCTION
The advantages of rainwater tanks to meet domestic demand are obvious, as mirrored by the international trend towards including rainwater tanks in water conservation strategies. It is therefore surprising that there are relatively few locations in South Africa where rainwater tanks have been systematically incorporated into new housing developments. The resistance to their wider adoption may be due to a lack of clear and simple guidelines of how they should be sized, and their associated risk of failure. The paper will briefly review the available methods for rational tank sizing and then propose a simplified framework for local application. The proposed procedure will be demonstrated by a design example for three selected locations in South Africa.
EXISTING APPROACHES TO RAINWATER TANK SIZING
The models previously proposed in the literature rely on three different approaches. Both the demand side approach (Centre for Science and Environment) and the supply side approach (Rees & Ahmed 2002) require information on the rainfall pattern, which can be obtained from historical data. The demand side approach starts with the daily water requirement, and sizes the tank according to the longest consecutive number of days without rain, whereas the supply side approach is based on the premise that all the available water running from the roof should be harvested. The latter therefore isolates the wet season from the remainder of the year, and then suggests a tank size to contain all the runoff during the wet season. Both these methods have obvious weaknesses. The demand side approach assumes that the roof is large enough to fill the tank prior to the dry season, therefore possibly leading to a less reliable supply. The supply side approach only considers the available water, even if it is much more than the demand, therefore possibly leading to an overly large and expensive storage tank.
A variation on the demand side approach for sizing rainwater tanks has been developed in the United Kingdom (Fewkes & Warm 2000). The method requires the calculation of an input ratio, which is defined as A*(MAP)/D, where A is the catchment area, MAP is the mean annual precipitation and D is the average annual demand. This ratio is then used along with a desired performance level to determine the number of days' storage that ought to be provided by means of a set of design curves. Each design curve shows the storage period versus the volumetric reliability for a specific value of the input ratio. The justification for using only one curve for a given input ratio comes from the fact that very little difference exists in the United Kingdom from one location to another (Fewkes & Warm 2000).
The United Kingdom's Environment Agency recommends a method which combines the supply and demand side approaches. The method determines the required size of the tank as being either a user-defined percentage of the MAP (5% is suggested for the UK), or of the average annual demand, whichever is smaller (Ward et al 2010). Ward et al (2010) state that the size is then calculated as:
S = P.A.CpF.MAP (1)
Where:
P = user defined percentage
A = area of the roof
CF= runoff coefficient
F = system filter efficiency
MAP = mean annual precipitation
The runoff coefficient is a function of the roof surface and gutter integrity, and is usually taken as close to 1 for impervious roof materials. The system filter efficiency is determined by the presence and nature of a filtering device included for water quality purposes before the storage tank. If D < MAP, MAP would be replaced by the annual demand (D).
The mathematical simulation of the tank level provides a third approach which eliminates the main weaknesses of the other two approaches, but it requires a detailed rainfall record covering at least ten years, preferably longer. It furthermore requires more computational effort, which is only possible with computer simulation. A number of computer models which are capable of doing such a simulation are available. These include the Model for Urban Stormwater Improvement Conceptualisation (MUSIC), Aquacycle and Raincycle (Ward et al 2010). The mathematical simulation approach, however, has the additional power of coupling the reliability of supply with the tank size, which is a prerequisite when considering rainwater tanks for domestic water supply.
SIMPLIFYING THE PROCESS
Rainwater tank sizing to meet constant demand, in its simplest form, reduces to finding a mathematical relationship linking five key variables:
■ The rate at which water is withdrawn from the tank, expressed as a constant daily withdrawal, or annual average daily demand (AADD) in ℓ/d. Where water is used for indoor demand and the number of inhabitants stay the same, the assumption of constant demand is reasonable.
■ The supply security (S), expressed as the fraction of the total water demand met by the tank. If secondary or emergency supplies with tankers, for example, are available, the supply security could typically be around say 90%. In the absence of secondary supplies, the required supply security should be higher, say around 98%.
■ The roof plan area (aerial view) from which the water is harvested, expressed in m2.
■ The tank volume (V), expressed in ℓ.
■ The mean annual precipitation (MAP), expressed conventionally in mm/year.
The first simplification is to combine A and the MAP to get the total volume of harvest-able water in a year, and to express this as a ratio of the total water demand in a year. This is called the runoff parameter X. Using the units provided above:
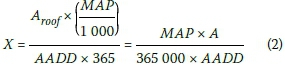
If the runoff parameter X would be 1, the total water harvested from a roof in an average year would be just enough to provide the total annual water demand. This provides the theoretical lower limit of X. To account for the fact that (a) the annual rainfall is variable from year to year, and (b) that the rainfall is unevenly distributed within any year, X has to be in excess of 1.
The second simplification is to introduce the storage parameter Y, linking V and the AADD:
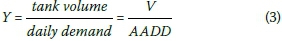
The storage parameter Y, in practical terms, simply provides the number of days of average demand that can be supplied from a full tank, provided no water flows into the tank. Y also has a lower limit determined by the length of the longest dry spell during the year, which corresponds to the volume predicted by the demand side approach reviewed earlier.
The proposed simplifications reduce the tank sizing problem to three parameters, namely the:
■ Runoff parameter (X)
■ Storage parameter (Y)
■ Supply security (S)
The idea of simplifying the process in this way is not altogether a new one. As mentioned above, Fewkes and Warm (2000) used a simplifying parameter A*MAP/D, which is equal to the runoff parameter X, suggested above. Ghisi (2010) developed a ratio F, which is the inverse of the runoff parameter.
THE SUGGESTED MATHEMATICAL RELATIONSHIP
It is intuitive that there should be an inverse relationship between X and Y - a larger, more continuous supply of water from the roof will obviously require less storage. In addition, for both X and Y, asymptotic limits exist. As the runoff parameter X approaches 1, the required tank size, and thus the storage parameter Y, will approach infinity, as no water may be lost by spillage. On the other hand, as the storage parameter Y approaches its lower limit, the runoff parameter X will approach infinity, as the tank has to be completely filled by even the very small rainfall events, thus requiring a very large roof surface.
From the above the general relationship follows, as shown in Figure 1.
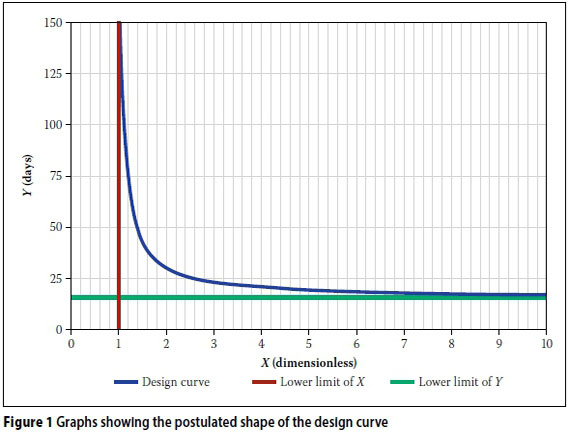
The relationship in Figure 1 follows a power curve of the general form:
Y = aXb (4)
By incorporating the asymptotic limits discussed above the following equation is obtained:
Y = a(X - 1)b+ c (5)
Where:
Y = storage parameter, defined above
X = runoff parameter, defined above
a, b, c = constants specific to each graph
SIMULATING THE BEHAVIOUR OF A RAINWATER TANK
Volume balance approach
The mathematical simulation of a rainwater tank is based on a volume balance approach. The idea is simply that the volume of water in the tank at the end of a given time-step must be equal to the volume of water in the tank at the beginning of the time-step (end of the previous time-step), after accounting for addition of the volume of water that has entered the tank, and subtracting the volume that has left the tank during the same time-step. Mathematically (Ming-Daw et al 2009; Kennedy & Male 2006):
Vt = Vt-1 + Qt- Dt (6)
This is subject to the constraint that the maximum volume of water in the tank is limited to the size of the tank:
0 ≤ Vt≤ S (7)
Where:
Vt= volume of rainwater in the tank at the end of time interval t
Qt= volume of rainwater that enters the tank during time interval t
Dt= (volume of water that is removed from the tank) during time interval t
S = maximum storage capacity
Yield-after-spill and yield-before-spill
In order to simulate the behaviour of a rainwater tank, rainfall data was used as an input with a preselected roof area, tank volume and water consumption from the tank, to obtain the reliability of the water supply from the tank for the selected parameters. In order to obtain an exact representation of the rainwater tank it is necessary to add rain to the tank and simultaneously subtract the water demanded from the tank. When working with discretised time intervals, the calculation sequence of inflow, spillage and outflow is important. Two different approaches can be used:
The first option is the yield-after-spill option. For this option the rainwater is added to the tank and the spillage is immediately removed by limiting the tank volume. The water demanded from the tank is then removed at the end of the same time-step, from a volume which can never exceed the maximum storage volume. In reality the water could be removed and rainwater added to the tank simultaneously. This could mean that the maximum limit would not be reached in reality, even though computationally it is reached. When spillage does occur, this option effectively decreases the tank capacity and, thus, underestimates the amount of water which can be supplied by the tank. For this approach the following equations can be used to determine the yield from the tank and the volume of water in the tank (Liaw & Tsai 2004; Palla et al 2011):
Yt= min{Dt; Vt-1} (8)
Vt= min{Vt-1+ Qt- Yt; S - Yt} (9)
Where:
Yt= yield from the tank during the time interval t
The second approach, the yield-before-spill approach, effectively does not allow the tank to spill during the time-step. It collects all the inflow, and satisfies the full demand first. If any surplus remains at the end of the time-step, this surplus is spilled. This has the opposite effect on the tank capacity and thus overestimates the water which can be supplied by the tank. This approach is described by the following equations (Liaw & Tsai 2004; Palla et al 2011):
Yt= min{Dt; Vt_1+ Qt} (10)
Vt= min{Vt-1+ Qt- Yt; S} (11)
The difference between the water supply reliability calculated by the two methods is typically approximately 0.3%. However, when small tank sizes are investigated, spillage will occur more often and the difference in reliability obtained from the two methods may be as high as 3%.
CALIBRATING THE EQUATION
The structure of the proposed equation was tested by simulating the behaviour of a rainwater tank at three stations (Kimberley, Mossel Bay and Rustenburg). The stations were selected to include both seasonal and year-round rainfall regions, as well as differences in mean annual precipitation. The simulations were conducted using daily rainfall data over a 16-year period (1994-2009), obtained from the South African Weather Services. The validity of the equation was tested at S = 90%, S = 95°% and S = 98%, using the method for simulating a rainwater tank, as described above. Each simulation was done using both the yield-after-spill and the yield-before-spill approaches, and their average value was then used for model calibration.
The parameters a and b were determined with least-square fitting of the simulated data points. Figures 2, 3 and 4 show the resulting graphs for the three stations in solid lines, as fitted to the data set shown with markers. The coefficient of determination for each of the fitted graphs to its corresponding data set was also calculated.
RESULTS
Table 1 provides a measure of the goodness-of-fit of the proposed equation. All the results show coefficients of determination of more than 94%, which is considered to be adequate for design purposes, given the inherent variability and deficiencies of the available hydrological records. Figures 2 to 4 also show a relatively sharp inflection point at a storage parameter of about X = 2, which means that the equation should be restricted to values of X > 2.
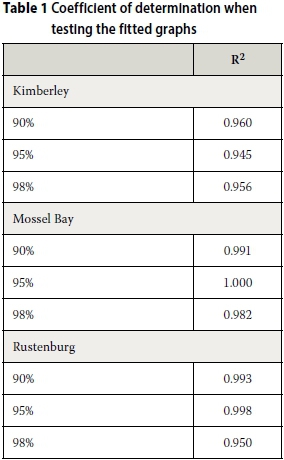
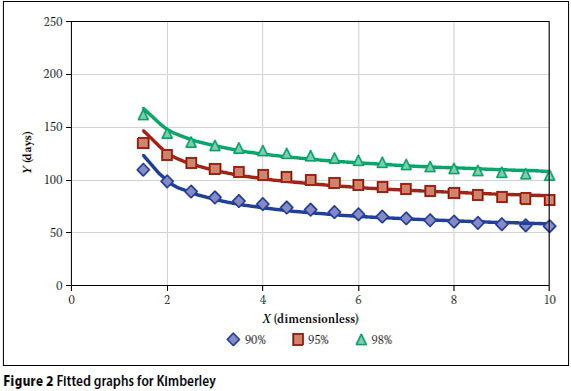
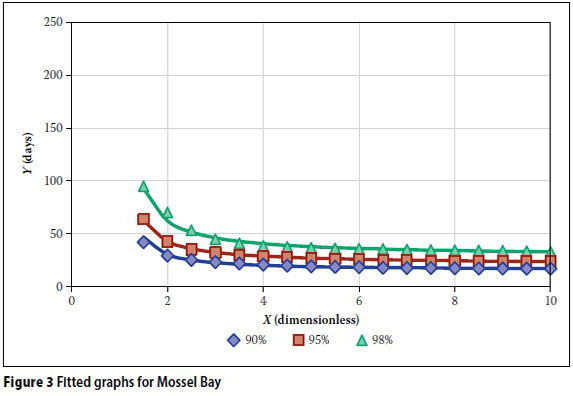
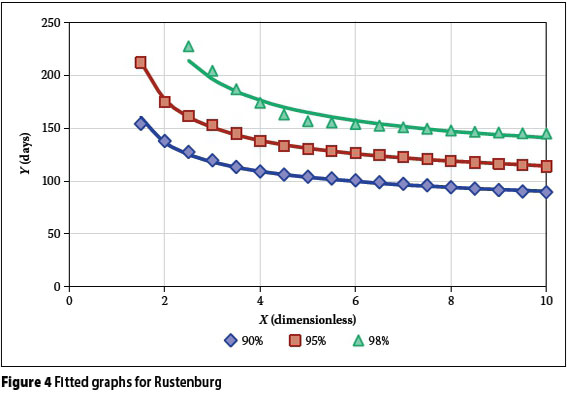
Table 2 shows the results for the total AADD that can be supplied by a tank for various combinations of roof area, tank volume, certainty of supply and location. The results were obtained by using the equations determined by using the simplifications discussed above. The roof area and tank volume were substituted into the relevant equation for the location and certainty of supply, and a solver was then used to determine the maximum AADD that could be obtained from the tank.
The results show clearly that there is no correlation between the MAP and the AADD that can be supplied. The MAP for Mossel Bay (532 mm) and the MAP for Rustenburg (579 mm) are much closer to each other than the MAP for Kimberley (428 mm). However, the AADD which can be supplied at Rustenburg is much closer to the results obtained for Kimberley than those obtained for Mossel Bay. The sizing of rainwater tanks is therefore more dependent on the seasonal variability of the rainfall than on the MAP. The only way to take this into account for a large region like South Africa, with its significant differences in rainfall characteristics, is to work from first hydrological principles as done in this paper.
The results also show clear links between the AADD that can be supplied, the roof area and the tank volume. As expected, the AADD will increase as the roof area increases, but the increase is significantly larger when a larger tank is used. This is due to the fact that increasing the roof area will have no effect if the tank is not large enough to store the increased volume of runoff. The effect of a larger roof area, however, is smaller when the certainty of supply is increased. Increasing the tank volume will also create an increase in the AADD that can be supplied. Similar to an increase in roof area, the increase in AADD is larger when the tank volume is larger. The equations that are obtained by using the simplifications discussed above thus account adequately for changes in roof area, tank volume, certainty of supply and location.
APPLICATION EXAMPLE
Consider a typical low-cost housing development with the roof areas of individual homes being 65 m2. Estimate the constant daily demand that can be harvested if every home is supplied with a storage tank of 3 000 ℓ. The calculations are shown in tabular form in Table 3.
CONCLUSION
■ The results of the study show that an equation of the form Y = a(X-1)b + c can be fitted to simulated data for rainwater tanks with a minimum coefficient of determination of 0.94. Rainwater tank sizing can therefore be performed with good precision in terms of a storage parameter Y and runoff parameter X.
■ The determination of the constants a, b and c requires a long, reliable record of daily rainfall records. The analysis presented for three randomly selected sites in South Africa needs to be extended to more South African sites before general expressions for the constants may be determined.
■ The amount of annual rainfall seems to be less critical for rainwater tank sizing than its seasonal variation, which further underlines the need for analysis at different sites.
■ The design examples for the three reported sites indicate that rainwater tank harvesting could go a long way in providing the domestic demand of developing communities, and therefore deserves closer scrutiny by water supply engineers.
FUTURE RESEARCH
The current study assumed that 100% of the rain which falls on a roof is available for collection. However, in reality this is not the case. Losses are created by the uneven texture of the roof, the guttering system used, as well as possible evaporation losses. The study also did not consider the effect of a water treatment system, such as a first flush system, which will also create losses in the system. Further research should be done to refine the suggested equation when these losses are considered.
REFERENCES
Centre for Science and Environment. n.d. Design of storage tanks. Available at: http://www.rainwaterharvesting.org/urban/design_storage.htm [accessed on 8 October 2011]. [ Links ]
Fewkes, A & Butler, D 2000. Simulating the performance of rainwater collection and reuse systems using behavioural models. Building Services Engineering Research and Technlogy, 21(2): 99-106. [ Links ]
Fewkes, A & Warm, P 2000. A method of modelling the performance of rainwater collection systems in the UK. Building Services Engineering Research and Technology, 2(4): 257-265. [ Links ]
Ghisi, E 2010. Parameters influencing the sizing of rainwater tanks for use in houses. Water Resources Management, 24(10): 2381-2403. [ Links ]
Kennedy, J W & Male, M S 2006. Reliability of rainwater harvesting. Eco-Architecture: Harmonisation between Architecture and Nature, 86: 391-400. [ Links ]
Liaw, C & Tsai, Y 2004. Optimum storage volume of rooftop rain water harvesting systems for domestic use. Journal of the American Water Resources Association, 40(4): 901-912. [ Links ]
Ming-Daw, S, Chun-Hung, L, Ling-Fang, C, Jui-Lin, K & Mei-Chun, L 2009. A probabilistic approach to rainwater harvesting systems design and evaluation. Resources, Conservation and Recycling, 53: 393-399. [ Links ]
Palla, A, Gnecco, I & Lanza, L 2011. Non-dimensional design parameters and performance assessment of rainwater harvesting systems. Journal of Hydrology, 40(1): 65-76. [ Links ]
Rees, D & Ahmed, S 2002. Rainwater harvesting. The Schumacher Centre for Technlogy and Development. Available at: http://practicalaction.org/docs/technical_information_service/rainwater_harvesting.pdf [accessed on 8 October 2011]. [ Links ]
Ward, S, Memon, F & Butler, D 2010. Rainwater harvesting: Model-based design evaluation. Water Science and Technology, 61(1): 85-96. [ Links ]
 Correspondence:
Correspondence:
Jacqui Allen
SMEC South Africa
Urban Development PO Box 1462
Pinegowrie 2123
South Africa
T: +27 (0)11 369 0759
E: Jacqui.Allen@smec.com
Dr Johannes Haarhoff
50A Cradock Street
Graaff-Reinet 6280
South Africa
T: +27 76 569 0852 / +27 (0)49 891 0473
E: johannes@haarhof.org.za

JACQUI ALLEN obtained a degree in Civil Engineering from the University of Johannesburg in 2008 and a Master's in Civil Engineering from the same university in 2012. Her research focused on tank sizing for roof top rainwater harvesting. She is currently working as a civil engineer for SMEC South Africa.

DR JOHANNES HAARHOFF graduated as a civil and environmental engineer at the University of Stellenbosch, South Africa, and Iowa State University, USA. He spent the first part of his career in municipal employ, civil construction, and design and project management, before joining the University of Johannesburg in 1990, where he led the Water Research Group. This group focuses on both applied and fundamental aspects of drinking water treatment and supply.














