Serviços Personalizados
Artigo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em Google
Similares em Google
Compartilhar
Journal of the South African Institution of Civil Engineering
versão On-line ISSN 2309-8775
versão impressa ISSN 1021-2019
J. S. Afr. Inst. Civ. Eng. vol.57 no.1 Midrand Jan./Mar. 2015
http://dx.doi.org/10.17159/2309-8775/2015/v57n1a2
TECHNICAL PAPER
Review of current methods for estimating areal reduction factors applied to South African design point rainfall and preliminary identification of new methods
J P J Pietersen; O J Gericke; J C Smithers; Y E Woyessa
ABSTRACT
Design point rainfall estimates assume a uniform distribution of rainfall over a catchment, and hence are only representative for a limited area. For larger areas, areal reduction factors (ARFs) are used to convert design point rainfall depths/intensities to an average areal design rainfall depth/intensity for a catchment-specific critical storm duration and catchment area. This paper presents a review of ARF estimation methods used nationally and internationally, with comparisons of the South African methods in the C5 secondary drainage region using standard input variables. The comparison of different ARF estimation methods confirmed that the empirical methods adopted for general use in South Africa are based on a limited database of observed rainfall data and are used without local correction factors beyond their original developmental regions. This results in the characterisation of the actual rainfall process over a catchment, and translation into questionable design peak discharge estimates. Therefore, the ARFs in South Africa need to be re-investigated in the light of recent extreme flood events, utilising the longer periods of record and denser rain-gauge networks which are now available for analysis. The variation of ARFs with return period and with rainfall producing mechanisms also needs to be investigated. Updated ARFs developed and verified using local rainfall data will improve the accuracy of design hydrology for large catchments in South Africa when event-based rainfall-runoff deterministic methods are used.
Keywords: areal reduction factor, areal design rainfall, critical storm duration, design point rainfall, return period
INTRODUCTION
In flood hydrology, the practising engineer or hydrologist frequently needs to estimate catchment design rainfall, i.e. rainfall information derived from observed rainfall data which comprises a depth or intensity, and duration associated with a given return period (T) or annual exceedance probability (AEP) (Gericke & Du Plessis 2011). However, design point rainfall estimates assume uniform spatial rainfall in a catchment, and hence are only representative for a limited area. For larger areas, areal reduction factors (ARFs) are used to convert design point rainfall depths/intensities into an average areal design rainfall depth/intensity for a particular critical storm duration and catchment area (Alexander 2001).
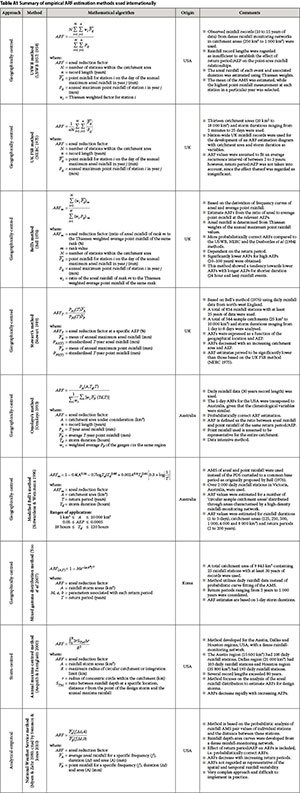
ARFs are estimated using either empirical and/or analytical methods. In many countries, the current ARF approaches are mostly based on empirical methods, using either storm-centred or geographically-centred approaches. Studies into the large-scale estimation of ARFs have generally been limited to the United States of America (USA) (USWB 1957; 1958), the United Kingdom (UK) (NERC 1975) and Australia (Siriwardena & Weinmann 1996). Despite these studies, ARFs are still regarded as inconsistent in most cases, mainly as a consequence of the variation in predominant weather types, storm durations, seasonal factors and recurrence interval (Skaugen 1997; Asquith & Famiglietti 2000; Allen & DeGaetano 2005). Omolayo (1993) identified insufficient rain-gauge networks and a lack of short duration (sub-daily) rainfall data as the main reasons behind the limited research in this field and the inconsistent results.
According to Asquith and Famiglietti (2000), the storm-centred approaches have not seen widespread application, due to the difficult inclusion of multi-centred storms. Omolayo (1993) indicated that storm-centred approaches are not suitable for estimating areal design rainfall from design point rainfalls, since extreme design point rainfall and extreme areal design rainfall are unlikely to be produced by the same rainfall event or rainfall type.
The empirical methods used to estimate ARFs in South Africa are based on the limited research conducted using a storm-centred approach, e.g. Van Wyk (1965) and Wiederhold (1969), and a geographically-centred approach, e.g. Alexander (1980; 2001). The latter attempt is based on the United Kingdom Flood Studies Report (UK FSR) methodology (NERC 1975) using observed daily rainfall data up until the 1980s. There has also been a concern in the hydrological community in South Africa that the UK FSR results may not be appropriate to South African conditions.
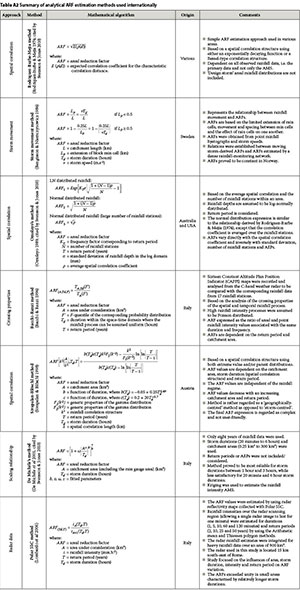
During the last three decades, several new analytical methods have been proposed to estimate ARFs, e.g. storm movement (Bengtsson & Niemczynowicz 1986), crossing properties (Bacchi & Ranzi 1996), spatial correlation structure (Sivapalan and Bloschl 1998) and scaling relationships (De Michéle et al 2001). According to Svensson and Jones (2010), the level of agreement between the empirical and analytical methods currently in use is limited to a specific scaling regime, namely short storm durations and small catchment areas. Thus, these methods are regarded as inappropriate to use over a wide range of temporal and spatial scales, e.g. small catchment to a quaternary catchment level. On the other hand, a number of these empirical (storm-centred) and analytical (correlation-based and annual maxima-centred) methods do not provide probabilistically correct areal design rainfall estimates, as it is assumed that the AEP of both the point and areal rainfall is similar. Most of these methods are also based on a limited amount of observed rainfall data and use assumptions that are not entirely true descriptions of the actual rainfall process (Svensson & Jones 2010).
This paper provides preliminary insight into the applicability of the various methods used in South Africa and internationally to estimate ARFs. The objectives of the study reported in this paper are discussed in the next section, followed by an overview of the location and characteristics of the pilot study area. Thereafter, the methods used to estimate ARFs are reviewed. The methodologies involved in assessing the objectives are then expanded on in detail, followed by the results, discussion and conclusions.
OBJECTIVES OF STUDY
The objectives of this study are:
i. to review the ARF estimation methods currently used nationally and internationally, with emphasis on the inconsistencies introduced by the use of different approaches;
ii. to assess a selection of graphical and numerical ARF estimation methods used in South Africa, using standard input variables, e.g. catchment area, critical storm duration and rainfall intensity, in order to provide preliminary insight into the consistency between methods; and
iii. to compare the results from applying the selected ARF estimation methods using the C5 secondary drainage region of South Africa as a pilot study in order to confirm or to reject the results as established in (ii).
In this study it was hypothesised that:
i. The graphical ARF estimation methods used in South Africa, as listed in Table 1, need to be updated with the longer data sets currently available compared to data used in their development, and these updates may influence the accuracy of the resulting average areal design rainfall and subsequent peak discharges as estimated with different design flood estimation methods.
ii. Most of the numerical ARF estimation methods used in South Africa are probabilistically incorrect, since these methods were derived from the original graphical ARF estimation methods, and possible differences between the recurrence intervals of point and areal design rainfall are not accounted for. In addition, the variation of ARFs with recurrence interval and rainfall-producing mechanisms is also not clearly understood. However, numerical ARF estimation methods are frequently used in practice due to the ease of calculation of the ARF, irrespective of the possible errors that could be introduced in doing so.
The recent compilation of the South African National Roads Agency Limited (SANRAL) Drainage Manual (SANRAL 2013), which is regarded by many practising engineers as an authoritative reference document, still proposes the use of these 'outdated' ARF estimation methods. This recent publication, along with the shortcomings identified during the literature review conducted on ARFs, served as a further motivation for this study.
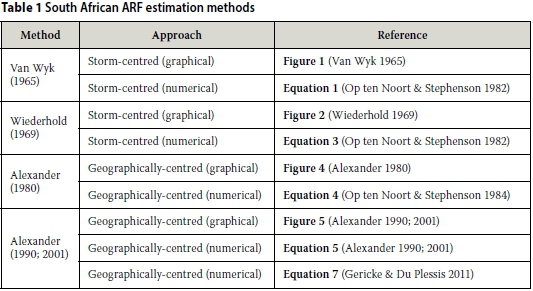
REVIEW OF SOUTH AFRICAN ARF ESTIMATION METHODS
The following subsections provide a review of the storm-centred and geographically-centred empirical ARF estimation methods currently used in South Africa.
Storm-centred ARF estimation methods
Van Wyk's method (1965)
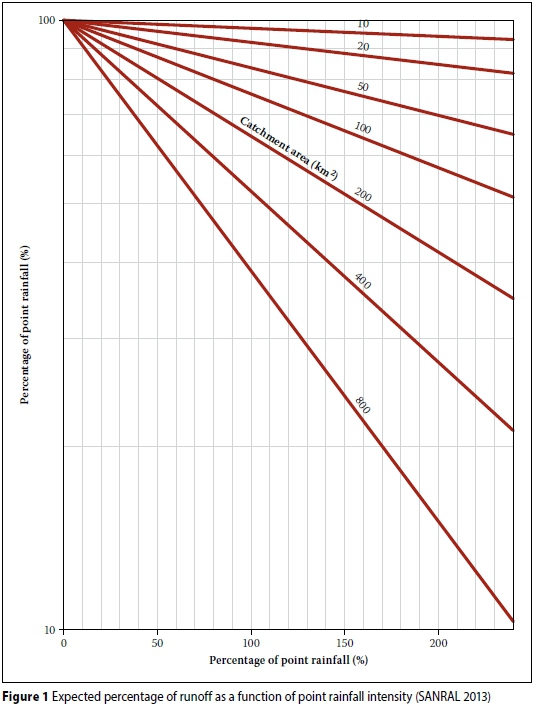
The first South African attempt to analyse ARFs based on a storm-centred approach was conducted by Van Wyk (1965; cited by Lambourne & Stephenson 1986) on a small scale (catchment areas ≤ 800 km2) in the Pretoria region, Gauteng. In addition, a few rainfall storm areas from the USA and Canada were also analysed for comparison purposes. Isohyetal maps of several storms were plotted based on the average areal rainfall depths in catchments ranging from 10 km2 to 800 km2 centred on the maximum point rainfall and expressed as a percentage of point rainfall at the storm centre. The ARFs were also expressed as a function of the point source rainfall intensity, i.e. an average intensity over the storm duration at the storm centre. As a result, depth-intensity-area envelope diagrams (Figure 1) were developed, as included in the Drainage Manual (SANRAL 2013). In small catchment areas (≤ 800 km2) the ARF is mainly a function of the area and design point rainfall intensity, since the relationship between rainfall intensity and the infiltration rate of the soil is predominant (Alexander 2001; SANRAL 2013).
Op ten Noort & Stephenson (1982) converted the ARF diagrams in Figure 1 to a mathematical algorithm (Equation 1) using regression analysis.
ARF = Exp(-0.000068 iA0.77) (1)
where:
ARF = areal reduction factor for point rainfall (fraction)
A = catchment area (km2), and
i = point rainfall intensity at the storm centre (mm.h-1).
Wiederhold's method (1969)
In the late 1960s, Wiederhold (1969; cited by Lambourne & Stephenson 1986) used a variable location, storm-centred approach, i.e. a modified version of Van Wyk's (1965) method to establish ARFs for 170 storms over large catchment areas between 500 km2 and 30 000 km2 within 18 regions delineated for South Africa. In these medium to large catchment areas (≤ 30 000 km2), the ARF is mainly a function of the area and storm duration, since the quantity of rainfall relative to the number of storage areas is of great importance (Alexander 2001; SANRAL 2013). The large area storms were delineated, while the point rainfall depths at each rainfall station were used to fit a sixth-order polynomial surface to enable the plotting of isohyets. Regionalised depth-area curves were produced for each storm with a time resolution of one day, resulting in co-axial diagrams to estimate the rainfall equalled or exceeded for storm durations of one day or longer. In the case of large area storms with associated storm durations less than 24 hours, the areal average rainfall over increasing areas (durations of one to six days) within each of the 18 regions were expressed as percentages of the maximum point rainfall observed. Depth-area curves were produced for durations of one to six days. Conservative upper envelope curves (of individual durations) were then re-plotted to produce depth-duration-area curves. Thereafter, the 24 hour to one hour durations were linearly extrapolated through these points to express the rainfall associated with a given area as a proportion of the point rainfall between one and 72 hours (Lambourne & Stephenson 1986). As a result, depth-duration-area ARF diagrams (Figure 2) for short to medium duration and large area storms were developed as included in the Drainage Manual (SANRAL 2013).
Op ten Noort and Stephenson (1982) converted the ARF diagrams in Figure 2 to a mathematical algorithm (Equation 2) using regression analysis.
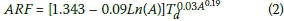
where:
ARF = areal reduction factor for point intensity (fraction),
A = catchment area (km2), and
Td= storm duration (hours).
Op ten Noort and Stephenson (1982) compared Equations 1 and 2 and established that the use thereof could cause a discontinuity in storm runoff estimation. Subsequently Figure 2 was extrapolated so that the ARFs approach unity at short durations. This relationship is expressed in Equation 3.
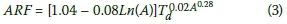
where:
ARF = areal reduction factor for point intensity (fraction),
A = catchment area (km2), and
Td= storm duration (hours).
Geographically-centred ARF estimation methods
Alexander's method (1980; 2001)
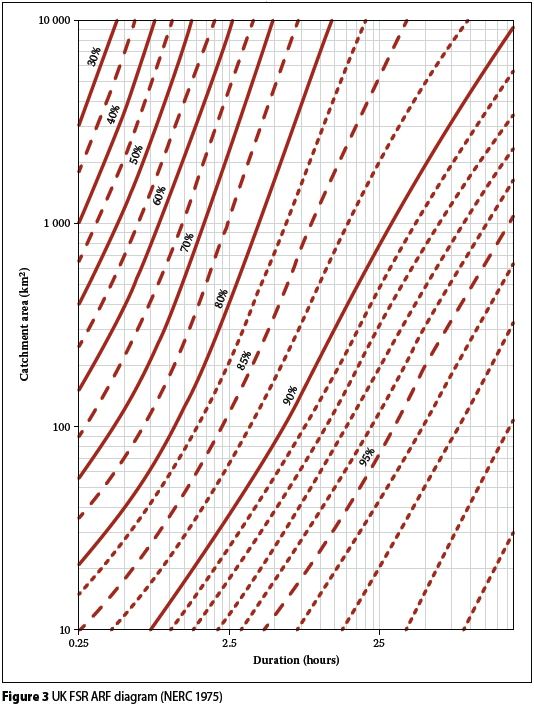
Alexander (1980) developed a geographically-centred ARF relationship based on the ARF diagrams (Figure 3) contained in the UK FSR (NERC 1975). Alexander (1980) claimed that the developed ARF diagram (Figure 4) should be used when uniform temporal and spatial rainfall distribution over a catchment is assumed.
Op ten Noort (1984; cited by Lambourne & Stephenson 1986) converted these ARF diagrams (Figure 4) to a mathematical algorithm (Equation 4) using regression analysis.
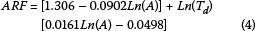
where:
ARF = areal reduction factor (%),
A = catchment area (km2), and
Td= storm duration (hours).
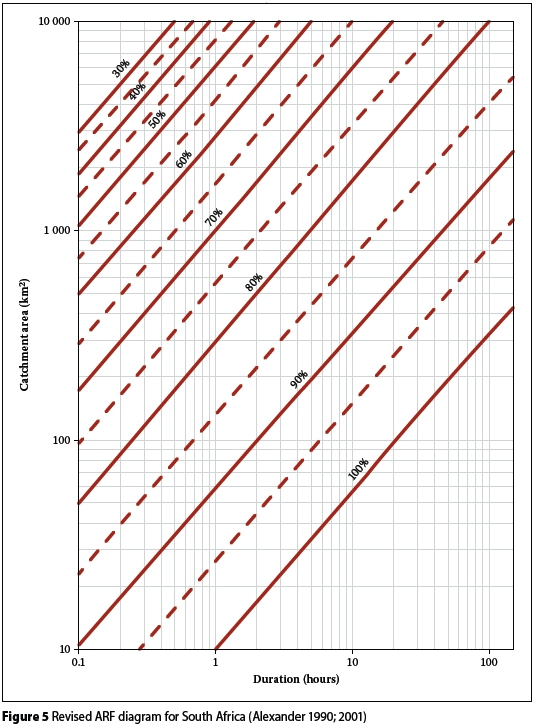
Figure 4 was adjusted to account for short duration rainfall over small catchment areas, which are mostly characterised by severe storm mechanisms producing very high intensity rainfall with cell core areas exceeding 10 km2 and durations exceeding 10 minutes. Estimates of shorter duration rainfall based on extrapolation from longer durations are unreliable when viewed in the light of the storm mechanisms which produce high-intensity rainfall for durations less than 10 minutes (Alexander 1980). Alexander (1980) argued that there is little justification in assuming ARFs less than 100% in these area and duration regions; subsequently Figure 4 was adjusted accordingly to provide a set of geographically-centred ARF diagrams (Figure 5) which enable the user to estimate average catchment rainfall from point rainfall statistics (Alexander 1990; 2001).
Alexander (1990; 2001) also converted Figure 5 to a mathematical algorithm (Equation 5). Alexander (1990; 2001) noted that the use of both Equations 4 and 5 resulted in slightly more conservative results when compared to the original UK FSR and United States Weather Bureau (USWB 1958) values.
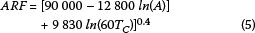
where:
ARF = areal reduction factor (%),
A = catchment area (km2), and
Tc= time of concentration/critical storm duration (hours).
A recent study confirmed that a relationship existed between the catchment area, Tc and ARFs (Gericke & Du Plessis 2011). The validity of Equation 5 was assessed by plotting the Tc within each catchment under consideration against the catchment area, after which a power-law curve fitted through the data points was superimposed on Figures 3 and 4 respectively. The fitted power-law relationship as expressed in Equation 6 provided a good indication of Tc associated with any catchment area under consideration. Equation 7 resulted from the substitution and simplification of Equation 6 into Equation 5.
TC = 0.2284 A0.596 (6)
ARF = [-69443 Ln(A) + 115731.9]0.4 (7)
where:
ARF = areal reduction factor (%),
A = catchment area (km2), and
TC= time of concentration (hours).
INTERNATIONAL ARF ESTIMATION METHODS RELATED TO THIS STUDY
The following subsections provide a brief review of the UK FSR (NERC 1975) ARF estimation method, which formed the fundamental basis of Alexander's ARF diagrams in the early 1980s, and Bell's method (1976). In this paper, the latter method is proposed as the most suitable for the re-investigation towards more up-to-date ARF estimation methods applicable to South African conditions. The justification of such a proposal is evident from the literature review to follow.
UK FSR method
The UK FSR method (NERC 1975) was developed by using nation-wide UK rainfall records. The final results from this study were represented using an ARF diagram (Figure 3), which allows the user to estimate geographically-centred ARF values based on a range of catchment areas and storm durations as input variables. Although this method allows for the area and duration to vary as input parameters, it remains invariant to the location within the UK and recurrence interval (Siriwardena & Weinmann 1996).
The method is reliant on the areal annual maximum event to recognise the date of the station/point annual maximum event. The point rainfall values corresponding to the same day as the areal maximum rainfall values (P'ij) and the maximum point values at each rainfall station in the same year (Pij) were recorded. This enabled the computation of ratios between P'ij and Pij at each rainfall station for each year. The final ARF values were derived from the overall mean values between the ratios for all stations and all years (Siriwardena & Weinmann 1996).
Bell's method
Bell (1976) conducted probabilistic rainfall analyses at rainfall stations (reasonably complete records over a 14 year period) situated in 1 000 km2 circular catchment areas in the UK. The estimated frequency curves of areal and averaged point rainfall were used to establish ARFs, i.e. the ARFs were computed as the ratio of areal to average point rainfall with associated AEPs. A modified Thiessen weighting procedure was used to estimate the daily areal rainfall values, after which these values were ranked to obtain the 20 independent highest values for each sample area. In other words, a partial duration series (PDS) using equally ranked observations curtailed to a common base period were used and fitted to an exponential distribution, with parameters estimated by the Method of Maximum Likelihood (MML). The average point rainfall frequency curves were estimated using the 20 highest daily rainfall values at each rainfall station. Instead of deriving separate frequency curves for each rainfall station to estimate weighted averages, a simpler, equivalent procedure was adopted. Each ranked weighted average point rainfall value was determined using the same modified Thiessen weighting procedure, followed by fitting an exponential distribution to provide estimates of the average point rainfalls for return periods from two to 20 years. The ARFs were then estimated directly using the corresponding areal and average point rainfall values associated with each return period or AEP (Bell 1976).
Bell's method, or modified versions thereof, have been used in several large-scale ARF studies conducted internationally, especially in the UK and Australia (Stewart 1989; Avery 1991; Masters 1993; Meynink & Brady 1993; Nittim 1989; Porter & Ladson 1993; Masters & Irish 1994; Siriwardena & Weinmann 1996). All these studies were conclusive that the basic procedure proposed by Bell (1976) is probabilistically more correct than other commonly used methods (e.g. USWB and UK FSR), since AEPs are explicitly included in the derivations of the ARFs.
Other international ARF estimation methods
Tables A1 and A2 in Appendix A provide the reader with a detailed summary of additional empirical and analytical ARF estimation methods used internationally.
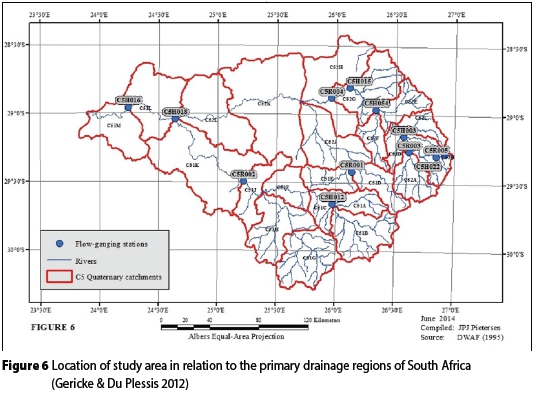
STUDY AREA
The C5 secondary drainage region was selected as the pilot study area, since most of the required data is available from previous studies (Gericke & Du Plessis 2011; 2012) conducted in this region. South Africa is delineated into 22 primary drainage regions, which are further delineated into 148 secondary drainage regions. The pilot study area (Figure 6) is situated in primary drainage Region C and comprises the C5 secondary drainage region (Midgley et al 1994). The rainfall intensity in this region is normally high to very high with associated thunder activity and can be classified as convective rainfall. The average Mean Annual Precipitation (MAP) is 424 mm, ranging from 275 mm in the west to 685 mm in the east (Lynch 2004), and rainfall is characterised as highly variable and unpredictable. The rainy season starts in early September and ends in mid-April with a dry winter (Midgley et al 1994). Twelve gauged catchments, ranging from 38 km2 to 33 277 km2, were selected in the pilot study area to investigate the study objectives.
METHODOLOGY
This section provides the detailed methodology followed during this study which focuses on the evaluation and comparison of the numerical and graphical empirical ARF estimation methods currently used in South Africa in two distinctive phases.
First phase: Comparison of ARF estimation methods using standard input variables
The standard input variables and their associated ranges, e.g. catchment area (10 to 30 000 km2), critical storm duration (one to 72 hours) and rainfall intensity (50 to 200 mm.h-1) as depicted in Figures 1 and 2 were used as input with the mathematical algorithms derived from these ARF diagrams in order to assess the consistency between the numerical and graphical ARF estimation methods compiled by Van Wyk (1965) and Wiederhold (1969). In each case Microsoft Excel ARF diagrams were reproduced by manually extracting values from the original ARF diagrams (Figures 1-5). Thereafter the graphical results, as obtained from each reproduced ARF diagram, were compared to the ARF computed using the individual mathematical algorithms to highlight any biases and inconsistencies present. The Van Wyk (1965) and Wiederhold (1969) results were not included in the comparisons as these two methods are applicable to different areal ranges.


Second phase: Comparison of ARF estimation methods in the pilot study area
All the ARF estimation methods evaluated in Phase 1 were compared and evaluated in the 12 gauged catchments located in the C5 secondary drainage region described above to establish the biasness/consistencies/inconsistencies determined during Phase 1, as well as to establish the need for further research in this field. All the required catchment geomorphological variables (e.g. catchment area), time parameters (e.g. time of concentration/critical storm duration) and climatological variables (e.g. design rainfall depths and intensities) were obtained from Gericke & Du Plessis (2011). In this study, the design rainfall depths with return periods ranging from 10 to 200 years were based on the Regional Linear Moment Algorithm and Scale Invariance (RLMA&SI) approach developed by Smithers & Schulze (2003; 2004).
RESULTS AND DISCUSSION
The results based on the methodology used in this study are discussed below.
Review of ARF estimation methods
The estimation of ARFs based on either empirical or analytical estimation methods was evident from the literature review conducted. The review also highlighted that most of these methods could not be regarded as entirely true descriptions of the actual rainfall process, especially when the empirical methods, based on a limited amount of observed rainfall data, are applied outside their original developmental regions.
Comparison of ARF estimation methods using standard input variables
As expected, all the ARF estimates decreased with an increase in catchment area, while significant differences, e.g. variation in the results obtained, also highlighted the presence of inconsistencies between the results from the numerical and graphical ARF estimation methods.
The comparison between Van Wyk's graphical (Figure 1) and numerical (Equation 1) results, as shown in Figure 7, is characterised by increasing averaged percentage differences associated with an increase in the catchment area, e.g. 7.1% (10 km2), 7,8% (20 km2), 12.20% (50 km2), 18.30% (100 km2), 23.8% (200 km2), 27.3%% (400 km2) and 28% (800 km2). A similar trend was also evident for the catchment area and rainfall intensities, in other words an increase in rainfall intensity associated with a specific catchment area resulted in larger percentage differences. However, despite these percentage differences, an overall coefficient of determination (r2) of 0.96 confirmed the high degree of association between the ARFs estimated using the two methods. It is essential to keep in mind that different practising engineers might yield different ARF values when using graphical procedures to estimate ARFs, whereas the same values should be estimated using the numerical estimation method.
The comparison between ARF estimates using Wiederhold's graphical approach (Figure 2) and Equation 3, as shown in Figure 8, is characterised by a high degree of association (r2= 0.92) and increasing percentage differences associated with an increase in the catchment area, e.g. averaged differences of 1.1% (500 km2), 1.7% (1 000 km2), 8.0% (5 000 km2), 13.6%% (10 000 km2), 22.5% (20 000 km2) and 28.9% (30 000 km2). In considering different storm durations associated with a specific catchment area, the ARF estimates increased with increasing storm duration.
Based on the above results, practising engineers should use the original graphical methods (Figures 1 and 2) as contained in the Drainage Manual (SANRAL 2013). However, it is important to note that both Van Wyk's and Wiederhold's methods are storm-centred empirical methods which are not suitable for estimating catchment areal design rainfall from design point rainfalls. In doing so, the practising engineer would by default incorrectly assume that extreme design point rainfall and extreme areal design rainfall are produced by the same rainfall event or rainfall type.
In the literature review it was highlighted that Alexander (1980) based his original methodology (Figure 4) on the UK FSR ARF diagrams (Figure 3, NERC1975), from which Op ten Noort and Stephenson (1984) developed Equation 4. In applying these approaches, and Alexander's revised methodology (Figure 5 and Equation 5), the results shown in Figures 9 and 10 were obtained.
Typical average percentage differences varied from 2.2% to 5.6% (Figure 3 vs Figure 4); 0.2% to 6.9% (Figure 4 vs Equation 4) and 0.4 to 8.5% (Figure 5 vs Equation 5); 15.4% to 21.4% (Figure 2 vs Equation 5), with an overall tendency for larger percentage differences in the smaller catchment areas (10 km2 ≤ A ≤ 100 km2). The latter tendency also confirmed the findings of Alexander (1980), especially with specific reference when severe storm mechanisms produce very high intensity rainfall with cell core areas exceeding the areal range and storm duration under consideration. The coefficient of determination (r2) results showed a high degree of association; 0.91 (Figure 3 vs Figure 4); 0.94 (Figure 4 vs Equation 4) and 0.96 (Figure 5 vs Equation 5); 0.87 (Figure 2 vs Equation 5). Based on these results it is evident that the geographically-centred numerical methods are generally more consistent, and this could likely also be one of the reasons why these methods are preferred to the storm-centred approaches, especially if multi-centred storms are to be considered.
Comparison of ARF estimation methods in the pilot study area
The application of the ARF estimation methods listed in Table 1 in the pilot study area showed some significant biases and systematic inconsistencies, which are summarised in Table 2.
The results contained in Table 2 are characterised by percentage differences ranging from 17.6% to 27.6% in the smaller catchments (38 km2 to 937 km2), 27.1% to 38% in medium sized catchments (1 650 km2 to 6 331 km2) and 44% to 71.5% in the large catchments (10 260 km2 to 33 277 km2). Similar to the results shown in Figures 9 and 10, these comparisons showed that the geographically-centred numerical ARF estimation methods are more consistent. However, the geographically-centred ARF estimates did not account for the variation of ARFs with return period.
CONCLUSIONS AND RECOMMENDATIONS
The comparison of the performance of ARF estimation methods over a range of input variables (e.g. catchment area, critical storm duration and rainfall intensity), and/or as applied in medium to large catchment areas in the C5 secondary drainage region in South Africa, highlighted that:
■ The geographically-centred methods used in South Africa were either transposed from the UK with little local verification, or were developed using very limited local data. Hence, all these methods could potentially show significant variation from the observed areal rainfall characterising South African catchments, and thus ARFs developed from local rainfall data need to be developed.
■ Ultimately, the significance of variation using different ARF estimation methods will only be appreciated when translated to design peak discharges. However, such an exercise is not possible at this stage of the study, but forms part of this high-priority on-going research area.
Based on the above it is evident that the ARFs currently used in South Africa need to be updated utilising the longer periods of records (40 years of additional data since the 1970s) which are now available for analysis. The variation of ARFs with return period and with rainfall-producing mechanisms also needs to be investigated. It is envisaged that Bell's method (1976) based on a geographically-centred approach would be the most appropriate to use, since:
■ the literature review conducted confirmed its large-scale preferential application internationally;
■ the use of a geographically-centred approach would be most appropriate for a national-scale investigation bounded within a 'fixed' catchment area, e.g. at a quaternary catchment level; and
■ currently in South Africa the storm-centered ARF methods (Van Wyk 1965 and Wiederhold 1969) are incorrectly applied in a geographically-centred manner, while assuming that extreme design point rainfall and extreme areal design rainfall are produced by the same rainfall event or rainfall type; given the use of point design rainfall to estimate ARFs, it is thus necessary to derive updated ARFs using a geographically-centred approach.
However, the use of a modified version of Bell's (1976) method, based on the annual maximum series (AMS) of point and areal rainfall as opposed to the PDS, is proposed. This modification would enable the development of probabilistically correct ARFs, namely the variation of ARFs with return period will be reflected, instead of using equally ranked observations curtailed to a common base period. The final results should be presented in a suitable format to be useful to a practitioner, such as a set of ARF diagrams and associated algorithms.
REFERENCES
Alexander, W J R 1980. Depth-area-duration-frequency properties of storm rainfall in South Africa. Technical Report TR103. Pretoria: Department of Water Affairs. [ Links ]
Alexander, W J R 1990. Flood hydrology for southern Africa. Pretoria: SANCOLD. [ Links ]
Alexander, W J R 2001. Flood risk reduction measures: Incorporating flood hydrology for southern Africa. Pretoria: Department of Civil and Biosystems Engineering, University of Pretoria. [ Links ]
Allen, R J & DeGaetano, A T 2005. Areal reduction factors for two eastern United States regions with high rain-gauge density. Journal of Hydrologic Engineering, 10(4): 327-335. [ Links ]
Asquith, W H & Famiglietti, J S 2000. Rainfall areal-reduction factor estimation using the annual- maxima centered approach. Journal of Hydrology, 230(1-2): 55-69. [ Links ]
Avery, D R 1991. Design flood analysis in coastal New South Wales using areal average rainfall data. Paper presented at the Hydrology and Water Resources Symposium 1991, Perth, Australia, IEAust. Nat. Conf. Pub. No. 91/22: 627-628. [ Links ]
Bacchi, B & Ranzi, R 1996. On the derivation of the areal reduction factor of storms. Atmospheric Research, 42: 123-135. [ Links ]
Bell, F C 1976. The areal reduction factor in rainfall frequency estimation. Institute of Hydrology, Report No 35. Swindon, UK: Natural Environment Research Council. [ Links ]
Bengtsson, L & Niemczynowicz, J 1986. Areal reduction factors from rain movement. Nordic Hydrology, 17(2): 65-82. [ Links ]
De Michéle, C, Kottegoda, N T & Rosso, R 2001. The derivation of areal reduction factor of storm rainfall from its scaling properties. Water Resources Research, 37(12): 3247-3252. [ Links ]
Desbordes, M, Raous, P & Trévisiol, Y 1984. Areal reduction factors on short time and space intervals. Water Science Technology, (16): 189-198. [ Links ]
Gericke, O J & Du Plessis, J A 2011. Evaluation of critical storm duration rainfall estimates used in hydrology in South Africa. Water SA, 37(4): 453-470. [ Links ]
Gericke, OJ & Du Plessis, JA. 2012. Catchment parameter analysis in flood hydrology using GIS applications. Journal of the South African Institution of Civil Engineering, 54(2): 15-26. [ Links ]
Lambourne, J J & Stephenson, D 1986. Research in urban hydrology and drainage: Factors affecting storm runoff in South Africa. Water Systems Research Programme Report No 2/86, Johannesburg: University of the Witwatersrand. [ Links ]
Lombardo, F, Napoletano, F & Russo, F 2006. On the use of radar reflectivity for estimation of the areal reduction factor. Natural Hazards and Earth System Sciences, 6: 377-386. [ Links ]
Lynch, S D 2004. Development of a raster database of annual, monthly and daily rainfall for southern Africa. WRC Report No 1156/1/04, Pretoria: Water Research Commission. [ Links ]
Masters, C J 1993. Areal reduction of point rainfall using Australian data. MEng Sc Project Report. Sydney, Australia: School of Civil Engineering, University of New South Wales. [ Links ]
Masters, C J & Irish, J L 1994. Areal reduction factors for the Sydney region derived from spatial characteristics of heavy rainfall. Paper presented at the Hydrology and Water Resources Symposium 1994, Adelaide, Australia, IEAust. Nat. Conf. Pub. No. 94/15: 27-32. [ Links ]
Meynink W J C & Brady, D K 1993. Areal reduction factors for design storms. Paper presented at the Hydrology and Water Resources Symposium 1993, Newcastle, Australia, IEAust. Nat. Conf. Pub. No. 93/14: 257-271. [ Links ]
Midgley, D C, Pitman, W V & Middleton, B J 1994. Surface water resources of South Africa. Vol 2, Drainage Region C, Vaal: Appendices. Report No 298/2.1/9. Pretoria: Water Research Commission. [ Links ]
Myers, V A & Zehr, R M 1980. A methodology for point-to-area rainfall frequency ratios. NOAA Technical Report No 24. Washington DC: United States Department of Commerce, National Oceanic and Atmospheric Administration, National Weather Services. [ Links ]
NERC (Natural Environment Research Council) 1975. Flood studies report. Swindon, UK: NERC. [ Links ]
Nittim, R 1989. Areal distribution of design rainfall. Paper presented at the Hydrology and Water Resources Symposium 1989, Christchurch, New Zealand, IEAust. Nat. Conf. Pub. No. 89/19: 487-488. [ Links ]
Omolayo, A S 1989. Relationships between point and areal rainfall for flood and drought assessments. Unpublished PhD thesis, Sydney, Australia: University of New South Wales. [ Links ]
Omolayo, A S 1993. On the transposition of areal reduction factors for rainfall frequency estimation. Journal of Hydrology, 145(1-2): 191-205. [ Links ]
Op ten Noort, T H & Stephenson, D 1982. Flood peak calculation in South Africa. Water Systems Research Programme Report No 2/1982. Johannesburg: University of the Witwatersrand. [ Links ]
Porter, J W & Ladson A R 1993. An application of fixed-area rainfall reduction factors. Paper presented at the Hydrology and Water Resources Symposium 1993, Newcastle, Australia, IEAust. Nat. Conf. Pub. No. 93/14: 273-279. [ Links ]
Rodriguez-Iturbe, I & Mejia, J M 1974. On the transformation of point rainfall to areal rainfall. Water Resources Research, 10(4): 729-735. [ Links ]
SANRAL (South African National Roads Agency Limited) 2013. Drainage manual, 6th ed. Pretoria: SANRAL. [ Links ]
Siriwardena, L & Weinmann, P E 1996. Derivation of areal reduction factors for design rainfalls in Victoria. Report No 96/4. Victoria, Australia: Cooperative Research Centre for Catchment Hydrology. [ Links ]
Sivapalan, M & Bloschl, G 1998. Transformation of point rainfall to areal rainfall: Intensity-duration-frequency curves. Journal of Hydrology, 204(1-4): 1 5 0-167. [ Links ]
Skaugen, T 1997. Classification of rainfall into small- and large-scale events by statistical pattern recognition. Journal of Hydrology, 200(1-4): 40-57. [ Links ]
Smithers, J C & Schulze, R E 2003. Design rainfall and flood estimation in South Africa. WRC Report 1060/01/03. Pretoria: Water Research Commission. [ Links ]
Smithers, J C & Schulze, R E 2004. The estimation of design rainfall for South Africa using a regional scale invariant approach. Water SA, 30(4): 435-444. [ Links ]
Stewart, E J 1989. Areal reduction factors for design storm construction: Joint use of rain gauge and radar data. Association of Hydrological Sciences, 181: 31-40. [ Links ]
Svensson, C & Jones, D A 2010. Review of methods for deriving areal reduction factors. Journal of Flood Risk Management, 3(3): 232-245. [ Links ]
USWB (United States Weather Bureau) 1957. Rainfall intensity-frequency regime, the Ohio Valley. Technical Paper 29. Washington DC: United States Department of Commerce. [ Links ]
USWB (United States Weather Bureau) 1958. Rainfall intensity-frequency regime, south-eastern United States. Technical Paper 29. Washington DC: United States Department of Commerce. [ Links ]
Van Wyk, W 1965. Aids to the prediction of extreme floods from small watersheds. Johannesburg: Department of Civil Engineering, University of the Witwatersrand. [ Links ]
Wiederhold, J F A 1969. Design storm determination in South Africa. HRU Report No 1/1969. Johannesburg: Hydrological Research Unit, University of the Witwatersrand. [ Links ]
Yoo, C, Kim, K, Kim, H S & Park, M J 2007. Estimation of areal reduction factors using a mixed gamma distribution. Journal of Hydrology, 335(3-4): 271-284. [ Links ]
 Correspondence:
Correspondence:
Jaco Petersen
Faculty of Engineering and Information Technology
Department of Civil Engineering, Central University of Technology Free State (CUT)
Private Bag X20539, Bloemfontein, 9300
South Africa
T: +27 (0)51 507 3693; F: +27 (0)51 507 3254
E: jpietersen@cut.ac.za
Jaco Gericke
Faculty of Engineering and Information Technology
Department of Civil Engineering, Central University of Technology Free State (CUT)
Private Bag X20539, Bloemfontein, 9300
South Africa
T: +27 (0)51 507 3516; F: +27 (0)51 507 3254
E: jgericke@cut.acza
Prof Jeff Smithers
School of Engineering, University of KwaZulu-Natal, Pietermaritzburg Campus
Pietermaritzburg, 3201
South Africa
T: +27 (0)33 260 5490; F: +27 (0)33 260 5818
E: smithers@ukzn.ac.za
Dr Yali Woyessa
Faculty of Engineering and Information Technology
Department of Civil Engineering, Central University of Technology Free State (CUT)
Private Bag X20539, Bloemfontein, 9300
South Africa
T: +27 (0)51 507 3452; F: +27 (0)51 507 3254
E: ywoyessa@cut.ac.za

JACO PETERSEN, who is a Civil Engineering Technologist and a member of SAICE, has lectured the practical components in Water Engineering and Geotechnical Engineering at the Central University of Technology, Free State (CUT FS), for the past three years. He has a special interest in flood hydrology, especially the influence of flood peaks on hydraulic structures. After obtaining the BTech Eng (Civil) degree from the CUT FS, he worked for five years at a civil engineering consulting firm in Bloemfontein, before joining the CUT FS. The results included in this paper will partially contribute towards his MTech Eng (Civil) degree from the CUT FS.

JACO GERICKE Pr Tech Eng has been lecturing in Hydrology, Irrigation and Water Engineering at the CUT FS for the past nine years. He has a special interest in flood hydrology, water resources management and hydrological modelling. He was awarded the BTech Eng (Civil) and MTech Eng (Water) degrees fromthe CUT FS, the BSc (Hons) Applied Science: Water Resources Engineering degree from the University of Pretoria (UP) and the MSc Eng degree from the University of Stellenbosch. He worked for six years at the Department of Water Affairs before joining the CUT FS. He is currently registered for a PhD Eng at the University of KwaZulu-Natal.

PROF JEFF SMITHERS Pr Eng graduated with a BSc Eng (Agric), MSc Eng and PhD degrees from the University of KwaZulu-Natal (UKZN). He has extensive academic and professional experience and has numerous publications in the design hydrology field to his credit. He is currently Professor of Agricultural Engineering at the UKZN and has a part-time appointment at Jeffares & Green Engineering and Environmental Consulting. He also serves as Adjunct Professor at the University of Southern Queensland, Australia, in the National Centre for Engineering in Agriculture. He is a Fellow of the South African Institute of Agricultural Engineers.

DR YALI WOYESSA Pr Tech Eng has an MSc in Irrigation Engineering and a PhD in Soil Physics. He has been involved in teaching and research for more than 20 years at higher education institutions. His research interests include catchment management, water resources management and hydrological modelling. He currently leads a research group on Sustainable Water Resources and Environment, and is Head of the Department of Civil Engineering at the CUT FS.
APPENDIX