Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
Journal of the South African Institution of Civil Engineering
On-line version ISSN 2309-8775
Print version ISSN 1021-2019
J. S. Afr. Inst. Civ. Eng. vol.56 n.3 Midrand Oct. 2014
TECHNICAL NOTE
Soil collapse from an effective stress perspective
G Brink; G Heymann
ABSTRACT
The behaviour of collapsible soil is often quantified by conducting a Collapse Potential Test or double oedometer test. However, these tests interpret the soil behaviour in terms of total stress, while it is well known that the behaviour of soil is governed by its effective stress. This article shows the results of a test conducted on undisturbed residual granite to study the collapse of the soil in terms of effective stress. The test was conducted in a modified oedometer which allowed the incremental addition of water to the sample during the test. The matric suction was quantified as a function of the moisture content of the soil during the test. The results indicate that the reduction in effective stress plays an important role during soil collapse. In addition it was found that much of the collapse settlement may be due to creep which occurs after the reduction in effective stress.
Keywords: creep, Collapse Potential Test, double oedometer test, effective stress, matric suction, soil collapse, unsaturated soil, vertical strain
INTRODUCTION
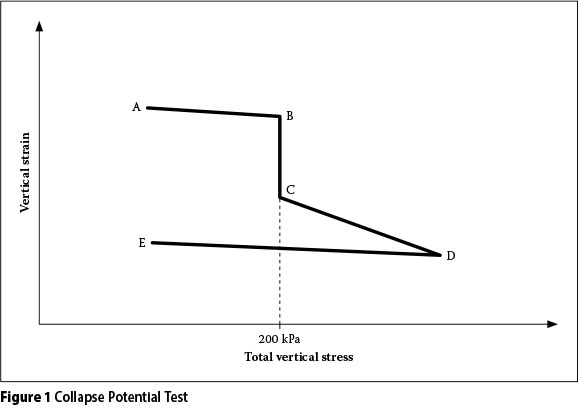
Collapsible soil was first recognised and studied by Jennings and Knight (1957), and Knight (1961). Soil collapse is typically evaluated in terms of total stress, as shown in Figure 1, where an unsaturated soil sample is placed in an oedometer at natural moisture content (A), loaded in stages to the desired vertical total stress (B), before the sample is inundated with water and the vertical strain is recorded. In South Africa, a collapse test inundated at 200 kPa is referred to as a Collapse Potential Test, and the vertical strain (B to C) during inundation is taken as the Collapse Potential. The sample is then loaded to point D and unloaded to point E under saturated or near-saturated conditions. This method is superficially attractive due to its simplicity, and is widely used as an indicator test to allow judgement on the severity of possible foundation settlement due to soil collapse. However, it is well known that soil behaviour depends on its effective stress, and a fundamental interpretation of the collapse phenomenon should be made in terms of effective stresses.
A number of theoretical frameworks have been developed to express the effective stress for unsaturated soil. Bishop (1959) formulated the following equation to quantify effective normal stress (σ') for unsaturated soil in terms of total stress (σ), pore air pressure (ua) and pore water pressure (uw):
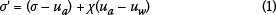
(σ - ua) is termed the net normal stress and (ua - uw) is the matric suction. χ is a parameter that quantifies the contribution of the matric suction to the effective normal stress. χ varies between 0 for a completely dry soil and 1 for a completely saturated soil. For these two conditions Equation 1 reduces to the classic Terzaghi equation (σ = σ - ua) for effective normal stress of a soil where the pores are completely filled either with air or water.
The difficulty with applying Equation 1 is quantifying the parameter χ. It is determined experimentally by conducting either shear tests or volumetric strain tests and quantifying the contribution of the matric suction to the behaviour of the soil. Bishop (1959) suggested that X is a function of the degree of saturation (Sr), soil structure and whether the soil is in a wetting or drying phase. Alonso et al (2010) suggested that χ also depends on the pore size distribution. The relationship χ = SrKhas been found to give good results with κ depending on the type of soil. Vanapalli and Fredlund (2000) developed the relationship for χ shown in Figure 2 by conducting unsaturated triaxial tests. Data from Alonso and Romero (2011) from volumetric strain tests are also shown in Figure 2.
Rust et al (2005) proposed a conceptual yield model to explain soil collapse, using effective stress paths as shown in Figure 3 and briefly explained below.
Consider an in situ collapsible soil with stress condition A in the figure. The stress condition is inside the "dry" yield surface. If wetted, the path will move to point A', and the in situ stress state will still be inside the now smaller "wet" yield surface for the in situ soil, which is now weaker than before it had been wetted. But since the stress state stayed inside the shrinking yield surface during wetting, no collapse of the in situ soil profile occurred. If the in situ soil at point A is loaded, the stress state may move to point B. Alternatively, if the soil is first sampled, it will move to point C where it does not experience any shear stresses (q = 0), before it is loaded in the oedometer to point B. At point B the soil is still at its in situ moisture content and hence still inside the "dry" yield surface. If the soil is now wetted, the yield surface will shrink as the soil weakens, and the stress state will move toward B' where the yield surface and stress state coincide with the one-dimensional strain (Ko-line), and large strains will occur as the soil collapses.
Even though this proposed framework has not been verified experimentally, primarily due to experimental difficulties, it is useful since it attempts to describe the collapse phenomenon in terms of effective stresses. It also shows that, from a fundamental effective stress perspective, the behaviour is much more complex than the behaviour shown in terms of total stresses in Figure 1.
SAMPLING AND TESTING
According to Brink et al (1982) and Schwartz and Yates (1980), the typical dry densities that could be expected for collapsible soils in South Africa range from 900 to 1 600 kg/m3, although Rust et al 2005 argued that collapse in materials with dry densities outside this range cannot be excluded. According to Schwartz (1985), it was originally assumed that the collapse phenomenon was largely restricted to loose aeolian deposits, with the result that most of the research and work dealt almost exclusively with such deposits. However, in South Africa numerous cases of collapse have been reported for the residual granitic soils of the Basement Complex (Schwartz 1985). Extensive foundation problems have been encountered with these soils, both in the central Highveld and eastern Lowveld regions of South Africa. The collapsible nature of the residual soils derived from these granites is associated with the deeply weathered soil profiles above the African Erosion Surface, encountered in the humid eastern parts of South Africa, with annual water surplus. During the weathering process, quartz remains unaltered in the form of sand grains, and mica particles remain partially unaltered, but the feldspars are thoroughly kaolinised through the chemical interaction with water charged with carbon dioxide, forming what is commonly known as ferralitic soils (Brink 1979). As the name suggests, ferralitic soils are rich in iron and aluminium hydroxides. Due to the duration of the weathering cycle and the moist nature of the climate, these ferralitic soils have a very low base status and are characterised by a friable and porous structure and the presence of 1:1 lattice kaolinitic clays (Brink 1979).
An undisturbed sample of decomposed residual granite was collected from the Bushbuck Ridge area, which is part of the Nelspruit Granite Suite. The material in its natural state was described as being slightly moist, dark pink with orange stains, gravelly silty sand with a medium dense to dense consistency and pinholed structure. It had a dry density of 1 392 kg/m3, natural moisture content of 7.2% and specific gravity of 2.64. The particle distribution consisted of 11% clay, 20% silt, 57% sand and 12% gravel-sized particles. The liquid limit was 36% and the plasticity index 13%. Quantitative XRD analysis indicated that more than 50% of the mineral composition was made up of quartz and kaolinite, with secondary percentages of microcline, muscovite and albite.
A modified oedometer was used to observe the collapse behaviour of the residual granite in the laboratory. It is similar to a standard oedometer apparatus, but allows the incremental addition of water to the sample through a small hole at the bottom of the loading cell during the test. The undisturbed sample was cut to fit into the oedometer ring with an inside diameter of 75 mm and a height of 20 mm. Once the sample had been cut into the ring, the sample surfaces at the top and bottom were carefully trimmed in order to minimise the effect of bedding errors during loading. Once the loading cap was in position the entire cell was sealed using petroleum jelly in order to minimise moisture loss. The cell was then connected to a water-filled burette using a small-diameter rubber tube to allow for the introduction of known quantities of water to the soil specimen. Since the gauge pore air pressure (ua) was zero throughout the test (equal to atmospheric pressure), the net vertical stress was equal to the total stress and the applied vertical stress.
At natural moisture content, the sample was loaded in increments, up to a total stress of 200 kPa. Dial gauge readings were taken and the load was only increased once the rate of creep of the sample was equal to or less than 0.25%/hour (Heymann 2000). Up to this point the testing procedure is similar to that of the widely used Collapse Potential Test. Once creep of the sample at a total vertical stress of 200 kPa had subsided sufficiently, additional moisture was introduced for the first time. Moisture was added in increments from the burette and the amount of water entering the sample was recorded. The process was continued until the sample no longer accepted free water. The sample was then inundated and left overnight. The next morning the loads were increased up to the final maximum load.
The moisture retention curve was determined using the filter paper method (Chandler & Gutierrez 1986) and the calibration relationship proposed by Hamblin (1981) for Whatman no 42 filter paper.
DISCUSSION
Figure 4 shows the behaviour of the soil in terms of total vertical stress (numerically equal to the applied vertical stress) and the effective vertical stress (Equation 1). For the purpose of these calculations χ was taken as equal to SrKwith κ = 1.94 at a plasticity index of 13% (Figure 2). The relationship between total stress and void ratio (e) is equivalent to that of a conventional Collapse Potential Test, except that the volumetric strain occurred incrementally as water was introduced to the specimen in stages. The Collapse Potential of 5.6% is taken as the vertical strain during inundation at a total stress of 200 kPa (point A to B in Figure 4).
At the start of the test the soil was at its in situ moisture content of 7.2% and it experienced a matric suction of 2 238 kPa. This translates to a 110 kPa difference between effective and total stress vertical at a degree of saturation of 21%. As the loading was increased prior to introducing water, the increase in effective vertical stress was different to the increase in total vertical stress. This is due to the fact that the moisture content remained constant, but the sample volume decreased. Hence the degree of saturation (Sr) increased, changing χ. This may be an oversimplification of a more complex phenomenon. When water was introduced to the specimen (points A and C in Figure 4), the effective vertical stress reduced rapidly and the void ratio decreased. This behaviour is in contrast with classical soil mechanics where a reduction in void ratio requires an increase in effective stress. As more water was introduced, the effective vertical stress eventually tended towards the total vertical stress as the matric suction approached zero. The collapse process appears to consist of two mechanisms. The first part is from point C to D in Figure 4, with a rapid reduction in effective stress which coincides with a reduction in void ratio. For the second part (D to B) sufficient water has been introduced to the specimen for the matric suction to approach zero, but void ratio reduction continues. This suggests that the introduction of water triggered the collapse process by reducing the effective stress, but that the reduction in effective stress cannot fully account for the reduction in the void ratio, as much of the void ratio reduction occurred at constant effective stress. Clearly creep is also an important mechanism contributing to volume reduction during soil collapse. Subsequent load increments, after inundation, occurred at or near full saturation, and the behaviour was similar to a conventional one-dimensional oedometer test.
CONCLUSIONS
The data shown in this article indicates that interpretation of soil collapse in terms of total stress leads to an oversimplification of the behaviour of the soil. This masks the contribution of the change in effective stress. The results indicate that the reduction in effective stress plays an important role during soil collapse. It appears to trigger the collapse process, but much of the collapse settlement may also be due to creep where volume reduction occurs at constant effective stress.
Effective stress due to matric suction may be higher than the stress applied to the soil as a result of operations related to construction of infrastructure. It follows that changes in moisture content will have a greater effect on the effective stress, and hence the strength and stiffness of the material, than stress changes due to engineering activity. Engineers therefore need to consider not only the effect of loading the soil due to construction, but also the consequence of moisture change on the effective stress experienced by the soil.
REFERENCES
Alonso, E E, Pereira, J M, Vaunat, J & Olivella, S 2010. Microstructurally based effective stress for unsaturated soils. Geotechnique, 60(12): 913-925. [ Links ]
Alonso, E E, Romero, E 2011. Experimental investigation on an effective stress law in compacted clayey/silty soil. In Jotisankasa, A, Sawangsuriya A, Soralump, S & Mairaing, W (Eds). Unsaturated soils: Theory and practice, Kasetsart University, Thailand, pp 331-336. [ Links ]
Bishop, A W 1959. The principle of effective stress. Tekniche Ukeblad, 39: 4-16. [ Links ]
Brink, A B A, Partridge, T C & Williams, A A B 1982. Soil survey for engineering. Oxford: Clarendon Press. [ Links ]
Brink, A B A 1979. Engineering geology of Southern Africa, Vol 1. Pretoria: Building Publications. [ Links ]
Chandler, R J & Gutierrez, C I 1986. The filter paper method of suction measurement. Geotechnique, 36: 265-268. [ Links ]
Hamblin, A P 1981. Filter paper method for routine measurement of field water potential. Journal of Hydrology, 53: 355-360. [ Links ]
Heymann, G 2000. Advances in triaxial testing. Journal of the South African Institution of Civil Engineering, 42(1): 24-31. [ Links ]
Jennings, J E & Knight, K 1957. The additional settlement of foundations due to a collapse structure of sandy subsoils on wetting. Proceedings, 4th International Conference on Soil Mechanics and Foundation Engineering, London, Vol 1, pp 316-319. [ Links ]
Knight, K 1961. The collapse structure of sandy subsoils upon wetting. PhD thesis. Johannesburg: University of the Witwatersrand. [ Links ]
Rust, E, Heymann, G & Jones, G A 2005. Collapse potential of partly saturated sandy soils from the east coast of southern Africa. Journal of the South African Institution of Civil Engineering, 47(1): 8-14. [ Links ]
Schwartz, K 1985. Collapsible soils: Problems of soils in South Africa - State-of-the-art. The Civil Engineer in South Africa, 27: 379-393. [ Links ]
Schwartz, K & Yates, J R C 1980. Engineering properties of aeolian Kalahari Sands. Proceedings, 7th International Conference on Soil Mechanics and Foundation Engineering, Accra, Ghana. [ Links ]
Vanapalli, S K & Fredlund, D G 2000. Comparison of different procedures to predict unsaturated soil shear strength. Proceedings, Geo-Denver Conference, ASCE Geotechnical Special Publication, 99: 195-209. [ Links ]
 Correspondence:
Correspondence:
George Brink
Exxaro resources
Po Box 1 Faerie Glen Pretoria 0043
South Africa
T: +27 12 307 3312
E: george.brink@exxaro.com
Gerhard Heymann
Department of Civil Engineering University of Pretoria
Pretoria 0002
South Africa
T: +27 12 420 3627
E: gerhard.heymann@up.ac.za

GEORGE BRINK has been practising as engineering geologist for the past five years and is currently employed as the Senior Geotechnical engineer at Exxaro resources in Pretoria. He graduated with BSc (Hons) and MSc degrees from the University of Pretoria, and is currently busy with his PhD on the topic ofthe evaluation and analysis ofthe engineering behaviour of tropical red soils.

PROF Gerhard Heymann graduated with BEng and MEng degrees from the University of Pretoria, and in 1990 he was appointed as lecturer at the same university. in the late 1990s he spent a number of years in the United kingdom conducting research on the stiffness behaviour of soils and weak rock, and subseguently obtained a PhDfromthe University of Surrey. He is currently a Professor in the Department of Civil Engineering at the University of Pretoria.














