Servicios Personalizados
Articulo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares en Google
Similares en Google
Compartir
Journal of the South African Institution of Civil Engineering
versión On-line ISSN 2309-8775
versión impresa ISSN 1021-2019
J. S. Afr. Inst. Civ. Eng. vol.56 no.3 Midrand oct. 2014
TECHNICAL PAPER
Review of pump suction reducer selection: Eccentric or concentric reducers
R M Mahaffey; S J van Vuuren
ABSTRACT
Eccentric reducers are traditionally recommended for the pump suction reducer fitting to allow for transportation of air through the fitting to the pump. The ability of a concentric reducer to provide an improved approach flow to the pump while still allowing air to be transported through the fitting is investigated. Computational fluid dynamics (CFD) were utilised to analyse six concentric and six eccentric reducer geometries at four different inlet velocities to determine the flow velocity distribution at the inlet to the pump. It was found that eccentric reducers with angles greater or equal to 15° and concentric reducers with an angle greater or equal to 20° did not pass the assessment criteria related to the inlet conditions. Air could be hydraulically transported through all of the concentric reducers modelled except for the 20° concentric reducer. A correctly designed concentric reducer will not only provide a more uniform velocity distribution in comparison to an eccentric reducer, but will allow for the hydraulic transportation of air through the reducer.
Keywords: pump station design, eccentric and concentric reducers, computational fluid dynamics (CFD), numerical modelling, air transport in pipelines
INTRODUCTION
The design of the pump inlet pipework defines the resulting hydraulic conditions experienced at the pump inlet/impeller. The importance of the pump inlet condition is often overlooked and, according to Jones et al (2008) is likely to be the single reason mostly responsible for the failure of pumps. Failure of the pump inlet design to produce a uniform velocity distribution at the pump inlet can lead to noisy operation, random axial load oscillations, premature bearing or seal failure, cavitation damage to the impeller and inlet portions of the casing, and occasional damage on the discharge side due to liquid separation (ANSI 2009). Typical components of pump inlet pipework (bends, valves, spool pieces, reducers, etc) create flow conditions that are prone to a non-uniform velocity distribution.
Reducer fittings used in pump inlet pipework are divided into two types: concentric reducers and eccentric reducers. Design guidelines, pump operating manuals and design standards prescribe which type of reducer to use for various conditions. An eccentric reducer with the flat side on top is typically the prescribed reducer to be used. This reducer prevents air to accumulate at the upstream end of the reducer. In a case study presented by Van der Westhuizen (2011) the incorrect reducer selection was noted as one of the causes of a reported pump failure; in this case study the reducers installed in the pump inlet pipework were eccentric reducers. In the failure investigation, field pressures in the installed eccentric reducer fitting were measured at eight circumferential locations towards the downstream end of the fitting. These pressure measurements presented a non-uniform pressure distribution within the reducer, with the greatest difference being 11 kPa (65% of the largest pressure reading). This contributed to the reported pump's failure. This pressure distribution is caused by an acceleration in velocity along the bottom edge (with the flat side on top) of the eccentric reducer as the flow path narrows from below.
The geometry of an eccentric reducer is asymmetrical, and asymmetrical flow conditions will result, introducing non-uniform velocity and pressure distributions at the pump inlet. These flow conditions are contradictory to the recommended pump inlet designs, which recommend symmetrical flow conditions with a uniform velocity and pressure distribution. The flow conditions resulting from a concentric reducer will be more uniform compared to the conditions resulting from an eccentric reducer. Prescribing eccentric reducers is based on the perception of the transportability of air.
Various relationships are used to evaluate the hydraulic transportability of air. The capacity for a pipeline to hydraulically transport air is a function of the velocity of the liquid, the diameter of the pipeline and the slope of the pipeline (Van Vuurn et al 2004). If air can be hydraulically transported in a pipeline, why will air not have the ability to be transported through a concentric reducer?
The velocity distributions resulting from various eccentric and concentric reducer designs were studied with the use of computational fluid dynamics (CFD) under various flow velocities. The velocity distributions were assessed according to criteria prescribed by ANSI (1998) and the guidelines provided by Wallingford (2001) in Sinotech CC (2005), and Van Vuuren (2011). With the CFD analyses, together with the theoretical assessment of the hydraulic transportability of air through the reducers, a design recommendation on the selection of reducer geometry can be made.
An introduction to pump inlet design and a theoretical overview into the hydraulic transportation of air are provided in the next section of this paper. The setup of the CFD models and the selection of the reducer geometries are then presented. The paper concludes with a brief presentation of the results and recommendations.
PUMP INLET DESIGN -SELECTION OF REDUCER TYPE
Reducers are typically placed immediately upstream of a pump in order to operate the suction pipework at acceptable energy losses (NPSH available). Figure 1 shows a schematic representation of the inlet side of typical parallel centrifugal pumps.
The selection of the type of reducer to be installed on the inlet side of a pump has an influence on the hydraulic transportation of air within the suction pipework and the flow conditions exiting the reducer and entering the pump. Numerous references prescribe the type of reducer to be used in a suction pipework - a summary of these design requirements is presented in Table 1. From this table it is observed that the eccentric reducer with the flat section on top is prescribed for all cases where the suction pipework enters in a horizontal plane. This prescription is to allow for the hydraulic transportation of air through the reducer by ensuring that an air pocket does not accumulate at the upstream end of the reducer, as illustrated in Figure 2. However, in the event of no potential for air accumulation or vertical inlet pipes, a concentric reducer is prescribed by ANSI (2009). A reason for this preference is, however, not provided by ANSI/HI.
The philosophy of prescribing the use of an eccentric reducer with the flat side on top will aid in the transport of air through the reducer. However, the following three aspects are not addressed:
-
The origin of air at this position in the pumping system. If a pump station sump, fore bay, intake bay, suction pipework and reservoir outlets are correctly designed it is impossible for air to accumulate. Pumps typically operate under positive suction pressure heads (when started) and therefore air should not be able to enter the system on the suction side. Under first-time start-up conditions after construction or after maintenance where air may be present in the system, the air may be released with a manual bleed-off valve.
-
The hydraulic capacity of the system to transport air. Trapped air in pipelines can be hydraulically transported along the length of a pipeline through valves and fittings depending on the pipeline slope, flow rate and fitting geometry. A concentric reducer with the correct flow rate and geometry will allow air to be hydraulically transported through it.
-
The non-uniform velocity distribution on the impeller created by the flow through the eccentric reducer. The geometry of an eccentric reducer is asymmetrical, and flow through a fitting of this nature will produce asymmetrical flow conditions, such as non-uniform velocity and pressure distributions. These flow conditions are contradictory to the recommended pump inlet designs, which recommend symmetrical flow conditions with a uniform velocity and pressure distribution.
PUMP INLET PIPING REQUIREMENTS
Pump inlet piping requirements are typically prescribed according to a maximum allowable velocity in the suction pipework and valves, and an allowable velocity distribution at the pump inlet. A summary of recommended maximum velocities for pump inlet piping as identified in a literature review is provided in Table 2. It can be observed that acceptable velocities for pump suction pipework are typically in the range of 0.75 m/s to 2.5 m/s, and the suction pipework is to be at least one size larger than the pump inlet nozzle, thereby defining the use of a reducer.
The requirements for maximum velocity distributions are to limit the radial thrust on the pump's shaft and couplings. The phenomenon of radial thrust is illustrated in Figure 3, where the pressure/velocity differential between positions P1 and P2 causes an additional imbalance of forces on the pump's impeller. The bearings, shafts and casings of a pump are designed to resist the anticipated radial load, but pumps have been destroyed within days, or even a few hours, through excessive wear in bearings, seals, shaft sleeves and wearing rings caused by excessive shaft deflections resulting from radial thrust (Jones et al 2008). The ideal is therefore that the approach flow to a pump should be an undisturbed flow - free from unequal velocity distributions, unequal pressure distributions, entrained air or gas bubbles, vortices and excessive pre-swirl at the pump inlet - to minimise the unbalanced forces directed onto the impeller in the axial direction (ANSI 1998; Sulzer 2010; Jones et al 2008).
HYDRAULIC TRANSPORTABILITY OF AIR
Source of air in pipelines
Air can enter a pipeline, and specifically on the suction end of a pump, in the following manners (Van Vuuren et al 2004):
-
Air present in the pipes due to first time start-up or start-up after maintenance
-
Air released from solution at sufficiently low pressures
-
Air that enters the pipework due to insufficient seals and/or faulty connections
-
Air entering the pipe from a free surface due to an incorrect design and/or incorrect operating conditions.
This air present in the pipeline negatively affects pumps and pumping systems, and these negative effects include:
-
A reduction in the water cross-sectional area (Jones et al 2008, ANSI 2009)
-
An increase to the flow resistance (Jones et al 2008, ANSI 2009)
-
Possible loss of prime to the pump if a slug of air is swept into the pump case during a restart, causing a partial or complete loss of prime (ANSI 2009)
-
The creation of an environment conducive to corrosion (Jones et al 2008)
-
Creation of turbulence and air entrain-ment (Mackay 2004)
-
Implosion of entrained air due to increasing pressure at the eye of the impeller causing damage identical to that of cavi-
-
tation (Mackay 2004)
-
Noisy operation (Bloch & Burdis 2010)
-
Unbalanced axial loads (Bloch & Burdis 2010).
It is therefore imperative to hydraulically transport air through the inlet pipework and pump, and not allow an accumulation of air in the upstream pipework of the pumping system.
Fundamental equations for the hydraulic transport of air
The hydraulic transportability of air refers to the ability of a fluid flowing within a conduit to transport free air in the direction of the flow. This free air is then normally transported within the conduit until it reaches an air valve where it can be mechanically removed, or until it reaches the end reservoir, or until it reaches a position within the conduit where the fluid cannot transport the free air any further. The minimum fluid velocity required to transport free air within a conduit is referred to as the critical velocity (Van Vuuren et al 2004). The hydraulic transportability of air within a pipeline is a function of the pipe slope, the amount of accumulated air and the flow characteristics of the fluid within the pipeline (i.e. Froude number, flow velocity and flow rate) (Pothof & Clemens 2011; Van Vuuren et al 2004).
Various relationships for the assessment of the hydraulic transportability of air have been developed by various researchers. According to Van Vuuren et al (2004), the two most widely used relationships to calculate the critical velocity are those presented by Kalinske and Bliss (1943) (Equation 1), and by Wisner et al (1975) (Equation 2). Van Vuuren et al (2004) also derived their own relationship to calculate the critical velocity (Equation 3).

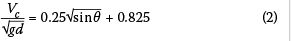

Where:
Qc = Critical flow rate (m3/s)
Vc = Critical velocity (m/s)
g = Gravitational acceleration (m2/s)
D = Diameter of the pipe (m)
θ = Slope of the pipeline (°)
a = Constant (0.2178)
b = Constant (0.4007)
These relationships can be utilised to evaluate the capacity of a pumping system to transport air through a concentric reducer, as it will represent flow conditions similar to that of a sloped pipe. The slope of the pipeline utilised in Equations 1 to 3 for a concentric reducer was calculated with the methodology described in Figure 4.
NUMERICAL MODEL (CFD SETUP)
Introduction
Computational fluid dynamics (CFD) is a defined set of methods that are used to numerically solve the governing laws of fluid motion in or around a material system, where its geometry is also modelled (Hirsch 2007). CFD has recently experienced remarkable growth in its application, and has been specifically elevated with the growth of the computational power of parallel computer processors, so that it now has a defined position in the parallel experimental investigations of fluid dynamic problems and research(Strum 2010).
The commercially available CFD software produced by CD-adapco: STAR-CCM+ (Version 8.04.007) was utilised to study the velocity distributions resulting from four velocity inputs in six concentric and six eccentric reducer geometries. Each of the simulations was run for 1 000 iterations, which were found to provide sufficient convergence and stable results.
Geometry and flow selection
The application of a range of constant velocities as inputs in the CFD calculations allows for a single reducer dimension to be modelled, i.e. the flow patterns resulting from a 1 m/s flow rate through a DN 200 to DN 150 reducer will be representative of the flow patterns through a DN 2000 to DN 1500 reducer if the reducer angles are equal. The DN 200 to DN 150 reducer was selected as the representative size reducer to be modelled with varying reducer angles (reducer transition lengths). With an increasing reducer angle (shorter reducer transition length) the uniformity of the pressure and velocity distributions will decrease and the hydraulic transportability of air through the concentric reducer will decrease.
The reducer angles were defined to represent the typical range of reducer geometries as defined by local fitting manufacturers and the guidelines presented in AWWA C208 (2008). The definition of the reducer geometries is illustrated in Figure 4, and the geometries modelled are summarised in Table 3. In order to provide flow information resulting from the application of additional downstream straight lengths of pipe requirements, as described by ANSI/HI (2009), and to model the effect of the discontinuities at the upstream and downstream ends of the reducer, a straight pipe length of 600 mm (3 x D1) was added upstream and downstream to all the reducer geometries. The 3D reducer geometries were created in Autodesk's Inventor and imported into STAR-CCM+ as Parasloid text files (*x.t).
The maximum velocity in the pump inlet pipework is typically recommended to be 2.4 m/s (see Table 2). By using the maximum velocity in the study, the non-uniform flow profiles will be exaggerated while the hydraulic transportability of air will be at its maximum. A velocity of 1 m/s is often used in the industry and this velocity will therefore provide velocity distributions typically experienced, and the capacity of flow to hydrauli-cally transport air through the fitting will be lower with this velocity than with a velocity of 2.4 m/s. Other flow velocities were selectee ranging from 1 m/s to the maximum velocity of 2.4 m/s (1 m/s, 1.5 m/s, 2 m/s and 2.4 m/s) to provide a complete set of results.
CFD input parameters
Model selection
The CR 10 model was selected to be used as the model where the CFD input parameters, such as meshing models and physics values, were tested to produce a numerical model that accurately represents the fluid flow problem and that could be solved within an acceptable period of time with adequate solution stability. After an iterative process the CR 10 model provided an acceptable solution, and the remaining 11 reducer geometries were set up with the final CR 10 model parameters. The significant inputs for the numerical models are described below (the numerous input parameters that were not changed, are not discussed).
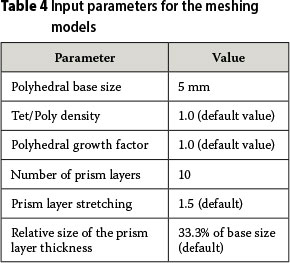
Meshing models
STAR-CCM+ provides various meshing models that can be selected to suit the specific problem. The following meshing model were selected in this instance:
-
Surface remesher. The surface remesher re-triangulates a closed starting surface to obtain a higher quality surface (CD-adapco 2012).
-
Polyhedral mesher. Polyhedral type cells (14 cell faces on average) produce a more accurate solution when compared to a tetrahedral mesh (4 cell faces) (CD-adapco 2012).
-
Prism layer mesher. Tu et al (2008) recommended that geometries with flows within bounded walls have locally refined or clustered mesh in the vicinity of the wall boundaries to ensure that the viscous boundaries are properly resolved.
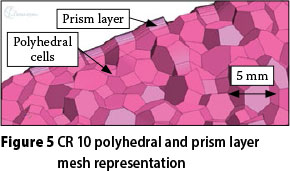
The input parameters for the meshing models used are provided in Table 4, and an example of the mesh of one of the models is provided in Figure 5.
Physics input parameters
The physics models and input parameters were selected to best suit the flow problem. Brief descriptions of the Star-CCM+ physics input parameters follow:
-
Space. The space model selected is the three-dimensional space model.
-
Time. The time physics model controls the iteration and/or time stepping of the solver. The steady time model was selected.
-
Material. The material model controls the definition of the substances being analysed, liquid in the case of this study.
-
Flow. Segregated flow was selected to represent the incompressible water flow.
-
Viscous regime. The flow being modelled is viscous and is in the turbulent zone. Therefore the turbulent viscous regime was selected. By selecting the turbulent viscous regime, the Reynolds-Averaged Navier-Stokes (RANS) turbulence model was auto-selected.
-
Equation of state. The equation of state model is used to compute the density and density derivatives relating to temperature and pressure. Temperature does not form part of this study, and the change density of the water will be insignificant due to the pressure loss experienced in the pump inlet piping. The constant density model was selected to model the equation of state.
-
Reynolds-Averaged turbulence. A model needs to be selected to provide closure to the RANS equations. The K-Epsilon model was selected for this study, as it provided a lower computational cost and was well suited to the flow properties of the study.
-
K-Epsilon model. STAR-CCM+ provides a choice of seven different K-Epsilon models The selection of the K-Epsilon turbulence model is determined by the wall treatment (near-wall modelling assumptions), the Reynolds number and the coarseness or the fineness of the mesh. The standard two-layer K-Epsilon model and the realisable two-layer K-Epsilon model offer the most mesh flexibility. They can be utilised on a wide range of y+ values (all - y+). The two-layer all y+ wall treatment and realizable K-Epsilon two-layer were automatically selected on selection of the K-Epsilon turbulence model. This selection corresponds to the guidelines described above and was not changed in the study.
Boundary conditions
Appropriate boundary conditions that represent the real physical fluid flow conditions are required to be selected in the CFD software. The boundary types selected to represent the fluid flow problem are velocity input, pressure outlet and fluid wall. The locations of these boundary conditions are illustrated in Figure 6. Descriptions and input parameters for the selected boundary types are provided below:
-
Velocity inlet. This boundary type was selected for the inflow boundary (upstream end) of the model and represents normal flow conditions entering the pipe perpendicularly, with a constant velocity that is supplied as an input parameter.
-
Pressure outlet. This boundary type was selected for the outflow boundary (downstream end) and represents a uniform constant pressure at the outlet that is supplied as an input parameter. The pressure was set to 150 000 Pa (150 kPa) to provide a positive pressure for the model.
-
Wall. A wall boundary represents an impermeable surface and is applicable as an impermeable boundary for inviscid flows and as an impermeable, non-slip boundary for viscous flow simulations (CD-adapco 2012). A roughness value (0.06 mm) was added to the fluid wall to enable near-wall turbulence and thereby apply friction to the model in order to accurately model the pipework. The roughness value utilised was obtained from Wallingford and Barr (2006) for an epoxy-lined steel pipe in a normal condition (typically the type of lining used for fittings in water pump stations in South Africa).
CFD visualisation and reporting
In order to visualise the magnitude of the velocity distribution through the pump inlet pipework, two scalar scenes were created. The first scene was created on the X-Y plane at the downstream end of the reducer - this scene allows for the visualisation of the simulation velocity results. The second scene was created on the Y-Z plane to visualise the propagation of the velocity differential through the reducer. In addition to the scalar scenes, X-Y plots of the velocity were generated along both the x-axis and y-axis of the pipe at four different positions (probe positions). The four probe positions are defined with Probe Position 1 starting at the downstream end of the reducer and repeated at intervals of 1 x D2 (downstream diameter), ending at Probe Position 4. XY velocity plots along two circles with diameters of 0.8 x ID2 and 0.6 x ID2 at Probe Position 1 were also created. The orientation of the scalar scenes, the locations of the four probe positions and the orientation of the x-axis, y-axis and z-axis are illustrated in Figure 7.
Limitations
In the analyses, uniform flow conditions were provided at the inlet of the geometry; in engineering applications this may seldom be the case. These non-uniform flow conditions may influence the velocity distribution in such a way that a concentric or eccentric reducer within the recommended range may produce a velocity distribution that is outside of the acceptance criteria, which needs to be quantified when designing the inlet pipework to a pump.
ASSESSEMNT CRITERIA
Further to the velocity and approach flow requirements provided in Table 2, assessment criteria were defined in order to compare the performance of the various reducer geometries. ANSI (1998) and Jones et al (2008) specified the requirement for time-averaged velocities at the pump suction to be within 10% of the cross-sectional area average velocity. Wallingford (2001) in Sinotech CC (2005), and Van Vuuren (2011) provided the following guidelines for velocity distribution variations in suction pipework:
-
Velocity variation along line ABCD is less than 10% of the average velocity (see Figure 8).
-
Maximum velocity variation along a circle AEDF is ± 5% of the average velocity (see Figure 8).
The requirement described by Wallingford (2001) in Sinotech CC (2005), and Van Vuuren (2011) did not indicate the location of the circle AEDF. Two circles were therefore defined (0.6 χ D2 and 0.8 χ D2) to assess the sensitivity of the location of the circle. The assessment criteria were labelled and the final assessment criteria used are summarised in Table 5.
RESULTS AND DISCUSSION
The results that were obtained are reflected under the following headings:
-
Scalar scene results
-
Results - Criterion 1 and Criterion 3 y-axis
-
Results - Criterion 2
-
Results - Criterion 3 x-axis
-
Results - Hydraulic transportability of air
-
Results matrix
Scalar scene results
The scalar scenes generated through the study allow for the development of the velocity distribution through the reducer to be visualised. Four scalar scenes for an input velocity of 1.5 m/s are provided as examples in Figure 9 and Figure 10 to illustrate the difference in velocity distributions resulting from the different reducer types and geometries. The main observations resulting from the scalar scenes are:
-
The downstream flow distribution evens out rapidly and presents a typical uniform distribution by the time it reaches a distance of 1 x D2 from the reducer (Probe Position 2).
-
The velocity distribution for the concentric reducers produce velocity distributions that are symmetrical around the centre of the pipe, i.e. the velocity contours are circular in shape.
-
The eccentric reducers produce areas of high velocities towards the bottom (sloped) side of the reducer, which result in non-uniform velocity distribution at the downstream end of the reducer (Probe Position 1).
-
The magnitude of variance in the velocity distributions increases with an increase in reducer angle.
-
In the case of the reducers with larger angles, the resulting velocities may be of such a nature that they will fall outside of the acceptance criteria.
Results -
Criterion 1 and Criterion 3 y-axes
Criterion 1 requires the velocity variation along line ABCD to be less than 10% of the average velocity along line ABCD. Criterion 3 y-axis requires the velocity variation along line ABCD (y-axis) to be less than 10% of the cross-sectional average velocity. The average velocities at the downstream end of the reducer (at ID2) were calculated and the average velocities along line ABCD (y-axis) at Probe Position 1 were calculated for all the simulations. The average velocities along line ABCD are within 0.9% (0.4 m/s) of the average velocity. Therefore the Criterion 1 and Criterion 3 y-axes were assumed to be equal for the assessment, and the assessment was conducted on the cross-sectional area average velocity. The results for Probe Positions 2, 3 and 4 are not provided due to the uniformity in the velocity distribution at these positions, as illustrated in Figure 9.
The results for all four velocities presented similar outcomes. The upper end of the eccentric reducers (ER 15, ER 20 and ER 30) and the CR 20 model concentric extend past the upper limit of the acceptance envelope and therefore do not pass acceptance Criterion 1 and Criterion 3 y-axes. The remaining concentric reducers (CR2, CR 2.5, CR 5, CR 10 and CR 15) and eccentric reducers (ER 2.5, ER 5 and ER 10) all fall within Criterion 1 and Criterion 3 y-axes. The results for the velocity distributions along the y-axis (line ABCD) for the 1.5 m/s velocity are provided as an example of the results obtained for Criterion 1 and Criterion 3 y-axes in Figure 11.
Results - Criterion 2
Criterion 2 HRW1 requires the velocity variation along circle AEDF to be less than 5% of the average velocity along circle AEDF, and Criterion 2 HRW2 requires the velocity variation along circle BGCH to be less than 5% of the average velocity along circle BGCH. The results for Probe Positions 2, 3 and 4 were not plotted due to the uniformity in the velocity distribution at these positions, as was demonstrated in Figure 9. The concentric reducers were not assessed according to Criterion 2, as their velocity distributions are symmetrical around the centre of the pipe, i.e. the velocity contours are circular in shape and will produce results that will fall within the acceptance envelope.
The velocities along the circumference of the two circles are plotted on the y-axis and an angle relating to the position of the cylinder is plotted on the x-axis. This angle is a component of the coordinate system illustrated in Figure 12. The result for the ER 15 Model at 1.5 m/s is provided in Figure 13 as example of the results obtained for Criterion 2. Models ER 20 and ER 30 fall outside both the HRW 1 and HRW 2 criteria, and the ER 15 model falls outside the HRW 1 criteria. Therefore ER 15, ER 20 and ER 30 do not pass acceptance Criterion 2. The remainder of the eccentric reducers (ER 2.5, ER 5 and ER 10) are within the acceptance envelope for Criterion 2.
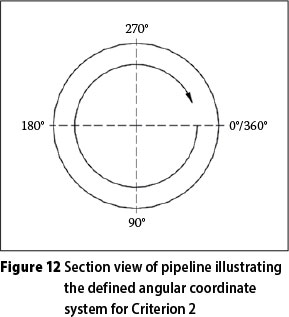
This highlights that the positions of the Criterion 2 circles have an effect on the outcomes of the results.
Results - Criterion 3 x-axis
Criterion 3 x-axis requires the velocity variation along line EGHF (x-axis) to be less than 10% of the cross-sectional average velocity. The results for Probe Positions 2, 3 and 4 are not provided, due to the uniformity in the velocity distribution at these positions, as illustrated in Figure 9.
The results for all four velocities presented similar results. The CR 20 model falls outside of acceptance Criterion 3 x-axis for all four flow velocities, and the ER 30 model falls outside of acceptance Criterion 3 axis for the 1.5 m/s, 2 m/s and 2.4 m/s velocities, and falls within the criteria for the 1 m/s velocity. The remainder of the models (CR 2, CR 2.5, CR 5, CR 10, CR 15, ER 2.5, ER 5, ER 10, ER 15 and ER 20) all fall within the Criterion 3 x-axis acceptance envelopes. The results of the velocity distributions along the x-axis (line EGHF) used in Criterion 3 x-axis for the 1.5 m/s velocity are provided as an example of the results obtained for Criterion 3 x-axis in Figure 14.
Comparison -
Hydraulic transportability of air
The critical velocity for each of the concentric reducers was calculated with the upstream (larger) diameter (D1) as the input diameter in the calculation, as the velocity increases through the reducer, thereby increasing the capacity to hydraulically transport the air. The calculated critical velocities are provided in Table 6. The values calculated with Equation 1 and Equation 3 are representative of one another. However, the values calculated with Equation 2 are not representative (this could be due to the addition of a constant of 0.825 x (gD)0.5 that affects the equation at low velocities). Only the values obtained with Equation 1 and Equation 3 were utilised to assess the hydraulic transportation of air through the models. The only model where air could not be hydraulically transported through it is the CR 20 model at 1 m/s. This model, however, also fails Criterion 1 and Criterion 3. It is noted that the critical velocity is a function of the pipe diameter (Equations 1, 2 and 3), and other results will differ from the results presented for the DN 200 upstream diameter utilised in this study. The hydraulic transportability of air will need to be assessed during the design of the pump station pipework.
Results matrix
The final assessment of the 48 models simulated with CFD according to the four criteria, is provided in Table 7. Concentric reducers CR 2, CR 2.5, CR 5, CR 10 and CR 15, and eccentric reducers ER 2, ER 5 and ER 10 all produce velocity distributions that fall within all four of the acceptance criteria at all four flow rates modelled. The CR 20 concentric reducer and eccentric reducers ER 15, ER 20 and ER 30 all fail one or more of the assessment criteria.
The range of angles modelled is representative of a wide range of reducers, separated by large increments in order to keep the sample group manageable (i.e. ER 2.5, ER 2, ER 10 and not ER 1, ER 2, ER 3, etc). The reducers that have been listed for the maximum allowable slopes (CR 15 and ER 10) may be conservative. For example, a concentric reducer of 16° may still provide acceptable results, as the slope is less than the CR 20 reducer that did not pass the various criteria.
CONCLUSIONS
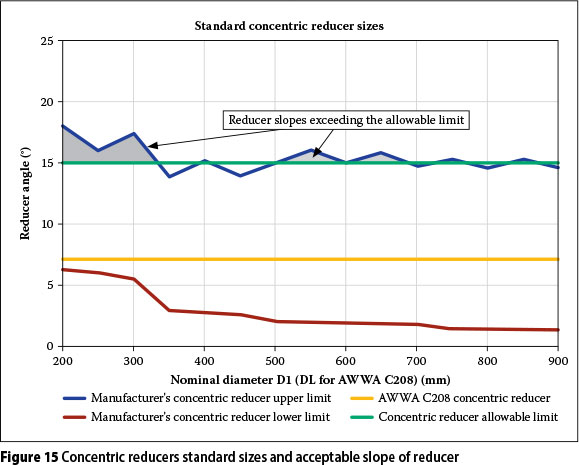
Figures 15 and 16 present charts illustrating the standard reducer sizes (from AWWA C208 and from the fitting manufacturers) and maximum slope of the acceptable size reducer, as defined in Table 7. From these charts it can be observed that various standard size reducer fittings fall outside of the acceptance criteria for the eccentric reducers. For the eccentric reducers this includes AWWA C208 standard eccentric reducer (angle of 14°). The addition of a straight length pipe may be used on the downstream end of the selected reducer to produce a more uniform velocity distribution at the pump inlet. This addition, however, decreases the NPSH available and increases the pump station's footprint and cost.
RECOMMENDATIONS
Review of pump inlet criteria
Based on the results obtained from this research it is recommended that concentric reducers be considered to improve the inlet conditions at pumps and that the following criteria should be considered during the assessment of pump suction pipe work:
-
Criterion 1: Velocity variation along line ABCD is less than ±10% of the average velocity along line ABCD.
-
Criterion 2: Velocity variation along line EGHF is less than ±10% of the average velocity along line EGHF.
-
Criterion 3: Maximum velocity variation along a circle AEDF is ±5% of the average velocity along circle AEDF; the diameter of circle AEDF is 0.8 x ID.
-
Criterion 4: Maximum velocity variation along a circle BGCH is ±5% of the average velocity along circle BHCG; the diameter of circle BGCH is 0.6 x ID.
-
Criterion 5: Time-averaged velocity at any point is to be within ±10% of the cross-sectional area average velocity.
-
Criterion 6: Air must be able to be hydraulically transported through the reducer.
Intended further research
It is recommended that:
-
Additional examples with various bends, elbows and sweep tees typically found in pump inlet pipework that could possibly create swirl or non-uniform flow conditions entering into the suction reducers, are to be modelled. With this information, guidelines on typical suction manifold and suction pipework can be developed.
-
Additional CFD modelling and/or physical model studies should be performed,
where the hydraulic transport of air through the concentric reducer is explored, to assess which one of the hydraulic transport of air equations best suits this problem.
REFERENCES
AWWA (American Water Works Association) 2008. C208-07: Dimensions for fabricated steel water pipe fittings. Denver: AWWA. [ Links ]
ANSI (American National Standards Institute) 1998. [ Links ]
ANSI/HI 9.8-1998: American National Standard for pump intake design. Parsippany, NJ: Hydraulic Institute. [ Links ]
ANSI (American National Standards Institute) 2009. ANSI/HI 9.6.6-2009: American National Standard for rotodynamic pumps for pump piping. Parsippany, NJ: Hydraulic Institute. [ Links ]
Bloch, H P 2010. Eccentric reducers and straight runs of pipe at pump suction. Hydrocarbon Processing, September, 9. Available at: http://www.hydrocarbonprocessing.com/article/2663961 [ Links ]
Bloch, H P & Burdis, A R 2010. Pump user's handbook life extension, 3rd ed. Lilburn, GA: The Fairmont Press. [ Links ]
CD-adapco. 2012. USER GUIDE STAR-CCM+ Version 7.04.006. [ Links ]
Hirsch, C 2007. Numerical computation of internal and external flows. Fundamentals of Computational Fluid Dynamics, 2nd ed. Oxford: Butterworth-Heinemann. [ Links ]
Jones, G M, Sanks, R L, Tchobanoglous, G & Bosserman II, B E (Eds) 2008. Pumping station design. Pumps: Intake design, selection, and installation, 3rd ed. Burlington, MA: Butterworth-Heinemann. [ Links ]
Kalinske, A A & Bliss, P H 1943. Removal of air from pipelines by flowing water. ASCE Journal, 13: 480. [ Links ]
KSB 2012. Operating instructions ETA centrifugal pump (A,B,C,Dpedestals). Available at: http://www.ksbpumps.co.za//products/etac&d/etacd_operating_instructions.pdf. [ Links ] [Accessed on 12 April 2012].
Mackay, R 2004. Practical pump handbook. Oxford: Elsevier Advanced Technology. [ Links ]
Pothof, I W M & Clemens, F H L R 2011. Experimental study of air-water flow in downward sloping pipes. International Journal of Multiphase Flow, 37: 278-292. [ Links ]
SAPMA (South African Pump Manufacturers Association) 2002. Pumps: Principles & practice, 4th ed. Johannesburg: K Myles and Associates. [ Links ]
Sinotech CC 2005. CFD modelling of the pipe work on the inlet side of the abstraction works. Unpublished Technical Report. Available from Sinotech CC: http://www.sinotechcc.co.za [ Links ]
Sturm, T W 2010. Water, water everywhere. Journal of Hydraulic Engineering, 136(1): 1-2. [ Links ]
Sulzer Pumps Ltd 2010. Centrifugal pump handbook, 3rd ed. Oxford: Butterworth-Heinemann. [ Links ]
Van Vuuren, S J 2011. Standards for sumps, pumps and pipe work. Report SHW 795 - Pump station design. Pretoria: University of Pretoria, Department of Civil Engineering. [ Links ]
Tu, J, Yeoh, G H & Liu, C 2008. Computational fluid dynamics - A practical approach. Oxford: Butterworth-Heinemann. [ Links ]
Van der Westhuizen, W 2011. Case study: Inlet conditions leading to problems - Knysna. Report SHW 795 - Pump station design. Pretoria: University of Pretoria, Department of Civil Engineering. [ Links ]
Van Vuuren, S J, Van Dijk, M & Steenkamp, J N 2004. Guidelines for effective de-aeration. WRC Report No 1177/2/04. Pretoria: Water Research Commission. [ Links ]
Wallingford, H R 2001. In: Sinotech CC 2005. CFD modelling of the pipe work on the inlet side of the abstraction works. Unpublished Technical Report. Available from Sinotech CC: http://www.sinotechcc.co.za [ Links ]
Wallingford, H R & Barr, D I H 2006. Tables for the hydraulic design of pipes, sewers and channels, 8th ed. Vol II. London: Thomas Telford. [ Links ]
Wisner, P E, Mohsen, F N & Kouwen, N 1975. Removal of air from water line by hydraulic means. Journal of the Hydraulic Division, ASCE, 101(HY2): 243-257. [ Links ]
 Correspondence:
Correspondence:
Ross Mahaffey
PO Box 14135 Lyttelton Manor 0140
South Africa
T: +27 12 427 2000
F: +27 86 764 3522
E: ross.mahaffey@aurecongroup.com
S J Van Vuuren
Department of Civil Enginering University of Pretoria
Pretoria 0001
South Africa
T: +27 12 420 2438
F: +27 12 362 5218
E: fanie.vanvuuren@up.ac.za

ROSS MAHAFFEY Pr Eng, who is an Associate Member of SAICE, obtained his BEng (Civil) and BEng Honours (Water Resource Engineering) degrees from the University of Pretoria, and is currently enrolled for his MEng degree at the same institution. He works for Aurecon in Tshwane (Pretoria), and has five years' experience in the water engineering field. His interests lie in the design and construction of bulk water supply infrastructure, and more specifically pump station design, large diameter steel pipelines and cathodic protection.

PROF S J VAN VUUREN Pr Eng holds an MBA and PhD (Engineering) from the University of Pretoria. He obtained extensive experience while working for the Department of Water Affairs, the Windhoek Municipality, various consulting engineering firms and contractors, and international academic institutions. Prof van Vuuren has widely published and presented technical papers. He was involved with a number of research projects, which included projects on closed-conduit flow systems, catchment development on surface discharge, sanitation, and hydropower generation. He also conducted a number of physical model studies, such as the Berg River Outlet Works, the energy dissipation for the proposed Necketal Dam (Namibia), the Sheikh Zayed Pump Station (Egypt), the VRESAP Pump Station Suction Manifold (South Africa), the Grootvlei Pump Station (South Africa), the Chanza Pump Station (Presa Del Arenosa, Spain), and the Askelon Pump Station (Israel). Prof van Vuuren developed software that is internationally used for the sizing and location of air valves, and he compiled, with other authors' input, the SANRAL Drainage Manual and the Namibian Road Drainage Manual. He also holds patents on the elimination of cavitation in control valves, real-time assessment of biofilm growth and climate control.














