Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
Journal of the South African Institution of Civil Engineering
On-line version ISSN 2309-8775
Print version ISSN 1021-2019
J. S. Afr. Inst. Civ. Eng. vol.56 n.2 Midrand Aug. 2014
TECHNICAL PAPER
The issue of personal safety on dolomite: A probability-based evaluation with respect to transient passage in a city centre
H A D Kirsten; G J Heath; I S Venter; A C Oosthuizen
Correspondence
ABSTRACT
For the past fifty years empirical knowledge guided the development of rules regarding population density on dolomite land. The insatiable demand for land, the improvement in transportation infrastructure and the associated need for improving the functionality of towns require that these rules on the risk of personal injury and damage to assets are revisited from a more scientific perspective. Probability theory provides a basis for decision-making in this regard.
SANS 1936:2012 defines development densities for different types of land usage, including non-residential improvement, high- and low-rise buildings and single-storey dwelling houses. The paper is devoted to public safety along the roads, thoroughfares and open spaces outside buildings in a heavily populated city centre as a study in "transient density" on dolomite land. People are transported through the city in a range of vehicles. Some people walk through the city and some appear in particular locations as dispersed groups. The densities at which people appear differ during peak hours, other times of the day, and at night.
The overall probability of fatal injury is determined by the mutually dependent probabilities of sinkhole occurrence, appearance of the sinkhole in a particular location, appearance of the sinkhole at a particular time, coincidence with the vehicle, people being unaware of the sinkhole, people falling into the sinkhole, people not being protected by the vehicle and the relative number of fatal injuries
Sinkholes are invariably caused by water-bearing services that tend to leak at isolated locations, as a result of which only one sinkhole occurs at a time in a particular stretch of land. In developed land the leaky service and the sinkhole are generally repaired soon after the sinkhole has occurred, which precludes the recurrence of sinkholes in that area for a very long period of time. The probability of sinkhole occurrence can therefore be evaluated on the basis of the binomial distribution. The infiltration regime that determines the sinkhole return period for this purpose is based on the water and wastewater reticulation infrastructure, stormwater control measures, landscaping and irrigation provisions, occurrence of impermeable pavements and dewatering protocols characteristic of a business district in a city centre.
It is shown that the probability of potential fatal injury during peak time is larger than an internationally prescribed threshold value for Inherent Hazard Classes 6, 7 and 8 for minibus taxis, buses and pedestrians at road intersections for sinkholes 10-20 m in diameter. These unacceptable cases may be resolved by marginally changing the values for some of the input probabilities that may be somewhat conservative. Alternatively, the adopted threshold level for tolerable risk could be relaxed from "As Low As Reasonably Practical" to "Slight", which may more accurately represent the fait accompli sense of risk in the brownfields situation in Centurion City. A further way to view the unacceptable cases is that they are largely compatible with the prescribed land usages in SANS 1936:2012, in that precautionary measures corresponding to area designations D3 + FP1, D3 + DL1 or D4 are required for all but Inherent Hazard Class 1. These requirements are fully justified for Inherent Hazard Classes 6, 7 and 8, may be somewhat conservative for Inherent Hazard Classes 4 and 5, and are quite likely too conservative for Inherent Hazard Classes 2 and 3 in the open spaces in a city centre environment. A fourth way of dealing with the unacceptable cases in a greenfields situation is to implement engineering designs to pavement structures that would mitigate the hazard.
Keywords: sinkhole, coincidence, personal safety, risk, hazard, probability, city centre, transient passage
INTRODUCTION
The hazard that sinkholes and surface subsidences pose to public safety has for the past fifty years played a fundamental role in township development on dolomite land. Empirical knowledge guided the development of rules on population and development density in different types of townships on such land. The rules were based on the observation that the likelihood that people would be affected by a sinkhole, as well as the severity of such effect, were related to the number of people who congregate in a particular area. Commercial demand for land development, the improvement in transportation infrastructure and the general need for densification to improve the functionality of towns bring people together in greater numbers and require that the empirical rules be revisited from a more scientific perspective. Probability theory informed by industry standards for sinkhole size and frequency per unit of area for different hazard classes, as propounded in SANS 1936:2012, provides the basis for such an approach.
Kirsten et al (2009, 2014a and 2014b) dealt with the issue of personal safety in single- and two- and three-storey residential accommodation. In the present paper the focus is on high-rise buildings commensurate with a cityscape similar to central Pretoria and Johannesburg, and with the volumes of vehicular and pedestrian traffic associated with such cities, as illustrated in the photograph in Figure 1.

In dealing with the exposure of people in residential accommodation, the likelihood of coincidence between the structure and the sinkhole is the point of departure. The likelihood of the home being occupied, structural collapse of the building, the occupants being in residence at the time and a number of occupants fatally injured, are dependent on the sinkhole occurring sufficiently close to the building to affect it. Transient density, which refers to people moving about in the open spaces between houses in cars and on foot, was not considered by Kirsten et al (2009, 2014a and 2014b) in dealing with single and two- and three-storey residential accommodation, because it was perceived to be low and the likelihood small that larger numbers of people would be injured out of doors in such environments. In a city centre, transient density in public spaces is very high at particular times of the day.
It is assumed in the paper that the buildings in which people are accommodated during most of the day in a city centre are safely founded and that the safety of the occupants is not compromised, even if a sinkhole were to develop directly beneath these buildings. The focus in this instance is rather on the large numbers of people who enter and exit buildings at various times of the day to occupy the roads and sidewalks and the open spaces in-between the buildings of the city in various ways and modes of transportation.
The purpose in the paper is to evaluate the risk of fatal injury in the various modes of transportation, and ways in which people appear in public spaces in the centre of a city on dolomite land subject to the infiltration of water peculiar to such an environment.
The infiltration regime is a fundamental determinant in the evaluation of sinkhole occurrence. Kirsten et al (2014a) distinguished between natural, residential and city centre infiltration regimes, as these are determined by the water-bearing services, measures to control stormwater, landscaping and irrigation provisions, occurrence of impermeable pavements and dewatering protocols characteristic to each regime.
The infiltration regimes are expressed in terms of potential sinkhole return periods for the eight Inherent Hazard Classes defined by Buttrick et al (2001), and the six sinkhole sizes as shown in Table 1. The two largest sinkhole sizes were added to the four sizes originally presented by Buttrick et al to extend their range. The research developments that preceded the definition of the return periods in Table 1 are presented by Kirsten et al (2009; 2014a).
Sinkhole occurrence is treated in this paper as a chance phenomenon, the qualifications of which are dealt with by Kirsten et al (2014a). It mainly needs to be observed that, as a result thereof that sinkholes are caused by waterbearing services that tend to leak at isolated locations, only one sinkhole occurs at any point in time in a neighbourhood, and that as a result of how the causes and the sinkhole itself are repaired, only that one sinkhole occurs at that location over a substantial period of time.
EVALUATION OF DOLOMITE RISK IN BUSINESS DISTRICTS
Before the advent of SANS 1936:2012 and SANS 10400:2012, the approach to developing on dolomite land was to strictly control residential development according to Inherent Hazard Class 5 or better land, and to allow different categories of commercial development on Inherent Hazard Classes 6 and 7 land. The motivation for this was that more effort can go into foundation systems for commercial development, that better control can be exercised on wet services systems and that corporate ownership is more robust to losses suffered when things go wrong than what individual home ownership is capable of. Inherent Hazard Class 8 land was considered to be irreparably unsuitable for any formal development. The promulgation of SANS 1936:2012 and SANS 10400:2012 considerably clarified the matter and to some extent relaxed these restrictions in some respects.
A business district in principle comprises low-rise shops and offices, garages, parking lots and high-rise office and apartment buildings. An extract of the land usage requirements in Table 2 in SANS 1936 -1:2012 on a business district including these improvements is given in Table 2. The land usage requirements in the standard are expressed in terms of maximum permissible population densities for four levels of precautionary measures represented by area designations D1, D2, D3 and D4 respectively, and are briefly defined as follows:
D1 No precautionary measures considered
D2 Precautionary measures prevent concentrated ingress of water into the ground
D3 Additional precautionary measures to D2 requirements as provided for in the standard
D4 Precautionary measures determined rationally and specifically for the particular site
It follows by inference that the maximum permissible population densities for land usage requirements D1, D2 and D3 by definition correspond to minimum population densities for land usage requirements D2, D3 and D4 respectively, i.e. for an area designation one level higher in each instance, hence the minimum inferred population densities denoted by superscript "1" in Table 2.
It can be seen in Table 2 that in all except Inherent Hazard Class 1, precautionary measures are corresponding to area designation D3 plus design level investigations FP1 and DL1 or area designation D4 required in business districts. It is required in SANS 1936 - 3:2012 that the land usage requirements apply to the entire site under development, including open areas outside buildings and all manner of infrastructure. The engineering design and construction of municipal township services and services in interconnected complexes, including stormwater management systems, roads, sewer mains and water supply systems, are specified in detail in SANS 1936 - 3:2012, irrespective of the Inherent Hazard Class. It is against this background that the purpose of the paper is to evaluate the risk of fatal injury in the various modes of transportation and appearance of people in the open spaces in a city centre.
DEFINITION OF MODES OF TRANSPORTATION, LOCATIONS AND TIMES OF EXPOSURE
The vehicles in a city centre, the locations at which the vehicles are used and the times at which people are exposed in the vehicles and on foot are defined as follows.
Vehicles
Sinkholes can affect people in different types of vehicles, such as cars, trucks, minibus taxis and buses, and by walking along or appearing as crowds in parking areas, sports fields and other open areas.
People on foot are assumed to be walking behind one another in single file or to appear in crowds. People in files or crowds are assumed to be equally far apart. Those in crowds are assumed to be in square formation.
There are as many of a particular type of vehicle per hectare as appear in terms of a particular traffic distribution pattern. A single file or a crowd of people encompassed by a sinkhole is also considered as a vehicle or mode of transport, since they are affected as a group by the sinkhole. There are as many files of people or crowds per hectare as encompassing sinkholes of a particular size can fit along a walkway or into an area without overlapping.
Locations of exposure
The places in which the various kinds of vehicles, including groups of people, occur are referred to as locations, and in this paper include roads, road intersections, sidewalks, parking areas, lanes, malls and open areas.
Times of exposure
The risk of sinkholes to people in the various types of vehicles and in the various locations referred to is considered separately during peak, day and night time to account for the daily variation in population density in public places.
TRAFFIC DISTRIBUTION REGIME
The objective of this paper is to determine the likelihood of sinkhole-induced fatal injury in a particular mode of transport or appearance in a city centre. The distribution of people moving through a city varies in terms of vehicle size and pedestrian dispersion. As a result, the likelihood of fatal injury varies across different locations in which different modes of transport carrying different numbers of passengers and different densities of pedestrians occur. The objective can therefore be met by determining the particular mode of transport and the time during which the probability of fatal injury is the largest. The frequencies of distribution for the modes of transport with lesser probabilities of fatal injury cannot be increased in isolation, because the frequencies of all the modes of transport are an integral part of the overall traffic distribution regime.
DETERMINATION OF PROBABILITY OF FATAL INJURY
The probability of fatal injury in a particular vehicle and location, and at a particular time, is determined by the joint occurrence of eight dependent events as represented in the following Expression.

The component probabilities may be defined as follows:
■ P1
Probability of sinkhole occurring
■ P2,location
Probability of sinkhole appearing at a particular location
■ P3,time
Probability of sinkhole appearing at a particular time
■ P4,location,vehicle,time
Probability of sinkhole coinciding with a vehicle
■ P5,awareness
Probability of people not aware of sinkhole
■ P6,vehicle =RsizeofvehicleRpavementfails
Probability of people falling into sinkhole
■ Rsizeofvehicle
Probability of sinkhole being larger than vehicle
■ Rpavementfails
Probability of supporting pavement failing structurally
■ P7,vehicle
Probability of vehicle not providing protection to people
■ P8,vehicle
Relative number of people sustaining fatal injury in a particular vehicle
The subscript "location" denotes the following specific locations that are separately provided for in subsequent expressions:
■ "cross" roads in intersections
■ "road" roads outside intersections
■ "inter" walkways in intersections
■ "side" sidewalks outside intersections
■ "lane" lanes and malls
■ "park" open parking areas
■ "next" stands outside, but adjoining buildings
■ "open" stands outside, but away from buildings
■ "under" under buildings
The subscript "vehicle" denotes the following specific vehicles that are separately provided for in subsequent expressions:
■ "car" cars
■ "truck" trucks
■ "taxi" minibus taxis
■ "bus" buses
■ "file" group of people in single file encompassed by a sinkhole
■ "crowd" group of people in square formation in crowds encompassed by a sinkhole
The subscript "time" denotes the following specific times that are separately provided for in subsequent expressions:
■ "peak" peak periods during the day
■ "day" daytime outside peak periods
■ "night" night-time (12 out of 24 hours) The probabilities of fatal injury per hectare at a particular time for all the vehicles of a particular type, but in different locations, should be combined as independent events as the overall probability of fatal injury Pvehicle,time for that particular vehicle in different locations. Let "location-1", "location-2"........... "location-n" denote the number of locations, n, in which the particular type of vehicle appears at a particular time. The overall probability of fatal injury may then be expressed as follows in Expression [2] based on Expression [1]. Expression [2] applies separately for the different types of vehicles (cars, trucks, taxis, buses, pedestrians in single file and pedestrians in crowds), and for every one of the different times (peak, day and night). The locations for cars, trucks, taxis and buses include roads and road intersections. The locations for pedestrians in single file include pedestrian crossings in road intersections, sidewalks, lanes, parks and areas outside buildings. The locations for pedestrians in crowds include parks and open areas outside buildings.

PROBABILITY OF SINKHOLE OCCURRENCE (P1)
An event of recurrence interval T years, i.e. a T-year event, is an event of such magnitude that the average time between events of larger magnitude is T years. This length of time is also referred to as the return period. The events considered in this paper refer to sinkholes in intervals of increasing diameter. Reference to a T-year event is therefore with regard to the occurrence of a size of sinkhole in a particular interval.
Let D denote the lifetime of a city centre development. The probability that a T-year event will be exceeded at least once in the lifetime of the development is given by Expression [3]. It is not necessary to consider the occurrence of more than one sinkhole in a business district, because of the way in which sinkholes occur and are repaired, as explained by Kirsten et al (2014a). A lifetime is defined as 70 years, i.e. D = 70 in Expression [3].

The sinkhole return period per 100 hectares is shown in Table 1 for three comparative regimes of infiltration, namely natural, residential and city centre, as presented by Kirsten et al (2014a). Photographs of sinkholes in the three regimes are presented in Figures 2, 3 and 4. The infiltration regime for a city centre development represents the conditions around the buildings and in the public spaces in a business district. The corresponding return periods per hectare, T3, given in Table 3 were obtained by substituting the return periods, T1, from Table 1 in the expression T1=N/[(1/100)N/T1]=100T1. The probabilities, P1, of exceeding the T-year sinkhole sizes at least once in a lifetime of 70 years are determined as shown in Table 4 from Expression [3].

FREQUENCY OF SINKHOLE APPEARING IN SPECIFIC LOCATION (P2)
Sinkholes are subjectively assumed by engineering judgement of the performance of the wet services to appear in the various locations considered at the following frequencies:

The effect of leaking services is illustrated in the photograph in Figure 5 in which a broken sewer gave rise to a 5 m sinkhole.

FREQUENCY OF SINKHOLE APPEARING AT PARTICULAR TIME (P3)
Two four-hour peak periods are assumed to occur at the start and end of the day, leaving daytime and night-time periods of four and twelve hours respectively. The frequencies of a sinkhole appearing during the three periods are therefore as follows:

PROBABILITY OF SINKHOLE COINCIDING WITH VEHICLE (P4)
An aerial view of traffic congestion at peak time in a city centre is shown in the photograph in Figure 6. A sinkhole is defined to coincide with a vehicle if it overlaps by 10% of its diameter in front and behind the vehicle, as shown in Figure 7. The overall distance (v+1.8d) may be referred to as the coincident distance. The diameter of the sinkhole is denoted by d and v is the length of the vehicle. The probability of a sinkhole coinciding with a particular kind of vehicle is defined as the proportion of the coincident distance to the length of road along which the vehicle is travelling, but which is not occupied by vehicles of another kind, multiplied by the likelihood of the sinkhole occurring in the stretch of road occupied by vehicles of the same kind. Different lanes in the same or opposite direction are taken as separate lengths of road along which the vehicle can travel. The probabilities of a sinkhole coinciding with other similar vehicles along the same length of road are taken as independent events and are accordingly added. Therefore, for any one kind of vehicle of which there are n along the length of road considered:


The probability of a sinkhole coinciding with a particular kind of vehicle in various locations at a particular time of day may therefore be expressed as follows:

PROBABILITY OF SINKHOLE COINCIDING WITH FILES OF PEOPLE (P4)
A view of pedestrian density during peak hour in a city centre is shown in the photograph in Figure 8. The probability of a sinkhole coinciding with a group of people walking in single file along a path as shown in Figure 9 is defined as the proportion of the diameter of the sinkhole to the length of the path. The number of persons within the diameter of the sinkhole defines the size of the group, j.. The diameter of the sinkhole, d, is a multiple α of the spacing between people, L ÷ h, where L denotes the length of the path and h the number of people along the path. Thus:

The number of people equally far apart within length d is by definition given by,

The number of groups of people, g, of size j along the path is given by:
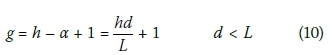
The probability that a sinkhole of diameter d coincides with any one of g number groups of people of size j along a path of length L along which h number people are present at equal distances from one another is therefore given by:

The probability of a sinkhole coinciding with groups of people along a particular walkway in various locations at a particular time of day may therefore be expressed as follows:

PROBABILITY OF SINKHOLE COINCIDING WITH CROWDS (P4)
The probability of a sinkhole coinciding with a group of people in a park in square formation, as shown in Figure 10, is defined as the proportion of the area of the sinkhole to that of the park. The number of persons within the diameter of the sinkhole defines the size of the group, j. The diameter of the sinkhole, d, is a multiple β of the grid spacing (A÷h)0.5, where A denotes the area of the park and h the number of people in the park in square formation. Thus,

The number of people in square formation within an area d2 is by definition given by:

Approximating the area of a sinkhole of diameter d by d2 does not give rise to a significant error in the context of the problem, since the number of people circumscribed by a sinkhole does not vary for variations of the diameter of the sinkhole within grid intervals. Adding the corners of an area d2 is no worse than not accounting for a change in the number of people circumscribed for variations of the diameter of a sinkhole between grid intervals.
The number of groups of people, g, of size j in the park is given by:
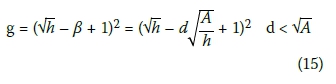
The probability that a sinkhole of diameter d coincides with any one of g number of groups of people of size j in a park of area A in which h number of people are present in square formation is therefore given by:

The probability of a sinkhole coinciding with crowds of people in square formation in open areas in various locations at a particular time of day may therefore be expressed as follows:

PROBABILITY OF PEOPLE UNAWARE OF SINKHOLE (P5)
It is assumed that people are 100% unaware of sinkholes that occur in any location and at any time. Thus, P5 = 1.0.
PROBABILITY OF PEOPLE FALLING INTO SINKHOLE (P6)
The probability that people fall into a sinkhole presupposes that the sinkhole is larger than the vehicle, and that the pavement fails as mutually dependent events in terms of the following expression:

The component probabilities in this expression are subjectively assumed by engineering judgement to have the values given in Tables 5 and 6, and the resulting probabilities of people falling into a sinkhole in Table 7 ("pedestrian" refers to both files and crowds of people).
The size of a vehicle relative to a sinkhole is illustrated in the photograph in Figure 11 in which a large passenger vehicle has fallen some distance into a 10 m sinkhole. The capping that a road pavement typically provides over a sinkhole is illustrated in the photograph in Figure 12, taken on the old Pretoria to Johannesburg road.


PROBABILITY OF VEHICLE NOT PROVIDING PROTECTION (P7)
It is presumably 100% certain that none of the vehicles provide any protection against fatal injury, i.e. P7 = 1.0. Even if the vehicle is not buried or badly deformed, the passengers would still be severely knocked around when a vehicle travelling at speed lands in a sinkhole.
PROBABILITY OF FATAL INJURY (P8)
Values for the probabilities of fatal injury, P8vehicle, are subjectively assumed by engineering judgement to be as given in Table 8 for various vehicles and sinkhole sizes. It is moot whether the values are not somewhat conservative, especially for the mid-range sinkhole sizes.

EVALUATION OF POPULATION DENSITY
Let svehicle denote the number of people in a particular vehicle, and Mvehicle the potential number of lives lost in the vehicle due to a sinkhole. It follows by definition that Mvehicle may be expressed as follows in terms of svehicle and the probability of fatal injury, P8,vehicle.

Let R denote the level of risk considered in terms of Figure 13, and Pvehicie the threshold lifetime probability of fatal injury per hectare for a potential number of lives lost per hectare of Mvehicle. Then in terms of Figure 13:

It follows from Expression [19] that:

Similar relationships apply to crowds.
The probability of fatal injury per hectare for a particular vehicle and time, Pvehicle.time' should be < Pvehicle, the threshold probability of fatal injury per hectare for the particular risk level considered, R. The number of people per hectare for whom this condition is satisfied are given from Expression [2] by:

The number of people in each vehicle and time slot may be varied until this condition is satisfied. The vehicle and time slot at which the potential number of lives lost is the least at F = 1.0, is the determining criterion. As an alternative approach, the likelihood of a sinkhole occurring can be reduced by mitigating the infiltration of water, propounded in SANS 1936:2012, or by upgrading the pavement to competently bridge over sinkholes of a pre-determined size.
DISTRIBUTION OF VEHICULAR AND PEDESTRIAN TRAFFIC IN A CITY CENTRE
Typical values for the parameters for the daily distribution of vehicular and pedestrian traffic in a city centre are given in Table 9, for typical layouts for the following four types of development, namely, single-storey dwelling houses, two- and four-storey dwelling units, city centre residential accommodation and city centre office accommodation. The symbols for the input parameters are given in the second column in Table 9. The typical layouts are shown in Figures 14 through 17. The values for the parameters in Table 9 are based on the assumption that the land is fully developed and all buildings are constructed complete as laid out. The figures are not adjusted downward for parking, because it is relatively minor.
The traffic distribution models in Table 9 are given to illustrate the different population densities in the various township types and to enable the theory presented in this paper to be illustrated in principle. The traffic distribution models need to be verified in terms of real-life situations. The findings on one of these models, presented further on, should not be considered as definitive of the conditions and situation in any city centre located on dolomite.
The transportation of people to/from city centre accommodation during peak time is based only on half of the length of roads and road intersections to allow for loading and off-loading of passengers, and for continuous movement of traffic. In all other instances the full lengths of roads and road intersections are taken to be available for the transportation of people. The overall lengths of trains or vehicles in single file are greatest during peak time and are equal to the total lengths of the intersections and the roads. Cycle times are also only considered to apply to the transportation of people to/from city centre accommodation during peak time. Otherwise they do not apply.
All the people are assumed to be vacated by way of vehicles and on foot in an hour from high-rise residential buildings and in an hour and a half from high-rise office buildings in cycle times of 10 minutes. The total number of people in the various kinds of vehicles in intersections and on roads is therefore equal to the total number of occupants in the buildings. The people shown in Table 9 in intersections, on sidewalks, in lanes and malls, in parking areas, outside buildings and on stands in open areas represent the influx into the city centre area in addition to the permanent occupants in buildings.
EVALUATION OF PROBABILITY OF INJURY IN A CITY CENTRE
Based on the input values in Table 9 for a city centre office development, the values for parameter F in Expression [26] for the various places, times of day and sinkhole sizes are respectively given in Tables 10, 11 and 12 for Inherent Hazard Classes 6, 7 and 8 for a risk factor R = 0.07, corresponding to a level of risk "As Low As Reasonably Practical". This enables the particular vehicles and time slots for which F < 1.0 to be readily identified as highlighted in blue.


The findings may be summarised as follows:
Parameter F is a minimum turning point phenomenon, as expected for all instances considered. The minimum turning point for parameter F corresponds generally to a sinkhole diameter of 10-20 m.
Unacceptable cases occur only for minibus taxis, buses and files of people, which can be shown to relate largely to pedestrians at intersections.
The number of unacceptable cases increases with Inherent Hazard Class.
Although not shown, it can be confirmed that no unacceptable cases occur for the development considered (high-rise offices) for Inherent Hazard Classes 1 through 5. One minimally (F > 0.9) and two moderately (0.7 < F < 0.9) unacceptable cases occur for Inherent Hazard Class 6 as evident from Table 10. Two moderately (0.7 < F < 0.9), two considerably (0.5 < F < 0.7) and one highly (0.3 < F < 0.5) unacceptable case/s occur for Inherent Hazard Class 7 as shown in Table 11. One minimally (F > 0.9), three moderately (0.7 < F < 0.9), four considerably (0.5 < F < 0.7), one highly (0.3 < F < 0.5) and three totally (F < 0.3) unacceptable cases occur for Inherent Hazard Class 8 as evident from Table 12. The ranges given above for factor F are chosen in terms of subjective engineering judgement.
The unacceptable cases referred to above may be dealt with in a number of ways. The values adopted for probabilities, P5, people not being aware of sinkholes, P6, people falling into sinkholes, P7, conveyance not offering any protection, and possibly P8, people fatally injured, may in the first instance be considered to be conservative, especially for sinkholes larger than 10 m in diameter. Since marginal changes in these values will resolve the observed unacceptable cases, it should be carefully considered whether such changes could be convincingly motivated.
It should in the second instance be observed that the unacceptable cases are a result of the level of risk, "As Low As Reasonably Practical", adopted, for which R = 0.07, and that the unacceptable cases would be resolved if a "Slight" level of risk for which R = 0.7 from Figure 13 is instead adopted. It may be that the general perception of the risk of fatal injury in the open spaces in Centurion City as a brownfields situation corresponds more accurately as fait accompli to "Slight" or even "Some" risk than "As Low As Reasonably Practical". The level of risk considered does not mean that fatal injuries will unavoidably occur in proportion thereto.
A third way of viewing the unacceptable cases is that they are by and large compatible with the land usage requirements for business districts as summarised in Table 2, in which precautionary measures corresponding to area designations D3 + FP1, D3 + DL1 and D4 are required for all except Inherent Hazard Class 1 in a business district. This requirement echoes the unacceptable risks of fatal injury in Inherent Hazard Classes 6, 7 and 8; may be somewhat conservative in respect of Inherent Hazard Classes 4 and 5; and is quite likely too conservative in respect of fatal injury in Inherent Hazard Classes 2 and 3 in the open spaces in a city centre environment.
A fourth way of dealing with the unacceptable cases in a greenfields situation is to implement engineering designs to pavement structures that would mitigate the hazard.
CONCLUSION
The objective of this paper is to present a methodology in terms of which the various factors that determine the risk of fatal injury in the open spaces in a city centre, due to a sinkhole, can be rigorously accounted for, based on probability theory and in terms of which it can in principle be shown how mathematical modelling can be applied to address some of the issues on personal safety that are involved. The values for the underlying parameters are estimates based on subjective engineering judgement and can be adjusted considerably. However, the overall result of the proposed methodology based on the parameter values considered is in principle compatible with long-standing observation by the authors.
ACKNOWLEDGEMENTS
The support of the Council for Geoscience to undertake the work described in this paper is gratefully acknowledged. The contribution that Dr Kleywegt made to the development of the geological time-based sinkhole return periods is in particular sincerely appreciated.
REFERENCES
Buttrick, D B, Van Schalkwyk, A, Kleywegt, R J & Watermeyer, R B 2001. Proposed method for dolomite land hazard and risk assessment in South Africa. Journal of the South African Institution of Civil Engineering, 43(2): 27-36. [ Links ]
Kirsten, H A D, Heath, G J, Venter, I S, Trollip, N Y G & Oosthuizen, A C 2009. The issue of personal safety on dolomite: A probability-based evaluation with respect to single-storey residential houses. Journal of the South African Institution of Civil Engineering, 51(2): 26-36. [ Links ]
Kirsten, H A D, Heath, G J, Venter, I S & Oosthuizen, A C 2014a. The issue of personal safety on dolomite: Update of probability-based evaluation with respect to single-storey residential houses. Journal of the South African Institution of Civil Engineering, 56(2): 78-87. [ Links ]
Kirsten, H A D, Heath, G J, Venter, I S & Oosthuizen, A C 2014b. The issue of personal safety on dolomite: A probability-based evaluation with respect to two-and three-storey residential houses. Journal of the South African Institution of Civil Engineering, 56(2): 54-64. [ Links ]
 Correspondence:
Correspondence:
H A D Kirsten
PO Box 17, Fontainebleau
Johannesburg, 2032
South Africa
T +27 11 782 5861, F: +27 11 782 0817
E: hadk@mweb.co.za
G J Heath
Private Bag X5
Westonaria, 1780
South Africa
T +27 83 579 3806
E: greg.heath@sibanyegold.co.za
I S Venter
PO Box 36114, Menlo Park
Pretoria, 0102
South Africa
T +2 7 82 5 70 1914, F: +27 1 2 460 0021
E: isak@thegeohub.co.za
A C Oosthuizen
Private Bag X112
Pretoria, 0001
South Africa
T +2 7 82 410 1148, F: +27 86 615 6682
E: toosthuizen@geoscience.org.za

DR HENDRIK KIRSTEN Pr Eng co-founded SRK Consulting in 1974. For 50 years he has specialised in complex practical geotechnical engineering problems, and has carried out 150 projects and published 90 papers. He is a member of CESA (Consulting Engineers South Africa) and a Fellow of SAICE, SAIMM and SANIRE (South African Institution of Civil Engineering, Southern African Institute of Mining and Metallurgy, and South African Institute of Rock Engineering respectively). His current projects include assuring statutory compliance of dolomite land use, geotechnical site safety licencing for nuclear power generation, design of sub-level open stope mine stability, and expert witnessing on construction and mining contracts. Dr Kirsten recently published guidelines on the implementation of quality and risk management in consulting engineering practice.

GREG HEATH completed his BSc Hons (Engineering Geology) at the University of Pretoria in 1990. He worked for the Council for Geoscience until 2012, where he undertook dam, dolomite and township investigations, as well as led research on dolomite. He completed his MSc Eng (Wits) in 2009 on the location and closure of unsafe, abandoned mine shafts. He currently leads the Ground Stability Unit at SibanyeGold.

ISAK VENTER is a generalist engineering geologist with 42 years' experience. He studied geology at the University of Pretoria, obtained an MSc (Engineering Geology) cum laude from the University of London and a DIC from Imperial College in 1976. He subsequently worked at the Geological Survey of South Africa, the University of Pretoria and at SRK. He joined Van Wyk and Louw (which later became Africon and now is Aurecon), where he was the Director for Geotechnics and the Environment from 1987 to 2004. He is now with the Geotechnical Hub.

THARINA OOSTHUIZEN PrSci Nat completed BSc (Hons) and MSc degrees in Engineering and Environmental Geology at the University of Pretoria in 2003 and 2013 respectively. She started her career in the mining environment where she was involved in high-wall stability monitoring and exploration until late 2005. When she joined the Council for Geoscience in 2005 she was initially involved with foundation investigations for dams. She currently works in the field of dolomite, where she conducts research and oversees the dolomite stability peer review reports. Tharina is a member of the South African Institute for Engineering and Environmental Geologists (SAIEG)














