Servicios Personalizados
Articulo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares en Google
Similares en Google
Compartir
Journal of the South African Institution of Civil Engineering
versión On-line ISSN 2309-8775
versión impresa ISSN 1021-2019
J. S. Afr. Inst. Civ. Eng. vol.56 no.2 Midrand ago. 2014
TECHNICAL PAPER
The issue of personal safety on dolomite: A probability-based evaluation with respect to two- and three-storey residential units
H A D Kirsten; G J Heath; I S Venter; A C Oosthuizen
Correspondence
ABSTRACT
While single-storey (single-house) residential developments were considered in a previous paper, two- and three-storey (multiple house) residential developments, which result in significantly higher densities of land occupation, are considered in this paper.
The overall probability of injury for the occupants of two- and three-storey dwelling units is defined as co-dependent probabilities of sinkhole occurrence, coincidence of the sinkhole with a dwelling unit, structural collapse of the dwelling unit, occupancy of the dwelling unit, occupants in residence when the sinkhole occurs and fatal injury as a result of the event.
The probability of sinkhole occurrence is determined by the associated infiltration regime for residential development, and the geological ground profile. The probability of coincidence between a sinkhole and a dwelling unit is treated in terms of overlapping geometric shapes. The probabilities for the remaining events are subjectively assigned by engineering judgement. The resulting overall probability of injury enables the number of dwelling units and the associated population densities for each of the Inherent Hazard Classes to be determined.
It is found that the allowable population densities for two- and three-storey residential units amount to 890, 425, 170, 125, 40, 0, 0 and 0 people per hectare respectively for the eight Inherent Hazard Classes of dolomite land. This corresponds in principle with the allowable population densities for single-storey dwelling houses of 800, 400, 150, 100, 30, 0, 0 and 0 people per hectare respectively for the eight Inherent Hazard Classes.
Keywords: dolomite, sinkhole, risk, hazard, coincidence, probability, multiple housing
INTRODUCTION
The purpose of the paper is to determine the permissible population densities for two- and three-storey dwelling units in townships on dolomite land based on a residential infiltration regime as defined by Kirsten et al (2014).
The infiltration regime is a fundamental determinant in the evaluation of sinkhole occurrence. Kirsten et al (2014) distinguished between natural, residential and city centre infiltration regimes, as these are determined by the water-bearing services, measures to control stormwater, landscaping and irrigation provisions, occurrence of impermeable pavements and dewatering protocols characteristic to each regime.
The infiltration regimes are expressed in terms of potential sinkhole return periods for the eight Inherent Hazard Classes defined by Buttrick et al (2001) and the six sinkhole sizes as shown in Table 1. The two largest sinkhole sizes were added to the four sizes originally presented by Buttrick et al to extend their range. The research developments that preceded the definition of the return periods in Table 1 are presented by Kirsten et al (2009 and 2014).
Sinkhole occurrence is treated in the paper as a chance phenomenon, the qualifications for which are dealt with by Kirsten et al (2014). It mainly needs to be observed that, as a result thereof that sinkholes are caused by water-bearing services that tend to leak at isolated locations, only one sinkhole occurs at any point in time in a neighbourhood, and that, as a result of how the causes and the sinkhole itself are repaired, only that one sinkhole occurs at that location over a substantial period of time.
CURRENT APPROACH TO DOLOMITE RISK EVALUATION IN TWO- AND THREE-STOREY RESIDENTIAL DEVELOPMENTS
Two- and three-storey developments are market driven options in which much higher densities of land occupation can be achieved than in conventional single-house type developments. Various layout options, footprint sizes and multi-storey options can be considered to achieve higher population densities. Representative two- and three-storey residential developments are shown in Figure 1.

Despite the fact that multi-house two-and three-storey developments may be more competent structurally and may have more robust wet services, a rigorous way of accounting for these advantages is not yet available. SANS 1936:2012 defines population density limits for the eight Inherent Hazard Classes in terms of land usage design specifications. However, it is not indicated how these limits that are higher than those for single-storey houses may be definitively determined in terms of the underlying parameters. The methodology developed by Kirsten et al (2014) for the determination of population density for single-storey residential houses was adapted to determine the permissible population densities for two-and three-storey dwelling units, accounting for the particular structural competence of such buildings and the associated robustness and more optimal use of wet services as presented in this paper.
LAYOUT OF LOW-RISE RESIDENTIAL ACCOMMODATION CONSIDERED
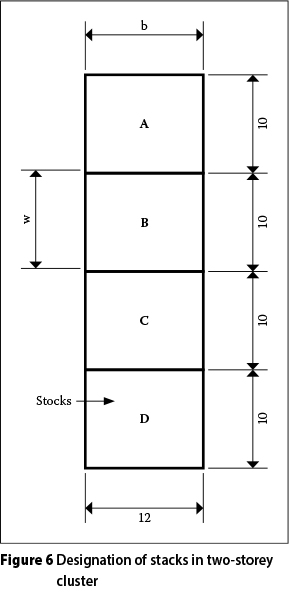
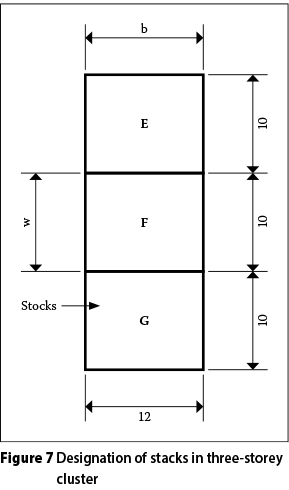
A dwelling unit denotes the living accommodation for a group of five people. A cluster denotes a single two- or three-storey building containing three or four dwelling units per floor. Dwelling units overlying one another on different floors are referred to as a stack of units. The low-rise multiple-house residential township considered in the paper is assumed to consist of one or more two-and three-storey clusters as shown in Figures 2 to 5 for various stages of development respectively.
PROBABILITY OF INJURY
Let the following symbols denote:
Ps Probability of sinkhole occurrence
Pc Probability of sinkhole coinciding with two- or three-storey stack
Pf Probability of two- or three-storey stack collapsing when affected by a sinkhole
Pr Probability of occupants in residence when affected by a sinkhole
Ph Probability of stack occupied when affected by a sinkhole
Pd Probability or relative number of fatal injuries of occupants of stack when affected by a sinkhole to provide for the case in which not all the occupants are fatally injured
The overall probability of injury, PO, is then given by the following products of the above dependent component probabilities:

PROBABILITY OF OCCURRENCE
An event of recurrence interval T years, i.e. a T-year event, is an event of such magnitude that the average time between events of larger magnitude is T years. This length of time is also referred to as the return period. The events considered in the paper refer to sinkholes in intervals of increasing diameter. Reference to a T-year event is therefore with regard to the occurrence of a size of sinkhole in a particular interval.
Let D denote the lifetime of a residential development. The probability that a T-year event will be exceeded at least once in the lifetime of the development is given by the expression in Equation 2. It is not necessary to consider the occurrence of more than one sinkhole in a neighbourhood because of the way in which sinkholes occur and are repaired, as had been explained in the Introduction. A lifetime is defined as 70 years.

The sinkhole return period per 100 hectares is shown in Table 1 for three comparative regimes of infiltration, namely natural, residential and city centre, as presented by Kirsten et al (2014). The infiltration regime for a residential development represents the conditions around two- and three-storey dwelling units. The corresponding return periods per hectare, T2, given in Table 2, were obtained by substituting the return periods T1 from Table 1 in the expression T2=N/[(1/100)N/T1] =100T1.
PROBABILITY OF COINCIDENCE
Let A, B, C and D denote the various stacks of units in a two-storey cluster, and E, F and G those in a three-storey cluster, as shown respectively in Figures 6 and 7. A sinkhole coincides with any stack of two-or three-storey units in a cluster if it lies within the hatched zones in Figures 8 and 9, representing the respective situations for the sinkhole less than and larger than the width of the unit w, as shown in Figures 6 and 7. Observe, as already defined above, that units that overlie one another on different floors are referred to as a stack of units. The probability of coincidence Pc is accordingly given by the larger value of the following two expressions:

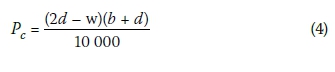
where d denotes the sinkhole diameter and b the width of the cluster, as shown in Figures 8 and 9. The resultant probabilities of coincidence for the range of sinkhole sizes considered are shown in Table 3 for b = 12 m and w = 10 m.

PROBABILITY OF BUILDING COLLAPSE
A two-storey residential building is structurally damaged by a 15 m sinkhole, as shown for example in Figure 10. Consider the potential collapse of two- and three-storey stacks of dwelling units as follows.
Two-storey dwelling unit - Figure 6
Consider the designation of stacks of units for a two-storey cluster as defined in Figure 6 and let,
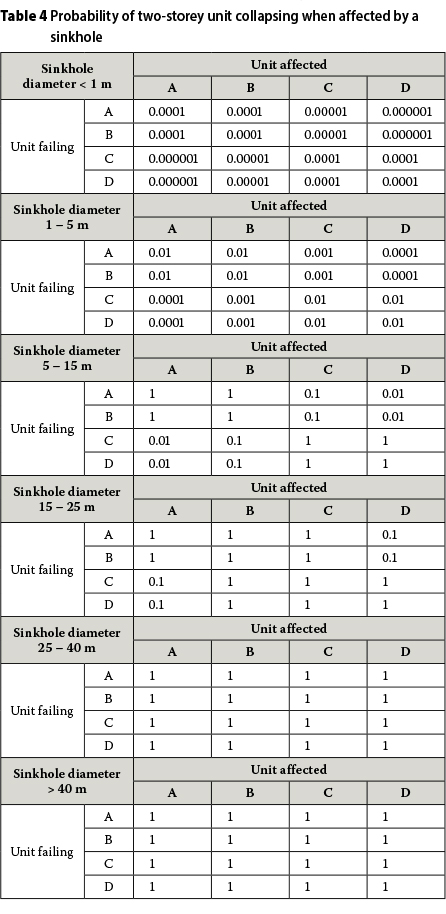
■ PfAA, PfAB, PfAC and PfAD denote the probabilities of two-storey stack A collapsing when stacks A, B, C and D are respectively affected by a sinkhole;
■ PfBA, PfBB, PfBC and PfBD denote the probabilities of two-storey stack B collapsing when stacks A, B, C and D are respectively affected by a sinkhole;
■ PfCA, PfCB, PfCC and PfCD denote the probabilities of two-storey stack C collapsing when stacks A, B, C and D are respectively affected by a sinkhole; and
■ PfDA, PfDB, PfDC and PfDD denote the probabilities of two-storey stack D collapsing when stacks A, B, C and D are respectively affected by a sinkhole.
Note that:
PfAA= PfDD, PfAB = PfDC, PfAC = PfDB,
PfAD = PfDA, PfBA = PfCD, PfBB = PfCC, PfBC = PfCB and PfBD = PfCA.
Values for these probabilities of two-storey dwelling stack, sinkhole-induced collapse may be assigned by subjective engineering judgement as given in Table 4.
Three-storey dwelling unit - Figure 7
Consider the designation of stacks of units for a three-storey cluster as defined in Figure 7 and let,
■ PfEE, PfEF and PfEG denote the probabilities of three-storey stack E collapsing when stacks E, F and G are respectively affected by a sinkhole;
■ PfFE, PfFF and PfFG denote the probabilities of three-storey stack F collapsing when stacks E, F and G are respectively affected by a sinkhole; and
■ PfGE, PfGF and PfGG denote the probabilities of three-storey stack G collapsing when stacks E, F and G are respectively affected by a sinkhole.
Note that:
PfEE = PfFF, PfEF = PfGF, PfEG = PfGE and PfFE = PfFG.
Values for these probabilities of three-storey dwelling stack, sinkhole-induced collapse may be assigned by subjective engineering judgement as given in Table 5.
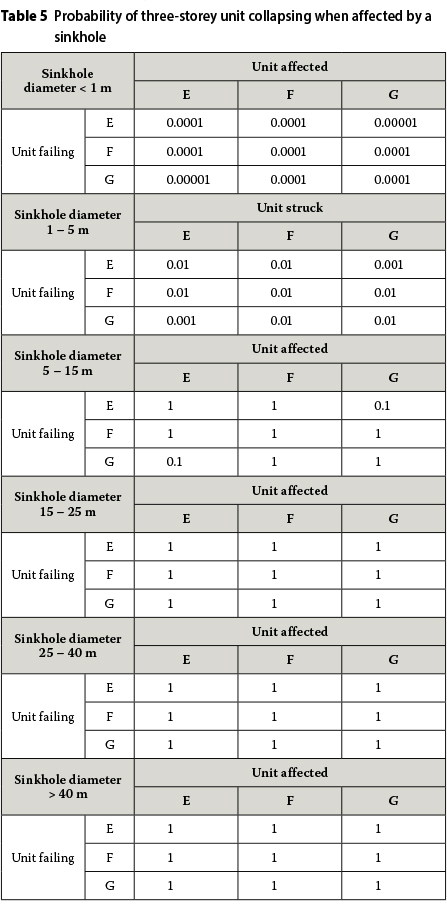
PROBABILITIES OF OCCUPANTS AT HOME AND UNITS OCCUPIED
The probabilities of the occupants being at home and the dwelling stacks being occupied when affected by a sinkhole are assumed to be 0.5 and 1.0 respectively in all instances.
PROBABILITY OF FATAL INJURY
Let Pd2 denote the probability of fatal injury of the occupants when any of the stacks in a two-storey cluster are affected by a sinkhole. Likewise, let Pd3 denote the probability of fatal injury of the occupants when any of the stacks in a three-storey cluster are affected by a sinkhole.
Values for these probabilities of fatal injury in sinkhole-induced collapse of two- and three-storey dwelling stacks may be assigned by subjective engineering judgement for various sizes of sinkhole as given in Table 6.
POPULATION DENSITY
Let j denote the average number of people per dwelling unit and N2 and N3 the potential numbers of fatal injuries in two- and three-storey stacks of units respectively. In this instance j = 5. By definition then:

The number of people accommodated per hectare, h, may be expressed in terms of the average number of people per unit, j, and the respective numbers of two- and three-storey clusters per hectare, m and n, by:

THRESHOLD LEVELS FOR FATAL INJURY
Lifetime probability is defined as the probable unit number of times that a detrimental event could occur during the life of the person affected. A natural lifetime is on average 70 years. Parameter D in Expression [1] is therefore taken as 70.
Threshold levels for fatal injury may be presented after Whitman (1984), as shown in Figure 11, in terms of lifetime probability Pt and potential number of fatal injuries N in the units in two- or three-storey stacks. The ordinate axis may alternatively represent the relative lapse of time in anecdotal terms as shown. The relationship between lifetime probability of injury Pt and the potential number of fatal injuries per stack of units N for any particular risk level R is given in principle by Expression 8.

For a fully developed mixture of two- and three-storey clusters as shown in Figure 5, the weighted average potential number of fatalities per stack may be determined from Expression [8] by substituting N2 and N3 from Expressions [5] and [6], and observing that there are 4m stacks in total in the two-storey clusters and 3n stacks in total in the three-storey clusters:
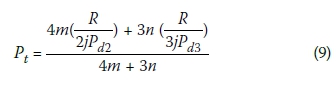
Thus, on simplifications
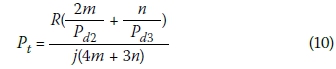
COLLECTIVE PROBABILITY OF INJURY
Consider two- and three-storey dwelling units separately as follows for determining the collective probability of injury.
Two-storey dwelling unit - Figure 6
Let PAA, PAB, Pac and Pad denote the overall probabilities of injury in two-storey stack A when stacks A, B, C and D are respectively affected by a sinkhole. A number of events need to happen simultaneously for people in stack A to be fatally injured, namely, the sinkhole has to occur, the sinkhole has to coincide with the stack, the stack has to collapse catastrophically, the stack has to be occupied by people, the people have to be at home at the time, and people in the stack need to be fatally injured. The overall probabilities Paa, Pab, Pac and Pad can therefore be obtained as given in Expression [1] by multiplying the probabilities for the six underlying events as follows in terms of the parameters defined above:
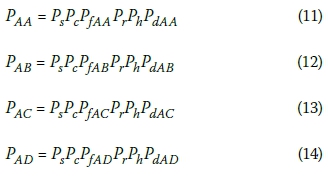
The collective overall probability that people are injured in stack A is therefore given by:
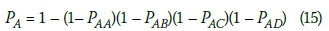
The collective overall probabilities of injury in stacks B, C and D are given as follows by cyclic rotation of subscripts:
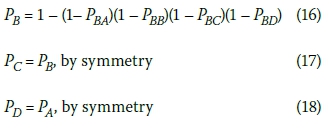
The collective overall probability of injury in a two-storey cluster is given by Expression 19:
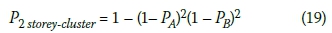
Three-storey dwelling unit - Figure 7
Let Pee, Pef and Peg denote the overall probabilities of injury in three-storey stack E when stacks E, F and G are respectively affected by a sinkhole. A number of events need to happen simultaneously for people in stack E to be fatally injured, namely, the sinkhole has to occur, the sinkhole has to coincide with the stack, the stack has to collapse catastrophically, the stack has to be occupied by people, the people have to be at home at the time, and people in the stack need to be fatally injured. The overall probabilities PEE, PEF and Peg can therefore be obtained as given in Expression [1] by multiplying the probabilities for the six underlying events as follows in terms of the parameters defined above:
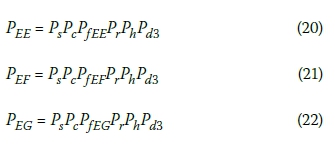
The collective overall probability that people are injured in stack E is therefore given by:
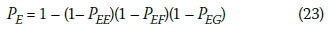
The overall probabilities of injury in three-storey stacks F and G are given as follows by cyclic rotation of subscripts:
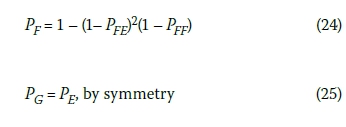
The collective overall probability of injury in a three-storey cluster is given by Expression 26:
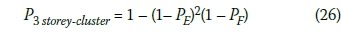
OVERALL PROBABILITY OF INJURY
The overall probability of injury per hectare Po is given by Expression 27:

The powers m and n in Expression [27] respectively represent the numbers of two-and three-storey clusters per hectare. For example, m = n = 1, 2, 3 and 4 respectively in Figures 2, 3, 4 and 5. Observe that m and n need not have the same value.
The overall probability of injury Po should be < Pt for the particular risk level considered. The number of people per hectare for which this condition is satisfied may be determined from Expression [28] by substituting Pt and Po from Expressions [10] and [27] respectively:

EVALUATION OF PERMISSIBLE POPULATION DENSITIES
Based on the input parameter values presented in the preceding sections, values for ratio F are shown for ranges of population density and sinkhole size in Tables 7 to 14 for Inherent Hazard Classes 1 through 8 respectively. The values for F correspond to a "negligible risk level" as defined in Figure 11, i.e. to R = 0.007. The values for F in these tables have a minimum turning point character for particular population densities. The maximum population density for any Inherent Hazard Class corresponds to that value for which F > 1.0 for all sinkhole sizes.
The maximum permissible population densities determined, as described above for two- and three-storey residential buildings, are summarised in Table 15 in terms of the sinkhole size for which factor F is approximately equal to unity. Owing to the minimum turning point character of factor F, the maximum population densities in Table 15 apply to all sinkhole sizes.
The maximum permissible population densities for two- and three-storey developments correspond to 890, 425, 170, 125, 40, 0, 0 and 0 people/ha respectively for the eight Inherent Hazard Classes compared to 800, 400, 150, 100, 30, 0, 0 and 0 people/ha for single-storey dwelling house developments.
A fully developed township consisting of two- and three-storey clusters as shown in Figure 5 can at most accommodate 340 people per ha, which approaches the permissible number of 425 people per ha in Inherent Hazard Class 2, but which is still far below that permissible in Class 1 of 890 people per ha. A population density of 340 people per ha is as expected almost three times as much as the maximum number of 160 people per ha that can be accommodated in single-storey houses.
The most probable number of fatal injuries will be determined by the number of stacks affected by a 20 m sinkhole, since this size of sinkhole corresponds to the minimum turning point with regard to population density as shown in Table 15. A 20 m sinkhole can only affect two stacks in either a two- or a three-storey cluster. As a result the most probable number of fatalities will in principle be 0.5 x 20 = 10 for a two-storey cluster and 0.75 x 30 = 22.5 for a three-storey cluster.
It should be emphasised that the parameter values adopted are not definitive for all two- and three-storey residential developments, and were only considered to illustrate the principles presented in the paper. The parameter values should be verified for every specific application. The probability of structural failure should in particular be rigorously assessed.
EVALUATION OF SANS 1936:2012 LAND USAGE REQUIREMENTS
The permissible land usage requirements in terms of SANS 1936 - 1:2012 are compared with the population densities determined in this paper in Table 16, which is an extract of the land usage requirements in the standard on two- and three-storey residences. The land usage requirements in SANS 1936 -1:2012 are expressed in terms of maximum permissible population densities for four levels of precautionary measures represented by area designations D1, D2, D3 and D4 respectively, and are briefly defined as follows:
D1 No precautionary measures considered
D2 Precautionary measures prevent concentrated ingress of water into the ground
D3 Additional precautionary measures to D2 requirements as provided for in the standard
D4 Precautionary measures determined rationally and specifically for the particular site
It follows by inference that the maximum permissible population densities for land usage requirements D1, D2 and D3 by definition correspond to minimum population densities for land usage requirements D2, D3 and D4 respectively, i.e. for an area designation one level higher in each instance, hence the minimum inferred population densities denoted by superscript "1" in Table 16.
The permissible population densities determined in the paper are not subject to the implementation of any specified precautionary measures. SANS 1936:2012 does not allow any people to be accommodated on dolomite land unless precautionary measures as specified in Table 16 are provided. The population densities corresponding to area designation D1 in the table are accordingly zero.
SANS 1936:2012 land usage requirement D2 for Inherent Hazard Class 1 is more onerous with regard to population density than determined in the paper, but is sensible, because it is always good practice to prevent the concentrated ingress of water into dolomite ground.
SANS 1936:2012 land usage requirement D2 for Inherent Hazard Class 2 is less onerous with regard to population density than determined in the paper and is sensible, because it is always good practice to prevent concentrated ingress of water. Inferred land usage requirement D3 or D4 for Inherent Hazard Class 2, if appropriate, is sensible.
SANS 1936:2012 land usage requirement D3 + FP1 for Inherent Hazard Class 3 is less onerous than determined in the paper, except perhaps for the limitation on sinkhole size. Inferred land usage requirement D4 for Inherent Hazard Class 3 is sensible.
SANS 1936:2012 land usage requirement D3 + FP1 for Inherent Hazard Class 4 is sensible compared to that determined in the paper, except perhaps for the limitation on sinkhole size. Inferred land usage requirement D4 for Inherent Hazard Class 4 is sensible.
SANS 1936:2012 land usage requirement D3 + FP1 for Inherent Hazard Class 5 is sensible compared to that determined in the paper, except perhaps for the limitation on sinkhole size. Inferred land usage requirement D4 for Inherent Hazard Class 5 is sensible.
SANS 1936:2012 land usage requirements D1, D2 and D3 for Inherent Hazard Classes 6, 7 and 8 are sensible compared to that determined in the paper. Inferred land usage requirement D4 for Inherent Hazard Classes 6, 7 and 8 is sensible.
CONCLUSION
The objective of the paper is to present a methodology in terms of which the various factors that determine the risk of fatal injury when a sinkhole gives rise to the collapse of a two- or three-storey residence, can be rigorously accounted for on the basis of probability theory and in terms of which it can in principle be shown how mathematical modelling can be applied to address some of the issues on personal safety that are involved. The values for the underlying parameters are estimates based on subjective engineering judgement and can be adjusted considerably. However, the overall result of the proposed methodology, based on the parameter values considered, is in principle compatible with long-standing observation by the authors.
ACKNOWLEDGEMENT
The support of the Council for Geoscience to undertake the work described in this report is gratefully acknowledged.
REFERENCES
Buttrick, D B, Van Schalkwyk, A, Kleywegt, R J & Watermeyer, R B 2001. Proposed method for dolomite land hazard and risk assessment in South Africa. Journal of the South African Institution of Civil Engineering, 43(2): 27-36. [ Links ]
Kirsten, H A D, Heath, G J, Venter, I S, Trollip, N Y G & Oosthuizen, A C 2009. The issue of personal safety on dolomite: A probability-based evaluation with respect to single-storey residential houses. Journal of the South African Institution of Civil Engineering, 51(2): 26-36. [ Links ]
Kirsten, H A D, Heath, G J, Venter, I S & Oosthuizen, A C 2014. The issue of personal safety on dolomite: Update of a probability-based evaluation with respect to single-storey residential houses. Journal of the South African Institution of Civil Engineering, 56(2): 78-87. [ Links ]
Whitman, R V 1984. Evaluating calculated risk in geotechnical engineering. Journal of Geotechnical Engineering, 110(2): 145-188 (paper no 18569). [ Links ]
 Correspondence:
Correspondence:
PO Box 17, Fontainebleau
Johannesburg, 2032
South Africa
T +27 11 782 5861, F: +27 11 782 0817
E: hadk@mweb.co.za
 Correspondence:
Correspondence:
Private Bag X5
Westonaria, 1780
South Africa
T +27 83 579 3806
E: greg.heath@sibanyegold.co.za
 Correspondence:
Correspondence:
PO Box 36114, Menlo Park
Pretoria, 0102
South Africa
T +2 7 82 5 70 1914, F: +27 1 2 460 0021
E: isak@thegeohub.co.za
 Correspondence:
Correspondence:
Private Bag X112
Pretoria, 0001
South Africa
T +2 7 82 410 1148, F: +27 86 615 6682
E: toosthuizen@geoscience.org.za

DR HENDRIK KIRSTEN Pr Eng co-founded SRK Consulting in 1974. For 50 years he has specialised in complex practical geotechnical engineering problems, and has carried out 150 projects and published 90 papers. He is a member of CESA (Consulting Engineers South Africa) and a Fellow of SAICE, SAIMM and SANIRE (South African Institution of Civil Engineering, Southern African Institute of Mining and Metallurgy, and South African Institute of Rock Engineering respectively). His current projects include assuring statutory compliance of dolomite land use, geotechnical site safety licencing for nuclear power generation, design of sub-level open stope mine stability, and expert witnessing on construction and mining contracts. Dr Kirsten recently published guidelines on the implementation of quality and risk management in consulting engineering practice.

GREG HEATH completed his BSc Hons (Engineering Geology) at the University of Pretoria in 1990. He worked for the Council for Geoscience until 2012, where he undertook dam, dolomite and township investigations, as well as led research on dolomite. He completed his MSc Eng (Wits) in 2009 on the location and closure of unsafe, abandoned mine shafts. He currently leads the Ground Stability Unit at SibanyeGold.

ISAK VENTER is a generalist engineering geologist with 42 years' experience. He studied geology at the University of Pretoria, obtained an MSc (Engineering Geology) cum hide from the University of London and a DIC from Imperial College in 1976. He subsequently worked at the Geological Survey of South Africa, the University of Pretoria and at SRK. He joined Van Wyk and Louw (which later became Africon and now is Aurecon), where he was the Director for Geotechnics and the Environment from 1987 to 2004. He is now with the Geotechnical Hub.

THARINA OOSTHUIZEN PrSci Nat completed BSc (Hons) and MSc degrees in Engineering and Environmental Geology at the University of Pretoria in 2003 and 2013 respectively. She started her career in the mining environment where she was involved in high-wall stability monitoring and exploration until late 2005. When she joined the Council for Geoscience in 2005 she was initially involved with foundation investigations for dams. She currently works in the field of dolomite, where she conducts research and oversees the dolomite stability peer review reports. Tharina is a member of the South African Institute for Engineering and Environmental Geologists (SAIEG)














