Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
Journal of the South African Institution of Civil Engineering
On-line version ISSN 2309-8775
Print version ISSN 1021-2019
J. S. Afr. Inst. Civ. Eng. vol.56 n.2 Midrand Aug. 2014
TECHNICAL PAPER
Resistance model uncertainty factors for ultimate limit state design of pile foundations
M Dithinde; J V Retief
Correspondence
ABSTRACT
The current limit state design procedure for pile foundations presented in geotechnical codes (e.g. SANS 10160-5, EN 1997-1) stipulates that, when the pile capacity is determined using an analytical approach, such as the static analysis using engineering properties of the soil as determined from laboratory or in-situ field testing, the prescribed partial resistance factors (γr) need to be corrected by a partial factor for the uncertainty in the resistance model (γR, d) or the resistance model uncertainty factor. The international position is to derive model uncertainty factors for both actions and resistances from available experimental data. Accordingly this paper makes use of a local pile load test database to derive the appropriate γR, d values for ultimate limit state design of pile foundations. The analysis indicates that γR, d values of 1.3 and 1.5 for piles in cohesive and non-cohesive materials respectively are appropriate. Alternatively, a single value of γR, d = 1.4 for all piles in all soils can be adopted with different γr values for the two distinctive pile classes of piles in cohesive and non-cohesive soils.
Keywords: ultimate limit state, pile foundation design, pile load tests, model factor, static formula
INTRODUCTION
Limit state design has been internationally accepted as the standard basis on which the new generation of geotechnical design codes are being developed today. The move is motivated by the need to provide a rational and consistent framework for managing design uncertainties. For most geotechnical designs, two predominant sources of uncertainty can be distinguished: (i) uncertainties associated with the evaluation of design soil properties, and (ii) calculation model uncertainties. With the current format of limit state design of pile foundations, partial resistance factors (γR) and partial factors for uncertainty in the resistance model (γR,d) are applied to account for soil properties and calculation model uncertainty respectively. For brevity γr, d will be referred to as the resistance model uncertainty factor.
This paper will be primarily concerned with the determination of appropriate values for γR,d to be used in South African pile design practice, as based on the Standard SANS 10160-5:2011, Basis of geotechnical design and actions. For this purpose a published dataset of model factor statistics will be employed to represent the uncertainty of pile resistance models. The probability treatment of model factor statistics serving as basis for deriving γr, d values is subsequently presented and implemented. Various classifications of pile conditions are investigated in order to evaluate differences of γr, d values for respective pile classes. A sensitivity analysis is performed by treating model factor statistics at higher confidence levels, rather than in terms of expected values. The basis for deriving γr, d values under local conditions is set in perspective by comparison to an elaborate dataset representing a wide range of pile conditions and design methods, for which γr, d values are also calculated to indicate comparative values and trends.
The results are assessed in terms of achieving sufficient and consistent reliability without undue complications for standardised design. The results obtained also serve as useful guidance beyond the strict scope of application represented by this analysis, to be applied to situations where safety measures in terms of safety factors are predominantly, if not solely, selected on experienced-based judgement.
A brief review of standardised geotechnical limit state design is first presented by way of an introduction to the general design approach taken. The special design verification format for piles provides the background for the investigation on appropriate values for partial factor for uncertainty in pile resistance models γr, d.
STANDARDISED GEOTECHNICAL LIMIT STATE DESIGN
To keep pace with international trends, South Africa has now converted to the limit state design through the publication of SANS 10160-1:2011, Basis of structural design and actions on buildings and industrial structures. Within this suite of standards, Part 5 (SANS 10160-5:2011) is devoted to Basis for geotechnical design and actions. SANS 10160:2011 is essentially a loading code and presents the general principles, and requirements for design of buildings and industrial structures, in accordance with the limit state design approach in South Africa. However, due to the absence of a geotechnical limit state code in the country, SANS 10160-5 also provides guidance on geotechnical design aspects of structures within the scope of SANS 10160, including pile foundations.
With limit state design, partial factors are applied to various elements of the design according to the reliability with which the parameters are known or can be calculated. In this regard EN 1997-1 provides for three design approaches which give alternative ways of applying partial factors to pile design variables. The selection of a particular design approach is a matter for national determination. Accordingly SANS 10160-5 has opted to follow Design Approach 1 for two main reasons (Day and Retief 2009): (i) partial factors are applied directly to the source of uncertainty (i.e. actions, calculation models and material properties), and (ii) the results obtained using this approach agree reasonably with the current South African practice based on the overall factor of safety approach. Furthermore, Design Approach 1 accounts for uncertainties in a more rational way, as partial factors are applied to basic variables (material properties and actions), or to quantities derived later in the calculation (resistances and action effects) according to where their effect will be most severe. Where the greatest uncertainties are with the geotechnical parameters (e.g. slope stability problems, spread foundations, earth retaining structures), partial factors are applied to the geotechnical properties. When the predominant uncertainty is associated with the calculation model (e.g. pile foundations and anchors), partial factors are applied to the calculated resistance. In terms of safety and economy, model solutions for Eurocode 7 workshop examples (Orr 2005) revealed that Design Approach 3 produces the most conservative designs, Design Approach 2 the least conservative designs, while Design Approach 1 generally yields designs between the other two approaches. The foregoing discussions reiterate that Design Approach 1 seems to be the best alternative for southern Africa.
The partial factors prescribed in SANS 10160-5 for use in conjunction with Design Approach 1 are presented in Table 1.
It is apparent from Table 1 that three ultimate limit states need to be considered. These are (a) GEO: for failure or excessive deformation of the ground, in which the strength of the soil or rock is significant in providing resistance; (b) STR: for internal failure or excessive deformation of the structure or structural elements (e.g. footings, piles, pile caps, basement walls), in which the strength of the structural materials is significant in providing resistance; and (c) STR-P: for dominant permanent action. Based on these limit states, in general two calculation combinations are required, as follows:
Combination 1
A1.1 "+" M1 "+" R1 (STR)
A1.2 "+" M1 "+" R1 (STR-P)
Combination 2 (GEO)
A2 "+" (M1 or M2) "+" R4
As already mentioned, set M2 is applied to unfavourable actions emanating from negative skin friction or lateral loading. The notion of a partial factor for uncertainty in the resistance model γr, d is also stipulated, as discussed below.
ULTIMATE LIMIT STATE DESIGN OF PILE FOUNDATIONS
SANS 10160-5 provides for four pile design methods as follows: (i) full-scale pile load tests, (ii) empirical analysis by directly using standard field test results (e.g. SPT and CPT), (iii) static analysis using engineering properties of the soil as determined from laboratoryor in-situ field testing, and (iv) dynamic driving resistance (pile driving formulae and wave equation).
Of the four pile design methods, static analysis using engineering properties of the soil as determined from laboratory or in-situ field testing constitutes the main pile design method in South Africa. When this analytical method is used, SANS 10160-5 stipulates that the prescribed partial resistance factor γR needs to be corrected by a partial factor for uncertainty in the resistance model γR, d (or resistance l model uncertainty factor) to explicitly account for pile resistance calculation model uncertainty. Clauses B.3.3, C.3.2.4.1 and C.3.2.4.2 of SANS 10160-5 provide guidance on the issue of the resistance model uncertainty factor for pile foundations. A resistance model uncertainty factor of γr, d = 1.5 has been prescribed. This value is reported by Day and Retief (2009) to be based on a preliminary analysis of data compiled by Dithinde (2007).
Further guidance clauses (C.3.2.4.1 and C.3.4.2) point out that ideally such a factor should be determined by comparing calculated pile resistance with the resistance determined from load tests. Furthermore, Holický (2009) reiterates that numerical values of action and resistance model uncertainty factors should be derived from previous experience and available experimental data. Accordingly, this paper derives γr, d values from test data comprising measured and predicted pile resistances within a probabilistic framework.
CONCEPT OF MODEL FACTOR AS APPLIED TO PILE FOUNDATIONS
The analysis is based on an extensive southern African database of pile load tests and comparative calculated resistances that were previously published. The database is extensively described by Dithinde et al (2011) by providing the interpreted test results, the way in which the corresponding resistances were calculated from recorded soil parameters and the statistical treatment of the comparisons for the main pile classes. Extended analyses and statistical assessment were reported by Dithinde and Retief (2013a). An assessment of reliability levels of present practice, as based on the database, is reported by Retief and Dithinde (2013).
The technical basis for the database of pile tests and the comparison to resistance prediction are provided by Dithinde et al (2011), with additional information and background presented by Dithinde (2007). The cases selected for the database are deemed to be representative of pile construction and soil conditions for southern Africa. Similarly the pile test, interpretation and calculation of pile resistance were deemed to be representative of local practice. Only a brief outline of the database is presented here, as summarised from the cited references.
Pile load tests were used to determine the measured pile resistance, while the geotechnical data was used to compute the predicted resistance. For trial piles, the measured resistances from the respective load-settlement curves were interpreted on the basis of Davison's offset criterion (Davison 1972), while for working piles, Chin's extrapolation (Chin 1970) was carried out prior to the application of Davison's offset criterion. The predicted resistance was based on the classic static formula, which is essentially the generic theoretical pile design model based on the principles of soil mechanics. The soil data that was obtained from the survey, and used for the predicted resistance, was mainly in the form of borehole log descriptions and standard penetration (SPT) results. Soil design parameters were selected on the basis of common southern African practice. To capture the distinct soil types for the geologic region of southern Africa, as well as the local pile design and construction experience base, pile load tests and associated geotechnical data from the southern African geologic environment are used. The cited references present detailed information on pile construction, testing procedures and the interpretation of the results; and classification of soil types, determination of soil parameters and resistance calculation for the respective soil types.
The systematic comparison of calculated and measured pile resistance provides a rational basis for the derivation of γr, d. In reliability terms the value of γr, d can be determined consistently with the target level of reliability set for pile design. The derivation of resistance model uncertainty factors in a probabilistic framework explicitly accounts for uncertainties, and thereby contributes to international initiatives towards more rational, transparent and improved design procedures.
In EN 1997-1, and by extension SANS 10160-5, provision is made for the inaccuracy of the pile capacity calculation model by the introduction of the concept of the model factor (M), defined as the ratio of the measured over predicted capacity and mathematically expressed as:

(1) where
Qm = measured pile capacity, and
Qp = predicted pile capacity.
The model factor M calculated as per Equation (1) is a random variable, and in principle captures all the sources of uncertainties (i.e. model uncertainty, systematic error, inherent spatial variability, statistical error and errors related to load tests). However, previous studies (e.g. Ronold & Bjerager 1992; Phoon & Kulhawy 2005; Teixeira et al 2011) demonstrate that, for pile foundations, calculation model uncertainty is the predominant source of uncertainty reflected by M. Furthermore, the predominance of model uncertainty in pile design has led to the exception in Design Approach 1 that, for piles, partial factors be applied to the resistance rather than on the materials, as is the case for other geotechnical structures.
Model factor statistics from the southern African database
Mathematical modelling of any physical process generally requires simplifications to create a useable model. Inevitably, the resulting engineering mechanics models are simplifications of complex real-world phenomena leading to uncertainty in the model prediction. Similarly, models used to calculate pile capacity never yield precise predictions of the actual capacity as measured from load tests.
The statistical characteristics of the uncertainty of a given calculation model can be obtained from the comparison of the results of load tests, and the resistance calculated from geotechnical parameters at locations of the test piles. Systematic differences can be obtained from the mean of the model factor given by Equation (1), or the bias, with variability based on higher order statistics of such observations. Therefore the characterisation of the model factor for a given calculation model requires a database of pile load tests and associated geotechnical data. In this regard, the database compiled by Dithinde (2007), and also reported in Dithinde et al (2011), and Dithinde and Retief (2013a), have been adopted for the analysis. The ensuing model factor statistics, as reported in Dithinde and Retief (2013a), are shown in Table 2.
The complete set of 170 cases was further classified in terms of four theoretical principal pile design classes based on both soil type and installation method. These fundamental sets of classes include: (i) driven piles in non-cohesive soil (D-NC), (ii) bored pile in non-cohesive soil (B-NC), (iii) driven piles in cohesive soils (D-C), and (iv) bored pile in cohesive soils (B-C). These principal four data sets were further combined into various practical pile design classes considered in design codes such as SANS 10169-5:2011 and EN 1997-1:2004 as follows: (a) classification based on pile installation method irrespective of soil type, which leads to two classes of driven (D) and bored (B) piles as per EN 1997-1:2004; (b) classification based on soil type comprising piles in non-cohesive (NC) and cohesive (C) soils in accordance with the general practice where a higher factor of safety is applied to pile capacity in clay as compared to sand; and (c) all pile cases as a single data set irrespective of pile installation method and soil type (ALL), in line with the practical consideration presented in SANS 10160-5:2011 where a single partial factor is given for all compressive piles.
DERIVATION OF γR,d VALUES FROM M STATISTICS
In accordance with EN 1990 Annex D, the realisations of the model factor M represented by Equation (1) constitute test results with distinct statistical characteristics. The resistance model uncertainty factor γR,d constitutes the design value of the available test results, which in this paper denotes the design value of M. The derivation of a design value of a given variable (material property, model parameter or resistance) from test results is carried out either by: (i) assessing a characteristic value, which is then divided by a partial factor and possibly multiplied if necessary by an explicit conversion factor; or (ii) direct determination of the design value, implicitly or explicitly accounting for the conversion of results and the total reliability required. In the case of the model factor, assessment via the characteristic value is rather complicated, as both the conversion factor (to be assessed on the basis of type of tests and type of material) and the partial factor (selected according to the field of application of the test results or should be taken from the appropriate Eurocode) are not known. Accordingly, in this paper the direct assessment approach was employed to derive the design value of the model factor M on the basis of the statistics presented in Table 2.
Direct assessment of γR,d values
With the direct assessment method, the design value (xd) of a given variable (X) is selected such that the probability of having a more unfavourable value is given by Equation (2) (EN 1990):
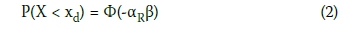
where β is the target reliability index, αr is a FORM sensitivity factor taken as 0.8 for resistance model variables, and Φ is the cumulative distribution function of the standardised Normal distribution.
In EN 1990, the design value of M, is generally incorporated into the design expressions through the resistance model uncertainty factor γR,d applied as follows:
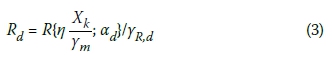
where Ed is the design resistance, Xk is the characteristic values of the variable, η is a convention factor appropriate to the material property, γm is the material property factor, ad is the design geometric parameter, and γR,d is the design value of the partial factor uncertainty in the resistance model which is also referred to here as the resistance model uncertainty factor.
When applied to design of pile foundations in accordance with SANS 10160-5, Equation (3) reduces to:

where Rk denotes the characteristic resistance as determined from an analytical model and γr is the partial resistance factor to account for uncertainty in soil properties.
The numerical values of γr are given in Table 1 while those for γRd are to be derived on the basis of M statistics in accordance with Equation (2). It is apparent from Equation (4) that the overall pile resistance uncertainty is a combination of model and soil strength represented by γr,d and γR respectively. The European pile design practice as captured by EN 1997-1, which is the reference code for SANS 10160-5, considers both model and soil strength uncertainty to be equally important. Accordingly, γr,d values reported in the literature (e.g. Orr 2005; Bauduin 2001) are of the same magnitude as γr values. Therefore, despite the current notion that model uncertainty is the dominant source, current practice considers the contributions of γRdand γr to the overall uncertainty to be equal. Since the contributions of the two sources of uncertainty are considered equal, both γrd and Yr are considered as non-dominant parameters. In accordance with EN 1990 for non-dominant variables, the design value of a design parameter (xd) is selected such that the probability of having a more unfavourable value is given by:
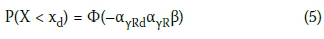
where α γRd and αγr are the contributions of model and soil strength uncertainties respectively.
Let the model and the soil strength uncertainties be represented by their respective coefficients of variation V1 and V2. From the premise of equal contributions, V1 = V2. Then total uncertainty is given by:
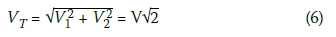
Then:
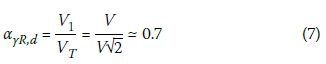
Therefore P(X < xd) = ф(-0.7 x 0.8β) = ф(-0.56β). For the target β of 3.0, corresponding to the reference reliability class RC2 for which reliability procedures are specified in SANS 10160, this corresponds to P(X < xd) = ф(-1.68) = 0.05. This gives a probability of observing a lower value than xd of 5% (i.e. a 5% fractile). Therefore xd s essentially a design fractile at 95% confidence level. Although a 5% fractile is generally interpreted as a characteristic value, here it should be strictly interpreted as design fractile corresponding to a target β of 3.0. In the context of model factor, Bauduin (2001, 2002, 2003) interprets the 5% fractile, that if pile load tests were performed, there is only a 5% probability that the measured capacity will be lower than the predicted. This also means that there is a 95% chance that measured capacities would be greater than the predicted capacities, which gives a safe design situation.
Expression for design fractile at P% confidence level
Mathematical representation of fractiles at a given confidence level can be found in various sources (e.g. EN 1990 Annex D; Bauduin 2003; Holický2009). For a 95% confidence level for a variable following a normal distribution, the fractile is given by:
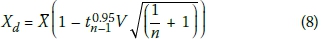
where Xd = the design fractile which in the context of model uncertainty data is equivalent to γr, d , X = mean of the model factor for a given pile class, V = coefficient of variation of the model factor for a given pile class, n = number of pile cases considered, and t0.95n-1 = student t factor for 5% fractile and n-1 degree of freedom.
If the model factor follows a lognormal distribution, Equation (8) becomes:
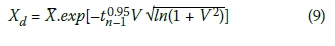
where the symbols are as previously defined.
Equations [8] and [9] represent design values in accordance with a multiplicative factor with a value of less than one; the same convention of a resistance factor φ < 1 is applied by North American, Asian and Australian codes. In accordance with the convention of dividing by a factor γ > 1 (as implied by Equation (3)) Xd is inverted according to Equation (10):
RESULTS AND DISCUSION
The obtained resistance model uncertainty factors γr,d for normal and lognormal distributions of M are presented in Table 3 and Table 4 respectively. These values are considered to be best estimates, since they are based on the direct application of the model factor parameters without any adjustment for the degree of confidence in parameter estimation.
General observations
Analysis of the results indicates the following:
■ Values of the resistance model uncertainty factor are influenced by the type of distribution assumed. In this respect, for a given pile class, values for normal distribution are higher than that for lognormal distribution. Therefore, the normal distribution seems to be relatively more conservative. However, in an analysis to determine which of the two distributions best fit the model factor data, Dithinde and Retief (2013a) concluded that the lognormal distribution is the most suitable, especially at the lower tail. From this premise, values based on the lognormal distribution (Table 4) are considered to be more realistic and have been adopted for the subsequent analyses.
■ In addition to the distribution, the numerical values of the resistance model uncertainty factors are also dependent on the model factor M statistics (i.e. mean and COV). In general high COV yields high Yr d values, as is the case for D-NC pile class. Also, the lower the mean, the higher the Yr,d value, as is the case for B-NC. Such trends have also been reported by Bauduin (2003).
■ Variation of Yr d values with pile class is within a narrow range (1.3 - 1.6). Piles in cohesive materials (D-C, B-C and C) depict the lowest Yr d value of 1.3, as compared to piles in non-cohesive materials with γr, d values ranging from 1.5 to 1.6. The differences in γr, d values between piles in cohesive and non-cohesive materials is more evident when comparing values for all piles in cohesive materials (C) versus all piles in non-cohesive (NC). It can be seen from Table 4 that γr, d = 1.3 for C and 1.5 for NC. The higher γr,d value in non-cohesive soil indicates that pile design in non-cohesive soil is more uncertain. This is attributed to the coupled effects of limited understanding of the soil failure mechanism around the pile shaft and base, and the resulting unrealistic pile design parameters (bearing capacity factors (Nq), coefficient of horizontal stress (ks) and soil-pile interface friction (5)).
■ A comparison of all bored (B) versus all driven (D) piles, irrespective of soil type, indicates no difference in terms of γr,d values. This suggests that the pile installation method has little influence on γr,d values. This further implies that pile design should be classified on the basis of soil type only, with model partial factors being differentiated on the basis of soil properties. In accordance with Table 4
γr, d values of 1.3 and 1.5 can be adopted for piles in cohesive and non-cohesive soils respectively.
■ The γr, d value for the all piles dataset is 1.4, which is not significantly different from that of the subgroups of the database.
Pile classes based on γR,d values
The critical question is whether to adopt a single YR, d for the combined dataset or different values as per the various subgroups. Bauduin (2001) argues that, although organisation into subgroups leads to refined values of the model partial factor, the number of tests in the subgroups decreases, thereby increasing statistical uncertainty on the characteristics of the distribution. On the basis of this argument it appears that taking one single value of the γr,d for all piles in all soils is the way to go. However, this will lead to an inconsistent situation where piles in cohesive materials will benefit favourably while those in non-cohesive will systematically be on the unsafe side. As mitigation to this problem, two possibilities are suggested: (i) Use a single γr,d for all piles with different γr values based on soil type. This implies a single γr,d value of 1.4 (i.e. γr, d for the ALL case), with different γr values for piles in cohesive and non-cohesive soil. (ii) Use different γr, d values with a single γr factor. In this regard the computations carried out here (Table 4) support a γr,d value of 1.3 for piles in cohesive soil and 1.5 for piles in non-cohesive soils. However, for piles in non-cohesive soils a single γr, d value of 1.5 seems to be not sufficient for driven piles. It appears that the poor understanding of soilpile interaction in non-cohesive soil is more prevalent for driven piles, and therefore the case D-NC warrants further investigations.
Bauduin (2000) suggests that the first option is the European proposal where, for instance, in the BS EN 1997-1 Annex, a single γr. d factor of 1.4 for all piles, irrespective of soil type, is given for use with different Yr factors for bored and driven piles.
Sensitivity of γR,d to parameter estimation uncertainty
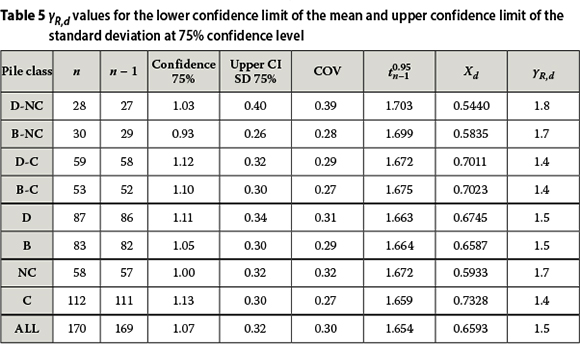
To provide for uncertainties in parameter estimation γr, d values are calculated for model factor statistics (i.e. mean and standard deviation at 75% confidence level). As explained in Dithinde and Retief (2013a), a 75% confidence level is recommended in EN 1990 for parameter estimation to serve as input in reliability models. In this regard the lower confidence limit of the mean (mM:-75) and the upper confidence limit of the standard deviation (sm+75) are used to represent the worst-case scenario of the model factor statistical parameter estimates. The results of the analysis are presented in Table 5. A comparison of γr,d values in Table 5 with those in Table 4 indicate an increase of 0.2 for D-NC, B-NC and NC, and 0.1 for ALL, D-C, B-C and C. It appears that γr,d values are not radically sensitive to parameter estimation uncertainties, and therefore the values presented in Table 4 can be used with confidence. However, it is the most severe case (D-NC) that is most sensitive to parameter estimation, to a limited degree also for B-NC and the combined NC. This provides some additional concern on how to provide for the special case of D-NC.
Comparison with γR,d values from other databases
The results discussed seem to indicate that γr,d values for piles in non-cohesive materials are relatively higher than that for piles in cohesive materials. The relatively higher γr,d values in non-cohesive materials is attributed to the higher variability of the model factor statistics in this material, which in turn is an indication of lack of precision or reliability of the static formula in non-cohesive soil. This trend seems to be supported by results of previous studies. For example Orr (2005) recommended a model factor of 1.5 for piles in sand, while Bauduin (2001) derived a value of 1.2 for piles in over-consolidated clay.
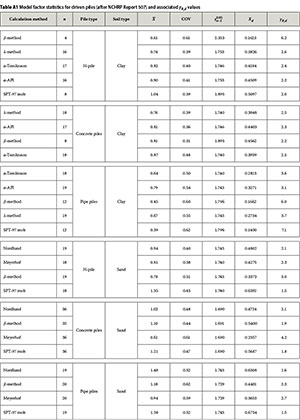
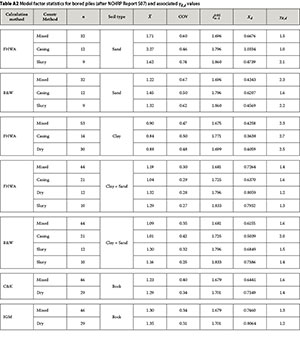
To get further insight into the general characteristics of γr d values based on other databases, model factor statistics from the NCHRP Report 507 (Paikowsky et al 2004) are used to compute γr d values. The NCHRP Report 507 contains, among other things, databases used for the statistical evaluation of model factors and associated resistance factors for a study to develop resistance factors for driven pile and drilled shaft foundations. The databases, which present the pile capacity calculation methods, pile construction methods, soil data and the model factor statistics are shown in Table A1 and Table A2 of the Appendix. These tables also present the results of the γr,d values calculated from the published parameters, calculated similarly to the values presented in Table 4 for the local M database. In principle, NCHRP Report 507 databases cannot be directly compared with the southern African database on the grounds of different calculation models, pile test procedure, methods for determining ultimate measured capacity from pile tests results, soil conditions and general pile design experience base. However, there are some comparable relevant general trends that provide more insight into the characteristics of γr,d values as follows:
■ As expected, the γr d values vary significantly with the calculation methods, suggesting that a model partial factor developed for a particular pile design method cannot be just applied to another method.
■ In agreement with the southern African database, the design methods in general provide more accurate and precise predictions in bored piles than in driven piles, as indicated by the mean model factor being closer to one and relatively lower COV. Therefore the relatively high γr,d value for the D-NC case is corroborated, thereby eliminating statistical uncertainty due to small sample size and quality of the data as the cause of the deviation from results of other cases. This strengthens the point made earlier that the root cause is that current calculation models do not realistically capture the behaviour of driven piles in non-cohesive soils.
■ For a given pile class (bored or driven piles), there seem to be in general slightly higher γr,d values in clay compared to sand, indicating that pile design in clay is more uncertain. This is the direct opposite of what was observed with the southern African database. The difference is attributed to the fact that in the southern African database, cohesive materials do not entirely refer to clay soils, but predominately refer to residual soils. Full-scale load tests on instrumented piles in residual soils (e.g. Chang & Broms 1991) behave in the same way as in stiff clays and weak rocks.
CONCLUSIONS
The paper presents a systematic derivation of resistance model uncertainty factors Yr d for pile foundations on the basis of test data in accordance with the probabilistic approach recommended in EN 1990 for reliability-based design. Probabilistic considerations in treatment of data, as well as reliability-based design procedures, are at the forefront of international efforts to ensure safety and economy of engineering designs. Accordingly, this paper contributes to the development of a reliability approach to geotechnical design.
The main observations based on the analysis are as follows:
■ A single value for the resistance model uncertainty factor of γr d = 1.4 (pile class ALL, Table 4) is close to the present value of 1.5 stipulated by SANS 10160-5:2011. This is not surprising, since the stipulated value is based on a preliminary analysis of information from Dithinde (2007) as reported by Day and Retief (2009). The upper confidence value of 1.5 (Table 5) indicates that γr,d = 1.4 is a proper best estimate value.
■ Differentiation in terms of pile construction is not warranted, since exactly the same results are obtained for driven (D) and bored (B) pile classes - for both the best estimate (1.4) and confidence level (1.5) values, as compared to the undif-ferentiated set.
■ Differentiation in terms of soil type indicates a distinct improvement, resulting in values of 1.3 for cohesive soils (C) and 1.5 for non-cohesive soils (N-C). The confidence level value of 1.4 for cohesive soils also confirms that the value of 1.3 represents a reasonable best estimate value.
■ However, for non-cohesive soil an increased sensitivity to parameter estimation is indicated by the increase from the best estimate value of 1.5 to a confidence level estimate of 1.7. The same observations apply to the other two pile classes of driven and bored piles in non-cohesive soil (D-NC and B-NC).
■ The most inconsistent case is therefore for driven piles in non-cohesive soils (D-NC), with a value of 1.6 and a confidence level value of 1.8. Acceptance of this deviation in reliability and confidence, when a value of 1.5 is applied, can only be based on acceptance of existing practice (Eetief & Dithinde 2013), and general calibration indicating that the target level of reliability is generally just achieved in this case (Dithinde & Retief 2013b).
To summarise it is concluded that:
■ The present value of γr,d = 1.5 for the partial factor for uncertainty in the pile resistance model stipulated in SANS 10160-5:2011 will achieve the target level of reliability under all conditions considered here, and for pile design in accordance with static pile resistance models for cohesive and non-cohesive soils, albeit with a degree of inconsistency in the reliability achieved.
■ A reduced value of γr,d = 1.4 can be justified, as based on an undifferentiated dataset, however, with concern about consistency and confidence in reliability for the special case of driven piles in non-cohesive soils.
■ A differentiated scheme of values of 1.3 and 1.5 for cohesive and non-cohesive soils respectively complies with exceeding the target level of reliability with improved consistency.
■ The anomalous behaviour of the case of driven piles in non-cohesive materials, and more generally resistance predictions in such soils, warrant further investigation.
■ The results from this relatively large data-set of pile tests and prediction methods are relatively coherent when compared to a representative range of pile and soil types and calculation methods from the NCHEP dataset and γr d values calculated from this database.
REFERENCES
Bauduin, C 2000. Design of axially loaded compression piles according to Eurocode 7. Proceedings, 9th International Conference on Piling and Deep Foundations, Nice, France, pp 301-312. [ Links ]
Bauduin, C 2001. Design of axially loaded compression piles according to Eurocode 7 and analysis of the test results. Proceedings, Symposium on Screw Piles: Installation and Design in Stiff Clay. Rotterdam: Balkema, pp 275-303. [ Links ]
Bauduin, C 2003. Assessment of model factor and reliability index for ULS design of pile foundations. Proceedings, 4th International Geotechnical Seminar on Deep Foundations on Bored and Auger Piles, 2-4 June, Ghent. [ Links ]
Chang, M F & Broms, B B 1991. Design of bored piles in residual soils based on field-performance data. Canadian Geotechnical Journal, 28(2): 200-209. [ Links ]
Chin, F K 1970. Estimation of the ultimate load of piles not carried to failure. Proceedings, 2nd Southeast Asian Conference on Soil Engineering, Singapore, 11-15 June, pp 81-90. [ Links ]
Davison, M T 1972. High-capacity piles. Proceedings, Soil Mechanics Lecture Series on Innovation in Foundation Construction, American Society of Civil Engineers, Illinois Section, Chicago, 22 March, pp 81-112. [ Links ]
Day, P W & Eetief, J V 2009. Provision for geotechnical design in SANS 10160. Background to SANS 10160. Stellenbosch: SunMedia. [ Links ]
Dithinde, M 2007. Characterisation of model uncertainty for reliability-based design of pile foundations. PhD Thesis University of Stellenbosch. Available at: http://www.hdl.handle.net/10019.1/21612. [ Links ]
Dithinde, M, Phoon, K K, De Wet, M & Retief, J V 2011. Characterisation of model uncertainty in the static pile design formula. Journal of Geotechnical and Geoenvironmental Engineering, ASCE, 137(1): 333-342. [ Links ]
Dithinde, M & Retief, J V 2013a. Pile design practice in southern Africa. I: Resistance statistics. Journal of the South African Institution of Civil Engineering, 55(1): 72-79. [ Links ]
Dithinde, M & Retief, J V 2013b. Reliability index of pile foundations designed to SANS 10160-5. Proceedings, 4th International Symposium on Geotechnical Safety and Risk (ISGSR 2013), 4-6 December, Hong Kong. [ Links ]
EN 1990. 2002. Eurocode: Basis of Structural Design. Brussels: Committee for Standardization (CEN). [ Links ]
EN 1997. 2004. Eurocode 7: Geotechnical Design. Part 1: General Rules. Brussels: European Committee for Standardization (CEN). [ Links ]
Holicky, M 2009. Reliability analysis for structural design. Stellenbosch: SunMedia. [ Links ]
Orr, T L L 2005. Model solutions for Eurocode 7. Workshop examples. Proceedings, International Workshop on the Evaluation of Eurocode 7, Dublin, Ireland, pp 75-108. [ Links ]
Paikowsky, S G, Birgisson, B, McVay, M et al 2004. Load and resistance factors design for deep foundations. NCHRP Report 507, Washington DC: Transportation Research Board. [ Links ]
Phoon, K K & Kulhawy, F H 2005. Characterisation of model uncertainty for laterally loaded rigid drilled shafts. Geotechnique, 55(1): 45-54. [ Links ]
Retief, J V & Dithinde, M 2013. Pile design practice in southern Africa. II: Implicit reliability of existing practice. Journal of the South African Institution of Civil Engineering, 55(1): 21-28. [ Links ]
Ronold, K O & Bjerager, P 1992. Model uncertainty representation in geotechnical reliability analysis. Journal of Geotechnical Engineering, ASCE, 118(3): 363-376. [ Links ]
SANS 10160-1: 2011. Basis of structural design and actions for buildings and industrial structures. Part 1. Basis of structural design. Pretoria: South African Bureau of Standards.
SANS 10160-5: 2011. Basis of structural design and actions for buildings and industrial structures. Part 5: Basis for geotechnical design and actions. Pretoria: South African Bureau of Standards. [ Links ]
Teixeira, A, Correia, A G, Honjo, Y & Henriques, A 2011. Reliability analysis of a pile foundation in a residual soil: Contribution of the uncertainties involved and partial factors. Proceedings, 3rd International Symposium on Geotechnical Safety and Risk (ISGSR 2011), 2-3 June, Munich, Germany. [ Links ]
 Correspondence:
Correspondence:
M Dithinde
Department of Civil Engineering, Stellenbosch University
Private Bag X1 Matieland, 7602
South Africa, Department of Civil Engineering, University of Botswana
Private Bag UB 0061
Gaberone, Botswana
T: +267 355 4297
F: +267 395 2309
E: dithinde@mopipi.ub.bw
J V Retief
Department of Civil Engineering, Stellenbosch University
Private Bag X1
Matieland, Stellenbosch, 7602
T: +27 21 808 4442
F: +27 21 808 4947
E: jvr@sun.ac.za

DR MAHONGO DITHINDE (Visitor) holds a PhD in Civil Engineering from the Stellenbosch University, an MSc in Foundation Engineering from the University of Birmingham (UK), and a BEng in Civil Engineering from the University of Botswana. He works as a Senior Lecturer at the University of Botswana. His specialisation and research interests are in the broad area of geotechnical reliability-based design. In addition to academic work, he is also a geotechnical partner for Mattra International where he is active in consultancy work in the field of geotechnical engineering.

PROF JOHAN RETIEF (Fellow of SAICE) has, since his retirement as Professor in Structural Engineering, maintained involvement at the Stellenbosch University, supervising graduate students in the field of risk and reliability in civil engineering. He is involved in various standards committees, serving as the South African representative to ISO TC98 (basis of structural design and actions on structures). He holds a BSc (cum laude) and a DSc from the University of Pretoria, a DIC from Imperial College London, and an MPhil from London University. Following a career at the Atomic Energy Corporation, he joined Stellenbosch University in 1990.
APPENDIX
Table A1 Model factor statistics for driven piles (after NCHRP Report 507) and associated γR,d values