Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
Journal of the South African Institution of Civil Engineering
On-line version ISSN 2309-8775
Print version ISSN 1021-2019
J. S. Afr. Inst. Civ. Eng. vol.56 n.2 Midrand Aug. 2014
TECHNICAL PAPER
A CPM-based scheduling method for construction projects with fuzzy sets and fuzzy operations
Ö Ökmen; A Öztaş
ABSTRACT
The Critical Path Method (CPM), which is used to schedule construction activities that depend on one another through network relationships, is deterministic with regard to the duration assigned to the execution of the activities and the results produced in certain values. Unfortunately, construction activities are performed under uncertain conditions. Project risks cause variations in activity duration, and in turn the entire network is affected by uncertainty. In this context, activity duration can be represented by fuzzy sets, and CPM network calculations can be performed by fuzzy operations through a method developed in this study. Since the duration of activities is represented by fuzzy sets, and network calculations can be performed by fuzzy operations, the activity early/late start/finish times and the project completion time are calculated as fuzzy sets by the proposed method. An example CPM application with fuzzy sets is also presented in the paper. The findings show that CPM is applicable with fuzzy sets, and the developed method operates well for modelling the uncertainty in CPM calculations.
Keywords: construction management, critical path method, scheduling, fuzzy sets, uncertainty
INTRODUCTION
Construction projects are realised by carrying out various activities which are dependent on one another by finish-to-start (FS), start-to-start (SS), finish-to-finish (FF) or start-to-finish (SF) relationships, and by lag or lead times. Therefore, construction activities constitute networks. In order to provide managerial information - such as the project completion time, the activity early start (ES), late start (LS), early finish (EF) and late finish (LF) times, the activity float times and the activity criticalities - the dependency relations between the activities should be analysed. Bar charts, Line of Balance and Critical Path Method (CPM) have been the popular methods of construction activity scheduling since the 1950s (Griffis & Farr 2000; Halphin & Woodhead 1998; Oberlender 2000). CPM, which was first developed in 1956 by the DuPont Company with Remington Rand as consultants in the USA, is accepted as the most suitable means of scheduling activity networks (Oberlender 2000). This is due to its capabilities, such as showing the dependency relations between activities, detecting the critical activities and revealing the activity float times (Ökmen & Öztaş 2008).
In spite of its wide usage and popularity, CPM has some limitations and criticised features. The limitations of CPM are related to its deterministic calculation procedure, which is insufficient for modelling uncertainty. CPM is deterministic because of the invariable duration values assigned to activities in network calculations, as if these durations are known certainly and do not vary by various risk factors. This deficiency may lead to inaccurate critical path identification and project duration measurement (Jaafari 1984; Ahuja & Thiruvengadam 2004). Unfortunately, construction network schedules are under the influence of uncertainty due to risk factors such as weather conditions, soil properties, labour productivity, etc (Edwards 1995; Flanagan & Norman 1993; Öztaş & Ökmen 2004). All of the risk factors in a construction project might be schedule risks, because they are directly or indirectly related to time schedules. Moreover, due to uncertainties, all activities might become critical in practice, even those that are not critical according to CPM.
In this context, this study aims at proposing a method of the CPM network calculations (forward and backward pass calculations) with fuzzy sets. The activity durations are represented by special kinds of fuzzy sets called fuzzy numbers in this method, and accordingly the CPM forward and backward pass calculations are executed by fuzzy operations. The representation of activity durations by fuzzy numbers enables modelling the uncertainty effect. In construction projects, the duration of an activity cannot be proposed with certainty in advance. Predictions such as "this activity can be completed most probably between seven and ten days, but perhaps it takes 15 days maximum and five days minimum depending on the conditions" are frequently made. Fuzzy numbers are suitable to model these kinds of linguistic propositions mathematically. Since the activity durations are represented by fuzzy numbers and the network calculations are performed by fuzzy operations, the activity early/ late start/finish times and the project completion time or the project duration are calculated as fuzzy numbers through this new method. In other words, the effect of uncertainty on the results of CPM is modelled. Furthermore, the evaluation of activity/path criticalness is realised by using the geometric centres of the activity early/late times.
Simulation-based, probabilistic- or fuzzy set-based methods have been used in the past by researchers to model the uncertain activity durations and the uncertainty effect on the activity networks (Ayyub & Haldar 1984; AbouRizk & Halphin 1992; Diaz & Hadipriono 1993; Wu & Hadipriono 1994). Program Evaluation and Review Technique (PERT) is the most popular probabilistic method developed for this purpose. While certain durations are assigned to the activities in CPM, activity durations are assumed as variables and represented by minimum, maximum and most likely durations in PERT. Through a simplification process, the expected durations and the variances of variable activity durations are calculated by utilising the minimum, maximum, and most likely durations. Subsequently, the traditional CPM calculations are performed by using the expected activity durations, and then the critical path is detected. The expected durations and variances of the activities on the critical path are added, and the project completion time is assumed to follow normal probability distribution having these calculated values as the distribution parameters, i.e. the mean and variance. Since the project completion time is obtained as a normal probability distribution in PERT, it becomes possible to draw some inferences regarding the uncertainty of the activity network and project completion time, such as the probability of completing the project within a specific percentage (Halphin & Woodhead 1998; Griffis & Farr 2000; Oberlender 2000; Plotnick & O'Brien 2009). However, PERT has been criticised in the literature because of its limitations, such as taking only the critical path into account, assumption of normal probability distribution for the project completion time, simplification process used in the calculation of expected activity durations and variances through estimated minimum, maximum and most likely durations, etc (Ahuja & Thiruvengadam 2004; Diamantas et al 2007; Kerzner 2009).
In order to overcome the limitations of CPM and PERT, CPM-based risk analysis models have been developed by utilising Monte Carlo Simulation Technique (Ökmen & Öztaş 2008; Wang & Demsetz 2000). Some of the researchers have tried to implement the CPM network calculations through fuzzy sets and operations instead of utilising probabilistic or simulation techniques (Chanas & Kamburowski 1981; Dubois & Prade 1988; Lorterapong & Moselhi 1996). Lorterapong and Moselhi (1996) developed a complete project network analysis technique by using a fuzzy set theory named FNET. This technique includes a new procedure for performing the forward and backward pass calculations of CPM with fuzzy sets in cases where the activities are dependent on one another having only finish-to-start relations, and where no lag or lead times are used between the activities. However, if other types of network dependencies, such as finish-to-finish, start-to-start or start-to-finish, and lag/lead times are used, this technique fails. In this study, it is aimed to propose a new method to be used for the full implementation of CPM with fuzzy sets, in case lag/lead times and all dependency types are used.
The details of the new method are described after introducing the basic information about fuzzy set theory and fuzzy numbers, and then an example application is carried out. The paper ends with the conclusions and recommendations for future work.
FUZZY SET THEORY AND FUZZY NUMBERS
In classical set theory, the membership of an element to a specified set is described by two definite and opposite situations: belonging to the set (membership degree = 1.0) or not belonging to the set (membership degree = 0.0). However, in fuzzy set theory, the membership of an element to a specified set is described by the membership degrees between 0.0 and 1.0 (Zadeh 1965; Sen 2004; Ross 2010). This provides the opportunity of modelling the uncertain expressions of real life mathematically, performing fuzzy set operations between these uncertainties and finally reaching fuzzy results that cannot be achieved analytically otherwise.
Consider a fuzzy set A of the universe U.
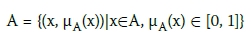
where µA(x) is a function called membership function, and µA(x) exactly states the grade or degree to which any element x in A is a member of the fuzzy set A.
The definition given above combines each element x in A with µA(x) in the interval [0, 1] which is assigned to x. Larger values of µA(x) indicate higher degrees of membership (Bojadziev & Bojadziev 1997; Han 2005; Ross 2010).
A fuzzy number is a continuous fuzzy set that possesses two properties: convexity and normality. The convexity indicates that the membership function has only one distinct peak, while the normality ensures that at least one element in the set has a degree of membership equal to 1.0. These two properties make the concept of fuzzy numbers attractive and naturally appropriate for modelling imprecise fuzzy quantities such as "approximately one week," or "more or less than seven days". Theoretically, fuzzy numbers can take various shapes. In modelling real-life problems, however, linear approximations such as trapezoidal and triangular fuzzy numbers are frequently used (Chanas & Kamburowski 1981; Dubois & Prade 1988). Mathematical definitions and general shapes of triangular and trapezoidal fuzzy numbers are given below:
Triangular fuzzy numbers
A triangular fuzzy number with membership function µA(x) is defined by:
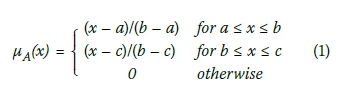
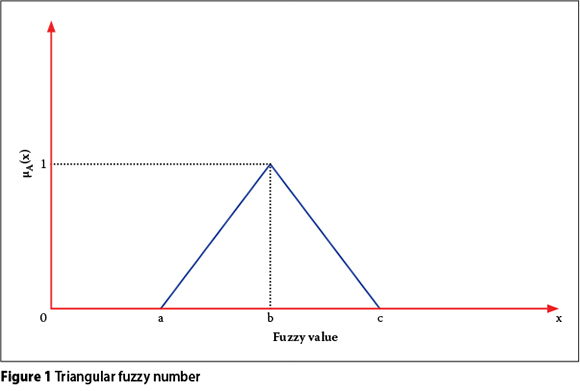
This set is graphically shown in Figure 1.
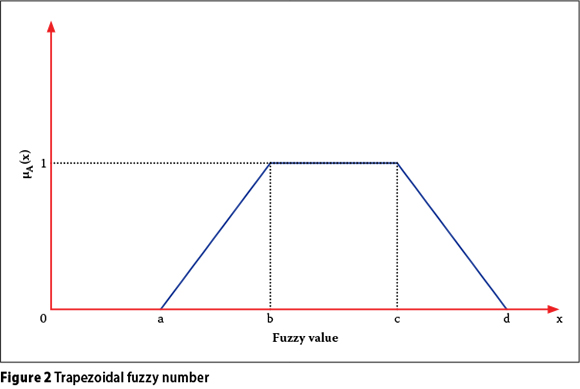
Trapezoidal fuzzy numbers
A trapezoidal fuzzy number with membership function µA(x) is defined by
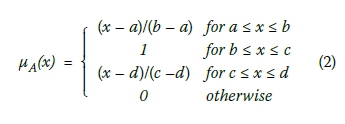
This set is graphically shown in Figure 2.
CPM NETWORK CALCULATIONS WITH FUZZY SETS AND FUZZY OPER ATIONS
The early/late start/finish times, total float times, criticalness of the activities and the project completion time of a network are explored by applying forward and backward pass calculations on the network. In other words, forward and backward pass calculations constitute the network calculations of CPM. In order to carry out the CPM network calculations, activity durations, activity interdependencies in the form of FS, FF, SS or SF, and lag/lead times between the activities are required. The activity durations should be predicted as invariable fixed values (most likely durations) for the CPM execution. However, if the activity durations and lag/lead times are represented by fuzzy sets, traditional forward/backward pass calculation of CPM becomes inapplicable. In this regard, a method has been developed for the purpose of making the CPM network calculations applicable with fuzzy sets and fuzzy operations.
Forward pass calculations with fuzzy sets
Forward pass calculations should be performed through fuzzy operations in an activity network of which the activity durations and lag/lead times are represented by fuzzy sets. For this reason, fuzzy addition, fuzzy subtraction, fuzzy maximisation and fuzzy minimisation have been utilised in order to develop the procedure of the CPM forward pass calculation with fuzzy sets. The procedure is described below:
If X and Y are the two trapezoidal fuzzy numbers, such that
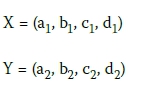
then
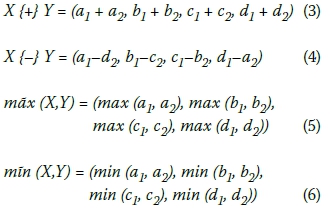
where {+}, {-}, mãx, mĩn are fuzzy addition, fuzzy subtraction, fuzzy maximisation and fuzzy minimisation, respectively.
These fuzzy operations are only applied between the fuzzy values possessing the same membership degrees, which is a rule based on the logic of fuzzy operations (Lorterapong & Moselhi 1996).
If all of the activity dependencies are FS and there is no lag/lead time between activities in an activity network, fuzzy forward pass calculation is performed as follows (Lorterapong & Moselhi 1996):

where p Є P (the set of predecessor activities); FESx, FEFx, FDx are the fuzzy early start time, fuzzy early finish time and fuzzy duration of activity x respectively; and Tproj and FEFe are the fuzzy project duration and fuzzy early finish time of the last activity respectively.
However, the construction project activity networks may include lag or lead times, and other dependencies such as SS and FF between activities. This problem is resolved by the following algorithm:
i. Subtract lead time from lag time with fuzzy subtraction for each activity pair having a predecessor/successor relation.
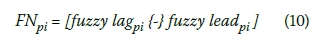
where pi denotes the predecessor activity so that i takes values depending on the number of predecessors.
ii. Add the fuzzy number calculated in step (i) with fuzzy addition to the corresponding early time of the predecessor activity. For instance, if the relation is FF between an activity and one of its predecessors, then early finish time of this activity is calculated by adding the fuzzy number calculated in step (i) to the early finish time of the predecessor activity.
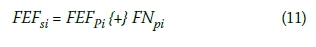
where si denotes the successor activity. Once more, i takes values depending on the number of predecessors.
iii. Fuzzy early start times of an activity are calculated by employing the fuzzy duration of this activity to the fuzzy early start times found in step (ii). However, this step is executed if the dependency is SF or FF. If the dependency is SS or FS, the fuzzy early time found in step (ii) is already the fuzzy early start time.
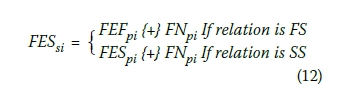
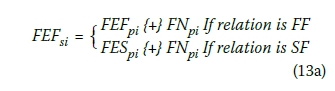
Then
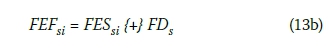
(13b) where FDs shows the fuzzy duration of the successor activity in question. iv. In step (iii) different fuzzy early start times are calculated as many as the number of predecessors (pi) of the successor activity (si) in question. Therefore, the final fuzzy early start time of an activity is found with fuzzy maximisation of the fuzzy early start times calculated in step (iii).
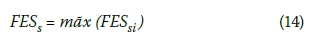
The procedure of fuzzy forward pass calculation described above is clarified by an application in a short example network portion (four predecessors - one successor network portion), which is shown in Figure 3.
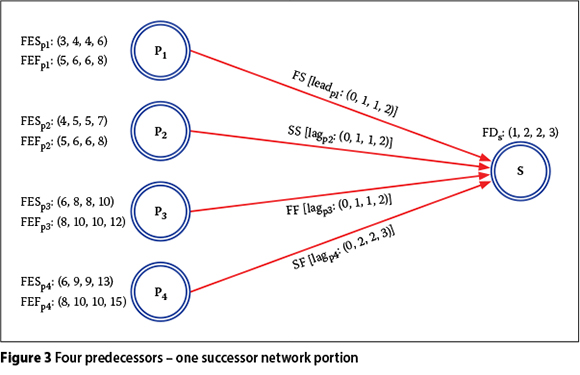
All of the fuzzy numbers in the Figure 3 example are accepted as trapezoidal. However, the mode values, b and c, are accepted as equal to each other for the purpose of modifying the trapezoidal fuzzy numbers to triangular fuzzy numbers in order to simplify the calculations. The network consists of a single activity whose fuzzy early start and fuzzy early finish times are being searched, and four predecessor activities whose dependency and lag/lead times differ as shown in Figure 3. FES and FEF designate the fuzzy early start and fuzzy early finish times respectively. Fuzzy forward pass calculations of this example network are performed as follows:
■ Predecessor 1 (p1) :
FESs1 = FEFp1 {+} [fuzzy lagp1 {-} fuzzy leadp1]
FESs1 = (5,6,6,8) {+} [(0,0,0,0) {-} (0,1,1,2)]
FESs1 = (5,6,6,8) {+} (-2,-1,-1,0)
FESs1 = (3,5,5,8)
■ Predecessor 2 (p2) :
FESs2 = FESp2 {+} [fuzzy lagp2 {-} fuzzy leadp2]
FESs2 = (4,5,5,7) {+} [(0,1,1,2) {-} (0,0,0,0)]
FESs2 = (4,5,5,7) {+} (0,1,1,2)
FESs2 = (4,6,6,9)
■ Predecessor 3 (p3) :
FEFs3 = FEFp3 {+} [fuzzy lagp3 {-} fuzzy leadp3]
FEFs3 = (8,10,10,12) {+} [(0,1,1,2) {-} (0,0,0,0)]
FEFs3 = (8,11,11,14)
FEFs3 = FESs3 {+} Fuzzy Act. Dur.s (FDs) (8,11,11,14) = FESs3 {+} (1,2,2,3)
FESs3 = (7,9,9,11)
■ Predecessor 4 (p4) :
FEFs4 = FESp4 {+} [fuzzy lagp4 {-} fuzzy leadp4]
FEFs4 = (6,9,9,13) {+} [(0,2,2,3) {-} (0,0,0,0)]
FEFs4 = (6,11,11,16)
FEFs4 = FESs4 {+} Fuzzy Act. Dur.s (FDs) (6,11,11,16) = FESs4 {+} (1,2,2,3)
FESs4 = (5,9,9,13)
■ FESs:
FESs = mãx (FESs1, FESs2, FESs3, FESs4)
FESs = (7,9,9,13)
■ FEFs:
FEFs = FESs {+} Fuzzy Act. Dur.s (FDs)
FEFs = (7,9,9,13) {+} (1,2,2,3)
FEFs = (8,11,11,16)
This example application shows that the fuzzy early start time of the successor activity S in Figure 3 is (7,9,9,13), i.e. the early start time of the activity S is certainly between the 7th and 13th unit times (day, month, etc), and it is most plausibly at the 9th unit time from the starting date of the network.
Backward pass calculations with fuzzy sets
If the activity durations and lag/lead times are represented by fuzzy sets, fuzzy backward pass calculations should be performed through fuzzy operations just as in the case of fuzzy forward pass calculations. For this reason, fuzzy subtraction has been utilised in order to develop the fuzzy backward pass calculation procedure. However, a problem occurs due to the usage of fuzzy subtraction. Fuzzy subtraction produces unrealistically large uncertainties associated with fuzzy late start and fuzzy late finish times of activities.
These uncertainties accumulate quickly as the backward pass calculation progresses. Moreover, earlier activities may be assigned with negative early finish and late finish times at the end of the calculation which has no meaning from the scheduling point of view. Lorterapong and Moselhi (1996) tried to overcome this problem by developing a procedure while developing their so-called model, FNET. However, only FS relation was considered and lag/lead times were ignored in FNET. For this reason, their method has been carried one step further in this study to circumvent these limitations. The used assumptions and the developed backward pass calculation procedure are described below.
Assumptions
■ All the values in fuzzy numbers (lower, upper and mode values - a,b,c,d) should have a positive value.
■ Each value should not exceed its successor (a < b < c < d).
■ The values of the fuzzy early start time or fuzzy early finish time of an activity found by fuzzy forward pass calculation should not exceed the values of the fuzzy late start or fuzzy late finish times found by the fuzzy backward pass calculation.
■ The right spread of fuzzy late times (the difference between d and c) should be at least as uncertain as their respective fuzzy early times.
Procedure
i. First, lag/lead times between the activities are processed. Since the operation is now the backward pass, lag times are considered just like the lead times of forward pass, and lead times are considered just like the lag times of forward pass. In other words, lag time is subtracted from lead time, with fuzzy subtraction for each activity pair having predecessor-successor relation.
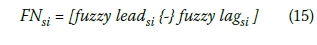
where si denotes the successor activity so that i takes values depending on the number of successors.
ii. The fuzzy number calculated in step (i) is added with fuzzy addition to the corresponding late time of the successor activity. For instance, if the relation is FF between an activity and one of its successors, then late finish time of this activity is calculated through fuzzy adding of the fuzzy number calculated in step (i) to the late finish time of the successor activity.
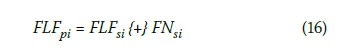
where pi denotes the predecessor activity. Once more, i takes values depending on the number of successors.
iii. Fuzzy late finish times of an activity x are calculated with employing fuzzy duration of this activity to the fuzzy late times found in step (ii). However, this step is executed if the dependency is SF or SS. If the dependency is FS or FF, the fuzzy late time found in step (ii) is already the fuzzy late finish time.
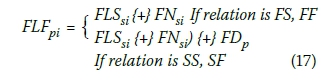
where FDp shows the fuzzy duration of the predecessor activity in question.
iv. Final fuzzy late finish time of an activity is found with fuzzy minimisation of the fuzzy late finish times calculated in step (iii).
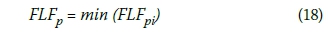
v. The fuzzy number found in step (iv) is accepted as the preliminary fuzzy late finish time (PFLFp).
vi. FEF and PFLF are compared to find which of the two fuzzy numbers has a greater right spread. Suppose that FEFp is represented by (a,b,c,d) and the PFLFp is represented by (p,q,e,f). In this case, the comparison is made between (f - e) and (d - c) (Lorterapong & Moselhi 1996).
vii. If (d - c) > (f - e), which means that the right spread of FEFp is more uncertain, the right spread of the final fuzzy late finish time (FLFp) is set equal to the right spread of FEFp. In this case, FLFp is calculated by Equation 19 (Lorterapong & Moselhi 1996).
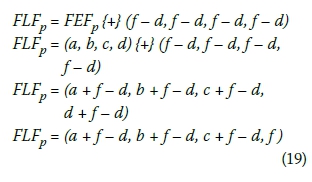
viii. If (d - c) < (f - e), which means that the right spread of FEFp is less uncertain, the right spread of FLFp is set equal to the right spread of PFLFp. In this case FLFp is calculated by Equation 20 (Lorterapong & Moselhi 1996).
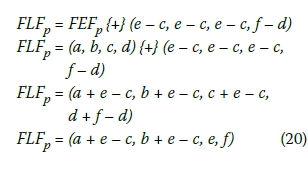
ix. Fuzzy late start time (FLSp) is computed by substituting FLFp and fuzzy duration (FDp) into Equation 21 (Lorterapong & Moselhi 1996).
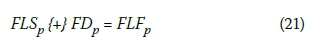
x. The procedure described up to now is applied to all activities starting from the last activity towards the start activity by following the paths in the backward direction.
The fuzzy backward pass calculation procedure described above is clarified by an application on a short example network (one activity with four successors) shown in Figure 4.
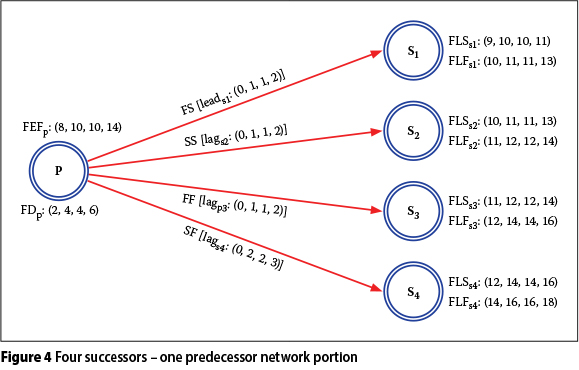
All of the fuzzy numbers are taken as trapezoidal. However, mode values b and c are taken equal for the purpose of modifying the trapezoidal fuzzy numbers to triangular fuzzy numbers in order to provide simplicity in this example. The network consists of a single activity whose fuzzy late start and fuzzy late finish times are being searched, and four successor activities whose dependency and lag/lead times differ, as shown in Figure 4. Fuzzy backward pass calculations of this network are as follows:
■ Successor 1 (s1) :
FLFp1 = FLSs1 {+} [fuzzy leads1 {-} fuzzy lags1]
FLFp1 = (9,10,10,11) {+} [(0,1,1,2) {-} (0,0,0,0)]
FLFp1 = (9,11,11,13)
■ Successor 2 (s2) :
FLSs2 = FLSs2 {+} [fuzzy leads2 {-} fuzzy lags2]
FLSp2 = (10,11,11,13) {+} [(0,0,0,0) {-} (0,1,1,2)]
FLSp2 = (10,11,11,13) {+} (-2,-1,-1,0)
FLSp2 = (8,10,10,13)
FLFp2 = FLSP2 {+} Fuzzy Act. Dur.p (FDp)
FLFp2 = (8,10,10,13) {+} (2,4,4,6)
FLFp2 = (10,14,14,19)
■ Successor 3 (s3) :
FLFp3 = FLFs3 {+} [fuzzy leads3 {-} fuzzy lags3]
FLFp3 = (12,14,14,16) {+} [(0,0,0,0) {-} (0,1,1,2)]
FLFp3 = (12,14,14,16) {+} (-2,-1,-1,0)
FLFp3 = (10,13,13,16)
■ Successor 4 (s4) :
FLSp4 = FLFs4 {+} [fuzzy leads4 {-} fuzzy lags4]
FLSp4 = (12,14,14,16) {+} [(0,0,0,0) {-} (0,2,2,3)]
FLSp4 = (12,14,14,16) {+} (-3,-2,-2,0)
FLSp4 = (9,12,12,16)
FLFp4 = FLSP4 {+} Fuzzy Act. Dur.P (FDp)
FLFp4 = (9,12,12,16) {+} (2,4,4,6)
FLFp4 = (11,16,16,22)
■ PFLFp :
PFLFp = mĩn (FLFp1, FLFp2, FLFp3, FLFp4
PFLFp = mĩn [(9,11,11,13), (10,14,14,19), (10,13,13,16), (11,16,16,22) ]
PFLFp = (9,11,11,13)
■ FLFp :
PFLFp = (9,11,11,13) and
FEFp = (6,8,8,11) (11 - 8) > (13 - 11) then,
FLFp = FEFp {+} (f - d, f - d, f - d, f - d)
FLFp = (6,8,8,11) {+} (13 - 11, 13 - 11, 13 - 11, 13 - 11)
FLFp = (8,10,10,13)
■ FLSp :
FLSp {+} Fuzzy Act. Dur.P (FDp) = FLFp
FLSp {+} (2,4,4,6) = (8,10,10,13)
FLSp = (6,6,6,7)
Fuzzy backward pass calculation may sometimes produce negative values, especially for the lower and mode fuzzy values (a,b,c) or it may produce zero for the mode fuzzy values (b,c) of the activities at the beginning of the network. In the former case, negative values are converted to zero and in the latter case all the fuzzy values (a,b,c,d) are accepted as zero.
AN EXAMPLE APPLICATION
This section introduces an example application of the proposed fuzzy set CPM-based methodology on a hypothetic activity network. Network information and the results of the application are given in Tables 1 and 2, respectively. The network is a short and simple one, but it contains all types of network dependencies, i.e. FS, FF, SS, SF with lag and lead times. Therefore, it stands as a good example for showing the application of all of the features of CPM with fuzzy sets.
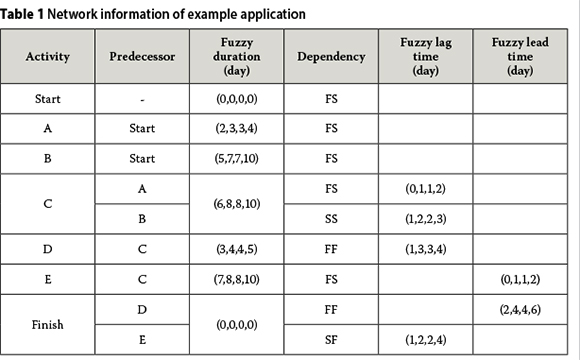
The results given in Table 2 reveal that the total float times of activities were calculated by using geometric centres of fuzzy early and fuzzy late times of the activities, and critical and uncritical activities have been determined with respect to the total float times. The calculation procedure of total float times (TF) by using the geometric centres of the fuzzy numbers is given by Equations 22 and 23 as follows (Lorterapong and Moselhi 1996):
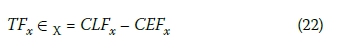
where the C designation denotes the geometric centre of the early and late times, x Є X (the set of activities), and CEF and CLF show geometric centres of fuzzy early finish and fuzzy late finish times respectively.
The geometric centre of a trapezoidal fuzzy set is calculated by Equation 23.
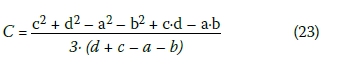
It should be mentioned that the activities with total float times close to zero, and with early and late times very close to one another, have been considered as critical in this study for the sake of detecting the critical path. For example, total float time, fuzzy early finish and fuzzy late finish times of activity C have been found as 1.67, (8,12,12,16) and (8,12,12,21), respectively (refer to Table 2). Therefore, activity C has been considered as a critical activity.
Another float type examined in Table 2 is the independent float. While the total float time is the amount of time that an activity can be delayed without delaying the project completion time, the independent float time is the amount of time that an activity can be delayed without delaying the start of any of its successor activities (Newitt 2008). In other words, independent float is the delay possible for an activity if all preceding activities start as late as possible and all subsequent activities start at their earliest time. The independent float times (IF) given in Table 2 have been calculated through Equations 23 and 24.
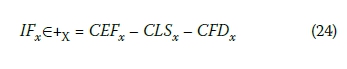
where the C designation denotes the geometric centre of the early and late times; xgX (the set of activities); CEF, CLS, and CFD show geometric centres of fuzzy early finish time, fuzzy late start time, and fuzzy activity duration respectively (refer to Equation 23). If IF is calculated below zero, then it is accepted equal to zero as in the case of the activity network examined in the example application (refer to Table 2). Otherwise, it would be meaningless to have a negative time value.
CONCLUSIONS AND FUTURE WORK
Construction activities are performed under uncertain conditions. Various risks cause variation in activity duration, and in turn the values found by CPM, such as the activity early/late times, become uncertain. In this context, activity durations are represented by fuzzy sets and the CPM network calculations are performed by fuzzy operations through a new method developed in this study. In this method, fuzzy sets are utilised to model the uncertainty in activity durations, activity early/late times and project completion time. An example CPM application with fuzzy sets was also presented. The findings show that CPM is applicable with fuzzy sets, and the developed method operates well for modelling the uncertainty in CPM network calculations.
The representation of activity durations by fuzzy sets enables modelling the uncertainty effect. In construction projects, it is not possible to predict the duration of an activity with certainty. Predictions such as "this activity can be completed most probably between seven and ten days, but perhaps it takes 15 days maximum and 5 days minimum depending on the conditions" are frequently made. Fuzzy sets are suitable to model these kinds of linguistic propositions mathematically. Since the activity durations are represented by fuzzy sets and the network calculations are performed by fuzzy operations, the activity early/ late start/finish times and the project completion time or the project duration are calculated as fuzzy sets through this new method. In other words, the effect of uncertainty on the results of CPM is modelled. Furthermore, the evaluation of activity/path criticalness is realised by using the geometric centres of the activity early/late times.
Execution of CPM by using fuzzy sets and fuzzy operations through the proposed method possesses some advantages over the traditional use of PERT, such as the following:
■ While PERT takes only the critical path into account by ignoring the other activity paths, the proposed method evaluates the uncertainty in all of the activities, and accordingly on all of the activity paths.
■ While PERT applies a simplification process to the estimated minimum, maximum and most likely durations in order to calculate the expected activity durations and variances, the proposed method does not require any simplifications, because the activities are represented by fuzzy sets, and CPM calculations are performed by using these fuzzy sets as a whole.
■ While PERT assumes that project completion time follows normal probability distribution represented by the mean and variance parameters found by adding the expected durations and variances of the activities on the critical path, the proposed method computes the project completion time as a fuzzy set through fuzzy forward and backward CPM calculations performed by using the fuzzy durations of all of the activities, both on the critical and uncritical paths.
The new method for the CPM network calculations with fuzzy sets, as proposed in this study, can also be compared with the other uncertainty analysis methods such as the Monte Carlo simulation-based models. Furthermore, it can be used for developing a fuzzy schedule risk analysis model operating with simulation, on which the authors currently focus their studies. It can also be computerised easily by utilising table processor software or computer programming languages. These issues are proposed as future work.
REFERENCES
AbouRizk, S & Halpin, D W 1992. Statistical properties of construction duration data. Journal of Construction Engineering and Management, 118(3): 525-544. [ Links ]
Ahuja, V & Thiruvengadam, V 2004. Project scheduling and monitoring: current research status. Construction Innovation: Information, Process, Management, 4(3): 19-31. [ Links ]
Ayyub, B M & Haldar, A 1984. Project scheduling using fuzzy set concepts. Journal of Construction Engineering and Management, 110(2): 189-204. [ Links ]
Bojadziev, G & Bojadziev, M 1997. Fuzzy logic for business, finance and management. Singapore: World Scientific. [ Links ]
Chanas, S & Kamburowski, J 1981. The use of fuzzy variables in PERT. Fuzzy Sets and Systems, 5(1): 11-19. [ Links ]
Diamantas, V K, Kirytopoulos K A & Leopoulos V N 2007. Project's duration prediction: traditional tools and simulation? World Review of Entrepreneurship, Management and Sustainable Development, 3(3): 317-333. [ Links ]
Diaz, C & Hadipriono, F 1993. Nondeterministic networking methods. Journal of Construction Engineering and Management, 119(1): 40-57. [ Links ]
Dubois, D & Prade, H 1988. Possibility theory: an approach to computerized processing of uncertainty. New York: Plenum Press. [ Links ]
Edwards, L 1995. Practical risk management in the construction industry. London: Thomas Telford. [ Links ]
Flanagan, R, & Norman, G 1993. Risk management and construction. Cambridge: Backwell Scientific. [ Links ]
Griffis, F H & Farr, J V 2000. Construction planning for engineers. Singapore: McGraw-Hill. [ Links ]
Halphin, D W & Woodhead, R W 1998. Construction management. New York: Wiley. [ Links ]
Jaafari, A 1984. Criticism of CPM for project planning analysis. Journal of Construction Engineering and Management, 110(2): 222-223. [ Links ]
Han, S 2005. Estimation of cost overrun risk in international projects by using fuzzy set theory. MSc Thesis, Ankara: Middle East Technical University. [ Links ]
Kerzner, H R 2009. Project management: a systems approach to planning, scheduling, and controlling. New Jersey: John Wiley & Sons. [ Links ]
Lorterapong, P & Moselhi, O 1996. Project network analysis using fuzzy sets theory. Journal of Construction Engineering and Management, 122(4): 308-318. [ Links ]
Newitt, J S 2008. Construction scheduling: principles and practices. New Jersey: Prentice Hall. [ Links ]
Oberlender, G D 200 0. Project management for engineering and construction. Boston: McGraw-Hill. [ Links ]
Ökmen, Ö & Öztaş, A 2008. Construction project network evaluation with Correlated Schedule Risk Analysis Model. Journal of Construction Engineering and Management, 134(1): 49-63. [ Links ]
Öztaş, A & Ökmen, Ö 2004. Risk analysis in fixed-price design build construction projects. Building and Environment, 39(2): 229-37. [ Links ]
Plotnick, F & O'Brien, J 2009. CPM in construction management. New York: McGraw-Hill. [ Links ]
Ross, T J 2010. Fuzzy logic with engineering applications. Singapore: John Wiley & Sons. [ Links ]
Şen, Z 2004. Mühendislikte bulanık (fuzzy) mantık ve modelleme prensipleri (The principles of fuzzy logic and modelling in engineering). İstanbul: Su Vakfı Yayınları [ Links ].
Wang, W-C & Demsetz, L A 2000. Model for evaluating networks under correlated uncertainty -NETCOR. Journal of Construction Engineering and Management, 126(6): 458-466. [ Links ]
Wu, R K & Hadipriono, F C 1994. Fuzzy modus ponens deduction technique for construction scheduling. Journal of Construction Engineering and Management, 120(1): 162-179. [ Links ]
Zadeh, L A 1965. Fuzzy sets. Information and Control, 8(3): 338-353. [ Links ]
 Correspondence:
Correspondence:
Devlet Su Işleri Genel Müdürlüğü
(General Directorate of State Hydraulic Works)
Proje ve İnşaat Dairesi Başkanlığı
Devlet Mah
İnönü Bulvarı
No: 16, 06100 Çankaya
Ankara
TURKEY
T: +90 532 288 1322
E: onderÖkmen@hotmail.com / onderok@dsi.gov.tr
A Öztaş
University President
Ishik University
100 Meters Avenue
Erbil
IRAQ
T: +964 66 252 9841
+964 750 704 6969
E: ahmet.Özta@ishik.edu.iq / president@ishik.edu.iq

DRÖNDER ÖKMEN is an engineer at the General Directorate of State Hydraulic Works in Turkey. He obtained his BSc degree in Civil Engineering from the Middle East Technical University, and his MSc and PhD degrees in Construction Management (Civil Engineering) from the Gaziantep University in Turkey. He did post-doctoral research at the Epoka University in Albania. Currently he is busy with irrigation and drainage projects. His research interests include project management, risk analysis, scheduling, cost estimation, irrigation channels and pipe networks.

PROF DR AHMET ÖZTAŞ is the President of Ishik University in Erbil, Iraq. He obtained his BSc degrees in Mathematics from İnönü University and in Civil Engineering from İstanbul Technical University in Turkey, and his MSc and PhD degrees in Management from İstanbul University and in Civil Engineering from Manchester University, respectively. After lecturing at the Gaziantep University for many years, he worked as faculty dean and lecturer at the Epoka University in Albania. His research interests include construction project management, expert systems, risk analysis, scheduling and cost estimation.














