Servicios Personalizados
Articulo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares en Google
Similares en Google
Compartir
Journal of the South African Institution of Civil Engineering
versión On-line ISSN 2309-8775
versión impresa ISSN 1021-2019
J. S. Afr. Inst. Civ. Eng. vol.56 no.1 Midrand ene. 2014
TECHNICAL PAPER
Accounting for moment-rotation behaviour of connections in portal frames
H L Albertyn; T N Haas; P E Dunaiski
ABSTRACT
Portal frames are steel structures used to construct industrial buildings. Conventional analysis techniques used by practising engineering professionals assume that the eave, ridge and base connections are either infinitely rigid or perfectly pinned. This approach leads to less accurate analysis of the displacement behaviour of portal frames when subjected to external loading. Portal frames must therefore be analysed with rotational springs at all connections to yield accurate displacement behaviour. This investigation focused on determining the accuracy and economic feasibility of modelling portal frame connections with rotational springs. The rotational spring stiffnesses of all connections were required before the portal frame could be analysed in a second-order two-dimensional non-linear analysis. The rotational spring stiffnesses unique to each connection were determined from the moment-rotation behaviour obtained from a series of finite element analysis simulations of each connection. Thereafter these stiffnesses were used to determine the vertical and horizontal displacements of the portal frame. These displacements were compared with experimental test results. The reasons for the discrepancies between the numerical and experimental results were investigated through a sensitivity analysis. The findings suggest that it is not computationally feasible to analyse portal frames with rotational springs, even though the model's predicted results are more accurate than those of conventional analysis using rigid and pin connections.
INTRODUCTION
Portal frames are steel structures composed of columns and rafters with various types of connection between the structural elements. Figure 1 shows a two-dimensional view of a portal frame with a ridge connection without a haunch and eave connections with a haunch.

Column bases can be designed either as pinned (hinged) or moment-fixed (infinitely rigid) connections. Most column bases in portal frames are designed as pinned connections. This approach leads to a more economical design than portal frames with rigid column bases. Pinned bases are less expensive to manufacture and foundations are smaller since no moment resistance is required. Eave and ridge connections are usually designed as moment-fixed connections, i.e. a transfer of bending moment takes place between the connecting members. However, tension bolts within the rafter height are inadequate for developing sufficient moment capacity at the connections (Narayanan & Kalyanraman 2003). Therefore, haunched elements using tapered I-sections are introduced on the bottom flange of the rafters at the connection to increase the moment capacity of the element, instead of increasing the rafter size (Moore & Wald 2003) and (Narayanan & Kalyanraman 2003).
The current practice of design engineering professionals in South Africa is to model the portal frame as a two-dimensional structure during the analysis procedure. It is the norm for column base connections to be modelled as perfectly pinned, while the eave and ridge connections are modelled as infinitely rigid. These assumptions are flawed, resulting in incorrect displacement behaviour of the portal frame which leads to incorrect steel sections being used (Kruger et al 1995).
In addition, higher grades of steel have been rolled in South Africa over the past few decades. The yield strength of structural steel has increased from 300 MPa for 300WA to 355 MPa for S355J (SAISC Handbook 2008). This results in members having greater axial and bending resistances due to the increase in yield strength for the same member size. These stronger elements are now used in design, and result in lighter sections being used. The elastic design of steel structures for normal use is mainly governed by serviceability limit state requirements, which are controlled by the displacements of the structure (Narayanan & Kalyanraman 2003). Members are therefore initially sized in analysis according to the serviceability limit state criteria. Final design of the structure is then conducted according to the ultimate limit state requirements, which are controlled by the strength capacity of the elements. The displacement of the structure is controlled by the flexural stiffness of the member and not by the yield strength of the material. Thus, the use of higher grade steel has no effect on the allowable, informative, codified guidelines for such structures as recommended by SANS 10162-1:2005 (SANS 2005). The increase in the yield strength of structural steel does not result in a codified reduction in the displacement behaviour of the portal frame.
It has thus become necessary to determine the displacement behaviour of portal frames accurately by using proper modelling techniques and by taking the increased yield strength of structural steel into account. This paper focuses on determining the real displacement behaviour of a portal frame by modelling the real behaviour of connections in portal frames with appropriate material properties.
LITERATURE BACKGROUND
Moment-rotation connection behaviour
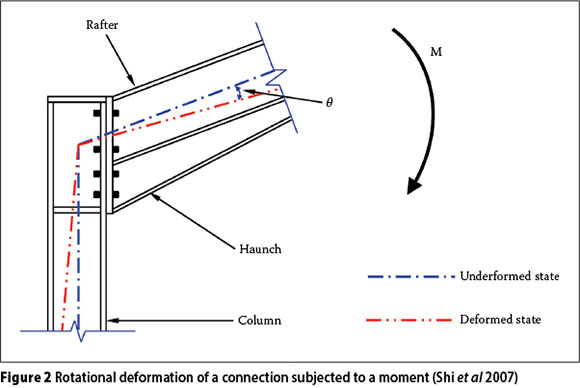
Infinitely rigid connections transfer axial forces, shear forces and bending moments between structural members. Under loading, the connections will undergo deformations as forces and bending moments are transferred between the members. Deformations caused by axial and shear forces are negligible in comparison with the rotational deformations that will occur and will therefore not be considered in this study (Kruger et al 1995). In-plane rotation of the connection is the most prominent type of deformation in portal frames, and is caused by the bending moment acting at the connection. It can thus be stated that the rotation of a connection is a function of the moment applied to it. The rotation (8) of a connection is defined as the change in angle of the structural components connected to it, that is, the change in angle between the centre lines of the column and the beam due to the loading of the portal frame resulting in a moment being generated at the connection. This is illustrated in Figure 2 (Shi et al 2007).
Conventional analyses and steel design procedures assume connections to be either infinitely rigid or perfectly pinned. Pinned connections do not transfer bending moments between structural elements and such a connection is modelled as a hinge, i.e. elements are free to rotate about each other. Fixed connections do transfer bending moments between structural elements and are assumed to be infinitely rigid, i.e. elements are not allowed to rotate about each other, although the joint with the connecting members can rotate. The real behaviour of steel connections, however, lies somewhere between these two extremes. It is illustrated in Figure 3.
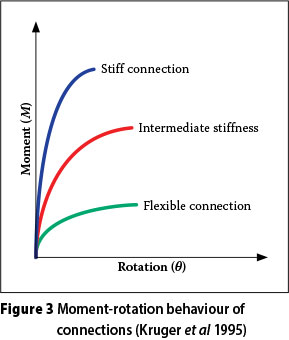
Referring to Figure 3, the vertical axis (M) represents a rigid connection, whereas the horizontal axis (8) represents a hinged connection. Experimental investigations (Kruger et al 1995) indicate that the real behaviour of a connection is as indicated by the curves shown in Figure 3. The moment-rotation curve of a connection provides an indication of the characteristics of a connection in terms of stiffness, strength and ductility. The stiffness of the connection is determined by the slope in the elastic region, whereas the peak of the curve indicates the ultimate moment capacity of the connection (Kruger et al 1995).
The effect of moment-rotation behaviour of connections on portal frames
Modelling of the real behaviour of the connections will reveal the distribution of forces, the bending moments and the displacements of the structure (Gerstle 1988).
Joint behaviour
In practice a rigid connection under loading exhibits rotation as a moment develops. Before the moment is transferred between the members, some rotational deformation occurs as a result of the elasticity and real behaviour of the connection, which delays the transfer of the ultimate moment (Lui & Chen 1987). This leads to greater displacements occurring in the structure before the ultimate capacity of the connection is achieved.
Column base behaviour
Modelling column base connections using pinned supports results in greater displacements than the actual (as-built) displacements. This is due to the rotational restraint provided by the column base plate/concrete interaction of the actual connection. The rotational restraint caused by the concrete results in a moment developing at the base of the column, which is contradictory to what is assumed in the design of the base connection (Jaspart et al 2008).
Bending moments will develop at the column base if the connection is assumed to be rigid, thus resulting in greater displacements being recorded in practice compared with the theoretical analysis due to the flexibility exhibited by the actual base.
Rotational springs in structural analysis
Past research found that different types of connection can be modelled as rotational springs (Simitses et al 1984; Chan et al 2005).
As stated previously, deformations caused by shear and axial forces are negligibly small compared with rotational deformations. A rotational spring permitting in-plane rotational deformations can be incorporated between various members of the portal frame to simulate the joint stiffness. The reader is referred to Chan and Chui (2000) for the mathematical formulation of rotational springs.
Rotational springs can be assigned to individual nodes in most structural analysis software. The spring stiffness is usually provided in terms of the relationship of the bending moment to the rotation of the connection. The stiffness of each connection is obtained by taking the derivative of the moment-rotation behaviour, i.e. the slope of the initial curve. The slope of the initial linear elastic region of a moment-rotation curve is referred to as the "initial stiffness" of the connection. Serviceability limit state design guidelines refer to "limiting the elastic deflections of the structure" (SANS 2011). The structure is therefore analysed with all components remaining within their elastic response regions. In this investigation the connection stiffnesses are modelled with their "initial" stiffness, which is sometimes referred to as their "elastic" stiffness.
RESEARCH METHODOLOGY
The investigation was conducted on a 5 m portal frame. It was divided into the following tasks:
1. An experimental investigation was conducted to determine the actual displacement behaviour of the portal frame with hinged supports (idealised conditions) and grouted supports (construction conditions) for three different loading conditions.
2. A two-dimensional numerical second-order analysis of the portal frame was conducted for the same conditions as the experimental configuration. In the analysis various methods of modelling the connections of the portal frame were considered. These included pinned, fixed and rotational spring connections. The rotational spring stiffnesses were determined from the moment-rotation curves which were obtained from a finite element analysis.
3. The experimental displacement results were compared with the numerical analysis displacement results for various types of connections to assess their accuracy.
EXPERIMENTAL SET-UP
The purpose of the experimental investigation was to determine the actual displacement behaviour of the portal frame when subjected to different loading and support conditions. The results were used as the benchmark to determine the accuracy of the displacement behaviour of the portal frame obtained from the numerical analysis.
Experimental configuration
Figure 4 shows a two-dimensional view of the experimental 5 m span portal frame with a column height of 1.5 m. All the sections are manufactured from IPE aa 100 sections. The portal frame was subjected to the load cases LC1, LC2 and LC3 shown in Figure 4, which were individually applied to the portal frame.
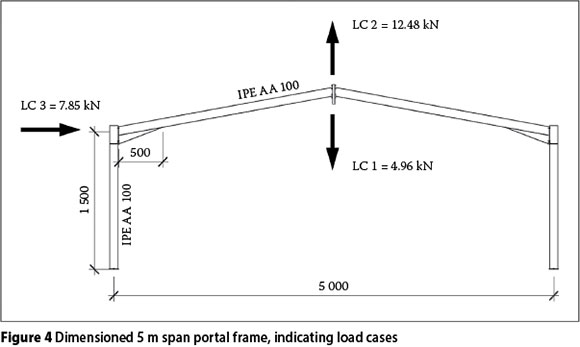
The individual load cases shown in Figure 4 are now described.
■ LC 1: a vertical downward load of 4.96 kN applied at the ridge which simulates the permanent load of the rafters, sheeting and purlins.
■ LC 2: a vertical upward load of 12.8 kN applied at the ridge which simulates the wind load.
■ LC 3: a horizontal load of 7.85 kN applied at the apex of the column perpendicularly to the portal frame which simulates the wind load.
Column bases are usually numerically analysed using pin supports as shown in Figure 5a, whereas the actual (grouted) support used in practice is shown in Figure 5b. From Figure 5b it is clear that the actual support does provide some degree of rotational restraint, which is due to the base plate/ concrete interaction. Both cases were experimentally investigated to determine their effect on the displacement behaviour of the portal frame.


NUMERICAL MODEL
A numerical model of the full-scale experimental test configuration was developed in Strand 7, a commercially available structural analysis software. The 1.5 m columns and the 2.54 m rafters were meshed with 0.1 m quadratic shear flexible (Timoshenko) beam elements. A series of different connections types were modelled, namely:
■ Rigid connection: These connections transfer moments between the members and are modelled as fixed. This type of connection was initially used to model the interaction at the ridge and eaves.
■ Pin connection: These connections only transfer shear and axial forces between the members and are modelled as hinged connections. This type of connection was initially used to model the column bases.
■ Rotational spring connection: These connections are neither fixed nor pinned and thus they allow the transfer of shear and axial forces, as well as a percentage of the moment, depending on the degree of fixity of the joint. This type of connection was subsequently used to accurately model the semi-fixed connections at the eaves, ridge and column bases.
A pinned support prevents vertical and horizontal displacements of the node, thus inducing vertical and horizontal forces. The same applies to the fixed support, except that the rotation of the node is restricted, thus inducing an additional bending moment. With a rotational spring, both vertical and horizontal displacements are restricted, while providing some resistance to rotation. Therefore the stiffness of the rotational spring must be determined before rotational springs can be implemented in the numerical analysis.
Rotational spring stiffness
Rotational spring stiffness is unique to each connection that is affected by the following attributes, among others: the size of the steel profiles, the size of the haunch, the number and size of the bolts, the position of the bolts, the torque of the bolts and the size of the connection end-plate. The rotational spring stiffness in the numerical simulation can also be affected by the element type, element mesh density, contact formulation, material properties and the type of analysis. The rotational spring stiffnesses were obtained by modelling a part of each connection with all members connected to the joint, using ABAQUS version 6.10-2, a general finite element (FE) analysis software. The FE simulations were conducted based on the guidelines presented by Prabha et al (2007).
These simulations resulted in a moment-rotation relationship for each connection. The rotational spring stiffness was obtained from the linear region of the moment-rotation curve within the elastic range. A previous experimental study conducted by Truter (1997) determined the moment-rotation behaviour of a haunched eave connection. The experimental rotational spring stiffness was used to determine the accuracy of the FE model. Figure 6 shows the experimental results obtained by Truter (1997) with a fourth-order regression line superimposed through the experimental results, as well as the FE simulation results.
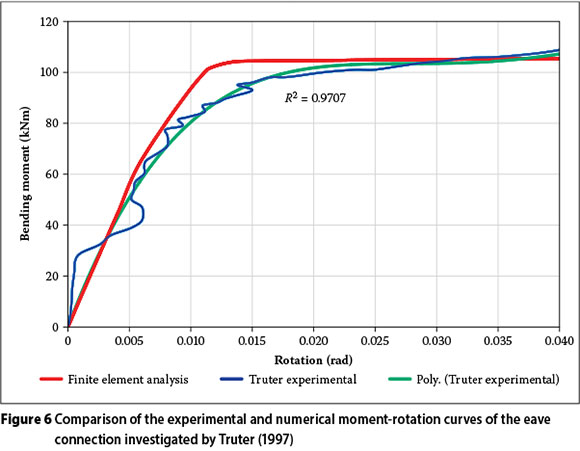
The regression line and the FE simulation response yield results that are virtually identical for the initial linear region. Only the linear region is important for this study, as serviceability limit state requirements refer to the elastic response of the structure. Based on the exceptionally good fit, it was accepted that the techniques used in the numerical model yield accurate results for this investigation and they were thus used to obtain all the other rotational spring stiffnesses.
The reader is referred to Albertyn (2011) for a detailed description of how the moment-rotation curves were obtained for each connection. Table 1 presents the rotational spring stiffnesses for each connection.
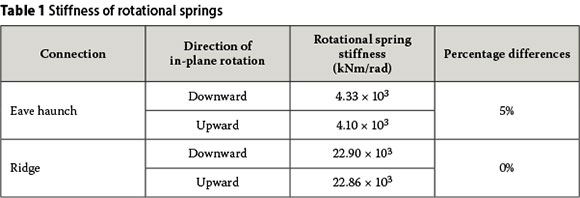
The differences between the clockwise and anti-clockwise rotations of the eave, as well as the ridge connections, fall within acceptable limits.
RESULTS AND DISCUSSION
The vertical and horizontal displacement responses of the 5 m span portal frame with hinged and grouted supports are presented for load cases 2 and 3. The responses of load case 1 are omitted as they yield displacement patterns similar to those of load case 2. Table 2 lists the types of connection investigated for both types of support, with a description of each displacement response used in Figures 7a through 7d and 8.
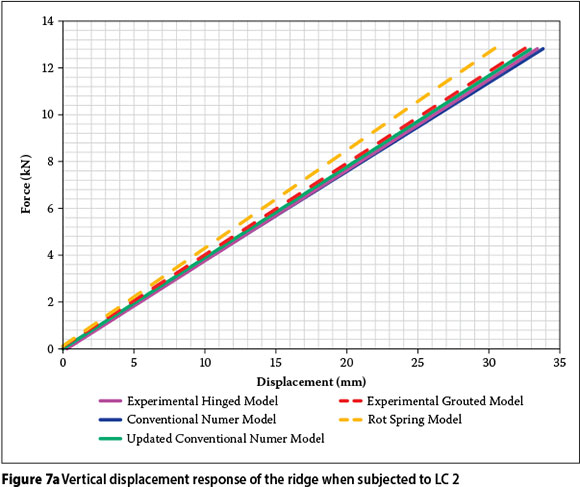
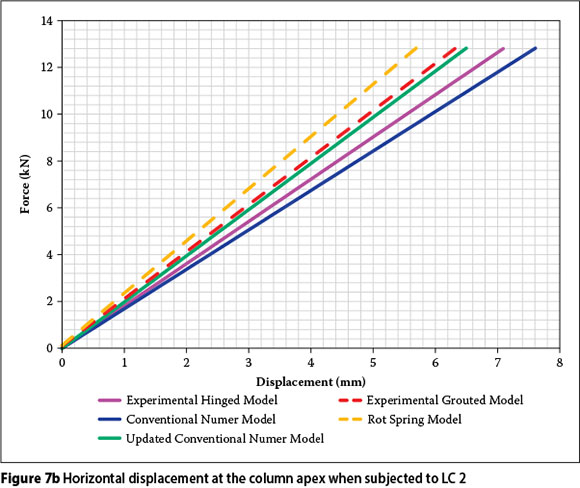
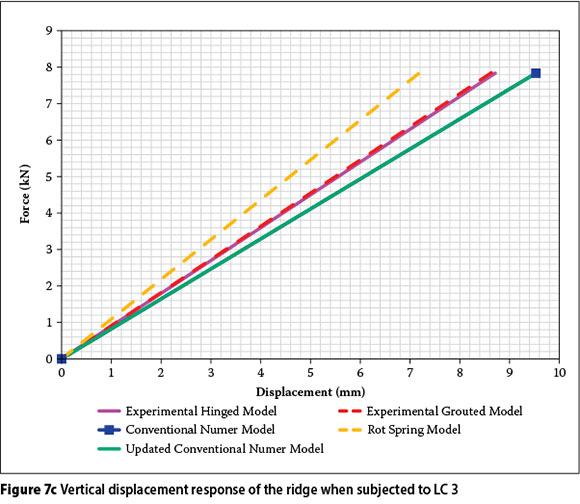
Results for load cases 2 and 3
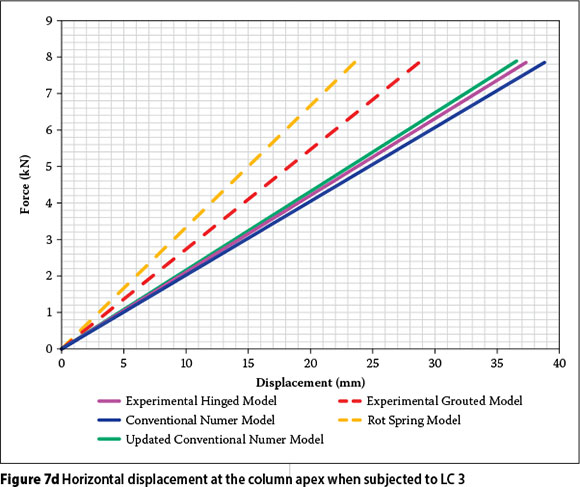
Figure 7a presents the vertical displacement of the ridge and Figure 7b presents the horizontal displacement at the column apex when subjected to LC 2. Figure 7c presents the vertical displacement of the ridge and Figure 7d presents the horizontal displacement at the column apex when subjected to LC 3.
For ease of reference, the models that refer to the pin-supported column bases are shown as solid lines. The corresponding models referring to the grouted supports are presented as dashed lines. Table 3 presents a summary of the significant results that were extracted from Figures 7a to 7d.
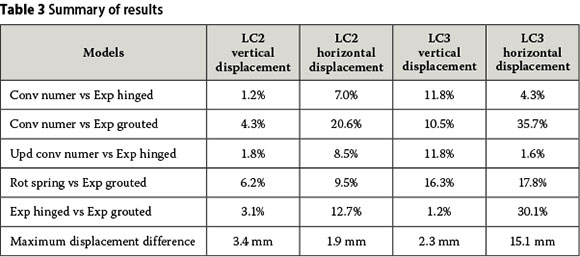
In Table 3 we notice that the maximum vertical displacement difference between the models is 3.4 mm, with a maximum percentage difference of 6.2% for LC 2. Larger percentage differences occur between the various models of the horizontal displacement for LC 2 and the vertical displacement of LC 3. However, the maximum displacement differences for these load cases are 1.9 mm and 2.3 mm, respectively. Due to the insignificant displacement differences in these models, it can be assumed that the numerical models yield sufficient accuracy. The differences obtained between the numerical and experimental models can be attributed to the accuracy with which the experimental measurements were obtained.
Large displacement and percentage differences occur in the horizontal displacement for LC 3. This is clearly evident between the displacement responses of the experimental hinged and experimental grouted models. There is a displacement difference of 8.7 mm or 30.1% between these experimental models. This implies that the grouted support interface has a significant effect on the horizontal displacement of the portal frame when subjected to a lateral force. A better correlation was expected between the displacement responses of the rotational spring and experimental grouted models since the numerical model incorporates rotational springs at all connections. This led to the conclusion that other influences contribute to the difference in displacement responses which were previously thought to be insignificant, and this led to a sensitivity analysis being conducted on the grouted interface.
SENSITIVITY ANALYSIS
The aim of the sensitivity analysis performed on the column base was to identify the possible cause(s) of the inaccurate horizontal displacement behaviour produced by the numerical model with rotational springs. Since only the column base connection was changed, the sensitivity analysis focused on the effect of this connection on the displacement behaviour of the portal frame. This led to an investigation of the effect of the preload on the holding-down bolts.
Effect of preload on holding-down bolts
Ordinary bolts in bolted steel connections are tightened according to the "turn of the nut" method (Kulak et al 2001). Various experimental studies indicate that the method referred to results in a bolt preload of approximately 70% of the bolt proof stress. A further investigation was conducted to determine the effect of this factor on the displacement response of the portal frame, since the bolt preload affects the rotation of the column base connection. This led to determination of the moment-rotation curves at bolt preloads of 0%, 5%, 35% and 70%. Table 4 shows the rotational spring stiffness of the grouted column base at these bolt preloads, which were obtained from the moment-rotation curves from the FE analysis.
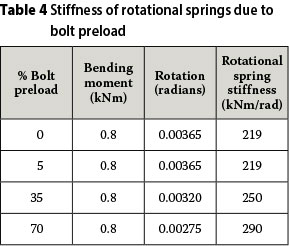
From Table 4 it can be concluded that bolt preload has a significant influence on the rotational spring stiffnesses. Rotational spring stiffness differences of 14% and 16% are obtained between bolt preloads of 0% and 35%, and 35% and 70%, respectively. This shows that the bolt preload could have an effect on the displacement behaviour of the portal frame.
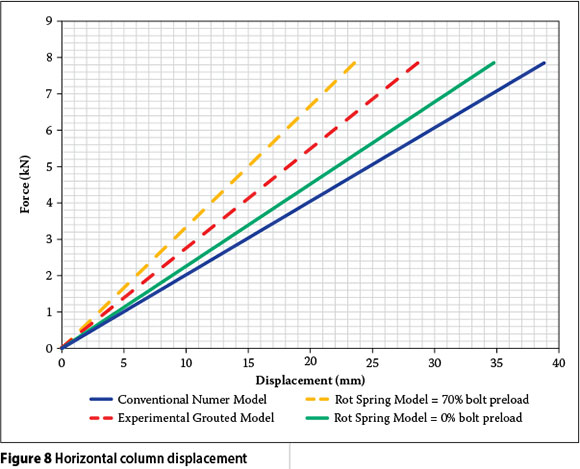
Figure 8 shows the numerical model's horizontal displacement responses for bolt preloads of 0% and 70%, with the experimental grouted model's displacement response superimposed. Figure 8 shows that the experimental grouted model produced a horizontal displacement of 28.6 mm when a horizontal load of 7.85 kN was applied to the apex of the column. The corresponding displacements at 0% and 70% bolt preload were 34.8 mm and 23.5 mm respectively. To obtain a similar horizontal displacement of 28.6 mm, the column base rotational spring stiffness in the rotational spring model was adjusted to 52 kNm/rad.
From a close examination of Figure 8 it can be seen that the experimental response lies midway between the 0% and 70% bolt preloads. This would suggest that the rotational spring stiffness of the experimental model is approximately the average of the rotational stiffnesses of the two numerical models' rotational stiffnesses, i.e. ± 250 kNm/rad. The actual column base rotational spring stiffness in the numerical model was obtained as 52 kNm/rad, which is approximately a quarter of the expected value. This implies that the column base of the experimental grouted model is less stiff than expected. It also suggests that some slip may have occurred between the holding-down bolts and the foundation, or that the holding-down bolts were not torqued to the required 70% bolt preload. After completion of the experimental tests, careful examination of the holding-down bolts revealed that an insignificant slip had occurred at the column base. For this reason the effect that in-plane rotation has on the horizontal displacement of the portal frame was determined. Table 5 presents the magnitude of the horizontal displacement of the portal frame as a function of the column base plate rotation.
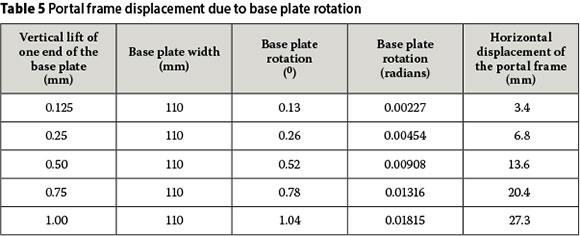
From Table 5 it can be observed that an insignificant base plate rotation of 0.260 or 0.00454 radians will result in a horizontal column apex displacement of 6.8 mm. Therefore, if the column base plate rotated insignificantly by 0.260, this would result in an additional 6.8 mm horizontal displacement of the portal frame compared with when no slip occurs. If no slip of the holding-down bolts occurred, an experimental displacement of 21.8 mm would be observed if we assume that the column base plate rotated by 0.260. A difference of 1.7 mm or 7.2% is found when this displacement is compared with the 70% bolt preload of the numerical model. Also, a difference of 0.6 mm or 1.9% is observed when the actual experimental displacement is compared with the average displacements of the 0% and 70% bolt preloads. This proves that the numerical model with rotational springs yields accurate results.
The conventional numerical approach overestimates the displacement response, which lies beyond the 0% bolt preload displacement response. The conventional approach overestimates the displacement response by 11.5% and 65.1% compared with the displacement responses of the 0% and 70% bolt preloads.
CONCLUSION
This study confirms that the numerical model with rotational springs can be used to model a portal frame, and that it does yield more accurate displacement results than the conventional analysis. The important question that must now be asked is whether the numerical model with rotational springs (updated numerical model) is an economically viable option to use in a consulting engineering practice in South Africa. This question is best answered in terms of the expertise of the designer, available software, time required for the analysis and the potential cost saving.
In terms of time, there is an insignificant computational time difference between the conventional model and the updated numerical model when a two-dimensional second-order non-linear analysis of the portal frame is performed. Accurate rotational spring stiffnesses of each connection are required before the two-dimensional analysis of the updated numerical model can be performed. This was achieved by conducting a finite element analysis of each connection, which required 12 hours of computational time per connection using a four-quad core computer with 32 GB RAM.
Also, considerable expertise in finite element analysis is required to develop a model of all the connections, taking into account the level of complexity to develop accurate numerical models. This could be achieved by an experienced graduate professional with the necessary theoretical and practical knowledge of finite element analysis. These individuals, however, attract a higher cost to company and greater consultancy fees to conduct an analysis.
The software required to perform advanced finite element analysis are expensive and usually not readily available in local consulting engineering design offices. Conventional and affordable structural engineering design software used in most design offices cannot perform the required advanced simulations to obtain moment rotation curves of connections. This leaves the design engineer unable to perform sophisticated analysis.
Based on the aforementioned reasons, and since most of the portal frame structures require a limited number of portal frames, the cost saving achieved using the updated numerical model would not make this type of analysis economically viable in a design office.
Thus, based on the findings of this research, it is recommended that portal frames in practice be analysed using the conventional approach, as it is reliable and safe. Since more accurate displacement results were obtained modelling connections as rotational springs, the recommendation is that this approach be followed for structural engineering research applications.
The scope of this study did not include focusing on the buckling behaviour of portal frames. It is therefore recommended that further research on portal frames be conducted at ultimate limit state behaviour accounting for the real behaviour of connections. Further research could also be conducted in the dynamic behaviour of portal frames with connections modelled as rotational springs
REFERENCES
Albertyn, H L 2011. The effect of moment-rotation joint behaviour on the displacements of portal frames. MSc dissertation, South Africa: Stellenbosch University. [ Links ]
Chan, S L & Chui, P P T 2000. Nonlinear static and cyclic analysis of steel frames with semi-rigid connections. Amsterdam: Elsevier Science. [ Links ]
Chan, S L, Huang, H Y & Fang, L X 2005. Advanced analysis of imperfect portal frames with semi-rigid base connections. Journal of Engineering Mechanics, 131(6):633-640. [ Links ]
Gerstle, K H 1988. Effect of connections on frames. Journal of Constructional Steel Research, 10:241-267. [ Links ]
Jaspart, J P, Wald, F, Weynand, K & Gresnigt, N 2008. Steel column base classification. HERON, 53(1/2):69-86. [ Links ]
Kruger, T S, Van Rensburg, B W J & Du Plessis, G M 1995. Non-linear analysis of structural steel frames. Journal of Constructional Steel Research, 34(2-3):285-206. [ Links ]
Kulak, G L, Fisher, J W, Struik, J H A & Geoffrey L 2001. Guide to design criteria for bolted and riveted joints (revised edition). New York: Wiley. [ Links ]
Lui, E M & Chen, W F 1987. Steel frame analysis with flexible joints. Journal of Constructional Steel Research, 8:161-202. [ Links ]
Moore, D B & Wald, F 2003. Design of structural connections to Eurocode 3 - Frequently asked questions. Watford, UK: Building Research Establishment Ltd. [ Links ]
Narayanan, R & Kalyanraman, V 2003. The INSDAG guide for the structural use of steelwork in buildings. Calcutta, India: Institute for Steel Development & Growth (INSDAG). [ Links ]
Prabha, P, Seetharaman, S, Arul Jayachandran, S & Marimuthu, V 2007. Proceedings, Mimicking Expensive Experiments using ABAQUS, Third Abaqus User's India Meet, Bangalore, India, 24 October. [ Links ]
SAISC (Southern African Institute of Steel Construction) 2008. Southern African steel construction handbook. Johannesburg: SAISC [ Links ]
SANS 2005. SANS 10162-1:2005: The structural use of steel. Part 1: Limit-state design of hot-rolled steelwork. Pretoria: South African Bureau of Standards. [ Links ]
SANS 2011. SANS 10160:2011: Basis of structural design and actions for buildings and industrial structures. Pretoria: South African Bureau of Standards. [ Links ]
Shi, G J, Shi, G & Wang, Y 2007. Experimental and theoretical analysis of the moment-rotation behaviour of stiffened extended endplate connections. Journal of Constructional Steel Research, 63(9):1279-1293. [ Links ]
Simitses, G J, Swisshelm, J D & Vlahinos, A S 1984. Flexibly-jointed unbraced portal frames. Journal of Constructional Steel Research, 4(1):27-44. [ Links ]
Truter, A N 1997. An experimental and theoretical investigation into the non-linear moment-rotation response of bolted endplate connections in single-storey haunched steel portal frames. MSc dissertation, South Africa: Stellenbosch University. [ Links ]
 Contact details:
Contact details:
Heindrich Albertyn
51 4th Avenue
Newton Park
Port Elizabeth
6055
South Africa
T: +27 41 364 0574
F: +27 41 364 0578
E: hlalbertyn@gmail.com
 Contact details:
Contact details:
Trevor Haas
Stellenbosch University
Department of Civil Engineering
Private Bag X1
7602
Matieland
South Africa
T: +27 21 808 4438
F: +27 21 808 4947
E: trevor@sun.ac.za

HEINDRICH ALBERTYN completed his undergraduate and MSc (Eng) degrees at Stellenbosch University in 2011. His research focused on the feasibility of optimising steel structures by modelling the real behaviour of connections in portal frame analysis. He is currently employed by Sigma Consulting Civil & Structural Engineers In Port Elizabeth.

DR TREVOR HAAS Pr Tech Eng is a Senior Lecturer in Structural Engineering at Stellenbosch University. He obtained a National Diploma and National Higher Diploma in Civil Engineering from the Peninsula Technikon in 1991 and 1992, an M.S. in Civil Engineering from Southern Illinois University at Carbondale, USA, in 1999, and a PhD In Civil Engineering from Stellenbosch University in 2007. His research interests include earthquake engineering, numerical modelling, structural dynamics and engineering education. He is developing an earthquake engineering centre at Stellenbosch University. He also serves on the Engineering Council of South Africa's team for the accreditation of universities of technology.

PROF PETER DUNAISKI Pr Eng, who sadly passed away in September 2011, was Professor in Structural Engineering at the Stellenbosch University. He obtained the HBEng (1974), the MEng (1984) and the PhD (1991) degrees from the same university. His research interests were experimental mechanics and steel construction, with a focus on design aspects of commercial and industrial structures. At the time of the preparation of this paper, he was also involved in code development for the South African structural engineering practice.














