Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
Journal of the South African Institution of Civil Engineering
On-line version ISSN 2309-8775
Print version ISSN 1021-2019
J. S. Afr. Inst. Civ. Eng. vol.56 n.1 Midrand Jan. 2014
TECHNICAL PAPER
Soil-structure-interaction provisions: A potential tool to consider for economical seismic design of buildings?
A Worku
ABSTRACT
Contemporary seismic design codes have become more stringent with respect to the requirements for design forces and deformations in building design. This paper demonstrates that it could be worthwhile to consider the introduction of soil-structure-interaction provisions into local design codes. This is partly to be able to offset the costs incurred by the high magnitude of base shear demand in most buildings attributed to site amplifications due to soft soil sites, as per the requirements of current codes, including the recent South African seismic design code. This beneficial effect of site soils is as a result of lengthening of the fundamental period and of the increased effective damping of the overall system due to soil-structure interaction, which in most cases lead to reduced design spectral values. The paper shows that, if pertinent provisions in some international codes are properly adapted, a substantial reduction in the base shear force can be achieved, in many cases resulting in structural-work cost saving. With this, the paper attempts to address the legitimate concern of design engineers regarding the potential escalation of construction costs associated with the introduction of stringent requirements of contemporary seismic design spectra, especially for soft soil sites.
Keywords: soil-structure-interaction, fixed-base structure, flexible-base structure, period lengthening, effective damping, base shear, site amplification
INTRODUCTION
The behaviour of site soils is one of the three major factors that can significantly influence the intensity of ground shaking due to an earthquake at any given site, the other two factors being the earthquake source mechanism and the geology of the seismicwave path. The influence of site geotechnical conditions on ground-shaking intensity is studied following one of two approaches. The first is an empirical approach based on comparison of ensembles of recorded ground motions at nearby rock and soil sites of known geotechnical characteristics whenever these are available. The results of such studies are presented in the form of smoothened, statistically averaged site-dependent design spectra. These spectra are factored forms of the basic design spectrum for the corresponding rock site. The amplification factors are in general dependent on the nature of the site and the seismicity of the region. In the absence or scarcity of recorded ground motions for a given seismic region, it is common practice to adapt design spectra from regions of similar geologic and tectonic setup.
The second approach is appropriate for site-specific studies which involve modelling of the site soil as any other dynamic system subjected to the ground motion at the rock level. The soil can be modelled as a continuous or discrete mass system. The end results could be ground motion time histories, peak ground motions or response spectra at the ground surface.
This effect of site soils to amplify the rock-level ground motion is generally detrimental to the integrity of structures built on them.
Another important influence of site soils on structures is related to soil-structure interaction (SSI), which is rendered unfairly less attention, especially in routine building design. When the ground motion, amplified by the site soil in the manner described above, strikes the foundation, two forms of SSI take place. The first is attributed to the difference in rigidity between the foundation unit and the soil, which causes, among others, reflection and refraction of the seismic waves back into the soil mass. As a consequence, the motion of the foundation and the free ground become different, with the foundation motion usually being smaller. This aspect of SSI is known as kinematic SSI. Ideally, the foundation motion should be used as input motion in the analysis of the structure. However, studies have shown that the difference between the two motions can be regarded as negligible. For this reason, the free-ground motion is used as the input ground motion in practice (Fenves & Serino 1992; Stewart et al 1999; Stewart et al 2003).
The second, and more important, form of SSI is manifested when the superstructure starts to vibrate as a result of inertial forces triggered by the excitation at the foundation level. The inertial forces distributed over the height of the structure cause a resultant base shear and an overturning moment at the foundation, which in turn cause deformation of the soil. This deformation initiates new waves propagating into the soil mass. These waves carry away part of the energy imparted on the structure by the incoming earthquake waves and act as a means of energy dissipation in addition to the material/hysteretic damping inherent in the system. This form of SSI is known as inertial SSI. Its effect in most structures is to increase total displacement due to the additional soil deformation, and to decrease the base shear demand due to the associated reduced structural inertia forces as a result of the additional energy dissipation into the soil (Fenves & Serino 1992; Worku 1996; Stewart et al 1999; Stewart et al 2003; Tileylioglu et al 2011).
In the sense of the reduced base shear, the consideration of SSI effect is beneficial for most building structures. Unfortunately this important effect is mostly ignored by engineers, with the notion that the design is on the safe side without the additional computational effort needed to account for SSI effects (Stewart et al 1999; Stewart et al 2003). This tendency lacks scientific rationality and is happening despite the fact that provisions for this phenomenon have been made available in some design codes since the 1980s. The original versions of these provisions have meanwhile been updated through calibrations with actual records from relatively recent strong earthquakes, including the 1989 Loma-Prieta and the 1994 Northridge earthquakes (Fenves & Serino 1992; Stewart et al 2003; BSSC 2004; BSSC 2010). Results of such calibration works and recent experimental verifications are encouraging the use of the recent versions of code-based SSI provisions (Stewart et al 1999; Stewart et al 2003; Tileylioglu 2011). However, it is also worth pointing out that, in certain seismic and soil environments, an increase in the fundamental natural period of a moderately flexible structure due to SSI may have detrimental effects on the imposed seismic demand (Mylonakis & Gazetas 2000; Ziotopoulou & Gazetas 2010). In both cases it is becoming more evident that neglecting seismic SSI is not sustainable.
The recently revised South African seismic code (SANS 10160-4) adapted the site-dependent design spectra of EC8 (2004) with some modifications. These spectra are in general more demanding than those of the previous versions (SABS 0160 1989; EC8 1994). Some South African engineers have expressed concern during the preparation period leading to the issue of the recent design code regarding the potential escalation of material and construction costs associated with such stringent requirements (Wium 2010).
With due account for this concern, this paper attempts to demonstrate that a good potential exists for some of the costs associated with site amplification to be partially offset by the beneficial effects of inertial SSI on many structures. This happens if engineers are allowed to exercise some degree of freedom to employ SSI provisions available in some international codes until these make their way to the South African seismic code in due course.
INERTIAL SOIL-STRUCTURE INTERACTION AND IMPEDANCE FUNCTIONS
In order to understand the influence of inertial SSI on the response of building structures subjected to seismic ground motions, it is helpful to briefly introduce the basic principles and concepts of dynamics of foundations supported by flexible media like soils. For this purpose, we consider the vibration of the rigid circular foundation of radius .R0 resting on the surface of the soil idealised as a homogenous elastic half space shown in Figure 1 (a) and excited by the vertical harmonic load. Let the half space have an elastic modulus of E and a mass density of p. For purposes of mathematical expediency and better insight, let us further represent the half space by the rudimentary model of the truncated solid cone of cross-sectional area of A0 at the ground level which is the same as the contact area of the foundation. The cone defines the angle α with the horizontal and the height h0 up to its apex above the ground (Worku 1996; Wolf & Deeks 2004).
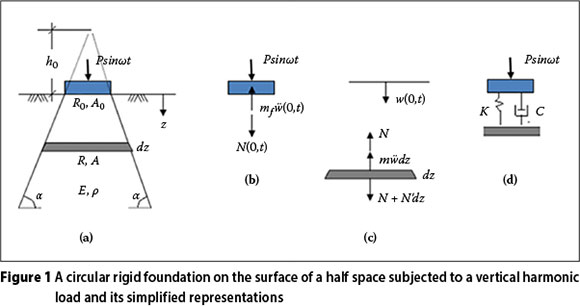
After formulating the equation of motion of the conical soil beam based on the equilibrium of the differential soil element shown in Figure 1(c), it can be shown, without resorting to the details, that the differential equation for the capping rigid circular foundation of Figure 1(b) becomes (Worku 1996):
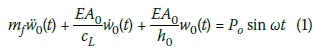
where mf is the mass of the foundation, Cl = √E/ρ is the velocity of the longitudinal elastic wave travelling away from the foundation through the conical soil column, and w0 is the vertical displacement of the foundation.
This equation is similar to the conventional equation of motion of the replacement single-degree-of-freedom (SDOF) oscillator shown in Figure 1(d) and given by:
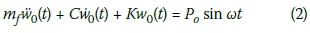
where K and C are the spring and dashpot coefficients of the mechanical model respectively. Comparison of the two equations results in the following expressions for the parameters of the SDOF model of Figure 1(d) in terms of the geometry of the foundation and the elastic properties of the soil:

This result obtained on the basis of a rudimentary idealisation of the soil-foundation system as a truncated conical column capped by the rigid foundation (Figure 1(a)) demonstrates the following fundamental facts:
■ The semi-infinite continuum can be replaced by a simple SDOF mechanical massless model supported by a spring and a dashpot of coefficients, K and C, respectively, arranged in parallel, and these parameters can be expressed in terms of the foundation geometry, the elastic parameters of the continuum and a pertinent wave velocity.
■ Unlike in conventional dynamic models of structures, the damping term - the second term in Equation (1) - is not an assumed addition of viscous damping; it is a mathematical outcome showing that the damping is an intrinsic behaviour of the system. This term represents an additional equilibrant force due to energy dissipation through waves propagating away from the foundation as represented by the wave velocity in the coefficient. It is in addition to the material damping of the continuum not considered in this discussion.
The truncated-cone approach was first devised and the above important outcomes observed about eight decades ago (Reissner 1936; Ehlers 1942). Interestingly, this seemingly primitive approach is extensively used in the recent book authored by Wolf and Deeks (2004) in a systematic manner. The new simplified approach has the potential of enabling engineers to easily solve a range of practical problems in structural dynamics involving SSI without reverting to complex finite-element techniques to model the site soil.
In a more rigorous treatment of the soil-foundation system, the spring and dashpot coefficients of Equation (3) are dependent on the frequency of excitation among many other factors (Luco & Westman 1971; Veletsos & Wei 1971). These coefficients, commonly termed as impedance functions, are now available in the literature for a wide range of conditions after several decades of intensive research works. They have meanwhile been well compiled, and have already made their ways into design codes starting from around 1980 (Gazetas 1983, 1991; Pais & Kausel 1988; Worku 1996; BSSC 2004; BSSC 2010).
Reverting to the mechanical model of Figure 1(d), its equation of motion given by Equation (2) for zero mass takes, for any degree of freedom considered, the form:
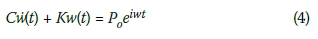
The subscript of the deformation is dropped for brevity reasons, and the harmonic load is represented in its complex form for purposes of generality. The trial solution to this differential equation should also be complex. After substituting a complex function for w(t) and solving for the complex-valued impedance function, which by definition is the ratio of the load to the response, yields:
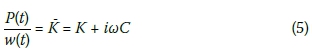
On the other hand, the complex-valued impedance functions obtained from rigorous mathematical treatments of the semi-infinite continuum are often presented in the literature in the following form:
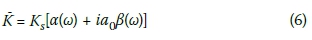
where Ks is the static spring stiffness, a0 is a dimensionless frequency parameter given by a0 = wRlVs , Vs is the shear wave velocity of the continuum, α(w) and β(w) are frequency-dependent dynamic impedance coefficients (also known as dynamic modifiers). By equating Equations (5) and (6) one obtains the following important relationships for the real-valued, frequency-dependent parameters of the massless spring-dashpot model in Figure 1(d):
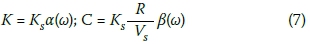
As indicated above, the impedance coefficients, α(w) and β(w), are available for various foundation conditions, soil conditions and vibration modes.
A circular foundation on the surface of the homogenous viscoelastic half space is the most basic and most important case. Studies have shown that use of an equivalent circular foundation gives satisfactory results for foundations of other shapes, provided that the aspect ratio of the encompassing rectangle of the foundation plan does not exceed 4:1. For other cases, suggested modifications are available (Gazetas 1991). The subsequent discussion will thus focus on circular foundations. The same discussion can easily be expanded to other shapes and soil-foundation conditions.
The static spring coefficients in Equation (7) for a circular foundation are given by the expressions in Equation (8) for the horizontal translation and rocking degrees of freedom respectively that are important in seismic design (Gazetas 1991; Worku 1996):
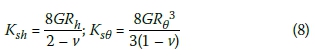
Note that the radii in the two cases are different for non-circular foundations and are determined by equating the area A and moment of inertia Iθ for rocking motion of the actual foundation to those of the equivalent circular foundation. Thus,
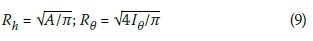
The corresponding dynamic modifiers for a surface circular foundation were originally provided by Vlelestos and his co-workers (Veletsos & Wei 1971; Veletsos & Verbic 1973) and Luco and Westmann (1971), independently of one another, as functions of the frequence parameter, a0. For other cases, appropriate impedance functions are available and should be used in order to determine the dynamic spring and dashpot coefficients as per Equation (7). Important factors to be further accounted for when using impedance functions include foundation embedment depth, foundation depth, foundation flexibility, soil layering and increase in stiffness of soil with depth. Relevant literature should be consulted for this purpose (Gazetas 1991; Pais & Kausel 1988; Worku 1996; Stewart et al 1999).
FLEXIBLE-BASE MODEL PARAMETERS
In the most general three-dimensional case, a single mass oscillator fixed at its base acquires six additional degrees of freedom (DOF) when the base is released. The additional DOFs consist of a translational DOF in each direction of the Cartesian coordinate axes and a rotational DOF around each of them.
For an excitation due to upward propagating seismic shear waves, inclusion of the horizontal and rocking DOFs alone is sufficient in planar analysis. This condition is depicted in Figure 2 for a superstructure represented by an SDOF model, in which the complex-valued springs are lumped at the base in each of the horizontal and rotational DOFs. Accordingly, the system now has three degrees of freedom. This representation is equivalent to a real-valued spring and dashpot arranged in parallel for each DOF. The height h refers to the height of the roof in the case of a single-storey building and to the centroid of the inertial forces associated with the fundamental mode in the case of a multi-storey building which is commonly taken as 0.7h assuming a linear fundamental mode of vibration (Stewart et al 1999; BSSC 2004).
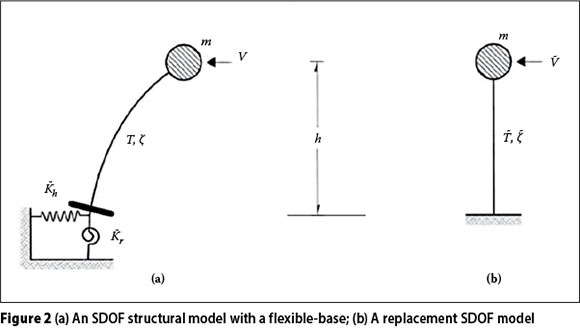
In time-history analysis (THA), the frequency dependence of the foundation parameters and the nature of the system damping renders flexible-base models more difficult to analyse than fixed-base models. Such systems are termed as non-classically damped systems and can be solved using specially tailored closed-form or iterative analysis methods (Worku 1996, 2005, 2012).
In contrast to THA, in response-spectrum and pseudo-static analyses, SSI is accounted for by dealing with an equivalent SDOF system as shown in Figure 2(b) with modified parameters to account for the foundation flexibility. This was proposed by Veletsos and Meek (1974), who drew a parallel between the two models and found that the maximum displacement of the mass in Figure 2(a) can be accurately predicted using the replacement SDOF system in Figure 2(b) with a modified natural period of T and a modified damping ratio of ζ. These modified parameters are called flexible-base parameters and have the convenience of enabling the engineer to use the conventional code-specified seismic design spectra as usual.
Veletsos and Meek (1974) found out that the flexible-base period may be determined from:
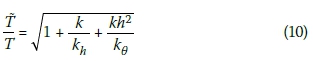
The fixed-base period is given by the well-known relationship of T = 2π/√k/m, where k is the stiffness of the structure and m is its mass. According to Equation (10), the flexible-base period T is always larger than the fixed-base period and increases with decreasing stiffness of the foundation. Measured period lengthening of more than 50% are reported by researchers (Stewart et al 2003). Note that the period ratio is dependent on frequency (or period) because of the frequency-dependent foundation stiffnesses. It is, however, sufficient to establish the stiffnesses for the fundamental frequency/period of the fixed-base system (Stewart et al 2003; BSSC 2004).
The effective flexible-base damping ζ is contributed from both the structural viscous damping ζ and the foundation damping ζ0 consisting generally of radiation and material damping components. Veletsos & Nair (1975) established the following relationship for the system damping based on equivalence of maximum deformations of the two oscillators in Figure 2:

The plots of Equation (11) against the period ratio are given in Figure 3 for the commonly assumed fixed-base structural damping (FBSD) of 5% and a number of foundation damping (FD) values ranging from 3% to 20%. Such ranges of foundation damping ratios have been reported in the past (Stewart et al 2003).
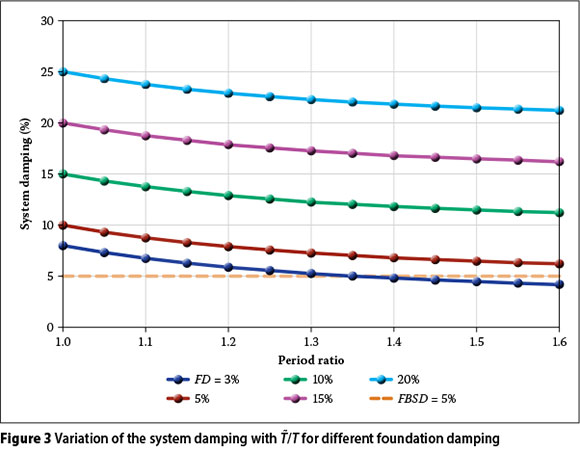
The plots show that the overall effective damping of the flexible-base system is larger than the fixed-base damping (FBSD = 5%) with the exception of the rare case of the foundation damping itself being very low (smaller than 5%), and the period ratio being large. For any given foundation damping, the system damping gradually decreases with increasing period ratio due to the decreasing contribution of the structural damping with increasing period ratio. It should, however, be noted that the effective damping may not generally be taken less than the structural damping of 5% (BSSC 2004, BSSC 2010).
INFLUENCE OF INERTIAL SSI ON DESIGN SPECTRA
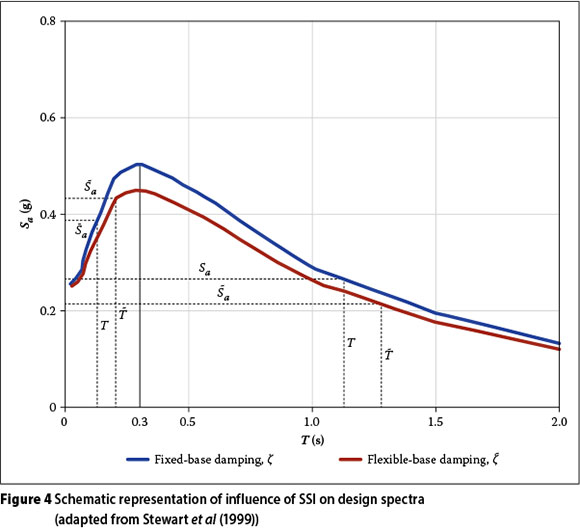
The influence of the lengthened period and the modified damping on a smoothened response spectrum is shown schematically in Figure 4. The figure shows that, for a fixed-base period of up to around 0.3 seconds, SSI has the effect of increasing the spectral response of the structure. However, for the most common case of building structures having a fundamental natural period larger than about 0.3 seconds, SSI has the effect of reducing the spectral response and thereby reducing the design base shear force (compare ordinates of the two curves corresponding to the pairs of T and T on either sides of T ≈ 0.3 s).
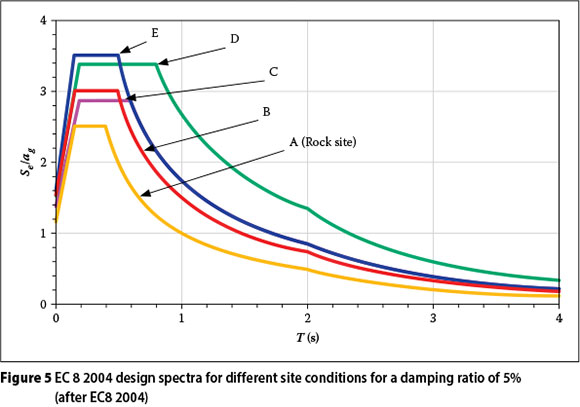
A more direct insight into the influence of SSI on code-specified design spectra can be obtained by considering the EC8 (2004) Type 1 design spectra specified for five different site soil classes shown in Figure 5 for a structural damping ratio of 5%. The various site soil classes are defined in the code (EC8 2004). The amplification potential of the site soils is evident from the spectral curves. These spectra are incorporated into the provisions of the recently revised South African seismic code, with the exception of the spectrum for Site Class E (SANS 10160-4).
Let us consider the two soft site soil classes of C and D characterised by an average shear-wave velocity of 180 to 360 m/s and less than 180 mls, respectively, over the upper 30 m depth in accordance with EC 8 (2004). The corresponding design spectra for the two site classes are presented separately in Figures 6(a) and 6(b) together with the spectrum for Site Class A - rock site.
Based on the definition of Site Class C, the maximum attainable foundation damping ratio including both material/hysteretic and geometric damping is estimated at 10% for the purpose of this study, even though larger damping ratios are reported for such a class of soil in the literature (Stewart et al 2003). The corresponding period lengthening of the SDOF system due to SSI is also conservatively estimated at 10% so that T/T reaches up to 1.10. With the effective system damping calculated from Equation (11) or read from Figure 3 as 13.76%, the corresponding design spectral curve is determined as per the provisions of EC 8 (2004) by scaling down the site-dependent spectral curve using a scaling factor to account for the modified damping. The factor is given by:
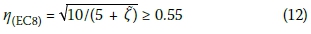
In this equation ζ is the effective system damping in percentile that accounts for both structural and foundation damping. The plot is given in Figure 6(a) by the dashed curve, which indicates that a significant reduction in the design base shear of up to 30% could be achieved for structures with a fundamental period larger than 0.2 seconds. Many classes of buildings belong to this period range. Most actual cases are expected to plot on or above the dashed curve.
Similarly, a little larger maximum limit for the foundation damping of 15% is assumed for the much softer Site Class D with corresponding period lengthening of up to 15%. The effective damping calculated as 18.3% resulted in the dashed curve shown in Figure 6(b). A larger reduction in the design base shear than in Site Class C seems attainable in this case. It is, however, important to point out that current code provisions for SSI cap the maximum permissible base-shear reduction to 30% (BSSC 2004).
The modified spectral curves for the two site classes are compared in Figure 7 against the corresponding site-dependent design spectra specified by the older version of EC8 (1994). In Figure 7(a), the design spectra for Site classes A and B of EC8-1994 are compared with the EC8-2004 design spectrum for Site Class C modified for SSI. Similarly, the spectra for site classes A and C of EC8 (1994) are compared in Figure 7(b) against the EC8 (2004) design spectrum for Site Class D modified for SSI.
It is interesting to note from the plots that the design spectra, and thus the design base shear, as per EC8 (2004) modified for inertial SSI effects can even be significantly lower than the values specified by the older EC8-1994 spectra for the corresponding soil classes over a significant range of fundamental period. The reduction is particularly significant in long-period structures.
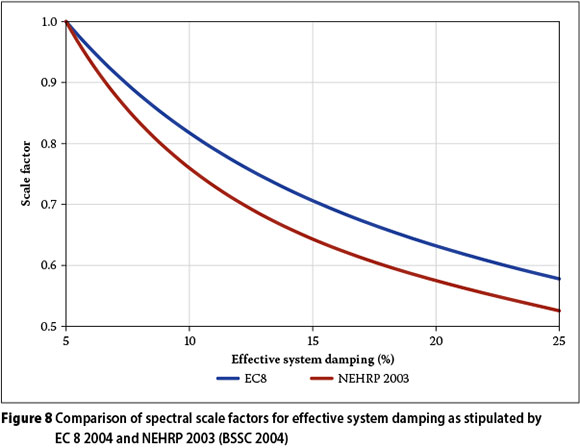
The factor in the National Earthquake Hazard Reduction Program (NEHRP) document - a resource document for most seismic codes in the USA - for scaling down the site-dependent spectral curves corresponding to Equation (12) is given by (BSSC 2004):

The plots of Equations (12) and (13) are compared in Figure 8, which shows that the reduction proposed by the NEHRP document (BSSC 2004) is slightly larger than that of EC 8 (2004).
Finally, to be emphasised is the fact that the foundation damping and the period lengthening are key factors that affect the amount of spectral reduction due to SSI. It is, however, important to note that the reductions demonstrated in the above plots are based on assumed ranges of foundation damping and period lengthening for the purpose of this study, even though these are based on reasonable engineering judgment and reported cases (Stewart et al 2003). Hence, the actual gains must be established by the design engineer on a case by case basis, and no generalisation is warranted on the basis of the presented material alone.
Nevertheless, the plots in Figures 6 to 8 demonstrate that the magnitude of spectral amplification by soil sites could be substantially offset by inertial SSI effects. If properly employed, SSI provisions could have the potential of leading to a significant financial saving in many cases, as is evident from the plots.
However, to be remembered is also the other important effect of inertial SSI that increases the lateral displacement of the building. This effect must be taken into account when considering ductility issues, secondary effects like P-∆ and possibilities of pounding with contiguous structures - considerations that are important in the design of tall buildings regardless of whether reduction in base-shear is achievable or not.
EXAMPLES
In order to illustrate the use of code provisions of SSI in seismic design of buildings and of the potential benefits, the site-soil classification and SSI procedures proposed in NEHRP are employed (BSSC 2004, 2010). EC8 (2004) does not have provisions for SSI.
Four different idealised reinforced-concrete buildings of height ranging from 5 to 25 storeys founded on the site soils types of D and E, according to the NEHRP classification system, are considered. Thus, the influence of SSI on eight different cases of dynamic system is studied simultaneously. The buildings are assumed to be located at sites characterised by a design peak ground acceleration (PGA) of 0.1 g, where g is the gravitational acceleration. Most sites in South Africa, where seismic design is required, are assigned a PGA of 0.1 g. According to the current response-spectra based on NEHRP seismic hazard mapping (BSSC 2004, 2010), a site of such seismicity can be represented by a short-period normalised spectrum Ss of about 0.25 and an intermediate-period (1 second) spectrum S1 of 0.1. Note that the US codes are no longer using PGA for seismic hazard characterisation.
A small-strain shear-wave velocity of 220 m/sec and 150 m/sec, a Poisson's ratios of 0.4 and 0.45 are assigned to the two site classes D and E respectively, whereas an effective soil unit weight of 18 kN/m3 is assumed for both. The characteristics of the site soils are summarised in Table 1, in which the small-strain shear modulus is also computed from the direct relationship with the small-strain shear-wave velocity.
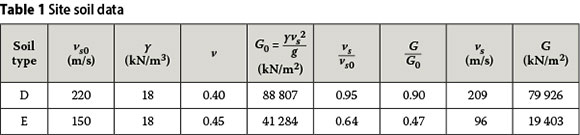
The actual shear-wave velocity and shear modulus corresponding to the large strains sustained during strong earthquakes at any given site are smaller and depend on the actual strain level, which in turn depends on the intensity of the anticipated earthquake shaking as represented by the seismicity of the site. The pertinent NEHRP provisions specify the ratios of va/vs0 and G/G0 as per the seismicity of sites. These recommended ratios are given in columns 6 and 7 of Table 1, and the reduced values of the two dynamic properties are provided in the last columns of Table 1. It can be noted that the reduction is larger in the softer soil E due to the expected larger strains.
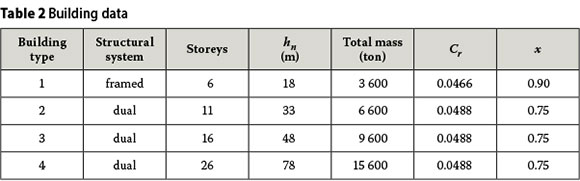
The data pertaining to the building structures are given in Table 2. All four building types considered are supported by a 20 m by 30 m rectangular raft foundation, have an additional basement storey and have a uniform story height of 3 m including the basement floor. The radius of the equivalent circular foundation for the horizontal and rocking (around the longer side of the rectangular foundation) degrees of freedom are computed from Equation (9) as 13.82 m and 12.63 m respectively.
The fundamental period is estimated using the relationship provided in the code:

The constants Cr and x, which depend on the structural system, are also provided in Table 2 as proposed by the provisions of the code. The height hn is the total height of the building measured from the foundation level.
The periods computed using Equation (14) are presented in Table 3. A uniformly distributed permanent gravity load of 10 kNlm2 is assumed on each floor for the subsequent computation of the building mass. The structural stiffness is computed using the natural period and the effective mass m obtained by reducing the total mass by a factor of 0.7 as recommended by the code using the relationship in Equation (15).

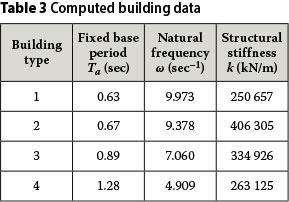
The structural stiffnesses computed in this manner are given in the last column of Table 3.
The dynamic foundation stiffnesses are dependent on the soil type, foundation shape, foundation embedment and structural properties. Neglecting the effect of foundation embedment due to the shallow depth, the stiffnesses are calculated using the relationships in Equation (16):
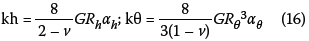
The coefficients αh and αθ are generally frequency-dependent dynamic modifiers applied on the respective static stiffness given by Equation (8) for the horizontal and rocking motion, respectively. Whereas the modifier αh may be taken as unity for all practical purposes, the modifier αθ must be established depending on the ratio Rmvs/Tα (BSSC 2004, 2010). Both the modifiers and the stiffnesses are computed and provided in Table 4.
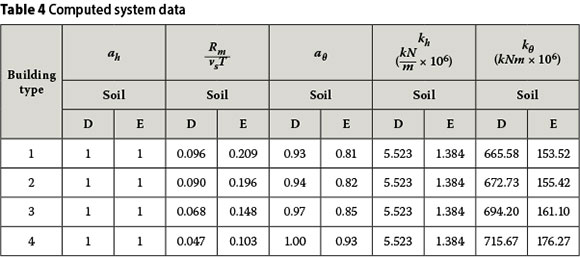
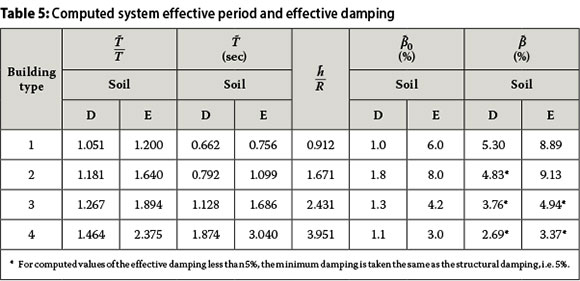
Once the stiffnesses are established, the system (effective) period is calculated from Equation (10). The computed values are given in Table 5. The foundation damping β0 is dependent on the aspect ratio T/T of the building, the period ratio T/T and the seismicity of the site, where h is the effective height taken equal to 0.7hn. It is determined in accordance with graphs provided in the code document. Then the effective system damping is determined as per Equation (11), in which a structural damping of 5% is assumed for concrete structures as usual. The foundation damping and the system damping are given in the last columns of Table 5. Note that for computed values of the effective damping that are less than 5%, a minimum damping of 5% is taken according to the recommendations of NEHRP.
The seismic response coefficient corresponding to the fixed-base period T is given by (for an elastic response and a normal-occupancy building):
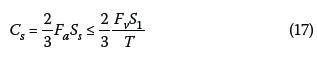
The coefficients Fa and Fv are the site amplification factors for the short-period and the intermediate-period regions of the design spectrum, respectively. They are determined from tables provided in the design code. Fa assumes the values of 1.6 and 2.5 for soils D and E, whereas Fv takes the values 2 and 3.2, respectively. Similarly, the seismic response coefficient Cs corresponding to the flexible-base period T is determined from Equation (17).
Finally, the effective system damping and the modified seismic response coefficient are employed together with the structural damping and the fixed-base seismic coefficient to calculate the reduction in base shear due to SSI using Equation (18). The results are presented in the last column of Table 6 as percentages of the base shear of the fixed-base system.
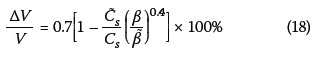
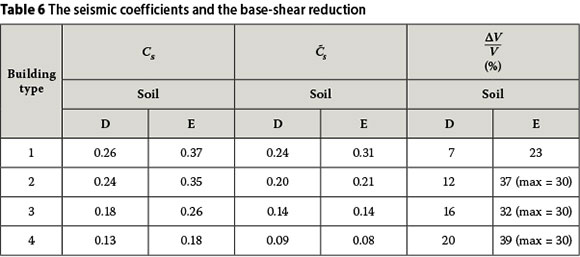
The results obtained demonstrate that a significant amount of reduction in design base shear can be achieved if SSI provisions of design codes are properly used. In these particular examples a reduction in base shear of 7% to 39% is achieved. However, it is important to point out that the series of NEHRP documents (BSSC 2004, 2010) limit the maximum base-shear reduction due to SSI to a maximum of 30% as shown in brackets in the last column of Table 6. Obviously, the resulting cost saving in general could be of significant proportion, especially in medium-height buildings. The percentage saving increases with decreasing stiffness of the soil. However, the increasing trend of reduction in base shear with increasing building height seen in Table 6 is not expected to continue with further increase in the number of storeys outside the range considered, as the influence of SSI generally decreases with increasing slenderness of the building in taller buildings.
CONCLUSIONS AND RECOMMENDATIONS
The material presented in this paper demonstrated the importance of inertial SSI, which has the beneficial effect of reducing design spectral values or base shear in most building structures, but also increasing their lateral deformation. It was observed that effects of SSI increase with decreasing stiffness of the site soil. This effect of soils is in addition to their amplification potential and tends to compensate for part of the seismic base shear demand associated with response amplification.
According to the state of the art, the actual amplification potential of site soils is much more than stipulated in older design codes like EC8 (1994) and SABS (1989). It has been shown in this paper that the cost implications due to site amplifications, which in some cases could be prohibitive, may be significantly offset if SSI provisions are introduced in design codes. The necessary procedures are available in recent code provisions such as the NEHRP series (BSSC 2004, 2010).
Recent research has shown that code-specified relationships in design codes for computing the period lengthening, the effective damping and the reduction in base shear are meanwhile calibrated using recorded and measured data from the near past such that these provisions can give reliable results. In fact, it can be said that the state of current knowledge and confidence attained with regard to seismic SSI is comparable with that of the amplification potential of site soils. The examples considered in the paper demonstrated that substantial savings could indeed be achieved by accounting for seismic SSI effects. It is thus suggested that engineers are encouraged to use such provisions for a potentially economical structural design until these provisions make their way into the local code.
As a final note, it should be recalled that SSI has also the effect of increasing the total lateral deformation of buildings, which will in turn have an impact on the ductility requirements of the structure and on secondary effects like P-∆. This aspect of SSI should also be duly accounted for in the design process, especially for tall structures.
REFERENCES
BSSC (Building Seismic Safety Council) 2004. National Earthquake Hazard Reduction Program (NEHRP): Recommended Provisions (and Commentary) for Seismic Regulations for New Buildings and Other Structures. Washington DC: BSSC, FEMA 450-1 and 450-2. [ Links ]
BSSC (Building Seismic Safety Council) 2010. National Earthquake Hazard Reduction Program (NEHRP): Recommended Provisions for Seismic Regulations for Buildings and Other Structures. Washington DC: BSSC, FEMA 750. [ Links ]
EC8: 1994. Design Provisions for Earthquake Resistance for Structures. Brussels: European Committee for Standardization. [ Links ]
EC8: 2004. Design of Structures for Earthquake Resistance. Brussels: European Committee for Standardization. [ Links ]
Ehlers, G 1942. The effect of soil flexibility on vibrating systems. Beton und Eisen. 41(21/22):197-203 (in German). [ Links ]
Fenves, G & Serino, G 1992. Evaluation of soil-structure interaction in buildings during earthquakes. Sacramento, CA: California Department of Conservation, Division of Mines and Geology, Data Utilization Report, CSMIP/92-01. [ Links ]
Gazetas, G 1983. Analysis of machine foundation vibration: State of the art. Soil Dynamics and Earthquake Engineering, 2(1):2-42. [ Links ]
Gazetas, G 1991. Formulas and charts for impedances of surface and embedded foundations. Journal of Geotechnical Engineering, ASCE, 117(9):1363-1381. [ Links ]
Luco, J & Westmann, R 1971. Dynamic response of circular footings. Engineering Mechanics Division, ASCE, 97(5):1381-1395. [ Links ]
Mylonakis , G & Gazetas, G 2000. Seismic soil structure interaction: Beneficial or detrimental? Journal of Earthquake Engineering, 4(3):277-301. [ Links ]
Pais, A & Kausel, E 1988. Approximate formulas for dynamic stiffnesses of rigid foundations. Soil Dynamics and Earthquake Engineering, 7(4):213-227. [ Links ]
Reissner, E 1936. Stationaere, Axialsymmetrische durch schuettelende Masse erregte Schwingungen eines homogenen elastischen Halbraums. Ingenieur-Archiv, 7(6):191-243. [ Links ]
SABS (South African Bureau of Standards) 1989. SABS 0160:1989. South African Standard Code of Practice for the General Procedures and Loadings to be adopted in the Design of Buildings. Pretoria: SABS. [ Links ]
SABS (South African Bureau of Standards) 2010. SANS 10160-4: Basis of Structural Design and Actions for
Buildings and Industrial Structures. Part 4: Seismic Actions and General Requirements for Buildings. Pretoria: SABS.
Stewart, J, Fenves, G & Seed, R 1999. Seismic soil-structure interaction in buildings. I: Analytical methods. Journal of Geotechnical and Geoenvironmental Engineering, ASCE, 125(1):26-37. [ Links ]
Stewart, J, Kim, S, Bielak, J, Dobri, R & Power, M 2003. Revision to soil-structure interaction procedures in the NEHRP design provisions. Earthquake Spectra, 19(3):677-696. [ Links ]
Tileylioglu, S, Stewart, J & Nigbor, R 2011. Dynamic stiffness and damping of shallow foundation from forced vibration of a field test structure. Journal of Geotechnical and Geoenvironmental Engineering, ASCE, 137(4):344-335. [ Links ]
Veletsos, A & Meek, J 1974. Dynamic behavior of building foundation systems. Earthquake Engineering and Structural Dynamics, 3(2):121-138. [ Links ]
Veletsos, A & Nair, V 1975. Seismic interaction of structures on hysteretic foundations. Journal of Structural Engineering, 101:109-129. [ Links ]
Veletsos, A & Verbic, B 1973. Vibration of viscoelastic foundations. Journal Earthquake Engineering and Structural Dynamics, 2(1):87-102 [ Links ]
Veletsos, A & Wei, W 1971. Lateral and rocking vibrations of footings. Soil Mechanics and Foundation Division, ASCE, 97(9):1227-1248. [ Links ]
Wium, J 2010. Background to SANS 10160 (2009). Part 4: Seismic loading. Journal of the South African Institution of Civil Engineering, 52(1):20-27. [ Links ]
Wolf, J & Deeks, A 2004. Foundation Vibration Analysis: A Strength-of-Materials Approach. Oxford: Elsevier. [ Links ]
Worku, A 1996. Bauwerksschwingungen infolge Erdbeben unter Berucksichtigung der Wechselwirkung zwischen Fundament und Boden. Doctoral dissertation, University of Wuppertal, Germany. [ Links ]
Worku, A 2005. A closed-form solution procedure to the vibration of non-classically damped systems subjected to harmonic loads. Zede, Journal of the Ethiopian Engineers and Architects, 22:1-9. [ Links ]
Worku, A 2012. An analytical solution procedure for dynamic analysis of soil-structure systems subjected to periodic loads. Electronic Journal of Geotechnical Engineering, 17(Y):3835-3852. [ Links ]
Ziotopoulou, A & Gazetas, G 2010. Are current design spectra sufficient for soil-structure interaction on soft soils? In: Fardis, M N (Ed.), Advances in Performance-based Earthquake Engineering, London: Springer Science and Business Media. [ Links ]
 Contact details:
Contact details:
Asrat Worku
PO Box 30020
Nairobi 00100
Kenya
T: +254 20 225 1880/0577
M: +254 725 617420
F: +254 20 221 0694 / +254 20 224 4493
E: aworku@gibbinternational.com
E: asratie@gmail.com

PROF ASRAT WORKU is an Associate Professor of Civil Engineering at Addis Ababa University (AAU), Ethiopia, and is currently also working as Operations Manager for Geotechnics at Gibb International in Nairobi. He completed his BSc degree in Civil Engineering in 1983, and, specialising in geotechnics, his MSc degree in 1989, both from AAU, IN 1996 he earned his DrIng degree from Wuppertal University, Germany, with a dissertation on seismic soil structure interaction. He has practised in both structural and geotechnical engineering. His industry experience in geotechnics spans various types of major projects in several African countries.














