Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
Journal of the South African Institution of Civil Engineering
On-line version ISSN 2309-8775
Print version ISSN 1021-2019
J. S. Afr. Inst. Civ. Eng. vol.55 n.2 Midrand Jan. 2013
TECHNICAL PAPER
Experimental study of turbulence and water levels in shoaling and breaking waves using digital image processing techniques
R Mukaro; K Govender
Contact details
ABSTRACT
In this article we present results of laboratory experiments undertaken to study the structure of turbulence generated by mild plunging waves breaking on a sloping beach bed. Measurements of water levels and instantaneous fluid velocities were conducted on a 1:20 sloping beach fitted inside a glass flume. The instantaneous water levels were measured using calibrated capacitive wave gauges, while the instantaneous velocity flow fields were measured using video techniques together with digital correlation techniques. A digital camera was employed to capture images of the breaking waves at 20 phases. For each phase, 100 image pairs were captured from which 100 instantaneous velocity fields were derived using a digital correlation image velocimetry technique. The 100 instantaneous velocity flow fields were averaged to provide information on the mean flow. Further analysis of the acquired data yielded turbulence quantities such as turbulence intensity, turbulent kinetic energy and vorticity at each phase of the flow. Results are presented for four phases where turbulence is predominant. Contour plots are used to provide a temporal and spatial distribution of the evolution of the turbulence characteristics. Vertical profiles of these quantities at different phases are also presented. These results may provide guidance on the approximations that can be expected in computational fluid model studies.
Keywords: breaking waves, wave height, still water line, digital correlation image velocimetry (DCIV), cross correlation, velocity flow fields, turbulence intensities, turbulent kinetic energy, vorticity
INTRODUCTION
Turbulence is recognised as irregularly fluctuating and unpredictable motion which is composed of a number of small eddies that travel in the current. Turbulence is ubiquitous in nature but its measurement and analysis has not been easy. In the coastal regions of the ocean, turbulence is generated by breaking waves. The coastal regions are characterised by a sloping bottom. Waves moving from deep water towards the shore begin to slow down, due to the decreasing water depth, while at the same time increasing in wave height to maintain a constant energy flux. At a certain critical wave height the wave becomes unstable and breaking occurs. Breaking is characterised by the top of the crest falling onto the front face of the wave, forming a body of fluid, called the wave roller that rides on the wave front.
The roller interacts with the fluid below it in a complicated way, exchanging energy and momentum in the process. The roller will eventually dissipate and be completely absorbed by the wave. However, if breaking continues to occur, like on a plane slope beach, then the roller will be sustained for the greater portion of the surf zone. Thus there will be shoreward mass transport occurring above the trough level. For a closed system there has to be a return current. In a 2-D wave system this return current, called the undertow, occurs below the trough level and flows seawards terminating in the vicinity of the break point. In 3-D wave propagation systems there will also be rip currents on the surface and long-shore currents. The roller has been identified as the major source of turbulence in the surf zone (see for example Govender et al 2002; Kimmoun & Branger 2007). The roller represents a vortex or eddy with a typical scale corresponding to the wave height. Shear within the roller, and between the roller and the fluid below, will generate eddies of smaller dimensions and so on, finally reaching micro scales where dissipation occurs. Thus there is a cascade of energy from the large scales to the small scales in a turbulent flow. The small scales that are of practical interest are the integral scales (Tennekes & Lumely 1972). In the surf zone the integral scales are typically 0.1h to 0.3h, where h is the local water depth (Pedersen et al 1998; Govender et al 2004; Stansby & Feng 2005).
Turbulence generated in the wave roller is transported to lower portions of the wave, and some of it will be transferred to the sediments on the sea floor, resulting in suspension. The suspended sediments will then be transported by the currents and deposited elsewhere. This will result in erosion of the beach at certain places, while accumulation of sediments will occur at other places. Under natural conditions there will be a balance occurring between erosion and accumulation of sediments. This balance will be shifted when coastal structures are erected in the surf zone. An understanding of turbulence generation, transport and dissipation, as well as of the currents that are generated, is essential for predicting coastline changes and the effect that coastal structures will have on surf zone processes.
In addition to the above, currents generated during breaking contain large amounts of wave energy and momentum. These exert huge forces on structures and obstacles in their path, sometimes with destructive consequences. With the view to protecting harbours and coastal structures, breakwater structures are used. As pointed out by Massel (1996), a reliable estimation of the maximum wave height at a particular location is a fundamental requirement in the design of these coastal and offshore structures. This, to a large extent, is dependent on the description of the local wave climate, and in particular knowledge of the water surface elevations and the underlying kinematics (Baldock & Swan 1996).
The Navier-Stokes equations are commonly used in models to describe processes occurring in turbulent flows. These equations are highly nonlinear and are often intractable. Thus there is a need to develop simplified models to describe wave breaking and turbulence in the surf zone. Mathematicians, coastal engineers and computational physicists alike have proposed several models to describe surf zone waves and turbulence (see for example Battjes & Janssen 1978; Svendsen 1984; Deigaard & Fredsoe 1989). These models, however, still require input data from experiments for verification, calibration and improvements. Treatment of turbulence naturally leads to a discussion about statistics of the flow (usually velocity). The conceptual framework for understanding turbulence is largely statistical, where a set of equations based on averaged quantities (such as transport of mass, momentum and energy) are often used by coastal engineers. It is therefore important in such studies to first undertake experiments that give information on the kinematics and dynamics of wave breaking, as well as measurements of the statistics of breaking. As Sou et al (2010) pointed out, it is difficult to fully model the boundary-dominated swash zone flows with fundamental mass, momentum and energy transport equations because of the strong turbulence and the complexity of boundary conditions, namely the mobile bed, the multi-phased flows and the dynamic free surface.
Various investigators have used different contact-free measuring techniques, like Laser-Doppler Anemometry (LDA), to get an insight into the mechanics of breaking waves (e.g. Liiv & Lagemaa 2008). Hwung et al (1998) and Petti & Longo (2001) were able to study the vertical turbulence structure in the swash zone using Laser-Doppler Velocimentry (LDV). Stive (1980) investigated the internal flow velocity field of a quasi-steady spilling breaker in the surf zone. Nadaoka & Kondoh (1982) studied the velocity flow field inside the surf zone to clarify the dependence of sand movements upon the bottom velocity. Chang & Liu (1996, 1998, 1999) examined the flow field and turbulence structure of quasi-periodic breaking waves. They measured the velocity near the tip of an overturning jet and found that the maximum velocity is 1.68 times that of the phase speed. Cox & Anderson (2001) observed large vortices in the horizontal plane in the outer surf zone, which indicated the existence of obliquely descending eddies in the outer surf zone. Melville et al (2002) studied the coherent structures of breaking waves in a channel flow. Other researchers have taken advantage of the ability of the particle image velocim-etry (PIV) technique to obtain two-dimensional flow fields in wave environments. Sou et al (2010) examined the evolution of the turbulence structure from the outer surf zone to the swash zone using PIV. Successful efforts have also been made to measure velocity in the surf and swash zones in the field (Raubenheimer 2002; Raubenheimer et al 2004; Butt et al 2004). More recently Sou & Yeh (2011) studied the flow structure of oscillatory broken waves within surf and swash zones of a laboratory flume using PIV. They directly computed vorticity from the resolved spatial distribution of the velocity field. Their results showed that the flow separation at the bed occurred during the interaction between the uprush bore front and the downwash flow. An internal flow circulation was observed to be generated at the flow reversal phase, as the flow near the bed responds to the gravitational force earlier than the flow in the upper water column, where the uprush momentum is sustained later in phase.
In this paper we investigate the fundamental characteristics of the flow structure in the vertical cross-shore plane as mild plunging waves evolve from the outer surf zone. As pointed out by Sou & Yeh (2011), little attention has been focused on the flow structure. The objectives of the series of experiments reported here were to examine the sea level rise and variability, and to determine the temporal and spatial distribution of the evolution of the turbulence characteristics in the entire water column. Velocity flow fields at various positions along the flume were measured using the digital correlation image velocimetry (DCIV) technique. This digital technique, which allows rapid acquisition and processing of flow data, is just an extended principle of PIV that is based on a two-phase flow. Unlike the point measurement techniques utilised in earlier laboratory and field studies, the technique used here provides full-field two-dimensional instantaneous velocity fields. By tracking the motion of neutrally buoyant particles, as well as bubble structures within the crest of the wave, we were able to measure velocities well into the crest of the wave.
EXPERIMENTAL SETUP AND PROCEDURES
Experiments were conducted in a glasswalled flume in the Coastal and Hydraulics Engineering Laboratory at the Council for Scientific and Industrial Research (CSIR) in Stellenbosch, South Africa. The objective was to study the variation of the wave height near the break point and to study the 2-D velocity flow fields during the breaking process. For this purpose, regular waves were generated in the wave flume. They were generated by a computer-driven, servo-controlled, piston-type wave maker, manufactured by HR Wallingford. The wave maker has a maximum paddle stroke of 0.8 m and is designed for water depths of up to 0.75 m. The wave maker has been fitted with an active absorption system to prevent waves being reflected back by the paddle. Complementary documentation of the wave maker specifications and wave generation mechanism may be found on the web page given at the end of the references section.
Figure 1 shows a schematic diagram of the flume giving the overall dimensions in addition to showing the position of the 1:20 sloping bottom and the coordinate system that was used. For water level measurements, the intersection of the still water line (swl) and the beach slope was taken as the reference point (x = 0, z = 0). Thus distances are negative from the swl towards the wave generator. For velocity measurements, the position of the flume bed was taken as the vertical reference, (z = 0) with the left edge of each image as x = 0. The flume is approximately 20 m long, 0.75 m wide and 0.8 m deep. Quarry stones were used at the end of the sloping bed to absorb any wave energy remaining after breaking.
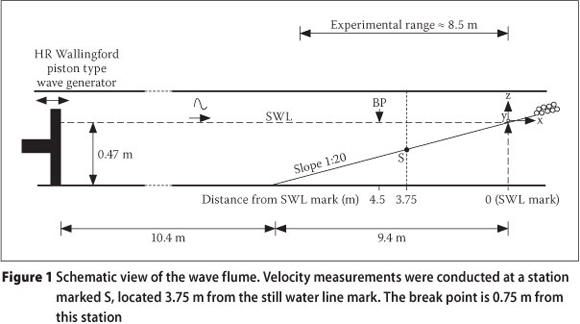
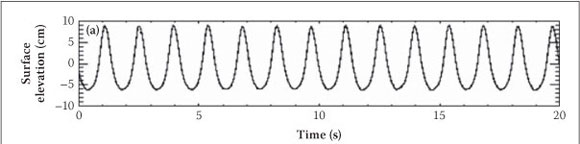
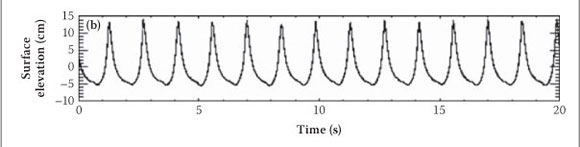
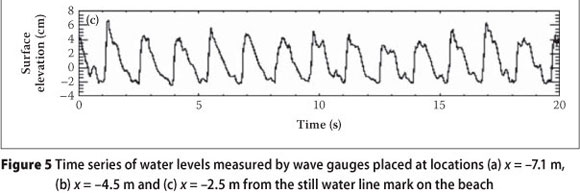
The flume was filled with water up to a height of 47 cm. The wave-generating computer was pre-programmed to drive the wave maker generating 0.7 Hz regular waves. This resulted in spilling/mild plunging waves of wave height 0.16 m which broke at a point 4.5 m from the still water mark on the beach. The first series of experiments involved free surface measurements which were performed to obtain a first assessment of the breaking wave behaviour in terms of its wave height and position of the break point. Prior to taking these measurements, the waves were allowed to run for 30 minutes to ensure that steady state conditions were reached. Surface displacements were measured using a set of three pre-calibrated capacitive wave gauges. The three wave gauges were initially positioned at x = -7.1 m, -4.5 m and -2.5 m, respectively. The gauges were simultaneously sampled at 20 Hz for two minutes at these positions. The gauges in the surf zone were then moved 10 cm towards the wave maker and measurements repeated. This procedure was repeated until time series measurements were captured over the entire experimental range. The experimental range which is marked on Figure 1 spans about 8.5 m. Fluid velocity measurements were then performed at a station marked S located -3.75 cm from the still water mark on the beach. A schematic diagram showing the interconnection of the experimental setup used for image acquisition is shown in Figure 2.
The water was seeded with partially expanded polystyrene beads. A longitudinal section of the flume was illuminated with a strobed light sheet from above. The illuminated section was imaged from the side using a progressive scan digital camera connected to a frame grabber residing in a computer. Pairs of images, separated by a few milli-seconds, of the beads and aeration due to breaking were obtained by appropriately strobing the light sheet. On receiving a trigger signal from the wave generator, the computer strobed the light sheet at the end of one video frame time and again at the beginning of the next, capturing a pair of images. While a particular frame is being exposed, the previous frame is downloaded to the frame grabber. The time between flashing of the light sheet corresponds to the time between the images in each pair. Our imaging setup can view only a small section of the wave at any time. In order to conduct measurements over the entire wavelength, a wave cycle was imaged at twenty equally spaced phase positions as follows: we began with phase 0 and, on receiving a trigger pulse, the computer was programmed to captured 100 image pairs of a 38 cm section of the wave over a number of cycles. This enabled ensemble averaging to be performed.
After getting the trigger pulse, the data acquisition computer waited a delay time proportional to the phase number before capturing images at the other remaining phases. All the image pairs were then analysed to obtain the instantaneous velocity flow fields. Mean and fluctuating velocity fields were obtained from the instantaneous fields by means of phase-ensemble averaging. Fluctuating velocities, together with preliminary analysis of the averaged vorticity, will be presented.
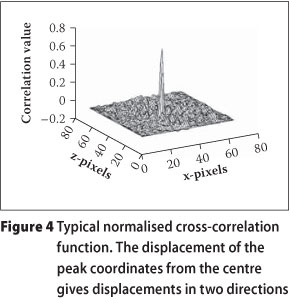
Figure 3 shows a schematic view of the digital signal processing procedure employed to extract instantaneous velocity fields from each pair of images. At a given point (i,j) in the first image an interrogation window of 32x32 pixels centered at (i,j) was placed. The sub-image contained within this interrogation window was then cross-correlated with a corresponding subimage in the second image. The coordinates of the peak in the cross-correlation result gave a measure of the displacements (in the respective directions) of the beads and/or aeration structures between the sub-images. Figure 4 shows a typical normalised cross-correlation function obtained from two sub-images. The displacement extraction procedure was implemented using Fast Fourier Transforms (FFT). To improve on the accuracy of the results, coordinates of the peak in the cross correlation function was estimated to sub-pixel resolution using sub-pixel interpolation. Dividing the displacements by the inter-image time gave velocity components at the point (i,j) in the images. The interrogation window was then moved in regular steps of eight pixels (vertically and horizontally) across the entire image to obtain the velocity flow field over the entire image. Theoretical details and validation of this DCIV measurement technique can be found in Govender et al (2002b) and Govender et al (2009), while a good reference which deals with most of the aspects of PIV and its application to water waves is a book by Raffel et al (1998) and an article by Grue et al (2003).
EXPERIMENTAL RESULTS
Table 1 shows parameters relating to water level measurements - fs is the sampling frequency, ts is the total sampling time, ns is the number of samples captured per wave period, Ns is the sample size captured in two minutes, and Nf is the number of full waves in the two-minute durations. With a sampling frequency of a reading every 0.05 s (i.e. 20 Hz) there were at least 28 samples over one wave period of 1.43 s, and a total of 2 350 over a test time of 120 s. The 2 350 samples thus contained about 84 full waves. The wave gauges provided a measure of the instantaneous displacement of the water level with respect to the still water line. Each wave cycle in the time series was analysed to extract the height of the crest and trough relative to the still water level.

These crest and trough positions were then averaged over 84 cycles to provide the mean crest and trough positions.
Water level measurements
Figure 5 shows a sample of the instantaneous water level results measured at three positions along the flume by wave gauges positioned at (a) x = -7.1 m, (b) x = -4.5 m and (c) x = -2.5 m. The wave gauges were sampled for 120 s. However, the time series shown have been truncated to show only up to 20 s. It is evident from the figure that, as the waves move from deep to shallow water (due to the sloping bottom), the wave profile changes from being sinusoidal to being more peaked at the crests while the troughs become drawn out. The wave height increases as the waves move into shallow water, reaching a maximum at which breaking occurs, and decreasing thereafter. The reason for the increase during pre-breaking is due to the fact that the wave speed decreases as the waves move up the slope. From linear theory this wave speed is given by:

where g is acceleration due to gravity and k is the local water height. However, since the energy flux is constant, the wave height has to increase. The decrease in wave height after breaking is due to the loss of wave energy to turbulence and currents.
Wave height measurements in the vicinity of the break point are shown in Figure 6. In this figure, the still water line (swl) is at z = 0 cm. Crests and troughs were measured from the swl and the wave height was taken as the vertical distance from the troughs to the crests. Troughs are observed to get up to 6 cm below the swl. In deep water (Figure 5(a)), the results show a wave height of about 16 cm, rising to 19.5 cm at the breakpoint, which is at x = -4.5 m from the swl mark. Thus there is a 21.8% increase in wave height at the breakpoint. Our results are consistent with those of Stive (1980) who conducted water level measurements in waves having a period of 1.79 s and found a 22.75% increase in wave height at the breakpoint. In the present investigation, the deep water wave length was LO = 3.20 m, and the local water depth at the breakpoint was hb = 22.5 cm. The wave height at the break point was Hb = 19.5 cm. The maximum wave height that can be sustained for a given water depth is given by (Miche 1951):
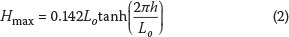
In deep water Equation (2) reduces to a maximum wave steepness Hmax/LO = 0.142, and in shallow water it reduces to a maximum height-to-depth ratio Hmax/d = 0.88 (McKee Smith 1999). This criterion is powerful, because it includes both the impacts of depth and steepness-limited breaking. Our experimental value of Hmax/d at the break point is 0.87, which is consistent with the result quoted above.
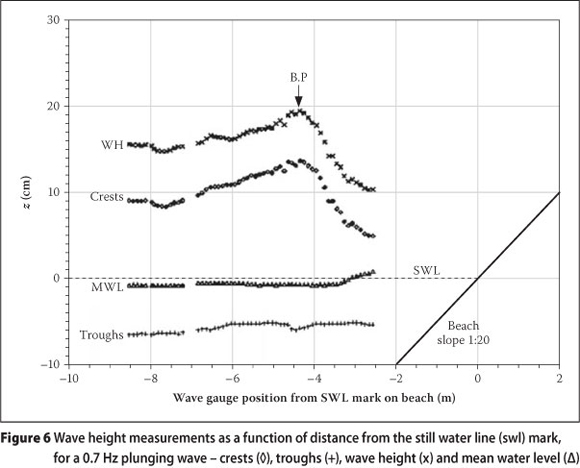
Note that there are 84 full waves measured at one position. Standard deviations of the 84 wave height measurements were used to determine the variability of the wave heights at each position. Standard deviations of the order ± 0.2 cm were observed before breaking, while after breaking they were of the order 2.0 cm. This amounts to a variability of about 10% in the wave height.
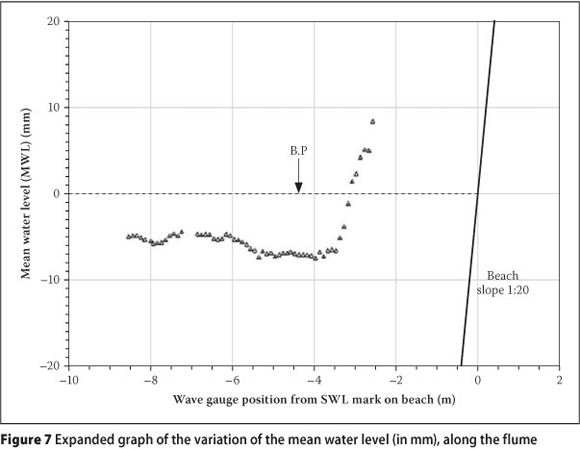
Figure 7 shows an expanded view of the variation of mean water level across the flume. Note that the variation is given in millimetres. Clearly there is a lowering of the mean water level before breaking, called the set-down, of about 5 mm, and a rising of the mean water level after breaking, called the set-up. A higher mean water level in the surf zone coupled with high levels of turbulence and currents will result in greater amounts of sediment suspension and transport.
Velocity measurements
The actual fluid flow velocity can be described as a sum of the averaged velocity and the fluctuating components. For the horizontal component we have:

where u is the measured velocity in the x direction, < u > is the phase-ensemble averaged horizontal velocity and u' reflects the instantaneous turbulent fluctuations. The average of the fluctuations is zero, i.e. < u' > = 0, while the ensemble average of the square of the fluctuations is not zero. This is similar for the other components.
The phase-ensemble average of a measured periodic quantity 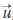 , at a given spatial position and with replication period T, and total temporal length T' = NT, where N is the number of samples captured at a particular phase (i.e. 100 in the present case), is defined as:
, at a given spatial position and with replication period T, and total temporal length T' = NT, where N is the number of samples captured at a particular phase (i.e. 100 in the present case), is defined as:
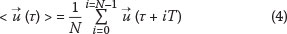
where τ lies in the interval {0; T} (Liiv & Lagemaa 2008; Sou & Yeh 2011).
Figure 8 shows typical images of the wave corresponding to four consecutive phases, but captured from different wave cycles. The sequence of images shown can be viewed as snapshots of the flow field covering four different timings. These images correspond to phases 10, 11, 12 and 13 (as indicated) of a wave propagating from left to right. These four phases have the most dynamic information about the wave, so we will only show turbulence results pertaining to these phases. Bubble structures and beads that were used as tracers are faintly visible in the images. The whitecap at the crest of the wave shows the high-speed wave roller.
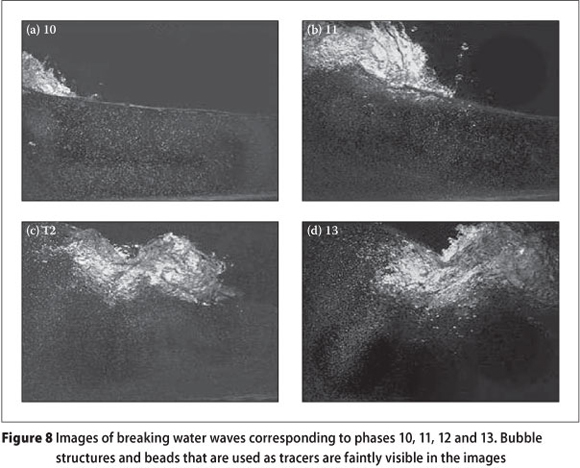
The corresponding instantaneous velocity flow fields for these four phases are shown in Figure 9. Every alternate row and column of vectors has been omitted for clarity. Clearly we were able to measure velocities over the entire image, including the aerated portion of the waves, which is not possible using techniques such as LDA. The theoretical wave-phase speed calculated using a local water depth of 18.75 cm at station S was 1.36 m/s. A vertical profile of the horizontal velocity component measured through a vertical section passing through the crest (first peak in the wave profile in Figure 9 (d)) of the wave and through the wave roller (second peak in the wave profile in Figure 9 (d)) is given in Figure 10. Also shown in Figure 10 is a plot of the horizontal component below the wave crest predicted using linear theory (dashed line) for a wave of height corresponding to that observed at station S. Near the crest the maximum instantaneous velocities are approximately 3-4 times greater than those predicted by linear theory, while below the trough level, the measured horizontal components underneath the wave crest are fairly similar to those given by linear theory for this particular position and wave case. The observed velocity profiles over depth deviate substantially from uniform, exhibiting complex vertical structures in such shallow water flows.
Phase-ensemble-averaged velocity flow fields for phases 10 to 13 are shown in Figure 11. Again every second row and column of vectors has been omitted for clarity. A legend shown in the upper left corner of each vector field shows an arrow vector of magnitude 100 cm/s. The position z = 15 cm corresponds to the still water line. The continuous line at the free surface now shows the average profile for that phase.
Phase averaging was performed using 100 velocity fields. It is important to note that the wave profile for each cycle differs from the next (i.e. no two cycles are exactly the same). As pointed out by Svendsen (1987), even for waves that are generated monochromatically, the wave period in the surf zone is not exactly the same. This is because irregularities in the propagation speed of the individual breakers, caused by nonlinearities, tend to accumulate as the waves move shoreward. This inevitably results in smearing at the crests of the phase averaged results as seen for phases 12 and 13 of Figure 11. Each sample of the phase average may not exactly come from the same phase in the wave relative to a characteristic point (such as zero up-crossing, the toe or the wave crest). A very strong shear layer is evident around an elevation of z = 15 cm. As observed by Sou & Yeh (2011), the horizontal velocity near the bed is still directed offshore.
Figure 12 shows contour plots of the mean horizontal velocity component. The colour bar represents the magnitude and direction of the velocity vector, with red pointing in the positive x-direction and dark-blue in the negative x-direction. Thus, for the horizontal velocity component, negative values represent seaward flow, while positive indicate onshore flow. Peak values of up to 250 cm/s are observed near crest. The fluid with fast longitudinal mean velocity moves near the free surface between z = 15 cm and the free surface, while the fluid with low velocity is confined to below the elevation z = 15 cm. Figure 13 shows contour plots of the mean vertical velocity component. The red colour points in the positive z-direction (upwards) while the dark-blue points downwards. Unlike fluid with high longitudinal velocity which occurs in the crest, fluid with high transverse velocity is observed to occur at lower elevations below the crest. Peak vertical velocity is about 60 cm/s. Figure 14 shows the vertical profile of both horizontal and vertical components, which is almost uniform from the flume bed up to the swl (z = 15 cm) and rising to peak values towards the crest.
Turbulence intensity
Turbulent fluctuations are usually quantified by the turbulent intensities, which are defined as the root-mean-square of the fluctuations. The turbulence intensity in the x-direction for a given spatial position is defined by (Stull 1988; Liiv & Lagemaa 2008; Misra et al 2008) as
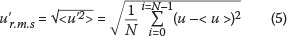
Similar equations were used for the other component. In the remainder of the paper the primed turbulent velocity components will be used to represent the root mean square values of the turbulent fluctuations as given by Equation (5).
The instantaneous velocity fields were further analysed using Equation (5) to quantify the turbulence intensity of the flow. Figures 15 and 16 are contour plots showing the spatial and temporal distribution of the horizontal and vertical turbulence intensities respectively for the phases of interest. From Figure 15 it can be observed that the highest levels of horizontal turbulence intensities are of the order of 120 cm/s, while Figure 16 shows peak vertical turbulence intensity values of the order of 60 cm/s for this breaker. Peak values for both horizontal and vertical turbulence intensities occur near the front face of the wave, above elevation z = 15 cm. The region of high horizontal turbulence intensity values corresponds to the wave roller.
Figure 17 shows the variation of the horizontal and vertical turbulence intensities through a vertical section passing through x = 20 cm for the four phases shown in Figures 12 and 13. Below the trough level the turbulence intensities are very much smaller than those in the wave crest and roller. From the flume bed up to elevation z = 15 cm, both turbulence intensity components are of the order of 10 cm/s.
From the still water line towards the crest, horizontal turbulence intensity rises to peak values of nearly 120 cm/s, while the vertical goes up to 60 cm/s. The turbulence intensities are observed to gradually decrease as the wave crest passes.
Turbulent kinetic energy (TKE)
The turbulent kinetic energy (TKE) per unit mass is defined as follows:

In the results reported here, only two components (u and w) were measured, so turbulent kinetic energy was estimated as suggested by Svendsen (1987) as:

The value of 1.33 is based on the assumption that breaking waves have turbulence characteristics similar to that of plane wakes (Svendsen 1987). A similar estimation of TKE was also used by Ting & Kirby (1995), Chang & Liu (1999), Shin & Cox (2006) and Liiv & Lagemaa (2008).
Contour plots of the computed TKE values for phases 10 to 13 are shown in Figure 18. Once again high TKE values are observed between the shear boundary layer and the crest. Figure 19 (a) shows the variation TKE through a vertical section passing through x = 20 cm for the four phases shown in Figure 18. Figure 19 (b) is an expanded plot showing TKE only for positions below the trough level. Below the trough level TKE is very much smaller than those in the wave crest and roller. Peak values of k ~ 1.0 m2/s2 occur in the crest and roller region. Normalised peak values of k/c2 ~ 0.01 occur just below the trough level for all the phases. Previous measurements by Ting & Kirby (1995) for a strongly plunging wave at a similar position indicate normalised peak TKE (k/c2) just below the trough level of 0.02 to 0.03. Thus our kinetic energy results are consistent with earlier measurements.
Vorticity
Vorticity of a fluid is an important factor in fluid dynamics and mechanics and is a natural way to describe turbulence. A vortex can be described as a fluid structure that possesses circular or swirling motion. It is the principal quantity to define the flow structure (Kim et al 1995; Wu et al 2006), and is mathematically defined as the curl of the velocity field:
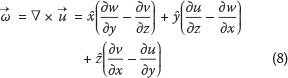
where the x, y and z indices denote the respective orthogonal directions and  , and ž are the unit basis vectors for the three-dimensional Euclidean space R3, and u, v and w are velocities in the x, y and z directions, respectively.
, and ž are the unit basis vectors for the three-dimensional Euclidean space R3, and u, v and w are velocities in the x, y and z directions, respectively.
If a two-dimensional fluid flow in the x-z plane is considered, the phase-averaged vorticity component, which points in the y-direction, is defined as (Sou & Yeh 2011):
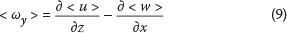
Several numerical schemes exist for performing this calculation. The central difference method is the mostly adopted method, especially when dealing with PIV measurements affected by a non-negligible noise level. Vorticity is then estimated from (Lee & Lee 2001; Sou & Yeh 2011):
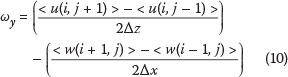
where Δx and Δz are the x and z-grid spacing respectively, and (i, j) represents the spatial grid point in (x, z) plane.
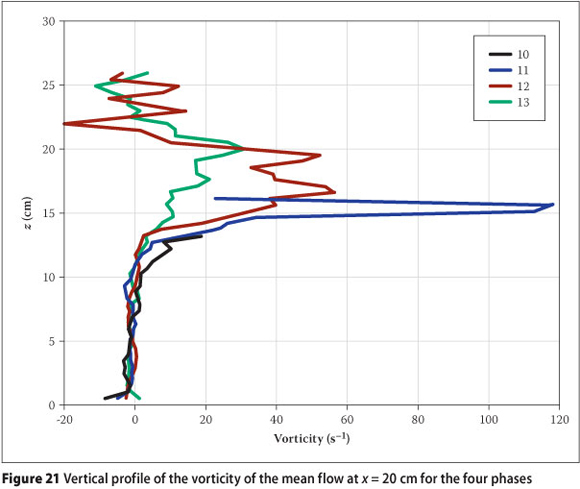
Figure 20 shows contour plots of the spatial variation of the vorticity of the phase-ensemble averaged flow for the four phases. Positive vorticity indicates clockwise rotation and the direction is into the plane of the figure, while negative vorticity indicates anticlockwise rotation with the direction out of the plane of the figure. Figure 21 shows the vertical variation of vorticity at position x = 20 cm for the four phases under consideration. From the flume bed up to the swl, vorticity is about zero and increases to peak values of up to 100 s-1 just above the swl before dropping to negative vorticity values towards the top of the crest. Again, just like the turbulence intensity components and the kinetic energy, peak vorticity lies near the shear boundary layer. The strong shear layer generated peak vorticity because of the interaction between the downwash and uprush flows. In a similar study, Sou & Yeh (2011) observed that an internal flow circulation is generated at the flow reversal phase, as the flow near the bed responds to the gravitational force earlier than the flow in the upper water column where the uprush momentum is sustained later in the phase. Similarly to results presented here, they also observed that, in the surf zone, the maximum intensity of the phase-averaged vorticity occurs at the shear boundary layer, and the strength of vorticity in the water column decays as the phase advances.
CONCLUSIONS
Results of an experimental study of spilling/ mildly plunging water waves breaking in a laboratory surf zone have been presented. Water level measurements show the usual increase in wave height in the shoaling region followed by rapid decrease in wave height beyond the breakpoint. An increase in wave height by a factor of approximately 22% has been observed at the breakpoint. Fluid velocities were measured by tracking the motion of almost neutrally buoyant particles, as well as aeration structures formed by breaking waves. For each phase 100 instantaneous velocity flow fields were averaged to provide information on the mean and turbulent flow. Instantaneous velocities in the wave roller were observed to go up to 3-4 times greater than the wave phase speed. Further analysis of the instantaneous velocity yielded turbulence quantities such as turbulence intensity, turbulent kinetic energy and vorticity at each phase of the flow. Peak turbulence intensities, turbulent kinetic energy and vorticity were observed in the crest part of the wave, around the shear boundary layer. Contour plots were used to provide a temporal and spatial distribution of the evolution of the turbulence characteristics. According to the evolution processes the vertical profiles of the turbulence parameters were observed to change systematically during the advance of the breaking crests.
From the flume bed towards the swl, turbulence quantities measured were observed to be negligible, rising sharply from the swl towards the crest. For the phase-ensemble-averaged flow, high rotation rates of up to nearly 100 s-1 were observed near the shear-boundary layer created by the fast-moving crest and the sea-bound trough water.
ACKNOWLEDGEMENTS
The authors would like to acknowledge the Research Office at the University of KwaZulu-Natal for a Competitive Research Grant that enabled this project to be carried out. We would also like to acknowledge the Council for Scientific and Industrial Research (CSIR), Stellenbosch, for financial assistance and allowing us access to their research facilities where this work was carried out.
REFERENCES
Baldock, T E & Swan, C 1996. Extreme waves in shallow and intermediate water depths. Coastal Engineering, 27(1-2): 21-46. [ Links ]
Battjes, J A & Janssen, J P F M 1978. Energy loss and set-up due to breaking of random waves. Proceedings, 25th International Conference on Coastal Engineering , 569-587. [ Links ]
Butt, T P, Russell, J, Puleo, J, Miles, J & Masselink, G 2004. The influence of bore turbulence on sediment transport in the swash and inner surf zones. Continental Shelf Research, 24: 757-771. [ Links ]
Chang, K-A & Liu, P L-F 1999. Experimental investigation of turbulence generated by breaking waves in water of intermediate depth. Physics of Fluids, 11: 3390-3400. [ Links ]
Chang, K-A & Liu, P L-F 1996. Measurement of breaking waves using particle image velocimetry. Paper presented at the 25th International Conference on Coastal Engineering, AMCE, Orlando, Florida. [ Links ]
Chang, K-A & Liu, P L-F 1998. Velocity, acceleration and vorticity under a breaking wave. Physics of Fluids, 10: 327-329. [ Links ]
Cox, D T & Anderson, S L 2001. Statistics of intermittent surf zone turbulence and observations of large eddies using PIV. Coastal Engineering, 43: 121-131. [ Links ]
Deigaard, R & Fredsoe, J 1989. Shear stress distribution in dissipative water waves. Coastal Engineering, 13: 357-378. [ Links ]
Govender, K, Mocke, G & Alport, M J 2002a. Dissipation of isotropic turbulence and length-scale measurements through the wave roller in laboratory spilling waves. JGR Oceans, 109: C08018, doi: 10.1029/2003JC002233. [ Links ]
Govender, K, Alport, M J & Mocke, G 2002b. Video imaged surf zone wave and roller structures and flow fields. Journal of Geophysical Research, 107(C7), 3072, doi: 10.1029/2000JC000755. [ Links ]
Govender, K, Michallet, H, Alport, M J, Pillay, U, Mocke, G P & Mory, M 2009. Video DCIV measurements of mass and momentum fluxes and kinetic energies in laboratory waves breaking over a bar. Coastal Engineering, 56: 879-885. [ Links ]
Govender, K, Mocke, G P & Alport, M J 2004. Dissipation of isotropic turbulence and length-scale measurements through the wave roller in laboratory spilling waves. Journal of Geophysical Research, 109, C08018, doi: 10.1029/2003JC002233. [ Links ]
Grue, J, Clamond, D, Huseby, M & Jensen, A 2003. Kinematics of extreme waves in deep water. Applied Ocean Research, 25: 355-366. [ Links ]
Hwung, H H, Hwang, K S, Chiang, W S & Lai, C F 1998. Flow structures in swash zone. Paper presented at 26th International Conference on Coastal Engineering, ASCE, Reston, Virginia, US. [ Links ]
Kim, W Y, Walker, P G & Pedersen, E M 1995. Left ventricular blood flow patterns in normal subjects: A quantitative analysis by three-dimensional magnetic resonance velocity mapping. Journal of the American College of Cardiologists, 26: 224-238. [ Links ]
Kimmoun, O & Branger, H 2007. A particle image velocimetry investigation on laboratory surf-zone breaking waves over a sloping beach. Journal of Fluid Mechanics, 588: 353-397. [ Links ]
Lee, S-J & Lee, S-H 2001. Flow field analysis of a turbulent boundary layer over a riblet surface. Experiments in Fluids, 30: 153-160. [ Links ]
Liiv, T & Lagemaa, P 2008. The variation of the velocity and turbulent kinetic energy field in the wave in the vicinity of the break point. Estonian Journal of Engineering, 14(1): 42-64. [ Links ]
Massel, S R 1996. On the largest wave height in water of constant depth. Ocean Engineering, 23(7): 553-573. [ Links ]
McKee Smith, J 1999. Wave breaking on an opposing current. Coastal Engineering Technical Note IV-17, US Army Corps of Engineers. [ Links ]
Melville, W K, Veron, F, White, C J 2002. The velocity field under breaking waves; coherent structures and turbulence. Journal of Fluid Mechanics, 454: 203-233. [ Links ]
Miche, M 1951. Le Pouvoir reflechissant des ouvrages maritimes exposes a l' action de la houle. Annals des Ponts et Chaussess, 121: 285-319 (translated by Lincoln and Chevron, University of California, Berkeley, Wave Research Laboratory, Series 3, Issue 363, June 1954). [ Links ]
Misra, S K, Kirby, J T, Brocchini, M, Veron, F, Thomas, M & Kambhamettu, C 2008. The mean and turbulent flow structure of a weak hydraulic jump. Physics of Fluids, 20(3): 035106-03121. [ Links ]
Nadaoka, K & Kondoh, T 1982. Laboratory measurements of velocity field structure in the surf zone by LDV. Coastal Engineering, 25: 125-145. [ Links ]
Pedersen, C, Deigaard, R & Sutherland, J 1998. Measurements of the vertical correlation in turbulence under broken waves. Coastal Engineering, 35: 231-249. [ Links ]
Petti, M & Longo, S 2001. Turbulence experiments in the swash zone Coastal Engineering, 43: 1-24. [ Links ]
Raffel, M, Willert, C E & Kompenhans, J 1998. Particle Image Velocimetry, A Practical Guide, Berlin: Springer. [ Links ]
Raubenheimer, B 2002. Observations and predictions of fluid velocities in the surf and swash zones. Journal of Geophysical Research, 107(C11), 3190, doi: 10.1029/2001JC001264. [ Links ]
Raubenheimer, B, Elgar, S & Guza, R T 2004. Observations of swash zone velocities: A note on friction coefficients. Journal of Geophysical Research, 109, C01027, doi: 10.1029/2003JC001877. [ Links ]
Shin, S & Cox, D 2006. Laboratory observations of inner surf and swash-zone hydrodynamics on a steep slope. Continental Shelf Research, 26: 561-573. [ Links ]
Sou, I M & Yeh, H 2011. Laboratory study of the cross-shore flow structure in the surf and swash zones. Journal of Geophysical Research, 116, C03002, doi: 10.1029/2010JC006700. [ Links ]
Sou, I M, Cowen, E A & Liu, P L-F 2010. Evolution of the turbulence structure in the surf and swash zones. Journal of Fluid Mechanics, 644: 193-216. [ Links ]
Standsby, P K & Feng, T 2005. Kinematics and depth-integrated terms in surf zone waves from laboratory measurements. Journal of Fluid Mechanics, 529: 279-310. [ Links ]
Stive, M J F 1980. Velocity and pressure field of spilling breaker. Paper presented at the 17th International Conference of Coastal Engineering, ASCE, Sydney, Australia. [ Links ]
Stull, R B 1988. An Introduction to Boundary Layer Meteorology. Vancouver, Canada: Kluwer Academic. [ Links ]
Svendsen, I A 1984. Wave heights and set-up in a surf zone. Coastal Engineering, 8: 303-329. [ Links ]
Svendsen, I A 1987. Analysis of surf zone turbulence. Journal of Geophysical Research - Oceans, 92(5): 5115-5124. [ Links ]
Tennekes, H & Lumley, J L 1972. A First Course in Turbulence. Cambridge: MIT Press. [ Links ]
Ting, F C K & Kirby, J T 1995. Dynamics of surf-zone turbulence in a strong plunging breaker. Coastal Engineering, 24: 177-204. [ Links ]
Weng, W G, Fan, W C, Liao, G X & Qin, J 2001. Wavelet-based image de-noising in (digital) particle image velocimetry. Signal Processing, 81: 1503-1512. [ Links ]
Willert, C E & Gharib, M 1991. Digital particle image velocimetry. Experiments in Fluids, 10: 181-193. [ Links ]
Wu, J Z, Ma, H Y & Zhou, M D 2006. Vorticity and Vortex Dynamics. Berlin-Heidelberg: Springer. [ Links ]
 Contact details:
Contact details:
Raphael Mukaro
School of Chemistry and Physics
University of KwaZulu-Natal
Private Bag X54001
Durban 4000
South Africa
T: +27 31 260 1163
F: +27 31 260 7795
E: mukaror@ukzn.ac.za
 Contact details:
Contact details:
Kessie Govender
Department of Electrical Engineering Cape Peninsula University of Technology
PO Box 1906
Bellville 7535
South Africa
T: +27 76 134 570'
School of Chemistry and Physics University of KwaZulu-Natal
Private Bag X54001
Durban 4000
E: kessie.gov@gmail.com

RAPHAEL MUKARO has been a lecturer at the Jniversity of KwaZulu-Natal (UKZN) since 2008, where he teaches third-year modules in Applied Physics (mainly Electronics, Signal Processing Techniques and Measurement Systems), and where he is also the coordinator of the Applied Physics programme. He received his MPhi degree, BSc Honours Physics and BSc Genera (Physics & Statistics) all from the University of Zimbabwe. In 2006 he was awarded Young Scientist of the Year for Zimbabwe, an award by the Research Council of Zimbabwe on behalf of the Third World Academy of Sciences (TWAS), in recognition of his published research on microprocessor-based measurement and control systems and the associated supervisory software that he developed for research and teaching in physics. His current research interests are in digital, statistical and wavelet study of laboratory plunging water waves. The work reported here forms part of his PhD dissertation, which has just been submitted for examination. In 2010 he received the student prize for best paper in the PhD category at the 7th South African Conference on Computational and Applied Mechanics (SACAM10) that was held at the University of Pretoria.

DR KESSIE GOVENDER has a wide range of work and research experience ranging from electrical engineering to physics. One of his research interests is in signal processing with application to geophysical problems. He has recently taken up a post as senior lecturer in the Department of Electrical Engineering at the Cape Peninsula University of Technology. Prior to this he worked for the South African Space Agency in Hermanus as a research support unit manager for two years and as a lecturer in physics for the University of KwaZulu-Natal for ten years. Dr Govender is also currently an Honorary Research Fellow in the School of Chemistry and Physics at the University of KwaZulu-Natal.
NOTE
Complementary documentation of the wave maker specifications and wave generation mechanism may be found at: http://www.hrwallingford.co.uk/index.aspx?facets=equipment