Serviços Personalizados
Artigo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em Google
Similares em Google
Compartilhar
Journal of the South African Institution of Civil Engineering
versão On-line ISSN 2309-8775
versão impressa ISSN 1021-2019
J. S. Afr. Inst. Civ. Eng. vol.55 no.2 Midrand Jan. 2013
TECHNICAL PAPER
Strong winds in South Africa: Part 1 Application of estimation methods
A C Kruger; J V Retief; A M Goliger
Contact details
ABSTRACT
The accurate estimation of strong winds is of cardinal importance to the built environment, particularly in South Africa, where wind loading represents the dominant environmental action to be considered in the design of structures. While the Gumbel method remains the most popular applied method to estimate strong wind quantiles, several factors should influence the consideration of alternative approaches. In South Africa, the most important factors influencing the choice of method are the mixed strong wind climate and the lengths of available wind measurement records. In addition, the time-scale of the estimations (in this case one hour and 2-3 seconds) influences the suitability of some methods.
The strong wind climate is dominated by synoptic scale disturbances along the coast and adjacent interior, and mesoscale systems, i.e. thunderstorms, in the biggest part of the interior. However, in a large part of South Africa more than one mechanism plays a significant role in the development of strong winds. For these regions the application of a mixed-climate approach is recommended as more appropriate than the Gumbel method.
In South Africa, reliable wind records are in most cases shorter than 20 years, which makes the application of a method developed for short time series advisable. In addition it is also recommended that the shape parameter be set to zero, which translates to the Gumbel method when only annual maxima are employed. In the case of the Peak-Over-Threshold (POT) method, one of several methods developed for short time series, the application of the Exponential Distribution instead of the Generalised Pareto Distribution is recommended. However, the POT method is not suitable for estimations over longer time scales, e.g. one hour averaging, due to the high volumes of dependent strong wind values in the data sets to be utilised. The results of an updated assessment, or the present strong wind records reported in this paper, serve as input to revised strong wind maps, as presented in the accompanying paper (see page 46).
Keywords: strong wind climate, South Africa, extreme-value distributions, wind statistics
INTRODUCTION
The primary input to the development of a strong wind climatology or atlas is observed wind data. This data should be analysed by the application of the most relevant statistical techniques available, by taking the underlying theoretical statistical distribution into account, and also the assumptions that are accompanied by the application of such a distribution.
Typical methodologies applied in the development of strong wind climatology mainly comprise a broad discussion of statistical extreme-value theory, but relevant to wind data. Discussions of the methodologies developed for special cases in extreme-value analysis, such as those developed for short time series and time series subjected to an underlying mixed strong wind climate (where the sources of the measured strong wind values are forthcoming from more than one type of strong wind producing mechanism), are also presented. The consideration of the latter methodologies is crucial, firstly because some of the time series to be utilised in this study can be considered to be quite short, but also due to the fact that a large part of South Africa exhibits a mixed strong wind climate (Kruger et al 2010). It should be noted that, although the statistical analysis applied in this paper is based on extreme-value theory, reference is made to strong winds as the outcome of the analysis; extreme winds are typically applied for winds exceeding the design base for structures, or treated as accidental situations (SANS 10160:2011).
Extreme-value theory comprises the statistical methodologies developed to determine the probabilities of specific extreme values to occur, from observed data sets. The optimum statistical method to be applied ultimately depends on the underlying features of these data sets.
BACKGROUND
Wind loading plays a prominent role in the new South African national standard SANS 10160:2011, but is still based on the extreme wind analysis conducted in 1985 (Milford 1985a & b). This study was predominantly based on the Fisher-Tippet Type I or Gumbel distribution. The Gumbel method is the most widely applied to estimate strong winds, mostly because of the relative simplicity of application, but also the conservative assumption that the shape parameter of the extreme-value distribution is equal to zero. However, due to the utilisation of only annual maxima, this method is most suitable for long time series, preferably 30 years or longer. In addition to this, Milford (1985a) identified apparent mixed climatic conditions in the parent distributions of the wind data sets analysed. Kruger et al (2010) confirms this, and indicates that the larger part of South Africa is influenced by more than one strong wind mechanism.
The purpose of the analyses performed in this paper is the identification of the most appropriate strong wind estimation methods to be applied to the available wind speed data in South Africa. The analysis is based on a data set of strong winds extracted from 209 Automatic Weather Stations (AWS) deployed by the South African Weather Service (SAWS) since 1995. Following quality scrutiny an initial set of 94 AWS records was selected and ultimately reduced to 76 records used for the final analysis. An important constraint was to have at least ten years of records at the selected AWS. A limitation of the data set is that the maximum record length is 20 years. A critical feature of the extracted strong wind record is that it includes an observation of the meteorological conditions for each occurrence.
In the fitting of the various statistical distributions, the Anderson-Darling goodness-of-fit test has been applied, as this test is particularly sensitive to deviations in the tails of the distribution (D'Agostino & Stephens 1986). The results from this test implied that all the applied statistical distributions fitted the data in a satisfactory manner.
The results of the extreme-value analysis of the recent extensive strong wind data set are applied in the update of mapping the strong wind statistics for South Africa, as reported in the accompanying paper (Kruger et al 2013).
APPLICATION OF GENERALISED EXTREME-VALUE DISTRIBUTIONS
The most widely used methods to estimate extreme wind speeds are based on the classical or Generalised Extreme-Value (GEV) theory, of which a short review is presented by Palutikof et al (1999). The GEV distribution is only fitted to the extreme values, usually the annual maxima.
In the annual maxima method, an Extreme-Value (EV) distribution is fitted to the annual maximum wind speed values. By using this method only independent annual extreme values are used in the fitting of the distribution. For sufficiently long sequences of independent and identically distributed random variables, the maxima of samples of size n, for large n, can be fitted to one of three basic families. These three families were combined into a single distribution (Jenkinson 1955), and is known as the GEV distribution, with cumulative distribution function (cdf):
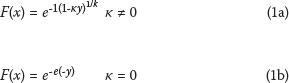
where κ is the shape parameter, which determines the type of extreme-value distribution, and y is the standardised or reduced variate. The Gumbel or Fisher-Tippett Type I distribution has a value of κ = 0, the Fisher-Tippett Type II has κ < 0, while the Type III has κ > 0. Types I and II are unbounded at the upper end, while Type III is bounded. This means that there will be an upper bound for the quantile values estimated with the Type III distribution, while no upper bound exists for Types I and II.
Gumbel method
The Gumbel method is the most often applied method to estimate extreme wind speeds. This is firstly because of the fact that the shape parameter, κ, of the Gumbel distribution is equal to zero, and therefore simplifies the calculations. The second reason is that one of the parent distributions of the Gumbel distribution is the Weibull distribution, which is considered to be a good model for the distribution of the wind speed (Hennessey 1977; Perrin et al 2006).
There are different options of methodologies which are often applied to estimate the parameters of the Gumbel distribution, i.e. the scale or shape α, and the mode β. These methods include graphical methods, probability weighted moments, maximum likelihood solutions and the method of moments. All of these methods should produce similar results. A graphical solution to the estimation of α and β is often preferred (Palutikof et al 1999).
The graphical method is based on the standardised or reduced variate y given by:

where α is the scale or dispersion parameter, β is the mode of the extreme-value distribution, and x is the extreme value, which is then modified to

where the slope α gives the scale or dispersion, and β, the mode. To estimate a value for y, the Gumbel reduced variate
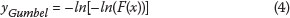
is used. F(x) is empirically estimated for each of the observed annual maxima. For the Gumbel distribution, the most unbiased estimates are given by

where xm is the mth ranked annual maximum wind speed, and N is the number of annual maxima (Gringorten 1963 in Palutikof et al 1999). A value for yGumbel can be calculated for each value of x, and a least-squares fit is used to fit a straight line to this data set. From this straight line the parameters α and β can be found.
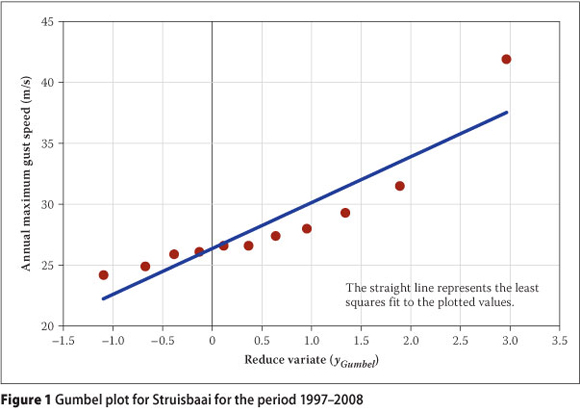
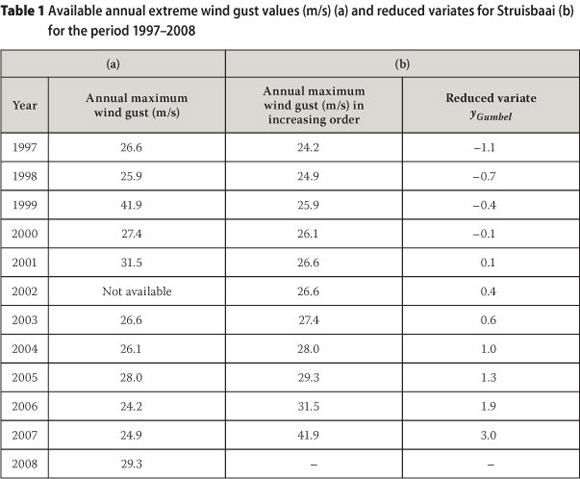
As an example, the graphical method is applied to the annual extreme wind gust data for Struisbaai, on the southern Cape coast, which is presented in Table 1. In the third column the wind gust values are shown in increasing order, xm, from the smallest to the largest, from which the plotting positions F(xm) were determined from Equation 5. Values for the reduced variate, yGumbel, could then be calculated with Equation 4.
Figure 1 presents the Gumbel plot, yGumbel against x (the annual maximum wind gust values), as well as the least-squares fit to the plotted values. The fitted straight line has equation y = 3.8x + 26.4, from which the estimations for α and β are then acquired as 3.8 and 26.4 respectively.
Alternatively, the estimation of the Gumbel parameters by the method of moments (Wilks 2006), which only uses the sample mean and standard deviation to estimate the Gumbel parameters, would be:

where s is the standard deviation of the sample, x is the sample mean, and γ = 0.57721... is Euler's constant. The estimations of the Gumbel parameters were calculated using the above method, and produced estimates for α as 3.7 and β as 26.3.
The estimated 1:50 year quantiles are 40.8 m/s and 40.6 m/s for the above two methods respectively. Comparisons of the results between the two methods for the data sets of other weather stations produce similar small differences between the results. According to Abild (1994) and Hosking et al (1985), in Larsén & Mann (2009), the method of moments yields less bias and variance on the parameter estimates, and has been proved highly efficient even for small sample sizes. It was therefore decided to estimate the coefficients of all the fitted Gumbel distributions with the method of moments. To be noted, the level of confidence of the estimations, and therefore the uncertainties, is not taken into consideration here.
The quantile XT, which is the value of X to be expected every T years, can now be calculated with
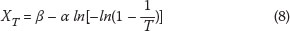
The quantiles of the annual maximum gust speeds and annual maximum hourly wind speeds, with return periods 50, 100 and 500 years, were then calculated accordingly. It is recognised that there should be substantial reservations in the estimations of quantiles for long return periods such as 100 and 500 years based on the short time series; these are only estimated for comparative purposes between the different methodologies. For illustrative purposes, the degree of extrapolation of the quantiles beyond the data record for Struisbaai is presented in Figure 2.
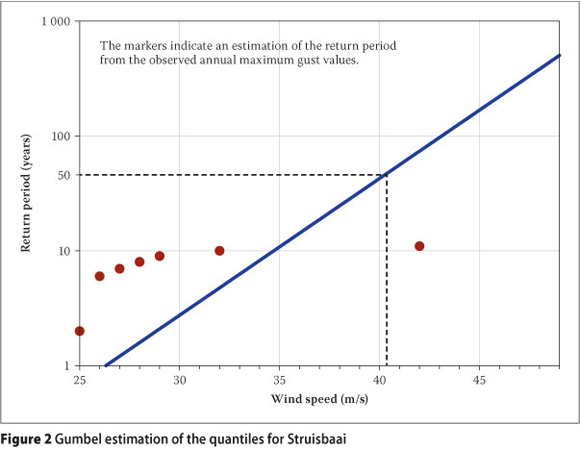
The Gumbel results for the main centres in South Africa, as well as other significant weather stations, are presented in Table 2. The results for a set of 84 selected weather stations are included in Kruger (2011).
Fitting of the GEV distribution
In fitting the Gumbel distribution to a set of data, it is assumed that the shape parameter, κ, of the GEV distribution equals zero.
Various authors dispute this, and often give a choice between the Type I (κ = 0) and Type III form (κ > 0) of the GEV distribution.
It is assumed that the Type II form (κ < 0) is usually indicative of a wind data series composed of wind speeds forthcoming from different strong wind producing mechanisms (Gomes & Vickery 1978), producing a thicker tail to the distribution, which can cause unrealistically high values for wind speed quantiles at longer return periods. Such wind series should ideally be decomposed, and the wind speeds forthcoming from the different strong wind producing mechanisms treated separately, and a method for mixed strong wind climates applied.
The biggest criticism of the application of the Type III form is that the distribution is bounded from above, and Palutikof et al (1999) argue that there is no physical justification for a natural upper bound for wind speed, especially at the order of magnitude at which wind speeds are naturally observed. However, Walshaw (1994) argues that a Type III distribution should be fitted if it fits the data better than a Type I. Lechner et al (1992) showed that for 100 wind time series in the United States, 36 showed a Type I form, three a Type II form and 61 a Type III form.
By assuming that the shape parameter, κ, is not equal to zero, GEV distributions were fitted to the annual maximum wind gusts, as well as the annual maximum mean hourly wind speeds, of the set of weather stations. Three distribution parameters, κ, α, and β, therefore needed to be estimated, i.e. the shape parameter, the scale or dispersion parameter, and the mode, respectively. The estimations of these values can be mathematically intensive and therefore the use of applicable software is advisable. Here the EasyFit software (www.mathwave.com) was employed, which estimates the distribution parameters by the ML solutions. This method follows an iterative procedure until the iterations reach a specified maximum, in this case 1 000 iterations, which are deemed sufficient to obtain accurate estimates.
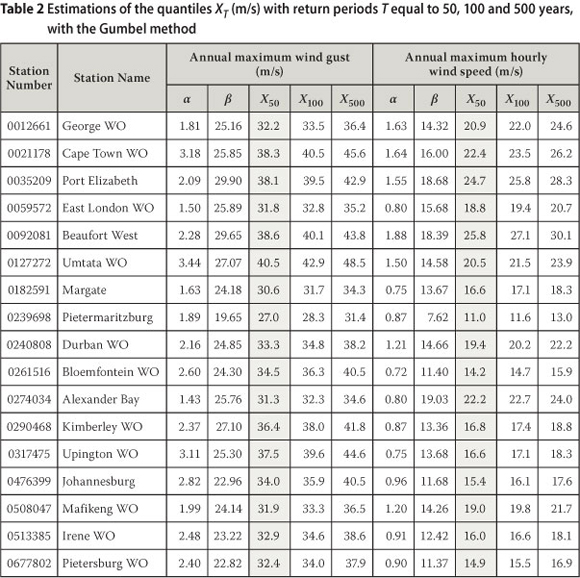
Figure 3 presents the fitting of the GEV distribution to the annual maxima of the wind gusts of Struisbaai, for which the value of the κ parameter was estimated as -0.47, i.e. a very strong form of Type II. Interesting to note is that, while the quantile estimations for the Type II is much higher than Type I for the longer return periods, the quantile estimations for the shorter return periods, e.g. ten years, are actually lower, due to the shape of the distribution.
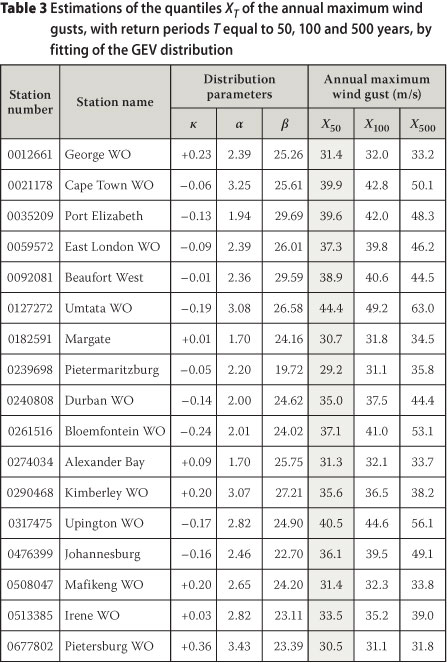
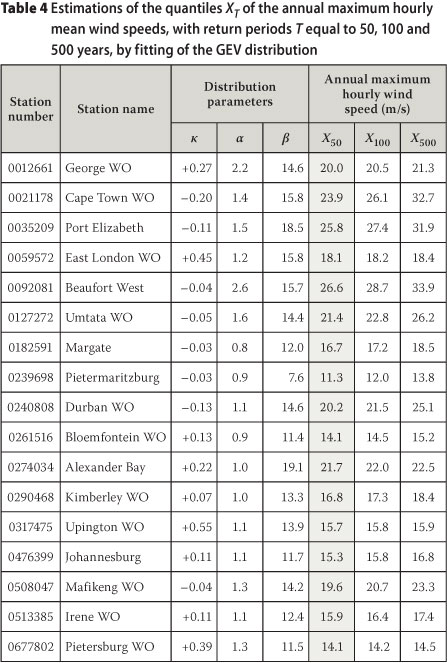
Tables 3 and 4 present the results of the estimations of the annual maximum gusts and annual maximum hourly wind speeds, for the quantiles of the same return periods as those estimated with the Gumbel distribution, presented in Table 2.
Further analysis and discussion of results
From the results presented in Tables 3 and 4 it is apparent that fitting of the GEV distribution to the available data sets led to the shape parameter, κ, almost as a rule, to be estimated not close to zero. For the set of 94 weather stations utilised by Kruger (2011) the estimated values for κ range from -0.47 to 1.07; and for the annual maximum hourly mean wind speeds from -0.35 to 0.55.
Figures 4 and 5 illustrate the annual extreme wind gusts, and annual maximum hourly mean wind speeds estimated with the GEV and Gumbel distributions differ as a function of the value of κ. As can be expected, a negative value of κ corresponds to a quantile value estimated with the GEV distribution to be higher than that estimated with the Gumbel distribution. This is because a negative shape parameter implies a thicker tail of the GEV distribution, compared to the Gumbel distribution.
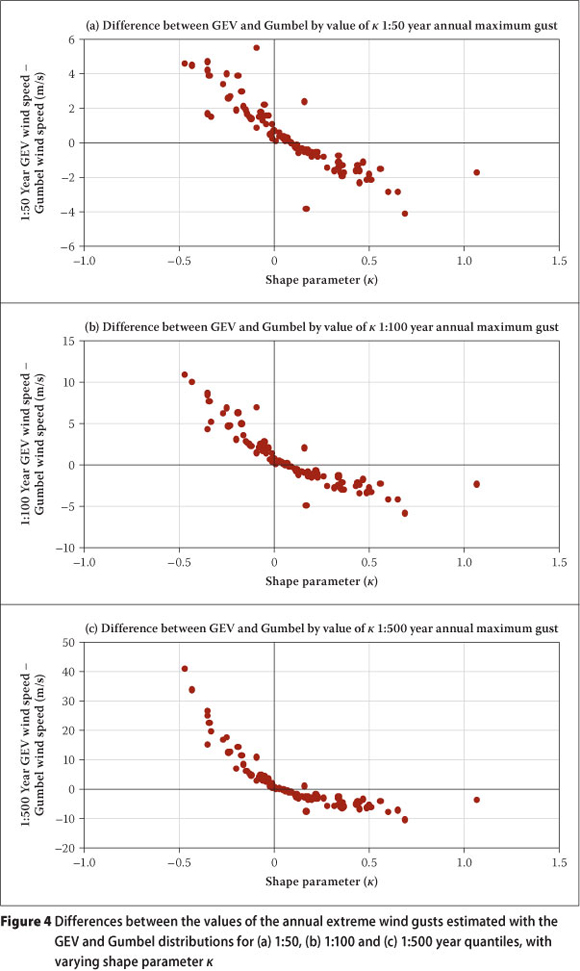
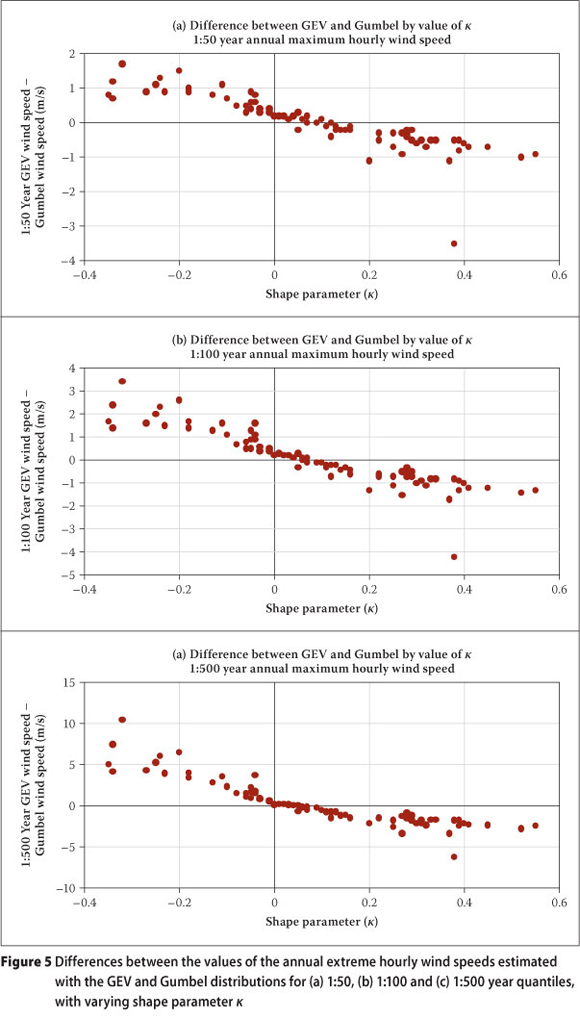
A positive value of κ corresponds to a quantile value estimated with the GEV distribution to be lower than that estimated with the Gumbel distribution, as a positive shape parameter implies that there is an upper bound to the quantile values which are estimated with the GEV distribution. As the deviations of the values of κ from zero become larger, the differences between the values of the quantile values estimated with the GEV distribution and that estimated with the Gumbel distribution also become larger. This is especially true when the quantiles for annual extreme wind gusts are estimated for long return periods, with negative values for κ.
As mentioned before, the Type II distribution is seldom resolved from a GEV analysis, and might indicate a mixed wind series (Abild et al 1992; Brabson & Palutikof 2000; Palutikof et al 1999). However, the data analysed in Kruger (2011) suggest quite a high percentage of weather stations in South Africa with annual maximum wind series exhibiting negative values for κ. For the annual maximum wind gusts 39% of weather stations had negative values for κ, while for annual maximum hourly wind speeds the figure is 32%. Also, negative κ values were found for weather stations where strong winds are caused by only one strong wind producing mechanism. No link between the sign of κ and the particular strong wind producing mechanisms could be found.
It is argued here that another possible cause for negative values for κ could be anomalous values, where the annual maximum values for one or a few years are much higher than the other values in a particular data set. These values are not regarded as possibly incorrect, as the data values utilised in these analyses have been thoroughly quality controlled. The fitting of a GEV distribution to data series is affected by these values, and can therefore indicate a Type II distribution when it is physically not justifiable - this is particularly relevant to short time series. To take Cape Town (κ = -0.20) as an example - the quantiles are estimated from strong winds measured during the passages of cold fronts. One should therefore assume that the quantile estimations for Cape Town should fall within the range expected from the strongest winds that can be generated by cold fronts, even for long return periods. However, this is not the case, as the 1:500 year quantile from the GEV method, for the hourly mean wind speeds shows: the estimated quantile of 32.7 m/s falls in the maximum wind category of the Beaufort wind scale, an empirical measure to describe wind speed, which indicates hurricane strength winds. However, the Gumbel estimate for the 1:500 year hourly mean wind speed for the same station is 24.6 m/s, which falls into the category for a storm or gale, and is consistent with wind strengths to be expected during a very strong cold front.
With regard to the above, Brabson & Palutikof (2000) illustrated the effect of the addition of four very large annual maxima, when the time series for Sumburgh (UK) was extended from a 13-year sample to a 25-year sample. The addition of these values dramatically raised the 100-year quantile value from 45.3 m/s to 56.8 m/s, well outside the standard errors calculated on the basis of the 13-year sample. However, the Gumbel predictions were less affected by the addition of the new data. It is also important to note from that analysis that the extension of the data set caused the difference between the quantile estimations with the GEV and Gumbel to be smaller, than with the shorter time series (0.1 m/s compared to 6.4 m/s). Brabson & Palutikof also showed, using additional weather stations, that the longer the time series utilised, the closer the value for κ is estimated to zero. With additional analyses they concluded that the generalised models, whether GEV or GPD, if brought to rely on 13 years of data, fail to predict the actual maximum gust speeds observed over a longer 25-year period. They attributed this failure largely to the non-stationarity in the wind climate in the region. This has the effect that the extreme values are not evenly distributed in a wind time series - this of course will apply to South Africa, as well, because of the cyclical behaviour of the climate.
The median of a data set is robust to outliers or anomalous values, while the average is not. The difference between the median and the average can therefore provide an indication of the magnitude of anomalous values in a data set. Figure 6 presents the relationship between κ and the difference between the median and the average, of all the data sets of the annual maximum wind gusts. The graph illustrates the fact that there is a statistically significant correlation between the value of the difference between the median and the average, and the value of κ.
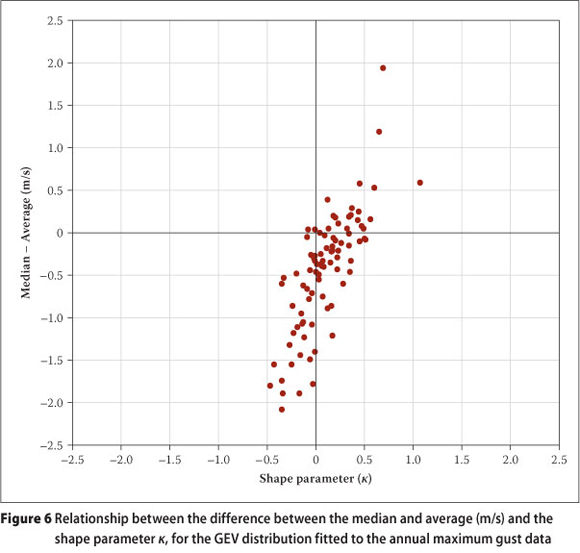
An example of how an anomalous value in a data set can make a significant difference in the values of the estimated quantiles, is for the data set for Umtata. The annual maximum gust speed for Umtata for 1999 is a verified 39.3 m/s, which was measured on 3 November 1999. This value is much higher than the mean of the annual maximum gust speeds, which is 27.8 m/s. If, for illustrative purposes, the value of 39.3 m/s is removed from the data set, the 1:50 year quantile for the wind gust becomes 35.6 m/s, compared to the 40.5 m/s with the high value included. It is concluded here, with the analyses presented in this section and those by Brabson & Palutikof (2000), that the fitting of the GEV distribution to small data sets of annual extreme winds should be treated with caution, and is in general not recommended.
METHODS FOR SHORT TIME SERIES
The problems in fitting the GEV distribution will be more pronounced for smaller data sets, such as those utilised in this research, which are all shorter than 20 years. Therefore other approaches to estimate the extreme wind speeds, specifically developed for shorter time series, were investigated to compare the results with those from the traditional methods and, by doing so, to identify the most appropriate statistical method to apply to the available wind data sets.
The well-known approaches to estimate extreme winds for shorter time series are discussed in Palutikof et al (1999), of which the methodologies in most cases contain some elements of subjectivity. At the same time, it has to be ensured that wind speed values extracted from the original wind data sets, for fitment to the statistical distributions, should be as independent and identically or evenly distributed as possible.
Regarding the extension of a single extreme value per epoch to include the r-largest values (Weissman 1978), decisions have to be taken on the size of r, as well as the minimum separation distance or time between extreme values. The separation distance might depend on the type of wind data, whether wind gusts or mean wind speeds over longer periods, as well as the type of strong winds experienced at the location where the wind measurements were taken.
Using the Method of Independent Storms (MIS) a decision has to be taken on the threshold value which separates individual storms. This value should be high enough to ensure that the storms identified are independent and eliminate the possibility of one larger storm which contains a lull in wind speed during the period it occurred. Also, individual storms might be separated by lulls with wind speeds of different values, complicating the choice of the threshold value.
With the Peak-Over-Threshold (POT) method a decision also has to be taken regarding the threshold value, as well as the separation distance, similar to the method that employs the r-largest values. However, if a separation distance is deemed sufficient by taking the prevailing weather systems into account, the threshold value can be inferred or derived without deciding on a specific value beforehand. The POT approach is the most widely used method to estimate extreme winds from short wind data time series and, due to the above considerations, it was decided to apply this method to the available wind data sets.
Application of Peak-Over-Threshold (POT) method
With POT methods, all values exceeding a specific threshold are used for analysis. A General Pareto Distribution (GPD) is fitted to the selected values. The CDF (Cumulative Distribution Function) of the GPD is
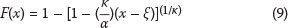
where ξ is the selected threshold. For κ = 0, the GPD simplifies to the exponential (EXP) distribution

The crossing rate of the threshold is defined as

where n is the total number of exceedances, and M is the total number of years of the time series. Quantiles for specific return periods (in years) can be calculated from Abild et al (1992):
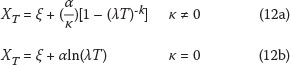
The distribution parameters α and k can be estimated by

which are valid within the range -0.5 < κ < 0.5. The threshold value should ensure a sufficient separation time between selected strong winds to avoid the interdependence of values. A separation time of 48 hours was selected by various authors for European wind climates (Cook 1985; Gusella 1991). The European wind climate is dominated by synoptic-scale strong wind producing mechanisms, especially the passages of extratropical cyclones. In South Africa the situation is similar for hourly mean wind speeds and gusts in many regions, and therefore this separation time was deemed to be appropriate. However, in a large part of the country most strong wind gusts are produced by thunderstorms in which individual systems can easily be separated by a period of one day only. Therefore, in the analysis of hourly mean wind speeds, the separation time was strictly deemed to be 48 hours, while for wind gusts, more flexibility was allowed by taking the particular strong wind mechanism and synoptic conditions into account.
To obtain a sufficient number of strong wind data values, one must accept that not all of the data values will be independent. In this regard the finding by Brabson & Palutikof (2000) was taken into account, in which the value of the independent event index, ε, is defined as
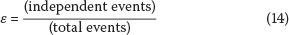
which can be as low as 0.8 to obtain accurate quantile estimates from the GPD.
In analysing the wind data, a range of threshold values were selected in 2.5 m/s increments. The data sets extracted according to these thresholds were then checked to identify the data set with the largest number of wind speed values and a value of ε that is at least 0.8. The GPD was then fitted to the selected series of values. The POT method is not compatible with hourly mean wind speed data, with too high percentages of values, even with very high thresholds, showing dependency. Table 5 presents the quantiles XT of the annual maximum wind gusts for return periods T equal to 50, 100 and 500 years, for the weather stations in Table 2, by application of the POT method. In Kruger (2011) the number of values n that could be selected varied widely between stations, with λ (the average number of values per year) ranging from 1.50 to 19.20. A high value for λ indicates a better separation of individual storms than when λ is low, because a larger number of independent strong wind values could be utilised. A low value of λ indicates that the strong winds tend to be clustered in the time series. It is, therefore, not surprising that the weather stations in those regions in the interior where thunderstorms are likely to occur frequently, exhibit in general higher λ values than those closer to the coast, where synoptic scale systems tend to cause most strong winds.
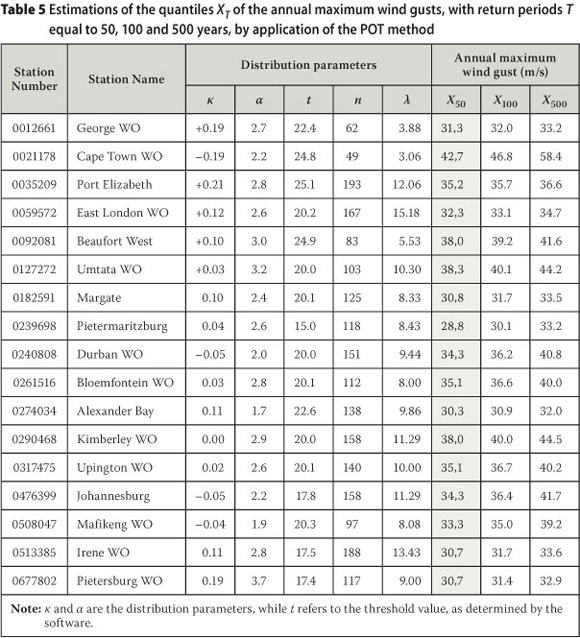
The advantage of the POT method, above methods which employ only one value per epoch, is that usually significantly more values can be utilised, which will in turn result in more confident estimates of the extreme wind quantiles. On the other hand it can be argued that a very large number of values can dilute the effect of the more extreme values in the data. However, it is assumed here that in general greater confidence can be given to quantiles estimated with values of λ much larger than 1, compared to a situation when only one value per epoch is utilised, as long as the values are independent and therefore assumed to be Poisson distributed.
Fitting of the exponential distribution
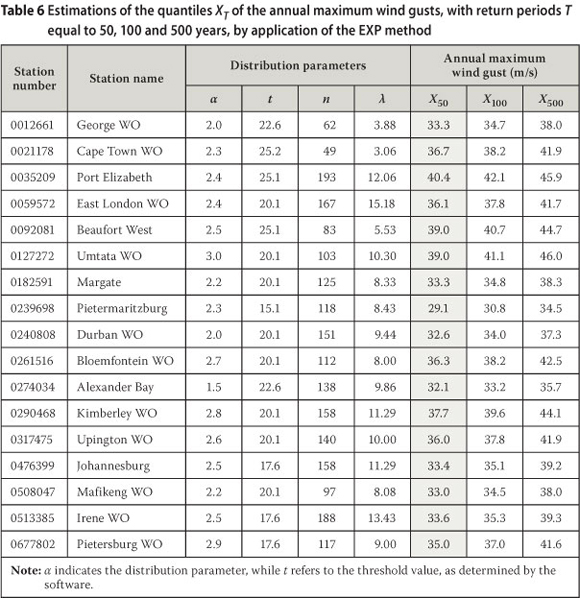
When the POT method is applied with the GPD, one of the parameters to be estimated is the shape parameter κ, similar to the GEV distribution. However, it was shown with the results of the fitting of the GEV distribution to a small number of data values, that κ can then be under- or overestimated. In fact, Brabson & Palutikof (2000) show in their analyses that the value of κ varies with a varying threshold value. From Table 5 it can be seen that the number of data values available for POT analysis, and the threshold values deemed most appropriate, vary substantially between the weather stations. In this section we fit the same data sets to which the GPD was fitted to the Exponential (EXP) distribution, i.e. the GPD with κ = 0. Table 6 presents the results of the analyses, also with estimations of the quantiles XT, with return periods T equal to 50, 100 and 500 years, for the same weather stations as in Table 2.
Comparison between application of GPD and EXP distributions
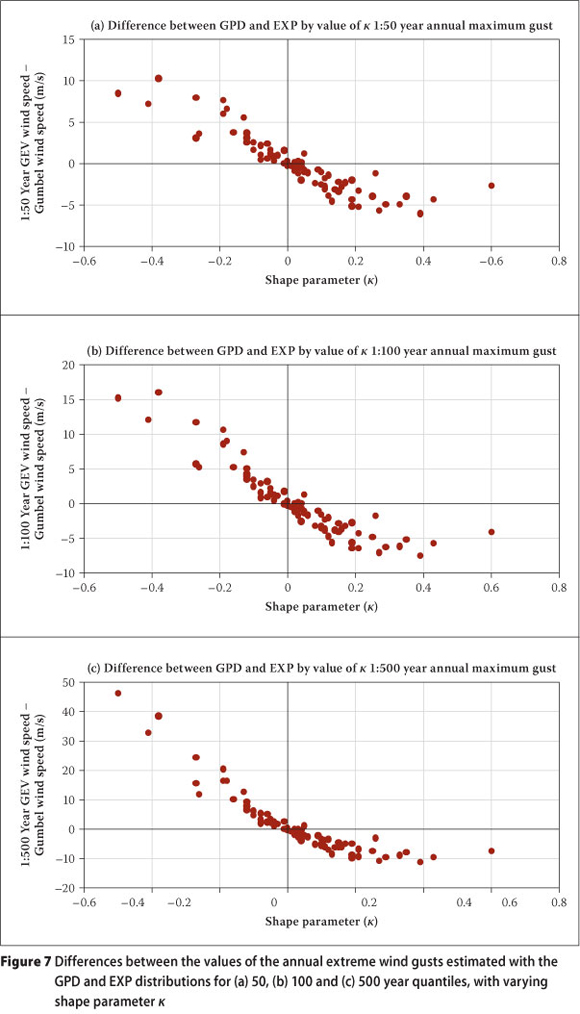
As with the comparison between the results of the Gumbel and GEV methods, it can be seen that the estimated quantiles are sensitive to the value of κ, which confirms the finding of Simiu & Heckert (1996). The general result is that with the GPD method, positive values of κ render quantile values lower, while negative values of κ render quantile values higher than that estimated with the EXP method. Figure 7 illustrates how the difference between annual extreme wind gusts estimated with the GPD and EXP distributions differ, with the estimated value of κ. The trends which can be observed are similar to those in the analysis which was presented in Figure 4. Because the GPD method is more flexible than the EXP method, the GPD distribution should fit the data better than the EXP distribution, as demonstrated by Brabson & Palutikof (2000). However, it was also illustrated that the downside of this flexibility is that estimated values of κ which are highly positive, strongly truncate the tail of the distribution causing a low bound at the upper end. Unlikely low extreme quantile values are then predicted. On the other hand, highly negative estimations of κ predict extreme speeds that are unrealistically strong for the longer return periods. The same argument than that developed for Gumbel vs GEV applies here, that short time series tend to render unrealistic values for κ.
COMPARISON OF THE ANNUAL MAXIMA AND POT METHODS
The κ parameter
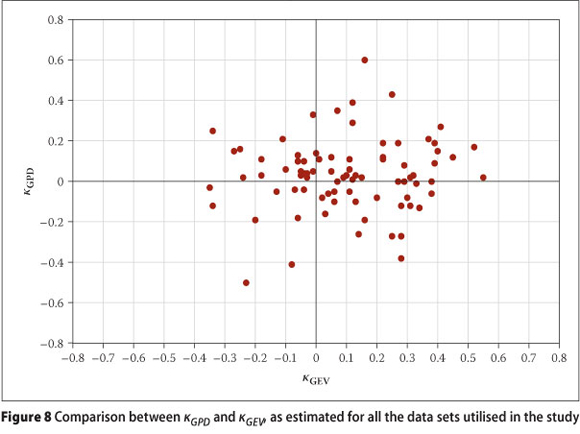
If the gust speed extremes are well described by a single GPD distribution, then κGPD (κ estimated with the GPD) should equal κgev (κ estimated with the GEV), or should approach this value with increase in the threshold value (Brabson & Pautikof 2000). However, this can of course only be true if the estimations for κgpd and κgev are realistic, which may ultimately depend on the size of the data sets utilised to estimate the distribution parameters with. Figure 8 presents a scatterplot comparison between κgpd and κgev for the weather stations utilised in the research. One can see that there is no apparent relationship between the two parameters. This could be due to either the inaccurate estimations of κgpd or κgev, or both.
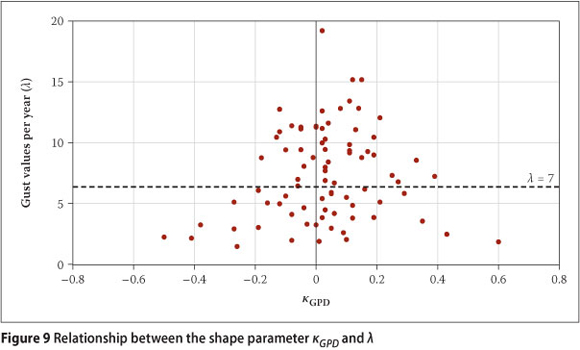
From the above discussion it is apparent that the value of the shape parameter should be treated with suspicion when generalised distributions are applied to short time series. However, the sizes of the data sets utilised in the application of the GPD distribution vary a lot between weather stations, as reported in Kruger (2011), with λ ranging from 1.5 to 19.2, with a median value of 7. It is assumed that the larger the data set utilised, the more accurate the estimated distribution parameters. Figure 9 presents the relationship between κgpd and λ. It is apparent that the values for κgpd tend to be clustered around zero, with the average for the values calculated as 0.05. Another observation is that the values for κgpd show lower variability for the upper half of the data pairs where λ > 7, compared to where λ < 7. The standard deviation for the values of κgpd where λ > 7 is equal to 0.12, while for κgpd where λ < 7 the standard deviation is equal to 0.22; the difference of which is statistically significant.
From the above, and results elsewhere in this paper, it follows then that it can be assumed that, with the available data for this study, the safest estimation for the value of κ is zero. This is consistent with Brabson &
Palutikof (2000) who, after analysing shorter and longer periods of data for the same location, came to the conclusion that the κ = 0 versions of the models make more accurate predictions of extreme wind speeds, even when a shorter period of data is utilised (in their case 13 years).
Abild et al (1992) came to a similar conclusion, namely that, while the GPD and GEV distributions are powerful in detecting outliers, and a possible two-component population in exponential data, the tail behaviour is strongly influenced by the estimation of κ, and will therefore not provide reliable estimates of upper quantiles when fitted to a short record. This shows that the poor behaviour of κ is indicative of the insufficiency of the short time series.
Gumbel and exponential distributions
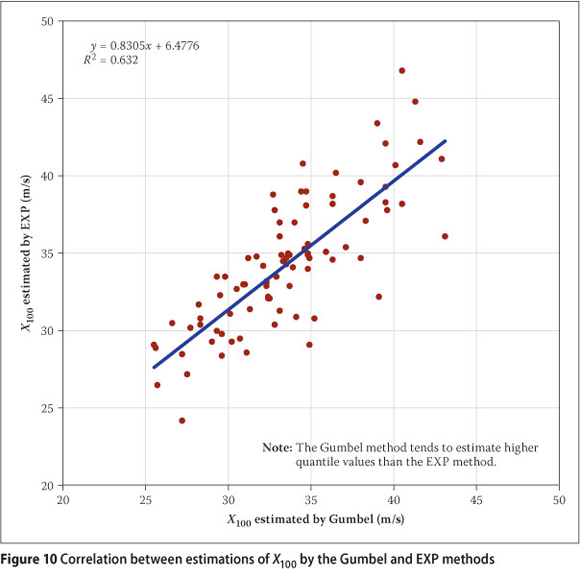
It was concluded in the previous section that, while the GEV and GPD distributions provide a better fit to the data, they do not necessarily make accurate predictions of high wind speeds, when based on a short period of data, or a small average number of data values per year. Figure 10 presents the relationship between X100 estimated by the Gumbel and EXP methods, with the correlation statistically significant at the 95% level of confidence. There is a general tendency for X100 to be estimated higher by the EXP method than with the Gumbel method, when X100 is estimated by the Gumbel method to be below about 38 m/s. This observation applies to about 82% of the X100 Gumbel estimates.
The question arises now which estimates, by the Gumbel or EXP method, can be considered to be the most reliable. Abild et al (1992) suggests that T-year estimates should never be given only as point estimates but should at least also contain some information regarding the uncertainty of the estimate related to the statistical model chosen. Brabson & Palutikof (2000) state that critical to the usefulness of maximum gust speed predictions are their associated standard errors. Calculation procedures for the standard errors of the T-year estimates are described by Hosking et al (1985) and Abild et al (1992). The derivations of the equations for the calculations of the standard deviations or variances will not be repeated here, but for the Gumbel distribution
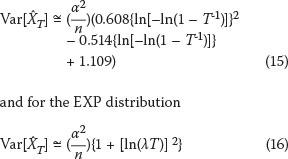
where a is the scale or dispersion parameter, n is the number of wind speed values utilised (in the case of the Gumbel distribution the number of years), T is the return period, and λ is the cross-over rate per year in the case of the POT. It follows then that the standard errors of the quantiles for a specific return period, which express the precision of the estimates of the quantiles, essentially depend on the variability of the wind speed values of the sample, and the number of values in the sample. Table 7 presents the standard deviations S50, S100 and S500 associated with the estimated annual maximum wind gust quantiles X50, X100, and X500 by the Gumbel and EXP distributions, as presented in Tables 2 and 6 respectively.
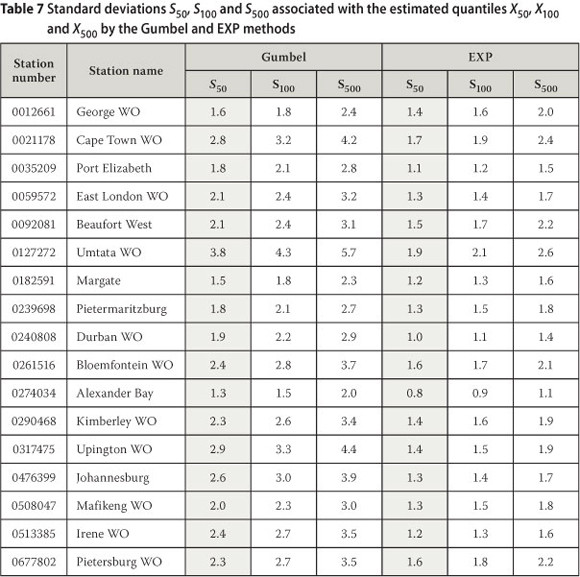
In Kruger (2011) only seven of the 94 weather stations analysed indicate standard errors of the Gumbel method to be smaller than that of the EXP method. For all these stations a was estimated larger for the EXP distribution than for the Gumbel distribution which, referring to Equations 15 and 16, caused the larger values. However, one can conclude that in general more confidence can be put on the quantile values estimated by the EXP method than by the Gumbel method.
MIXED STRONG WIND CLIMATES
As previously mentioned, in the application of the GEV and GPD methods, the estimation of a negative value for the shape parameter κ is often seen as an indication of a mixed strong wind climate, i.e. the data set contains values from two or even more populations or types of events. While these methods are powerful in detecting outliers or a possible two-component (or more) population in exponential data, they will not provide reliable estimates of upper quantiles when fitted to a short record (Abild et al 1992). Twisdale & Vickery (1992), in their analysis of the wind speed data of four weather stations, came to the conclusion that places where thunderstorms dominate the extreme wind climatology, the traditional approach by the Gumbel or POT methods will tend to underestimate the design wind speeds.
These methods assume that all of the winds used to describe the probability distribution of wind speed are produced by the same phenomena, such as large-scale extra-tropical storms. However, this is not always the case, especially for the 2-3 second wind gusts, as in the greater part of the interior of South Africa thunderstorms tend to dominate the strong wind climate (Kruger et al 2010). Therefore, for such data sets extreme wind estimation methodologies should be explored that explicitly take the mixed strong wind climatology into account.
Application of a mixed distribution method
The optimum application or fitting of the mixed speed distribution is described by Gomes & Vickery (1978). This method requires preferably the identification of all strong wind producing mechanisms, which will probably be the cause of the occurrence of an annual extreme wind at a specific station. Gomes & Vickery (1978) disaggregated four extreme wind generating mechanisms, i.e. extra-tropical low-pressure systems, thunderstorms, hurricanes and tornadoes, while Twisdale & Vickery (1992) distinguished between two mechanisms, i.e. extra-tropical low-pressure systems and thunderstorms.
In this study the causes of each of the annual maximum wind gusts and annual maximum hourly mean wind speeds were identified for the individual weather stations. To be noted, the thunderstorms were not considered to be a possible cause of high hourly mean wind speeds, due to their strong winds of usually short duration. Strong winds during a thunderstorm are usually shorter than ten minutes; therefore only the underlying synoptic-scale situation was taken into account.
The descriptions of the different strong wind mechanisms are presented in Kruger et al (2010). The identified causes for each weather station were then considered to be the main strong wind producing mechanisms at a particular station. The disaggregations of the strong wind sources, in the synoptic scale, in the current research are more detailed than in both of the examples of Gomes & Vickery (1978) and Twisdale & Vickery (1992). This approach may improve the accuracy of the extreme wind estimations, and additional information can also be gained from the extreme wind analyses, such as the most likely causes, directions and the time of year of extreme wind estimations for specific return periods. For the annual extreme wind gusts 86% of the 94 weather stations in Kruger et al (2010) exhibited a mixed strong wind climate by application of the disaggregation procedure, while for the annual extreme hourly mean wind speeds the fraction is much lower at 57%.
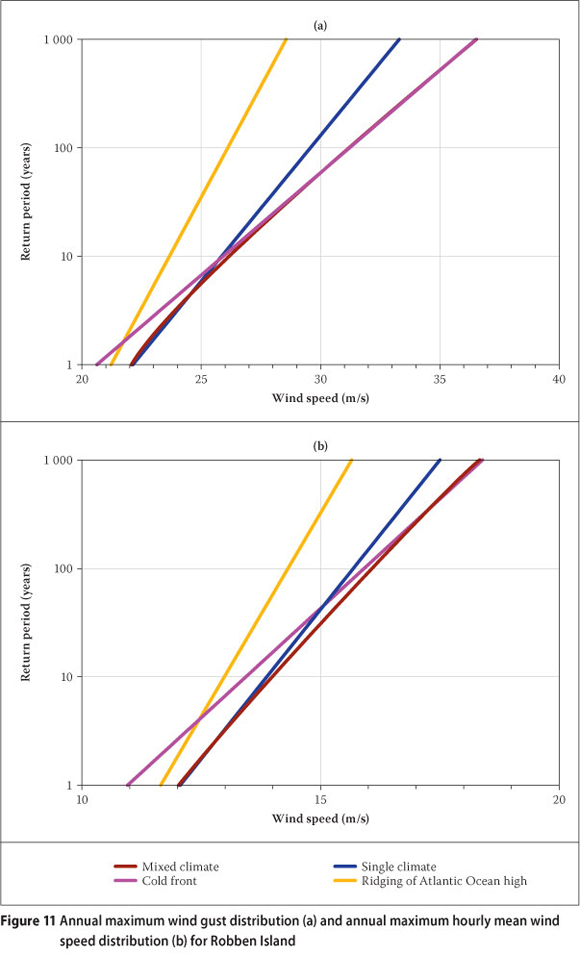
After the identification of the strong wind mechanisms involved at each weather station, the strongest wind gusts and hourly mean wind speeds were determined which were caused by each of the identified mechanisms, for each year of available data. An example of the results of this procedure is presented in Table 8, for the weather station at Robben Island. Here the annual maximum wind gusts, as well as the annual maximum hourly winds, are caused by two mechanisms, namely the passage of cold fronts and the ridging of the Atlantic Ocean high-pressure system. The maximum wind gust values and hourly mean wind speeds produced by each of the mechanisms are also given.
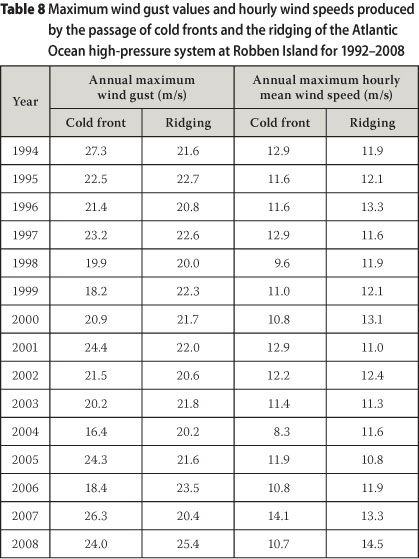
For both the wind gusts and the hourly mean wind speeds, assuming that the values are Gumbel distributed, the combined distribution of these events is determined as the sum of the individual risks of exceedance, given as
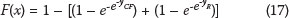
where yCF and yR are the reduced variates for the data sets for the cold fronts and ridging respectively.
Therefore,
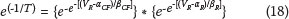
where T is the return period, αcf and βCF are the dispersion and the mode parameters of the cold front values, αR and βR are the dispersion and the mode parameters of the values associated with ridging, and VR is the wind speed associated with the return period T. The return period estimations for a specific wind speed could then be determined by
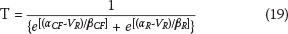
Figure 11 presents the quantile estimates for the annual maximum wind gusts as well as the annual maximum hourly mean wind speeds, by the method for mixed strong wind climates and the Gumbel method. Also shown are the quantile estimates where the Gumbel method has been applied to the data sets for cold fronts and ridging, presented in Table 8. One can see that the distribution patterns are similar for extreme wind gusts and hourly mean wind speeds. One may also assume that from a return period of about 50 years for the wind gusts, and 100 years for the hourly mean wind speeds, the annual extreme winds will probably be caused by the passage of cold fronts, of which the strongest usually occur during the winter months. The wind directions of these winds are usually north-westerly.
An example of a weather station where thunderstorms are one of the main causes of extreme wind gusts is Jamestown in the Eastern Cape Province. Figure 12 presents the annual maximum wind gust distribution for this weather station, from which one notices large differences between the quantile estimates by the mixed climate method and the conventional Gumbel method.
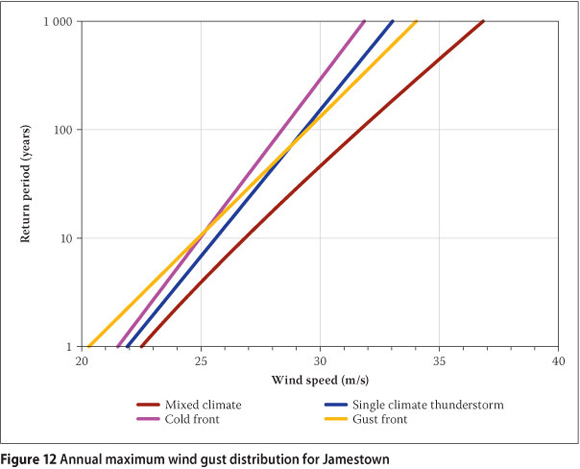
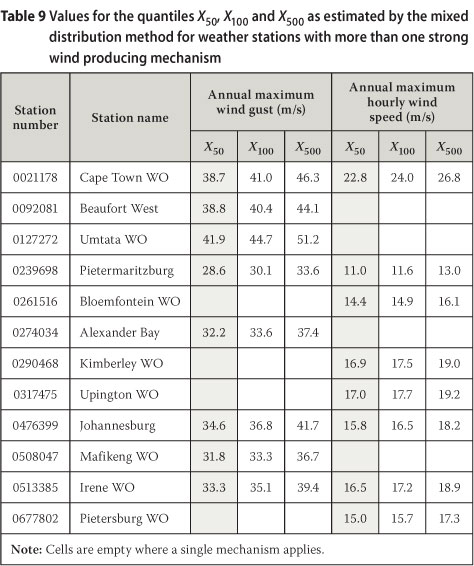
Table 9 presents the values for the quantiles X50, X100, and X500, as estimated by the mixed distribution method, for both annual maximum wind gusts and mean hourly wind speeds, for the weather stations listed in Table 2 which exhibit a mixed strong wind climate (cells are empty where a single mechanism applies).
Further analyses and discussion of results
The κ parameter and mixed distributions
The assumption that a negative shape parameter κ, estimated by fitting of the GEV distribution, or GPD distribution with the POT method, might indicate a mixed distribution of the wind values in the data samples is here investigated further. With the data sets utilised in Kruger (2011), more than one strong wind mechanism was identified for 23 of the 35 weather stations with κ < 0, estimated by fitting of the GEV distribution to annual maximum gust speeds. For mean hourly winds, 15 of the 29 weather stations with κ < 0, estimated by the fitting of the GEV distribution to annual maximum mean hourly wind speeds, had more than one identified strong wind mechanism. It is therefore apparent that mixed distributions are not the only cause for negative estimations of κ, as not all weather stations with κ < 0 have mixed strong wind climates.
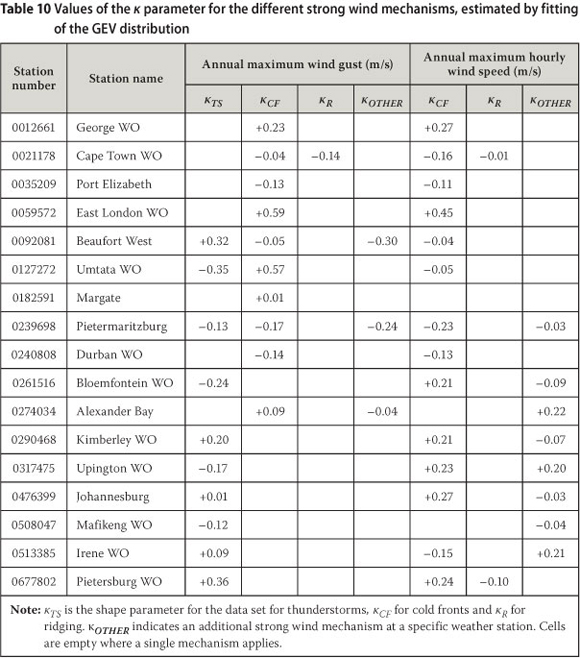
The GEV distribution was fitted to the data samples for each strong wind mechanism, e.g. to the data sets in the four columns of Table 8 for Robben Island. The results of these analyses are presented in Table 10, for the same weather stations as in Table 2. It can be noted that the analyses in Kruger (2011) revealed that there is no real consistency between the sign or magnitude of κ and specific strong wind mechanisms.
A conclusion can be made that the values of κ, for the data samples utilised, probably depend in most cases on the internal variability of the values in the data samples, and not on the strong wind mechanisms involved. Therefore it is reiterated again that for shorter time series, the estimation of quantiles should be based on the application of a method restricting the value of κ to zero, as previously suggested. It might be possible that, if the time series utilised were significantly longer, there would be some consistencies evident in the sign and magnitude of κ between the different weather stations, and specific strong wind producing mechanisms.
Comparison between quantile estimations of Gumbel and mixed distribution methods
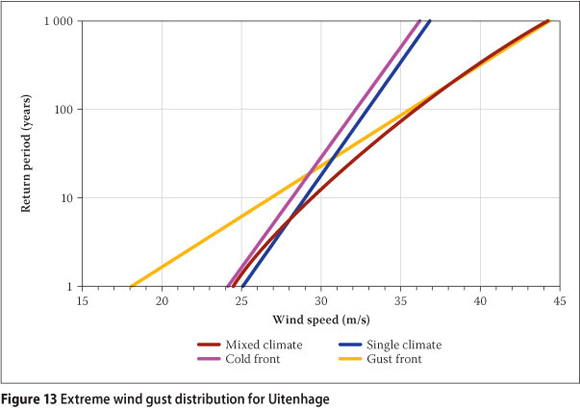
The differences between the values of the quantiles X50, X100, and X500, estimated by the method for mixed distributions and the Gumbel method, e.g. for the 1:50 year quan-tiles, are presented in Table 11, for the weather stations in Table 9. As expected, and also noted by Gomes & Vickery (1978), quantile estimations by the mixed distribution method are usually larger than the estimations by the Gumbel method, with the differences increasing with increasing return periods. In Kruger (2011), for X50 the mixed distribution method estimates are, on average, 0.7 m/s larger than the Gumbel method for annual maximum wind gusts, and 0.2 m/s larger for annual maximum hourly mean wind speeds. For longer return periods the mean differences become larger. For X100, the mean differences are 1.0 m/s and 0.3 m/s, while for X500 the mean differences are 1.7 m/s and 0.5 m/s respectively.
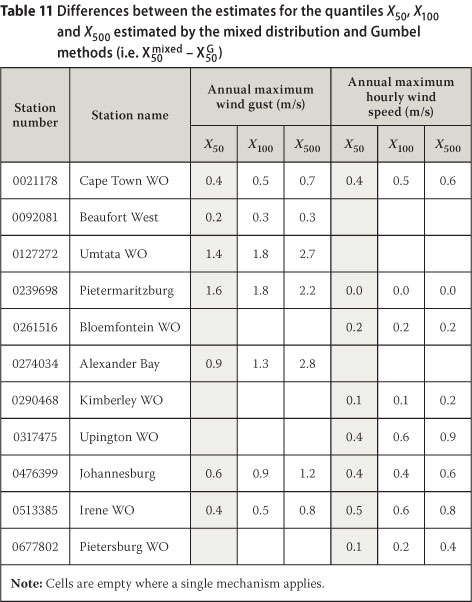
Where there are large differences between the estimates of the two methods it is usually because the strong wind mechanism that is causing the most extreme wind speeds is underrepresented in the sample of annual maximum wind speeds of a weather station. The dispersion of the annual maximum values of this particular strong wind mechanism is then also always larger than that for the other strong wind mechanism(s) taken into account. To illustrate this, the annual maximum wind gust distribution for Uitenhage and the annual maximum hourly mean wind speed distribution for Malmesbury are discussed.
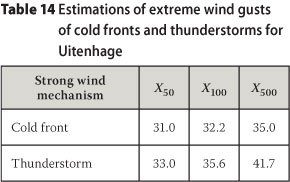
In the case of Uitenhage the most extreme wind gusts are caused by thunderstorms. Table 12 presents the annual maximum wind gust values, as well as the annual maximum values produced by the passage of cold fronts and the occurrence of thunderstorms at Uitenhage for the period 1996 to 2008.

Cold fronts are the causes of the annual maximum wind gusts on eight of the available 11 years of data. The average of the values for cold fronts is 25.2 m/s, which is higher than the average of the values for thunderstorms at 19.8 m/s. However, the value of the dispersion parameter, α, is 1.8 for cold fronts and 3.8 for thunderstorms. This larger value for α results in a shallower slope in the extreme wind gust distribution graph for thunderstorms, as well as for the mixed climate, as presented in Figure 13.
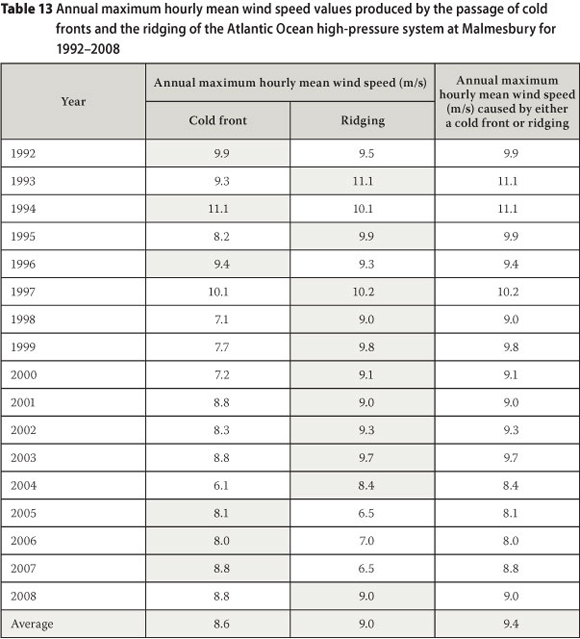
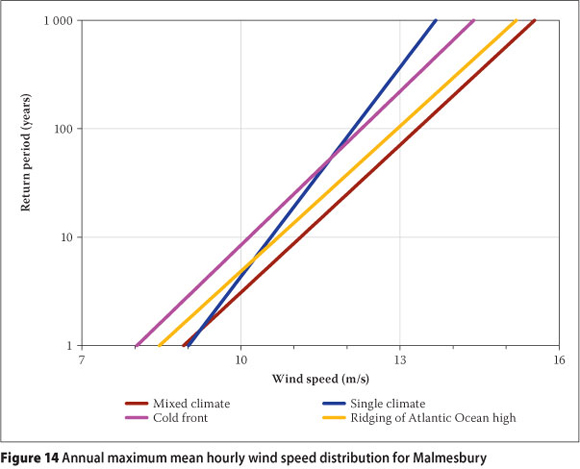
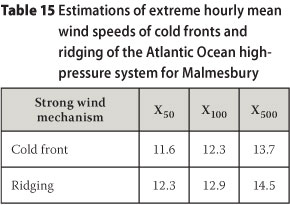
Another interesting example is that for the extreme hourly mean wind speed distribution for Malmesbury. Table 13 presents the maximum hourly mean wind speed values produced by the passage of cold fronts and the ridging of the Atlantic Ocean high-pressure system at Malmesbury, for the period 1992 to 2008. Cold fronts are the causes of the annual maximum hourly mean wind speeds on six of the available 17 years of data, while the ridging of the Atlantic Ocean high-pressure system is the cause for the remaining 11 years. The average of the annual maximum values for the cold fronts is 8.6 m/s, while for the ridging it is 9.0 m/s. The value of a for the cold fronts is 0.9, while for the ridging it is 1.0. Therefore the extreme hourly wind distributions for cold fronts and ridging are very similar. However, the mean of the annual maximum hourly mean wind speeds, regardless of the cause, is 9.4 m/s and a is equal to 0.7. The result is an extreme wind distribution as presented in Figure 14. The slope of the mixed climate distribution is similar to the distributions for cold fronts and ridging, while the single climate slope for the traditional Gumbel method is much steeper, causing a significant underestimation of wind speeds for the longer return periods.
The conclusion is that, for the estimation of quantiles for long return periods, it is advisable or "safer" to follow a mixed distribution approach. This is especially applicable to strong wind estimations in South Africa, where most of the land area is influenced by more than one strong wind producing mechanism.
The disaggregated data sets developed in this analysis also make it possible to predict extreme wind estimations caused by the different strong wind mechanisms. For the above examples, the estimated wind gust quantiles X50, X100 and X500 for the strong wind mechanisms identified for Uitenhage are shown in Table 14. Table 15 presents hourly mean wind speed quantiles for the same return periods for the strong wind mechanisms identified for Malmesbury.
SUMMARY AND RECOMMENDATIONS
It is demonstrated that, amongst others, the background information on the strong wind climatology and record length are imperative considerations in the selection of appropriate methods for extreme-wind estimations.
The various steps taken in the analysis of the strong wind data can be summarised as presented in the overview in Figure 15. Due to the short time series and the complex wind climate of South Africa, some extreme wind estimation methods can be recommended above others.
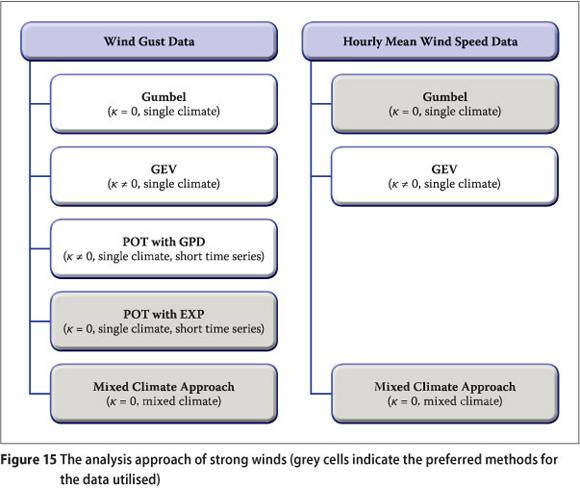
Firstly all the data sets were analysed with the traditional Gumbel method. As it cannot readily be assumed that κ = 0, the data sets were subsequently analysed with the GEV approach, and from the results it was seen that no spatial consistency between stations in terms of the value of κ is evident. This indicated the influence of outliers on the analysis; and that the GEV approach is not recommended for the analysis of short time series.
The POT method, specifically developed for the analysis of short time series, was then applied. This method is not applicable to hourly mean wind speeds, and therefore only the data sets for the wind gusts were analysed. With the POT method applied to the GPD, again no spatial consistency between stations in terms of the value of κ was evident. The POT method was then applied with the EXP distribution, which is essentially the GPD distribution with κ = 0. This approach is deemed to produce the best estimates of extreme wind values from the methods investigated, if a single strong wind climate is assumed.
Subsequently a method for analysing mixed strong wind climates was applied to the wind gust as well as the hourly mean wind speed data sets, where almost all of the weather stations showed increased quantile estimates.
For wind gusts, in the case of wind data of single climatic origin, the POT approach applied with the EXP method is recommended. In the case of a strong wind climate of various origins the mixed strong wind climate approach is recommended, especially for longer return periods where the quantile estimations by the mixed climate method become much larger than that with the traditional Gumbel method. It is not feasible to apply the POT method to a mixed climate approach, due to the large number of strong winds of which the causes would have to be determined.
For hourly mean wind speeds the traditional Gumbel approach is satisfactory. However, in the case of a mixed strong wind climate of various origins, it is recommended that the method providing the highest quan-tile values is applied.
REFERENCES
Abild, J 1994. Application of the wind atlas method to extremes of wind climatology. Technical Report Risoe-R-722 (EN), Roskilde, Denmark: Risø National Laboratory. [ Links ]
Abild J, Andersen, E Y & Rosbjerg, D. 1992. The climate of the extreme winds at the Great Belt, Denmark. Journal of Wind Engineering & Industrial Aerodynamics, 41-44: 521-532. [ Links ]
Brabson, B B & Palutikof, J P 2000. Tests of the Generalized Pareto Distribution for predicting extreme wind speeds. Journal of Applied Meteorology, 39: 1627-1640. [ Links ]
Cook, N J 1985. The designer's guide to wind loading of building structures. Part 1: Background, damage survey, wind data and structural classification. London: Building Research Establishment, Garston, and Butterworths. [ Links ]
D'Agostino, R B & Stephens, M A 1986. Goodness-of-fit techniques. New York: Marcel Dekker. [ Links ]
Gomes, L & Vickery, B J 1978. Extreme wind speeds in mixed wind climates. Journal of Industrial Aerodynamics, 2: 331-344. [ Links ]
Gringorten, I I 1963. A plotting rule for extreme value probability paper. Journal of Geophysics Research, 68: 813-814. [ Links ]
Gusella, V 1991. Estimation of extreme winds from short-term records. Journal of Structural Engineering, 117: 375-390. [ Links ]
Hennessey, J P Jr 1977. Some aspects of wind power statistics. Journal of Applied Meteorology, 16: 119-128. [ Links ]
Hosking, J R, Wallis, M J R & Wood, E F 1985. Estimation of the generalized extreme value distribution by the method of probability-weighted moments. Technometrics, 27: 251-261. [ Links ]
Jenkinson, A F 1955. The frequency distribution of the annual maximum (or minimum) values of meteorological elements. Quarterly Journal of the Royal Meteorological Society, 81: 158-171. [ Links ]
Kruger, A C 2011. Wind climatology of South Africa relevant to the design of the built environment. Unpublished PhD thesis, Stellenbosch: University of Stellenbosch. [ Links ]
Kruger, A C, Goliger, A M, Retief, J V & Sekele, S 2010. Strong wind climatic zones in South Africa. Wind & Structures Journal, 13(1): 37-55. [ Links ]
Kruger, A C, Retief, J V & Goliger, A M 2013. Strong winds in South Africa. Part II: Mapping of updated statistics. Journal of SAIcE, 55(2): 46-58. [ Links ]
Larsén, X G & Mann, J 2009. Extreme winds from the NCEP/NCAR reanalysis data. Wind Energy, 12(6): 556-573. [ Links ]
Lechner, J A, Leigh, S D & Simiu, E 1992. Recent approaches to extreme value estimation with application to wind speeds. Part 1: The Pickands method. Journal of Wind Engineering & Industrial Aerodynamics, 41-44: 509-519. [ Links ]
Milford, R V 1985a. Extreme-value analysis of South African mean hourly wind speed data. Unpublished Internal Report 85/1, Pretoria: Structural and Geotechnical Engineering Division, National Building Research Institute, CSIR. [ Links ]
Milford, R V 1985b. Extreme value analysis of South African gust speed data. Unpublished Internal Report 85/4, Pretoria: Structural and Geotechnical Engineering Division, National Building Research Institute, CSIR. [ Links ]
Palutikof, J P, Brabson, B B, Lister, D H & Adcock, S T 1999. A review of methods to calculate extreme wind speeds. Meteorological Applications, 6: 119-132. [ Links ]
Perrin, O, Rootzén, H & Taesler, R 2006. A discussion of statistical methods for estimation of extreme wind speeds. Theoretical & Applied climatology, 85, 203-215. [ Links ]
SANS 10160:2011: Basis of Structural Design and Actions for Buildings and Industrial Structures. Pretoria: South African Bureau of Standards. [ Links ]
Simiu, E & Heckert, N A 1996. Extreme wind distribution tails: A "peak-over-threshold" approach. Journal of Structural Engineering, 122: 539-547. [ Links ]
Twisdale, L A & Vickery, P J 1992. Research on thunderstorm wind design parameters. Journal of Wind Engineering & Industrial Aerodynamics, 41-44: 545-556. [ Links ]
Walshaw, D 1994. Getting the most from your extreme wind data: A step-by-step guide. Journal of Research of the National Institute of Standards and Technology (NIST - US), 99: 399-411. [ Links ]
Weissman, I 1978. Estimation of parameters and large quantities based on the k largest observations. Journal of the American Statistical Association, 90: 812-815. [ Links ]
Wilks, D S 2006. Statistical Methods in the Atmospheric Sciences. Amsterdam, Boston: Elsevier Academic Press. [ Links ]
 Contact details:
Contact details:
Andries Kruger
Climate Service
South African Weather Service
Private Bag X097
Pretoria, 0001
T: +27 12 367 6074
F: +27 12 367 6175
E: andries.kruger@weathersa.co.za
 Contact details:
Contact details:
Johan Retief
Department of Civil Engineering
University of Stellenbosch
Private Bag X1, Matieland
Stellenbosch, 7602
T: +27 21 808 4442
F: +27 21 808 4947
E: jvr@sun.ac.za
 Contact details:
Contact details:
Adam Goliger
CSIR Built Environment
PO Box 395
Pretoria, 0001
T: +27 12 841 2472
F: +27 12 841 2539
E: agoliger@csir.co.za

DR ANDRIES KRUGER obtained his MSc degree from the University of Cape Town in the Geographical and Environmental Sciences, and his PhD from the University of Stellenbosch in Civil Engineering, with research topic "Wind Climatology and Statistics of South Africa relevant to the Design of the Built Environment". Since 1985 he has been involved in the observation, analysis and research of historical climate at the South African Weather Service. This included climate change and variability research, the authoring of general climate publications, and other climatological studies through consultation. He is the author or co-author of a substantial number of scientific publications.

PR0F J0HAN RETIEF, who is a Fellow of the South African Institution of Civil Engineering, obtained his first degree in Civil Engineering from Pretoria University, MPhil from London University, Engineer from Stanford, and DScEng again from Pretoria University. He joined Stellenbosch University after many years at the Atomic Energy Corporation. Since retirement he is still involved in supervision of graduate students and is involved nationally and internationally in standards development.
 .
.
DR ADAM GOLIGER obtained his MSc degree from Warsaw Technical University and his PhD from Stellenbosch University, both in Structural Engineering. Since 1985 he has been involved in research and consulting work at the CSIR. This included wind-tunnel simulation and modelling techniques, wind damage and environmental studies around buildings. For several years he served as the South African representative on the International Association for Wind Engineering (IAWE) and participated in various local and international committees. He is the author or co-author of more than 80 scientific publications and various technical reports.














