Servicios Personalizados
Articulo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares en Google
Similares en Google
Compartir
Journal of the South African Institution of Civil Engineering
versión On-line ISSN 2309-8775
versión impresa ISSN 1021-2019
J. S. Afr. Inst. Civ. Eng. vol.55 no.1 Midrand abr. 2013
TECHNICAL PAPER
2D Linear Galerkin finite volume analysis of thermal stresses during sequential layer settings of mass concrete considering contact interface and variations of material properties. Part 2: Stress analysis
S Sabbagh-Yazdi; T Amiri-SaadatAbadi; F M Wegian
ABSTRACT
In this research, a 2D matrix-free Galerkin finite volume method on the unstructured meshes of triangular elements is utilised to compute thermal stress fields resulting from the predefined transient temperature distribution in a mass concrete structure (dam wall). In the developed numerical model, the convergence of the force equilibrium equations are achieved via some iterative solutions for each given computed temperature field. Since the mechanical properties of concrete may vary over time due to concrete ageing, the presented numerical model considers the variation of mechanical properties corresponding to the degree of concrete hydration and concrete temperature. In addition, the geometry of the dam wall and foundation is not considered integrated any longer, so the mechanical contact is considered at concrete-rock foundation interface to achieve more realistic simulations of the strain-stress fields in this part. In this work we present the comparison of thermal stress analysis numerical results (of a clamped plane which is exposed to constant temperature) with the results of finite element-based ALGOR software to assess the accuracy and efficiency of the developed model, and prove that the results correlate well. As an application of the developed model for a real-world problem, thermal stress analysis of a mass concrete structure which is gradually constructed on a natural foundation is performed with regard to variable mechanical properties.
Keywords: variable mechanical property, mass concrete, Galerkin finite volume solution, unstructured meshes of triangular elements
INTRODUCTION
The volume changes in concrete that take place during the hydration process and cooling phase will cause tensile stress development. The external and internal constraints often exist simultaneously and will limit the thermal strains corresponding to the temperature changes. Therefore, critical thermal stresses may appear in the concrete members. The concrete has a relatively low tensile strength (compared to other building materials) and is susceptible to cracking. Therefore, if thermal stresses exceed the tensile strength of concrete, they could cause visible cracking in the concrete members. Hence, mass concrete structures such as concrete dams, nuclear reactor containments and bridges may be subject to thermal cracking due to thermal stresses. Thermal cracking can influence the durability and serviceability of concrete dams, and should therefore be studied in detail.
Calculating the temperature and stress distribution is one of the most important considerations in solid mechanics. These phenomena have therefore been modelled by various numerical techniques, such as the finite difference method (FDM), the finite element method (FEM), the finite volume method (FVM), etc. Traditionally, solid body problems were addressed by the FEM. The FDM has, however, become one of the most popular methods in the area of computational fluid mechanics, and recently some problems in continuum mechanics have been solved successfully by FVM (Demirdzic et al 1993). The FDM is the oldest method and is based on the application of a local Taylor expansion to approximate the differential equations, which are truncated usually after one or two terms. The number of terms determine the accuracy of the solution (the more there are, the more accurate the solution), but this is a complex matter (Yip 2005). The FDM is suitable for structured grids associated with regular boundaries, and is not as accurate for complex geometries as the FVM is. However, for dealing with irregular boundaries, the use of unstructured meshes provides considerable flexibility and accuracy for modelling projects (Sabbagh-Yazdi et al 2009).
This is a potential bottleneck of the FDM when handling complex geometries in multiple dimensions. The issue motivated the use of an integral form of the governing equations (PDE), and subsequently the development of the FEM and FVM (Yip 2005). Both methods have surpassed the FDM and other numerical methods, and researchers typically use one of them for numerical simulations of all types of physical phenomena. The FEM has become very popular in structural analysis due to the great practical value of the results, especially in cases where deformations are limited to elastic ones (Demirdzic et al 1993).
The FEM is based on the variational principle and uses the predefined shape functions dependent on the topology of the element, easily extends to higher order discretisation, produces large block-matrices, usually with high condition numbers, and as a consequence relies on direct solvers. The FVM is usually second-order accurate, based on the integral form of the governing equation, uses a segregated solution procedure, where the coupling and non-linearity are treated in an iterative way, and creates diagonally dominant matrices well suited for iterative solvers.
The question here is a trade-off between the high expense of the direct solver for a large matrix in FEM or the cheaper iterative solvers in FVM. The reason for this may be the fact that the FVM is inherently good at treating complicated, coupled and non-linear differential equations, widely present in fluid flows. By extension, as the mathematical model becomes more complex, the FVM should become a more interesting alternative to the FEM. Another reason to consider the use of the FVM in structural analysis is its efficiency. In recent years industrial computational fluid dynamics has been dealing with meshes of high order which are necessary to produce accurate results for complex mathematical models and full-size geometries (Jasak et al 2000).
It is well known that the numerical analysis of solids in incompressible limit could lead to difficulties. For example, fully integrated displacement-based lower-order finite elements suffer from volumetric locking. Also, some difficulties are experienced producing a stiffness matrix and shape function in order to increase the convergence rate.
From the results of several benchmark solutions, the FVM appeared to offer a number of advantages over equivalent finite element models. For instance, unlike the FDM solution, the FVM solution is conservative, and incompressibility is satisfied exactly for each control volume of the computational domain. In principle, because of the local conservation properties, the FVMs should be in a good position to solve such problems effectively. Furthermore, numerical calculation with meshes consisting of triangular cells showed excellent agreement with analytical results (Sabbagh-Yazdi et al 2009).
The presented results show that both local and global norms of error for the FVM are similar to the FEM. Using the constant strain triangles leads to a similar stiffness matrix and consequently a comparable level of accuracy in both the FVM and FEM. It is interesting that the execution time for the FVM is less than that of the FEM for sufficiently fine mesh (Ekhteraei-Toussi et al 2007).
As mentioned before, the FVM is a popular method in thermal analysis, while the FEM is a conventional technique in the solid mechanics field. The use of both methods would inevitably necessitate the transferring of data. However, the transformation of results between the FVM and FEM is time-consuming. By using the FVM for the analysis of solids and temperature, the time-consuming transfer of data can be avoided, while the method is also more stable when simulating complicated problems (Suvanjumrat et al 2011).
For determining the displacement fields and elastic stress distribution in structures, Wheel (1996) introduced an implicit finite volume method for axisymmetric geometries using structured meshes. Wenke et al (2003) presented a finite volume-based discretisation method for determining displacement, strain and stress distributions in two-dimensional structures on unstructured meshes. They incorporated rotation variables in addition to the displacement degrees of freedom. Slone et al (2003) evaluated the dynamic structural response of solids on unstructured meshes. In this work, a three-dimensional vertex-based method with a Newmark implicit scheme was presented and the neutral frequency was predicted accurately by employing viscous damping. Demirdzic et al (2000) extended their numerical technique for the stress analysis in isotropic bodies subjected to hygro-thermo-mechanical loads. In this research, the temperature, stress, displacement and humidity fields were calculated using the fully implicit time differencing, whereas the source term and diffusion fluxes were treated explicitly. Fainberg et al (1996) performed similar work for thermo-elastic material.
In one of the numerical research efforts, ANSYS software was used for 2D and 3D thermo-structural analyses of roller-compacted concrete (RCC) (Malkawi et al 2003). Both thermal and mechanical properties of the concrete were considered constant during the analysis. In this research, a 2D finite element programme was used to simulate the construction process of a mass concrete structure. A computer code for thermo-structural analysis of the mass concrete structures was also implemented by these researchers. They predicted the time of crack occurrence via the crack index with regard to the constant mechanical properties of concrete over time. Noorzaei et al (2006) and Jaafar et al (2007) implemented a 2D computer code based on the finite element method for the thermal analysis of a mass concrete structure. In this research the thermal properties of concrete were assumed to be constant during analysis. Azenha & Faria (2008) proposed a 2D numerical method for the prediction of temperature and stress distribution considering the evolution of mechanical properties during the early ages of concrete.
It should be noted that, as the reactions proceed, the products of the cement hydration process gradually grow to form the skeleton of hardened cement paste as a solid mass which bears the applied loads. Hence, the mechanical properties of concrete change with respect to concrete age. This process is known as concrete ageing and must be considered in precise thermal stress analysis. Luna & Wu (2000) predicted the temperature and stress distribution during RCC dam construction considering the temperature effect on the elastic modulus and creep behaviour of concrete, but the other concrete properties were assumed to be constant over time. Cervera et al (2000) implemented a numerical simulation for construction of the mass concrete structure with regard to the ageing effects. In that work the numerical analyses were performed under different scenarios of dam construction. Chen et al (2001) developed the finite element relocating mesh method for stress analysis of RCC dams during the construction period. The ageing effects on the elastic modulus of concrete were considered by Chen et al.
Another module of NASIR (Numerical Analyzer for Scientific and Industrial Requirements) solver, which uses a matrix-free Galerkin finite volume method on the unstructured meshes of triangular elements, was recently introduced for strain-stress analysis of plane-strain problems under external loads considering constant mechanical properties (Sabbagh-Yazdi et al 2008). In Part I of this two-part paper, a new explicit 2D numerical solution has been presented to compute the temperature field which is caused due to the hydration and thermal conductivity by the Galerkin finite volume method on the unstructured meshes of triangular elements with respect to the variation of temperature and age of concrete.
In this research, NASIR plane-strain solver, the finite volume method solver of Cauchy equations for plane-strain problems, is developed to predict the strain-stress fields during multi-layer concrete setting of a mass concrete structure considering the variations of mechanical properties. For this purpose, a strain-stress solver based on the Galerkin finite volume method for plane-strain problems is developed for stress analysis during the various stages of gradual construction of mass concrete structures. In this modelling strategy, the convergence of 2D force equilibrium equations is achieved via some iterative matrix-free solutions for a given (previously computed in Part I of this two-part paper) temperature field at each stage of the gradual construction of the mass concrete structure. The thermal stresses are computed considering the effect of concrete ageing on the mechanical properties of concrete. The variations of mechanical properties are considered corresponding to the concrete temperature, the time dependent degree of hydration and the concrete age.
After the detailed description of the numerical modelling, the accuracy of the introduced numerical model is assessed by comparison of the computed principle thermal stress contours of a clamped plate due to a uniform temperature field with the finite element method solution which has been reported by Logan (2000). Finally, the thermal stress solution during the multi-layer construction of a mass concrete structure on a natural foundation is performed considering the variable mechanical properties of concrete
FORCE EQUILIBRIUM AND STRESS FIELD MATHEMATICAL MODEL
Force equilibrium equations
It is well known that the Cauchy equations are the predominant equations of solid mechanics. The following equation is attained from the equilibrium equations which can be used on each body with any material (Sabbagh-Yazdi et al 2008).
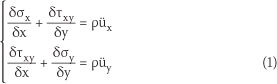
where p (kg/m3) is the material's density and üi (m/s2) is the acceleration of the body.
Strain-stress relations
The stress field for plane-strain problems is expressed as:
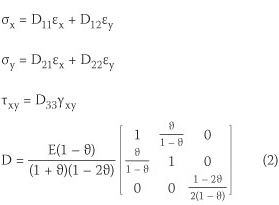
where σx,σy,τxy are the normal stresses in the x and y directions and shear stress, respectively; εx,εy,yxy are the normal strains in the x and y directions and shear strain, respectively; and E, 9 denote the elastic modulus and Poisson's Ratio coefficient.
The strain field is expressed as:

where (εEth)n is the external thermal strain of node n which is calculated from Equation 4
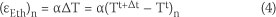
where
α(l/°C) : coefficient of thermal expansion
Ttn(°C) : temperature of node n at time (t)
Ageing effects on mechanical properties
The changes of concrete properties during the hydration reaction are called the concrete ageing. The evolution of elastic modulus and strength of concrete must be considered for a precise thermal stress analysis.
Elastic modulus
The elastic modulus is defined as the ratio between the constrained strains and stresses. The elastic modulus of concrete relates to the hydrated cement paste of concrete, which is able to support the applied loads. The hydrated cement paste of concrete grows with time and causes considerable increase of the concrete elastic modulus. Equation 5 may be used for the evolution of the concrete elastic modulus over time (Noorzaei et al 2006).
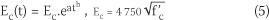
where Ec(MPa) is the elastic modulus of concrete at time (t), Ec(MPa) is the ultimate elastic modulus of concrete, t(day) is the equivalent age of concrete, f'c is the characteristic cylinder strength of concrete, and a, b are the fit parameters which were determined for one mass concrete structure as follows: a = -0.5, b = -0.63.
Poisson's Ratio
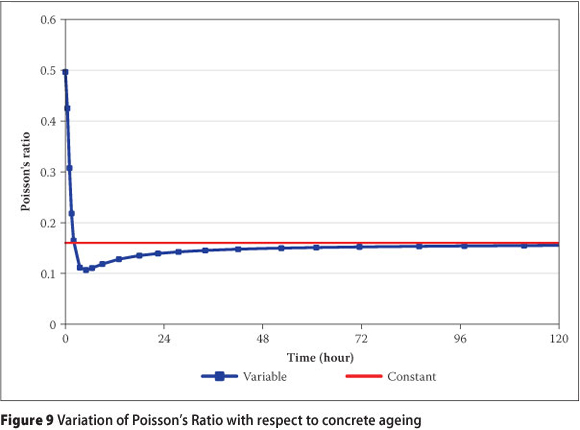
The Poisson's Ratio coefficient is required for stress modelling in multi-dimensional structures. This coefficient is defined as the ratio of transverse strain to longitudinal strain under uniform axial stress. De Schutter & Taerwe (1996) presented a model to calculate the variation in the Poisson's Ratio of concrete over time based on the degree of concrete hydration.
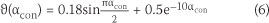
where 9(αcon) is the Poisson's Ratio of concrete at the degree of hydration (αcon).
Coefficient of thermal expansion
Coefficient of thermal expansion is one of the most important parameters of thermal stress analysis. The mixture proportions, type of aggregate, degree of saturation and concrete age are the effective parameters on the coefficient of thermal expansion of concrete. The coefficient of thermal expansion is dependent on the coefficient of thermal expansion of the concrete components. Since the aggregate content of concrete is relatively high, the coefficient of thermal expansion of the aggregate has the greatest effect on the coefficient of thermal expansion of concrete.
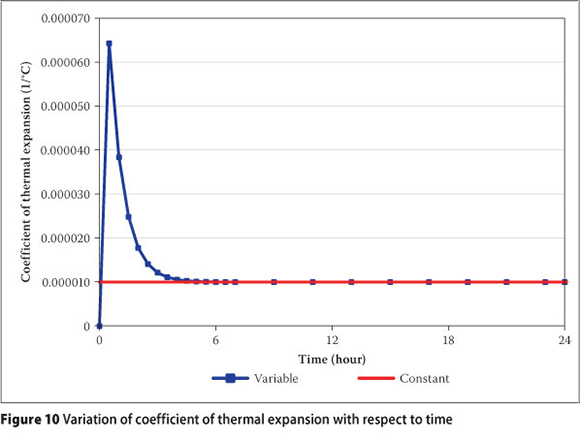
The Loukili model expresses the evolution of the coefficient of thermal expansion of concrete over time (Equation 7). According to this relationship, the coefficient of thermal expansion of concrete decreases over time and converges to 10-5(1/°C).

where α(10-6/°C) is the coefficient of thermal expansion of concrete, and t(hr) is the equivalent age of concrete (Loukili et al 2000).
NUMERICAL SOLUTION
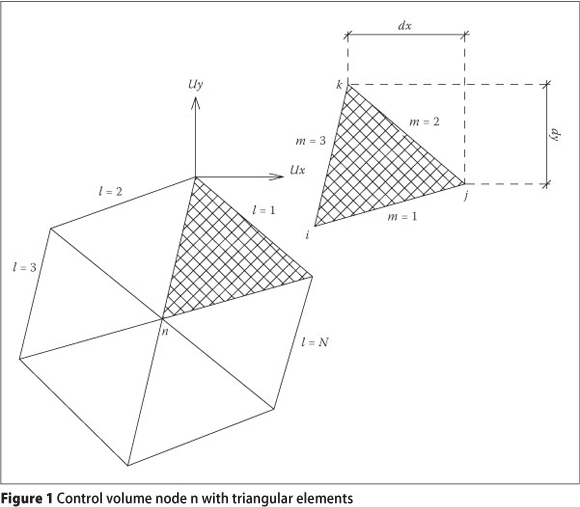
Galerkin finite volume formulations
The compact form of Cauchy equations can be expressed as:
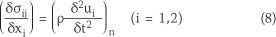
For j = 1,2 the stress vector can be defined as 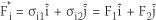 where uim) is displacement in the i direction.
where uim) is displacement in the i direction.
By application of the Galerkin weighted residual method, after multiplying the residual of the above equation by a weight function (which can be considered as the nodal shape function of a linear triangular element φn) and integrating over a subdomain Ω (which is formed by gathering all the elements sharing node n), the weak form of Equation 8, after omitting zero boundary terms, is expressed as:
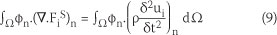
The first term on the right-hand side of Equation 9 can be written as Equation 10:
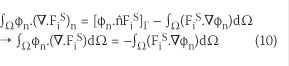
The approximate relationship given in Equation 11 can be used to calculate the spatial derivative term of Equation (10):
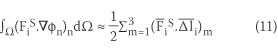
Here (Δli)m is the i direction component of the normal vector of edge m of the subdomain Ωn
The weighting function φ has a value of unity at the desired node n, and zero at the other neighbouring nodes k of each triangular element.
For an equilibrium condition in which time stepping can be considered as a strategy to perform the iterative computation until the desired convergence is achieved, the transient term of the equation can be expressed as:
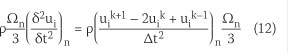
The discrete form of the Cauchy equation for a node n is written as Equation 13:
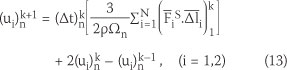
where 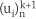 is the displacement of node n at k+1 iteration in the i direction (Figure 1).
is the displacement of node n at k+1 iteration in the i direction (Figure 1).
Computation of stress vector components
The stress field can be calculated using the following equations:
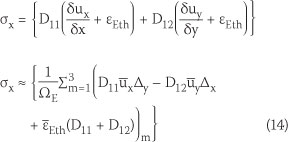
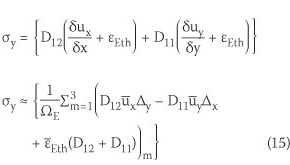
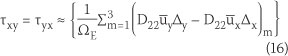
where
: the external thermal strain which is the average strain of each edge
ΩE : the area of triangular element
n : the external edges number of control volume
Boundary conditions
The boundary conditions of the force equilibrium equation are presented as follows:
Clamped constraint
In this boundary condition, not only the displacement, but also the rotation must be limited (Figure 2).
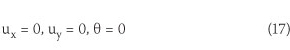
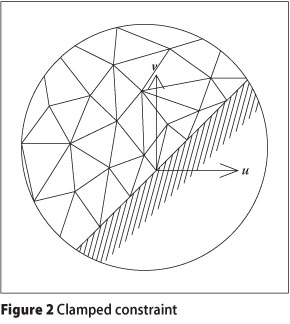
Sliding constraint
This boundary condition provides only the tangential displacement, and the normal displacement is prevented (Figure 3).

Iterative computation
The iterative computations are resumed until the steady state condition and desired convergence are achieved. In order to maintain the stability of the iterative computations, the time stepping size must be limited. Using the local time stepping method can reduce the run-time required to reach equilibrium. In order to have the stable explicit solution, the Courant's number must be less than unity.
According to the proposed relation (Sabbagh-Yazdi et al 2008), the time step size must be limited to the following equations:

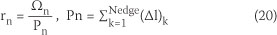
where Ωn and Pn are the area and perimeter of the control volume, respectively.
C is the speed of information transition which is calculated from Equation 21:

Every node has its own time step size. Using the concept of the local time stepping method accelerates the convergence to the equilibrium condition for steady state problems.
CONTACT ANALYSIS
Contact mechanics involves the study of forces transmitted from one solid to another and the consequent stresses in those solids.
Contact mechanics has widespread application in many engineering problems and no one can disregard its importance. The general goals of contact analysis are to determine the contact stresses transmitted across the contact interfaces of the solids that are brought into contact. Nowadays computational mechanics is a useful tool to simulate contact problems numerically so that one is able to analyse large-scale problems. One of the interesting applications of contact mechanics is the modelling of dam-rock foundations interface. Interface may not only affect the mechanical behaviour of the dam and foundation system, but also the diffusion properties, such as moisture transmission. The safety against sliding has to be assessed for the interface between the dam and the foundation, especially in dynamic analysis.
In the contact area, the constraint equations for normal and tangential contact have to be formulated. Let us assume that two solids are brought into contact (Figure 4). In this case, the non-penetration condition (constraint equation) is given by the following equation:
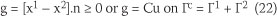
where Γc denotes the contact surface; n is the normal to solid 2; x1,x2 are the deformed positions of solids 1 and 2, respectively; u is the displacement matrix; and  is the relative motion in normal and tangential direction, respectively.
is the relative motion in normal and tangential direction, respectively.
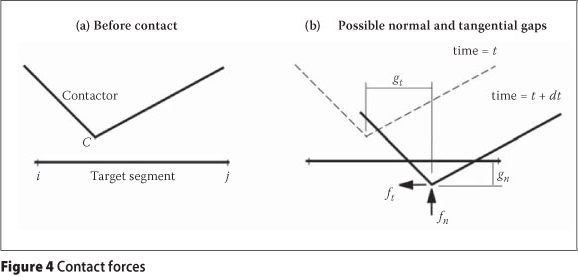
If the above relationship isn't exactly satisfied, we have some penetration in the contact surface which could be interpreted as the g function:

In this research, the penalty method is considered for enforcing a constraint condition in contact analysis. The stiffness equation of a constrained problem is determined by minimising the total potential energy (Equation 24). As is clear from this, the stiffness matrix and force vector are modified to incorporate the impenetrability constraint stiffness.
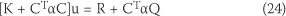
where α is the penalty number.
The contact force vector is calculated from the following equation:
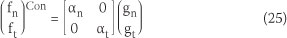
where fn, ft are the normal and tangential contact forces, respectively, and αn, αt are the normal and tangential contact stiffness, respectively.
One has to distinguish two cases which are called stick state and slide state in the tangential direction of the contact surface. In the first situation (stick state) a point which is in contact cannot move in the tangential direction, but in the slide state situation relative slip between two solids occurs and friction law is applied to the contact surface. A slip criterion is used to indicate whether stick or slip state occurs, which is stated as in Equation 26:
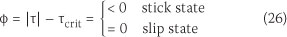
where |τ| denotes the norm of the tangential traction and is determined by the friction law.
The Coulomb friction law, which is adequately applicable to common frictional contact problems, is adopted in this research as (Mohammadi 2003):

where µ is the friction coefficient and σn denotes the normal stress. The value of the friction coefficient for mass concrete on sound rock is considered to be 0.7 so that the stick state always occurs (ETL 1110-3-446 1992).
VERIFICATION AND APPLICATION
Verification test
External thermal stresses are induced in concrete structures because the coefficients of thermal expansion of the body and adjacent structures are different. When the temperature difference between the body and its adjacent structures is the same, the thermal strains in the body and its adjacent structures due to the difference between their coefficients of thermal expansion are different, which cause thermally induced stress.
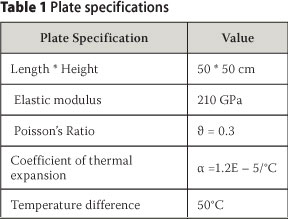
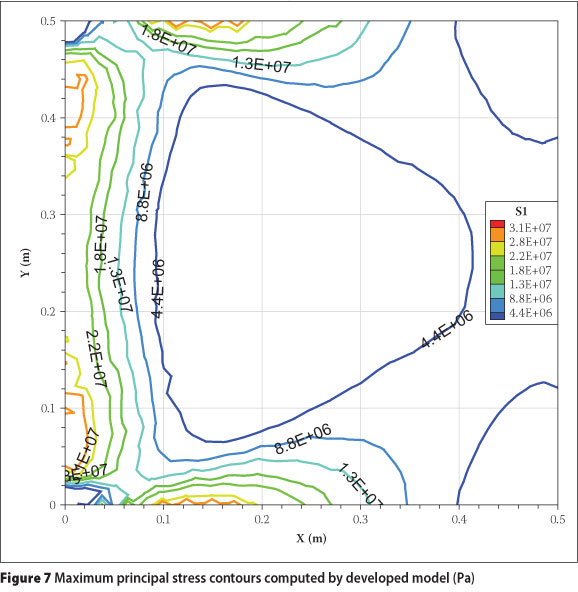
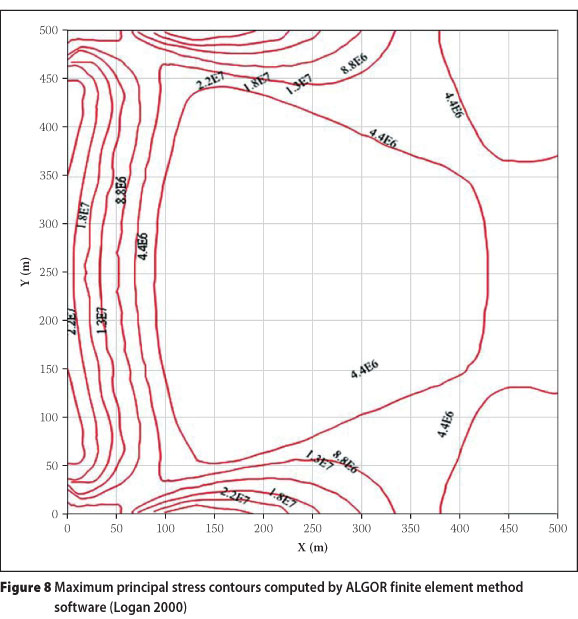
A plate specimen is clamped at the left and is subjected to a uniform temperature of 50°C as shown in Figure 5 (Logan 2000). The properties of the material are given in Table 1.

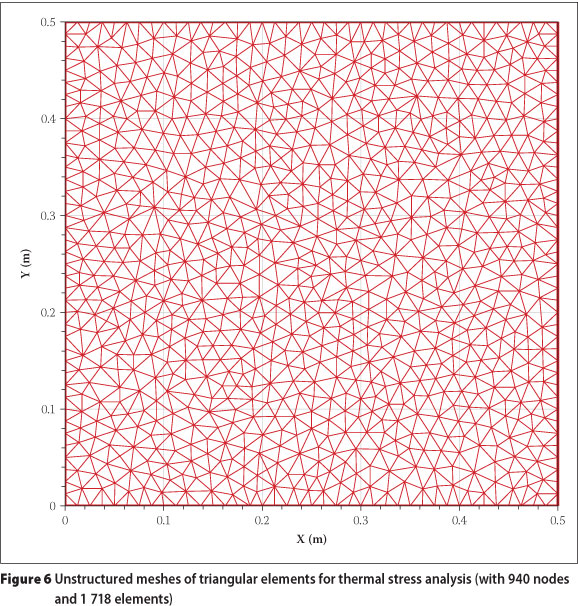
The unstructured mesh of triangular elements, as shown in Figure 6, is used to perform the Galerkin finite volume method solution. In order to assess the computed results of the present solver with other developed methods, the results of the finite element-based ALGOR commercial software (presented in the previous literature review) are used to compare the computed results. Under a uniform temperature, the thermal stresses are induced by the restraint boundary conditions. The computational stress field is the same as the results from the ALGOR software (Logan 2000), as are shown in Figures 7 and 8.
Application case
The applicability of the developed solver to simulate real-world problems is shown in this section. Using the developed software, the simulation of a thermally-induced stress field of a typical mass concrete structure is performed with regard to the variations of mechanical properties of the material. The mechanical properties of the concrete and foundation are tabulated in Table 2. For more geometrical details please refer to Part I of this two-part paper.
Using the presented relationships, the mechanical properties of concrete can be determined according to concrete ageing during analysis. Their variation diagrams over time are shown in Figures 9-11.
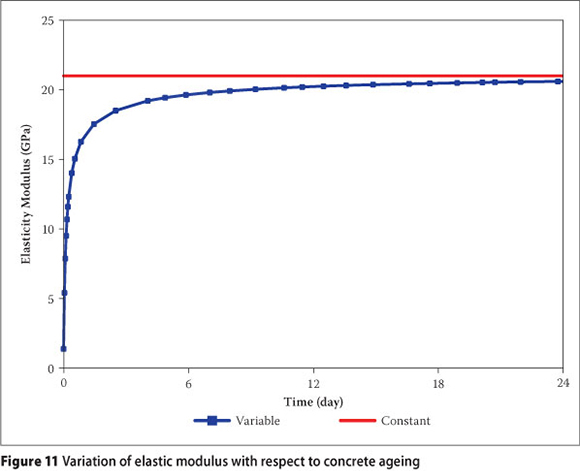
The numerical analysis of a typical mass concrete structure is performed using the above-mentioned relationships of the mechanical properties and the computed results of both simulations (constant and variable properties of concrete), as demonstrated in Figure 12 (see page 112) in terms of the transient principal stress contours in a concrete dam wall during the different stages of construction.
In order to provide a better understanding of the effects of the gradual load imposing technique and to ensure the convergence of the presented results, the root mean square of the computed displacements is shown in Figure 13.
CONCLUSION
Considering the temperature and time-dependent mechanical properties of concrete is an essential task for the precise thermal stress analysis of mass concrete structures. In this research, a plane-strain matrix-free Galerkin finite volume method was used to develop a numerical solver which is able to predict the temperature-induced stress-strain fields in mass concrete structures due to concrete heat of hydration and thermal conduction between the concrete and surrounding air through the boundary surfaces, considering the concrete ageing dependent mechanical properties.
Building on the computed transient temperature field from the similar solver in Part I of this two-part paper, stress analysis was performed on the same mesh, and the converged stress-strain fields were achieved via some iterative solution of Cauchy equilibrium equations. The time step of the Cauchy equation formulation was used for the iterative solution of the equilibrium equation at each desired time step of the thermal analysis. The thermal stresses were computed using the previously computed displacements and the thermal strains which had been accumulatively calculated from the results of performed thermal analyses between the two sequential stress-strain computation stages. In addition, dam wall and foundation geometry were not considered integrated anymore, so the mechanical contact was considered at concrete-rock foundation interface to achieve more realistic simulations of stain-stress fields in this area. The accuracy of the developed model was evaluated by the comparison of thermal stress analysis numerical results of a clamped plane, which was exposed to constant temperature (constant mechanical properties), with the results of finite element-based ALGOR software. The calculated results correlated well with the finite element results. Then the applicability of the developed numerical solver was demonstrated by the simulation of the transient stress-strain field during the gradual construction of a concrete dam wall on a natural foundation. The numerical computations were performed for a typical mass concrete structure on a natural foundation for the variable mechanical properties. The simulation results showed that significant tensile stresses may develop at the concrete surfaces due to the severe temperature gradient.
The thermal stress module of the NASIR Galerkin finite volume solver can be used as a helpful simulation tool to predict the thermal stresses of the multi-layer construction programme of a mass concrete structure considering the variable mechanical properties.
NOTATION SECTION
bi : Body force
p : Material density
üi : Acceleration of body
D : Stiffness matrix
εEth : External thermal strain
α : Coefficient of thermal expansion
Ttn : Temperature of node n at time t
: Stress vector in the direction
Ω : Subdomain
φ : Test function
(un)it+Δt : Displacement of node n at k iteration number
ΩE : Area of the triangular element
n : External edges number of control volume
Ωn : Area of the control volume
Pn : Perimeter of the control volume
C : Speed of information transition
Δtn : Virtual time step of node n
Ec : Ultimate elastic modulus of concrete
t : Equivalent age of concrete
f'c : The characteristic cylinder strength of concrete
a,b : Fit parameters
9 : Concrete Poisson's Ratio
acon : Degree of concrete hydration
Ec(t) : Elastic modulus of concrete at time (t)
(Δli)m : The i direction component of the normal vector of edge m of the subdomain Ωn
REFERENCES
Azenha, M & Faria, R 2008. Temperatures and stresses due to cement hydration on the R/C foundation of a wind tower - A case study. Engineering Structures, 3: 2392-2400. [ Links ]
Cervera, M, Oliver, J & Prato, T 2000. Simulation of construction of mass concrete structures. II: Stress and damage. Journal of Engineering Mechanics, 126(9): 1062-1069. [ Links ]
Chen, Y, Wang, C, Li, S, Wang, R & He, J 2001. Simulation analysis of thermal stress of RCC dams using 3-D finite element relocating mesh method. Advances in Engineering Software, 32(9): 677-682. [ Links ]
De Schutter, G & Taerwe, L 1996. Degree of hydration-based description of mechanical properties of early age concrete. Materials and Structures, 29(6): 335-344. [ Links ]
Demirdzic, I & Martinovic, D 1993. Finite volume method for thermo-elasto-plastic stress analysis. Computer Methods in Applied Mechanics and Engineering, 109: 331-349. [ Links ]
Demirdzic, I, Horman, I & Martinovic, D 2000. Finite volume analysis of stress and deformation in hygrothermo-elastic orthotropic body. Computer Methods in Applied Mechanics and Engineering, 190(8-10): 1221-1232. [ Links ]
Ekhteraei-Toussi, H & Rezaei-Farimani, M 2007. Comparative analysis using the numerical methods of finite element, boundary element, element free Galerkin and finite volume in the field of solid mechanics. Proceedings, International Conference on Engineering and Mathematics, Madrid, Spain, 57-64. [ Links ]
ETL 1110-3-446 1992. Revision of thrust block criteria. TM 5-813-5/AFM 88-10, (5): Appendix C. Department of the Army, US Army Corps of Engineers, Washington DC, US. [ Links ]
Fainberg, J & Leister, H J 1996. Finite volume multigrid solver for thermo-elastic stress analysis in anisotropic materials. Computer Methods in Applied Mechanics and Engineering, 137(2): 167-174. [ Links ]
Jaafar, M S, Bayagoob, K H, Noorzaei, J & Thanoon, W A 2007. Development of finite element computer code for the thermal analysis of roller-compacted concrete dams. Advances in Engineering Software, 38: 886-895. [ Links ]
Jasak, H & Weller, H G 2000. Application of the finite volume method and unstructured meshes to linear elasticity. International Journal for Numerical Methods in Engineering, 48: 267-287. [ Links ]
Logan, D L 2000. A First Course in the Finite Element Method Using Algor, 2nd edition. Platteville, US: Thomson Brooks/Cole. [ Links ]
Loukili, A, Chopin, D, Khelidj, A & Le Touzo, J Y 2000. A new approach to determine autogenous shrinkage of mortar at an early age considering temperature history. Cement and Concrete Research, 30(6): 915-922. [ Links ]
Luna, R & Wu, Y 2000. Simulation of temperature and stress fields during RCC dam construction. Journal of Construction Engineering and Management, 126(5): 381-388. [ Links ]
Malkawi, A H, Mutasher, S A & Qiu, T J 2003. Thermal-structural modeling and temperature control of roller-compacted concrete gravity dam. Journal of Performance of Constructed Facilities, ASCE, 17(4): 177-187. [ Links ]
Mohammadi, S 2003. Discontinuum Mechanics Using Finite and Discrete Elements. Tyne and Wear, UK: WIT Press. [ Links ]
Noorzaei, J, Bayagoob, K H, Thanoon, W A & Jaafar, M S 2006. Thermal and stress analysis of Kinta RCC dam. Engineering Structures, 28(13): 1795-1802. [ Links ]
Sabbagh-Yazdi, S R & Alimohammadi, S 2009. Comparison of finite element and finite volume solvers results for plane-stress displacements in plate with oval hole. Proceedings, 4th International Conference on Continuum Mechanics, Cambridge, UK, 168-173. [ Links ]
Sabbagh-Yazdi, S R, Esmaeili, M & Mastorakis, N E 2008. NASIR explicit matrix free Galerkin finite volume solver for analyzing arbitrarily shaped solid mechanics problems on unstructured triangular meshes. Proceedings, WSEAS Conference on Engineering Mechanics, Structures and Engineering Geology, Rodos, Greece, 104-110. [ Links ]
Slone, A K, Bailey, C & Cross, M 2003. Dynamic solid mechanics using finite volume methods. Applied Mathematical Modelling, 27(2): 69-87. [ Links ]
Suvanjumrat, C & Chaichanasiri, E 2011. Implementation and validation of finite volume C++ codes for plane stress analysis. Proceedings, 2th International Conference on Mechanical Engineering, Krabi, Thailand. [ Links ]
Wenke, P & Wheel, M A 2003. A finite volume method for solid mechanics incorporating rotational degrees of freedom. Computers and Structures, 81(5): 321-329. [ Links ]
Wheel, M A 1996. A finite-volume approach to the stress analysis of pressurized axisymmetric structures. International Journal of Pressure Vessels and Piping, 68(3): 311-317. [ Links ]
Yip, S 2005. Handbook of Materials Modeling, Volume I: Methods and Models. Dordrecht, Netherlands: Springer Science and Business Media. [ Links ]
 Contact details:
Contact details:
Prof Dr Saeed-Reza Sabbagh-Yazdi
Civil Engineering Department
KN Toosi University of Technology
Valiasr St Mirdamad Cross
Tehran, Iran
T: +98 21 8 8 77 9 623
F: +98 21 88 77 9476
E: syazdi@kntu.acir
 Contact details:
Contact details:
Tayebeh Amiri-Saadatabadi
Civil Engineering Department
KN Toosi Jniversity of Technology
Valiasr St Mirdamad Cross
Tehran
Iran
T: +98 21 8 8 7 7 9 623
F: +98 21 88 77 9476
E: t_amiri@dena.kntu.acir
 Contact details:
Contact details:
Prof Dr Falah M Wegian
Chairman: Civil Engineering
Department College of Technological Studies
PAAET, Kuwait
PO Box: 42325
Shuwaikh
70654 Kuwait
T: +965 9 975 2002
F: +965 2 4 89 0767
E: fmwm@yahoo.com

PROF DR SAEED-REZA SABBAGH-YAZDI is professor in the Civil Engineering Department of the KN Toosi University of Technology, Tehran, Iran. He obtained his PhD from the Jniversity of Wales, Swansea, United Kingdom. He has more than twenty years' academic and professional experience in management, design, computation, hydraulics, structura engineering, computer simulation of fluid flow and heat transfer, and stress analysis of hydraulic structures.

TAYEBEH AMIRI-SAADATABADI is a PhD student in the Department of Civil Engineering at the KN Toosi Jniversity of Technology. She obtained her MSc in hydraulic structures from the KN Toosi Jniversity of Technology and started her PhD research in 2010. Currently she is developing software to analyse concrete structures. Her main research interest is in finite volume numerical methods, cracking and creep.

PROF DR FALAH M WEGIAN has more than 20 years' academic experience, including the research work for his Masters and Doctorate. Prof Wegian is currently chairman of, and professor in, the Civil Engineering Department at the College of Technological Studies, Public Authority for Applied Education and Training (PAAET), Kuwait. His wide range of research interests includes the use of Fiber Optic Bragg Grating Sensors embedded in concrete structures to evaluate strains and cracks and the performance of bridge structures. Prof Wegian has published numerous research papers and has also authored two textbooks on concrete structures.














