Servicios Personalizados
Articulo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares en Google
Similares en Google
Compartir
Journal of the South African Institution of Civil Engineering
versión On-line ISSN 2309-8775
versión impresa ISSN 1021-2019
J. S. Afr. Inst. Civ. Eng. vol.55 no.1 Midrand abr. 2013
TECHNICAL PAPER
2D Linear Galerkin finite volume analysis of thermal stresses during sequential layer settings of mass concrete considering contact interface and variations of material properties. Part 1: Thermal analysis
S Sabbagh-Yazdi; T Amiri-SaadatAbadi; F M Wegian
ABSTRACT
In this research, a new explicit 2D numerical solution is presented to compute the temperature field which is caused due to hydration and thermal conductivity by the Galerkin finite volume method on unstructured meshes of triangular elements. The concrete thermal properties vary, based on the temperature variation and the age of the concrete in the developed model. A novel method for imposing natural boundary conditions is introduced that is suitable for the Galerkin finite volume method solution on unstructured meshes of triangular elements. In addition, the thermal contact is considered at the concrete-rock foundation interface to achieve more realistic simulations in this section. In this work we present the comparison of the thermal analysis numerical results of a plane wall, which had different thermal boundary conditions applied to its edges, with its analytical solution to assess the accuracy and efficiency of the developed model. The applicability of the developed numerical algorithm for thermal analysis is presented by the solution of thermal fields during gradual construction of a typical mass concrete structure.
Keywords: variable thermal property, mass concrete, Galerkin finite volume solution, unstructured meshes of triangular elements
INTRODUCTION
Gradual setting of concrete layers during construction of mass concrete structures may give rise to drastic temperature gradients due to the cement hydration and heat conduction properties of the concrete. Cement is a basic ingredient of concrete which, by the process of hydration, mixes with aggregates and water and produces concrete. This process is exothermal and causes the concrete temperature to rise. After achieving maximum temperature, the temperature decreases until it reaches the ambient temperature. Predicting the temperature field resulting from the concrete hydration process during a particular construction programme is an important consideration in the design and construction of mass concrete structures like concrete dams. However, the thermal properties of concrete (specific heat and thermal conductivity) vary according to the concrete temperature and the degree of concrete hydration. These changes can be considered in the thermal analysis of the mass concrete structures by the adoption of available empirical relationships.
The finite volume method has been widely applied to heat transfer and fluid dynamic problems through relatively simple discretisation (Vaz Jr et al 2009). In recent years the finite volume method has been used for the solution of temperature analysis, stress-strain computations and thermal stress solutions of solid mechanical problems, some of which are listed in the following review.
For the computation of temperature fields, an unstructured finite volume node-centered formulation was implemented, using an edge-based data structure for the solution of two-dimensional potential problems (Lyra et al 2002). Lyra et al used an edge-based unstructured finite volume procedure for the thermal analysis of steady state and transient problems (Lyra et al 2004). Recently, a 2D finite volume method to solve a heat diffusion equation was developed to predict the transient temperature field in an RCC (roller-compacted concrete) dam wall during concreting of sequential layers, taking into consideration the constant thermal properties during concrete setting (Sabbagh-Yazdi et al 2007).
The variation in concrete properties significantly influences the prediction of the temperature history of mass concrete structures. Much research has been done to calculate temperature fields, and different numerical models have been used in the various solution methods to simulate the temperature field in mass concrete structures. For example, a 2D finite difference method for predicting the hydration-induced temperature profile in mass concrete was developed, considering a sinusoidal function for the surrounding air changes (Ballim 2004).
A 3D finite element solution was proposed for thermal analysis by Kim et al (2001) who considered the effect of pipe cooling systems. Ilc et al (2009) also developed a numerical model for the thermal analysis of young concrete structures, based on the finite element method. Considering the constant thermal properties of concrete, the NASIR (Numerical Analyzer for Scientific and Industrial Requirements) concrete temperature solver, a 2D finite volume method solver for heat generation and transfer equation, was developed to predict the transient temperature field in an RCC dam wall during sequential layers of concrete setting (Sabbagh-Yazdi et al 2001). The accuracy and efficiency of the proposed model were assessed by comparing the numerical results from the analysis with analytical solutions for problems with constant concrete properties and various boundary conditions (Sabbagh-Yazdi et al 2007). In this research, the variation in the heat conduction properties of concrete that occurs due to changes in concrete temperature and the ageing process is considered in terms of the NASIR concrete temperature solver. For this purpose, a 2D matrix-free Galerkin finite volume solution is utilised for computing the temperature fields in mass concrete structures on unstructured meshes of triangular elements. In the developed numerical model, the heat generation and transfer equation is explicitly solved to compute the temperature field. For the cases where the boundary normal vector is parallel to the direction of the grid in the coordinate system, it is easy to impose the natural gradient boundary condition. To overcome the difficulties that may appear when imposing such a boundary condition at inclined boundaries of unstructured meshes of triangular elements, a technique is applied in this work to modify the gradient flux vectors at the centre of the boundary elements. This method is adopted for the implementation of the natural gradient boundary condition for the solution of heat generation and transfer equation using the Galerkin finite volume method.
HEAT GENERATION AND TRANSFER MATHEMATICAL MODEL
Heat transfer mathematical model
The heat generation and transfer equation is produced from different thermodynamics and heat transfer references (Sabbagh-Yazdi et al 2007).
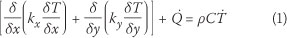
where k(J/m.h.°C) is the thermal conductivity of concrete, T(°C) is concrete temperature, Q (J/m3.h) is the rate of heat generation per volume, p(kg/m3) is the density of concrete, and C(J/kg.°C) is the specific heat of concrete.
The two main boundary conditions at the external surfaces are:

where Tair(°C) and q(w/m2) are the air temperature and the rate of heat exchange.
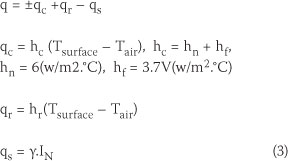
where qc, qr and qs are heat flux by convection, long wave radiation and solar radiation, respectively; hn, hf and hr are natural, forced and radiation convection; and γ,IN (w/m2) and V(m/s) are surface absorption, incident normal solar radiation and wind speed, respectively.
In this research, the effects of long wave radiation and solar radiation in heat flux have been disregarded and the wind speed has been supposed to be zero.
Cement hydration heat generation
Cement is a basic ingredient of concrete which gains its cementitious property after mixing with water. This chemical reaction called hydration causes the paste to harden and gain strength. Because of its significance, several research efforts into the concrete heat of hydration field and the appropriate mathematical models, have already been presented (Noorzaei et al 2006; Riding 2007).
In general, hydration is a thermo-activated reaction, and temperature primarily affects the rate of hydration. Hence, the equivalent age parameter and maturity function are used to consider this feature. Through the maturity function, the effect of concrete temperature on the rate of hydration is regarded.
Equation 4 is used to calculate the heat of hydration.
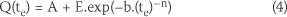
where A, E, b, n are variables which are calculated by appropriate fitting of Equation 4 to experimental data, and te(hr) is the equivalent age.
By adopting the Rastrup maturity function, the following equation is used to calculate the equivalent age:
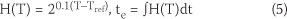
where H(T), T, Tref(°C), are the relative speeds of hydration reaction, concrete temperature and reference temperature, respectively.
Finally, Equation 6 is used to calculate the rate of concrete hydration (Sabbagh-Yazdi et al 2007):
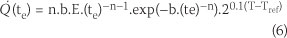
The hydration process is a long-term reaction, with different hydration products developing over time as a result of the chemical reaction of water with the cement components. Through this process, a skeleton of hardened cement paste is formed. Due to the ageing process, therefore, the concrete properties (thermal and mechanical) may change during the hydration reaction. The degree of hydration is equivalent to the amount of heat liberated at any point during the hydration stage to the total heat corresponding to the end hydration. Many different relationships are presented to calculate the degree of concrete hydration. One of these models is the Schindler model, in which the degree of hydration is calculated by the mixture proportions and the concrete age, as presented in Equation 7.
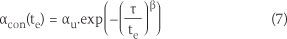
where au(unitless) is the ultimate degree of hydration, τ is hydration time parameter, te(hr) is the equivalent age, and β is the hydration slope parameter. The fit parameters (αu, τ,β) are specified according to the mixture proportions (Schindler 2004).
Using Equation 7, the rate of heat generation due to the concrete heat of hydration can be represented by the source terms, heat generation and transfer equation. In addition, the variation of concrete thermal properties (such as specific heat and thermal conductivity) during the ageing process can be considered in the computational thermal analysis.
Ageing effects on thermal properties of concrete
The concrete temperature and degree of concrete hydration affect the thermal properties of the concrete. The relationships below, which are related to change in the thermal properties of concrete over time, are used in the present thermal analysis.
Specific heat
The specific heat of concrete, which is equal to the required heat for 1°C increase of concrete temperature per unit mass of the concrete, depends on the mixture proportions, the degree of hydration, concrete temperature and the relative humidity of concrete.
The following equation is used for changes in the specific heat of concrete over time, as provided by Van Breugel (1998):
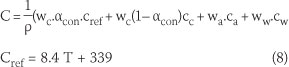
where C(J/kg.K) is the specific heat of concrete; p(kg/m3) is the density of concrete; wc, wa, ww(kg/m3) are the weight of cement, aggregate and water per unit volume; cc, ca, cw(J/kg.K) are the specific heat of cement, aggregate and water respectively; αcon is the degree of concrete hydration; and T(°C) is the concrete temperature.
Thermal conductivity
The thermal conductivity of concrete, which is the concrete's ability to conduct heat, represents the amount of heat transition through a unit thickness of concrete in a direction normal to a surface area at the unit time. This parameter is dependent on the relative humidity, type and amount of aggregate, porosity and the density of the concrete.
Schindler (2002) stated that a higher degree of hydration decreases the thermal conductivity of concrete. The following equation was proposed by Schindler:
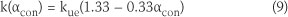
where k(w/m.K) is the transient thermal conductivity, kue(w/m.K) is the ultimate thermal conductivity of concrete, and αcon is the degree of concrete hydration.
NUMERICAL SOLUTION
Galerkin finite volume formulations
The heat generation and transfer Equation 5 can be written as:
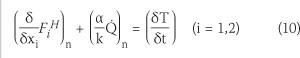
where FiH is diffusive flux in i direction.
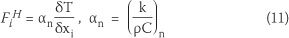
In each time step, the values of thermal properties (k, C) are updated considering the concrete temperature and degree of concrete hydration. Then the source term (Sn) is computed for every node (n) of the concrete body.
By application of the Galerkin weighted residual method, after multiplying the residual of Equation 10 by a weight function (which can be considered as the nodal shape function of a linear triangular element, (φn) and integrating over a subdomain On (which n is formed by gathering all the elements sharing node n), the weighted integral form of Equation 10 is written as Equation 12:
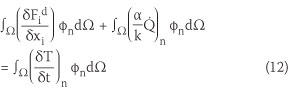
The weak form of Equation 12, after the omission of zero boundary terms, is expressed as:
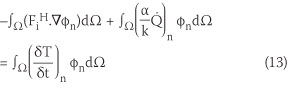
The approximate ratio given in Equation 14 can be used to calculate the spatial derivative term of Equation 13:
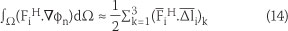
Here 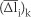 is the i direction component of the normal vector of edge k of the subdomain Ωn which is opposite to its central node n (Figure 1).
is the i direction component of the normal vector of edge k of the subdomain Ωn which is opposite to its central node n (Figure 1).
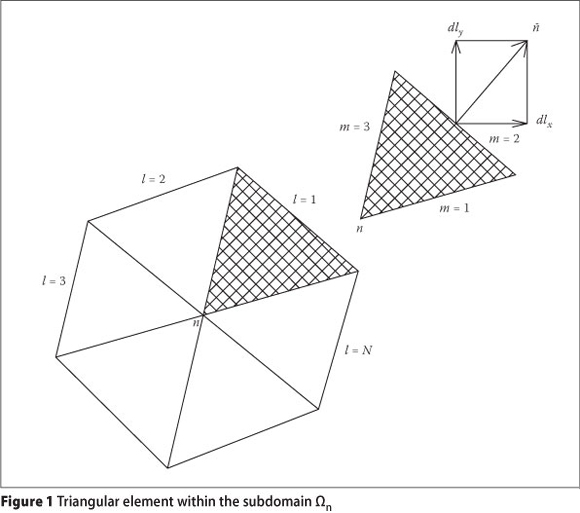
The source term of the Equation 13 can be approximated as:
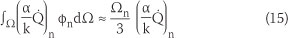
Using the forward differencing method, the discrete form of the transient term of the governing equations can be written as follows:
The explicit form of the heat generation and transfer equation for subdomain Ωn is expressed as Equation 17:
where Tnt+Δt is temperature of node n at time t+Δt, and N is the number of edges surrounding the subdomain Ωn (Figure 1).
Computation of heat flux vector components
The components of the heat flux vector  must be calculated at the centre of the elements corresponding to the boundary edges of the subdomain Ωn (Figure 1). The integration over an element can be converted to a boundary integral using the Gauss divergence theorem:
must be calculated at the centre of the elements corresponding to the boundary edges of the subdomain Ωn (Figure 1). The integration over an element can be converted to a boundary integral using the Gauss divergence theorem:

where Ωe is the area of a triangular element. The discrete form of the line integral can be written as:
where Δli is the component of the mth edge normal vector of a triangular element which is perpendicular to the i direction, and T is the average temperature at the same edge (Figure 1).
Hence, diffusive flux at each triangular element for both directions can be calculated using the following equation:
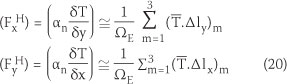
Boundary conditions
Two types of boundary conditions, known as essential and natural boundary conditions, are usually applied in thermal analysis. The essential and natural boundary conditions are used for certain temperature and temperature gradient flux at boundaries, respectively.
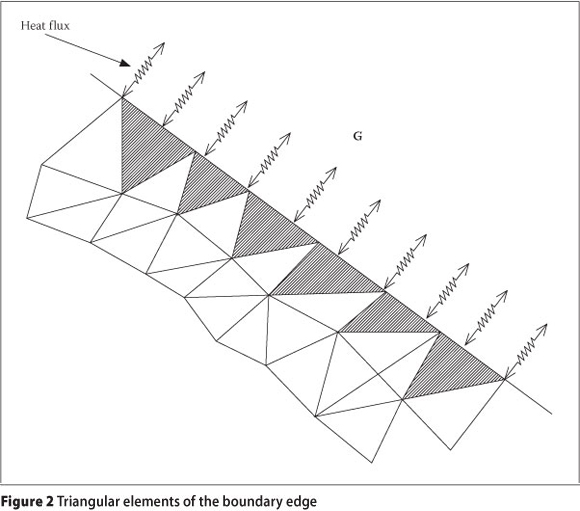
For the cases where the boundary normal vector n = (nx,ny) is parallel to the direction of the grid in the coordinate system, the given normal gradient due to heat flux by convection, G, can simply be inserted, but the computational difficulties arise for inclined or curved boundaries. To solve this problem, the computed gradient flux vector (Equation 20) at the centre of the boundary elements (hatched elements in Figure 2) at the end of each computational step may be modified as Equation 23.
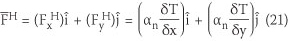
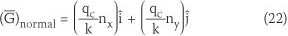
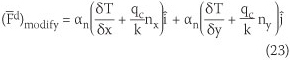
where k is thermal conductivity and qc is heat flux by convection, which was defined previously.
Time integration
If the propagation speed of heat is considered proportional to an, the critical time step size solution of the heat generation and transfer equation can be written as Equation 24:

where M is a coefficient that is less than unity.
In order to maintain the stability of the explicit solution, the minimum time step size of the computational domain must be used in the computation of the unsteady problems. For the steady state cases, the concept of local time stepping can be used where every node has a special time step which reduces the programme execution time.
THERMAL CONTACTS
When two solids, of initially different temperatures, are brought into contact, thermal coupling must be considered within the contact analysis. Heat normally flows from one solid to another one at the interface between the two solids; this affects the temperature distribution near the contact surfaces. A constitutive equation is required for the determination of heat flux in the contact zone. In addition, the heat conduction is dependent on contact pressure in the contact area. The following equation is often assumed to be the constitutive equation for heat flux:

Where T2 is the temperature of the slave node and  is the temperature of the closest point in the master surface to the slave node. The heat transfer coefficient
is the temperature of the closest point in the master surface to the slave node. The heat transfer coefficient 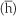 depends on the temperature of the contact surfaces and the contact pressure. The heat transfer can be accomplished in three possible ways, i.e. heat conduction through spots (hs), gas (hg) and radiation (hr). The following equation is obtained when one assumes that the above-mentioned mechanisms act in parallel:
depends on the temperature of the contact surfaces and the contact pressure. The heat transfer can be accomplished in three possible ways, i.e. heat conduction through spots (hs), gas (hg) and radiation (hr). The following equation is obtained when one assumes that the above-mentioned mechanisms act in parallel:

In this research, the heat conduction through gas and radiation has been disregarded and Equation 27 is used to determine the heat conduction through the spots in the contact interface.

where P is the contact pressure and coefficients hr, Hv and ξ are the thermal resistance coefficient, Vickers hardness and an exponent, respectively, which are given as hr = 1.0, Hv = 3.0 and ξ = 1.5.
The thermal boundary condition is applied by the following equations for each node in the contact interface:
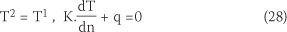
where T1 and T2 are the temperature of solids 1 and 2, respectively, and  and q are the thermal conductivity, normal temperature gradient and heat flux, respectively (Wriggers 2002).
and q are the thermal conductivity, normal temperature gradient and heat flux, respectively (Wriggers 2002).
VERIFICATION AND APPLICATION
Verification test
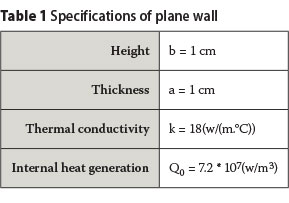
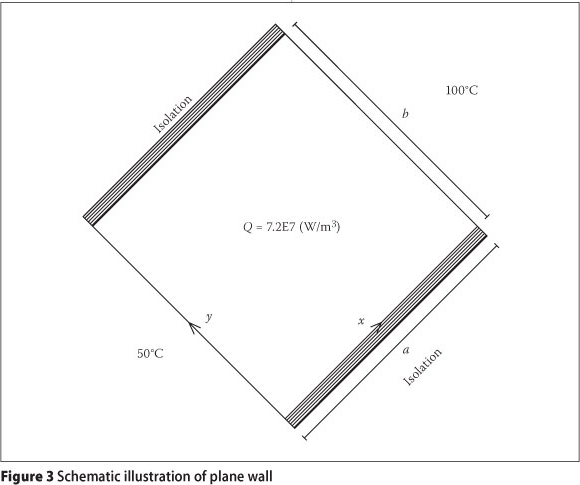
In this section, the solution for a steady state problem with inclined boundary is presented. Using the developed solver, the time stepping limit of the formulation is utilised to maintain the stability of iterative computation from the assumed initial condition towards the steady state condition. Furthermore, use of the local time stepping method speeds up the computation towards equilibrium. Consider a plane wall with specifications as presented in Table 1.
The boundary at y = 0,b of the domain is assumed to be insulated. The boundary at x = 0 is maintained at T0 = 50°C, and the boundary at x = a is exposed to ambient temperature Tc = 100°C (Figure 3). The film coefficient is hc = 200(w/m2°C). The assumption of an insulated boundary condition at y = 0,b of the domain results in the 1D heat flowing along the x direction. In this case, the analytical temperature field is given as Equation 29 (Reddy et al 2000).
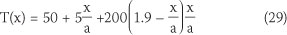
where x(m) is the distance from the edge, which is held at a constant temperature of 50°C, and a(m) is the dimension of the plate.
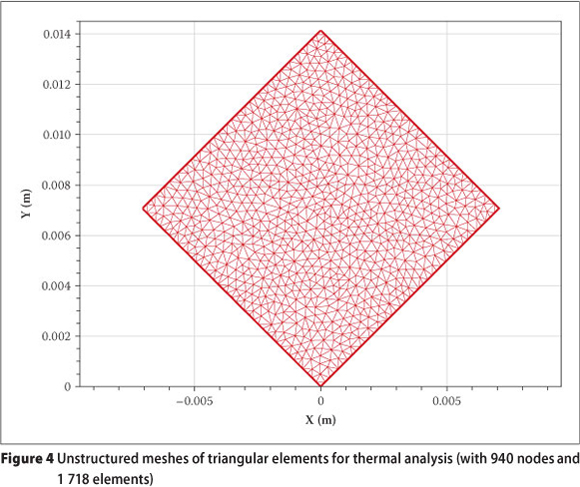
Unstructured meshes of triangular elements are shown in Figure 4, and computed temperature contours are illustrated in Figure 5.
Using the Dell Vostro 1500 with an Intel Core 2 Duo T7100 CPU with 1.8 GHz, 2 GB main memory, the CPU time measured 44.6 seconds.
The root mean square of the computed temperature during iterations, which is calculated by Equation 30, is shown in Figure 6. In Figure 7 the temperature changes along the x direction are compared with the analytical results. The good correlation between the computed results and the analytical solution is promising.
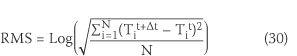
Application case
In this section, the developed algorithm is utilised to analyse the transient temperature field during the gradual construction of a typical mass concrete structure. The dam is 30 m high, while the base and crest are 30 m and 4.35 m wide, respectively. The left and right slopes are 0.1:1, 0.8:1 respectively (Figure 8). Layer thickness at every concreting is 0.5 m, and the interval between consecutive concrete placing lasts 48 hours. The portion of the dam foundation that is considered for thermal analysis is shown in Figure 8.
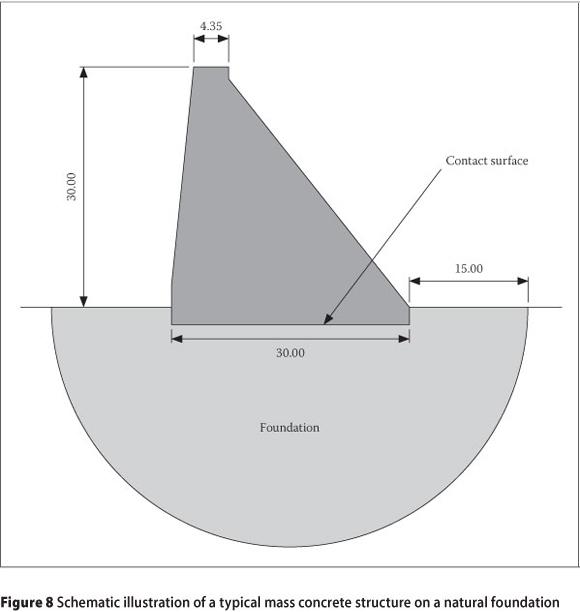
The far field boundary of the foundation is treated as a zero gradient boundary condition, and the Newman thermal boundary condition is used for the external surfaces of the dam wall and ground surface (Figure 8).
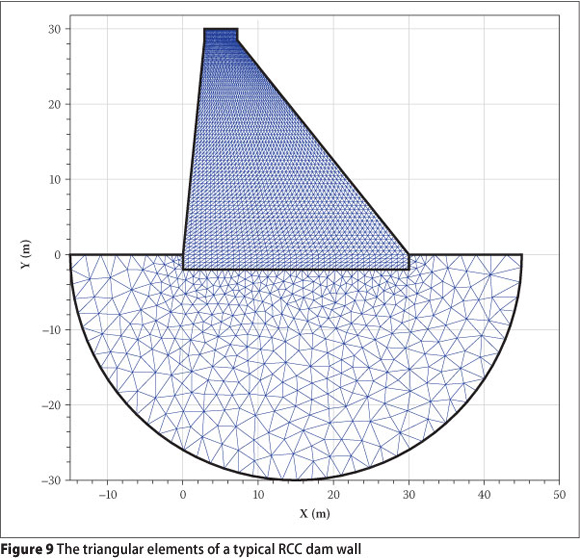
The use of unstructured meshes of triangular elements for the geometric modelling of the foundation media (Figure 9) facilitates simulation of the geo-structure layers with irregular formation and material variation. Likewise, application of structured meshes of triangular elements for the dam wall (Figure 9) provides the development of concrete media in the vertical direction (proportional to the construction stage and concrete layer). The sinusoidal function is utilised for air temperature changes.
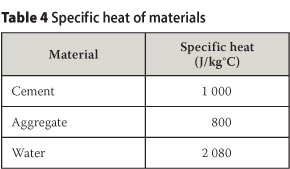
The thermal properties and mixture proportions of concrete are presented in Tables 2 and 3. The specific heat of materials, which is needed to calculate the specific heat of concrete, is presented in Table 4.
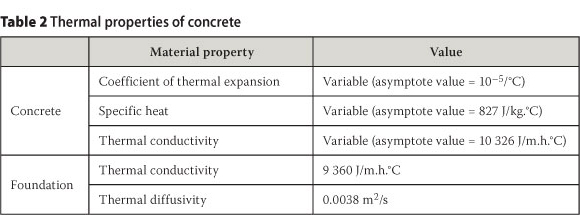
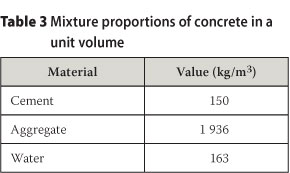
As mentioned, thermal properties of concrete vary with the ageing process. In the present analysis, the relationships as presented above are used for the simulation of the changes in the thermal properties of concrete over time. The thermal properties of the mass concrete structure are summarised in Table 2.
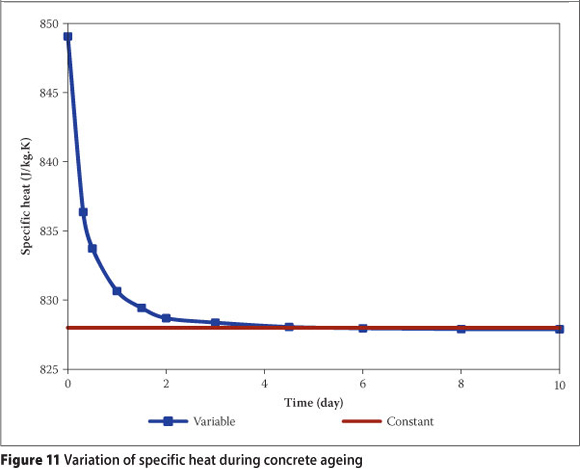
Using the presented relationships, the thermal properties of concrete can be determined according to concrete ageing over time, as shown in Figures 10 and 11. Having the transient changes of the thermal properties, these properties are assigned to each node considering the temperature and age of every concrete layer during thermal analysis. The simulation results for the various stages of gradual construction of a typical mass concrete dam are presented in terms of the transient temperature contour in Figure 12 (see page 102).
CONCLUSION
A 2D matrix-free Galerkin finite volume solution is presented to compute the transient temperature field, considering the variable thermal properties on the developing linear triangular elements due to the heat of hydration and thermal conduction through boundary surfaces during gradual concreting of concrete structures. The represented explicit solution is a computationally efficient algorithm which can achieve results of time-dependent heat generation and transfer problems with considerably low computational effort and CPU time consumption. However, for the steady state problems, the time stepping of the formulation may be utilised for iterative stable computation towards equilibrium, and using the local time stepping method, the programme execution time can be reduced.
Due to the hydration progress of concrete and the ageing process, the thermal properties of concrete vary over time. In the present transient thermal analysis of the concrete media, the proposed relationships by previous researchers, as mentioned above, are used for the simulation of the transient changes in the thermal properties of concrete according to concrete temperature and the degree of concrete hydration. The method presented in this research resolves the problem of imposing a normal temperature gradient at the inclined boundaries of unstructured meshes of triangular elements. In the developed algorithm, the temperature gradient boundary condition is applied by the modification of the gradient flux vector at the centre of the boundary elements.
In addition, the geometry of the dam wall and foundation is not considered integrated anymore, so the thermal contact is considered at concrete-rock foundation interface to achieve more realistic simulations in this part. In this work we present the comparison of the thermal analysis numerical results of a plane wall, where different thermal boundary conditions are imposed at its edges, with its analytical solution to assess the accuracy and efficiency of the developed model. The computed results presented promising correlation with the analytical solution. In order to present the applicability of the developed solver to simulate real-world problems, the developed model was used for transient thermal analysis of a typical mass concrete structure on a natural foundation in which the concrete media were gradually developed via sequential setting of fresh concrete layers.
The concrete temperature module of the NASIR Galerkin finite volume solver can be applied as a useful modelling means for the prediction of transient temperature profiles during the desired sequential setting construction programme of a mass concrete structure, considering variations in thermal properties.
NOTATION SECTION
k : Thermal conductivity of concrete
kuc : Ultimate thermal conductivity of concrete
C : Specific heat of concrete
ρ : Density of concrete
Sn : Source term te : Equivalent age of concrete
T : Concrete temperature Tref : Reference temperature
Tsurface : Concrete surface temperature
Tair : The air temperature
Tnt+Δt : Temperature of node n at t + Δt time
: Average temperature of edge
Q : Heat of hydration
Q: Rate of heat generation per volume
Q0 : Internal heat generation
αcon : Degree of concrete hydration
αu : Ultimate degree of hydration
A,E,b,n : Fit parameters
τ : Hydration time parameter
β : Hydration slope parameter
q : Rate of heat exchange
qc : Heat flux by convection
qr : Heat flux by long wave radiation
qs : Heat flux by solar radiation
hn : Natural convection
hf : Forced convection
hr : Radiation convection
γ : Surface absorption
IN : Incident Normal Solar Radiation
V : Wind speed
Ω : Subdomain
: Normal component of boundary edge at the i direction for the subdomain
Ω N : Number of control volume outside faces
: Normal vector of the boundary edges
Ωε : Area of the triangular element
Δl : Edge of triangular element
FiH : Diffusive flux in i direction.
G : Given normal temperature gradient
Δt : Time step size for heat generation and transfer equation
M : Coefficient that can be considered less than unity
wc,wa,ww : Weight of cement, aggregate and water, respectively
cc,ca,cw : Specific heat of cement, aggregate and water, respectively
hc : Film coefficient
x : Distance
a : Dimension of plate
REFERENCES
Ballim, Y 2004. A numerical model and associated calorimeter for predicting temperature profiles in mass concrete. Cement and Concrete Composites, 26(6): 695-703. [ Links ]
Ilc, A, Turk, G, Kavčič, F & Trtnik, G 2009. New numerical procedure for the prediction of temperature development in early age concrete structures. Automation in Construction, 18(6): 849-855. [ Links ]
Kim, J K, Kim, H K & Yang, J K 2001. Thermal analysis of hydration heat in concrete structures with pipe-cooling system. Computers and Structures, 79(2): 163-171. [ Links ]
Lyra, P R M, Lima, R D C F D, Guimarraes, C S C & Carvalho, D K E D 2002. An edge-based unstructured finite volume method for the solution of potential problems. Mecanica Computational, XXI: 1213-1231. [ Links ]
Lyra, P R M, Lima, R D C F D, Guimarães, C S C & Carvalho, D K E D 2004. An edge-based unstructured finite volume procedure for the numerical analysis of heat conduction applications. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 26(2): 160-169. [ Links ]
Noorzaei, J, Bayagoob, K H, Thanoon, W A & Jaafar, M S 2006. Thermal and stress analysis of Kinta RCC dam. Engineering Structures, 28(13): 1795-1802. [ Links ]
Reddy, J N & Gartling, D K 2000. The Finite Element Method in Heat Transfer and Fluid Dynamics, 2nd edition. New York: CRC Press. [ Links ]
Riding, K A 2007. Early age concrete thermal stress measurement and modeling. PhD Thesis, Austin, Texas, US: University of Texas at Austin. [ Links ]
Sabbagh-Yazdi, S R & Bagheri, A R 2001. Thermal numerical simulation of the laminar construction of RCC dams. Proceedings, 6th International Conference on Computational Modeling of Free and Moving Boundary Problems, Lemnos, Greece, 183-192. [ Links ]
Sabbagh-Yazdi, S R & Mastorakis, N E 2007. Efficient symmetric boundary condition for Galerkin finite volume solution of 3D temperature field on tetra-hedral meshes. Proceedings, 5th IASME/WSEAS International Conference on Heat Transfer, Thermal Engineering and Environment, Athens, Greece, 48-55. [ Links ]
Schindler, A K 2002. Concrete hydration, temperature development, and setting at early-ages. PhD Thesis, Austin, Texas, US, University of Texas at Austin. [ Links ]
Schindler, A K 2004. Effect of temperature on hydration of cementitious materials. ACI Materials Journal, 101(1): 72-81. [ Links ]
Van Breugel, K 1998. Prediction of temperature development in hardening concrete. In: Springenshmid, R (Ed), RILEM Report 15, Prevention of Thermal Cracking in Concrete at Early Ages, London: E & FN Spon, 51-75. [ Links ]
Vaz Jr, M, Munoz-Rojas, P A & Filippini, G 2009. On the accuracy of nodal stress computation in plane elasticity using finite volumes and finite elements. Computers and Structures, 87(17-18): 1044-1057. [ Links ]
Wriggers, P 2002. Computational Contact Mechanics. Weinheim, Germany: Wiley. [ Links ]
 Contact details:
Contact details:
Prof Dr Saeed-Reza Sabbagh-Yazdi
Civil Engineering Department
KN Toosi University of Technology
Valiasr St Mirdamad Cross
Tehran, Iran
T: +98 21 8 8 77 9 623
F: +98 21 88 77 9476
E: syazdi@kntu.acir
 Contact details:
Contact details:
Tayebeh Amiri-Saadatabadi
Civil Engineering Department
KN Toosi Jniversity of Technology
Valiasr St Mirdamad Cross
Tehran
Iran
T: +98 21 8 8 7 7 9 623
F: +98 21 88 77 9476
E: t_amiri@dena.kntu.acir
 Contact details:
Contact details:
Prof Dr Falah M Wegian
Chairman: Civil Engineering
Department College of Technological Studies
PAAET, Kuwait
PO Box: 42325
Shuwaikh
70654 Kuwait
T: +965 9 975 2002
F: +965 2 4 89 0767
E: fmwm@yahoo.com

PROF DR SAEED-REZA SABBAGH-YAZDI is professor in the Civil Engineering Department of the KN Toosi University of Technology, Tehran, Iran. He obtained his PhD from the Jniversity of Wales, Swansea, United Kingdom. He has more than twenty years' academic and professional experience in management, design, computation, hydraulics, structura engineering, computer simulation of fluid flow and heat transfer, and stress analysis of hydraulic structures.

TAYEBEH AMIRI-SAADATABADI is a PhD student in the Department of Civil Engineering at the KN Toosi Jniversity of Technology. She obtained her MSc in hydraulic structures from the KN Toosi Jniversity of Technology and started her PhD research in 2010. Currently she is developing software to analyse concrete structures. Her main research interest is in finite volume numerical methods, cracking and creep.

PROF DR FALAH M WEGIAN has more than 20 years' academic experience, including the research work for his Masters and Doctorate. Prof Wegian is currently chairman of, and professor in, the Civil Engineering Department at the College of Technological Studies, Public Authority for Applied Education and Training (PAAET), Kuwait. His wide range of research interests includes the use of Fiber Optic Bragg Grating Sensors embedded in concrete structures to evaluate strains and cracks and the performance of bridge structures. Prof Wegian has published numerous research papers and has also authored two textbooks on concrete structures.














