Servicios Personalizados
Articulo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares en Google
Similares en Google
Compartir
Journal of the South African Institution of Civil Engineering
versión On-line ISSN 2309-8775
versión impresa ISSN 1021-2019
J. S. Afr. Inst. Civ. Eng. vol.55 no.1 Midrand abr. 2013
TECHNICAL PAPER
Pile design practice in southern Africa Part 2: Implicit reliability of existing practice
J V Retief; M Dithinde
ABSTRACT
Limit state design has become the basis of geotechnical design codes worldwide. With the semi-probabilistic limit state design approach, load and resistance factors of (deterministic) design functions are calibrated on the basis of reliability theory. The calibration is done to obtain procedures that will ensure that a target level of reliability is exceeded under the design conditions within the scope of the design function. This is conventionally expressed in terms of the reliability index (β), which is related to the probability of failure (Pf). Acceptable existing design practice is an important source of information on appropriate levels of reliability.
This paper uses the results from a pile load test database to evaluate the reliability levels implied in the current South African pile design approach. The results of the analysis indicate that the reliability index values for ultimate limit state failure of single piles implicit to present design practice vary with the pile class. However, the influence of the probability model applied is more significant. Based on conventional and standardised procedures for reliability analysis, a representative implicit reliability index value βI Rep 3.5 is obtained, corresponding to a probability of failure Pf = 2.10-4. The values for various sets of pile conditions range from βI = 3.1 (Pf = 1.10-3) to βI = 4.3 (Pf = 1.10-5). This compares well with target levels of reliability for structural and geotechnical performance of βT = 3.0 as set in SANS 10160-1:2011 Part 1 Basis of structural design.
These indicative results provide a useful reference base to establish the reliability of existing and therefore acceptable South African pile design practice. It could also be interpreted as indicative of geotechnical design practice in general. The standard SANS 10160-5:2011 Part 5 Basis for geotechnical design and actions provides the framework for future calibration investigations.
Key words: pile foundations, South African practice, geotechnical design, reliability level
INTRODUCTION
The model factor statistics presented in the accompanying paper (Dithinde & Retief 2013 - please turn to page 60) provide a clear indication of the need for a systematic treatment of the variability and uncertainty of design parameters and procedures in geotechnical design practice. The principles of reliability-based design providing the conceptual basis for such systematic treatment are sufficiently established to be captured in standardised procedures such as the International Standard ISO 2394:1998 (adopted as SANS 2394:2004) and converted into operational basis of design procedures such as Eurocode EN 1990:2002. The standardised procedures are based on limit states design format with a reliability-based framework to ensure appropriate performance levels for the load-bearing capacity and characteristics of the structure or civil engineering works.
Sufficient advances in the theory of reliability have been made to derive guidelines for levels of performance as expressed in terms of reliability representing probability of failure (Pf) for classes of structures and facilities. For various reasons, however, there is insufficient information available to develop reliability-based procedures purely on frequentist or statistical probability models. The most compelling argument for taking information from existing practice into account when reliability-based design procedures are developed comes from the success of present practice and codes which primarily rely on experience-based expertise and judgement.
Capturing the reliability performance from existing practice which is deemed to be acceptable, such as presented in the accompanying paper, is an important source of information for the development of standardised design procedures. One of the possible applications of the information on existing practice is to obtain an indication of acceptable levels of reliability, in comparison to other ways in which target reliability is established. This is the purpose of the present paper. In the process, representative probability models for pile resistance are obtained, that could subsequently be used for reliability calibration of standard design procedures.
A brief overview is firstly provided of the state of limit states design in South Africa -the standardised way in which the principles of reliability is formulated and related to limit states design, including a discussion of target levels of reliability in general and as established for South Africa, serves as basis for comparison of implicit levels of reliability derived for existing practice. Ultimately such implicit levels of reliability are derived, considering alternative probability models from the results of the accompanying paper, and determining representative cases and probability models.
RELIABILITY-BASED GEOTECHNICAL LIMIT STATES DESIGN
The need of converting the now defunct Code of Practice for Pile Foundation Design (SABS 088:1972) to limit states design principles was recognised by the South African piling industry as far back as 1993. A concerted effort was also made by the Geotechnical Division of the South African Institution of Civil Engineering (SAICE) to adopt and apply geotechnical limit state design in South Africa, as summarised by Day & Retief (2009). Recent international and local developments have now added impetus to the introduction of probabilistic-based limit state geotechnical design in South Africa. These include:
i. Increased interest in harmonisation of technical rules for design of building and civil engineering works internationally as is demonstrated for instance by the activities of the ISSMGE (Orr et al 2002) and across disciplines, as demonstrated by the Eurocode set of design standards (CE 2002).
ii. The international acceptance of semi-probabilistic limit states as the standard basis on which the new generation of geotechnical codes are being developed today, such as Eurocode EN 1997:2004 Geotechnical design (EN 1997:2004) and the FHWA Manual for Load and Resistance Factor Design (LRFD) of bridge substructures (FHWA 2001).
iii. The publication of the revised South African Loading Code (SANS 10160:2011 Basis of structural design and actions for buildings and industrial structures) providing the reliability framework in Part 1 Basis of structural design, with the implication that the subsequent materials codes will be based on the same framework. Geotechnical design is included in this framework with the first step taken in Part 5 Basis of geotechnical design and actions as related to buildings and similar industrial structures.
The main advantage of the derivation of geotechnical limit states design procedures from the principles of reliability is that it provides a rational basis for such practice. In addition to enhancing the rationality of design for a specific situation (limit state, failure mode, construction type, etc) it also improves the consistency between the various situations within a single construction (geotechnical, substructure, superstructure, structural materials) or extends to the scope of application of the design procedures.
Common principles of reliability provide the rational basis for unification of geotechnical and structural design. This is an essential requirement for interrelated but specialised design procedures, not only since both elements are shared by individual constructions, but also for the purpose of technical communication between geotechnical and structural design practitioners.
At the highest level a rational basis for the underlying models and procedures is the only way in which international harmonisation of design practice can be maintained. The importance of sharing the wealth of international experience on the basis of harmonisation is usually appreciated, but the ability to provide optimally for local conditions whilst maintaining fundamental alignment with internationally accepted procedures is not always achieved or even attempted.
The theory of reliability, as applied to determine the performance of civil engineering works, is sufficiently mature to formulate standardised procedures for its application in design practice: The International Standard General principles on reliability for structures, ISO 2394:1998, was adopted as a South African National Standard SANS 2394:2004. The Joint Committee on Structural Safety Probabilistic Model Code (JCSS-PMC 2001) provides more detailed pre-normative reliability procedures and models. A notable development is the conversion of general reliability concepts into operational procedures as captured in the Eurocode Standard EN 1990:2002 Basis of structural design which provides a common basis for the set of Eurocodes. SANS 10160-1:2011 and SANS 10160-5:2011 respectively provide harmonisation with the Eurocode for the basis of design and geotechnical design. EN 1990 Annex C Basis of partial factor design and reliability analysis serves as reference for standardised reliability practice, with probabilistic models taken from Annex D Design assisted by testing in this paper.
A critical element of converting reliability analysis into design procedures is the establishment of acceptable levels of reliability. Some guidance on appropriate levels of reliability is given in SANS 2394:2004 and JCSS-PMC:2001. Application of appropriate levels of reliability in South African structural design is discussed by Retief & Dunaiski (2009). The implicit levels of reliability of existing design practice are recognised in standardised procedures such as SANS 2394:2004, EN 1990:2002 and FHWA HI-98-032 (FHWA 2001) as a basis for selecting target levels of reliability.
MOTIVATION AND PURPOSE OF INVESTIGATION
Given the importance of the reliability performance of existing practice serving as starting point for the calibration of more refined limit states design procedures, the purpose of this paper is to provide such an assessment of present pile construction and design practice in southern Africa. Implicit reliability serves as baseline for acceptable practice. Inconsistency in reliability across the scope of application can be identified, considering possible remedies and adjustments. Systematic calibration of the provisions of SANS 10160-5:2011 is another possible application of the results reported here.
The purpose of this paper is to assess the reliability performance of southern African pile design practice by exploring the application of the database of model uncertainties of pile resistance as reported by Dithinde et al (2011) where particulars of pile load tests and associated geotechnical information, design parameters and descriptive statistics are fully reported. Information from this pile database, together with additional statistical treatment as reported in the accompanying paper, serves as input to the reliability assessment reported here. A comprehensive range of soil conditions, pile geometry and resistance is incorporated in the database, to provide extensive representation of southern African pile construction practice in this assessment.
RELIABILITY CONCEPTS
The concepts of reliability, as developed for geotechnical and structural design, are defined in SANS 2394: 2004. The operational basis for partial factor design and reliability analysis as presented in EN 1990:2002 is followed here since these guidance procedures also apply to SANS 10160-1:2011 for the general basis of design and SANS 10160-5:2011 specifically for the geotechnical basis of design.
The reliability-based performance function for a structure g(X1; . Xj) as a random function of the random variables (X1; . Xj) is expressed as a limit state function indicating the state beyond which the structure no longer satisfies the design performance requirements, as shown in Equation 1. The random variables consist of a specified set of variables representing physical quantities which characterise actions, and material properties (including soil properties and geometrical quantities) conventionally defined as basic variables. The probability of failure of the structure Pf is given by Equation 2. Pf can also conveniently be expressed in terms of the reliability index β and the cumulative normal distribution function Φ or the inverse normal distribution function Φ-1 as given by Equation 3.

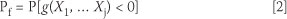
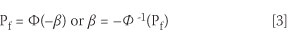
Two distinct formats of reliability-based design applies, with Equation 1 representing the probabilistic format. The deterministic partial factors format for standardised limit states design is defined in SANS 101601:2011; the application of the partial factors format to geotechnical limit states design is defined in SANS 10160-5:2011. Reliability calibration is the process of determining appropriate values for the partial factors to achieve a specified level of reliability for a given limit state as derived from Equation 1. Since partial factors design procedures are expressed in deterministic format with various partial factors calibrated on principles or probabilistic reliability, it is classified as a semi-probabilistic procedure or Level 1 reliability-based design (EN 1990:2002).
Although the theory of reliability is firmly rooted in the mathematical theory of probability and related statistics, its success as an operational basis for geotechnical and structural design is directly related to the simplification and approximation applied to the representation of the basic variables (Xi) and solving of the performance function, Equation 1. The ultimate approximation comes from the conversion of Equation 1 into a deterministic design function which employs partial factors that are based on the theory of reliability (see for example Holický et al 2007).
The most important level of approximation is related to the degree to which sources of variability and uncertainty are treated comprehensively. On the one hand it is granted that reliability modelling does not provide for a vital component of failure, which derives mainly from phenomena such as gross human error. Therefore reliability levels are often referred to as notional reliability. On the other hand reliability modelling presents a powerful tool for identification of critical sources of uncertainty, providing the basis for quality management measures in defence against gross error. The most compelling argument for reliability theory to provide for variability and uncertainty is its modelling and predictive capability, equivalent to structural mechanics modelling of load bearing behaviour for structural and geotechnical design.
TARGET LEVEL OF RELIABILITY
Central to the reliability basis of design procedures is the calibration of partial factors, which consists of an inverse reliability analysis process of calculating partial factors to exceed a given or target level of reliability (βτ) as an initial step. The establishment of an appropriate level of reliability in accordance with the design case under consideration therefore plays a key role in reliability-based limit states design, or more specifically the calibration of standardised design procedures.
Several approaches for setting the target reliability index are available. A pragmatic approach which is mostly followed is to apply a combination of the various methods. The methods include:
■ Risk-based cost-benefit analysis and optimisation
■ Failure rates estimated from actual case histories
■ Value set by regulatory authorities for a given limit state
■ Range of beta values implied in the current design practice.
Risk-based optimisation of reliability
The most rational approach for establishing the target level of reliability is through cost-benefit analysis and optimisation. Cost-benefit analysis entails the study of the variation of the initial cost, maintenance costs, and the costs of expected failure. It therefore represents the determination of reliability in the context of risk optimisation. The matter of the necessary inclusion of the loss of human life leads this process to be highly controversial. However, the relatively recent development of the concept of the Life Quality Index (LQI) which relates human life in neutral terms of marginal changes in life expectancy and working life (see for example Rackwitz 2008) should resolve this controversy. Although the LQI concept developed rapidly in recent years, no operational guidelines are available as yet, particularly for South African conditions.
Reliability levels for geotechnical design
The target probability of failure for a given structure can be established on the basis of failure rates estimated from actual case histories. For the case of foundations it is estimated that probability of failure (Pf) ranges from 0.001 to 0.01 - about one-and-a-half orders of magnitude below a "marginally acceptable" level and half an order of magnitude below an "acceptable" level according to the FHWA Manual for LRFD bridge pile design (FHWA 2001). However, many authors (e.g. Phoon 1995; Baecher & Christian 2003; Christian 2004) have cautioned that the probability of failure for constructed facilities is not solely a function of the design process uncertainties, as is the case for the calculated failure probabilities. Therefore, for comparison with calculated failure probabilities, the rate of failure from FHWA (2001) should be adjusted by one order of magnitude downward (Phoon 1995). If the suggested adjustments are effected, the probability of failure for foundations becomes 0.001 to 0.0001 which corresponds to target reliability index values (βT) of between 3.1 and 3.7.
Reliability levels for South African practice
The target levels of reliability for South African constructions within the scope of the revised Loading Code SANS 101601:2011 are discussed by Retief & Dunaiski (2009). Motivation is provided for maintaining the reference level of βT = 3.0 to be the same as that applied in SABS 0160:1989 (Milford 1988). The decision was based mainly on the argument that there was no evidence or justification for adjusting the level of reliability for South Africa. The reference reliability agrees with practice in countries such as the USA and Canada. It is consistent with guidance given in SANS 2394:2004 when South African economic conditions are taken into account.
The most serious challenge to maintaining the reference level of reliability for South Africa came from the default value of βT = 3.8 applied in Eurocode. It should be noted, however, that this value is not normative in Eurocode, but since safety is treated as a national issue βT can be selected by member countries. The high value of reliability applied in Eurocode was also judged to reflect higher levels of economic development, which implies lower relative cost of construction (or higher affordability) and consequent higher safety levels obtained in risk-based optimisation.
A factor which moderates the difference between South African target reliability and the Eurocode default value is that in calibration the reliability is seen as a constraint, whilst the Eurocode value is often seen as a target to be attained on average (SAKO 1999). The implication is that βT = 3.0 as a constraint differs less from βT= 3.8 as an average target than it may appear at first glance.
Another moderating factor is that the South African reference value applies to a more restricted reliability class of construction (RC2, typically buildings up to four storeys high) which corresponds to the lower part of the corresponding Eurocode reliability class (RC2). For the next South African reliability class (RC3, typically buildings of five to fifteen storeys) βT = 3.5 approaches that of the undifferentiated Eurocode RC2.
Implicit reliability levels of acceptable practice
Keeping the design methodology compatible with the existing experience base is consistent with the evolutionary nature of codes and standards that require changes to be made cautiously and deliberately (Phoon 1995). In the spirit of a Bayesian approach towards reliability, proven experience is an important source of information that can be combined with other sources of data on variability and uncertainty in reliability-based design.
Accordingly this paper investigates the level of reliability of pile foundations designed in accordance with the static formula. This is done by determining the implicit levels of reliability for the current working stress design (WSD) methods for piles by comparing design values to reliability models for pile resistance. Reliability modelling of pile resistance is based on the uncertainty of pile resistance, as observed by the comparison of the interpreted resistance from pile tests and the predicted value for an extensive survey of pile tests done across southern Africa, representing a wide range of conditions, pile construction practices and configurations.
CONCEPTS OF RELIABILITY ANALYSIS AND CALIBRATION
Although reliability calibration and the analysis of existing practice form two distinct components of the application of reliability theory in design, they are so closely related that some concepts of their treatment in practice can share a common formulation. The common concepts are related to a specific level of reliability over a defined range of conditions. The following issues are relevant to reliability calibration of design procedure such as partial factor limit states design; therefore by implication also to reliability assessment of existing practice:
■ The representative level of reliability is either the target reliability in the case of calibration, or the implicit reliability in the case of assessing acceptable existing practice; conventionally expressed in terms of a reliability index as βτ and β! respectively. The following alternative approaches apply to the representative reliability:
■ An average value is taken across the range of conditions, although the value may be significantly exceeded in some cases - this is the view generally taken in Eurocode, also associated with relatively high levels of reliability (typically βT = 3.8).
■ A lower limit value is taken as a constraint, generally to be exceeded - this view is taken in South Africa, where the representative value is also relatively low (typically βT = 3.0).
■ Consistency of reliability over the range of application is an objective to ensure that significantly different levels do not occur under different design conditions or cases; in particular systematically as a function of classes of applications (for example construction and/or soil type in the case of piles) or other design parameters. The following effects need to be considered:
■ Conditions under which the lowest level of reliability is achieved will control the measures taken.
■ Systematic exceeding of the representative reliability represents conditions which may be unjustifiably conservative.
■ Consistency of reliability can be assessed in terms of the absence of different levels and the absence of trends, or at least smooth transitions related to continuous design parameters.
■ The level of confidence of calibration or assessment should take into account that it is at best an approximate process, due to the predictive nature of design. It is based on limited information, either for parametric calibration or assessment of existing practice such as presented here, or on the actual conditions in the case of design of a specific project. Calibration or assessment should therefore be moderated on the following basis:
■ A limited level of confidence applies to both the required reliability levels (target or implied) and measures to achieve these - all based on acceptable performance of present practice. ■ Best estimates of reliability is therefore generally acceptable, only reverting to conservative modelling when there is specific justification for such measures.
It should be noted that calibration back to existing practice does not imply maintaining the status quo just in a more complex format! With calibration, allowance can subsequently be made for rectifying conditions where reliability is inconsistent with the (present) general practice, either insufficient or unjustifiably conservative. Where insufficient reliability derives from uncertainty, as opposed to variability, appropriate measures can be considered, such as additional investigation consisting of gathering of data and improved modelling.
RELIABILITY MODELLING OF PILE RESISTANCE
The two predominant classes of uncertainty for geotechnical design can be distinguished as (i) uncertainties associated with design soil properties and (ii) calculation model uncertainties. With regard to geotechnical property uncertainties, significant research has been done to generate statistics on individual components of soil parameter uncertainty. Conversely, model statistics are relatively scarcer. In fact, the lack of model statistics is considered to be a key impediment to the development of geotechnical reliability-based design (Phoon 2005). This consideration provided the motivation for the investigation of model uncertainty of pile resistance as reported in the accompanying paper and by Dithinde et al (2011).
Model uncertainty, as defined for example in ISO 2394:1998, EN 1990:2002 and JCSS PMC (2001), reflects uncertainties of the structural mechanics model. Variability of variables, mainly actions, material properties and geometry is represented explicitly as basic variables in the performance function, as defined in Equation 1. In experimental determination of model uncertainty, values of basic variables are determined deterministically through testing. The implication is that model uncertainty represents not only the effect of the structural mechanics model, but also of all the sources of uncertainty, and even variability that is not explicitly captured in the testing process.
The modelling uncertainty reported in the accompanying paper not only reflects the uncertainty of the static pile design formula, but also the interpretation of site investigations and conversion of measurements into material properties. Due to the uncertainty of material properties and the absence of its representation as basic variables, the model factor can be considered to represent a probability model of pile resistance as predicted by the static pile formula. The procedure for using soil properties based on subsurface data surveys to predict pile resistance as described by Dithinde (2007) implies that the uncertainties from soil properties are incorporated in the predicted values. The pile resistance probability model can therefore be taken from the distributions and summary statistics presented in the accompanying paper.
In applying working stress design (WSD) procedures through the static pile design function, the emphasis is predominantly placed on pile resistance. Whilst loads are treated at nominal un-factored values, safety is treated by the application of a factor of safety to pile resistance. The initial parametric investigation of pile design practice is therefore based on considering pile resistance only. The effect of considering variability of loading is then considered subsequently.
Pile resistance only
In the definition of model uncertainty given in the accompanying paper, given here as Equation 4, the interpreted pile capacity (Qi) can be taken to represent the probability representation of the pile resistance (RRel), and the predicted capacity (Qp) the deterministic nominal pile resistance (Rn). RRel can therefore be expressed by Equation 5. The static pile design function is given by Equation 6 in terms of a factor of safety (FS) and nominal dead load (Dn) and live load (Ln). From Equations 5 and 6, the specific performance function given by Equation 7 can be converted into a parametric limit state function as shown in Equation 8. The implicit reliability index value (βI) an then be obtained from Equation 9 in terms of the probability model for M and the factor of safety FS which has a deterministic value.




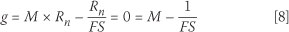

Values for βI can be obtained in terms of the pile classes identified in the accompanying paper. This is done by applying the reported statistics as parameter estimates for probability models for M. Comparison of βI -values for alternative pile classes provides an indication of the representativeness and consistency of implicit reliability across the range of conditions represented by the M statistics.
As a point of departure the case of a single combined pile class (ALL) is used as a representative case to estimate βI ,Rep. This case is then used to investigate the influence of the probability distribution on βI -values. The influence of pile class on βI -estimates is considered below.
The estimate for βI ,Rep is based on the lognormal distribution as standardised practice for resistance. Generally an overall factor of safety of 2.5 is regarded as an acceptable value for piles and has become a norm in southern Africa (Byrne & Berry 2008). As indicated in the accompanying paper, the normal distribution, which is conventionally used as the default first approximation distribution in reliability analysis, could also be considered. The mild degree of skewness indicated from the sample statistics presented in the accompanying paper can be taken into account by considering the general lognormal distribution. The results are summarised in Table 1, where values for the estimated distribution parameters are also given.
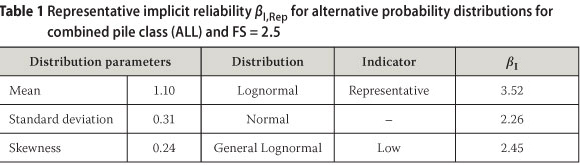
The value for βI ,Rep is clearly sensitive to the distribution applied to represent M and therefore needs some interpretation: The value of βI ,Rep = 3.5 as obtained from the lognormal distribution is taken as an estimate of acceptable practice in accordance with standardised reliability procedures. The value of βI ,Rep = 2.3 obtained from the normal distribution is considered to be too low to reflect acceptable practice. The low value of skewness taken into account by the general lognormal distribution provides a slight improvement on this apparently low level of reliability; this result should be considered as a lower limit estimate of implicit reliability, as βI ,Low = 2.4.
An indication of the representativeness of these values of βI across the range of pile classes is presented in Table 2. The value for βI ,Rep = 3.5 listed in Table 1 for the combined group (ALL) generally lies in the lower range of the values obtained for the various pile classes as listed in Table 2. The value of 3.5 is therefore taken to be in agreement with the approach of defining target reliability at a lower constraint value, and is thus ranked to indicate the mid-range value of implicit reliability.
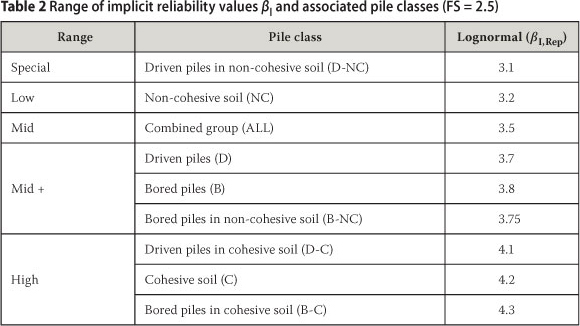
The class of piles driven in non-cohesive soil (D-NC) is ranked at a special-range due to its low value in comparison to the representative implicit reliability. The more general pile class of non-cohesive soil (NC) is classified to be in the low-range. For all other pile classes, higher values for βI ,Rep are obtained (Mid+); with significantly higher values (High) obtained for bored piles in cohesive soils (B-C), as listed in Table 2.
R is therefore concluded that the values for βI ,Rep and βI ,Low obtained from Table 1 provide a reasonable representation of the implicit reliability of existing practice, but that the special case of driven piles in non-cohesive soils (D-NC) should be considered separately for systematically lower levels of reliability.
In addition to obtaining a lower limit estimate of the implicit reliability as based on the probability distribution, confidence level estimates of the distribution parameters can be applied. For this purpose the confidence limit estimates presented in the summary statistics in the accompanying paper are utilised. A single-sided 75% confidence limit estimate is used, as suggested by Eurocode EN 1990:2002 for cases where parameter estimation is based on vague prior distributions. The lower confidence limit value is used for the mean and the upper limit for the standard deviation. The confidence limit estimates βI ,CONF are listed in Table 3 for the two cases identified above as representative (ALL) and the special lower pile class (D-NC). Values are based on the confidence level distribution parameters, also listed in Table 3, applied to the lognormal distribution.
Although the confidence limit implicit reliability listed in Table 3 is reduced for the representative case of the combined pile conditions listed in Table 1, the change from 3.5 to 3.2 is not too significant. For the special case D-NC the change from 3.3 to 2.2 is, however, indicative of not only the tendency of systematic lower value of implicit reliability, but also of the poor quality of its prediction.
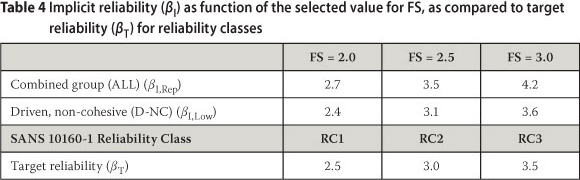
The influence of the FS-value selected in pile design on βI-estimates is shown in Table 4. For comparison, target levels of reliability (βT) are also listed, as given by SANS 10160-1:2011 for different reliability classes of building structures. The comparison indicates reasonable agreement between βI, Low for FS(2.0, 0.5 and 3.0) and βτ for reliability classes (RC1, RC2 and RC3}. The values for βI, Rep generally exceed that for the corresponding βτ showing a trend of widening of the difference for the higher FS values and reliability classes.
Implicit reliability based on resistance and loads
Expression of the performance function given by Equation 1 in terms of probabilistic models for resistance (R), dead (D) and live (L) is given in Equation 10.
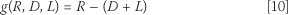
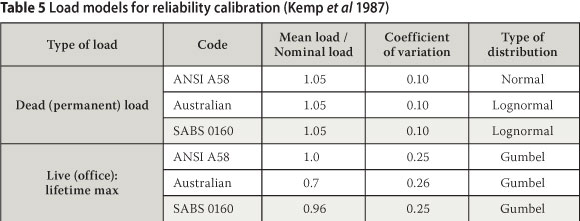
A normalised reliability model for Equation 10 can be obtained for parametric reliability analysis by representing each basic variable (X) by the ratio of mean to nominal value µX/Xn) and the relationship between the nominal values (Rn, Dn and Ln) given by the static pile design function (Equation 6). Similar to the treatment above, the resistance R is represented by the probability model for M as given by Equation 5. The load models reported by Kemp et al (1987) used for the conversion of structural design in South Africa from working stress to limit states design procedures listed in Table 5 can be used for models of D and L.
Different loading conditions can be treated parametrically through the ratio Ln/Dn. A typical range of Ln/Dn ratios is 0.51.5 for concrete structures and 1-2 for steel structures (Melchers 1999). For foundations dead load would dominate, tending towards the lower range of load ratios. Based on this information, a practical range of Ln/Dn ratio of 0.5 to 2 was adopted as sufficiently representative of structures in general. The special cases of dead and live loads only are indicative of the outer limits of load conditions. For this reason the range of analysis was done for Ln/Dn between 0 and 2; the case for Ln only was also calculated. Parametric reliability analysis of Equation 10 was done using Second Order Reliability Method (SORM) software provided by Holický (2009).
The results for the representative reliability analysis (βI, Rep) based on the model for the complete dataset (ALL) are shown in Figure 1(a); the results for the special case of driven piles in non-cohesive soil βI, d-nc) are shown in Figure 1(b). Separate graphs are provided for the values of FS (2.0, 2.5 and 3.0). The results for the analysis of the complete version of Equation 10 are labelled as M,D,L(FS); the off-scale case of live load only is indicated as an arrow (→) labelled M,L(FS); the results from the previous analysis considering pile resistance only are indicated as the horizontal line labelled M(FS).
As can be expected, the inclusion of the effects of loading reduces the level of implicit reliability. Furthermore, the effects are dependent on the ratio of live to dead load (Ln/Dn), with trends similar to that obtained with load calibration analyses (Holický & Retief 2005). The lower values of implicit reliability occur for conditions dominated by live load, which generally can only be expected under exceptional conditions for pile foundations. Over the operational conditions of loading dominated by Dn the values for βI, Rep compare well with the target reliability index values βτ listed for the various reliability classes listed in Table 4. For the special case of driven piles in non-cohesive soils, the values obtained for βI d-nc are systematically lower than the corresponding values for βT.
DISCUSSION AND CONCLUSIONS
The resistance statistics for pile design practice in southern Africa, as reported in the accompanying paper, are applied in this paper to assess the implicit levels of reliability of such practice. This is done by deriving reliability models for pile resistance by applying the model statistics as parameter estimates to internationally standardised probability distributions for geotechnical and structural resistance. Values for implicit reliability, as expressed by the reliability index βI), are determined to obtain a measure of the representative level of performance of pile design practice. In addition to obtaining best estimate values for βI, conservative estimates are also made in terms of more severe interpretation of parameter estimates or probability distributions for pile resistance. Consistency of reliability is also investigated across the range of pile construction practice.
Implicit levels of reliability are derived for two reliability performance models:
i. Considering pile resistance only and neglecting loading as basic variable, in accordance with design practice reflected by the working stress design format for pile design, where a single factor of safety is applied to pile resistance.
ii. Including reliability models for dead (permanent) and live (variable) loads into the performance function, using the models on which the implementation and calibration of limit states design for South Africa were based.
The two main issues of concern for determining model statistics and applying these to reliability models for pile resistance identified in the accompanying paper are (i) the probability distribution used, and (ii) the scope of application as based on differentiated classes of pile conditions. It was found that the different plausible probability distributions have a more significant influence on the levels of implied reliability than differentiation into classes of pile conditions.
The default distribution applied in reliability analysis is generally the normal distribution, to represent the basic step from deterministic design practice to at least provide for the dispersion of basic variables. The lognormal distribution function at the same basic level of approximation has the added utility of not predicting negative values. This is particularly relevant when the lower tail of the distribution is considered, such as for resistance. However, values for βI vary from a low value βI,n = 2.3 for the normal distribution to a relatively high value βI= 3.5 for the lognormal distribution, in both cases for the combined set of pile conditions and general design practice based on FS = 2.5. When skewness obtained from the model statistics is taken into account by applying the general lognormal distribution, βI= 2.4 is obtained.
Selecting the lognormal distribution as basis to obtain a representative value for the reliability index βI,Rep = 3.5 is based on consideration of standardised practice for reliability analysis, supported by the marginal preference obtained from the model statistics results presented in the accompanying paper. In accordance with Equation 3 the reliability index value corresponds with a probability of failure Pf of 2.10-4.
A lower estimate βI, Low= 2.4 (Pf = 8.10-3) is based on the general lognormal distribution. Another lower limit estimate of βI is based on the 75% confidence limit estimates of the distribution parameters, obtaining a value of βI, CL= 3.2 (Pf = 7.10-4).
Comparing the values for βI for the combined set of pile conditions to the various pile classes, the following observations can be made:βI,Rep= 3.5 provides a lower limit estimate value for βI values for other pile classes based on construction method and/or soil type generally provide higher values. The exception is the case for driven piles in non-cohesive soil, where βI,d-nc = 3.1 (Pf = 1.10-4) is obtained; alternatively for non-cohesive soil βI, NC= 3.2. When confidence level estimates are made, it is shown that the confidence limit value for driven piles in non-cohesive soil is as low as βI,Conf= 2.2 (Pf = 1.10-2).
When loads are also modelled as basic variables, the values for βI,Rep is somewhat reduced in the typical range of ratios for live to dead load to be expected for pile foundations. Values above 3.2 are obtained for live load less than dead load. The limited reduction in βI,Rep is indicative of the fact that reliability is dominated by the influence of pile resistance reliability. The reduction in βI values for situations dominated by live load is indicative of the increasing role of the reliability of live load, which should optimally be provided for in terms of partial load factors, rather than being of concern for pile design reliability as such.
Comparison of values for βI,Rep corresponding to commonly adopted values for factor of safety FS (i.e. 2 - 3) generally shows good agreement with the target reliability βT set in SANS 10160-1:2011 for different reliability classes. The values for implicit reliability for the three values of FS for dead load dominating conditions βI, Rep (2.5, 3.2 and 3.7) compares well with target reliability for the first three reliability classes βT (2.5, 3.0 and 3.5). Nonetheless, the range of βI, Rep values obtained seem to be on the higher side for single piles, suggesting that current practice is conservative.
The reliability assessment of pile design practice does not only provide insight into the sufficiency of existing practice, but could also form the basis for achieving appropriate performance levels through reliability calibrated procedures. The rational basis for reliability calibration provided in SANS 10160-1:2011 can be applied in accordance with geotechnical limit states design procedures presented in SANS 10160-5:2011.
LIST OF NOTATIONS FOR RELIABILITY INDEX (β)
β Reliability index, as related to prob- ability of failure given by Equation 3
βT Target level of reliability obtained through calibration of design expression
βI Reliability level implicitly achieved by existing practice, expressed in terms of the reliability index β
βI, Rep Indicative level of reliability taken to be representative of the set of pile conditions under consideration, usually considering pile design in general
βI, Low Lower limit estimates of implicit reliability based either on the selection of the probability distribution or the pile class
βI, Conf Reliability index value based on confidence limit estimates of distribution parameters
βI, d-nc Implicit reliability index value for the special case of driven piles in non-cohesive soil
REFERENCES
Baecher, G B & Christian, T 2003. Reliability and Statistics in Geotechnical Engineering. New York: Wiley. [ Links ]
Byrne, G & Berry, A D 2008. A Guide to Practical Geotechnical Engineering in Southern Africa, 4th edition. Germiston: Franki Africa (Pty) Ltd. [ Links ]
CE (Commision Européenne) 2002. Guidance Paper L: Application and Use of Eurocodes. Document CONSTRUCT 01/483 Rev.1, Brussels: CE. [ Links ]
Christian, J T 2004. Geotechnical engineering reliability: How well do we know what we are doing? The 39th Terzaghi Lecture. Journal of Geotechnical Engineering and Geoenvironmental Engineering, 130(10): 985-1003. [ Links ]
Day, P W & Retief, J V 2009. Provision for geotechnical design in SANS 10160, Chapter 5-1. In: Retief, J V & Dunaiski, P E (Eds), Background to SANS 10160. Stellenbosch: SUN MeDIA Press. [ Links ]
Dithinde, M 2007. Characterisation of model uncertainty for reliability-based design of pile foundations. PhD Thesis, Stellenbosch, South Africa: University of Stellenbosch. [ Links ]
Dithinde, M, Phoon, K K, De Wet M & Retief, J V 2011. Characterisation of model uncertainty in the static pile design formula. Journal of Geotechnical and Geoenvironmental Engineering, ASCE, 137(1): 333-342. [ Links ]
Dithinde, M & Retief J V 2013. Pile design practice in southern Africa. Part I: Resistance statistics. SAICE Journal, 55(1): 60-71. [ Links ]
European Committee for Standardization 1990. EN 1990:2002. Eurocode: Basis of Structural Design. Brussels: European Committee for Standardization (CEN). [ Links ]
European Committee for Standardization 1997. EN 1997:2004. Eurocode 7: Geotechnical Design. Part 1: General Rules. Brussels: European Committee for Standardization (CEN). [ Links ]
FHWA (US Federal Highway Administration) 2001. Load and Resistance Factor Design (LRFD) for Highway Bridge Substructures. Publication No.
FHWA-HI-98-032, Washington DC: FHWA. Holický, M & Retief J V 2005. Reliability assessment of alternative Eurocode and South African load combination schemes for structural design. SAICE Journal, 47(1): 15-20. [ Links ]
Holický, M 2009. Reliability Analysis for Structural Design. Stellenbosch: SUN MeDIA Press. [ Links ]
Holický, M, Retief, J V & Dunaiski, P E 2007. The reliability basis of design for structural resistance. Proceedings, 3rd International Conference on Structural Engineering, Mechanics and Computation (SEMC 2007), Cape Town, South Africa: Millpress, 1735-1740. [ Links ]
JCSS (Joint Committee on Structural Safety) PMC 200). Probabilistic model code. JCSS Working Materials [Online] http://www.jcss.ethz.ch (retrieved 1 Feb. 2011). [ Links ]
Kemp, A R, Milford, R V & Laurie, J P A 1987. Proposal for a comprehensive limit states formulation for South African structural codes. The Civil Engineer in South Africa, 29(9): 351-360. [ Links ]
Melchers, R E 1999. Structural Reliability: Analysis and Prediction. Chichester, New York: Wiley. [ Links ]
Milford, R V 1988. Target safety and SABS 0160 load factors. The Civil Engineer in South Africa, 30(10): 475-481. [ Links ]
Orr, T L L, Matsui, K & Day, P W 2002. Survey of geo-technical investigation methods and determination of parameter values. In: Honjo, Y (Ed), Foundation Design Codes and Soil Investigation in View of International Harmonization and Performance-Based Design. Proceedings, International Workshop on Foundation Design Codes and Performance-Based Design, Tokyo, Japan, 10-12 April, Lisse, Netherlands: AA Balkema. [ Links ]
Phoon, K K 1995. Reliability-based design of foundations for transmission line structures. PhD Thesis, Ithaca, NY, US: Cornell University. [ Links ]
Phoon, K K 2005. Reliability-based design incorporating model uncertainties. Proceedings, 3rd International Conference on Geotechnical Engineering combined with the 9th Yearly Meeting of the Indonesian Society for Geotechnical Engineering, 191-203. [ Links ]
Rackwitz, R 2008. Optimization with a LQI acceptance criterion, Annexure 5. In: JCSS Risk Assessment in Engineering - Principles, Systems Representation. pp 78-79. [Online] http://www.jcss.ethz.ch/publications/background/Risk_background Doc_LQI_Optimization.pdf (retrieved on 1 Feb. 2011). [ Links ]
Retief, J V & Dunaiski, P E 2009. The limit states basis of structural design for SANS 10160-1, Chapter 1-2. In: Retief, J V & Dunaiski, P E (Eds), Background to SANS 10160. [ Links ]
Stellenbosch: SUN MeDIA. SABS 1972. SABS 088:1972. Code of Practice for Pile Foundations. Pretoria: South African Bureau of Standards. [ Links ]
SAKO (Joint Committee of NKB and INSTA-B) 1999. Basis of Design of Structures. Proposal for Modification of Partial Safety Factors in Eurocodes. Oslo, Norway: NKB Committee and Work Reports. [ Links ]
SANS 2004. SANS 2394:2004. General Principles on Reliability for Structures. Adoption of International Standard ISO 2394-1998, Pretoria: South African Bureau of Standards. [ Links ]
SANS 2011a. SANS 10160-1:2011. Basis of Structural Design and Actions for Buildings and Industrial Structures. Part 1: Basis of Structural Design. Pretoria: South African Bureau of Standards. [ Links ]
SANS 2011b. SANS 10160-5:2011. Basis of Structural Design and Actions for Buildings and Industrial Structures. Part 5: Basis for Geotechnical Design and Actions. Pretoria: South African Bureau of Standards. [ Links ]
 Contact details:
Contact details:
Prof Johan Retief
Department of Civil Engineering
Stellenbosch University
Private Bag X1
Matieland
Stellenbosch
7602
T: +27 21 808 4442
F: +27 21 808 4947
E: jvr@sun.ac.za
 Contact details:
Contact details:
Dr Mahongo Dithinde
Department of Civil Engineering
Stellenbosch University
Private Bag X1 Matieland 7602
South Africa
Department of Civil Engineering
University of Botswana
Private Bag UB 0061
Gaberone Botswana
T: +267 355 4297
F: +267 395 2309
E: dithinde@mopipi.ub.bw

DR MAHONGO DITHINDE (Visitor) holds a PhD in Civil Engineering from the Stellenbosch University, an MSc in Foundation Engineering from the University of Birmingham (UK), and BEng in Civil Engineering from the University of Botswana. He works as a Senior Lecturer at the University of Botswana. His specialisation and research interests are in the broad area of geotechnical reliability-based design. In addition to academic work, he is also a geotechnical partner for Mattra International where he is active in consultancy work in the field of geotechnical engineering.

PROF JOHAN RETIEF (Fellow of SAICE) has, since his retirement as Professor in Structural Engineering, maintained involvement at the Stellenbosch University, supervising graduate students in the field of risk and reliability in civi engineering. He is involved in various standards committees, serving as the South African representative to ISOTC98 (basis of structural design and actions on structures). He holds a BSc (cum laude) and a DSc from the University of Pretoria, a DIC from Imperial College London, and an MPhil from London University. Following a career at the Atomic Energy Corporation, he joined Stellenbosch University in 1990.














