Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
Journal of the South African Institution of Civil Engineering
On-line version ISSN 2309-8775
Print version ISSN 1021-2019
J. S. Afr. Inst. Civ. Eng. vol.54 n.2 Midrand Jan. 2012
TECHNICAL PAPER
Definition and application of a cohesive crack model allowing improved prediction of the flexural capacity of high-performance fibre-reinforced concrete pavement materials
E Denneman; E P Kearsley; A T Visser
ABSTRACT
In conventional concrete pavement design methods the design parameters are determined using linear elastic analysis. Concrete is subject to significant size effect and as a result linear elastic design concepts, such as the modulus of rupture determined for a beam, have limited reliability in the design of elements of different size and geometry. The objective of this paper is to demonstrate that, in contrast to the modulus of rupture, fracture mechanics material parameters can be used to accurately and precisely predict the flexural capacity of elements of a different size and geometry. The experimental framework includes two high-performance fibre-reinforced concrete mix designs, used to produce beams of different sizes tested in three-point bending configuration, as well as centrally loaded round panels. The fracture energy of the material is determined from the flexural beam tests. An adjusted tensile splitting test procedure is used to determine the tensile strength. The flexural tests on the beams and panels are simulated numerically using two finite element implementations of a cohesive crack approach. The numerical simulation yields satisfactory prediction of the flexural behaviour of the beam and disk specimens. It is concluded that using a fracture mechanics approach, the flexural behaviour of structural elements of different size and/or geometry can be reliably predicted.
Keywords: fracture mechanics, fibre-reinforced concrete, cohesive crack, flexural strength, size effect
INTRODUCTION
South Africa boasts an extensive and mature road network. At present the bulk of pavement design activities are aimed at preserving and upgrading the existing road infrastructure. Innovative methods of pavement rehabilitation are required to increase the service life of wearing courses and to reduce the need for traffic hampering maintenance activities. To this aim, the South African National Roads Agency Limited (SANRAL) has sponsored the development of the ultra-thin continuously reinforced concrete pavement (UTCRCP). UTCRCP is intended as an overlay strategy for existing roads. The technology comprises a high-performance fibre-reinforced concrete (FRC) layer with a nominal thickness of approximately 50 mm. The material incorporates reinforcement in the form of fibres, as well as mesh, and is characterised by its ability to withstand large deflections. The technology is being implemented as part of major highway rehabilitation projects. The available design tools for the innovative UTCRCP system are currently based on conventional mechanistic-empirical concrete pavement design methodologies. These methodologies make use of linear elastic (LE) mechanics to determine the stress in the pavement slab. In these models the material strength is characterised by the modulus of rupture (MOR), using a standard test method such as SANS 5864:2006. The MOR is also calculated under the assumption of LE material behaviour. The nonlinear, non-elastic post-fracture behaviour of concrete is not taken into consideration. The ratio between the MOR and the stress in the pavement is used to predict the fatigue life of the pavement.
The first objective of this paper is to demonstrate that the fibre-reinforced concrete material under study exhibits a strong size effect due to its high post-crack stress capacity and that this limits the reliability of the MOR obtained for a specific specimen size and geometry, as a predictor of the peak load of elements of a different size and or geometry.
The second objective is to show that, in contrast to the MOR, fracture mechanics material parameters can be used to accurately and precisely predict the peak load, and importantly, the post-peak flexural behaviour of elements of different sizes and geometry.
Theoretical background on the size effect observed in flexural tests on concrete elements is provided in the next section. Following that, a cohesive crack fracture mechanics model for the FRC material is introduced. The material parameters required to define the model are obtained from experiments on beams and cylinders, as discussed in the section on the experimental work performed for this study. The final fracture mechanics model, defined using test results for a single beam size, is used to numerically predict the flexural performance of beams of different sizes, as well as of centrally loaded round panels. The main contribution of this paper is the generalisation of the cohesive crack model for FRC, previously used in two-dimensional space to simulate experiments on beams, to three-dimensional space for tests on centrally loaded disks. The paper presents a complete methodology, simple, yet effective, to determine the fracture parameters of FRC, and applies these to predict the flexural behaviour FRC structural elements.
SIZE EFFECT
The MOR, or flexural strength, is a design parameter often used in civil engineering designs. The MOR is obtained from flexural tests on beams and represents the stress in the extreme fibre of the specimen, calculated under the assumption that an LE stress distribution is present at the peak load condition. It is assumed that this material strength parameter obtained from laboratory experiments can be reliably generalised to predict the failure stress in full-size structural elements. Researchers have, however, long established that for concrete the MOR is not a true material property, because its value changes with specimen size (Reagel & Willis 1931; Kellerman 1932). In flexure tests, large beams fail at lower maximum tensile stress than small beams of the same material.
Studies at the University of Pretoria have shown the high-performance fibre-reinforced concrete material used in UTCRCP to have significantly increased post-crack load carrying capacity when compared to plain concrete (Kearsley & Elsaigh 2003; Elsaigh 2007). Subsequent studies found the MOR value of the fibre-reinforced concrete material to be subject to significant size effects (Denneman et al 2010a,b).
To illustrate the size effect, the average load-displacement (P - δ) curves of three-point bending (TPB) tests, performed by Denneman et al (2010b) on specimens of different sizes, are shown in Figure 1a. The TPB test configuration is shown in Figure 2a. The specimens have similar geometry, i.e. the span (s) to height (h) ratio, and span to notch depth (a) ratio are kept constant. To explore the size effect in the experiments, the nominal stress in the section is calculated assuming a linear elastic stress distribution using Equation 1:

where P is the load, and b the beam width.
The stress at the peak load condition (σΝι) represents the flexural strength, or MOR, parameter. An appreciation of the size effect can be obtained by plotting aN against the deflection (δ) as a ratio of the effective beam height (h) as shown in Figure 1b. The figure shows the effect of size not only on the peak stress, but also on the post-crack behaviour of the material.
The modulus of rupture is typically determined from an FPB test configuration, which is shown in Figure 2b. For this configuration aN is obtained from:

The effect of size on MOR values in FPB tests on high-performance fibre-reinforced concrete material is shown in Figure 3.
It is evident that MOR results are highly dependent on the height of the tested specimen. The main implication of the findings from size-effect studies is that the MOR is unsuitable as a design parameter; as the results obtained for a certain specimen size cannot be used to reliably predict the peak load of a specimen with the same geometry, but a different size. Much less can it be used to predict the flexural behaviour of elements of a different geometry.
The study presented in this paper is limited to high-performance fibre-reinforced concrete pavement materials. The findings are, however, relevant to plain concrete pavements as well, as plain concrete exhibits size effect similar in magnitude (Denneman 2011).
The main source of the size-effect phenomenon, is the fracture mechanics size effect (Bazant & Planas 1997). The fracture mechanics size effect is caused by the fact that concrete is a quasi-brittle material, and at the peak-load condition cracks would already have formed in the specimen. Due to the presence of a crack, LE stress distribution assumed in the MOR calculation no longer exists in the beam specimen. In different sizes of specimens, different amounts of fracture energy are released into the crack front, giving rise to the observed size effect.
Similarly, an LE stress distribution will not be present in a pavement slab loaded to failure, because it, too, would have cracked. Size effect in plain concrete has been well documented and can be predicted using fracture mechanics (Bazant & Planas 1997). In this paper a cohesive crack model is used to improve the prediction of the flexural behaviour of FRC elements.
DEFINING A COHESIVE CRACK FUNCTION
The complex behaviour of FRC composites calls for the use of advanced damage models. This has been the topic of many studies internationally. Local research in this field was performed by Kearsley & Elsaigh (2003), Boshoff & Van Zijl (2007), Shang & Van Zijl (2007), Elsaigh (2007) and Van Zijl (2009).
A fracture mechanics method for the analysis of crack propagation in concrete, favoured by various researchers for implementation in finite element analysis, is the fictitious crack model. The model, nowadays commonly referred to as the cohesive crack model, was introduced by Hillerborg et al (1976). According to the cohesive crack model, the material behaves linear elastically until the tensile stress reaches the tensile strength of the material. At this point a crack is induced. After crack nucleation, stresses are still transferred over the crack according to a softening relation. The crack bridging stress (σ) is written as a function of the crack width (w):

For plain concrete a bi-linear shape for the softening function is often used. For the more complex softening of fibre-reinforced concrete, tri-linear softening functions have been proposed (Lim et al 1987; Pereira et al 2004; RILEM 2003). Denneman et al (2011a) proposed a softening function which combines crack tip singularity with exponential softening. The softening behaviour is shown schematically in Figure 4. The softening function was proposed based on evaluation of direct tensile test results performed on material with similar fibres by Lim et al (1987). The softening model seeks to simulate the initial rapid reduction of stresses transferred across the crack as a crack is formed in the cement aggregate matrix. As the crack width increases, the steel fibres are activated. The point at the base of the crack tip singularity, where the fibres are activated, is represented in Figure 4 by stress σ1 and crack width w1. The values of σ1 and w2 are obtained through calibration. The function is defined by the following equations:
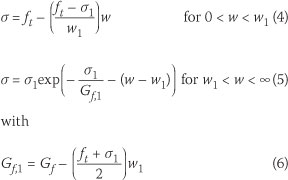
where Gf is the specific fracture energy of the material, which is equal to the area under the softening curve, and ft is the tensile strength, representing the stress at which a crack is formed, of the material need to be determined.
A method to obtain Gf for fibre-reinforced concrete from TPB tests was developed by Denneman et al (2011a). A best estimate of the tensile strength is determined using an adjusted tensile splitting test as described by Denneman et al (2011b). A summary of the methodologies to determine Gf and ft is provided in the following two sections.
Determining specific fracture energy
In order to determine Gf from TPB tests, the work of fracture (Wf) required to completely break the beam specimen needs to be determined. Figure 5a shows the load-displacement curve for a TPB test; the area underneath the curve represents Wf. TPB tests on fibre-reinforced concrete specimens will invariably be stopped short. Near the end of the test the crack would have grown to the top of the beam. However, not all fibres are completely pulled out, and therefore not all work of fracture has been recorded. In the standard test configuration it is physically impossible to run the test up to the high deflection required to pull out the fibres at the top of the beam. To determine Wf the load-displacement tail would have to be extrapolated as shown in Figure 5a. Denneman et al (2011a) proposed a method to model the tail of the curve, based on an earlier methodology proposed for plain concrete by Elices et al (1992).
The methodology makes use of the kinematic model in Figure 5b. It was shown that at large displacements, when the crack has propagated to the top of the beam, the two halves of the beam act as rigid parts, rotating around a hinge point. The angle of rotation (φ) of the individual parts around the hinge point is a function of the deflection (δ) at the centre of the span. The missing part of the tail can be modelled by determining the remaining moment capacity around the hinge point using the cohesive crack relation. Denneman et al (2011a) showed that the work of fracture under the missing tail (Wtail) can be determined from:

where δ is the deflection at the last recorded data point.
A is a parameter corresponding to the slope of a graph plotting the moment due to external loading (M) divided by the width of the beam (b) against 2φ-2. At large deflections, parameter A becomes a constant as shown in Figure 6 for TPB results on specimens of different sizes tested as part of this study. Wtail which may represent up to 20% of the total area (Denneman 2011) is added to the area under the recorded part of the curve to obtain the total Wf required to completely break the specimen. From Wf the fracture energy dissipated per unit fractured surface can be calculated:

The value of Gf thus obtained represents the area under the softening function in Figure 4. The remaining material parameter to be determined for the definition of the softening function is the tensile strength of the material.
Determining the tensile strength
In standard test methods for the cylinder splitting test, such as the ASTM C496 (ASTM 2008a), the maximum tensile strength is calculated from the peak load in the tests using the continuum mechanics solution for a circle loaded with two equal and opposed point loads, offered by Timoshenko & Goodier (1970). However, the loading is actually introduced to the specimen by means of loading strips with a certain width instead of through load points. Tang (1994) corrected the linear elastic plane stress solution for the stress distribution in the specimen for the effect of the width of the load strips.
Denneman et al (2011b) showed that, due to the high post-crack stress capacity of FRC, the ultimate peak load (Pu) recorded in the splitting test is not related to the assumed uniform cracking takes place at the edges of the specimen at Pu as shown in Figure 7b.
For the experiments reported on in this paper, the transversal deformation of the cylinders was measured using linear variable displacement transducers (LVDTs) on fixtures mounted to the base plate, as shown in Figure 8. Measurements were taken at the centre line of the specimen at the centre of its length. In later experiments, the transversal deformation was measured using LVDTs mounted to datum points which were glued to the specimens at either end of the cylinder (Denneman et al 2011b).

If the transversal deformation is measured in this way, the tensile strength ft can be obtained using Equation 9, which includes the correction for the width of the load strip proposed by Tang (1994).
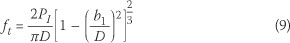
LE tensile stress condition along the loading plane. Through measurement of the transversal deformation of the specimen during the test it was found that the load-deformation curve has two distinct peaks, as shown schematically in Figure 7c. The first peak (PI) is related to principle crack formation along the loading plane, as shown in Figure 7a. After this initial crack has formed, stresses in the specimen redistribute and once again load increases until secondary where D is the diameter of the specimen, b2 is the width of the load strip and Pl is the initial peak load as identified from the load-transversal deformation curve.
Through numerical simulation of the experiments Denneman et al (2011b) confirmed that a close estimate of the true tensile strength of FRC may be obtained from this adjusted tensile splitting test procedure. The tensile splitting methodology for fibre-reinforced concrete proposed by Denneman et al (2011b) provides a relatively simple alternative to the more complex direct tensile testing approach. Direct tensile testing yields more detail on the post-cracking behaviour of the composite material, but if only a measure of the tensile strength is required, the presented tensile splitting methodology will suffice.
EXPERIMENTAL WORK
The fracture experiments for this study were performed at the University of Pretoria. The components by mass for the concrete mix designs are shown in Table 1. The designs are typical for the material used in UTCRCP. One mix was prepared with 80 kg/m3 steel fibres, the other with a steel fibre content of 120 kg/m3.
For the TPB tests, beam specimens of various sizes and geometry were prepared from both mix designs. To investigate fracture in a three-dimensional test, a centrally loaded round panel on three support points was used. The panels were cast in two different sizes. The test configuration for the tests on panels is shown in Figure 2c. The dimensions of the beam and panel specimens are shown in Table 2.
The procedure for TPB to determine fracture properties as recommended by RILEM technical committee 162-TDF (RILEM 2002) was used as the point of departure for the TPB tests. Besides the standard recommended beams of 150 x 150 mm2 cross section with a 550 mm length and a 25 mm notch, a number of other specimen sizes and geometries were used. Specimens with and without a notch were included to investigate the suitability of the eventual numerical models for fracture simulation for cases with and without a pre-formed crack.
During the TPB tests the vertical displacement at mid-span was recorded by means of LVDTs at either side of the beam. The reference frame for the displacement was mounted at half the height of the beam specimen. Mid-span displacement was measured relative to reference points above the supports.
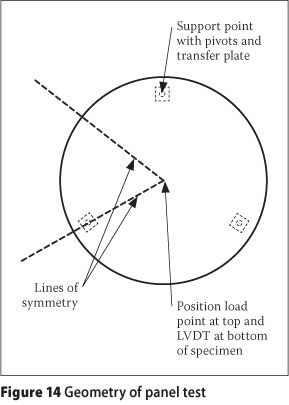
The tests on the concrete panels were performed in accordance with ASTM standard test method C 1550 - 05 (ASTM 2005). In this test the load-displacement response of a centrally loaded concrete panel supported on three pivot points is recorded. The vertical displacement is measured with an LVDT placed under the disk in line with the position of the loading point at the top of the disk.
All tests were run in displacement control, at the loading rates prescribed in the respective standard test methods.
Compressive strength tests were performed on the material in accordance with British Standard BS 1881 (BSI 1983). The static modulus of elasticity (E) and Poisson's ratio (υ) were determined in accordance with the standard procedures contained in ASTM C469-02 (ASTM 2008b). The average results for fc and E and υ are shown in Table 3. The table also shows the value of ft determined in accordance with the adjusted procedure for the tensile splitting test presented in the previous section. The load-transversal deformation curves for the split cylinder tests on the mixes are shown in Figure 9.
Table 4 shows the values of sNu obtained for the TPB specimens, as well as the fracture properties in terms of A, Wj and Gj determined from the TPB results in accordance with the procedure discussed earlier in the paper. The load-displacement curves for the TPB tests are shown in Figure 10. The results of the flexural tests on panels are shown in Figure 11. Also shown in the figures are the results of the numerical simulation performed using the material parameters in Table 3 and Table 4. The numerical models are discussed in the next section.
NUMERICAL SIMULATION OF FRACTURE
Two different finite element method (FEM) software frameworks were used for the simulation of fracture in the beams and panels. The numerical simulation of the beams can be reduced to a two-imensional problem and was performed using the embedded discontinuity method (EDM). The EDM was implemented in the open-source FEM framework OpenSees (2008) by Wu et al (2009). The flexural tests on panels were simulated in three-dimensional space using the commercial software Abaqus (2009); this was necessary as the EDM implementation in OpenSees is at present limited to two-dimensional space.
Simulation of fracture in beams with EDM
The implementation of the embedded discontinuity method by Wu et al (2009) is based on work by Sancho et al (2007). An advantage of EDM over other cohesive crack FEM models is that it allows cracks to propagate through elements, independent of nodal positions and element boundaries. In the earlier work by Wu et al (2009), a simple exponential softening function was used for damage evolution. The softening function was found suitable to predict the fracture behaviour of a plain concrete pavement material (Denneman et al 2010c). The simple exponential shape, however, over-predicts the peak load of fibre-reinforced concrete (Denneman et al 2010a). The EDM code was updated by Denneman et al (2011a) to allow for the more suitable exponential softening function with crack tip singularity described earlier in this paper.
The two-dimensional numerical model consists mainly of triangular elastic bulk elements. These elements require the modulus of elasticity and Poisson's ratio as input. A narrow band of triangular-shaped embedded discontinuity elements is provided at the notch facilitating a vertical crack path to the top of the specimen. It is possible to run the analysis using EDM elements for the entire model. In the numerical simulation, a crack will invariably form at the position with the highest stress. To make the calculation more efficient, a narrow vertical band of triangular EDM elements was provided in the ligament area at the mid-span position of the beam specimens. An impression of the deformed meshes for the TPB tests at high displacements near the end of the test is provided with the simulated load-displacement curves for the various beam types in Figure 10.
Figure 12 shows the calibrated softening curves for Mix A and Mix B. As Gf is determined from the TPB results and ft is obtained from tensile splitting tests, w1 and o1 are the only unknowns to be calibrated in the model. The softening curves were developed based on a parameter study aimed at achieving the best fit for both the flexural beam and tensile splitting tests. w1 was initially set to 0 for the simulation of flexural beam tests. It was later found that if a small displacement w1 is used, a better fit of the model can be obtained for the simulation of tensile splitting tests (Denneman et al 2011b). For the simulation of the flexural beam tests under study, the difference between w = 0 and w = 0.005 is insignificant. The main calibration is therefore the value of sj, which is chosen based on a parameter study for a single beam size after which the fit for other sizes is checked. As shown in Figure 10, the simulation of the TPB tests using the softening curves in Figure 12 results in a satisfactory, size-independent reflection of the physical measurements. As part of this study it will be investigated whether the softening behaviour can be generalised to a geometrically different test setup, i.e. the centrally loaded panel test.
Simulation flexural tests on panels with Abaqus
The commercial FEM software package Abaqus includes a number of fracture mechanics models that can be applied to concrete. The software includes a brittle cracking model intended specifically for the simulation of cracking in concrete. Damage evolution takes place using the cohesive crack relation as introduced by Hillerborg et al (1976). Because the Abaqus brittle crack model uses the cohesive crack principle for damage evolution in the principle tensile stress direction, the softening functions developed for the material in Figure 12 can be used unaltered.
In contrast to the EDM in which both shear and tension are handled using a crack width softening function, the brittle cracking model in Abaqus has a separate strain softening function for shear. To ensure that the response of the Abaqus model in shear was similar to that in the EDM simulation, the shear strain softening function was defined in accordance with the relation:

This relation relates the softening as a result of the fracture strain (ef) over a certain width (hc) in smeared crack models to the softening as function of crack width (w) in cohesive crack models.
To verify that the fracture simulation using the Abaqus brittle cracking model is equivalent to the results obtained from the EDM in Opensees, both approaches were applied to simulate a TPB test using the same softening relation. The results are shown in Figure 13. A characteristic element size of 1 mm was used for both the triangular OpenSees elements and the Abaqus quadrilateral elements in the ligament area above the notch. At the far edges of the mesh, the characteristic size of the elements was set to 25 mm. The results obtained from the simulations are almost equivalent. Only at large displacements do the load displacement curves diverge slightly. This was taken as proof that the Abaqus brittle cracking model was correctly configured, allowing its use for the simulation of the flexural disk tests.
The layout of the disk tests is shown schematically in Figure 14. Owing to symmetry, only one sixth of the disk needs to be modelled as indicated in the figure. The model and boundary conditions are shown in Figure 15a. Fracture elements with the brittle crack damage model were used for the entire model, with exception of the area around the support. In this area linear elastic bulk elements were used to prevent cracks forming due to unrealistic stress concentrations. The support point is connected to a surface corresponding to the area of the transfer plate under the panel using a kinematic rigid coupling. Standard Abaqus 8 node brick elements of the C3D8R type were used for the mesh. The mesh is shown in Figure 15b. The characteristic size of the elements throughout the model is 5 mm, with exception of the area around the support where a size of 15 mm was used.
As the model consists mostly of fracture elements, multiple cracks will occur when stress redistribution after initial cracking leads to the development of new highly stressed areas. The results of the numerical simulation for the panels are shown in Figure 11. The results provide an accurate prediction of the pre-peak, peak load and early post-peak behaviour for the specimens. At larger deflections the crack tends to get locked, leading to unrealistic high stresses in the material. As a result, the load carried by the slab does not decrease at the pace observed in the experiments. The simulation was aborted when crack-locking started to occur. The simulation, however, yields satisfactory results in predicting the peak load for the panels.
To compare the results of the fracture mechanics-based analysis to a linear elastic design approach, the fracture elements in the panels were substituted for elements with linear elastic material behaviour. A load equal to the experimentally determined peak load per specimen type was applied to the models. Figure 16 shows the results in terms of the nominal tensile stress along the symmetry line midway between two supports from the centre of the panel to the edge. The maximum stresses at the centre of the disk are in the order of 22 MPa, almost twice the sNu values determined from beam tests shown in Table 4. These results indicate that if sNu (or MOR) was used to predict the peak load condition of the panels, as is done in pavement design, the flexural capacity of the panels would have been significantly underestimated - the error of the prediction would have been in the order of 70 to 100 per cent due to size effect.
CONCLUSIONS
The results in this paper show that, due to size effect, the MOR has limited reliability as a predictor of the peak load of FRC elements of a different size and/or geometry than the specimen for which the MOR was determined.
It was shown that the cohesive softening function with a crack tip singularity and exponential tail can be used to reliably predict the flexural behaviour of beams of different sizes and also of centrally loaded panels. The softening function was defined using a simple, but effective experimental methodology as presented in this paper. It is concluded that, in contrast to the MOR, the fracture mechanics models can be used to generalise the parameters obtained for a certain specimen size to reliably predict the flexural behaviour of specimens with a different size or geometry.
REFERENCES
ASTM 2005. C1550-05 Standard test method for Flexural Toughness of Fiber Reinforced concrete (using centrally loaded round panel). West Conshohocken: ASTM International. [ Links ]
ASTM 2008b. ASTM C469-02. Standard Test Method for Static Modulus of Elasticity and Poisson's Ratio of Concrete in Compression. In Annual book of ASTM standards 2008: section 04.02.
ASTM. ASTM 2008a. ASTM C496 / C496M-04e1 Standard Test Method for Splitting Tensile Strength of Cylindrical Concrete Specimens. In Annual book of ASTM standards 2008: section 04.02. ASTM. [ Links ]
Abaqus. 2009. Abaqus. Providence: Dassault Systemes Simlia Corp. [ Links ]
Bazant, Z P & Planas, J 1997. Fracture and size effect in concrete and other quasibrittle materials. Boca Raton and London: CRC Press. [ Links ]
BSI 1983. BS1881: Testing concrete. Part 116:1983 Method for determination of compressive strength of concrete cubes. British Standard Institute. [ Links ]
Boshoff, W & Van Zijl, G 2007. A computational model for strain-hardening fibre-reinforced cement. Journal of the South African Institution of Civil Engineering, 49(2): 24-31. [ Links ]
Denneman, E 2011. Fracture in high performance fibre reinforced concrete pavement materials, PhD thesis, University of Pretoria, Pretoria. [ Links ]
Denneman, E, Wu, R, Kearsley, E & Visser, A 2011a. Discrete fracture in high performance fibre reinforced concrete materials. Engineering Fracture Mechanics, 78(10): 2235-2245. [ Links ]
Denneman, E, Kearsley, E & Visser, A 2011b. Splitting tensile test for fibre reinforced concrete. Materials and structures, DOI: 10.1617/s11527-011-9709-x. [ Links ]
Denneman, E, Kearsley E & Visser, A 2010a. Size-effect in high performance concrete road pavement materials. In Van Zijl, G & Boshoff W, Advances in cement-based materials, London: CRC Press, pp. 53-58. [ Links ]
Denneman, E, Kearsley E & Visser, A 2010b. Measurement of size effect in monotonic and cyclic tests on fibre reinforced concrete pavement materials. Proceedings, 7th international DUT-Workshop on fundamental modelling of design and performance of concrete pavements. Sevilla. [ Links ]
Denneman, E, Wu, R & Harvey, J 2010c. Fracture behavior of concrete pavement material in bending under monotonic and cyclic loading. Proceedings, 2nd international symposium on service life design for infrastructure. Delft. [ Links ]
Elices, M, Guinea, G & Planas, J 1992. Measurement of the fracture energy using three-point bend tests Part 3-Influence of cutting the P-u tail.pdf. Materials and Structures, 25: 327-334. [ Links ]
Elsaigh, W 2007. Modelling the behaviour of steel fibre reinforced concrete pavements, PhD thesis, University of Pretoria, Pretoria. [ Links ]
Hillerborg, A, Modeer, M & Petersson, P 1976. Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements. Cement and Concrete. Research, 6. [ Links ]
Kearsley, E & Elsaigh, W 2003. Effect of ductility on load-carrying capacity of steel fibre reinforced concrete ground slabs. Journal of the South African Institution of Civil Engineering, 45(1): 25-30. [ Links ]
Kellerman, W 1932. Effect of size of specimens, size of aggregate and method of loading upon uniformity of flexural tests. Public roads. 13(11): 177-184. [ Links ]
Lim, T, Paramasivam, P & Lee, S 1987. Analytical model for tensile behavior of steel-fiber concrete. ACI Materials Journal, 84: 286-298. [ Links ]
OpenSees 2008. Open System for Earthquake Engineering Simulation v1.7.5. Berkeley: Pacific Earthquake Engineering Research Center, University of California. [ Links ]
Pereira, E N, Barros, J A, Ribeiro, A F & Camóes, A 2004. Post-cracking behaviour of selfcompacting steel fibre reinforced concrete. Proceedings 6th International RILEM Symposium on Fibre Reinforced Concrete-BEFIB 2004, Varenna, pp 1-10. [ Links ]
Reagel, F & Willis, T 1931. The effect of dimensions of test specimens on the flexural strength of concrete. Public Roads, 12: 37-46. [ Links ]
RILEM 2002. RILEM TC 162-TDF: Test and design methods for steel fibre reinforced concrete; bending test. Materials and Structures, 35: 579-582. [ Links ]
RILEM 2003. RILEM TC 162-TDF: 'Test and design methods for steel fibre reinforced concrete' σ-ε- design method. Materials and Structures, 36: 560-567. [ Links ]
Sancho, J, Planas, J, Cendón, D, Reyes, E & Gálvez, J 2007. An embedded crack model for finite element analysis of concrete. Engineering Fracture Mechanics, 74: 75-86. [ Links ]
SANS 2006. SANS 5864:2006 Concrete tests - Flexural strength of hardened concrete. Standards South Africa, Groenkloof. [ Links ]
Shang, Q & Van Zijl, G 2007. Characterising the shear behaviour of strain-hardening fibre-reinforced cement-based composites. Journal of the South African Institution of Civil Engineering, 49(2): 16-23. [ Links ]
Tang, T 1994. Effects of load-distributed width on split tension of unnotched and notched cylindrical specimens. Journal of testing and Evaluation, 22(5): 401-409. [ Links ]
Timoshenko, S & Goodier, J 1970. Theory of Elasticity (3rd edition). McGraw-Hill Book Company. [ Links ]
Van Zijl, G 2009. Constitutive model for fibre reinforced strain hardening cement composites (SHCC). Concrete Beton, 123: 8-15. [ Links ]
Wu, R, Denneman, E & Harvey, J 2009. Evaluation of Embedded Discontinuity Method for Finite Element Analysis of Cracking of Hot-Mix Asphalt Concrete. Transportation Research Record, 2127: 82-89. [ Links ]
 Contact details:
Contact details:
Principal Engineer, Bituminous Surfacing, ARRB Group Ltd 500
Burwood Highway, Vermont South VIC 3133, Australia
T: +61 3 9881 1535
E: erik.denneman@arrb.com.au
Contact details:
Head: Department of Civil Engineering,
University of Pretoria,
Pretoria, 00 02, South Africa
T: +27 12 420 2429
E: elsabe.kearsley@up.ac.za
Contact details:
Department of Civil Engineering,
University of Pretoria Pretoria,
00 02, South Africa
T: +27 12 420 3168
E: alex.visser@up.ac.za

DR ERIK DENNEMAN holds a BEng degree in Civil Engineering, an MSc degree in Technology & Society, and a PhD in Engineering from the Universities of Haarlem, Eindhoven and Pretoria -espectively. Erik is registered as a profess iona engineer with ECSA and is a member of SAICE. The work presented in this paper was oerformed at the University of Pretoria and the CSIR in Pretoria, and is related to his PhD study. For the past seven years Erik worked as a Principal Researcher specialising in road surfacing materials at the CSIR. In June 2012 he joined the ARRB Group in Melbourne, where he holds the position of Principal Engineer.

PROF ELSABÉ KEARSLEY graduated with a degree in Civil Engineering from the University of Pretoria, and holds a PhD from the University of Leeds. She worked in both South Africa and the UK before joining the staff at the University of Pretoria, where she currently is the Head of the Department of Civil Engineering. For the past 18 years she has been involved with cement and concrete materials research.

EMERITUS PROF ALEX VISSER recently retired as the SA Roads Board Professor in Transportation Engineering in the Department of Civi Engineering at the University of Pretoria, South Africa. He holds the degrees BSc (Eng) (Cape Town), MSc (Eng) (Wits), PhD (University of Texas at Austin) and BComm (SA). His fields of research interest are primarily low-volume road design and maintenance, roads for ultra-heavy applications, interlocking block paving, and road management systems. He has performed extensive research on non-traditional stabilisers for improving road materials, and has published extensively and lectured internationally on these topics. Since retiring he has also provided advice on projects around the world. Prof Visser s a Fellow and Past-President of the South African Institution of Civi Engineering (SAICE) and a Fellow of the South African Academy of Engineering. In 1998 he was awarded the SAICE Award for Meritorious Research for his contributions to low-volume road technologies, and in 2004 he received the Chairman's Award from the Transportation Division for contributions to transportation engineering. He was awarded emeritus membership of the US Transportation Research Board for Low-Volume Roads committee in 2006 for lifelong services rendered.














