Servicios Personalizados
Articulo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares en Google
Similares en Google
Compartir
Journal of the South African Institution of Civil Engineering
versión On-line ISSN 2309-8775
versión impresa ISSN 1021-2019
J. S. Afr. Inst. Civ. Eng. vol.54 no.2 Midrand ene. 2012
TECHNICAL PAPER
The wave climate on the KwaZulu-Natal coast of South Africa
S Corbella; D D Stretch
ABSTRACT
The east coast of South Africa has been the subject of numerous coastal developments over recent years. The design of such developments requires a thorough analysis of the local wave climate. Richards Bay and Durban's Waverider data are two relatively long east coast data sets (18 years). These data sets have not been formally reviewed since Rossouw (1984) analysed existing wave data for South African and Namibian coastal waters. This paper aims to provide a formal analysis of the KwaZulu-Natal wave data.
Seasonal exceedance probability plots, wave roses and typical wave parameter statistics are presented. Return periods for extreme waves are estimated from the generalised extreme value distribution, and the associated limitations are discussed.
The average peak period on the east coast of South Africa is 10.0 seconds, the average significant wave height is 1.65 m and the average wave direction is 130 degrees. Autumn has the most frequent and the largest wave events while summer is the only season unlikely to produce either large or frequent events. The recurrence interval of the largest recorded significant wave height (8.5 m) was estimated to be between 32 and 61 year.
Key words: wave climate, wave data, wave parameter, wave roses, KwaZulu-Natal coast, coastal developments, seasonal trends
INTRODUCTION
The estimation of statistical return periods (average recurrence interval) of storm events is imperative for coastal managers and design engineers. An average recurrence interval TR is the average time (usually expressed in years) between the realisations of two successive events. If the risk of engineering failure due to an event of a specified recurrence interval is not acceptable, it should be redesigned or relocated accordingly. In light of recent developments, from promenade and harbour upgrades to a prospective port and small craft harbour being undertaken in vulnerable coastal zones, the accurate estimation of design waves of specified return periods has become increasingly important.
The KwaZulu-Natal coastline on the east coast of South Africa (Figure 1) experienced its largest recorded wave event in March 2007. The storm coincided with the March equinox (highest astronomical tide of the year) and had devastating effects on the shoreline. Considering coincidence of tide and significant wave height, Theron & Rossouw (2008) (cited by Wright (2009) and Smith et al (2010)) referred to the event as having a 500 year recurrence interval. Phelps et al (2009) found the recurrence interval of the significant wave height to be between 34 and 85 years, but noting that a 35 year occurrence was more likely. CSIR (2008) estimated the significant wave height return period of the storm to be 10 to 35 years, but noted that it was probably closer to a 10 year return period. Apart from the 500 year recurrence interval that considers the coincidence of the tide and storm, the analysis of the significant wave height return period therefore ranges from 10 to 85 years. This wide range further highlights the need for additional research on the characteristics of design waves for the east coast of South Africa.
Once a coastal project has been designed in consideration of a specific return period, the construction or operation of the project becomes the point of focus. Construction and operation of a development often depends on the exceedance statistics of a given wave parameter (see METHODS). Exceedance graphs are a tool used to identify the percentage of time a parameter will be exceeded. Exceedance statistics are not very useful to the design engineer, as the probability of exceedance does not preclude dependent or related recordings of the same event. Therefore this does not yield a recurrence interval estimate of independent storm events. Exceedance graphs are, however, of value during coastal construction work as a management tool. It allows the contractor, resident engineer or project manager to estimate how often work will be disrupted. For example, if a specific height of a cofferdam is installed, exceedance statistics may be used to determine the probable number of days that the temporary works will be overtopped.
The wave climate on the east coast of South Africa has not been formally reviewed since Rossouw (1984) analysed existing wave data for South African and Namibian coastal waters. Rossouw concluded that only the Waverider data (refer METHODS) is reliable enough to consider for design purposes. The relatively long records of data (18 years) making up the current east coast record are from Durban and Richards Bay. Rossouw's analysis was of a time when no wave recording buoys were operational in Durban. Durban's reliable data has been analysed by various South African consultants and non-commercial authors (examples include Van der Borch van Verwolde (2004) and Rossouw (2001)). This paper provides a re-analysis and update of the KwaZulu-Natal wave recording data. It also places the analysed data into a formal design reference that is readily accessible.
From a coastal design point of view there was a need to identify what data was available for design applications and how representative it was, since Durban's record was made up of three different instruments at three different locations. Fortunately Richards Bay has a continuous wave data set from its Waverider buoy that could be used to verify the results.
Storm waves are generated off the KwaZulu-Natal coast by tropical cyclones, cold fronts or cut-off lows. Cold fronts move from west to east and generally exist closer to the coast than cut-off lows and cyclones. Cold fronts occur more regularly than the other forcings and produce relatively smaller wave heights and wave periods with southerly direction. Tropical cyclones are rarely responsible for extreme waves in Durban - between 1962 and 2005 only seven cyclones affected the eastern parts of South Africa (Kruger et al 2010). Generally tropical cyclones produce north-easterly swells. Cutoff lows have been associated with the largest wave events on the KwaZulu-Natal coast (March 2007). They form further offshore than cold fronts and are generally associated with large south-easterly waves with long wave periods. For a detailed description of South African weather conditions the reader is referred to Hunter (1987), Preston-Whyte & Tyson (1993), and Taljaard (1995).
This paper aims (1) to determine the reliability of the Durban and Richards Bay Waverider data, and to use it to establish return periods of wave heights for the east coast of South Africa; (2) to present exceedance statistics of wave heights and peak period and to provide other typical wave statistics; and (3) to analyse wave height return periods by different methods to illustrate the uncertainties and risks of basing designs on a short wave record.
The methods of analysis, as well as definitions of the wave parameters considered, are described under METHODS. We then present the exceedance statistics and other typical wave parameter statistics with seasonal variations. A discussion of multivariate return periods is given prior to summarising the conclusions.
METHODS
The first phase of the analysis was verifying the validity of the available data. Analysis of the wave climate could then be performed with respect to seasonal distributions, exceedance graphs, typical statistics, and a univariate statistical analysis of extreme wave heights.
The wave parameters analysed included the significant wave height, Hs, which, in deep water, is equal to 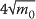 where mo is the area under the wave spectrum; the maximum wave height, Hmax, is the largest wave recorded in a recording period; the peak period, Tp, is the period at which the maximum energy density occurs and is the inverse of the peak energy frequency fp,
where mo is the area under the wave spectrum; the maximum wave height, Hmax, is the largest wave recorded in a recording period; the peak period, Tp, is the period at which the maximum energy density occurs and is the inverse of the peak energy frequency fp, 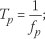 and the wave direction is the mean wave direction measured from true north.
and the wave direction is the mean wave direction measured from true north.
Hs should be used to model coastal process and shoreline response while Hmax is more appropriate to calculate wave loading on structures. Tp is used to define the surf similarity parameter and is consequentially used to quantify wave run-up, scour and forces on structures (the larger the period, the larger the wave run-up and forces on structures). An increase in period has also been shown to increase erosion (Van Gent et al 2008; Van Thiel de Vries et al 2008).
Validity of the wave data
Durban's 18 years of wave records are a combination of three different wave recording instruments at three different locations (Table 1), two Waverider buoys and an acoustic doppler current profiler (ADCP). Waverider, which is the trade name of Datawell's wave recording buoy, is a spherical accelerometer buoy that calculates wave heights from accelerations. The ADCP is located on the ocean floor and uses sonar to measure wave heights.
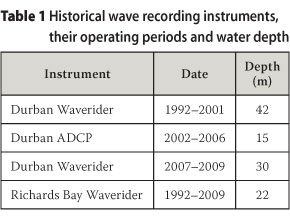
The different locations were a concern because of the shoaling and refraction effects of the different water depths. Diedericks (2009) found that the Richards Bay data has a good correlation with Durban's data. Diedericks' findings were verified by finding a Pearson correlation coefficient and a ratio between the Durban Waverider buoy and the Richards Bay Waverider buoy, and between the Durban ADCP and the Richards Bay Waverider buoy (Table 5).
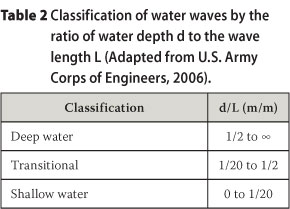
There was still a concern that the ADCP data was not representative enough of deep-water wave conditions and so the recorded waves were classified as either deep water, transitional or shallow water by considering the range of their depth over wave length ratio (Table 2). Newton's method was used to iteratively solve the wave length L using the peak wave period Tp, depth h and gravitational acceleration g (Equation 1).
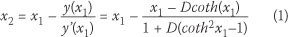
where
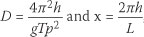 is the wave number
is the wave number
It was decided that since the ADCP did not record the 2007 event, in addition to being in much shallower water than the other instruments, this entire data set would be replaced by the Richards Bay data which had a strong correlation to the Durban Waverider buoys. The Richards Bay data is a continuous set from a constant location, and so it was also analysed to confirm and compare the Durban results. Unfortunately Richards Bay was not without its limitations and, although it recorded the 2007 event, it did not record the second and third largest events. These events had to be incorporated into the Richards Bay data from the Durban records.
Seasonal distribution of wave parameters
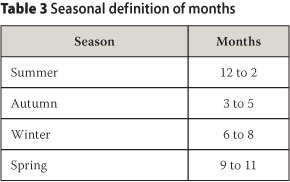
Each data set was analysed independently to establish if there were any inconsistencies or biases. The sets were analysed annually and seasonally. The months were divided into seasons using the meteorological convention as defined in Table 3.
All the recordings were counted and used to determine what percentage of a specific season and year made up a data set. The data sets were made up of measurements at three-hour intervals, which means that a season may contribute a larger percentage to the data set in terms of data points, but be missing a significant amount of days of data. This problem was resolved by calculating a percentage of days missing. The percentage of data and the percentage of days missing showed which seasons or years had the potential to skew results or create bias, and identified which periods needed to be supplemented by the other data set. A few days of missing data was deemed to be insignificant, if not during a storm event, but months to years of missing data was supplemented.
Average direction was only available from the Durban ADCP (2002 - 2006) and the Durban Waverider (2007 - 2009), making Hmax, Hs and Tp the only parameters analysed for the full 18 years of data. The Richards Bay data had wave directions from 1997 to 2009, but differed from the Durban data as a result of different local wind conditions.
Exceedance graphs
Supplementing Durban's data with Richards Bay's data created an 18 year data set for Durban. Exceedance graphs were created for Hs, Hmax and Tp for each of the four seasons. The exceedance graphs provided an initial idea of event occurrences and allowed an Hs value to be selected for the peak-over-threshold method.
The exceedance graphs were created by binning the parameter in question and then calculating the frequency of occurrence per bin. The frequencies were then used to find the frequency of events that exceeded each bin. The exceedance frequencies were then divided by the total number of data points and expressed as a percentage exceedance. The parameters were plotted against the percentage on a log scale to produce the exceedance graphs. A best fit line was then used to interpret the percentage of time a given wave height is equalled or exceeded.
Wave climate variation and typical statistics
The following parameters were extracted from the data set annually and seasonally: the maximum Hmax , Hs, Tp , and the average Tp, Hs and wave direction. Comparing the parameters seasonally illustrated the degree of seasonal variation.
The average wave direction was calculated, as well as the significant wave height weighted average direction. The results differed negligibly, so only the weighted average directions are presented.
Since minor events had the potential of dampening major events in specific seasons, the analysis of the Hs data was also done only considering events exceeding 3.5 m wave heights.
Univariate statistical analysis of extreme waves
The average recurrence interval or return period of independent wave events can be estimated by fitting a theoretical probability distribution to the data and using it to extrapolate to the event of interest. There are many available probability distributions, and the use of an appropriate one is important to accurately model the data and to realistically estimate the probability of rare events by extrapolation.
The literature identifies commonly used distributions, but does not state which is preferred or superior. The U.S. Army Corps of Engineers (1985, 2006) recommends the guidelines of Isaacson & Mckensie (1981) while providing guidelines for the Extremal Type I (Fisher Tippett I) distribution and also recommends Fisher Tippett II. Isaacson & Mckensie (1981) provide guidelines for the Lognormal, Extremal Type I and II, and the Weibull distribution. Chadwick et al (2004) noted that the Department of Energy recommends using the Gumbel, Fisher Tippett I or the Extremal Value Type I distribution. Goda (2008) provides guidelines for the use of the Fisher-Tippett I, Fisher-Tippett II, Weibull and Lognormal distributions. The Generalised Extreme Value distribution (GEV) encompasses the Fisher-Tippet distributions, and the Extreme Value distribution is equivalent to the Gumbel distribution. The GEV distribution has been used extensively for extreme value analysis of hydrological events and specifically for wave heights by Guedes Soares & Scotto (2004) and Chini et al (2010), while the Generalised Pareto (GP) distribution has been used by Callaghan et al (2008) and Hawkes (2002). Ruggiero et al (2010) considered both the GP and GEV distributions. Considering the above sources, the Weibull, Lognormal, Generalised Pareto, Extreme Value and the Generalised Extreme Value distributions were used in the analysis.

There are numerous fitting methods available, but probably the most popular is the maximum likelihood. The method maximises the probability of observing the data set that has been observed in the sample. This intuitive approach has led to the method being referred to as the most popular and best technique for deriving estimators (Casella & Berger 1990; Montgomery & Runger 2003). The maximum likelihood method is popular with statisticians as its characteristics can be examined mathematically (Goda 2008). It shows a small amount of negative bias, but seems to have the smallest degree of deviation (Goda 2008). The method requires lengthy iterative manipulation (Isaacson & MacKensie 1981), an issue that has largely been removed with modern computing capabilities. The maximum likelihood method is therefore used in this study. The Akaike information criterion (Equation 2) was used to determine the best fitting probability distribution.

where k is the number of parameters in the probability distribution and L is the maximised value of the likelihood function for the estimated parameters.
The length of the wave data record was only 18 years and so it was decided to statistically analyse the Hmax and Hs wave heights with both the annual maxima method and peak-over-threshold method (POT). The peak-over-threshold method was only applied to the Hs data for a threshold of 3.5 m. When performing the POT method it is imperative that only independent events are considered. To ensure this, data was divided into events using the following definition: a storm event commences when Hs exceeds 3.5 m and ends when Hs falls below 3.5 m, and remains below for approximately one month, based on the decay time of the autocorrelation. The Richards Bay data was similarly analysed.
The 95% confidence intervals were found for the return periods using bootstrapping. Bootstrapping is a resampling technique with replacement. The bootstrapped samples were used to calculate the critical t statistic, which was in turn used to bound the estimated return intervals. For a given value of a sample there is a probability (1-α) of selecting a sample for which the confidence interval will contain the true value of . The 100(1-α) percent confidence interval for the t distribution is given by Equation 3.
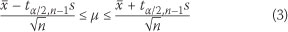
where χ is the mean of the bootstrapped sample, s is the standard deviation, n is the number of samples and ta/2,n-1 is the upper 100α/2 percentage point of the t distribution with n-1 degrees of freedom.
RESULTS
The Richards Bay data is shown to be a representative measure of the Durban wave conditions. The two data sets are used in conjunction to establish exceedance probabilities, typical wave parameter statistics, seasonal trends and average recurrence intervals of wave heights along the east coast of South Africa.
Wave data validity
The wave data showed that the Richards Bay data was an acceptable supplement to the Durban wave data. The waves recorded from all the recording instruments were largely transitional water waves (Table 4). The Durban Waveriders, being in deeper water, recorded the most deep water waves and, although the Richards Bay Waverider data consisted of only 2% deep water waves, it was still ten times larger than the ADCP, making Richards Bay's recorded waves more similar to that of the Durban Waveriders than the ADCP.
Richards Bay's Waverider showed a stronger correlation between the Durban Waverider than the ADCP (Table 5). When comparing the average ratios of significant wave heights, the Richards Bay data showed a 1.08 ratio with Durban's Waverider data, while only a 0.85 with the ADCP data.
The final justification in replacing the ADCP data is shown in Figures 2 and 3. These time series plots of the largest wave events (overlapping the data sets) illustrate that the Richards Bay data is more representative of the Durban Waverider than the Durban ADCP.
Figure 4 shows a comparison of the wave roses for the entire data sets of the Durban Waverider (2007-2009), the Durban ADCP (2002-2006) and the Richards Bay Waverider (1997-2009). The Durban and Richards Bay Waveriders show a similar southerly distribution reaffirming the strong representation of one another. The Durban ADCP has a dominant easterly component and is essentially the result of refraction occurring at the ADCP's shallow depth.
Consequently the Richards Bay data was substituted for the ADCP data and used to supplement other missing data points, and a complete 18-year data set was attained.
The Richards Bay data on the other hand was a continuous set from the same location, having wave direction recordings from 1997. The Richards Bay data did contain minor gaps and Durban's data was used to supplement two missing wave events. The Richards Bay data was analysed to compare and verify the results of the Durban data.
Exceedance probabilities and wave roses
As previously mentioned, exceedance graphs are not useful in a design application, but are valuable in project planning.
The exceedance graphs are shown seasonally. Figure 5 shows an exceedance graph of significant wave height (Hs) and Figure 6 shows an exceedance graph of maximum wave height (Hmax). Wave direction barely shows a seasonal variation and it is presented as wave roses in Figure 8.
Figures 5 and 6 show that autumn experiences the largest waves followed by winter and spring and then summer. Autumn, with regard to wave height exceedance (Hs and Hmax), is the only season that shows a significant statistical difference from the other seasons at a 95% confidence limit. Based on the available data, wave heights will exceed the 2007 event (Hs 8.5 m, Hmax 12.4 m) 0.01% of the time. However, from the regression line the Hs exceedance of 8.5 m is 0.0015% of the time and the Hmax exceed-ance is 0.005%. The event was evidently rare, relative to the data set. Tables 6 and 7 define the regression lines for Hs and Hmax respectively.
Figure 7 and Table 8 show that the peak period does not exhibit a statistically significant seasonal variation. The important result is that 90% of the peak periods fall between 10 and 20 seconds.
Figure 8 shows the seasonal wave direction roses for summer, autumn, winter and spring. The dominant wave angle is approximately south-east and is consistent with the south-north littoral drift as expected.
The wave parameters were compared over the entire data set annually and seasonally.
Referring to Figure 9 the highest wave height occurred in 2007. The next highest waves were in 2001. The year 2001 also had the highest average wave height, indicating a particularly rough year in terms of sea conditions. The average Hs for the entire data set was 1.65 m with an average direction of 130 degrees. The maximum Tp occurred in 2008.
Figures 10 to 13 are identical to Figure 9 except that they show the seasonal results as opposed to the entire data set.
Summer's maximum Hmax occurred in 1999 and summer's largest Hsmax occurred in 2001. Its largest average Hs occurred in 1997. The average Hs for summer is 1.58 m, the average peak period is 9.52 s and the average direction is 135 degrees.
Figure 11 highlights that the largest Hmax and Hsmax of autumn correspond to the 2007 event, while the largest average Hs was significantly higher in 2001 than in the other years. Autumn of 2001 had the second highest Hsmax and the third highest Hmax.
The average Hs was 1.65 m, the average peak period is 10.4 s and the average wave direction was 132 degrees.
Figure 12 shows that Hmax, Hsmax and the maximum average Hs of winter all occurred in 2001. This further enforces the expectation of 2001 being a particularly rough year. The average Hs of winter is 1.64 m, the average peak period is 10.8 s and the average direction is 124 degrees.
The largest Hmax and Hsmax of spring (Figure 13) occurred in 1993, while the largest average Hs occurred in 1996. The average Hs for spring is 1.72 m, the average peak period is 9.56 s and the average direction is 129 degrees.
The data illustrates that 2001 had particularly rough sea conditions. It also demonstrates that in terms of average Hs, Tp and direction there is not much seasonal variation. The above statistics are only those of the combined Durban and Richards Bay data sets.
Seasonal Trends
Seasonal trends, with regard to large wave heights, were identified by considering only the events that exceeded a significant wave height threshold of 3.5 m. Table 9 shows the seasonal percentage of events, the maximum and minimum Hs, and the average Hs for the events exceeding a wave height of 3.5 m.
Table 9 shows that autumn has the highest frequency of events, followed by spring and winter and then summer. Summer is definitely the calmest season having the lowest frequency and smallest Hsmax and average Hs. Autumn is the roughest period of the year having the largest Hsmax, Hsmin and average Hs. It is important to note that autumn still experienced the highest Hs of 6.3 m when not considering the 2007 event.
The results show that large events most frequently occur in autumn, as well as the largest events. Winter and spring have very similar events and event occurrences, while summer appears to be the only season unlikely to produce either large or frequent events.
Wave height return periods
For the estimation of average recurrence intervals of independent extreme wave events, Borgman & Resio (1977) suggest that a data set should not be extrapolated to more than three times the extent of the data set.
The results can also vary extensively based on the distribution used, as well as the data selected from the data set. These two limitations were considered by using numerous probability distributions and by applying the annual maxima method, as well as the POT method of sampling. The GEV was determined to be the best-fitting probability density function for all the data sets based on the Akaike information criterion.
Table 10 demonstrates the variations in the different methods. The annual maxima method of both Hs and Hmax have the largest return periods, estimated for the 2007 event, of 48 and 61 years respectively. The 95% confidence intervals are a function of the number of data points. Since the annual maxima method only uses 18 data points, the confidence intervals are relatively large, ranging between 37 and 60 years for Hs, and 49 and 76 for Hmax. It should be noted that the Hmax values and the Hs values do not always coincide with the same event, evident by the different results.
The POT method yields significantly lower return period estimates and confidence intervals. The Hs POT estimated the event to have a recurrence interval of 32 years, with a 95% confidence interval of 28 to 35 years. The estimates using the Richards Bay data were comparable (Table 10).
The variations in the estimates are indicative of the short data set. The estimates are limited to conclude that the event was between a 32 and 61 year event. This is similar to the 35 to 85 year return period that was determined by Phelps et al (2009). It should be noted that similar wave heights were experienced during Cyclone Imboa in 1984 (prior to the wave record analysed herein). The 23 year period between these major events suggests that the actual return period of the 2007 event is at the lower end of the estimated range. Figures 14 to 16 have been created to allow easy estimation of return periods using any of the two methods, considering the associated uncertainty demonstrated in Table 10.
DISCUSSION OF MULTIVARIATE RETURN PERIODS
We have demonstrated that the estimation of average recurrence intervals is dependent on the probability distribution used for estimation and the threshold used to sample wave heights. Apart from the analysis limitations, the estimation of a univariate return period is not a true estimate of the storm risk. The 2007 event's wave height occurrence was estimated as a 32 year return period, but its coincidence with the highest astronomical tide (HAT) would make the combined event far rarer. Considering two independent events, the probability of both events being exceeded is the product of the exceedance probability of each event. In the case of the 2007 event, coincidence of the HAT (an 18.6 year return period) and wave height (a 32 year return period) yields an average recurrence interval of 595 years.
This extreme return period is actually incorrectly defined, as it assumes that the HAT is a random process which has equal probability of occurrence each year. The HAT is deterministic and the coincidence of a wave height needs be described by the probability of a wave height exceedance for that period of heightened water level. Furthermore the 595 year return period is not a useful measure of risk, since the HAT only exceeds mean high water springs by approximately 30 cm. This demonstrates that the event characteristics should be related to their contribution to the risk of failure. For example, the same amount of damage may have occurred at any highest astronomical tide of the year for the given wave heights, but would have resulted in a significantly shorter return period estimate.
The estimation of risk becomes more complicated when events are interdependent and requires more advanced statistics. The Gumbel mixed model (Yue et al 1999), the Gumbel logistic model (Yue 2001) and copulas (De Michele et al 2007) are examples of multivariate models that may be appropriate for considering event dependencies in the estimation of return periods. Depending on the requirements of the risk estimation, the multivariate analysis can be extended to include storm duration, wave direction, peak wave period and any other parameters that may contribute to a storm's damage potential.
CONCLUSION
We have re-analysed 18 years of reliable wave data for the KwaZulu-Natal coast and provided a timely update to the existing statistics. Typical statistics of wave parameters are now available without having to re-analyse the integrity of the data sets. The average peak period of the data set is 10.0 seconds, the average significant wave height is 1.65 m and the average wave direction is 130 degrees. Exceedance curves are now available to aid the programming and risk identification for coastal and marine projects. Autumn has been shown to be responsible for the most frequent and the largest amplitude wave events, while winter and spring are similar. Summer is the only season where large events are infrequent.
Five probability distributions have been fitted to the extreme wave events of which the generalised extreme value distribution best modelled the available data. Design waves are now available for coastal projects and the return periods of future events can be quickly estimated. The largest wave event on record occurred in autumn and had an 8.5 m significant wave height, with an estimated return period between 32 and 61 years. Given past records, which have not been considered in the analysis, it is most probable that the average recurrence interval is at the lower end of the range. The Richards Bay return periods were found to be larger, so it is recommended that the more conservative return periods calculated for Durban's data be used in design.
The 32 year return period of the 2007 event would suggest that it was not very extreme. This return period highlights the limitations of risk analysis when only considering a single variable. Coastal storm damage is caused by a combination of high waves, long duration storms, sea levels, and possibly other factors. In order to fully assess the risks from the 2007 event, the probability of the event's wave heights coinciding with the highest astronomical tide, as well as other characteristics such as the storm duration, should be accounted for.
REFERENCES
Borgman, L E & Resio, D T 1977. Extremal prediction in wave climatology. Proceedings, Ports 77 Conference, Vol 1, New York, pp 394-412. [ Links ]
Callaghan, D P, Nielsen, P, Short, A & Ranasinghe, R 2008. Statistical simulation of wave climate and extreme beach erosion. Coastal Engineering, 55: 375-390. [ Links ]
Casella, G & Berger, R L 1990. Statistical inference. Pacific Grove, US: Wadsworth and Brooks/Cole. [ Links ]
Chadwick, C, Morfett, J & Borthwick, M 2004. Hydraulics in civil engineering and environmental engineering, 4th edition. Abingdon, UK: Spon Press. [ Links ]
Chini, N, Stansby, P, Leake, J, Wolf, J, Roberts-Jones, J & Lowe, J 2010. The impact of sea level rise and climate change on inshore wave climate: A case study for East Anglia (UK). Coastal Engineering, 57: 973-984. [ Links ]
CSIR 2008. Durban beach monitoring progress report: July 2006 to June 2007. Report No. CSIR/NRE/ECO/ER/2008/0424/B, Vol 1. CSIR: Stellenbosch. [ Links ]
De Michele, C, Salvadori, G, Passoni, G & Vezzoli, R 2007. A multivariate model of sea storms using copulas. Coastal Engineering, 54: 734-751. [ Links ]
Diedericks, H 2009. Personal Communication. eThekwini Municipality Coastal and Stormwater Department, Durban, 29 June 2009. [ Links ]
Goda, Y 2008. Random seas and design of maritime structures, 2nd edition. Singapore: World Scientific Publishing. [ Links ]
Guedes Soares, C & Scotto, M G 2004. Application of the largest-order statistics for long-term predictions of significant wave height. Coastal Engineering, 51: 387-394. [ Links ]
Hawkes, P J, Gouldby, B P, Tawn, J A & Owen, M W, 2002. The joint probability of waves and water levels in coastal engineering design. Journal of Hydraulic Research, 40 (3): 241-251. [ Links ]
Hunter, I 1987. The weather of the Agulhas Bank and the Cape Town South Coast. PhD thesis, Cape Town: University of Cape Town. [ Links ]
Isaacson, M Q & Mackenzie, N G 1981. Long-term distributions of ocean waves: a review. Journal of Waterway, Port, Coastal and Ocean Division, ASCE, 107(WW2): 93-109. [ Links ] Kruger, A C, Goliger, A M, Retief, J V & Sekele, S 2010.
Strong wind climatic zones in South Africa. Wind and Structures, 13(1): 37-55.
Montgomery, D C & Runger, G C 2003. Applied statistics and probability for engineers, (3rd edition). New York: Wiley. [ Links ]
Phelps, D, Rossouw, M, Mather, A A & Vella, G F 2009. Storm damage and rehabilitation of coastal structures on the east coast of South Africa. Proceedings, Institute of Civil Engineers Conference, Edinburgh, Scotland. [ Links ]
Preston-Whyte, R A & Tyson, P D, 1993. The atmosphere and weather of Southern Africa. Cape Town: Oxford University Press. [ Links ]
Rossouw, J 1984. Review of existing wave data, wave climate and design waves for South African and South West African (Namibian) coastal waters. Coastal Engineering and Hydraulics, National Research Institute for Oceanology, CSIR Report No T/SEA 8401, Stellenbosch: CSIR. [ Links ]
Rossouw, M 2001. Re-evaluation of the extreme wave climate of Southern Africa. PhD thesis (in preparation). Stellenbosch: University of Stellenbosch. [ Links ]
Ruggiero, P, Komar, P D & Allan, J C 2010. Increasing wave heights and extreme value projections: the wave climate of the U.S. Pacific Northwest. Coastal Engineering, 57: 539-552. [ Links ]
Smith, A M, Mather, A A, Bundy, S C, Cooper, J A G, Guastella, L A, Ramsay, P J & Theron, A 2010. Contrasting styles of swell-driven coastal erosion: examples from KwaZulu-Natal, South Africa. Geological Magazine, 147: 940-953. [ Links ]
Taljaard, J J 1995. Atmospheric circulation systems, synoptic climatology and weather phenomena of South Africa. Part 2: Atmospheric circulation systems in the South African region. Pretoria: South African Weather Bureau. [ Links ]
Theron, A & Rossouw, M 2008. Analysis of potential coastal zone climate change impacts and possible response options in the Southern African region. CSIR Report, Stellenbosch; CSIR. [ Links ]
U.S. Army Corps of Engineers 1985. Reliability of longterm wave conditions predicted with data sets of short duration. Coastal Engineering Technical Note, Report No CENT-I-5. [Online] http://chl.erdc.usace.army.mil/library/publications/chetn/pdf/cetn-i-5.pdf, retrieved 5 June 2009. [ Links ]
U.S. Army Corps of Engineers 2006. Coastal engineering manual EM 1110-2-1100, Part II, Chapter 1, p 8 and Part II, Chapter 8, pp 6-11. [ Links ]
Van der Borch van Verwolde, E 2004.Characteristics of extreme wave events and the correlation between atmospheric conditions along the South African coast. MSc dissertation, Cape Town: University of Cape Town. [ Links ]
Van Gent, M R A, Van Thiel de Vries, J S M, Coeveld, E M, De Vroeg, J H & Van de Graaff, J 2008. Large- scale dune erosion tests to study the influence of wave periods. Coastal Engineering, 55: 1041-1051. [ Links ]
Van Thiel de Vries, J S M, Van Gent, M R A, Walstra, D J R & Reniers, A J H M 2008. Analysis of dune erosion processes in large-scale flume experiments. Coastal Engineering, 55: 1028-1040. [ Links ]
Wright, K 2009. Storm warning. Wavescape. [Online] http://www.wavescape.co.za/severe-weather-watch/ storm-warning.html, retrieved 27 March 2009. [ Links ]
Yue, S, Ouarda, T B M J, Bobee, B, Legendre, P & Bruneau, P 1999. The Gumbel mixed model for flood frequency analysis. Journal of Hydrology, 226: 88-100. [ Links ]
Yue, S 2001. The Gumbel logistic model for representing a multivariate storm event. Advances in Water Resources. 24: 179-185. [ Links ]
 Contact details:
Contact details:
166 KE Masinga Road Durban 4001
South Africa
T: +27 31 311 7312
E: corbellas@durban.gov.za
Contact details:
School of Engineering
University of KwaZulu-Natal
Durban
South Africa
404
T +27 31 260 1064
E: stretchd@ukzn.ac.za

STEFANO CORBELLA (Member SAICE) received his BSc degree in civil engineering cum laude from the University of KwaZulu-Natal, South Africa. He completed the requirements for ar MSc in coastal engineering summa cum laude and is currently upgrading the MSc to a PhD. He s a practicing coastal engineer at the eThekwin Municipality's Coastal Stormwater anc Catchment Management Department.

PR0F DEREK STRETCH is Professor of Hydraulics and Environmental Fluid Mechanics at the University of KwaZulu-Natal. He currently occupies the eThekwini-sponsored Chair in Civi Engineering and is Director of the Centre for Research in Environmental, Coastal & Hydrologica Engineering. His research group focuses on the bio-hydrodynamics of estuarine systems, coasta and shoreline processes, and understanding turbulence and mixing in environmental flows.














