Servicios Personalizados
Articulo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares en Google
Similares en Google
Compartir
Journal of the South African Institution of Civil Engineering
versión On-line ISSN 2309-8775
versión impresa ISSN 1021-2019
J. S. Afr. Inst. Civ. Eng. vol.54 no.2 Midrand ene. 2012
TECHNICAL PAPER
Catchment parameter analysis in flood hydrology using GIS applications
O J Gericke; J A du Plessis
ABSTRACT
The use of Geographical Information Systems (GIS) has permeated almost every field in the engineering, natural and social sciences, offering accurate, efficient, reproducible methods for collecting, viewing and analysing spatial data. GIS do not inherently have all the hydrological simulation capabilities that complex hydrological models do, but are used to determine many of the catchment parameters that hydrological models or design flood estimation methods require. The purpose of this study was to perform catchment parameter analysis using GIS applications available in the ArcGISTM environment. The paper will focus on the deployment of special GIS spatial modelling tools versus conventional manual methods used in conjunction with standard GIS tools to estimate typical catchment parameters, e.g. area, average catchment and watercourse slopes, main watercourse lengths and the catchment centroid. The manual catchment parameter estimation methods with GIS-based input parameters demonstrated an acceptable degree of association with the special GIS spatial modelling tools, but proved to be sensitive to biased user-input at different scale resolutions. GIS applications in an ArcGISTM environment for the purpose of catchment parameter analyses are recommended to be used as the standard procedure in any proposed hydrological assessment.
Key words: catchment parameters, GIS, DEM, average slope, flood hydrology e.g. area, average catchment and watercourse slopes, main watercourse lengths and the catchment centroid.
INTRODUCTION
The use of Geographical Information Systems (GIS) has permeated almost every field in the engineering, natural and social sciences, offering accurate, efficient, reproducible methods for collecting, viewing and analysing spatial data. These spatial data sets represent the key components in the hydro-logical response of catchments to storm rainfall and the resulting runoff. GIS do not inherently have the hydrological simulation capabilities that complex hydrological models do, but are used to determine many of the catchment parameters that hydro-logical models or design flood estimation methods require.
In hydrological catchment parameter analyses, a Digital Elevation Model (DEM) and spatial data sets represent the two fundamental data sets initially required. The DEM contains raster information of the catchment and surrounding areas, while the spatial data sets contain the spatial information which originates from other sources than the DEM. The DEM is used to do a complete catchment parameter analysis, including the determination of flow directions, catchment areas, land surface and river channel characteristics. The spatial data sets contain layers of combined spatial information used to analyse the spatial distribution and associated attributes of geology, soil, land use and vegetation.
In addition to catchment parameter analysis, GIS also provide a powerful data management framework with a consistent, intuitive platform for organising and analysing relationships amongst the spatial variables and information associated with those variables encountered in the field of flood hydrology. Various GIS software packages exist. This paper will, however, only refer to the Environmental Systems Research Institute (ESRI) GIS software in the form of ArcGISTM 9.3.
The purpose of the study is discussed and explained in the next section, followed by an overview of the study area's spatial distribution and characteristics. In the section thereafter, the methods used in South Africa to estimate catchment parameters are reviewed in detail. The methodologies involved in assessing the paper's purpose and objectives are then expanded on in detail, followed by the results, discussion and conclusions.
PURPOSE OF STUDY
The purpose of this study was to perform catchment parameter analysis using GIS applications available in the ArcGISTM environment. The focus was on the deployment of special GIS spatial modelling tools versus conventional manual methods used in conjunction with standard GIS tools to estimate typical catchment parameters, It was hypothesised that the accuracy of conventional manual procedures used in flood hydrology to establish typical catchment parameters could be improved by using automated GIS input processing functionalities, since manual inputs are regarded as insufficiently accurate and outdated. It was further hypothesised that the spatial distribution of slope classes, used as primary input data to the deterministic flood estimation methods, are not sufficiently representative of the specific conditions under evaluation. Many practitioners in the field of flood hydrology typically ignore the importance thereof and follow a "thumb-suck" approach. In addition, hydrologists and engineers are frequently doubtful when deciding on, or determining, the position of the catchment centroid.
STUDY AREA
The study area covers 34 795 km2 between 28°25' and 30°17' South and 23°49' and 27°00' East, and comprises the C5 secondary drainage region. The tertiary drainage regions of concern are C51 (Riet River Catchment (RRC)) and C52 (Modder River Catchment (MRC)), covering an area of 17 435 km2 and 17 360 km2 respectively. The MRC and RRC consist of eleven and twelve quaternary catchments respectively (Midgley et al 1994). The topography is gentle (average quaternary catchment slopes between 2,4% and 5,5%), while the mean altitude above sea level varies between 997 m and 2 122 m (NASA 2002).
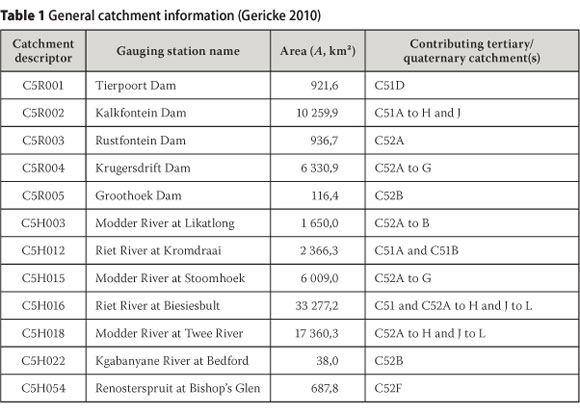
Twelve catchments with contributing catchment areas consisting of either single or multiple C51 or C52 quaternary catchments were evaluated individually in the study area. A Department of Water Affairs (DWA) flow- gauging station is situated at the outlet of each of these catchments. The flow-gauging station numbers were therefore used as the catchment descriptor for easy reference in all the Tables and Figures included in this paper. The general information applicable to these catchments is listed in Table 1, while the location thereof within the study area and in relation to the primary drainage regions of South Africa is shown in Figure 1.
REVIEW OF CATCHMENT PARAMETER ESTIMATION METHODS
To provide the background for further discussion, the manual and automated methods used in design flood estimation to establish catchment parameters, will now be discussed briefly.
Catchment area
The standard maps recommended to manually determine the catchment areas for use in flood hydrology are either the 1:50 000 scale topographical maps and/or 1:10 000 scale orthophotos. The latter are normally used if the catchment area under consideration is less than 10 km2. The manual procedure to determine the catchment area entails that the demarcated catchment boundary on the map is copied onto graph paper, after which the number of squares within the catchment are counted by including squares more than halfway into the catchment. A conversion factor is then used to convert the number of squares to the catchment area in km2 (Alexander 2001). Planimeters are also still in use to measure the manually demarcated catchment areas.
Alternatively, the aforementioned standard maps in an electronic format can be imported to a suitable Computer-Aided Design (CAD) environment as a picture file, after which standard CAD functions are used for the demarcation and area calculation respectively. The use of Google Maps as alternative is also worthwhile to consider.
In an ArcGISTM 9.3 environment, the Watershed tool contained in the Hydrology toolset of the Spatial Analyst Tools toolbox (Figure 2) can be used to identify catchment areas for specified pour points representative of the catchment outlet. However, a hydrologically correct and depressionless DEM must be prepared for these calculations, using most of the tools contained in the Hydrology toolset.

Average catchment slope
Slopes, whether gentle or steep, influence the catchment response time and hence the duration of critical rainfall intensity and resulting peak discharges and volumes (Alexander 2001). The average catchment slope (S) can be determined by using any one of the Grid, Empirical or Neighbourhood methods in conjunction with standard tools available in the ArcGISTM 9.3 environment.
Grid method
A grid of at least 50 squares must be superimposed over the catchment area. At each grid intersection point, the horizontal (shortest) distance between the contour intervals which straddle the grid point along a line that passes through the grid point, is measured. The average catchment slope is consequently defined as the average slope perpendicular to the nearest contour line at each grid point. This is presented diagram-matically in Figure 3 and expressed by Equation 1 (Alexander 2001).


where:
S1 = average catchment slope (m/m)
AH = contour interval (m)
Li = horizontal distance between consecutive contours (m), and
N = number of grid points.
Empirical method
According to Schulze et al (1992), the average catchment slope can be determined by making use of the following empirical relationship (Equation 2):

where:
S2 = average catchment slope (m/m)
A = catchment area (km2)
AH = contour interval (m), and
M = total length of all contour lines within the catchment (m).
Equation 2 is not widely used, especially due to the tedious task to determine the M values manually. However, the use of Equation 2 in its more rudimentary form (derived from first principles), in conjunction with standard functions in ArcGISTM, will be highlighted further in the Methodology.
Neighbourhood method
This method is also known as the Average Maximum Technique (Equation 3) and is included as the standard slope algorithm in the ArcGISTM environment to generate slope rasters from raw DEM and/or point elevation GIS data sets to enable the determination of average catchment slopes and steepness frequency distributions. The slope raster generation is based on a cell matrix approach which represents the maximum change in elevation over the distance between the cell and its eight neighbouring cells. Typically, in a 3 x 3 search window (grid network with nine cells, C1 to C9), eight grid points from the surrounding cells are used to calculate the average slope of the central cell (Cs) using unequal weighting coefficients, which are proportional to the reciprocal of the square of the distance from the kernel centre (Jones 1998; ESRI 2006b).
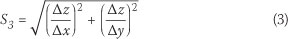
where:
S3 = average catchment slope (m/m) Az
 = rate of change of the slope surface in a horizontal direction from centre cell
= rate of change of the slope surface in a horizontal direction from centre cell

 = rate of change of the slope surface in a vertical direction from centre cell][
= rate of change of the slope surface in a vertical direction from centre cell][
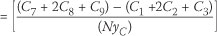
C1-4/6-9 = surrounding cells
Cs = centre cell
N = number of grid points or cells
Xc = horizontal cell size, and
yc = vertical cell size.
Length and average slope of main watercourses
The main watercourse is a defined flow path along which water will travel the longest time to reach the catchment outlet from a point on or near the catchment boundary. This distance can be measured manually on orthophotos or topographical maps by using dividers set at a predefined incremental distance which is a function of the map scale (Alexander 2001). The average main watercourse slope can be determined manually by using the following methods (Alexander 2001; Van der Spuy & Rademeyer 2010):
Equal-area method
An average slope line is drawn or positioned in relation to the longitudinal profile of the main watercourse in such a way that the area above (A1) this line equals the area below (A2) the line. This relationship is expressed by Equation 4 and illustrated in Figure 4.

where:
SCHI = average main watercourse slope (m/m)

HB = height at catchment outlet (m)
Hi = specific contour interval height (m)
L = length of main watercourse (m), and
Li = distance between two consecutive contours (m).
10-85 method
This method was developed by the United States Geological Survey (USGS) and is the most widely used in South Africa (SANRAL 2006). This relationship is expressed by Equation 5 and illustrated in Figure 5.

where:
SCH2 = average main watercourse slope (m/m)
L = length of main watercourse (km)
H0,085L = height (m) of main watercourse at length 0,85L, and
H010L = height (m) of main watercourse at length 0,10L.
Taylor-Schwarz method
This method is preferred by the Department of Water Affairs (DWA) and the Natural Environment Research Council (NERC 1975). The latter also proposed the use thereof in the United Kingdom Flood Studies Report (UK FSR 1975) (Van der Spuy & Rademeyer 2010). The main watercourse profile is subdivided into sub-reaches of which the velocities are related to the square root of the slope. The index is equivalent to the slope of a uniform channel with the same length as the longest watercourse and an equal travel time. This relationship is expressed by Equation 6 and illustrated in Figure 6.
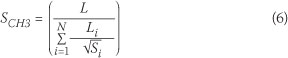
where:
SCh3 = average main watercourse slope (m/m)
L = length of main watercourse (m)
Li = distance between two consecutive contours (m), and
Si = slope between two consecutive contours (m/m).
In the ArcGISTM environment, both fully and semi-automated methods are available to estimate the main watercourse length. The Longest Flow Path tool which forms part of the ArcHydro toolbox automatically determines the longest watercourse. However, a hydrologically correct and depressionless DEM based on extensive input rasters with increased computing time is required. The use of semi-automated methods in conjunction with Equations 4 to 6 will be expanded on in detail in the Methodology.
Distance to catchment centroid
According to Alexander (2001), an eyeball estimate of the location of the catchment centroid is adequate. In practice, the distance to the centroid can be determined manually by using a cut-out of the catchment area to hang freely from a pin inserted close to a border of the catchment area. A string with a weight attached to the bottom, attached to the pin and hanging vertically under gravity from the pin, provides a guideline on the paper cut-out of the catchment. With the guideline drawn on the catchment, the pin is then moved to another position (approximately rotated 90° from the first position) close to the boundary of the catchment. The intersection of the two guidelines on the catchment provides the approximate position of the centroid.
In the ArcGISTM environment, the location of the catchment centroid can be automatically determined by making use of the Mean Center tool available in the Measuring Geographic Distributions toolset of the Spatial Statistics Tools toolbox, which will be expanded on in more detail in the Methodology.
METHODOLOGY
To evaluate the deployment of special GIS spatial modelling tools versus conventional manual methods used in conjunction with standard GIS tools to estimate typical catchment parameters, the following procedures were followed:
Projections and catchment geometry calculations
All the relevant GIS and catchment related data were obtained from the DWA (Directorate: Spatial and Land Information Management), which is responsible for the acquisition, processing and digitising of the data. These data sets are normally presented as geographical coordinate systems; in other words, the position of a geographical location on the earth's surface is described by using spherical measures of latitude and longitude (in degrees) from the centre of the earth to a point on the earth's surface.
These geographical input data sets need to be transformed to a projected coordinate system, which portrays the curved surface of the earth on a flat surface, during which the distance, area, shape and direction, or a combination thereof, might be distorted (ESRI 2006a).
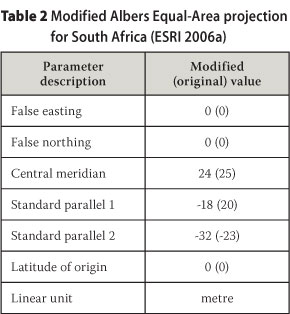
The Africa Albers Equal-Area projected coordinate system, with modification, was used during this study. This approach is best suited for land masses extending in an east-to-west orientation (as in the case of the study area), rather than those lying north-to-south. This conic projection uses two standard parallels to reduce some of the distortion of a projection with one standard parallel. Although neither shape nor linear scale is truly correct, the distortion of these properties is minimised in the region between the standard parallels. All areas are proportional to the same areas on the earth, while distances are most accurate in the middle latitudes (ESRI 2006a).
The standard parallels were established by using the one-sixth rule by determining the range in latitude (degrees) north to south, divided by six. The first standard parallel is positioned at one-sixth the range above the southern boundary and the second standard parallel minus one-sixth the range below the northern boundary (ESRI 2006a). These modifications are listed in Table 2.
The specific GIS data features classes (lines, points and polygons) applicable to the study area, and individual sub-catchments were extracted and created from the original GIS data sets by using the Clip tool available from the Extract toolset contained in the Analysis Tools toolbox. The Clip tool cuts out a piece of one feature class using one or more of the features in another feature class as a cookie cutter. Either the tertiary or quaternary drainage region polygons were used as clip feature classes, since a clip feature class has to be a polygon. The data extraction was followed by data projection and transformation, editing of attribute tables and recalculation of catchment geometry (areas, perimeters and distances).
Digital Elevation Model
The Shuttle Radar Topography Mission (SRTM) elevation data for southern Africa at 90 metre resolution (NASA 2002) was extracted, projected and transformed for the study area and used as the DEM. An alternative DEM was also generated by making use of point elevation and/or contour data as the input features. The Interpolation toolset contained in the Spatial Analyst Tools toolbox was used to generate rasters for the DEM interpolation process. The input features (contours or point elevations) were selected, the Output Surface Raster was specified and Tolerance 1 was set to a value of 10, which is equal to half the contour interval, or set to zero if point elevations are predominately used. The Output Cell Size, which specifies the output raster cell size, was then selected. A smaller cell size increases the amount of cells in the raster matrix with both an increased accuracy and computing time. A trade-off between time and accuracy was used in selecting the output cell size.
Average catchment slope
The average catchment slope of the study area, as well as of individual catchments, was determined by using the following manual methods with GIS-based input parameters:
Grid method
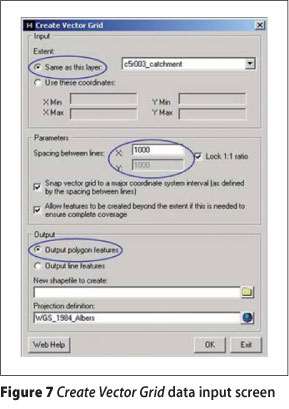
The Create Vector Grid tool available in the Sampling toolset of the Hawth's Analysis Tools toolbox was used to superimpose a grid over the catchment areas. Refer to Figure 7 for the Create Vector Grid data input screen. In Figure 7, the Extent selection was in accordance with the extent of the catchment boundary under consideration, while polygon features were selected as the required Output, since this option enables geometry (area) calculations. Shapefiles containing the polylines as feature type were created in ArcGISTM, via the Sketch tool accessible from the Edit toolbar, to represent the horizontal distances measured at each grid intersection point between two consecutive contours (e.g. Figure 8). The attribute table of each developed shapefile was edited and the length of each polyline was determined by making use of the Calculate Geometry function. These attribute tables were then exported to Microsoft Excel for further computations.

It is important to note that the Hawth's Analysis Tools Version 3.27 (Beyer 2004) is not a standard toolbox available in ArcGISTM 9.3, but it can be downloaded from either www.ESRI. com or www.spatialecology.com/htools. However, this toolbox is only compatible with ArcGISTM 9.3 or earlier versions, since the ArcGISTM programming interface (ArcObjects) changed with the update to ArcGISTM10. In this new version of ArcGISTM the Hawth's Analysis Tools was replaced with a toolbox known as the Geospatial Modelling Environment (GME). The GME incorporates most of the functionality of its predecessor, but has a greater range of analysis and modelling tools, supports batch processing, offers new graphing functionality, automatically records work-flows for future reference and supports geodatabases (Beyer 2009).
Empirical method
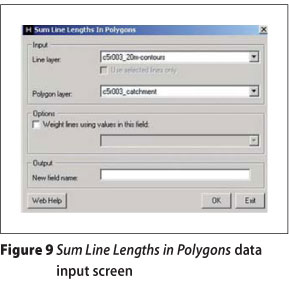
The Sum Line Lengths in Polygons tool (Figure 9) in the Analysis Tools toolset contained in the Hawth's Analysis Tools toolbox was used to calculate the total length of all contour lines (M) within each catchment, after which it was used as an input variable for Equation 2. The other input variables, area (A) and the contour interval (AH), were obtained from the relevant developed feature classes of the study area.
Neighbourhood method
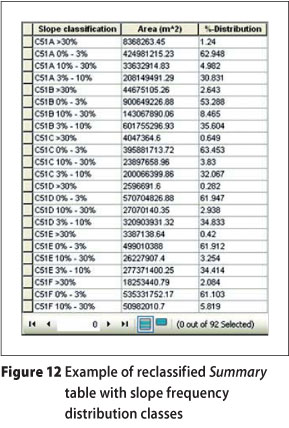
A slope raster was generated from the raw DEM data using the Slope tool available from the Surface toolset contained in the Spatial Analyst Tools toolbox. The generated slope raster is based on a cell matrix approach, which represents the maximum change in elevation over the distance between the cell and its eight neighbouring cells, thus the maximum slope for each cell. The Zonal Statistics as Table tool in the Zonal toolset contained in the Spatial Analyst Tools toolbox (Figure 10) was applied on the slope raster to generate a summary table containing the statistical information about the input data or raster for a defined zone within the data frame, thus the average slope for each catchment (Figure 11). The slope raster was converted to a feature class (polygons) and reclassified into four slope frequency distribution classes, e.g. 0-3%, 3-10%, 10-30% and >30% as required by the deterministic flood estimation methods (SANRAL 2006; Van der Spuy & Rademeyer 2010) to establish the surface slope coefficients associated with different Mean Annual Precipitation (MAP) ranges. This conversion was done by using the Raster to Polygon tool in the Conversion Tools toolbox of ArcToolbox, while the Reclassify tool in the Reclass toolset contained in the Spatial Analyst Tools toolbox was used for the reclassification. The reclassified summary table is shown in Figure 12.
Length and average slope of main watercourses
The main watercourse in each catchment was manually identified in ArcMap. A new shape-file containing polyline feature classes representative of the identified main watercourse was created by making use of the Trace tool in the Editor toolbar. Each identified main watercourse was traced using the polyline feature classes of the 20 m interval contour shapefile as the specified offset or point of intersection, resulting in chainage distances between two consecutive contours. The attribute table of each shapefile was then edited by using the Add Field function to include the reduced heights of the contour intervals, and the length of each polyline was determined by making use of the Calculate Geometry function. These attribute tables (e.g. Figure 13) can then be exported to Microsoft Excel for further computations and used as input data for the deterministic and empirical methods used in design flood estimation.
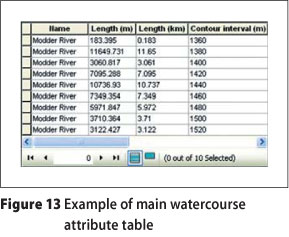
Distance to catchment centroid
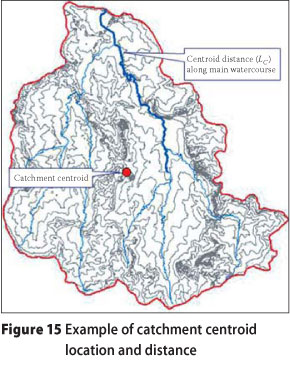
The centroid of each catchment under consideration was determined by making use of the Mean Center tool in the Measuring Geographic Distributions toolset contained in the Spatial Statistics Tools toolbox (Figure 14). Only the input polygon feature class representative of each catchment has to be selected to result in a point output feature class and associated attribute table representative of the x and y coordinate of the geometric centroid of each catchment (e.g. Figure 15). The length of the identified main watercourse in each catchment to a point opposite the identified centroid within the catchment was established by using the Measure tool in ArcMap. This measured length (LC) represents the distance along the main watercourse between the outlet and the point closest to the centroid of the catchment (e.g. Figure 15).

RESULTS AND DISCUSSIONS
The results based on the methodology used during this study will now be discussed.
Projections and catchment geometry calculations
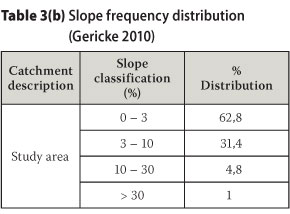
The frequency distribution of the altitude-above-sea-level classes present in the study area is summarised in Table 3 (a), while the slope-frequency-distribution classes based on the developed DEM (slope raster) are listed in Table 3 (b). The class-to-class variation and frequency distribution of the altitude-above-sea-level classes are indicative that the topography is relatively flat and that flood peaks will be attenuated and translated both in magnitude and duration respectively. The developed DEM for the study area is illustrated in Figure 16.

Average catchment slope
The results of the average catchment slope calculations based on the Neighbourhood method (DEM data), Grid method and Empirical method as used in the specific catchments, are listed in Tables 4 to 6. The scatter plots are shown in Figures 17 and 18. The developed DEM data was used as the baseline data for the evaluation of and/or comparisons with the two other methods.



According to Alexander (1990) there must be at least 50 grid points within a catchment, while Van der Spuy & Rademeyer (2010) suggested that the minimum number of grid points in catchments smaller or larger than 10 km2 must be 20 and 50 respectively. The number of grid points used varied from 50 to 7 200, with an overall average of 0,45 grid points per km2. The results indicated that either an increase or decrease in the number of grid points per km2 does not necessarily guarantee higher accuracies when compared with the Neighbourhood method (DEM data). For comparison purposes, the average catchment slopes (as %) for all the catchments were plotted as a scatter plot using the Neighbourhood method slopes against the Grid method slopes. The results are illustrated in Figure 17.
The Grid method underestimated the average catchment slope in all the catchments under consideration compared to the Neighbourhood method. The underestimation varied between 16,7% (0,48 grid points/km2) and 32,5% (0,34 grid points/ km2). Thus, if the DEM data based on the Neighbourhood method are accepted as true and accurate, then the average slope calculation using the Grid method with GIS-based input parameters must be increased with a value of between 17% and 33%. The inverse is also true. No definite relationship between the catchment area and these underestimations could be established.
The coefficient of determination (r2) of 0,88 is indicative of a high degree of association between the two methods. The Grid method is also useful for the development of slope frequency distribution classes used in the deterministic flood estimation methods. The Grid method is, however, time-consuming and sensitive to biased user input at different scale resolutions, extent of catchment areas and contour intervals used.
The results (Figure 18), based on the Empirical method (Equation 2), compared well with the Neighbourhood method. Since Equation 2 is a function of the catchment area (A), contour interval (AH) and total length of all contour lines within the catchment (Aí), the influence of each variable was evaluated. The results (Table 6) were indicative that there is only a direct relationship between A and A for slopes steeper than 4%, since flatter slopes will result in a lower contour density and associated M values. This trend was particularly evident for catchment areas exceeding 15 000 km2. The Empirical method underestimated the average catchment slope in all the catchments under consideration, except in catchment C5R005, where the average catchment slope result agreed with that of the Neighbourhood method.
M: A ratios of less than 1 500 resulted in an underestimation of between 20% and 30,2%, while M : A ratios between 1 700 and 2 750 were associated with underestimations between 18,7% and 0%. Thus, the higher the M: A ratios, the more accurate Equation 2 becomes. The coefficient of determination (r2) of 0,97 is also indicative of a high degree of association.
The visual comparison of results can be highly subjective. Therefore, the data pairs in each catchment under consideration were compared and evaluated using an array of conservation and regression statistics. Values of the y-intercept (a), slope (b), coefficients of efficiency (Ec) and determination (r2), which provide quantitative amplification of the results discussed above, are presented in Table 7.
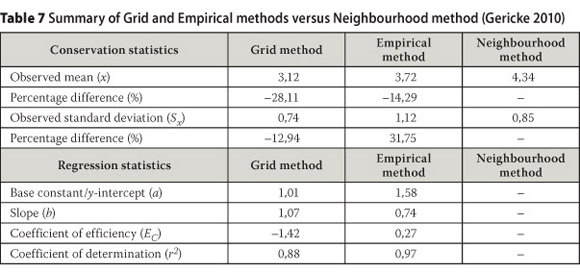
The conservation statistics percentage differences in Table 7 reflect the differences between the average results as obtained with the Grid and Empirical methods compared respectively to the Neighbourhood method results. In both cases, the objective function (OF) is to minimise these percentage differences, of which the Empirical method's OF proved to be the minimum, with, on average, the underestimation limited to 14,3%. The y-intercept (a) and slope values (b) of the Grid and Empirical methods showed that these two methods could have different predictive abilities at flat and steep slope classes respectively. In the case of the Grid method, the positive y-intercept (1,01) is indicative of a possible overestimation of flatter slopes, while the slope value (b) which slightly exceeded unity (1,07), highlighted that the overestimation of steeper slopes is neither excluded nor impossible. The Empirical method's positive y-intercept value (1,58) highlighted that this method is even more likely to overestimate flatter slopes, while the slope value (b) less than unity (0,74) is associated with the underestimation of steeper slope classes.
Length and average slope of main watercourses
The main watercourse average slope results based on the Equal-area, 10-85 and Taylor-Schwarz methods are listed in Table 8, while the scatter plots are shown in Figures 19 to 21.




The degree of association between these methods was very high, since the coefficient of determination varied between 0,995 and 0,998. In the past, preference was given to the 10-85 method, since the Equal-area method is largely a graphical procedure and the use of the Taylor-Schwarz method is not widely known in South Africa.
Distance to catchment centroid
The results contained in Table 9 are indicative that the length of the watercourse to a position closest to the centroid (Lc) is influenced by the size and shape of the catchment, but more importantly, influenced by the average catchment slope. It is clearly evident from Table 9 that an increase in the average catchment slope is associated with a decrease in the Lc: L ratio, which varied between 0,48 and 0,62.

CONCLUSIONS AND RECOMMENDATIONS
Projections and catchment geometry calculations
The DEM developed from the SRTM elevation data for southern Africa at 90 metre resolution proved to provide highly accurate raster information which can be used to calculate various catchment parameters (area, length and slope).
Average catchment slope
The developed DEM data based on the Neighbourhood method was assumed to be the most accurate representation of the actual average catchment slope and was therefore used as the baseline data to evaluate the Grid and Empirical methods. The Grid method underestimated the average catchment slope in all the catchments under consideration, while the results were indicative that either an increase or decrease in the number of grid points per km2 does not necessarily guarantee higher accuracies when compared with the DEM data. The use of at least 50 grid points in catchments up to 10 km2 is recommended; thereafter additional grid points at a grid density of 0,5 grid points/km2 in catchments up to a 1 000 km2 followed by 0,1 grid points/km^ in catchments exceeding 10 000 km2
The Empirical method also underestimated the average catchment slope in all the catchments under consideration, except in catchment C5R005, where the average catchment slope result agreed with that of the Neighbourhood method. The results were indicative that there is a direct relationship between the area (A) and the total length of all contour lines within the catchment (M).
The higher the M: A ratios, the more accurate the results calculated using the Empirical method.
Both the Grid and Empirical methods demonstrated high degrees of association with the DEM data and can be used along with suitable tools in the ArcGISTM environment to estimate the average catchment slope. The Grid method is especially useful for the development of slope frequency distribution classes, but the method is sensitive to biased user-input at different scale resolutions, extent of catchment areas and contour intervals used.
On the other hand, the Empirical method in its more rudimentary form (derived from first principles), in conjunction with standard functions in ArcGISTM, proved to be quicker and more accurate, while it is also very suitable for the development of slope frequency distribution classes. The higher accuracy was reflected by the higher r2 value (0,97) and the balance in tendency to either over- and underestimate the flat and steep average catchment slopes respectively. The results conclusively confirmed the preferential use thereof in conjunction with standard tools in the ArcGISTM environment.
Average main watercourse slope
The high degree of association between the Equal-area, 10-85 and Taylor-Schwarz methods proved that any of these methods can be used satisfactorily and with confidence in design flood estimation. However, this high degree of association between these methods does not necessarily guarantee the correctness thereof when used to estimate the time of concentration (Tc). In essence, the use of the average main watercourse slope as a suitable predictor variable for Tc estimation can only be justified when compared to Tc estimates based on the temporal distribution of rainfall (observed hyetographs) and runoff (observed hydrographs). In such a case, the validity of the established empirical relationship is also limited to the catchments or regions of original development.
Distance to catchment centroid
The average Lc: L ratio of 0,56 obtained from this study is indicative that the general assumption of using a Lc : L ratio of between 0,5 and 0,6 times the distance along the main watercourse is sufficiently accurate in most cases to be used in the various design flood estimation methods (Rademeyer 2012; Van der Spuy 2012). This is also a more definite guideline than the eyeball estimate thereof as proposed by Alexander (2001). However, practitioners are advised to evaluate each catchment individually using the tools available in ArcGISTM, before just using the proposed Lc : L ratios.
REFERENCES
Alexander, W J R 1990. Flood hydrology for Southern Africa. Pretoria: SANCOLD. [ Links ]
Alexander, W J R 2001. Flood risk reduction measures: Incorporating flood hydrology for Southern Africa. Pretoria: University of Pretoria, Department of Civil and Biosystems Engineering. [ Links ]
Beyer, H L 2004. Hawth's analysis tools for ArcGIS. Available at: http://www.spatialecology.com/htools/ (accessed on 20 March 2009). [ Links ]
Beyer, H L 2009. Geospatial modelling environment for ArcGIS. Available at: http://www.spatialecology. com/gme/ (accessed on 13 February 2012). [ Links ]
DWAF (Department of Water Affairs and Forestry) 1995. GIS data: Drainage regions of South Africa. Pretoria: DWAF. [ Links ]
ESRI (Environmental Systems Research Institute) 2006a. ArcGIS desktop help: Map projections and coordinat systems. Available at: http://www.webhelp.esri.com/arcgisdesktop. [ Links ]
ESRI (Environmental Systems Research Institute) 2006b. ArcGIS desktop help: Spatial analyst slope algorithm. Available at: http://www.web-help.esri.com/arcgisdesktop. [ Links ]
Gericke, O J 2010. Evaluation of the SDF method using a customised design flood estimation tool. Unpublished MSc Eng dissertation, Stellenbosch University, Stellenbosch. [ Links ]
Jones, K H 1998. A comparison of algorithms used to compute hill slope as a property of the DEM. Computers and Geosciences, 24(4): 315-323. [ Links ]
Midgley, D C, Pitman, W V & Middleton, B J 1994. Surface water resources of South Africa. Vol 2, Drainage Region C, Vaal: Appendices. Report No 298/2.1/9. Pretoria: Water Research Commision. [ Links ]
NASA (National Aeronautics and Space Administration) 2002. Shuttle Radar Topography Mission (SRTM) elevation data for Southern Africa at 90-meter resolution. Houston, TX, US: NASA. [ Links ]
NERC (Natural Environment Research Council) 1975. Flood studies report. London: NERC. [ Links ]
Rademeyer, P F, Directorate of Flood Studies, Department of Water Affairs, personal communication, 16 February 2012. [ Links ]
SANRAL (South African National Roads Agency Limited) 2006. Drainage Manual, 5th ed. Pretoria: SANRAL. [ Links ]
Schulze, R E, Schmidt, E J & Smithers, J C 1992. SCS-SA user manual: PC-based SCS design flood estimates for small catchments in Southern Africa. ACRU Report No 40, Pietermaritzburg, University of Natal, Department of Agricultural Engineering. [ Links ]
Van der Spuy, D & Rademeyer, P F 2010. Flood frequency estimation methods. In: Van der Spuy, D & Rademeyer, P F (Eds), Lecture Course: Flood Hydrology, 2.1-9, Stellenbosch: Stellenbosch University. [ Links ]
Van der Spuy, D, Directorate of Flood Studies, Department of Water Affairs, personal communication, 16 February 2012. [ Links ]
 Contact details:
Contact details:
Department of Civil Engineering
University of Stellenbosch
Private Bag X
Matieland
7602
South Africa
T: +27 21 808 4358
F: +27 21 808 4351
E: jadup@sun.ac.za
Contact details:
Department of Civil Engineering
University of Stellenbosch
Private Bag X'
Matieland
7602
South Africa
T: +27 51 507 3516
F: +27 51 507 3254
E: jgericke@cut.acza

JACO GERICKE has lectured in Hydrology, Irrigation and Water Engineering at the Centra University of Technology, Free State (CUT FS) for the past seven years. He has a special interest in flood hydrology, water resources management and hydrological modelling. He received the BTech Eng (Civil) and MTech Eng (Water) degrees from the CUT FS, and the BSc (Hons) Applied Science: Water Resources Engineering degree from the University of Pretoria (UP). He worked for six years at the Department of Water Affairs before joining the CUT FS. The results presented in this paper form part of his research towards the MSc Eng degree from the Stellenbosch University (2010).

DR KOBUS DU PLESSIS has lectured ir Hydrology, Water Engineering and Environmental Engineering at the Stellenbosch University (SU) for the past eight years. He has a special interest in water demand management and the implementation process as applied by municipalities. He served as a director in a municipal water division for seven years before joining the SU. After obtaining the B Eng (Civil) and M Eng (Water Resources Management) deg rees from the SU, he worked for the Department of Water Affairs, the City of Cape Town and the West Coast District Municipality. In 2011 he was awarded a PhD degree from the SU for his work done on ntegrated water management for local governance in South Africa.














