Serviços Personalizados
Artigo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em Google
Similares em Google
Compartilhar
Journal of the South African Institution of Civil Engineering
versão On-line ISSN 2309-8775
versão impressa ISSN 1021-2019
J. S. Afr. Inst. Civ. Eng. vol.54 no.1 Midrand Abr. 2012
TECHNICAL PAPER
Assessment of the behaviour factor for the seismic design of reinforced concrete structural walls according to SANS 10160 - Part 4
R C Le Roux; J A Wium
ABSTRACT
Reinforced concrete structures, designed according to proper capacity design guidelines, can deform inelastically without loss of strength. Therefore, such structures need not be designed for full elastic seismic demand, but could be designed for a reduced demand. In codified design procedures this reduced demand is obtained by dividing the full elastic seismic demand by a code-defined behaviour factor. There is, however, no consensus in the international community regarding the appropriate value to be assigned to the behaviour factor. The purpose of this study is to assess the value of the behaviour factor currently prescribed by SANS 10160-4 (2011) for the design of reinforced concrete structural walls. This is done by comparing displacement demand to displacement capacity for a series of structural walls. The first step in seismic force-based design is the estimation of the fundamental period of the structure. The influence of this first crucial step is investigated in this study by considering two period calculation methods. It was found that, regardless of the period calculation method, the current behaviour factor value prescribed in SANS 10160-4 (2011) is adequate to ensure that inter-storey drift of structural walls would not exceed code-defined drift limits.
Keywords: seismic design, behaviour factor, reinforced concrete, structural wall, inter-storey drift
INTRODUCTION
In the 1960s, with the development of inelastic time history analysis (ITHA), came the realisation that well designed structures can deform inelastically without loss of strength (Priestley et al 2007: 1-4). Engineers realised that structures need not be designed for the full elastic seismic demand (seismic load), but could be designed for a reduced demand. This reduced demand is obtained by dividing the full elastic seismic demand by a code-defined behaviour factor. There is, however, no consensus in the international community regarding the appropriate value to be assigned to the behaviour factor. This is evident in the wide range of behaviour factor values specified by international design codes (see Table 1). (These behaviour factor values should, however, not be directly compared, since various other code-related requirements also vary between international codes. Thus, each behaviour factor should be viewed from within the context of the corresponding code).
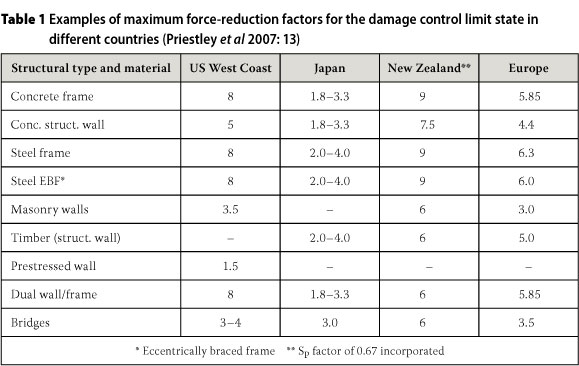
The purpose of this paper is to assess the current value of the behaviour factor in SANS 10160-4 (2011) for the seismic design of reinforced concrete structural walls. A value of 5 is specified in this standard.
Additionally, this paper evaluates the way in which the fundamental period of a structure is determined. Seismic design codes, including SANS 10160-4 (2011), provide a simple equation by which the fundamental period of a structure may be calculated, subject to certain limitations. It is well known that this equation results in seismic design forces to be overestimated, and lateral displacement demand to be underestimated (Priestley et al 2007: 11). An alternative period calculation procedure, based on moment-curvature analysis, will also be assessed. This method provides a more realistic estimate of the fundamental period of structures, but due to its iterative nature it is not often applied in design practice.
The influence of the behaviour factor becomes evident in seismic displacement demand. Therefore, in order to assess the current behaviour factor value, a comparison is required between seismic displacement demand and displacement capacity. A series of independent structural walls are assessed in this investigation. A first estimate of displacement demand of these walls is obtained from the equal displacement and equal energy principles. The displacement demand is then verified by means of a series of ITHA applied to these walls. Displacement capacity is defined by seismic design codes in terms of inter-storey drift limits to prevent non-structural damage in building structures. "Displacement capacity" could thus be described as "allowed displacement".
DUCTILITY DEMAND AND CAPACITY
Displacement ductility is a measure of the magnitude of lateral displacement of a structure, where a displacement ductility of greater than one represents inelastic response. In the remainder of this paper the term ductility will be used with reference to displacement ductility. Both the displacement demand and displacement capacity will be expressed in terms of ductility for comparison purposes.
Ductility demand
The displacement calculation method prescribed by seismic design codes such as SANS 10160-4 (2011) is based on the equal displacement principle. However, the validity of the equal displacement principle has recently been questioned (Priestley et al 2007: 26-29). Therefore, in this investigation ductility demand is calculated according to either the equal displacement or the equal energy principles (depending on the fundamental period), and then verified by means of ITHA.
Ductility capacity
Priestley et al (2007: 71) states that it is difficult to avoid excessive non-structural damage when inter-storey drift levels exceed approximately 0.025, and hence it is common for building design codes to specify inter-storey drift limits of 0.02 to 0.025. At these levels, most buildings would not have reached the structural damage-control limit state.
Separating non-structural infill panels from the structural system by means of isolation joints forms part of good conceptual design practice (Bachmann 2003: 40). For such buildings EN 1998-1 (2004) specifies the following drift limit:

where:
dr is the relative displacement between the top and bottom of a storey in the struc-ture, obtained from a seismic event with a 10% in 50 year probability of occurrence
hs is the storey height
v is a reduction factor which is equal to between 0.4 and 0.5, depending on the importance class of the structure.
SANS 10160-4 (2011: 30) imposes the following drift limits:

where:
T is the fundamental period of the structure
It may be seen that for a v value of 0.5, Eq 1 yields a drift limit of 0.02, which corresponds to the SANS drift limit for fundamental periods longer than 0.7 seconds. In this investigation ductility capacity is based on the period-dependent drift limits of Equations 2 and 3. The calculation of ductility capacity from these drift limits is discussed later.
PARAMETER STUDY
The following parameters are considered in this investigation:
■ Period calculation method
■ Wall aspect ratio
■ Number of storeys
Period calculation method
Method 1
According to SANS 10160-4 (2011: 27) the fundamental period of a structure may be calculated using Eq 4:

where:
CT = 0.05 was assumed for this investigation (as per SANS 10160-4 (2011))
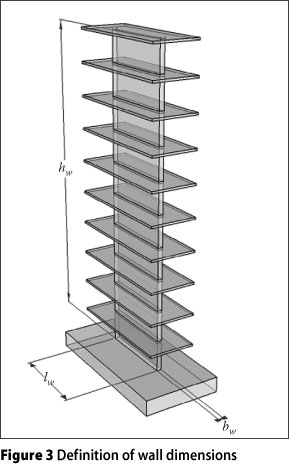
hw is the height of the building, in metres, from the top of the foundation or rigid basement (see Figure 3).
Equation 4 has been shown to correspond well to measured building periods (Priestley et al 2007: 11). These measurements were, however, taken at very low levels of vibration (normally resulting from wind vibration), where non-structural participation is high and concrete sections are uncracked (Priestley et al 2007: 11). Under seismic excitation, however, sections are allowed to crack and thus structures respond at much higher fundamental periods. It is often argued that using a too low period is conservative, since the acceleration demand is then overestimated (Priestley et al 2007: 11). This, however, is not true, since an underestimation in period results in an underestimation of displacements (Dazio & Beyer 2009: 5-15).
Because Eq 4 underestimates the fundamental period, Dazio & Beyer (2009: 5-16) suggest that it "should never be used". Eigenvalue analyses based on the stiffness derived from the cracked section should rather be used (Dazio & Beyer 2009: 5-16-18; Priestley et al 2007: 11).
Method 2
As an alternative approach, the stiffness of a cracked reinforced concrete section can be obtained from a moment-curvature analysis of the section. This is done by drawing a bilinear approximation to the moment-curvature curve as shown in Figure 1 (Priestley et al 2007: 144).
The fundamental period is then obtained from an eigenvalue analysis, assuming the same sectional stiffness, EIeff, over the height of the wall. The design of a wall, using this method, is unfortunately iterative, since the moment-curvature analysis cannot be done unless the reinforcement content and layout of the section is known, and the demand on the section depends on the stiffness of the section. For structures which comply with the requirements to allow for the use of the equivalent static force method, the iterative method depicted in Figure 2 should thus be followed.
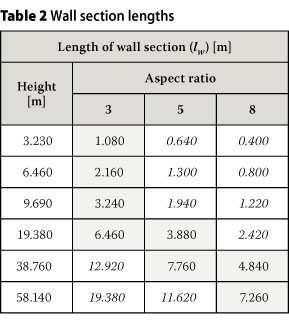
Wall aspect ratio
The aspect ratio of the wall, defined as the height of the wall hw divided by the length of the wall section lw (see Figure 3), is another variable to be considered.
The aspect ratio determines the extent to which a wall responds in flexure or shear. A wall with an aspect ratio of less than three responds predominantly in shear (Paulay & Priestley 1992: 371). A structural wall subject to seismic action should preferably respond in ductile flexural action (Paulay & Priestley 1992: 362).
The aspect ratio should also not be too large. Priestley et al (2007: 326) have shown that the elastic seismic force should not be reduced at all (behaviour factor < 1) for walls with an aspect ratio of more than approximately 9.
For the two above-mentioned reasons it was decided to consider walls with aspect ratios of 3, 5 and 8 in this study.
Number of storeys
This investigation focuses on the series of walls shown in Figure 4. The storey height was chosen as 3.23 m. The walls are all independent and free-standing. The behaviour of such a wall is, however, similar to that of a wall forming part of a symmetric structure.
Eq 4 is only applicable for buildings up to a height of 40 m. The 60 m wall is designed according to method 2 only.
The reason that the aspect ratio increases with height is that the wall section lengths need to remain within reasonable limits. The wall section lengths are shown in Table 2. It can be seen that only the shaded cells contain reasonable wall lengths.
Thus, the scope of this investigation is composed of the eight walls shown in Figure 4. These walls are designed according to both period calculation methods discussed earlier. Ground types 1 and 4 of SANS 10160-4 (2011) are used to define the range of seismic ground types. The methodology according to which seismic drift is assessed for these eight walls is presented next.
METHODOLOGY
The methodology used in this investigation is illustrated in Figure 5 and is listed in steps 1 through 6 below. These steps are applied to each of the eight walls defined in Figure 4 for both ground types 1 and 4. Thus, the steps are applied sixteen times. Steps 1 to 3 describe the design of the walls, while steps 4 to 6 describe the assessment of the walls.
Two period calculation methods were previously introduced. The difference between these two methods will be evaluated by using both these period calculation methods in the design of the walls.
Different period calculation methods would produce different force demands on the structure. In practice, the mass of a structure is fixed, and thus different force demands will be reflected in the longitudinal reinforcement content of the structural wall, or the wall cross-sectional dimensions. For this study, however, the cross-sectional dimensions are fixed (for the purpose of comparison), and thus it was decided to use an "inverse" design method, where the capacity of the cross-section is fixed at the start (step 1) and the associated floor masses are obtained as the final result of the design (step 3).
The methodology steps are the following:
1. The width of the wall section bw is chosen such that wall instability due to out-of-plane buckling in the plastic hinge region does not occur (Paulay & Priestley 1992: 403). An amount of reinforcement must be provided to comply with codified criteria. In this study the recommended reinforcement quantities of Dazio & Beyer (2009: 7-12) were used.
2. The moment capacity of the wall cross section at the base of the wall can be determined using either design equations or a moment curvature analysis. The moment capacity calculated using the design equations (M'n) corresponds to design material strengths. For analysis purposes it is important to predict the most likely response of the wall, thus the nominal yield moment (Mn) obtained from moment-curvature analysis corresponds to mean material strengths.
3. Given the chosen wall, the purpose of this step is to calculate floor masses and corresponding to the two period calculation methods respectively.
3.1 Method 1
3.1.1 The fundamental period (T1) is calculated using Equation 4.
3.1.2 The design pseudo acceleration (a1) is obtained from the design spectrum.
3.1.3 The floor mass m1 should be of such a magnitude that the resulting base moment is slightly less than the nominal yield moment (M'n) obtained from the design equations. This is to take the additional strength, due to reinforcement choice, into consideration.
3.1.4 For analysis purposes a better estimate of the fundamental period at which the wall would respond (T1(real)) is obtained by means of an eigenvalue analysis based on the cracked sectional stiffness obtained from the moment-curvature analysis.
3.2 Method 2
3.2.1 This step starts by assuming a value for the fundamental period (T2) A good estimate is T1(real) obtained in the previous step.
3.2.2 The design acceleration demand (a2) is obtained from the design spectrum.
3.2.3 Similar to 3.1.3 above, the floor mass m2 can be obtained.
3.2.4 A new estimate of T2 is calculated using the eigenvalue analysis. Iteration, such as shown in Figure 2, is required until the value of m2 does not change significantly between two iterations.
4. The purpose of this step is to estimate the ductility demand according to the equal displacement and equal energy principles. For this purpose the multi degree of freedom (MDOF) wall is converted into an equivalent single degree of freedom (SDOF) wall.
4.1 Firstly, the properties of the equivalent SDOF system need to be calculated. This includes the equivalent SDOF height h* and the effective first modal masses
and
. The equivalent height is obtained from Eq 12, while the effective first modal mass can be obtained from finite element modal analyses.
4.2 The shear (Vn) corresponding to nominal yield moment can be calculated from the nominal yield moment (Mn) obtained from moment-curvature analysis.
4.3 For both methods the acceleration
corresponding to the yield shear can be calculated.
4.4 The elastic acceleration demand (A1 and A2) can be obtained from the elastic pseudo acceleration spectrum.
4.5 The force reduction factors (R1 and R2) are calculated as the ratio between elastic demand
and yield capacity (a+(real) and ª+X
4.6 The ductility demand can now be calculated as a function of the force reduction factor according to the equal displacement and equal energy principles.
5. The ductility capacity based on code drift limits can be determined. This is discussed later.
6. Compare the ductility demand and capacity.
6.1 If the demand is greater than the capacity, choose a lower behaviour factor and repeat from step 3.
6.2 If the demand is less than the capa-city, the ductility demand needs to be verified by means of ITHA. If the ductility demand is found to be less than the ductility capacity, the current behaviour factor is adequate. It is not the intention of this study to increase the magnitude of the behaviour factor beyond 5. The current behaviour factor value is higher than most behaviour factor values in other codes. Refer to Priestley et al (2007: 13) for a comparison between international seismic codes. Hence, it was not the intention of the code committee to suggest the use of an even higher value.
MATERIAL PROPERTIES
For both the design and moment-curvature analyses of the walls, material properties are required. Material strength values are sufficient for design, while stress-strain relationships are required for moment-curvature analysis.
Material strengths
SANS 10160-1 (2011: 40) states that, if sufficient ductility for structural resistance can be provided, the partial material factors should be taken as 1.0. Thus, since sufficient ductility can be provided by designing walls in accordance with SANS 10160-4 (2011), characteristic material strengths should be used for design.
In order to predict the most likely strength and stiffness of a wall cross section it is necessary to use the mean material strengths. Therefore, mean material strengths are used for moment-curvature analysis. Table 3 lists the material strengths assumed for this investigation.
Stress-strain curves
Concrete
Mander's stress-strain relationship is used for unconfined and confined concrete (Mander et al 1988: 1807-1808). Both stress-strain curves are shown in Figure 6.
Reinforcing steel
A strain-hardening ratio of 1.15 was assumed, resulting in an ultimate stress (fu) of 569 MPa. The ultimate strain capacity was assumed to be 7.5%. The stress-strain relationship equations used for the steel material model are taken from Priestley et al (2007: 140):
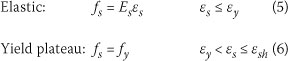
Strain hardening:
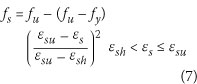
DESIGN EQUATIONS
Design equations are used in step 2 of the methodology. The moment capacity of a wall cross section may be determined using an equivalent stress block method such as the one set out by Bachmann et al (2002: 137). In this investigation the stress block method of SANS 10100-1 (2000) was used.
DUCTILITY CAPACITY AND DEMAND
It was stated in step 6 of the methodology that ductility demand will be compared to ductility capacity. This section shows how ductility capacity may be expressed as a function of inter-storey drift limits and how ductility demand may be calculated from ITHA results.
As shown in Figure 7, the displacement of a MDOF wall can be measured by an equivalent SDOF wall (Chopra 2007: 522-532). This equivalent SDOF wall must have the same dynamic characteristics as the first mode of the MDOF wall. In addition, the height of the wall is chosen such that the base moment of the SDOF wall due to the concentrated force F* is equal to the base moment of the MDOF wall due to the distributed force (Priestley et al 2007: 316). This height h* is referred to as the effective height.
In order to calculate ductility capacity as a function of a drift limit, equations for the drift profile and displacement profile at yield are sought. This is the point at which the curvature at the base of the wall is equal to the yield curvature (Φy). It is sufficient to assume a linear yield curvature profile (Priestley et al 2007: 317-319):

where:
 is the curvature at height
is the curvature at height
hi = 0, 1, 2, N is the storey number, and
hw is the height of the wall, defined in Figure 3.
Integration of Eq 8 with respect to the height produces an equation for the yield drift profile:
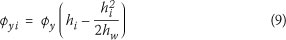
Integration of Eq 9 produces an equation for the yield displacement profile:
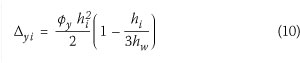
Defining ductility capacity in terms of a code drift limit
Ductility capacity is calculated in this study using both the plastic hinge method and an approximate equation.
Plastic hinge method
The yield displacement can be obtained from
Eq 11 (Priestley et al 2007: 96):

where:
 is obtained from Eq 10.
is obtained from Eq 10.
The effective height can be calculated from Eq 12 (Priestley et al 2007: 100):

where:
Δt is the ith value of the first mode shape vector.
The maximum yield drift can be calculated from Eq 9:
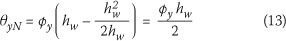
Since this would be the maximum yield drift for all values of i, the allowable plastic rotation is the difference between the code drift limit 6c and 6yN. Having obtained the allowable plastic rotation, the plastic displacement at the effective height is:

The ductility capacity in terms of the code drift limit is then 
Approximate equation
Based on the following simplifying assumptions, Priestley et al (2007: 325-326) derived a convenient equation which relates ductility to the code drift limit:
From a series of moment-curvature analyses, the yield curvature of a rectangular reinforced concrete structural wall is known to be (Priestley et al 2007: 158):

where:
ey = 0,00225 is the yield strain of the longitudinal reinforcement, and
lw is the length of the wall section, defined in Figure 3.
Thus, from Eq 13 the maximum yield drift is:
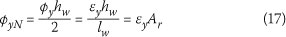
where:
Ar is the aspect ratio of the wall.
From Eq 10 the yield displacement profile can be described by:
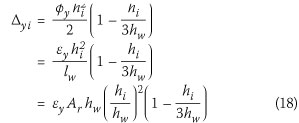
The equivalent yield displacement can be obtained by substituting Eq 18 in Eq 11 and assuming equal floor masses (Priestley et al 2007: 326):
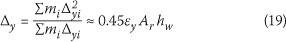
The effective height at yield, from Eq 12, is h* ≈ 0.77hw. Thus, by substituting Eq 17 in Eq 14, the plastic displacement is:
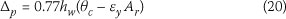
Hence, from Eq 15, the ductility capacity is:
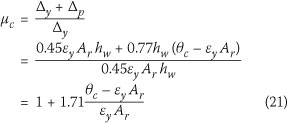
Both the plastic hinge method and Eq 21 are used in this paper to calculate the ductility capacity in terms of the code drift limits prescribed by SANS 10160-4 (2011: 30) (see Figures 16 to 19).
Calculating ductility demand from inelastic time history analysis (ITHA) results
As stated in step 6.2 of the methodology, ITHA is used here to validate the ductility demand obtained from the equal displacement and equal energy principles. For each wall, ITHA is performed for a number of ground motion records. For each ground motion record the peak displacement of each degree of freedom (DOF) is recorded. The equivalent displacement of the average of the peak displacements, obtained from the different ground motions, can be calculated from Eq 22 (Priestley et al 2007: 96):

where:
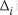 is the average of the peak displacement values of the ith DOF. The yield displacement is known from Eq 11, and thus the ductility demand can be calculated using Eq 23:
is the average of the peak displacement values of the ith DOF. The yield displacement is known from Eq 11, and thus the ductility demand can be calculated using Eq 23:

INELASTIC TIME HISTORY ANALYSIS
Degree of sophistication in element modelling
Line elements are beam-column elements with the ability to form plastic hinges at the ends of the member. With a suitable moment-curvature hysteresis rule assigned to the plastic hinges, the structural response can be predicted with remarkable accuracy (Priestley et al 2007: 193). In this investigation the student version of Ruaumoko (Carr 2007) was used for ITHA.
Beam properties
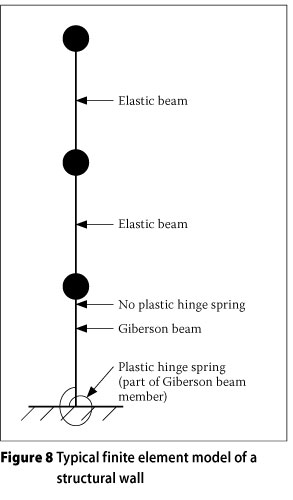
The two types of line elements available in Ruaumoko are the elastic beam (Timoshenko beam - shear deformable) and the Giberson beam. The first storey was modelled with a Giberson beam element which, in addition to the elastic beam properties, contains a rotational spring at one end of the member representing the plastic hinge which forms at the base of the wall.
The upper part of the wall is required to remain elastic. Thus all higher storeys were modelled with elastic beam elements. An illustration of a typical finite element model of one of the walls of the investigation is shown in Figure 8.
Elastic properties
The input required for the elastic beam is summarised in Table 4:
As indicated in Table 4, the cracked sectional moment of inertia is obtained from the pre-yield branch of the bilinear moment-curvature relationship. Only one moment-curvature analysis was done for each wall, namely at the base of the wall (Dazio, Beyer & Bachmann 2009). The stiffness obtained from this analysis was applied over the full height of the wall. The properties obtained from the moment curvature analysis are illustrated in Figure 9.
Inelastic properties
In addition to the elastic section properties, the Giberson beam requires the input listed in Table 5.
Hysteresis rule
The Modified Takeda Rule shown in Figure 10 with a β value of zero applies to structural walls (Priestley et al 2007: 201-202).
The unloading stiffness ku is a function of the elastic stiffness ko and the ductility at the onset of unloading 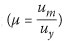 (Priestley et al 2007: 201):
(Priestley et al 2007: 201):

where:
a = 0.5 is considered appropriate for reinforced concrete structural walls (Priestley et al 2007: 201). Tables 4 to 6 thus contain all input required for the Giberson beam.
Time step integration parameters
For this study Newmark's average acceleration time-stepping method with time steps of 0.005 seconds was used (Chopra 2007: 175).
Ground motions
According to Priestley et al (2007: 210) it is sufficient to use the average response of a minimum of seven ground motion records. Spectrum-compatible accelerograms may be obtained through "manipulating existing 'real' records to match the design spectrum over the full range of periods" (Priestley et al 2007: 211). It has the advantage over purely artificial records that it preserves the essential character of the original real records (Priestley et al 2007: 211).
Thus it was decided to obtain real records with characteristics similar to that of ground types 1 and 4, and to manipulate these records to match the SANS 10160-4 (2011) elastic spectra. For this manipulation the student version of Oasys Sigraph (Oasys Limited 2010) was used.
Ground motion records were selected based on vs 30 values and peak ground acceleration (PGA). The selected ground motions are listed in Table 7. Each earthquake has two orthogonal components. The seven ground motions were thus obtained from both components of the first three earthquakes and one component of the fourth. The records were obtained from the PEER NGA Database (2007).
These fourteen records were manipulated to match the SANS 10160-4 (2011) spectra. The pseudo acceleration spectra of the manipulated records are plotted in Figure 11 with the elastic SANS spectra.
Damping
Tangent-stiffness proportional damping was used with a damping ratio of 0.05 for the first mode (Priestley et al 2007: 207). When applying stiffness proportional damping, one should also be careful that the damping of the highest mode is less than 100% (Carr 2007). Thus, the damping in the highest mode was limited to 100%, resulting in some cases in a damping of less than 5% in the first mode.
RESULTS
Design results (Figure 5(3) of the methodology)
Figures 12 to 15 show the elastic-, capacity-, and design spectra of ground types 1 and 4.
■ The design acceleration coordinates (a) of the eight walls of this investigation, each with a different fundamental period, are shown on the design spectrum.
■ The names of the walls, defined in Figure 4, are included in the figures. It may be seen that for design method 1, the design acceleration values (a1) are the same for walls of equal height, since Eq 4 depends only on the height of the wall.
■ The capacity of the walls is also shown in Figures 12 to 15. For the purposes of this discussion, we refer to this as the capacity spectrum1. The pseudo acceleration capacity was calculated from the yield moment capacity as described in step 4 of the methodology.
The relationship between the design spectrum and the capacity spectrum is influenced by three factors, namely over-strength, design conservatism, and period shift. These are briefly discussed below.
Over-strength
The capacity spectrum is higher than the design spectrum due to over-strength. The main factors which lead to over-strength are the following (Dazio & Beyer 2009: 3-21):
a. Mean material strengths, which are used to predict the most likely bending moment capacity of a section, are higher than the characteristic material strengths, used to predict bending moment capacity during design.
b. The provided reinforcement is always more than the required reinforcement.
Design conservatism
In this paper design conservatism is the name given to the assumption made during design that the design force is related to the total mass of the structure. To account in some way for the effect that higher modes inevitably have on the structure, the design seismic force is based on the total building mass, instead of the effective first modal mass. The effect of design conservatism is most clearly seen in Figure 13 by the steadily increasing capacity spectrum with increasing period.
Period shift
The term period shift here refers to the difference in fundamental period predicted by the code (SANS 10160-4, 2011) in Eq 4 and the "true" period predicted by moment-curvature analysis of the cross section. Period shift only occurs for design method 1. The fundamental period calculated according to design method 2 is based on moment-curvature analysis, and thus no period shift occurs.
The relation of the demand spectrum to the capacity spectrum determines the extent to which the walls respond inelastically. As stated in step 4 of the methodology, the force reduction factor (R) is equal to the ratio between acceleration demand (A1 or A2) and capacity 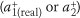 . Thus, if the demand is less than the capacity, the force reduction factor is less than one, and thus no inelastic action is expected. This is illustrated in Figures 12 to 15 by the dividing line which intersects at the intersection of the demand and capacity spectra.
. Thus, if the demand is less than the capacity, the force reduction factor is less than one, and thus no inelastic action is expected. This is illustrated in Figures 12 to 15 by the dividing line which intersects at the intersection of the demand and capacity spectra.
Analysis results (steps 4 to 6 of the methodology)
With the force reduction factor (R) known, the ductility demand can be calculated according to the equal displacement and equal energy principles and verified with ITHA. As previously discussed, the ductility capacity is based on code drift limits and is calculated according to the plastic hinge method and a simplified equation (Eq 21). Figures 16 to 19 show the comparison between ductility demand and ductility capacity for ground types 1 and 4, and design methods 1 and 2.
It is evident from Figures 16 to 19 that, on the capacity side, the plastic hinge method and the simplified equation (Eq 21) predict similar results. The simplified equation is, however, slightly conservative since it predicts a lower ductility capacity. The effect of the wall aspect ratio (Ar) on the ductility capacity is also evident. It was shown in Eq 21 (repeated here as Eq 25) that the ductility capacity reduces as the aspect ratio increases.
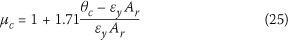
It may also be seen that the ductility demand predicted by the equal displacement and equal energy principles corresponds to that of the ITHA.
The only wall to which the equal energy principle applied is the single-storey wall on ground type 4. For this wall the ductility capacity is exceeded by the ductility demand. This implies that the drift of the single-storey wall would exceed the code drift limits, and would thus suffer non-structural damage in excess of the design limit state. This does, however, only apply to walls with an aspect ratio of three or higher. This wall was only included in the scope of this investigation to obtain structural walls with a very short period. The aspect ratio was limited to three, since flexural response was desired of structural walls. In general, structural walls used for single-storey construction would have aspect ratios of less than three, and would therefore fall outside the scope of this investigation. The reader is referred to Paulay & Priestley (1992: 473) for the design of squat structural walls.
For all the other walls the ductility demand is less than the ductility capacity. Inter-storey drift levels for these walls are thus below code drift limits. It can be seen that the ductility demand reduces as the period increases. This is due to the artificial acceleration plateau of the design spectrum (see Figures 12 to 15). It can also be seen that method 1 produces "safer" structures than method 2 because of the assumption of a short period, and thus higher acceleration demand. Method 1, however, severely underestimates structural displacement.
It is therefore concluded that the current value of 5 of the behaviour factor, as defined by SANS 10160-4 (2011), is adequate to ensure that code drift limits are not exceed-ed, whether design is done according to method 1 or 2. The designer is, however, still required by the code to calculate structural displacements as the final step in the seismic design process (SANS 10160-4, 2011, p. 30).
CONCLUSION
The purpose of this investigation was to assess the value of the behaviour factor currently prescribed by SANS 10160-4 (2011) for the seismic design of reinforced concrete structural walls. The behaviour factor is used in seismic design to reduce the full elastic seismic demand on structures, since well-designed structures can dissipate energy through inelastic response. The behaviour factor was evaluated by comparing displacement demand with displacement capacity for eight structural walls.
Displacement demand was calculated by means of the equal displacement and equal energy principles and confirmed by inelastic time history analyses (ITHA). Displacement capacity was based on inter-storey drift limits specified by SANS 10160-4 (2011). These drift limits serve to protect building structures against non-structural damage.
Displacement demand was evaluated for two period estimation methods. Firstly, the fundamental period may be calculated from an equation provided by the design code (SANS 10160-4, 2011), which depends on the height of the building. This equation is known to overestimate acceleration demand, and underestimate displacement demand. The second period estimation method involves an iterative procedure where the stiffness of the structure is based on the cracked sectional stiffness obtained from moment-curvature analysis. This method provides a more realistic estimate of the fundamental period of structures, but due to its iterative nature it is seldom applied in design practice.
The conclusion of this investigation is that the current behaviour factor value of 5, as found in SANS 10160-4 (2011), is adequate to ensure that structural walls comply with code-defined drift limits. This applies to both period estimation methods.
NOTE
1 Not to be confused with the "Capacity Spectrum Method" by Freeman (2004).
REFERENCES
Bachmann, H 2003. Basic principles for engineers, architects, building owners, and authorities. Available at: http://www.bafu.admin.ch/publika-tionen/publikation/00799/index.html?lang=en (accessed on 15 July 2010). [ Links ]
Bachmann, H, Dazio, A, Bruchez, P, Mittaz, X, Peruzzi, R & Tissiêres, P 2002. Erdbebengerechter Entwurf und Kapazitätsbemessung eines Gebáudes mit Stahlbetontragwanden. Available at: http://www.sgeb.ch/docs/D0171/SIA_D0171.pdf (accessed on 15 July 2010) (in German). [ Links ]
Carr, A J 2007. Ruaumoko - A program for inelastic dynamic analysis [CD-ROM]. Pavia, Italy: IUSS Press. [ Links ]
Chopra, A K 2007. Dynamics of Str-ct-res - Theory and Applications to Earthq-ake Engineering. Upper Saddle River, NJ, US: Pearson Prentice Hall. [ Links ]
Dazio, A & Beyer, K 2009. Short course: Seismic design of building structures. Unpublished class notes, Stellenbosch: Stellenbosch University. [ Links ]
Dazio, A, Beyer, K & Bachmann, H 2009. Quasi-static cyclic tests and plastic hinge analysis of RC structural walls. EngineeringStr-ct-res, 31(7): 1556-1571. [ Links ]
European Standard EN 1998-1:2004. Eurocode 8: Design of structures for earthquake resistance. Part 1: General rules, seismic actions and rules for buildings. Brussels, Belgium: European Committee for Standardization. [ Links ]
Freeman, SA 2004. Review of the development of the Capacity Spectrum Method. ISETJo-rnal of Earthq-ake Technology, 41(1):1-13. [ Links ]
Mander, J B, Priestley, M J N & Park, R 1988. Theoretical stress-strain model for confined concrete. Jo-rnal of Str-ct-ralEngineering, 114(8):1804-1826. [ Links ]
Oasys Limited 2010. Oasys Sigraph 9.0 Build 2. Available at: http://www.oasys-software.com/infor-mation/universities.shtml (accessed on 1 July 2010). [ Links ]
Paulay, T & Priestley, M J N 1992. Seismic Design of Reinforced Concrete and Masonry B-ildings. New York: Wiley. [ Links ]
PEER NGA Database 2007. Pacific Earthquake Engineering Research Center: NGA Database. Available at: http://peer.berkeley.edu/nga/index.html (accessed on 14 August 2010). [ Links ]
Priestley, M J N, Calvi, G M & Kowalski, M J 2007. Displacement-Based Seismic Design of Str-ct-res. Pavia, Italy: IUSS Press. [ Links ]
SANS 2000. SANS 10100-1: The structural use of concrete. Part 1: Design. Pretoria: South African Bureau of Standards. [ Links ]
SANS 2011a. SANS 10160-1: Basis of structural design and actions for buildings and industrial structures. Part 1: Basis of structural design. Pretoria: South African Bureau of Standards. [ Links ]
SANS 2011b. SANS 10160-4: Basis of structural design and actions for buildings and industrial structures. Part 4: Seismic actions and general requirements for buildings. Pretoria: South African Bureau of Standards. [ Links ]
 Contact details:
Contact details:
PostNet Suite 93
Private Bag X1
Melrose Arch 2076 South Africa
T: +27 11 218 7600
E: rudolf.leroux@arup.com
Contact details:
Department of Civil Engineering
Stellenbosch University
Private Bag x1
Matieland 7602 South Africa
T: +27 21 808 4498
F: +27 21 808 4947
E: janw@sun.ac.za

RUDOLF LE ROUX completed his undergraduate and MSc (Eng) degrees at the Stellenbosch university in 2010. His interest in structural dynamics started in 2008 when he studied the use of damped outriggers in high-rise buildings for his final year project. He is currently employed by Arup Consulting Engineers.

PROF JAN WIUM, PrEng, is professor in the Murray & Roberts chair for Construction Engineering and Management in the department of Civil Engineering at Stellenbosch university. He completed his undergraduate and MSc (Eng) degrees at the university of Pretoria and obtained his Phd from the Swiss Federal institute of Technology in Lausanne. He worked as a consultant for 20 years before joining the university of Stellenbosch in 2003. After first addressing the behaviour of concrete structures and seismic analysis of structures, he now focuses his research on the management and initiation of multidisciplinary capital projects.














