Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
Journal of the South African Institution of Civil Engineering
On-line version ISSN 2309-8775
Print version ISSN 1021-2019
J. S. Afr. Inst. Civ. Eng. vol.53 n.2 Midrand Oct. 2011
TECHNICAL PAPER
Validation of international concrete creep prediction models by application to South African concretes
G C Fanourakis
ABSTRACT
Creep deformation of concrete is often responsible for excessive deflections at service loads which can compromise the performance of a structure. National design codes therefore provide prediction models for the estimation of creep deformation. These models are empirical-based.
This paper assesses the accuracy of six international code type models, when compared with the actual strains measured on a range of South African concretes under laboratory control conditions. The models considered are those contained in AS 3600 (2001), AS 3600 (2009), Eurocode EC 2 (2004), GL (2000), GL (2004) and GZ (1993).
The results indicate that for the range of concretes tested, the GL (2000) model yielded the most accurate predictions, giving the lowest overall coefficient of variation (ωall) of 31,9%. The least accurate method was the AS 3600 (2009) which yielded an overall coefficient of variation (ωall) of 74,7%.
This paper also recommends a new approach to assessing the accuracy of creep models.
Key words: concrete, creep, models, design codes, testing
INTRODUCTION
Creep estimates are an important design consideration for durability, long-term serviceability and load carrying capacity of structures.
The rate and ultimate magnitude of creep, to be used in the design of a reinforced concrete structure, can be estimated at various levels, depending on the nature of the proposed structure and the extent of its deformation sensitivity.
In cases where the nature of the proposed structure warrants an approximate estimate of the extent and rate of creep strain, this can be estimated using design code type models. The input required by these models would be general information available at that stage, such as compressive strength of the concrete, applied stress, general environmental conditions of exposure and member geometry.
During a previous investigation, Fanourakis and Ballim (2006) assessed the accuracy of the following code-type creep prediction models when compared with the actual strains measured on a range of concretes under laboratory controlled conditions:
South African Bureau of Standards, SABS 0100 (1992), currently renamed SANS 10100 (2000).
Modified SANS 10100 model, discussed in Fanourakis and Ballim (2006).
British Standards Institution - Structural Use of Concrete, BS 8110 - Part 2 - (1985).
American Concrete Institute (ACI) Committee 209 (1992), reapproved by ACI Committee 209 in 2008.
Standards Association of Australia - Australian Standard for Concrete Structures - AS 3600 (1988).
Comité Euro-International Du Béton - Federation Internationale De La Précontrainte (CEB-FIP) Model Code (1970).
CEB-FIP Model Code (1978).
CEB-FIP Model Code (1990).
International Union of Testing and Research Laboratories for Materials and Structures (RILEM) Model B3 (1995), after Bazant and Baweja (1995).
Subsequently, some of the models listed above were superseded. This justified an assessment of the accuracy of the revised models, as well as other code-type models that were not previously considered. This paper assesses the accuracy of the following six international code type models when compared to the same experimental data used to assess the accuracy of the above models.
Standards Association of Australia - Australian Standard for Concrete Structures - AS 3600 (2001 and 2009 versions).
EUROCODE (EC 2) - BS EN 1992-11:2004, which will be referred to as EC 2 (2004).
Gardner and Lockman 2000 and 2004 versions, which will be referred to as GL (2000) and GL (2004), respectively. The GL (2000) model was published in 2001.
Gardner and Zhao (GZ 1993).
The BS 8110 (1985) was superseded by the EC 2 (2004) which is validated in this paper. The EC 2 (2004) model is the 1999 update of the CEB (1990) model.
The GL (2000 and 2004) and GZ (1993) models were considered as they are similar in their degree of complexity and approach to the other national code models considered. The GL (2000) model is a modification of the GZ (1993) model.
The accuracy of all the models was determined by comparing experimental total creep values based on laboratory testing over a period of 168 days, carried out as part of an investigation by Fanourakis (1998), against those predicted at the corresponding ages by all the models considered. A period of 168 days (approximately six months) was selected as it is accepted that approximately 60% of the ultimate creep strain will occur within the first six months after loading (Alexander 1994).
The models were assessed against the strains measured on six different concrete mixes, incorporating combinations of three aggregate types and two w/c ratios as detailed in Table 1. The three aggregate types were representative of common aggregates used in concrete and the two w/c ratios represented medium and high strength concretes.
STRUCTURE OF THE MODELS CONSIDERED
The models considered are all empiricalbased. The 28-day compressive strength is the only input parameter which necessitates testing. Other input parameters typically comprise certain variables, such as effective thickness, relative humidity and age at loading.
All the models considered express creep strain in terms of the creep coefficient, φ(t), where:

In Equation 1, εc(t, τ) is the creep strain at any concrete age t for a concrete loaded at age τ, where t > τ and εeτ is the elastic strain of eT the concrete at age τ. The creep coefficient is empirically determined by considering one or more intrinsic and/or extrinsic variables such as concrete stiffness and age at first loading.
Table 2 shows a summary of the factors accounted for by each of the prediction models considered in this paper. These factors include those required for the determination of the elastic modulus which is used in the calculation of εeτ in Equation 1.
As is evident from Table 2, the factors considered by the two AS 3600 models are almost identical. The same situation applies to the three models co-developed by Gardner (GL 2000; GL 2004 and GZ 1993).
The Australian models (AS 2001 and 2009) are the only two models that consider characteristic compressive strength in addition to actual compressive strength.
MATERIALS
A single batch of CEM I 42,5 cement, from the Dudfield factory of Alpha Cement (now AfriSam), was used for all the tests carried out in this investigation. Quartzite (Q) from the Ferro quarry in Pretoria, granite (G) from the Jukskei quarry in Midrand and andesite (A) from the Eikenhof quarry in Johannesburg were used as both the stone and sand aggregates for the concrete. The stone was 19 mm nominal size and the fine aggregate was crusher sand.
EXPERIMENTAL METHODS
Aggregate stiffness
Measurements of aggregate elastic modulus or stiffness were carried out on samples obtained from the representative boulders collected from the three sources of the aggregates used in the investigation. The stiffness of each rock type as determined on the boulder samples was taken to be representative of the stiffness of the corresponding aggregates used in the concrete specimens.
Three cores measuring 42 mm in diameter and 82 mm long were cut from each set of two boulders and these were tested according to the procedure described in BS 1881 (1983) to determine the elastic modulus of the aggregates used in this investigation. These cores were loaded to a maximum stress equal to approximately 25% of the average unconfined compression strength values respectively determined by Davis and Alexander (1992) as 250 MPa, 190 MPa and 527 MPa for the quartzite, granite and andesite from the same sources.
The average elastic modulus for each rock type is included in Table 1.
Creep and shrinkage measurements
For each of the concretes listed in Table 1, six prisms were prepared, measuring 100 x 100 x 200 mm and cast with the 200 mm dimension vertical. After de-moulding, these prisms were continuously water-cured up to an age of 28 days. A set of Demec targets were glued onto two opposite 200 x 100 mm faces of each prism, on a vertical axis symmetrically about the middle of the specimen, to accommodate a 100 mm Demec strain gauge.
After curing, three of the six prisms of each mix were used for creep tests and the remaining three were used for shrinkage measurements.
The creep test prisms were placed into creep loading frames and subjected to an applied load of approximately 25% of the 28-day compressive strength, for the 168-day period, in a room controlled at 22 ± 3ºC and RH of 65 ± 5%.
The shrinkage (companion) prisms were placed on a rack in the same room as the creep samples and, in order to ensure a drying surface area equivalent to the creep samples, the two 100 mm square ends were dipped in warm wax to prevent drying from these surfaces.
Elastic strain measurements of the loaded specimens were taken within 10 minutes of application of the loads. These measurements were used to determine the secant elastic moduli of the concretes, which were compared with the values estimated by each creep model assessed.
Creep and shrinkage measurements were recorded daily for the first week, thereafter weekly for the remainder of that month and then monthly until the culmination of the approximately six-month total loading period. This entailed measuring the strain across the targets using a Demec gauge with a resolution of 16,7 microstrain per division. At each measuring period, the strain of each prism was taken as the average of the strains measured on the two opposite faces of the prism. The strain of each group of prisms, that is the three creep prisms or the three companion shrinkage prisms of a particular mix, was taken as the average of the strains of the prisms in that group.
The results of shrinkage measurements were subtracted from the total time-dependent strain of the loaded specimens to determine the total creep strain.
RESULTS AND DISCUSSION
Elastic moduli of concrete
All the creep prediction models applied in this investigation include an empirical equation for estimating the elastic modulus of the concrete, which, in turn, is used in predicting the creep of the concrete. Hence, the reliability of estimation of the elastic modulus significantly influences the reliability of the prediction of creep. For this reason the accuracy of elastic moduli estimates are considered below.
The GL (2000), GL (2004) and GZ (1993) use a common equation for the estimation of elastic modulus.
All the equations of the models included in this paper consider the cylinder compressive strength of the concrete at the time of loading. The cylinder strengths used for the various mixes were inferred from the cube strengths of those mixes using the conversions given in the EC2 (2004) model.
The equations prescribed by the AS 3600 models also consider the density of the concrete. The AS 3600 (2009) model prescribes two equations for estimating the elastic modulus of the concrete, one for cylinder compressive strengths less than or equal to 40 MPa and the other for strengths in excess of 40 MPa. The equation pertaining to concretes with a maximum compressive strength of 40 MPa is the same equation that is used for estimating elastic modulus for all strength ranges in the AS 3600 (2001) version.
Table 3 shows the estimated elastic moduli for each of the concretes according to the different creep prediction methods, together with the average elastic moduli measured at 28 days after casting. The most and least accurate elastic modulus estimations are indicated in green and red, respectively.
This table includes the following statistics:
The coefficients of variation of errors (ωj) after Bazant and Panula (1979). This coefficient is expressed as a percentage and is defined by Equations 2 and 3. The more accurate the estimation, the lower the value of ωj.

in which,

where,
| ωj | = | coefficient of variation for data set j |
| Δij | = | the deviation (vertical) between the measured and predicted value for data point i on data set j. |
| Jij | = | the measured values (labelled by the subscript i in the data set number j). |
| n | = | the total number of data points in the set. |
The t-Test results, which relate to a comparison between the measured and the predicted values for each of the concretes, determined by a particular creep prediction method. T-test probabilities exceeding five per cent indicate that the difference between the estimated and the actual values is not due to chance, and hence significant.
It is evident from Table 3 that, in the case of the concretes containing the andesite aggregate (A1 and A2), which had an average density of 2 591 kg/m3, the models generally underestimated the elastic modulus. In the remaining mixes, which had an average density of 2 400 kg/m3, the creep prediction models generally overestimated the elastic modulus. No trend was established regarding the variance exhibited in the values predicted for the lower w/c ratio mixes (Q2, G2 and A2) in comparison with the higher w/c ratio mixes.
The AS 3600 (2009) method, which yielded a coefficient of variation (ωj) of 9,3%, was the most accurate method, while the EC 2 (2004) was the least accurate method (ωj = 16,4%).
The introduction of the additional equation (for strengths in excess of 40 MPa) for predicting elastic modulus in the recent AS 3600 (2009) model appears to yield more accurate results compared to those obtained using only the equation from the former AS 3600 (2001) model. The inclusion of concrete density in the AS 3600 models does appear to benefit the accuracy of the estimated elastic modulus.
The AS 3600 (2009) model generally yielded the most accurate estimates of elastic modulus of all the models considered, including those in the previous investigation by Fanourakis and Ballim (2006).
According to the t-Test results shown in Table 3, the discrepancies between the measured and predicted elastic moduli values, for the different mixes, were not significant for any of the models.
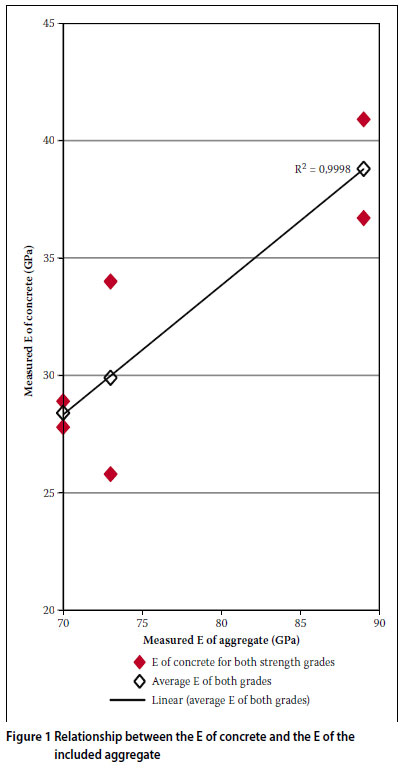
No trend was established regarding the influence of the included aggregate on the accuracy of the predicted modulus of elasticity. However, a trend was established between the average elastic modulus of the concrete (at 28 days) for both strength grades manufactured with each aggregate type and the elastic modulus of the included aggregate, as shown in Figure 1.
Total creep
Analytical procedures
The six creep prediction methods considered in this investigation were used to predict the specific creep at the same ages at which measurements were taken for the concrete of each of the six mixes used.
In order to provide a basis for comparing the creep strains of concretes with different strengths and different applied stresses, σ, the measured and predicted results were presented in the form of specific creep (Cc)which is defined as:

Substituting Equation 1 into Equation 4

where,

therefore,

Results
Figures 2 to 7 show comparisons between the measured results for the six mixes (Q1, Q2, G1, G2, A1 and A2) together with the corresponding strains predicted by the different models.
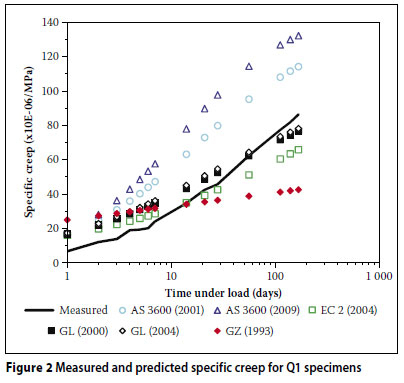
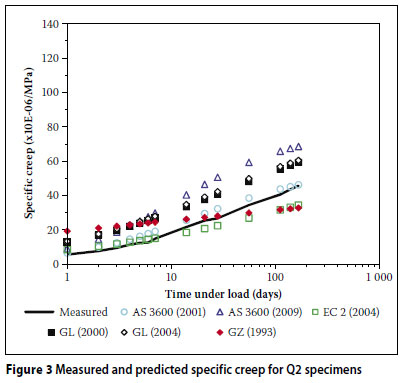
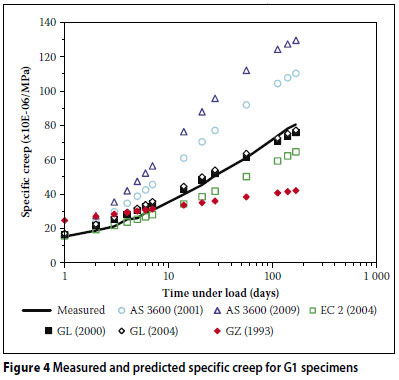
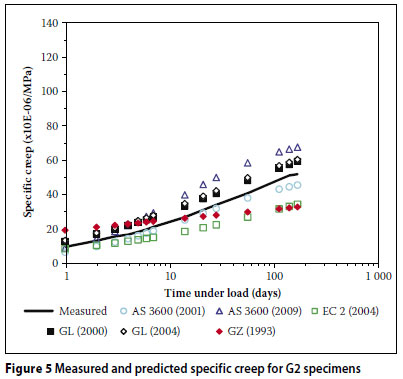
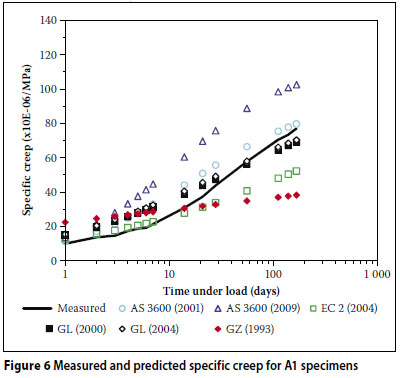
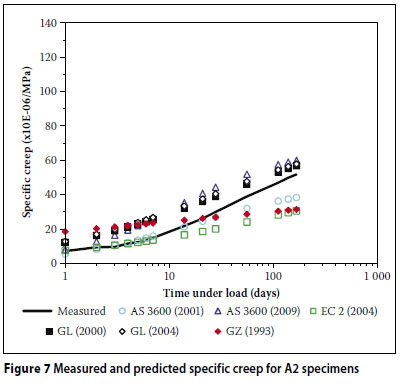
From Figures 2 to 7, the following is evident:
The AS 3600 (2009) model over-predicted the creep strain for all six of the concrete mixes.
The AS 3600 (2001) model overpredicted the creep strain in the case of the low strength mixes (Q1, G1 and A1). Furthermore, in all the mixes except G2, this model overestimated the early development of creep. This trend is in disagreement with the findings of Gilbert (2002) where the early development of creep is underestimated by this model.
The GL (2000) and GL (2004) models over-predicted the creep strain in the case of the high strength mixes (Q2, G2 and A2).
The GZ (1993) model initially over-predicted the creep strain (within the first three weeks) and then under-predicted thereafter.
The coefficient of variation of errors (ωj), which is defined by Equations 2 and 3 above, was used to quantify the extent to which predicted specific creep values at different ages after loading (determined by applying a particular model) deviated from the values measured at the relevant ages on the specimens of a particular concrete mix. The more accurate the prediction, the lower the value of ωj.
The overall coefficient of variation (ωall) was used to estimate the average (pooled) coefficient of variation of a number of independent coefficients of variation (ωj), as defined by Equation 8.

where,
N = the number of sets considered.
The calculated values of ωj and ωall for the different models assessed are shown in Table 4. The most and least accurate predictions and estimations are indicated in green and red, respectively.
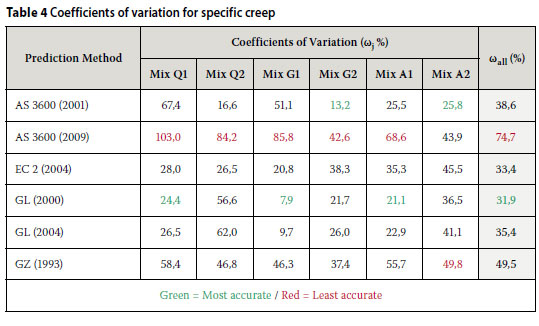
When considering specific mixes, the most accurate results were yielded by the GL (2000) in the case of the low strength mixes (Q1, G1 and A1) and generally by the AS 3600 (2001) in the case of the high strength mixes. Overall, the GL (2000) model yielded the most accurate predictions, giving the lowest overall coefficient of variation (ωall of 31,9%).
Ironically, the AS 3600 (2009), which yielded the most accurate elastic modulus of all the models considered (Table 3), showed the least accuracy of prediction (ωall = 74,7%) by exhibiting the least accuracy in five of the six mixes (all the mixes except A2).
No other trend was established between the accuracy of the specific total creep and the elastic moduli predicted by any of the models.
Although the GL (2000) model yielded the most accurate results in this investigation (ωall = 31,9º%), the CEB-FIP (1970), BS 8110 (1985) and SABS 0100 (1992) models, which were included in the previous investigation by Fanourakis and Ballim (2006), respectively yielded more accurate ωall values of 18,1º%, 23,6º% and 31,3%.
CONCLUSIONS
Based on the results of this investigation, the following was concluded:
All the creep prediction methods included in this project considered the value of a predicted elastic modulus of the concrete in calculating predicted creep strain. A comparison of the predicted elastic moduli, determined for each mix by the different creep prediction methods, with the measured elastic moduli of the relevant mixes, indicated that the differences were not significant in the case of all the models.
No trend was established regarding the influence of the included aggregate on the accuracy of the predicted modulus of elasticity.
The six models assessed show significant and wide variation in the magnitude of specific creep predicted over the time period considered. When considering specific mixes, the most accurate results were yielded by the GL (2000) in the case of the low strength mixes (Q1, G1 and A1) and generally by the AS 3600 (2001) in the case of the high strength mixes.
For the range of concretes tested, the GL (2000) model yielded the most accurate predictions, giving the lowest overall coefficient of variation (ωall of 31,9%). However, this model was not as accurate as the CEB-FIP (1970), BS 8110 (1985) and SABS 0100 (1992) models, which were assessed by Fanourakis and Ballim (2006), and yielded ωall values of 18,1%, 23,6% and 31,3%, respectively.
Ironically, the AS 3600 (2009), which yielded the most accurate elastic modulus of all the models considered, showed the least accuracy of prediction (ωall = 74,7%) by exhibiting the least accuracy in five of the six mixes. This method over-predicted the specific creep for all the mixes.
The current European model (EC 2, 2004), Australian model (AS 3600, 2009) and GL (2004) model yielded less accurate predictions than their immediate superseded versions.
The accuracy of the predictions did not increase with the complexity of the method applied or with increasing number of variables accounted for in the method. On that basis, it is recommended that the superseded BS 8110 (1985) model, which exhibited the greatest accuracy considering its simplicity, of all the models investigated by the author, be used for South African conditions.
Finally, it should be borne in mind that the findings of this investigation pertain to small-scale tests conducted over a 168- day period after loading for the specific materials used and environmental conditions. Hence, the accuracy of the models established may differ for other loading periods, materials or environmental conditions.
RECOMMENDATIONS FOR FUTURE RESEARCH
General
The following proposals should be considered with a view to improving the accuracy of creep predictions:
Characteristic strengths should not be considered in estimating creep.
The accuracy of creep coefficient (φ) should be evaluated separately from the accuracy of elastic modulus. These are discussed below.
Characteristic strength
Characteristic strength As mentioned earlier, the Australian models (AS 2001 and AS 2009) consider characteristic strength in the estimation of the creep coefficient (φ). This is probably why these models respectively ranked fourth and sixth (last) in terms of overall relative creep prediction accuracy.
The characteristic strength of the concrete may vary significantly from the actual strength achieved, depending on the degree of quality control exercised during the production of the concrete and its constituent materials.
Figure 8 shows the left half of a normal distribution curve. The relative positions of the target mean strength and characteristic mean strength are also indicated. Mixes are designed to achieve the target mean strength, which exceeds the characteristic strength by a margin which is equal to 1,65 times the standard deviation. The characteristic strength is defined as the strength below which not more that 5% of the actual strengths achieved will fall.
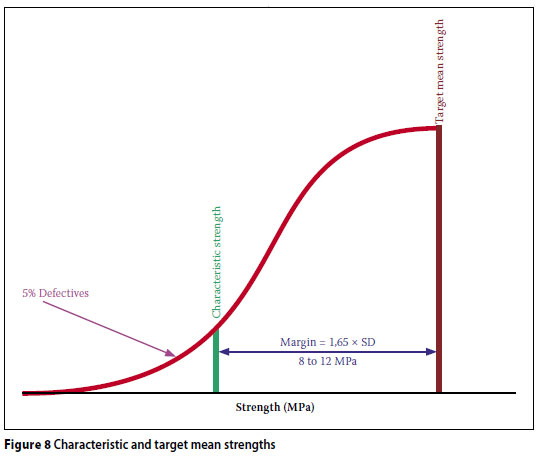
Therefore, depending on the degree of control exercised, which will be manifested in the standard deviation (e.g. good = 5 and poor = 7), and bearing in mind that the actual strength achieved may exceed the target mean strength, the difference between the characteristic and actual strength may be as large as 12 MPa or more.
Table 5 shows the overall coefficients of variation for creep predictions by both the AS 3600 (2001) and the AS 3600 (2009) models, using characteristic compressive strength (as prescribed by these models) and actual compressive strength (as proposed by the author).
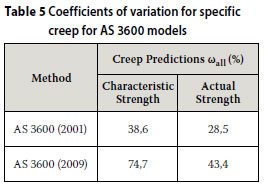
It is evident from Table 5 that use of actual compressive strength in place of characteristic compressive strength results in more accurate creep predictions, especially in the case of the AS 3600 (2009) where the ωall was reduced from 74,7% to 43,4%.
In view of the above, it can be concluded that characteristic strength is not sufficiently representative of the concrete to be considered as a criterion for predicting creep.
Accuracy of estimated creep coefficient (φ) and elastic modulus
As shown in Equation 7, the Specific Creep (Cc) predicted by a particular model is dependent on the ratio of the estimated creep coefficient (φ) to the estimated elastic modulus (E). The E is estimated by a particular model and then, in turn, used to determine the Cc.
It is proposed that, in further research, the accuracy of the φ estimated by a particular model at various ages be assessed separately from the accuracy of the E estimated by that model to ascertain which factors influence φ and which influence E.
This proposal is justified by the fact that, at times, the model which estimated the E most accurately proved to be the least accurate in predicting Cc at various ages. Table 6 shows the results of predicted Cc and estimated E values for all the creep models investigated by the author to date, including those in the paper by Fanourakis and Ballim (2006). The most and least accurate predictions and estimations are indicated in green and red respectively.
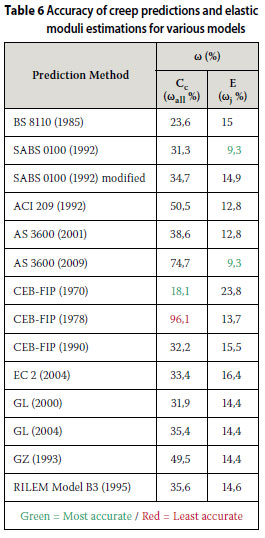
Referring to Table 6, it is evident that the most accurate creep prediction model, the CEB-FIP (1970), which yielded a ωall of 18%, was the least accurate in estimating E. Furthermore, in the case of the six models assessed in this paper, the AS 3600 (2009) yielded the most accurate estimation of E (Table 3) and the least accurate prediction of Cc (Table 4).
ACKNOWLEDGEMENTS
The author thanks the Information Centre of the Cement and Concrete Institute (C & CI -South Africa) and, in particular, Susan Battison for her assistance in sourcing publications.
REFERENCES
Alexander, M G 1994. Deformation and volume change of hardened concrete. In: Fulton's concrete technol ogy, 7th ed, Addis, B J (Ed), Midrand, South Africa: Portland Cement Institute, 123 p. [ Links ]
ACI (American Concrete Institute) 1992. Prediction of creep, shrinkage and temperature effects in concrete structures. Report ACI209, R-92, Detroit, US: ACI. [ Links ]
ACI (American Concrete Institute) 2008. Guide for modeling and calculating shrinkage and creep in hardened concrete, Report ACI 209, R-08, Detroit; US: ACI. [ Links ]
AS 3600 1988. Concrete structures - AS 3600 1988. Sydney: Standards Association of Australia. [ Links ]
AS 3600 2001. Concrete structures - AS 3600 2001. Sydney: Standards Association of Australia. [ Links ]
AS 3600 2009. Concrete structures - AS 3600 2009. Sydney: Standards Association of Australia. [ Links ]
Bazant, Z P & Baweja, S 1995. Creep and shrinkage model for analysis and design of concrete structures. Model B3. Draft RILEM Recommendation, Materials and Structures, Vol 28, pp 357-365, 415-430 & 488-495, with Errata in Vol 29 (1996), p 126. [ Links ]
Bazant, Z P & Panula, L 1979. Practical prediction of time dependent deformations of concrete, Parts I-VI. Materials and Structures, 12: 169-183. [ Links ]
BS 1881 1983. Testing concrete. Part 121: Method for determination of static modulus of elasticity in compression. London: British Standards Institution (BSI). [ Links ]
BS 8110 1985. Structural use of concrete. Part 2: Code of practice for design and construction. London: British Standards Institution (BSI). [ Links ]
BS EN 1992-1-1 2004. Eurocode 2: Design of concrete structures. Part 1-1: General - common rules for buildings and civil engineering structures. London: British Standards Institution (BSI). [ Links ]
CEB-FIP (Comité Européen du Béton - Fédération Internationale de la Précontrainte) 1970. International recommendations for the design and construction of concrete structures: Principles and recommendations. Proceedings, Sixth FIP Congress, Prague, Czech Republic, pp 27-28. [ Links ]
CEB-FIP (Comité Euro-International du Béton -Fédération Internationale de la Précontrainte) 1978. International system of unified standard codes of practice for structures, Vol II: CEB-FIP model code for concrete structures, 3rd ed. Lausanne, Switzerland, pp 56 & 331-344. [ Links ]
CEB-FIP (Comité Euro-International du Béton -Fédération Internationale de la Précontrainte) 1990. CEB-FIP model code 1990, 1st draft. Lausanne, Switzerland, (Information Bulletin, No 195), pp 2-3 & 2-28-2-40. [ Links ]
CEB-FIP (Comité Euro-International du Béton -Fédération Internationale du Béton) 1999. Structural Concrete: Textbook on behaviour, design and performance. Updated Knowledge of CEB-FIP model code 1990. Lausanne, Switzerland, (FIB Bulletin 2(2)), pp 35-52. [ Links ]
Davis, D E & Alexander, M G 1992. Properties of aggregates in concrete, Part 2. Sandton, South Africa: Hippo Quarries Technical Publication, pp 1-27, 42-43 & 46-47. [ Links ]
Fanourakis, G C 1998. The influence of aggregate stiffness on the measured and predicted creep behaviour of concrete. MSc (Eng) dissertation, Johannesburg: University of the Witwatersrand. [ Links ]
Fanourakis, G C & Ballim, Y 2006. An assessment of the accuracy of nine design models for predicting creep in concrete. Journal of the South African Institution of Civil Engineering, 48(4): 2-8. [ Links ]
Gardner, N J 2004. Comparison of prediction provisions for drying shrinkage and creep of normal strength concretes. Canadian Journal for Civil Engineering, 31(5): 767-775. [ Links ]
Gardner, N J & Lockman, M J 2001. Design provisions for drying shrinkage and creep of normal strength concrete. ACI Materials Journal, 98(2): 159-167. [ Links ]
Gardner, N J & Zhao, J W 1993. Creep and shrinkage revisited. ACI Materials Journal, 90(3): 236-246. [ Links ]
Gilbert, R I 2002. Creep and shrinkage models for high strength concrete - Proposals for inclusion in AS 3600. Australian Journal of Structural Engineering, 4(2): 96-106. [ Links ]
SABS 0100: 1992. Code of practice for the structural use of concrete. Part 1: Design. Pretoria: South African Bureau of Standards. [ Links ]
SANS 10100: 2000. The structural use of concrete. Part 1: Design. Pretoria: South African Bureau of Standards. [ Links ]
 Contact details:
Contact details:
Dept of Civil Engineering Technology University of Johannesburg
PO Box 17011
Doornfontein 2028 South Africa
T: +27 11 559 6416 F: +27 11 559 6057
E: georgef@uj.ac.za
 | GEORGE C FANOURAKIS is an Associate Professor in the Department of Civil Engineering Technology at the University of Johannesburg, South Africa. He received the degrees MSc (Eng) from the University of the Witwatersrand and DTech (Eng) from the University of Johannesburg. He is a Chartered Civil Engineer and Member of the Institution of Civil Engineers (UK), and a Member of the South African Institution of Civil Engineering (SAICE). His primary teaching and research interest areas are Concrete Technology and Geotechnical Engineering. Prof Fanourakis heads the Materials, Geotechnical and Transportation Engineering Research Group at the university. He is a member of the SABS SC 59P: Geotechnical Standards Committee. He received the 2006 Best Journal Paper Award from SAICE. |














