Services on Demand
Article
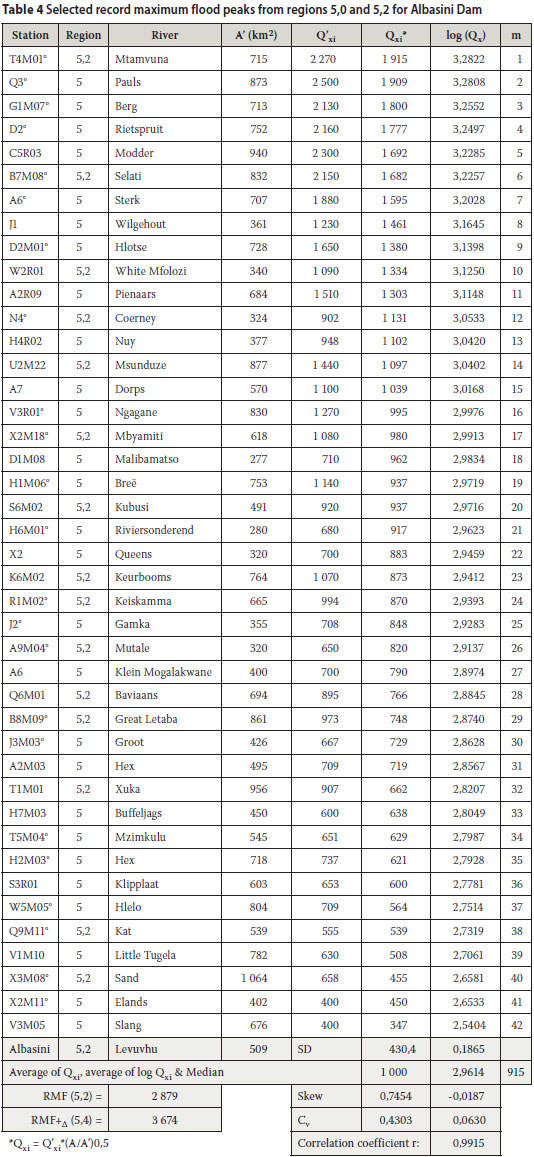
Indicators
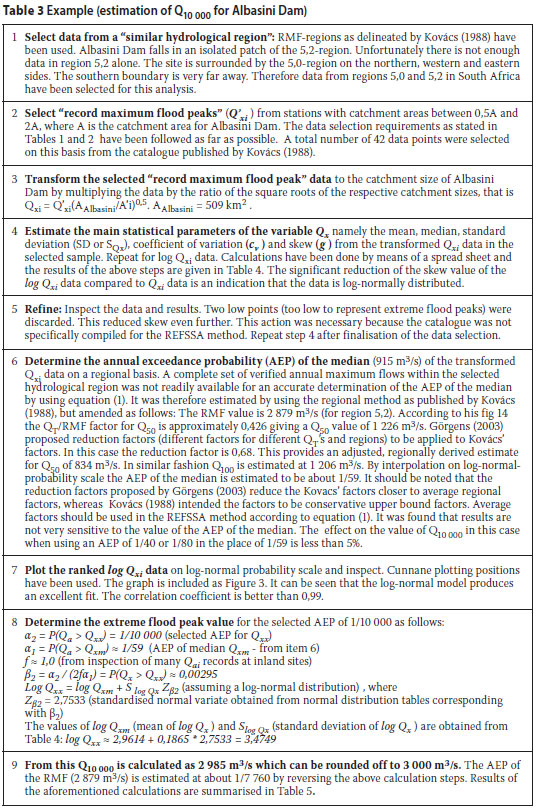
Related links
-
 Cited by Google
Cited by Google -
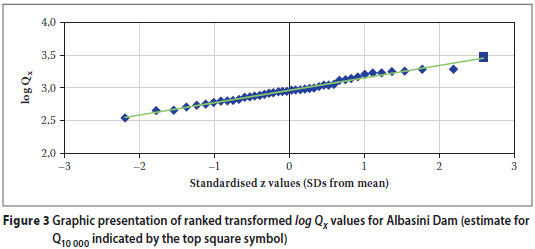
 Similars in Google
Similars in Google
Share
Journal of the South African Institution of Civil Engineering
On-line version ISSN 2309-8775
Print version ISSN 1021-2019
J. S. Afr. Inst. Civ. Eng. vol.52 n.2 Midrand Oct. 2010
TECHNICAL PAPER
Estimation of extreme flood peaks by selective statistical analyses of relevant flood peak data within similar hydrological regions
J H Nortje
ABSTRACT
This paper describes a new Regional Estimation of Extreme Flood Peaks by Selective Statistical Analyses (REFSSA) method to estimate extreme flood peaks from regional flood peak data. The method differs from current regional flood frequency analysis (RFFA) methods or approaches in that an additional separate statistical analysis is performed on "record maximum flood peaks" within a "similar hydrological region". Suitability of the method is demonstrated for the estimation of extreme flood peaks with annual exceedance probabilities between 0,001 (1/1 000) and 0,0001 (1/10 000) for two major hydrological regions in South Africa, and for catchment sizes between 100 and 7 000 km2. The applicability of the method for catchments outside these regions and limits has not been fully tested mainly due to a shortage of verified data. The theory and a practical example are presented. Excellent results have been obtained so far, displaying high correlation coefficients between extreme flood peak data and regression lines, namely 0,99 on average on log-normal scale. The method is considered to have universal application, especially in climates experiencing outlier type of extreme flood peaks.
Keywords: hydrology, extreme flood peak estimation, regional flood frequency analysis, regionalisation, regression
INTRODUCTION AND BACKGROUND
This paper describes a new approach termed the Regional Estimation of Extreme Flood Peaks by Selective Statistical Analyses (REFSSA) method, to estimate values for extreme flood peaks. The approach differs from current regional flood frequency analysis (RFFA) methods in the following respect: selective (and separate) statistical analyses are carried out on regional flood peak data after transformation (in proportion to the square roots of the respective catchment areas) from comparable sites within a "similar hydrological region" to the site under investigation. A distinction is specifically made between information contained within the whole spectrum of annual maximum flows (one value per site per year, thus including many low flows in the South African climate) and information contained within the "record maximum flood peaks" (only one record value per site for the full observation period), which better reflects the characteristics of extreme flood peaks.
For the purpose of this paper a "similar hydrological region" is provisionally defined as a space/area of demonstrated similarity with regard to the past occurrences of "record maximum flood peaks", thus not requiring homogeneity with regard to aspects such as catchment characteristics. This wide definition is considered admissible for the initial purpose of this study, namely to determine upper-bound values for extreme flood peaks within "similar hydrological regions". However, the REFSSA method is versatile and homogeneous regions, or alternatively clusters of similar basins as described by Wiltshire (1986), could be used in the place of "similar hydrological regions".
The REFSSA method is particularly suitable for hydrological environments where a flood record typically includes one or two extreme flood peak outliers (as in South Africa) and where record lengths are rather short. The initial focus of this paper is the estimation of upper bound values for extreme flood peaks between Q1 000 and Q10 000, where QT is defined as the flood peak value with an annual exceedance probability (AEP) of 1/T (Q10 000, for example, has an AEP of 1/10 000).
Traditionally, the Single Station Statistical Analysis (SSSA) method has been used for the estimation of extreme flood peak values even up to Q10 000. The SSSA method is certainly useful for estimating flood peaks within or close to its record length but, as motivated by Kovács (1988), a flow record should not be extrapolated to more than two times its length. Alexander (2000) also warned against extrapolation beyond Q100. The limitation of the SSSA method is demonstrated by the fact that different but equalfitting distributions (all with correlation coefficients in the order of 0,97), such as Lognormal, Log Pearson III and General Extreme Value (with either conventional moments or probability-weighted moment estimators), yield entirely different estimates of Q10 000 which could range from 2 000 to 13 000 m3/s for one site. Lesser annual maximum flows, such as Q1, Q2, Q3, ... Q30, play a major role in the SSSA method, but they do not necessarily contain information on the magnitude of extreme flood peaks. This is demonstrated by the flow record at Midmar Dam shown in Figure 1. In this case only one extreme flood peak occurred during a continuous 43-year record length. This is a typical picture for many inland sites in South Africa.
Integration of regional information helps to overcome the lack of long-term records at individual sites and this is addressed by RFFA methods in many parts of the world. Cunnane (1988) provides an evaluation of the merits of different RFFA methods. Current RFFA methods, however, do not fully overcome the statistical shortcomings of the SSSA method for estimating extreme flood peaks in an environment with outlier type of extreme flood peaks. The main reason is that the different statistical characteristics of extreme flood peaks are not taken into account. Also, in its purest form, the RFFA method requires a homogeneous region or pool (cluster of similar basins) and a common record period covered by all stations within the region or pool. As a result, the database is reduced in size and it is still dominated by low annual maximum flows, especially in the South African context. In addition, historical flood peaks cannot be added without making questionable statistical assumptions. Görgens (2007a) adapted the RFFA approach (using the flood index method) for South Africa, but it is unfortunately only considered suitable for the estimation of flood peaks and flood hydrographs up to about Q100.
Compared with the SSSA method, the REFSSA method achieves superior correlation coefficients between extreme flood peaks and regression lines. Another significant improvement is with respect to the coefficient of variation, cv (standard deviation divided by the mean in terms of logarithms of flood peak data), which typically reduces from about 0,2 (SSSA method) to about 0,06 (REFSSA method). Typically, a record length of 50 to 100 years is analysed by the SSSA method in South Africa, whereas the typical representative record length analysed by the REFSSA method is between 3 000 and 5 000 station years. In addition, historical (including palaeo) flood peaks could be added to the catalogue of "record maximum flood peaks" without the statistical difficulties experienced by current RFFA methods. These comparisons suggest that more reliable estimates of extreme flood peaks could be obtained by means of the REFSSA method.
In South Africa, the Regional Maximum Flood (RMF) method as developed by Kovács (1988) in accordance with the Francou- Rodier (1967) approach is a frequently used empirical method to determine appropriate safety evaluation flood peaks for dams. The RMF value is the value on an envelope curve drawn just outside "record maximum flood peaks" for different sites within a specific demarcated region. The RMF method thus also integrates regional information within "similar hydrological regions", but a serious shortcoming is that the annual exceedance probability (AEP) of the RMF value at a specific site is unknown. In addition, the AEP of the RMF is not constant but varies significantly from site to site and region to region.
Application of the Probable Maximum Flood (PMF) approach in South Africa is also problematic. Firstly, the AEP of the PMF is undefined. Secondly, PMF values as derived by the preferred unit graph method of HRU (1972) have poor correlation with actual record maximum flood peak data. This was demonstrated by Görgens et al (2007b) who found that PMF/RMF ratios vary from 0,6 to 9 from site to site and region to region in South Africa.
The new REFSSA method provides a sound statistical basis for estimating extreme flood peak values between Q1 000 and Q10 000 from regional data. Reliability depends mainly on the availability and accuracy of relevant record maximum flood peak data from comparable catchments. By means of the REFSSA method, estimates can also be made of the AEP of RMF and PMF values. This is considered very useful because the SANCOLD Guidelines (SANCOLD 1991), which are relevant when determining appropriate safety evaluation discharges or floods for dams in South Africa, are based largely on the RMF and PMF methods.
THEORETICAL PREMISE OF THE REFSSA METHOD
The REFSSA method distinguishes between the following two data sets: (1) the Qx data set which consists of transformed "record maximum flood peaks" (Qxi-values) and (2) the Qa data set which consists of all transformed annual maximum flows (Qai-values). The aforementioned data are selected from sites with comparable catchments and catchment sizes within a "similar hydrological region", and then transformed to the site under investigation in proportion to the ratio of the square roots of their respective catchment areas. It is inherently assumed that "storm event" is the major factor with regard to the magnitude of extreme flood peaks. It is expected that the REFSSA method would be less reliable for catchment sizes of less than about 100 km2, where catchment characteristics could become more important.
The crux of the method is the postulation that a variable termed the "regionally observed maximum flood peak" (Qx) for a specific site (based on the distribution of transformed "record maximum flood peaks" or Qxi-values, obtained from other sites with comparable catchments within a "similar hydrological region" during the same observation period of adequate length) can be regarded as a statistical variable and further that its statistical distribution parameters can be utilised to estimate the magnitude of extreme flood peaks, such as Q1 000 to Q10 000. It is postulated that information contained within record maximum flood peak data within a "similar hydrological region" is much more suitable for estimating the magnitude of extreme flood peaks than information contained within lesser annual maximum flow data, such as Q1, Q2, Q3, ... Q30, etc. Information from the latter or Qa data set is utilised to help "calibrate" the AEP of extreme flood peaks. An algorithm that combines the information from the two data sets in order to estimate both the magnitude and the AEP of extreme flood peaks is presented in the next section. The expected value of Qx for a site during a similar observation period can be calculated as the mean (or median if the data are log-normally distributed) of the Qxi -values. The other parameters of the distribution of Qx such as the standard deviation, coefficient of variation and skewness, can also be calculated from the Qxi -values. Estimates can then be made of extreme flood peak values such as Q10 000 by using a suitable theoretical statistical distribution model.
The following notes have further bearing on the theoretical premise of the postulation:
QT is defined as the flood peak value with an annual exceedance probability (AEP) of 1/T. T is traditionally referred to as the recurrence interval or return period in years, which is strictly speaking inappropriate because hydrological records are not statistically independent with respect to time. Records at many single stations show definite cyclic patterns over time. Alexander (2009) demonstrated that annual inflow volumes at Vaal Dam display low-high 'cycles' with periods of approximately 20 years. Long-term climate changes are also not reflected within short observation or record periods. The AEP of QT should thus be expressed as 1/T (e.g. 0,0001 or 1/10 000 - omitting years), with the qualification that it is based on a statistical analysis of data collected over a specified observation period.
If there were 50 independent Qxi-values available from 50 different sites with equal catchment areas within a "similar hydrological region", then each site will have a different record maximum flood peak value mainly because of differences in storm events, which do not occur uniformly over a whole region. This phenomenon will be reflected in the variance of Qx. It is assumed that independent storm events could occur on a relatively random basis anywhere within a "similar hydrological region", especially if the region is large relative to the catchment size of the site under investigation.
If each of the above sites had a record length of 100 years, then the artificially combined record of the 50 separate sites could be put at 5 000 "station years". As motivated above, this is not equivalent to a single station with a 5 000 year record because hydrological data even at single stations are not statistically independent. From a statistical perspective it could be expected that 5 000 station years or 50 data points of "record maximum flood peaks" could include flood peaks as low as Q30 and as high as Q1 000 or more. This expected wide spectrum of "record maximum flood peaks" is confirmed by Figures 9a to 9h of Kovács (1988) that show wide bands of the record maximum flood peak values within "similar hydrological regions".
The mean of say 500 Qxi -values from 500 sites would provide a reasonably good estimate of the population mean µQx at a site within a "similar hydrological region". Similarly the standard deviation of the 500 Qxi -values would provide a reasonably good estimate of the standard deviation σQx of the population. However, if the sample size is small, statistical uncertainty would be high and the estimates of µQx and σQx would lack in accuracy. This will have an influence on the reliability of the estimation of extreme flood peak values. It has been found that sample sizes (number of Qxi -values) should not be less than about 25 to 30 in order to obtain stable results.
Limitations and practical considerations impacting on accuracy of results
The REFSSA method is provisionally considered suitable for the estimation of extreme flood peaks between Q1 000 and Q10 000.
The estimation of extreme flood peaks for a specific site within a "similar hydrological region" but with catchment characteristics significantly different from the 'average' would be less accurate.
The reliability of the method depends on the quantity and quality of the source data.
The estimates for extreme flood peaks are valid for current climatic conditions (as reflected by the source data).
At some dams flood attenuation may play a significant role. In such cases extreme flood hydrographs should be constructed by using other methods, e.g. as proposed by Görgens (2007a), but these should be realistic compared to actual recorded extreme flood hydrographs at similar sites within the "similar hydrological region".
The demarcation of "similar hydrological regions" could be somewhat subjective due to limited available record maximum flood peak data and this could lead to inaccuracies.
Catchments bigger than 7 000 km2 typically cover two or more "similar hydrological regions" and the upper limit for the REFSSA method is provisionally set at 7 000 km2.
It is expected that catchment characteristics would play a bigger role in the case of smaller catchments and the lower limit is provisionally set at 100 km2.
SELECTION OF DATA
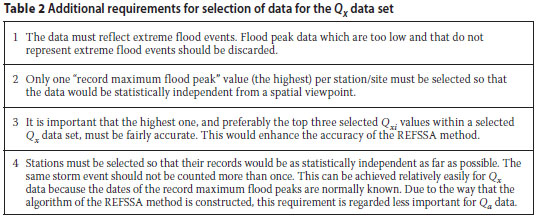
Requirements for selection of data for the Qx and Qa data sets
From a statistical viewpoint the data should be unbiased, statistically independent and relevant to the site for which an extreme flood peak is to be estimated. These criteria form the basis of the selection requirements as listed in Tables 1 and 2. Additional requirements for the selection of Qx data are listed in Table 2. Record maximum flood peak data selected according to the criteria as listed in Tables 1 and 2 should give a good indication of the mean and variance of extreme flood peaks.

Catalogue of "record maximum flood peaks" by Kovács (1988)
In South Africa record maximum flood peak data are readily available from the catalogue published by Kovács (1988). This catalogue was used as the main data source in this study. RMF-regions as demarcated by Kovács (1988) comply with the definition of and have been used as "similar hydrological regions" as a starting point for the purpose of this study. The following aspects relate to the suitability of the catalogue by Kovács (1988) as a data source for the REFSSA method (it should be borne in mind that this catalogue was not specifically compiled for the REFSSA method):
Record maximum flood peak data for catchments below 100 km2 and above 7 000 km2 are scarce. The sample size for an analysis should preferably be more than 30 in order to reduce statistical uncertainty to acceptable levels.
In the catalogue an indication of the accuracy of individual data points is given. Accuracy varies considerably. The accuracy of many flood peaks is indicated as "unknown".
Some data could have been influenced by flood attenuation by upstream dams and the data should be corrected to reflect natural un-attenuated flood peaks where and if applicable.
The data selected for an analysis should be as statistically independent as possible, especially with regard to the most important factor namely storm event. Fortunately the catalogue includes most of the dates of "record maximum flood peaks".
Ideally, all data should cover the same observation period of, say, at least 100 years to improve consistency (or to reduce bias). The observation period covered by the catalogue varies over the country and is generally rather short. The data might thus not include an adequate number of extreme flood peaks.
Regional boundaries should be refined as more data become available. The increments between some regions appear to be too large.
It can be seen that the catalogue as published by Kovács (1988) has a number of shortcomings for use as a database by the REFSSA method. Nevertheless, at the time of its publication (1988) a lot of work was done to make the catalogue as accurate and complete as possible and it contains a wealth of information. It is the only verified database of its kind that is readily available in South Africa. Taking all factors into account, it is regarded as suitable for current use until a more complete database becomes available.
ALGORITHM FOR ESTIMATING EXTREME FLOOD PEAKS
The algorithm for estimating the magnitude and AEP of extreme flood peaks is described below on the basis of the diagrammatic presentation in Figure 2.
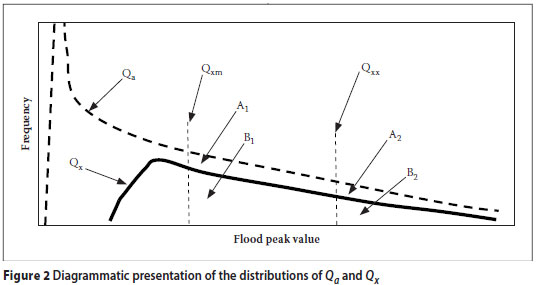
The symbols used in Figure 2 are defined below. All Q values in Figure 2 refer to flood peak values after transformation to a specific catchment size. The data reflect those of a selected number of stations within a "similar hydrological region" during the same observation period.
Qx Regionally observed maximum flood peak, measured as the "record maximum flood peaks" from many sites within a "similar hydrological region" (one Qxi-value per site for the full observation period). Note that the Qx data set is a subset of the Qa data set.
Qa Regional annual maximum flow, measured as "annual maximum flows" from the same sites as above (one Qai-value per site per year, e.g. 5 000 values for 50 sites during an observation period of 100 years, thus including 50 Qxi-values)
Qxm Median of all Qxi-values
Qxx Extreme flood peak value that must be determined for a site (e.g. Q10 000 )
In a very large sample the AEP of Qxx at a selected site (defined as α2 in Equation (2) below) would be approximately equal to the number of Qai-values that exceed Qxx divided by the total number of all Qai values, which constitute the total outcome or sample space of Qa.
In Figure 2 the areas A1 and A2 below the Qa curve represent the number of Qai data points exceeding Qxm and Qxx respectively (for a "continuous" probability density function Qa this can be visualised by selecting one flood peak unit to be equal to one class interval). Similarly, the areas B1 and B2 below the Qx curve represent the number of Qxi data points exceeding Qxm and Qxx respectively. If the total area below the Qa curve is A and the total area below the Qx curve is B, then the cumulative probabilities of selected events can be expressed as follows:

Note that α2 is the selected AEP for which Qxx must be estimated.
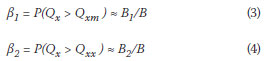
It should be noted that α1, α2, A1, A2 and A are within Qa sample space and β1, β2, B1, B2 and B are within Qx sample space.
It is reasonable to assume that the Qa curve and the Qx curve would coincide to the right of the Qxx value, because the Qxx value is a large and extreme value by definition. Thus:

Define f as the factor required to reduce A1 so that the Qa and Qx curves will approximately coincide to the right of the Qxm value. Thus:

or

From Figure 2 it is clear that f < 1,0. The Qxivalues represent record maximum flood peak values. Only one Qxi value is selected per station for the full observation period. It is therefore possible that there might be other Qai values that are also larger than Qxm but that are not the largest for a single station and thus do not qualify as Qxi values. That is why the Qx curve is shown below the Qa curve in Figure 2.
The equality of the proportions below follows from Figure 2 or Equations (5) to (7):

Substitute Equations (1) to (4) into Equation (8):

or

From the definition of the median:

thus

Equation (12) for β2 can also be obtained by using the theory of conditional probability (the above deduction is a simplified and illustrative version thereof). Equation (12) provides the necessary conversion to obtain the probability β2 in Qx space (Qxi data set) so that the value of Qxx can be determined by using the known (calculated) distribution characteristics of the variable Qx.
If it is assumed that Qx is log-normally distributed, then from the characteristics of the log-normal distribution:
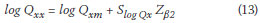
where
Zβ2 = standardised normal variate obtainable from normal distribution tables corresponding to β2
Slog Qx = standard deviation (SD) determined from the log Qxi data
In summary, the algorithm consists of solving Equations (1), (6), (12) and (13) consecutively. The value of Qxx is finally determined from Equation (13).
Inspection of Equation (13) shows that the value of log Qxx depends on three parameters: the first two, namely log Qxm and Slog Qx depend on the distribution of Qx alone. It is clear that the distribution of Qx dominates the magnitude of the calculated extreme flood peak Qxx. The third parameter, namely Zβ2 is related to the AEP of the median Qxm in Qa sample space and is determined mainly from the distribution of Qa in accordance with Equation (12). In this way the Qa data set (annual maximum flows) is utilised to help calibrate the AEP of Qxx.
It is recommended that the Qxi data be presented graphically to check that the lognormal model (or any other selected model) is indeed an appropriate model. In most cases investigated so far correlation coefficients better than 0,98 have been obtained, demonstrating that the log-normal model is indeed a good theoretical model for simulating the distribution of Qx. Only moderate extrapolation is required to estimate the magnitude of extreme flood peaks up to Q10 000 (in the sense that 50 data points with an observation period of 100 years each would represent 5 000 station years).
Application in cases where adequate or complete records of Qa are not available
Unfortunately, annual records covering adequate record lengths may not be available for all sites included in a catalogue of "record maximum flood peaks". In such cases the value of f cannot be determined from Equation (6) and the value of α1 cannot be determined from Equation (1).
The value of f could then be estimated from those sites that do have adequate annual records. It has been found that for inland sites in South Africa the value of f approaches 1,0. The calculated value for an extreme flood peak such as Q10 000 is not very sensitive to the f-value. For example, if the f-value is reduced from 1,0 to 0,8, the Q10 000 value reduces only by about 4%. Assuming f = 1 could then result in slightly conservative flood peak estimates in some cases.
To be consistent, the value of α1 (AEP of the median Qxm in Qa sample space) must also be determined from regionally integrated information. Equation (1) could be applied to those stations that do have adequate annual records, on condition that there are an adequate number of such stations available. Other methods could also be used to determine the AEP of the median, as long as they have a regional basis. It has been found that α1 values typically fall between 1/50 and 1/200, and could thus be calculated fairly reliably by using available regionally based methods.
EXAMPLE: ESTIMATION OF Q10 000 FOR ALBASINI DAM SITE
An example to demonstrate the procedures and calculation steps for estimating extreme flood peaks such as Q1 000 to Q10 000 for a specific site is given in Tables 3 and 4 and the final results are given in Table 5. Figure 3 demonstrates the excellent correlation between selected log Qxi values and the regression line on the log-normal probability scale.
It is always good practice to do sensitivity analyses. Sensitivity could, for instance, be tested by selecting only data from the eastern part of South Africa (in which the site under investigation is located), or by selecting only data from region 5,2 (in which the site is located) if enough data points were available. Sensitivity for the estimated value of the AEP of the median should also be tested as was done under item 6 in Table 3.
RESULTS OF SOME GENERALISED INVESTIGATIONS
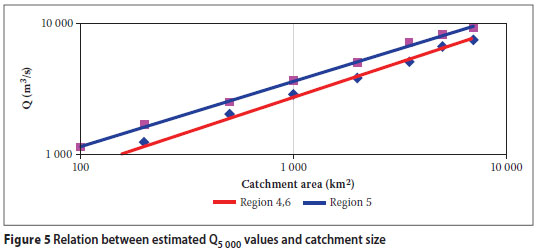
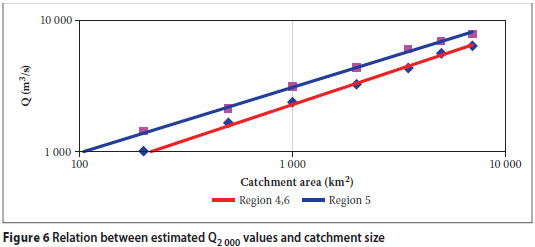
A number of different catchment sizes and hydrological regions have been analysed by means of the REFSSA method and the results are summarised in Table 6. The scope of the investigations was limited by the availability of verified data on extreme flood peaks. Consequently, the REFSSA method was tested only for South African regions 4,6 and 5,0 as demarcated by Kovács (1988) and for catchment areas between 100 and 7 000 km2.
Data were selected and handled as follows for the purpose of this investigation:
Record maximum flood peak data were selected from the catalogue as published by Kovács (1988) in accordance with the selection requirements as listed in Tables 1 and 2. Regions as demarcated by Kovács (1988) were used, but as amended below.
Data were selected from the RMF region in which the site under investigation falls, as well as from the adjacent RMF+Δ region which is one increment higher (more extreme). This conservative approach to the selection of data for a "similar hydrological region" was followed owing to statistical uncertainty (small sample sizes, short record lengths, inaccuracy of the source data and uncertainty regarding demarcation of boundaries). One could also argue that a storm event could blow over from the more extreme region to the less extreme region. This argument is supported by the record maximum flood peak data, which do not always abide by boundaries as demarcated.
The region in which a site under investigation falls was used for the calculation of the AEP of the median. Complete records of verified annual maximum flows were not readily available and the method used in the example in Table 3 (item 6) was used to estimate the AEPs of medians. Compared with site-specific analyses (e.g. the rational method), the above method appears to give conservative (higher) AEPs for the median in most cases. This would result in conservative estimates for extreme flood peaks. It was found that the results are not very sensitive to the value of the AEP of the median. The effect on the value of Q10 000 in the case of the above example when using an AEP of 1/40 or 1/80 in the place of 1/59 was less than 5%.
Where applicable, exceptionally low data points, which do not really represent extreme flood peaks and thus do not really comply with the definition of Qx were discarded. This reduced the absolute values of negative skewness coefficients to almost zero in most cases. Exceptionally low points have the undesirable effect of increasing the standard deviation, causing higher estimates for Qxx (e.g. Q10 000). Discarding low data points is considered to be compatible with the definition of Qx and the way in which the algorithm is constructed. In the same vein, in a few cases of high positive skewness, low data points were added to the data in order to reduce positive skewness to below 0,1. This latter action results in slightly higher estimates for Qxx, avoiding under-estimation of Qxx when using the log-normal model
Discussion of results in Table 6
The average correlation coefficient between actual log Qxi data and corresponding log-normal regression lines is 0,99 (and better than 0,98 in all cases if the sample size exceeds 25). The average correlation coefficients are the same for regions 4,6+ and 5,0+. The excellent correlation coefficients support the postulation that the estimation of the magnitude of extreme flood peaks should be based mainly on extreme flood peak data.
The skewness coefficients of selected log Qxi data are very low in most cases and significantly lower than those of natural Qxi data.
The above two points indicate that the selected Qxi data in the range of extreme flood peaks are generally log-normally distributed.
The average coefficient of variation cv (standard deviation divided by mean or SlogQx/log Qxm) for region 4,6+ is the same as that for region 5,0+ (namely 0,058). This indicates remarkable consistency. If cv (in terms of log Qx) can be accepted as a constant, this has an enormous impact on statistical certainty: calculations in one case with a sample size of 30 (not shown in Table 6) assuming cv is constant, reduced the one-sided 95% upper confidence limit for Q10 000 to 1,14(Q10 000) compared with 1,54(Q10 000) without the aforementioned knowledge.
The AEP of the RMF is not constant but varies from 1/879 to 1/2 877 for different catchment sizes and for different regions in Table 6. The average AEP of the RMF for region 4,6+ (1/1 071) is about double that for region 5,0+ (1/2 290).
The average AEP of the RMF+Δ for both regions is about 1/10 600 (not shown in Table 6).
The Q10 000/RMF ratio varies between 1,2 and 1,75. This is within the expectation of the SANCOLD Guidelines (1991) which state that PMF/RMF ratios exceeding 2,0 should not be accepted. In comparison, Görgens et al (2007b) found that for PMF values as calculated by the unit graph method of HRU (1972), the PMF/RMF ratio varies from 0,65 to 6,9 (for the same regions and range of catchment sizes considered in Table 6). The upper ratio exceeds all reasonable expectations. It is clear that the above PMF method produces unreliable results.
The estimated values for Q10 000 have not been exceeded by actual records in any of the analysed cases. In one case the estimated value for Q10 000 could have been exceeded, but the accuracy of the relevant record maximum flood peak (station K4, Goukamma River) is indicated as "unknown" and this record was therefore not used in the analysis. Estimated values for Q10 000 could have been exceeded in two additional cases if storm events had blown over from the adjacent, more extreme region. Kovács (1988) estimated the cumulative station years of independent flood peaks for the relevant regions and areas at approximately 6 700 station years. The probability that Q10 000 could have been exceeded during a record of 6 700 station years is estimated at roughly 49%. The estimated values for Q5 000 were equalled in one case and the estimated values for Q2 000 were equalled or exceeded in four cases. The probabilities that these flood peaks could have been exceeded during a record of 6 700 station years are estimated at roughly 74 and 97% respectively. The results of the REFSSA method seem plausible in view of the above probabilities. (However, it should be pointed out that the common probability equation P(Q>QT) = 1-(1-1/T)L - with L equal to the total observation period of 6 700 station years in the above case - for estimating the above probabilities is based on the Bernoulli sequence, which requires complete statistical independence of events, but this is not the case for hydrological data. The aforementioned probabilities are therefore rough estimates at best.)
Sensitivity analyses were done to compare the estimated values for Q10 000 in Table 6 with those obtained when using data from only region 5,0. It was found that combining regions 5,0 and 5,2 for data-selection purposes, as was done for Table 6, resulted in estimates for Q10 000 that are on average only 6% higher (varying between 0 and 20%) than when using data from only region 5,0. However, this preliminary finding could be inaccurate and biased because the sample sizes for region 5,0 alone were much smaller than when regions 5,0 and 5,2 were combined (25 compared to 35 on average).
Most of the assumptions made to produce Table 6 are considered to be slightly conservative. Consequently, the results in Table 6 should be regarded as slightly conservative for most of the cases at this stage.
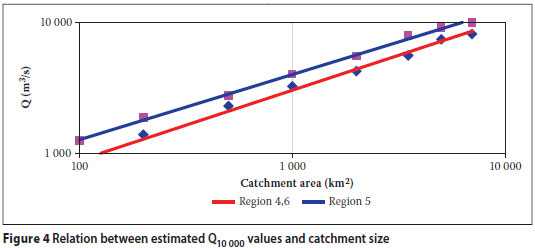
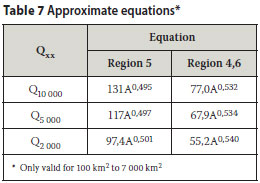
The estimated values for Q10 000, Q5 000 and Q2 000 in Table 6 are represented graphically against catchment size on logarithmic scales in Figures 4 to 6. Remarkably high correlation coefficients have been obtained between the estimated values and the regression lines (all better than 0,99). Approximate equations for these regressions lines are given in Table 7, but it is recommended that a complete analysis as shown in the example (Tables 3 to 5) be done for designs or safety evaluations of important projects.
CONCLUSIONS
The applicability of the REFSSA method has been demonstrated for the estimation of extreme flood peaks in two major hydrological regions in South Africa. Despite limitations with regard to the quality and quantity of available "record maximum flood peak" data, relatively high correlation coefficients have been obtained between transformed "record maximum flood peaks" and regression lines (0,99 on average on log-normal scale as given in Table 6). This indicates excellent reliability within the hydrological environment and supports the theoretical basis of the REFSSA method.
Because the REFSSA method is new, caution should be exercised. Data selection should be done carefully in accordance with the selection requirements proposed in this paper. Sensitivity analyses should always be done to test sensitivity, for instance by using only data closer to the site under investigation, but still within the "similar hydrological region". Sensitivity should also be tested by varying the AEP of the median.
Although the REFSSA method could currently be regarded as one of the better methods in South Africa for determining the magnitude and AEPs of extreme flood peaks larger than Q1 000, the following limitations should be borne in mind:
It is a regional method and would thus be more reliable for catchments with average catchment characteristics (corresponding to those of the source data).
An adequate number of relevant "record maximum flood peaks" of adequate accuracy must be available to do an analysis.
It is provisionally considered applicable for the estimation of extreme flood peaks between Q1 000 and Q10 000 and for catchment sizes between 100 and 7 000 km2.
RECOMMENDATIONS
The following further actions or investigations are recommended:
The catalogue of "record maximum flood peaks" as published by Kovács (1988) should be extended, updated and its accuracy improved as far as possible.
The applicability of the REFSSA method should be tested for all other regions in South Africa as has been done for regions 4,6+ and 5+ in Table 6 of this paper, after extension of the catalogue.
It should be investigated whether the REFSSA approach could also be employed to estimate extreme flood volumes from record maximum flood volumes.
The applicability of the REFSSA method for catchments smaller than 100 km2 and larger than 7 000 km2 should be investigated. Not enough verified data were available to do this investigation in the present study.
It is of critical importance that future flood events are accurately surveyed and documented.
ACKNOWLEDGEMENTS
Zoltan Kovács (1988) must be recognised for publishing a useful catalogue of verified "record maximum flood peaks" in South Africa. The catalogue was based on records, surveys, estimates and documents compiled by the Department of Water Affairs, other organisations and individuals and these efforts must be commended. Without this catalogue this paper would probably not have seen the light. My colleague Mr C L van den Berg is thanked for checking the algorithm for correctness. The anonymous reviewers are thanked for their valued comments. Permission by the Department of Water Affairs to publish this paper is gratefully acknowledged. It should be noted that the opinions expressed in this paper are those of the author and not necessarily those of the Department.
REFERENCES
Alexander, W J R 2000. Flood risk reduction measures. Pretoria: University of Pretoria, Department of Civil Engineering. [ Links ]
Alexander, W J R 2009. Mathematics vs pattern recognition in water resource studies. Civil Engineering, 17(5). [ Links ]
Cunnane, C 1988. Methods and merits of regional flood frequency analysis. Journal of Hydrology, 100. [ Links ]
Francou, J & Rodier, J A 1967. Essai de classification des crues maximales. Proceedings, Leningrad Symposium on Floods and their Computation, UNESCO. [ Links ]
Görgens, A 2003. Design flood hydrology. Unpublished lecture notes. University of Stellenbosch & Ninham Shand. [ Links ]
Görgens, A 2007a. Joint Peak-Volume (JPV) Design Flood Hydrographs for South Africa. WRC Report No 1420/3/07, Water Research Commission, Pretoria, South Africa. [ Links ]
Görgens, A, Lyons, S, Hayes, L, Markhabane M & Maluleke, D 2007b. Modernised South African Design Flood Practice in the Context of Dam Safety. WRC Report No 1420/2/07, Water Research Commission, Pretoria, South Africa. [ Links ]
HRU (Hydrological Research Unit) 1972. Design flood determination in South Africa. Report No. 1/72, Johannesburg: University of the Witwatersrand. [ Links ]
Kovács, Z 1988. Regional maximum flood peaks in southern Africa. Technical Report TR 137, Pretoria: Department of Water Affairs. [ Links ]
SANCOLD 1991. Guidelines on safety in relation to floods. Pretoria: SANCOLD. [ Links ]
Wiltshire, SE 1986a. Regional Flood Frequency Analysis I: Homogeneity Statistics. Hydrological Sciences Journal. [ Links ]
Wiltshire, SE 1986b. Regional Flood Frequency Analysis II: Multivariate Classification of Drainage Basins in Britain. Hydrological Sciences Journal. [ Links ]
 Contact details:
Contact details:
Department of Water Aff airs
Private Bag X313 Pretoria
0001 South Africa
Tel: 27 12 336 8010 Fax: 27 12 336 8674
e-Mail: nortjej@dwa.gov.za
 | JAN NORTJE (Pr Eng, Member SAICE) graduated in 1973 and obtained his Master's degree in 1993, both in civil engineering and at the University of Pretoria. He joined the Department of Water Affairs in 1972 and has since specialised in dam engineering covering various facets, including design, construction and planning of dams. Since 1987, when he joined the Dam Safety Office, he has been working in the dam safety engineering field. Determination of appropriate "safety evaluation floods" for dams is one of the major challenges in dam engineering and this is what has inspired the current paper. |














