Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
Journal of the South African Institution of Civil Engineering
On-line version ISSN 2309-8775
Print version ISSN 1021-2019
J. S. Afr. Inst. Civ. Eng. vol.52 n.2 Midrand Oct. 2010
TECHNICAL PAPER
Applications of response sensitivity analysis in earthquake engineering
C P Roth; M D Grigoriu
ABSTRACT
Response sensitivity analysis as a part of dynamic finite element structural analysis has many applications to structures of realistic scale and complexity in earthquake engineering. A demonstration project, consisting of a hospital structure and piping network, is used to demonstrate the potential applications of the method to practical problems. Nonlinear finite element analysis is done to determine displacements, stresses, etc, as well as sensitivity information by the direct differentiation method. The response sensitivity analysis is used for the identification of critical parameters of the systems, optimisation, calibration and the generation of fragility curves.
Keywords: sensitivity analysis, finite element analysis, seismic design, fragility curve
INTRODUCTION
The theory and implementation of response sensitivity analysis in dynamic structural analysis has been discussed by several authors (such as Zhang & Der Kiureghian 1993, Roth 2001, Conte 2001, Conte et al 2003). This paper illustrates potential earthquake engineering applications of the method to structures of realistic scale and complexity. A demonstration project, consisting of a hospital structure and associated piping network, is used to demonstrate the potential applications.
RESPONSE SENSITIVITY ANALYSIS PROBLEM STATEMENT
A dynamic earthquake engineering problem consists of a ground motion or input, which passes through the system, and results in an output such as a displacement response. Values for some of the parameters of the input and/or the system may be well known, while others may be uncertain. For example, the magnitude of the earthquake is highly uncertain and can be described probabilistically by seismic hazard analysis. Material parameters such as steel yield strength are less uncertain, but can also more accurately be described by probability distributions than by single deterministic values.
Let x be a vector whose elements consist of all of the uncertain parameters in both the input and the system. As the properties of the input and the system depend on x, the output u(t, x) will also be a function of x as well as time t. Response sensitivity analysis determines the effect on the output u of changing the parameters in x. It is useful to introduce a quantitative measure of the sensitivity of u to an arbitrary element xi of x. One fairly intuitive measure is the sensitivity factor, defined as the derivative of u with respect to xi and denoted by vi:
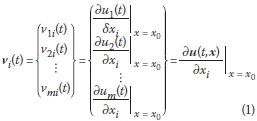
where x0 is the nominal value of x.
This paper will illustrate some of the practical uses of sensitivity factors defined in this manner.
GOVERNING EQUATIONS
The types of system under consideration are civil engineering structures such as buildings, piping systems and bridges. It will be assumed that the system is mathematically modelled by discrete elements. The model is characterised by a mass matrix m, a damping matrix c and a restoring force vector r, and is subjected to an applied load vector f. For linear elastic structures the vector r is simply ku, where k is the stiffness matrix. The definitions here are common in structural dynamics (Chopra 1995). It will be assumed that the mass matrix m is fixed, but that c, r and f may depend on uncertain parameters contained in x. For example, x may contain the damping coefficients and/or the yield stress of a material. The assumption that m is fixed is reasonable as it is typically easier to accurately determine the mass of a structure than it is to determine the damping, restoring force or applied load. For a general nonlinear structure r may also be a function of displacement u, velocity ú and certain path- or history-dependent variables, such as amount of plastic strain, which will be stored in vector z.
The governing equation of u with x at its nominal value x0 is:
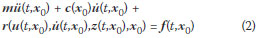
This is the equation that is solved by common existing structural dynamics programs to determine the displacement of a structure subjected to a ground motion. It is a seconddegree, nonhomogenous differential equation. For general nonlinear restoring force functions, it is also a nonlinear differential equation.
Several methods can be used to determine the sensitivity factors, with the direct differentiation method used here being one of the most suitable. By this method, the governing equation of vi is obtained by differentiating Equation (2) with respect to xi. After changing the order of differentiation with respect to t and xi and rearranging, it becomes:
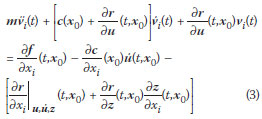
Equation (3) is similar in form to Equation (2) in that it is a second-degree, nonhomogenous differential equation. However, as the coefficients of  i,
i, 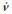 i and vi and the right-hand side of Equation (3) do not depend on vi, it is a linear differential equation with timevarying coefficients. This is true even if the structure is nonlinear in a structural engineering sense. Numerical methods are generally used to solve Equation (2). The Newmark method is one of the most commonly used methods. The same method can be extended to solve Equation (3) for the sensitivity factors (Roth 2001). The formulation given here is from Roth (2001) and is similar to that in Conte et al (2003). However, here the history-dependent variables z are explicitly included in the governing equation as this may be clearer to follow and to implement.
i and vi and the right-hand side of Equation (3) do not depend on vi, it is a linear differential equation with timevarying coefficients. This is true even if the structure is nonlinear in a structural engineering sense. Numerical methods are generally used to solve Equation (2). The Newmark method is one of the most commonly used methods. The same method can be extended to solve Equation (3) for the sensitivity factors (Roth 2001). The formulation given here is from Roth (2001) and is similar to that in Conte et al (2003). However, here the history-dependent variables z are explicitly included in the governing equation as this may be clearer to follow and to implement.
COMPUTER IMPLEMENTATION
The governing equations described in the previous section need to be implemented in computer software to allow the calculation of displacement and response sensitivity information for realistic systems. Two programs have been developed to perform the calculations:
1. a new MATLAB program that calculates both displacement and sensitivity factors, intended for a relatively simple, beam-element level of analysis; and
2. an existing finite element analysis program, DIANA, adapted with new subroutines to calculate the sensitivity factors, allowing more detailed analysis.
DEMONSTRATION PROJECT
A demonstration project will be used to illustrate some applications of the response sensitivity factors. The example chosen is a hospital in Buffalo, United States. Both primary and secondary systems in the hospital will be considered: the primary system is the hospital structure itself, while the secondary system is the piping system that supplies water for fire suppression.
Ground motion
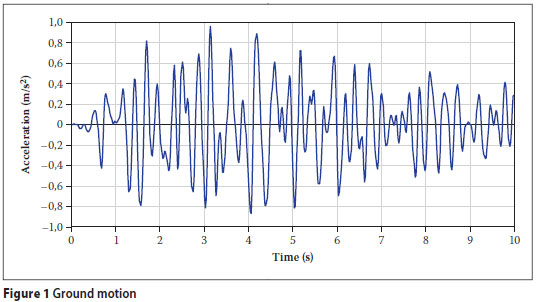
As insufficient real earthquake records exist for the Buffalo area, artificial motions are used as the input ground motions to the primary system. The ground motions are realisations of a Gaussian stochastic process with the amplitude modulated through time by an envelope function. The power spectral density g(ω) of the process is based on the specific barrier model for simulating earthquake ground motion (Papageorgiou & Aki 1983). Required parameters are the moment magnitude M and distance r of the earthquake event causing the motion, and the average soil shear wave velocity to a depth of 30 m at the site, V30. The values selected are M = 6, r = 50 km and V30 = 255 m.s-1. This magnitude-distance pair has a return period of 10 000 years at the site. The average shear wave velocity is for a typical soil.
To illustrate the use of the sensitivity factors, only one ground motion sample will be considered (Figure 1). However, for real analysis, design or selection of retrofit strategies, a suite of ground motions should be used. Each ground motion in the suite can be used in the same manner as the single ground motion used here, and all the results considered when making the necessary decisions.
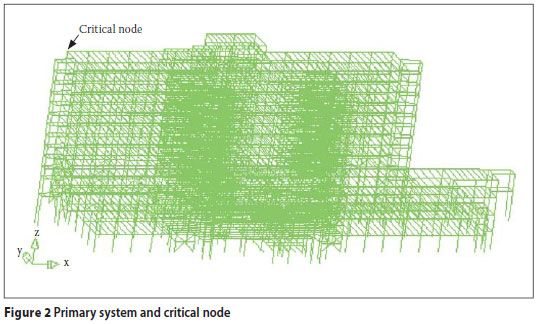
Primary system
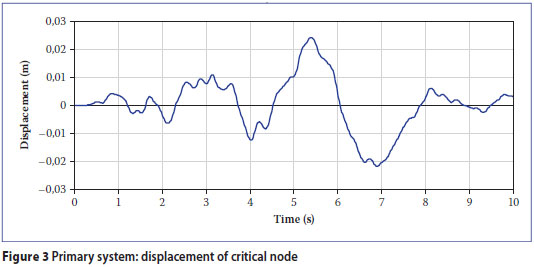
The hospital is a 14-storey steel frame structure. A DIANA computer model of the structure with 10 678 beam elements was prepared for the analysis. Figure 2 shows the model and the location of a node on the roof selected as the critical node. This node was selected as peak roof displacement in an earthquake can be used as an indicator of damage suffered by the building. Suggested maximum values are provided by the Federal Emergency Management Agency (2009). The calculated displacement of the critical node is shown in Figure 3. Rayleigh damping of the form c = am + bk was used for the analysis, where k is the initial global stiffness matrix.
Secondary system
The secondary system is the hospital fire suppression piping system. It is a steel piping system that runs from a tank in the basement to a standpipe on the roof. On floors 6 to 14, branches split off from the main riser pipe to supply water to ceiling-mounted sprinklers in the hospital wards. To reduce the size of the model, only two of the branches were analysed: the branch on the top floor, where the maximum displacement and damage to piping is expected (OSHPD 1995), and the branch at a typical intermediate floor. The system is shown in Figure 4. It was modelled in MATLAB using linear pipe elements for the straight pipe runs and nonlinear elbow hinge elements for the pipe elbows. The assumed boundary conditions were:
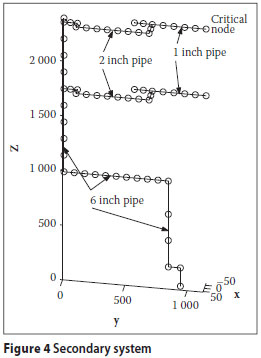
Tank: The pipe was assumed to be fully fixed to the tank on the basement level.
Pipe clamps: The vertical pipe sections were assumed to be attached to the primary system at each floor by means of pipe clamps constraining translation of the pipe in all directions.
Pipe hangers: The horizontal pipes were assumed to be suspended from pipe hangers from the floor beams. The pipe hangers provide only vertical support.
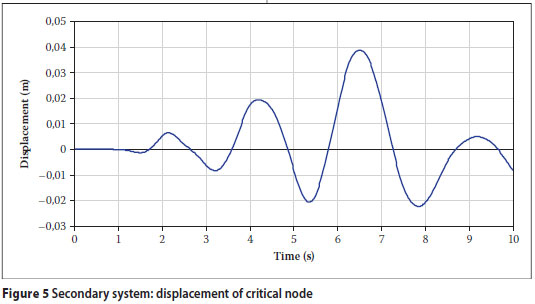
The input to the secondary system is the motion of the hospital structure. As the structure does not move as a rigid body, the motion is different at each support point of the secondary system. The motions were determined from the time-history analysis of the primary system. The critical output was assumed to be the relative displacement between the structure and the pipe at the critical node indicated in Figure 4. This output was selected as sprinkler damage due to relative motion between the pipe and hard ceilings was found to be a common problem for hospital piping systems in the Northridge earthquake (Ayres and Ezer Associates 1996). The relative displacement is plotted in Figure 5.
IDENTIFICATION OF CRITICAL PARAMETERS
The effect of a small change in the parameter values can be approximated using the sensitivity factors and a first-order Taylor expansion. If xi is varied by a small amount Δxi, then:
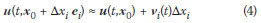
where ei is the i-th unit vector.
A critical parameter is one for which the product of the sensitivity factor (vi) and the uncertainty or variation in the parameter (Δxi) is large. The uncertainty in a parameter value is the amount by which the value may reasonably be expected to vary from the nominal value. It is clear from Equation 4 that the critical parameters will have the greatest influence on the response. These parameters need to be determined accurately for satisfactory modelling of the system. They should also be considered first when selecting optimum retrofit strategies.
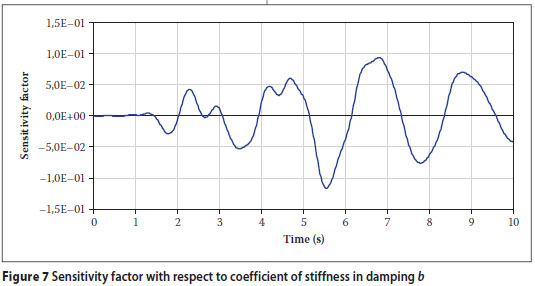
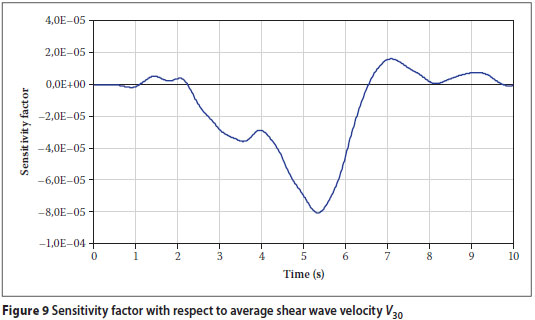
Consider the primary system. Suppose that we wish to evaluate which of the following parameters are more critical to the displacement of the critical node: the Young's modulus E of the steel sections in the structure, the coefficient b of the stiffness matrix in the specification of Rayleigh damping, the earthquake magnitude M, or the soil shear wave velocity V30. The sensitivity factors for the displacement of the critical node with respect to each of the parameters were calculated by DIANA and are shown in Figures 6 to 9. The assumed uncertainties in the parameter values for the demonstration project are described below.
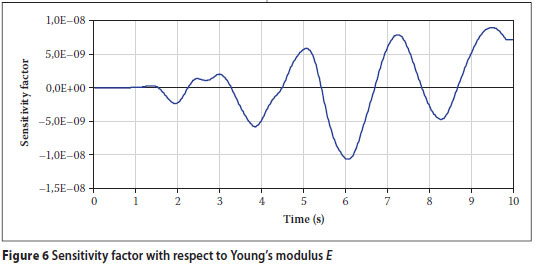

The Young's modulus E of the steel is usually known within 3% (Mirza & MacGregor 1979).
The damping of the structure is less accurately known. An uncertainty of 20% is assumed (Chopra 1995).
The average soil shear wave velocity V30 can typically only be estimated within 20% given the soil conditions at the site.
The earthquake magnitude M is highly uncertain. However, for illustration an uncertainty of 20% is assumed.
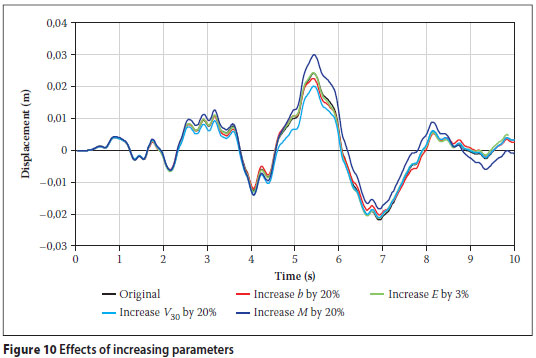
The effects on the displacement of the critical node of increasing the parameters by the assumed uncertainties are shown in Figure 10. The figure suggests that the output is more sensitive to the input parameters V30 and M than to the system parameters E and b. Without the use of response sensitivity analysis, preparing this graph would require a separate time-history analysis for each uncertain parameter, whereas using the sensitivity factors, only one time-history analysis is required. The information can be used to determine which parameters should be changed to improve the safety of the building.
Another way of presenting the same information about the parameters is to consider them to be random and to calculate the contribution of each to the variance of the response. Using upper case letters for random variables, assume that the parameter vector X is a random vector with mean µx and that element Xi has variance 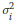 , i = 1,2,3,...,m. Using the generalised first-order Taylor expansion for a general displacement uj,
, i = 1,2,3,...,m. Using the generalised first-order Taylor expansion for a general displacement uj,
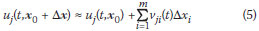
it can be shown that the variance of uj can be approximated by
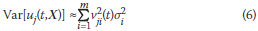
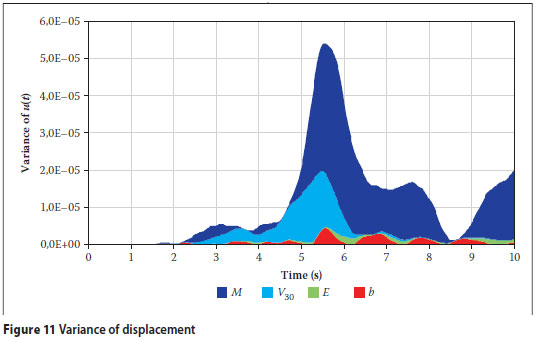
provided that the nominal parameter vector value at which the sensitivity factors are calculated is equal to the mean µx and the variables are uncorrelated. One possible assumption about the coefficients of variation of the random parameters is that they are the same as the uncertainties defined previously, that is, 0,03 for E, 0,2 for b, 0,2 for V30 and 0,2 for M. This assumption is followed here. Figure 11 shows the variance of the displacement of the critical node, calculated by Equation 6. The total variance is subdivided into different bands showing the contribution of each term on the right side of Equation 6 to the total. A critical parameter is one which has a large contribution to the total variance. Examination of Figure 11 shows that the earthquake magnitude M is the most critical parameter. Among the system parameters, it is clear that b is more critical than E.
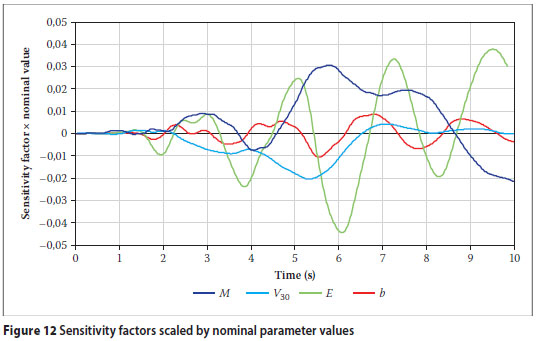
It should be noted that one other method of comparison that has been suggested is to multiply the sensitivity factors by the nominal parameter values (Zhang & Der Kiureghian 1993). This is shown in Figure 12. The result is a factor that indicates the sensitivity of the output to changes in the percentage of the parameter values. For example, if the factor in Figure 12 with respect to b is larger than that with respect to E, this indicates that the output is more sensitive to a 1% change in b than to a 1% change in E. In fact, multiplying the factor by 0,01 gives an estimate of the difference between the original displacement and the displacement found after changing the parameter value by 1%. However, this method of comparison is valid only if the uncertainty in the parameter value is the same percentage of the nominal value for each parameter. In general, the uncertainties in the parameters are very different so the method is not valid. For example, in this case a reasonable uncertainty in E is 3% while a reasonable uncertainty in b is 20%.
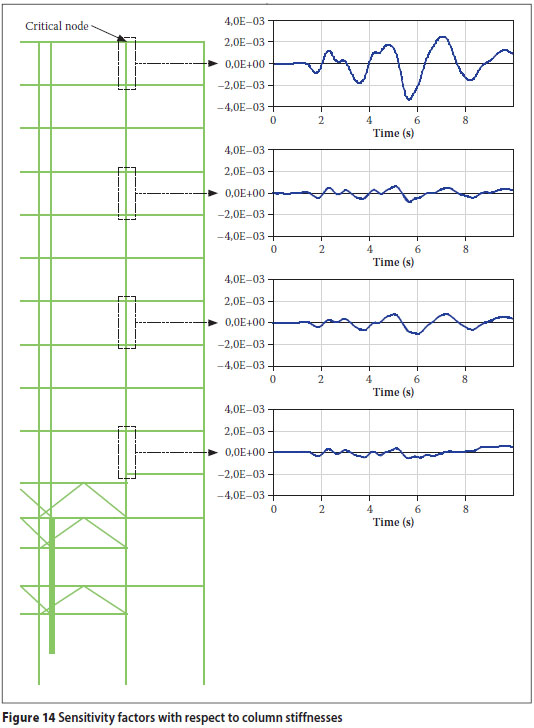
The sensitivity factors can also be used to identify the most critical elements of the system. Consider the line of columns in Figure 13. It may be useful to identify the column in that line to which the critical displacement is most sensitive. This information can be used to select columns for retrofit, to improve the design, or just to give insight into the behaviour of the structure. The sensitivity factors with respect to the initial stiffnesses of four of the ten columns are plotted in Figure 14. Interestingly, the roof displacement is most sensitive to the stiffness of the top column. It appears to be roughly equally sensitive to the stiffnesses of the two columns in the middle, and less sensitive to the stiffness of the bottom column.

OPTIMISATION AND CALIBRATION
Among the most useful applications of the sensitivity factors are the calibration of the parameters of the structural model to match experimental data, or the selection of an optimal value of one of the parameters. Both tasks can be accomplished by nonlinear programming methods. To formulate the problem, consider a scalar objective function of the displacement of the structure, g(u(t,x)). We wish to find the value of x that minimises the value of this function. This can be accomplished by a suitable nonlinear programming algorithm. Such algorithms are typically iterative, starting at a given point in x-space and at each iteration taking a "step" in a direction such that the objective function is reduced. Different algorithms use different methods to select the direction and size of the "step", and often use the gradient of g with respect to x. The iterative nature of the algorithm means that g(u(t,x)) will have to be evaluated at several values of x before the minimum is found. Each evaluation requires a time-history analysis of the system, which may be time-consuming. The usefulness of the sensitivity factors is in calculating the gradients of g with respect to x, which otherwise have to be calculated by finite difference methods requiring additional evaluations of g(u(t,x)).
As an example of a typical objective function, consider the common problem of calibrating a simple computer model of a structure against either experimental data or data from a more accurate but also computationally intensive model. More specifically, the problem is to find values of the parameters of the simple model so that the calculated timehistory of displacement of a selected degree of freedom of the structure, say uj(t), 0 < t < τ, matches a given time history η(t), 0 < t < τ. A commonly used objective function for this problem is the integral of the square of the difference between the two time histories:
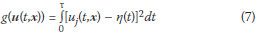
Minimising this objective function will tend to draw uj(t,x) closer to η(t) over the whole period under consideration.
The derivative of g is given by
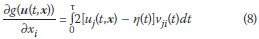
A second typical objective function is often found in seismic retrofit problems. The problem is to find the parameter values that minimise the peak absolute value of the displacement of a critical degree of freedom. The objective function for this problem is:
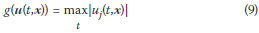
The derivative of g is:
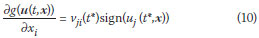
where
t* = arg maxt|uj(t,x)|, the time at which the maximum displacement occurs.
Consider the secondary system. Suppose that the peak displacement of 39 mm in Figure 5 is too high and that a suitable retrofit strategy has to be found to reduce the displacement. One possible strategy is to replace the rigid pipe clamp connections between the structure and the riser section of the pipe by snubbers. Snubbers are hydraulic or mechanical devices used as flexible supports for piping systems. A snubber can be modelled as a spring and a dashpot in series; however, for simplicity it is modelled here as a spring (Sharma et al 1985). For design, the spring stiffness that minimises the displacement of the critical node needs to be determined. This is an optimisation problem that can be solved using the sensitivity factors and the objective function in Equation 9. A nonlinear programming algorithm, the BFGS method, is included in the MATLAB program used to analyse the piping system. After 12 steps the routine indicates that the optimum stiffness is 560 N/m, which reduces the peak displacement from 39 to 16 mm.
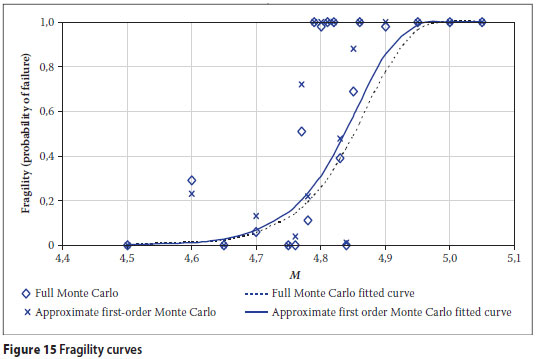
FRAGILITY CURVES
Consider a system with random properties subjected to a random input motion, and a failure criterion that determines if the response of the system to the input is satisfactory. Fragility curves are used to indicate the safety of the system as a function of the size of the input. More specifically, the curves show the probability that the system response exceeds the failure criterion, or in other words the system failure probability, as a function of a parameter or parameters of the input.
This section illustrates the generation of fragility curves for the secondary system. The failure criterion assumed is a relative Y-direction displacement of the critical node of 45 mm. The system parameters are assumed to be random and are stored in vector X. The random input motion is again a Gaussian process with a power spectral density from the specific barrier model. The parameters of the power spectral density are the magnitude M and distance r of the earthquake event causing the motion, and it is logical to plot the fragility curves as a function of both M and r. However, to illustrate the method it will be assumed that the distance r is fixed at 50 km and the fragility curves will be plotted against magnitude M.
One possible procedure for generating the fragility curve is the following, referred to here as the full Monte Carlo method:
1. Select a value of M.
2. Generate one sample of the input and a predetermined number Ns of samples of the parameter vector X.
3. Perform a time-history analysis of the primary system using the generated input sample.
4. Perform a time-history analysis of the secondary system using one of the samples of the parameter vector X, and the results from the primary system analysis. Check the failure criterion for the secondary system.
5. Repeat step 4 for each of the Ns samples of X.
6. If the number of failures in the Ns samples is Nf, the probability of failure at this value of M is approximately Nf/NS.
7. Repeat steps 2 to 6 for several different values of M.
8. Fit a regression curve through the resulting points. The curve must be monotonically increasing over the range [0, 1].
The probability of failure at each M value is conditional on the particular ground motion realisation used. However, a different realisation is used at each M value, so the final fitted fragility curve will reflect the average probability of failure of all of the realisations.
An alternative method using the sensitivity factors, referred to here as the approximate first-order Monte Carlo method, replaces steps 4 to 5 with the following:
4a. Perform a time-history analysis of the secondary system using the mean value µx for the parameter vector X, and the results from the primary system analysis. Calculate the sensitivity factors as well as the displacement.
4b. Calculate u(ti,x)
u(ti,µx) + v(ti)(x-µx) for i = 1,2,3,... for one of the samples x of X and check the failure criterion after each step.
5. Repeat step 4b for each of the Ns samples of X.
The system parameters that are assumed to be random are the diameter and Young's modulus of the pipes, and the damping. The coefficients of variation used are 0,2 for the pipe diameters, 0,06 for the Young's modulus and 0,5 for the damping.
The fragility curves calculated by the full Monte Carlo and approximate first-order Monte Carlo methods are shown plotted against M in Figure 15. Fragility curves of the following form were fitted by the weighted least squares method:

where y is the fragility, and a and b are regression constants.
In Figure 15, the curves generated by the full Monte Carlo and approximate first-order Monte Carlo methods are reasonably similar and the approximate curves may be accurate enough for most applications.
The curves indicate the failure probability of the system. For example, at M = 4,8 the probability of failure is 0,3 while at M = 5,0 it is 1,0, indicating that the system will almost certainly fail in an M = 5,0 earthquake.
The advantage of the approximate method is in the time taken. To illustrate the order of magnitude difference, the total time required for a 256 MHz computer to complete the calculations was less than one minute for the approximate method compared with two days for the full Monte Carlo method.
CONCLUSIONS
Response sensitivity analysis has many practical applications in earthquake engineering. The use of the method has been demonstrated here for structural (primary) and piping (secondary) systems. Critical parameters of the system can be identified after only one analysis. Optimisation of parameter values and calibration of models can be done in fewer steps than with traditional methods. Fragility curves indicating the safety of the system can be generated. The response sensitivity analysis allows the determination of results in less time than other traditional methods.
REFERENCES
Ayres and Ezer Associates 1996. Northridge Earthquake Hospital Water Damage Study. Los Angeles. [ Links ]
Chopra, A 1995. Dynamics of structures: Theory and applications to earthquake engineering. Englewood Cliffs: Prentice-Hall. [ Links ]
Conte, J 2001. Finite element response sensitivity analysis in earthquake engineering. Earthquake Engineering Frontiers in the New Millenium. Spencer & Hu/Swets & Zeitlinger: Lisse, Netherlands, pp 395-401. [ Links ]
Conte, J, Vijalapura, P & Meghella, M 2003. Consistent finite-element response sensitivity analysis. Journal of Engineering Mechanics, ASCE, 129: 1380-1393. [ Links ]
Federal Emergency Management Agency 2009. NEHRP recommended seismic provisions for new buildings and other structures (FEMA P-750). Washington DC. [ Links ]
Mirza, S & MacGregor, J 1979. Variability of mechanical properties of reinforcing bars. Journal of the Structural Division, ASCE, 105: 921-937. [ Links ]
OSHPD (Office of Statewide Health Planning and Development) 1995. The Northridge earthquake: A report to the Hospital Building Safety Board on the performance of hospitals. Sacramento, US. [ Links ]
Papageorgiou, A & Aki, K 1983. A specific barrier model for the quantitative description of inhomogeneous faulting and the prediction of strong ground motion. Bulletin of the Seismic Society of America, 73: 693-722. [ Links ]
Roth, C 2001. Sensitivity analysis of dynamic systems subjected to seismic loads, PhD thesis, School of Civil and Environmental Engineering, Cornell University. [ Links ]
Sharma, G, Manna, M, Ghosh, G & Chatterjee, S 1985. Seismic analysis of main primary heat transport system for the Kakrapar Atomic Power Project. Proceedings, 8th International Conference on Structural Mechanics in Reactor Technology, K: 229-234. [ Links ]
Zhang, Y & Der Kiureghian, A 1993. Dynamic response sensitivity of inelastic structures. Computer Methods in Applied Mechanics and Engineering, 108: 23-36. [ Links ]
 Contact details:
Contact details:
Department of Civil Engineering, University of Pretoria
Pretoria, 0002, South Africa
Tel: 27 12 420 2185
e-Mail: chris.roth@up.ac.za
Contact details:
Dept of Civil & Environmental Engineering Cornell University
Ithaca, New York, 14853
United States of America
Tel: 1 607 255 3334
e-Mail: Mdg12@cornell.edu
 | CHRIS ROTH (PrEng, Member SAICE), is Associate Professor in Civil Engineering at the University of Pretoria, working in the discipline of structural engineering. He started his career in consulting engineering before joining the University of Pretoria. He obtained a BEng degree in civil engineering at the University of Stellenbosch, and an MS and PhD at Cornell University in Ithaka, New York, USA. His interests are in structural reliability and structural analysis. |
 | MIRCEA GRIGORIU is Professor of Civil Engineering at Cornell University in Ithaca, New York, USA. He joined Cornell's structural engineering faculty in 1980 after several years of professional practice and research in Romania, Venezuela, Canada and the United States. His research interests are in structural dynamics, random vibration, system reliability, stochastic mechanics, fracture mechanics and applied probability. He is a member of numerous professional organisations. |














