Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
Journal of the South African Institution of Civil Engineering
On-line version ISSN 2309-8775
Print version ISSN 1021-2019
J. S. Afr. Inst. Civ. Eng. vol.52 n.1 Midrand Apr. 2010
Partial factors for selected reinforced concrete members: background to a revisionof SANS 10100-1
M Holický; J Retief; J Wium
ABSTRACT
The application of Eurocode EN 1992-1-1 in revising the South African standard for structural concrete design SABS 0100-1:1992 will require the determination of partial factors in accordance with the reliability requirements of the revised South African loading code SANS 10160:2010. The partial material factors γs for steel and γc for concrete are proposed in analysing the reliability of reinforced concrete slabs and short centrically loaded columns. It appears that the partial factors γs = 1,10 and γc = 1,40 are a suitable set of factors to be considered in the foreseen revision of the code. Further research is required on the model uncertainty for different structural members (flexural members, shear, columns, walls) and the theoretical models of basic resistance variables related to quality control.
Keywords: concrete reliability, partial factors, concrete design, flexural resistance, column resistance
INTRODUCTION
The South African Code of Practice for the design of reinforced concrete structures SABS 0100-1:1992 was initially formulated by using as reference document the British Code of Practice for the Structural use of Concrete BS 8110: Part 1: 1985. Apart from small corrections issued in subsequent amendments (1994 and 2000) no major revision of the Code has been done. The British Code (BS 8110) has recently been replaced by Eurocode EN 1992-1-1, which is an indication that a revision of the South African code is much needed.
A process therefore commenced in 2007 when a working group was established under the initiative of the Cement and Concrete Institute to consider the actions needed for a revision of SABS 0100-1:1992. A decision was made in principle that Eurocode EN 1992-1-1:2004 would be used as reference document. The decision was based on the fact that this code contains the most recent research and developments in the field of reinforced concrete design, and it forms part of a much larger suite of harmonised codes. This large suite of codes enables an integrated approach across different materials and includes a well-formulated part on the basis of design and loadings. Furthermore, the revised South African Loading Code (SANS 10160:2010), which is presently in the final stages of being published, has been formulated using Eurocode EN 1990:2002 and the relevant parts of EN 1991 as reference standards.
This paper presents the results of a reliability-based approach to define values for steel and concrete resistance variables (material factors) which can be used in the revised concrete design code. The approach which is followed assumes that the partial factors of resistance variables are limited to material strengths alone, while other basic variables related to resistance, such as geometry, are not explicitly factored.
Theoretical models are used in the study based on assumed uncertainty for basic variables which include geometry values. These assumptions should be linked to production quality and need to be verified for the South African market.
Although results show that different partial factors could be used for different structural member types, this would not be a practical design approach. Values are therefore proposed that would be valid for any structural member type albeit on the conservative side for some cases.
RELIABILITY ASSESSMENT
The reliability basis of structural design formulated in ISO 2394:1998 General principles on reliability for structures (also issued as SABS 2394:2004) is developed into operational procedures for the determination of partial factors for actions and resistance in Eurocode EN 1990:2002 Basis of structural design. General guidelines for reliability analysis procedures are provided in EN 1990:2002 Annex C (Informative) Basis for partial factor design and reliability analysis. Additional information on EN 1990:2002 is also given by Gulvanessian et al (2002), including background on its reliability basis.
Reliability basis for South African structural standards
With the publication of SABS 0160:1989 it was envisaged that the application of the principles of reliability to derive proper specifications for the treatment of loads or actions on structures should be followed by similar treatment of structural resistance by the following versions of the materials design codes. The South African National Conference on Loading (SAICE 1998) made it clear that such development for concrete design was not done (Retief et al 2002). One of the objectives of the revision of SABS 0100-1:1992 should therefore be to provide an appropriate reliability basis for the stipulated design procedures.
SANS 10160:2010 Part 1 Basis of structural design provides the requirements not only for the actions on structures as stipulated in subsequent Parts, but also for structural resistance. Since these requirements were largely derived from Eurocode EN 1990:2002, the wealth of reliability investigations and procedures done against the background of the development of the Eurocode (e.g. Holický & Marková 2003; Holický & Holická 2004) could assist in providing useful guidance also for South African conditions and requirements.
A critical reliability feature of the Eurocode is that allowance is made for the national selection of reliability performance levels, typically as expressed by target reliability levels in calibration studies. Provision for the appropriate performance levels required by SANS 10160-1:2010 is therefore an essential component of the reliability assessment of the revision of SABS 0100-1:1992.
Reliability calibration
Reliability calibration for partial factor limit states design consists of the derivation of a set of partial factors that would ensure sufficient reliability of structural performance across the scope of application. Structural performance can be expressed in terms of a reliability model g(X) as a function of probabilistic or basic variables X.
Reliability requirements for resistance
The aim of the submitted study is to analyse partial factors for resistance variables of reinforced concrete structural members. It is assumed that the overall reliability level of structural members, described by the reliability index β may be split into the resistance part, expressed by the resistance index βR= αR β and the load effects part, expressed by the load effect index βE = - αE β (EN 1990:2002). Here αR and αE denote FORM (First Order Reliability Method) sensitivity factors (the values αR = 0,8 and αE = 0,7 are recommended in Eurocode EN 1990:2002). Consequently, suitable combinations of the partial factors may be identified by the reliability analysis of the resistance part without simultaneous consideration of the load effects. A value of β = 3,0 is used in the present South African Loading Code SABS 0160:1989, and is maintained in the revised standard in SANS 10160-1:2010. It is then sufficient to require that the resistance index βR should be close to its target value βRt= 0,8 × 3,0 = 2,4 corresponding to the recommendation of SANS 10160-1:2010, thus:

The resistance index βR is given by the probability PR = P{R(X) < Rd (Xk, γ)} of the resistance R(X) being less than the design resistance Rd(Xk, γ), where X denotes the vector of basic variables, Xk the vector of their characteristic values and γ the vector of the relevant partial factors. The mutual relationship between the probability PR and the resistance index βR is given as:
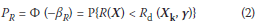
In Eq (2) Φ() denotes the distribution function of the standardised normal distribution. It follows from Eq (2) that the appropriate limit state function to be used in reliability analysis can be written in the form:
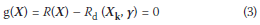
Reliability of structural concrete resistance
In the following, Eq (2) and the limit state function, Eq (3), are applied to analyse the resistance of reinforced concrete structural members. Well-established methods of structural reliability are used (probability integration and approximate analytical First Order Reliability Method (FORM)).
The design resistance Rd(Xk, γ) is a deterministic value dependent on the characteristic values Xk and the partial factors γ. The resistance can be determined using common design formulae given for example in SANS 10160-1:2010 and EN 1992-1-1:2004. As a rule, two partial factors γs and γc for reinforcement and concrete strength are commonly applied in design formulae, in which case the vector γ consists only of these two components. In this study the partial factors γs and γc are assessed using reliability analyses of two different reinforced concrete members, slab and column, as representative examples of flexural and compressive structural members. A slab was chosen as the representative bending member rather than a beam in view of the fact that the resistance of a slab is less reliable than that of a beam due to the important influence of concrete cover versus element depth for a slab.
However, in the case of the resistance of reinforced concrete structural members, the sensitivity factors of steel and concrete strength may be (in the case of flexural members) considerably less significant than the sensitivity factors of other variables (for example resistance uncertainty and some geometric data). Consequently the theoretical partial factors, derived from the design point (determined using the FORM method), generally differ from the partial factors applied to steel and concrete strength in design. Thus from the theoretical point of view, this oversimplification of using two partial factors only is somewhat simplistic and may lead to conservative design values.
Two different approaches to the analysis of the resistance of reinforced concrete structural members based on Eq (2) and (3) are applied in the following analysis:
a) Direct determination of the probability PR or index βR for given X, Xk and γ
b) Inverse determination of the partial factors γ for given PR or βR, X and Xk.
The straightforward approach a) provides a good overview of the variation of the probability PR or index βR with the partial factors γ and other parameters. The inverse approach b) provides particular values of the partial factors γ complying with the required reliability level (the probability PR or index βR) for given parameters (e.g. reinforcement ratio). Commercially available software (e.g. COMREL and the FORM method) may be effectively used in approach a). Both approaches are incorporated in specialpurpose software tools (based on probability integration methods) developed using the mathematical software MATHCAD.
THEORETICAL MODELS OF BASIC VARIABLES
Theoretical models of basic variables describing a slab and a column ( fc, fy, αcc, h, a, b, As and model uncertainty θR) are given in Table 1, where the symbols are defined. Conventional models of basic variables provided in working documents of JCSS (2002) are mostly accepted. In general, however, theoretical models of basic variables (including model uncertainty) should be linked to production quality and available data. In particular, the model uncertainty θR seems to be a very important basic variable significantly affecting the resulting reliability.
The following abbreviations are used in Table 1: LN for lognormal (two parameter), N for normal, GA for gamma distribution and DET for deterministic quantity. The theoretical models may be denoted by an abbreviation followed by the mean an standard deviation in brackets, for example the resistance uncertainty θR is described as LN(1,00; 0,05) in the case of slabs and LN(1,00; 0,10) in the case of columns.
European steel characteristics were used in the study. It can be shown that using local South African steel characteristics will have a negligible effect on the results (see Figures 9 and 10 and the related discussion below). Note that the mean values of the strength of concrete and steel equal to the characteristic values plus two times the standard deviation (Xk + 2 σX) are greater than the theoretical means (Xk+1,65σX) corresponding to the characteristic values Xk being equal to the lower 5% fractiles of the strengths. This is a common consequence of the sample inspection of the strengths.
It is also well known that in general the model uncertainties may significantly affect the resulting reliability. Although the working material from JCSS (2002) gives values as high as 1,2 for the mean value of modelling uncertainty, the theoretical models given in Table 1 have means equal to unity in order to avoid biased results and differ only in the coefficients of variability (0,05 for slabs and 0,10 for columns). However, the models indicated in Table 1 should be modified whenever convincing data are available. Note that the characteristic values of the model uncertainties θR are 1 and are consequently not explicitly considered in design formulae.
REINFORCED CONCRETE SLAB
The partial factors for resistance variables are assessed by analysing the probability of the design value Rd (Xk, γ) being exceeded by the random resistance R(X). In the case of a reinforced concrete flexural member (a beam or slab) exposed to a bending moment, this probability can be analysed considering the limit state function (1) and given as:
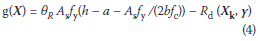
The design resistance Rd (Xk, γ) in Eq (4) is given by the partial factor method in Eq (5):
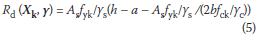
The characteristic values of the basic variables are used together with the partial factors. In this case, only two partial factors of material properties γs and γc for steel and concrete strength respectively are commonly used. The remaining variables As, h, a and b are considered by their mean (nominal) values, that is, they are not factored. It should be noted that strictly speaking the resistance model (Eq (4)) is only valid for ρ approximately < 1,2% as specified in standard procedures, to ensure ductile failure of under-reinforced sections.
Previous experience (Holický & Retief 2005; Holický et al 2007) shows that in the case of reinforced concrete members the resistance index βR is dependent on the basic variables including the model uncertainty θR and on the reinforcement ratio ρ. Figure 1 shows the variation of the resistance factor βR with the reinforcement ratio ρ for selected partial factors γs and γc.
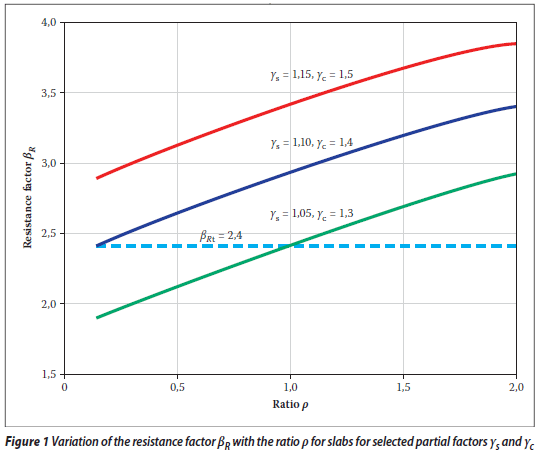
Figure 1 indicates that the resistance index βR is dependent on the reinforcement ratio ρ. It appears, however, that the target resistance factor βR = 2,4 is achieved for all reinforcement ratios ρ > 0,2 % when the combination of partial factors γs= 1,10, and γc= 1,40 is used in the design.
Figure 2 shows the results of inverse analysis when the partial factor γc is derived for selected factors γs from the given reliability level βRt = 2,4.

It follows from Figure 2 that for γs = 1,10 the partial factor γc would be almost independent of the reinforcement ratio ρ and for ρ> 0,5%, and could even be equal to unity, γc ≈ 1.
REINFORCED CONCRETE COLUMN
A short reinforced concrete column exposed to a centric load may be described by the general limit state function (1) in the following form:
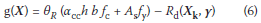
The design resistance Rd(Xk, γ) in Eq (6) is given by the characteristic values of the basic variables and appropriate partial factors:
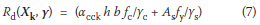
Similarly as in the case of a slab, only two partial factors of the material properties γs and γc for steel and concrete strength fy and fc are applied. The remaining basic variables αcc, As, h and b are also considered by their mean (nominal) values (not factored).
An analysis of a short reinforced column exposed to a centric load is graphically depicted in Figures 3 and 4. The resistance index βR seems to decrease with increasing reinforcement ratio ρ (see Figure 3). This is exactly the opposite trend to the case of a reinforced concrete slab. In general, similar to the case of a slab, the resistance index βR and the partial factors γs and γc are dependent on the reinforcement ratio ρ.
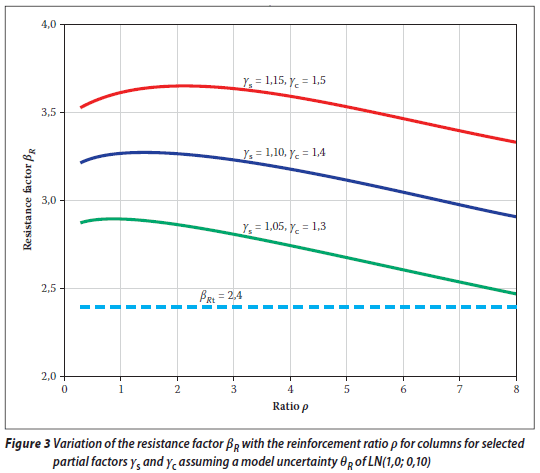
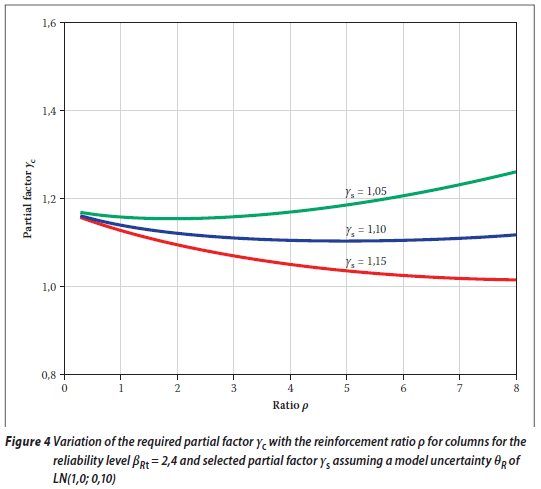
Figure 3 indicates that all the combinations of the partial factors considered (including the combination γs = 1,10 and γc= 1,40) are fully satisfactory for all reinforcement ratios ρ.
It appears that for γs = 1,10 the partial factor γc would again be almost independent of the reinforcement ratio ρ and could be equal to about γc ≈ 1,15.
Reinforced concrete column with increased uncertainty
The variability of the model uncertainty θR in reinforced concrete columns may in some cases be greater than the model LN(1,0; 0,10) indicated in Table 1. It may be a consequence of insufficient quality control and poor workmanship. In order to assess the sensitivity of the reliability of columns to the variability of model uncertainty, the coefficient of variation is increased from 0,10 to 0,15. Figure 5 shows the variation of the resistance factor βR with the reinforcement ratio ρ for selected partial factors γs and γc assuming the uncertainty θR described by the theoretical model LN(1,0; 0,15).
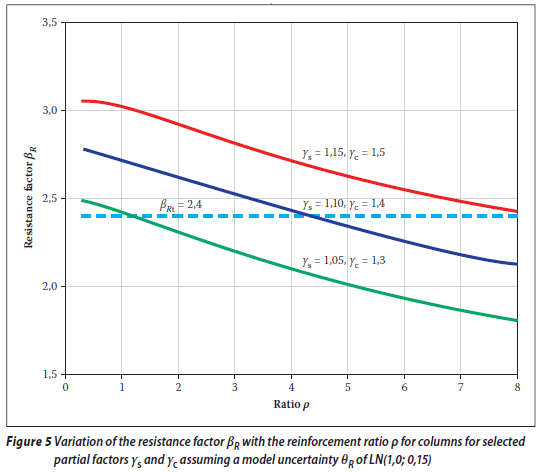
Figure 5 indicates that the reliability level considerably decreases (compared with Figure 3). The combination of partial factors γs= 1,10, γc= 1,40 would be satisfactory only for reinforcement ratios of ρ < 4 %. This limitation is, however, acceptable in most practical cases. When the reinforcement ratio ρ is greater than 4%, then increased production quality should be required.
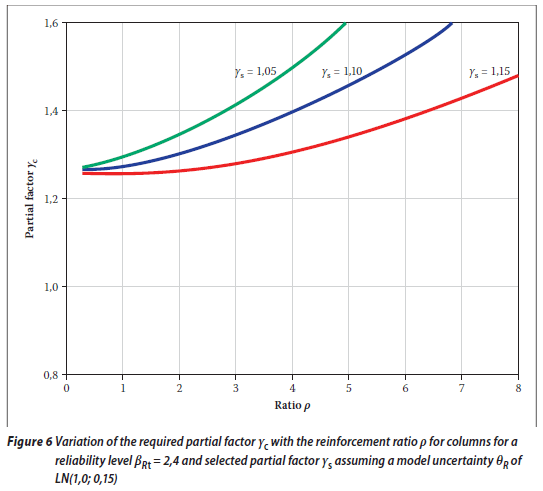
The results of the inverse analysis shown in Figure 6 confirm the previous finding that the combination of partial factors γs= 1,10 and γc= 1,40 would be satisfactory for a limited reinforcement ratio of ρ < 4 %. Comparison of Figures 4 and 6 shows that the required partial factor γc would be greater assuming a model uncertainty θR of LN(1,0; 0,15) than for a model uncertainty θR of LN(1,0; 0,10).
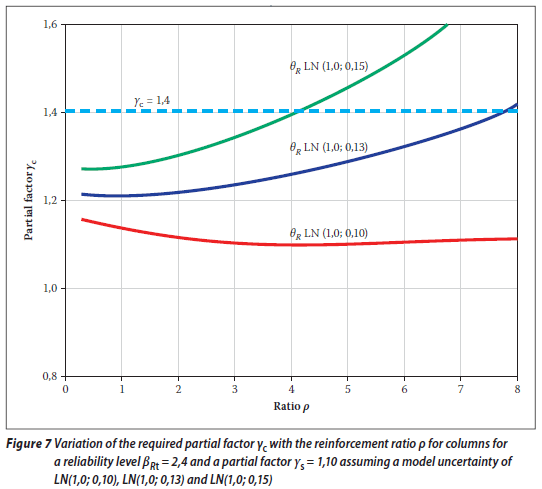
The effect of the increased variability of the model uncertainty θR (described by the increased coefficient of variability from 0,10 to 0,15) is apparent from Figure 7. Obviously the partial factor γc = 1,4 would be satisfactory for an increased variability of the model uncertainty.
ASSESSMENT OF PARTIAL FACTORS
The opposing reliability trends in the reinforcement of slabs and columns indicate some oversimplification of the design functions as expressed by Eq (5) and (7) respectively. This implies that the contribution of the respective partial factors to structural performance may not be a simple linear process in terms of factored material properties as indicated by these design functions. The results also demonstrate the difficulty of selecting partial factors based on judgement due to the counter-intuitive behaviour of the design functions. More insight into the contributions of partial factors to the reliability performance of a design function can be gained through further analysis of the reliability performance functions.
Extended reliability analysis
Various techniques are available to provide additional information on the reliability performance of slabs and columns, and the influence of the respective basic variables. The techniques for further analysis are generally based on the determination of the socalled design point (R*) for which the most likely set of basic variables (X*) are used to ascertain the (design) resistance for a given level of reliability (Ang & Tang 1984).
Global resistance factor
In performing inverse analysis to achieve the target level (βRt = 2,4) of resistance reliability and thereby to obtain the results in Figures 2 and 4, the design resistance (Rβt) that would achieve such reliability can be determined. This resistance can then be related to the mean resistance (µR) to obtain a global resistance factor (GRF); µR is obtained by using mean (unfactored) values for the basic variables (µx) in the design function, which are given by Eq (5) and (7) respectively. The characteristic GRF can be obtained in a similar manner by using unfactored characteristic basic variables (Xk) in the design function.
The GRF for slabs and columns as a function of the reinforcement ratio (ρ) are shown in Figure 8. Both the mean GRF (graph (a)) and characteristic GRF (graph (b)) values are shown. The differences in the attributes of the reliability behaviour of the two structural elements should be noted in terms of the magnitude of the required GRF, trends as a function of ρ and the change in GRF from mean to characteristic value.
Note that the difference between the mean and characteristic GRF derives only from the differences between the mean and characteristic values for fy and fc. The difference between graph (a) and graph (b) represents the contribution towards achieving sufficient reliability through the specification of the characteristic material properties fyk and fck. The difference between graph (b) and a value of 1,0 represents the contribution required from the partial factors γy and γc. From the results shown in Figure 8 it is clear that the specification of characteristic material properties fyk and fck, plays a more prominent role than the values of the partial factors in achieving sufficient reliability for both slabs and columns.
The effect of applying the specified characteristic concrete strength value fck = µfc - 1,64 σfc instead of the effective value (fck = µfc - 2σfc) shown in Table 1 to obtain R'k, is also shown. The difference between the two versions of the characteristic GRF represents a significant increase in the design bias required through the partial factors γs and γc for situations where quality control of concrete production is insufficient to achieve the effective characteristic concrete strength as used in this analysis.
Theoretical partial safety factors
The most likely set of values for the basic variables X*βt to obtain R* = Rβt can be determined to allow calculation of the theoretical partial factors as γ*x = µx / X*βt for each of the basic variables. Note that γ*x is the "unbiased" partial factor which applies to the mean value µx. The partial factor which applies to the characteristic value Xk is obtained by direct conversion, i.e. by multiplying γ*x by the ratio of the characteristic value to the mean (Xk / µx).
In Figure 9 the values of γ*x are shown for all the basic variables for slabs (Eq (4)) and columns (Eq (6)), with the indicated symbols in accordance with those given in Table 1. The factor for the cover distance (a) for slabs is off scale in Figure 9(a), with a value of γ*a ∼ 0,67 (or 1,5 as a multiplication factor) which applies across the range of ρ as indicated, implying that a design value of 30/0,67 = 45 mm should be used in the design!
Again the different values and trends for the two structural elements are noteworthy, particularly for the partial factor for concrete strength γ*fc, which has prominently high values for both cases, but opposing trends as a function of the steel ratio ρ. To obtain the partial factors applicable to characteristic values for fy and fc, the values shown in Figure 9 have to be multiplied by the factors 500/560 = 0,893 for steel and 20/30 = 0,67 for concrete, resulting in values of < 1 in both cases. The implication is that the characteristic bias for steel and concrete is sufficient with regard to the theoretical values. Additional conservatism is therefore required through γs and γc to provide for the other basic variables (geometric and modelling), which are unfactored.
Sensitivity factors
Whereas the theoretical partial factor gives an indication of the adjustment required to each respective basic variable to achieve βRt, the sensitivity factor (αX) provides information on the relative importance of the variables. Sensitivity factors also give an indication of the effectiveness of applying partial factors to the respective basic variable in order to achieve the target reliability βRt (Ang & Tang 1984).
Values of the sensitivity factors αX,i for slabs (Eq (4)) and columns (Eq (6)) as a function of the reinforcement ratio are presented in Figure 10 for βRt = 2,4 (symbols are in accordance with those given in Table 1). It should be noted that αX,i represents normalised factors since Σ(αX,i)2 = 1. As αX and γ*x are directly related, there is a similarity in the shape of the graphs in Figures 9 and 10. However, the relative values of αXi are of greater importance since a larger value indicates a larger contribution to reliability performance and greater effectiveness of applying a partial factor to the respective basic variable.
Figure 10 indicates that the reliability for both cases is dominated by unfactored variables, namely modelling uncertainty for both cases, with steel cover (α) even more important for slabs. For slabs γ s is clearly more effective to achieve sufficient reliability for low values of ρ, while γc is more effective for large ρ values. The partial factor γc is generally more effective throughout the full range of ρ for columns.
The source of differences in trends of behaviour for the two types of element is also apparent from Figure 10. In the case of slabs the reliability is dominated by basic variables which have a negative influence (reducing reliability) on the contribution of the lever arm to the resisting moment, viz a and fc. Lower values for fc result in a smaller lever arm, and thus a lower resistance moment; this effect becomes more prominent as ρ increases. Lower values for fy have a counterbalancing effect on the resistance moment by decreasing the force but increasing the lever arm, with the effect again becoming more prominent with increasing ρ.
In the case of columns, the relative importance of fy and fc simply changes with the relative contribution of steel and concrete to the resistance, although modelling uncertainty is generally the dominating factor.
CONCLUDING REMARKS
This paper presents the results of a reliabilitybased approach to defining the values of partial factors γs and γc for reinforced concrete slabs and short centrically loaded columns. Target reliability levels as expressed by the resistance index βR are set in accordance with South African practice. The reinforcement ratio ρ, which is considered as the main design parameter, was investigated across the range of practical values. The objective was to determine economic values for the partial factors that would ensure sufficient reliability across the range of design conditions.
In addition to some conclusions on appropriate values for the partial factors in accordance with the scheme at present in use, namely the material partial factors γs and γc, the results of the reliability analysis also enhance insight into the mechanisms and factors that have an influence on the reliability performance of the resistance of these elements. The following conclusions may be drawn, and some recommendations are made for using the results and further investigations:
The differences in reliability performance across the range of design parameters of structural element type and reinforcement ratio which was identified previously (Holický et al 2007) have been confirmed: The trends of various reliability parameters against reinforcement ratio are markedly different for slabs and columns. For example, compare Figures 1 and 3 for β versus ρ. Even the effectiveness of the partial factors γs and γc vary, as is demonstrated in Figures 2 and 4. These differences can be ascribed to the respective mechanisms of resistance, and their sensitivities to the effects of the basic variables, as shown in Figure 10.
The resistance reliability of slabs is dominated by basic variables related to the lever arm of the resistance moment. The importance of steel depth a results from its direct effect on the lever arm and its high variability, with a coefficient of variability of 30%. Concrete strength only plays a role through its effect on the lever arm, and therefore only becomes significant at high reinforcement ratios (Figure 10). This explains the counter-intuitive effect of reduced reliability with increasing reinforcement for slabs. While the variability of the steel strength reduces the reliability through the moment force, its effect on the lever arm causes an increase, with a net effect of reduced sensitivity with increasing reinforcement.
The resistance reliability of columns is dominated by model uncertainty, except in the case of low reinforcement ratios where concrete strength is also important (Figure 10). Although the contribution of steel increases with ρ, it is relatively unimportant, even less so than that of αcc, which represents the long-term effect of concrete strength.
The specified characteristic material strengths fyk and fck play an important role in achieving sufficient reliability, as indicated by Figure 8. This effect is further enhanced by the fact that strengths are systematically exceeded in practice. Since credit is taken for this effect, it is important to verify that the models for steel and concrete strengths are valid for South African conditions, and that they are realised in the application of quality control in individual projects.
The results verify that in terms of present South African practice of using a target reliability of βRt = 2,4 and partial factor scheme of material factors, values of γs = 1,10 and γc = 1,4 are sufficient, which also provide for the effects of modelling uncertainty and geometry across the operational range of ρ for the two classes of structural element.
It is also clear, however, that the partial factors not only reflect the effects of material strengths, but also provide for other sources of uncertainty which are applied at unfactored nominal values in design expressions. On the one hand this provides an indication that the use of resistance factors only may be reasonable, with values of γR,slab = 1,10 and γR,column = 1,15 being sufficient (Figure 8). A more refined but more elaborate scheme of providing a model factor in addition to the material factors could also be considered.
Further research is required on the following topics for which available information provided by the JCSS model code is incomplete and rather general, particularly when applied to the derivation of design procedures under South African conditions:
the model uncertainty θR for different structural members (flexural members, shear, columns, walls)
the theoretical models of basic resistance variables related to quality control.
ACKNOWLEDGEMENT
This study was partly supported by the research project GAČR 103/06/1562, Development of durability concepts for verification of structures and materials.
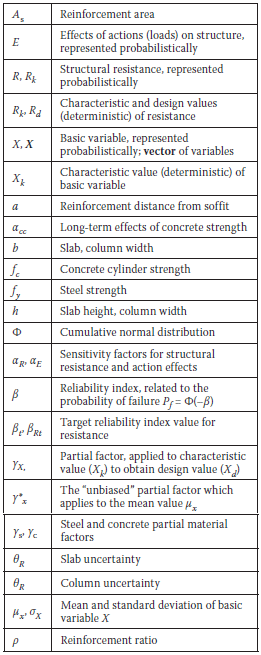
LIST OF NOTATIONS
REFERENCES
Ang, A H-S & Tang, W H 1984. Probability Concepts in Engineering Planning and Design. Vol. 2, Decision, Risk and Reliability. New York: Wiley. [ Links ]
BS 8110: Part 1: 1985. British Standard Structural Use of Concrete. Part 1. Code of Practice for Design and Construction. London: British Standards Institution. [ Links ]
EN 1990:2002. Eurocode: Basis of Structural Design. European Committee for Standardization. [ Links ]
EN 1992-1-1:2004. Eurocode 2: Design of Concrete Structures. Part 1-1: General Rules and Rules for Buildings. European Committee for Standardization. [ Links ]
Gulvanessian, H, Calgaro, J-A & Holický, M 2002. Designer's Guide to EN 1990 Eurocode: Basis of Structural Design. London: Thomas Telford. [ Links ]
Holický, M & Holická, N 2004. Global resistance factors for concrete members (in Czech). Betonářské dny, Hradec Králové, 11: 287-292. [ Links ]
Holický, M & Marková, J 2003. Reliability of concrete elements designed for alternative load combinations provided in Eurocodes. Acta Polytechnica, 1: 29-33. [ Links ]
Holický, M & Retief, J V 2005. Reliability assessment of alternative Eurocode and South African load combination schemes for structural design. Journal of the South African Institution of Civil Engineering, 47(1): 15-20. [ Links ]
Holický, M, Retief, J V & Dunaiski, P E 2007. The reliability basis of design for structural resistance. Proceedings, 3rd International Conference on Structural Engineering, Mechanics and Computation, Cape Town. [ Links ]
ISO 2394:1998. International Standard: General Principles on Reliability for Structures. International Standards Organisation. [Also issued as SANS 2394:2004] [ Links ]
JCSS 2002. Probabilistic model code. JCSS working materials. Available at: http://www.jcss.ethz.ch/ [ Links ]
Retief, J V, Maritz, G, Ter Haar, T R, Brand, W W & Muhimua-Joao, A 2002. Structural concrete reliability models for design code assessment. Proceedings, Concrete for the 21st Century, Midrand, Gauteng. [ Links ]
SABS 0100-1:1992. South African Standard. Code of Practice: The Structural Use of Concrete, Part 1. Design. South African Bureau of Standards. [ Links ]
SAICE 1998. South African National Conference on Loading. South African Institution of Civil Engineering, Midrand, 9-10 September 1998. [ Links ]
SANS 10160:2010. Draft South African Standard. Basis of Structural Design and Actions for Buildings and Industrial Structures. South African Bureau of Standards. [ Links ]
 | MILAN HOLICKÝ obtained his civil engineering degree at the Czech Technical University in Prague, and his doctoral degree at the University of Waterloo in Canada. He is Deputy Director of the Klokner Institute, CTU, in Prague. At present he is involved in research into structural reliability and risk assessment, and in the development and implementation of the ISO and European Standards Structural Eurocodes and he serves on the Joint Committee on Structural Safety. His latest publication is Reliability Analysis for Structural Design, published in Stellenbosch. |
 | JOHAN RETIEF, PrEng, retired in 2001 as professor in the Department of Civil Engineering, Stellenbosch University, but still does part-time research for the university. He has been actively involved in the recent revision of the SA Loading Code SANS 10160:2010 and other standards development activities, with specific interest in structural reliability considerations. He is the South African delegate for ISO TC98, Bases for the Design of Structures. He holds a BSc Eng and DSc Eng from the University of Pretoria, a DIC from Imperial College and an MPhil from London University, and Engineer from Stanford University. |
 | JAN WIUM, PrEng, is professor in the Murray & Roberts chair for Construction Engineering and Management in the Department of Civil Engineering at Stellenbosch University. He completed his undergraduate and MSc (Eng) degrees at the University of Pretoria and obtained his PhD from the Swiss Federal Institute of Technology in Lausanne. He worked as a consultant for 20 years before joining the University of Stellenbosch in 2003. After first addressing the behaviour of concrete structures and seismic analysis of structures, he now focuses his research on the management and initiation of multidisciplinary capital projects. |
 Contact details
Contact details
M Holický
Klokner Institute, CTU, Prague
Solinova 7, 16608 PRAHA 6
Czech Republic
T: +420 224 353 842
F: +420 224 355 232
E: holicky@klok.cvut.cz
Contact details
Department of Civil Engineering
University of Stellenbosch
Private Bag X1
Matieland, 7602
T: 021 808 4442
F: 021 808 4947
E: jvr@sun.ac.za
Contact details
Department of Civil Engineering
University of Stellenbosch
Private Bag X1
Matieland, 7602
T: 021 808 4498
F: 021 808 4947
E: janw@sun.ac.za














