RESEARCH ARTICLE

 

Efficient Removal of Sulfamethoxazole onto Sugarcane Bagasse-derived Biochar: Two and Three-parameter Isotherms, Kinetics and Thermodynamics

 

 

Victor O. Shikuku^{I, *}; Selly Jemutai-Kimosop^II

^IDepartment of Physical Sciences, Kaimosi Friends University College, P.O. Box 385-50309, Kaimosi, Kenya
^IIDepartment of Chemistry, Masinde Muliro University of Science and Technology, P.O. Box 190, Kakamega, Kenya

 

 

---

ABSTRACT

In this work, bagasse, an agricultural waste was used for the development of environmentally benign biochar (CBG) and the thermal pyrolysis product applied for adsorption of sulfamethoxazole (SMX) from water using a batch technique. The pseudo-first-order model best described the adsorption kinetics. Equilibrium adsorption data were modelled using six two-parameter and five three-parameter isotherm equations and the best-fitting models obtained using five error functions. The Sips isotherm best predicted the equilibrium data with an estimated adsorption capacity of 128.8 mg g^-1. Error analysis showed that three-parameter isotherms best explained the experimental data. The thermodynamic functions, viz. enthalpy (AH = -24.72 kJ mol^-1), Gibbs free energy (AG = -15.67 kJ mol^-1), entropy (AS = 32.65 kJ mol^-1), showed that the reaction is spontaneous and exothermic. The mechanism of adsorption involved charge-assisted hydrogen bonding (-)CAHB. The amount of CBG required for the removal of 99 % of SMX in a given volume of effluent was predicted. The results attest that CBG is an effective low-cost adsorbent for SMX adsorption.

Keywords: Sulfamethoxazole, adsorption, bagasse, pyrolysis, biochar.

---

 

 

1. Introduction

The accumulation of pharmaceutical ingredients in water and soil is a subject of increasing concern in recent decades.¹ Pharmaceutical compounds and veterinary drugs enter the environment through various means but not limited to: the discharge of treated wastewater effluents into recipient water bodies, landfills leachates, and indiscriminate dumping of residual and expired drugs.² Concerning the various categories of antibiotics, sulfonamides such as sulfamethoxazole (SMX) have often been reported in treated effluents from conventional wastewater treatment systems.³ This indicates their recalcitrance to traditional wastewater treatment techniques and underscores the demand for the evaluation of alternative efficient sequestration methods.⁴ Sulfonamides in the environment have been shown to cause a considerable variety of health-related disorders.⁵ A broad spectrum of adsorbents has been proposed for the elimination of sulfonamides from water. These include walnut shells,⁶ iron oxide modified clays,⁷ haematite nanoparticles,⁸ goethite,⁹ graphene oxide¹⁰ and biochars.¹¹

Biochars have received considerable attention in the removal of sulfonamides due to their inexpensiveness owing to the plethora of agronomical biomass.¹² Furthermore, biochars are environmentally friendly materials and the pyrolysis of wastes is not only an environmental management strategy but also converts waste materials to utilizable resources. However, the performance of the biochars as adsorbents and the concomitant adsorption mechanisms depend on the precursor material and preparation conditions.^13,14 Since there is no unifying theory combining the biomass type, preparation conditions, and performance, the adsorptive potential of biochars are normally examined individually and the performance compared with other adsorbents. As such, this study aimed to evaluate the adsorptive behaviour of carbonized bagasse biochar (CBG), derived from an abundant and unutilized agronomical waste, for the elimination of sulfamethoxazole from water. The effects of pH, temperature, SMX concentration, reaction time, and amount of adsorbent have been examined. Six nonlinear two-parameter isotherms models (Langmuir, Freundlich, Temkin, Elovich, Fowler-Guggenheim and Flory-Huggins models) and five three-parameter isotherms (Hill, Sips, Koble-Corrigan, Toth, and Redlich-Peterson) models were tested to provide insight on the adsorbate-adsorbent interactions and the best-fitted model determined using five error functions, viz. average relative error (ARE), hybrid fractional error function (HYBRID), chi-square (x²), Marquart's percentage standard deviation (MPSD), and the sum of absolute errors (EABS). Kinetic data were processed using the nonlinear regression of the widely used pseudo-first (PFO) and pseudo-second-order (PSO) kinetic models.

 

2. Materials and Methods

2.1. Adsorbent Preparation

The sugarcane bagasse derived biochar (CBG) was prepared by chopping the biomass into pieces followed by thorough washing with deionized water for the removal of all adhering dirt and then air-dried for 24 h before pyrolysis. Biochar was prepared by slow-pyrolysis at 350 °C at a heating rate of 10 °C min^-1 and a residence time of 60 min in a furnace. The biochar was then cleaned with deionized water and oven-dried at 100 °C for 2 h.¹⁵ The resultant product, CBG, was sieved through a 200 μm sieve and was ready for use.

2.2. Biochar Characterization

The elements present in the bagasse biochar (CBG) were acquired by XRF (Bruker S1 TITAN) technique. The functional groups in the CBG sample were obtained using FTIR (Nicolet iS-5, USA) spectroscopy. The mineralogical composition was obtained using X-ray diffraction (X-ray Brucker diffractometer D8 Advance with copper radiation, K_a = 1.5406) analysis. Surface morphology was inspected by a scanning electron microscopy (SEM) (Zeiss Evo LS 15 SEM) while the pH drift approach was used to estimate the point of zero charge (pH_pzc).

2.3. Adsorption Experiments

For the adsorption experiment, 0.1 g of CBG was added to 50 mL of 1 mg L^-1 solution of sulfamethoxazole (SMX), and the contents were shaken at 120 rpm at 298 K. At the predetermined time between 0 and 420 min, the SMX remaining in the aqueous phase was quantified. The effects of initial SMX concentration (0.25-1.25 mg L^-1) at room temperature and pH 6.4, and temperature (298, 308, 318, 328, and 338 K) were also examined. The effect of solution pH was performed between pH 2 and 10 using 0.1 M HCl and 0.1 M NaOH solutions to adjust the pH accordingly. Aliquots of 0.5 mL were extracted from the reaction vessels and sieved using 0.2-μm filters and analyzed for SMX. The experiments were conducted in triplicate. Sulfamethoxazole (SMX) was analyzed using HPLC with ultraviolet (UV) detection (Shimadzu LC 20AT) at 270 nm with acetonitrile and water (90:10 v/v) as the mobile phase.⁷ The chemicals used were analytical grade purchased from Kobian Limited (Kenya). The amount of SMX adsorbed onto CBG at equilibrium (q_e) and the percentage removal (%R) were calculated by the equations:

where V is the volume of solution (L), m is mass of CBG (g), and C_i and C_e represent the initial and equilibrium SMX concentrations, respectively.

 

3. Results and Discussion

3.1. Biochar Characteristics

3.1.1. Elemental Composition

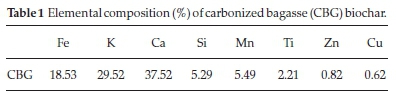
The elements present in the carbonized bagasse biochar (CBG) as obtained by XRF analysis is summarized in Table 1. The metal ions present in the highest amounts in CBG were calcium, potassium, and iron in descending order.

 

 

3.1.2. Surface Morphology Analysis

The SEM micrograph of CBG is displayed in Fig. 1. The micrographs depict spherical-like metal oxide dispersed on the surface of the material with a visibly large cavity and heterogeneous surface morphology. The open cavities seem to have the potential of trapping small-sized adsorbate molecules.

 

 

3.1.3. Crystallinity and Mineralogical Analysis

XRD analysis was done to obtain the mineralogical composition of CBG. The XRD diffractogram is depicted in Fig. 2. The carbonized bagasse was largely amorphous with SiO₂ as the only notable crystalline phase (Fig. 2).

3.1.4. FT-IR Analysis

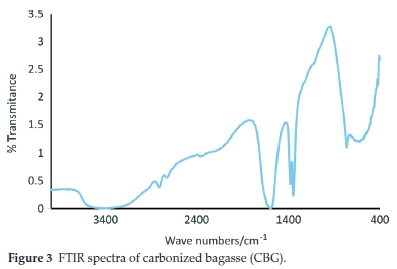
The FTIR spectra of the carbonized bagasse biochar are displayed in Fig. 3. The bands at 3600-3300 cm^-1 were assigned to both free and hydrogen-bonded -OH stretching vibrations from the phenols present. The bands in the 1700-1600 cm^-1 region were ascribed to C=O stretching vibrations resulting from ketones, carboxylic acids, anhydrides and esters.¹⁶ The bands around 1500-1400 cm^-1 were attributed to inorganic functional groups such as alumina-silicates and metal oxides.¹⁷

 

 

3.2. Adsorption Kinetics

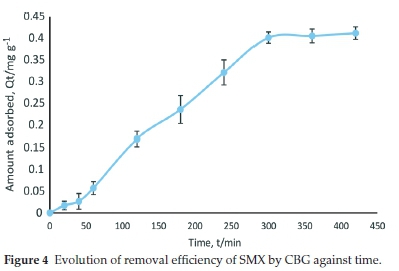
The abstraction efficiency (%R) of sulfamethoxazole (SMX) by the carbonized bagasse (CBG) increased steadily with time leading to saturation in 300 min (Fig. 4). The percentage removal (%R) at equilibrium was 78 %. The high instantaneous percentage removal is due to the vast number of unoccupied adsorption sites. However, the equilibrium phase is due to inaccessibility to adsorption sites with continued loading of SMX in the solid phase.

 

 

To obtain the adsorption rate, the nonlinear pseudo-first-order (PFO)¹⁸ and pseudo-second-order (PSO)¹⁹ kinetic rate equations were used. The relative applicability of the models was assessed using the coefficient of determination (R²) values and the extent of closeness between empirical equilibrium adsorption capacity (q_exp) and the predicted figures (q_cal) calculated from the models. The coefficient of determination (R²) is given by:

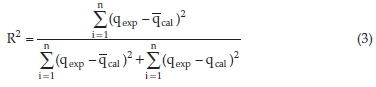
where q_cal is the model calculated equilibrium concentration adsorbed, q_exp is the experimentally determined equilibrium concentration adsorbed and q_cal(bar) is the mean of q_cal andnis the number of data points.

The kinetic models are represented by Equations 4 and 5 and the calculated parameters are listed in Table 2.

 

 

 

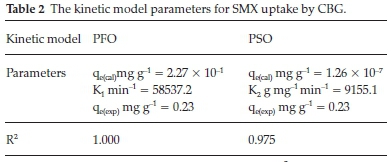
The PFO model depicted an accurate prediction power of the experimental data as shown by an R² value of unity and convergence of predicted and experimental equilibrium sorption capacities. Besides the relatively high R² value for the PSO model, it is evident that the prediction error of the PSO (q_cal) against the experimental adsorption capacities (q_exp) is huge and the model unsatisfactorily predicts the experimental data. Therefore, the huge deviation of the predicted equilibrium capacity from the empirical denotes that SMX adsorption onto the CBG cannot be a PSO process. The PFO model assumes a physisorption driven rate-controlling step.

3.3. Two-parameter Isotherm Modelling

The calculated two-parameter isotherm constants are summarized in Table 3. The coefficient of determination (R²) has been extensively used for the determination of the most applicable isotherms. However, Zheng el al.²⁰showed that solely used, R² is insufficient to determine best-fitting models. Furthermore, linear regression of nonlinear isotherms has also been shown to induce errors in parameter estimations resulting in misleading conclusions.^21,22 To overcome these challenges, nonlinear regression was used and mathematical error functions (HYBRID, MPSD, EABS, X², and ARE), shown in Table 4, applied for the determination for the most applicable isotherm.

3.3.1. Langmuir Isotherm

Langmuir²³ isotherm equation postulates monolayer adsorption of adsorbate molecules, with no lateral interactions, onto a morphologically homogeneous adsorbent surface with a fixed number of energetically identical adsorption sites. The nonlinear form of the Langmuir equation is expressed as:

where q_e is the amount of adsorbate in adsorbent at equilibrium (mg g^-1), C_e is the residual adsorbate concentration in the solution at equilibrium (mg L^-1), Q₀ is the theoretical maximum adsorption capacity (mg g^-1) and K_L is the Langmuir constant (L g^-1).

In the present work, the low R² value and a calculated theoretical maximum adsorption density of zero (0) (Table 3), which lack practical significance, denote that the predictions of the Langmuir model were unacceptable. This conclusion was further ascertained by the error function figures and therefore the assumptions of the Langmuir isotherm do not adequately account for the uptake of SMX onto the biochar.

3.3.2. Freundlich Isotherm

The Freundlich isotherm²⁴ (Freundlich, 1906) postulates a multilayer adsorption process onto a heterogeneous adsorbent surface and excludes lateral interactions. The Freundlich equation is represented as:

Treybal²⁵ associated Freundlich constant n with the favour-ability of an adsorption process. In this study, the n-value (0.749) (Table 3) would correspond to poor adsorption potential. To el al²⁶reported that the magnitude of 1/n indicates the strength of the adsorbate-adsorbent bonds. As such, the calculated 1/n value (1.335) in this study bespeak of weak adsorbate-adsorbent forces corresponding to physisorption. The 1/n values greater than 1 imply cooperative adsorption.²⁷ The R² value of unity and the least magnitude of error functions denote that the underlying theories of the Freundlich isotherm satisfactorily accounted for the adsorption of SMX onto the biochar.

3.3.3. Temkin Isotherm

Temkin isotherm model incorporates the impact of adsorbate-adsorbate interactions on the adsorption reaction. The model presupposes that the energy of adsorption (AH_ads) decreases linearly with increased surface coverage.²⁸ The Temkin isotherm is reported to be valid for a moderate space of ion concentrations.²⁹

Adsorption energy (B_Tln(A_T)) ranging between 8 and 16 kJ mol^-1 is associated with chemisorptions, as well as b_T values above 80 kJ mol^-130 As seen in Table 3, the computed value of B_Tln(A_T) was 0.613 kJ mol^-1 with a correspondingb_T value of 9.01 kJ mol^-1, suggesting physical interaction between SMX and CBG. Additionally, the b_T value was positive, implying an exothermic adsorption reaction.³¹ Both the relatively high coefficient of determination (R² = 0.967) and error functions attest to the suitability of the Temkin model to account for the sorption of SMX onto CBG.

3.3.4. Flory-Huggins Isotherm

This isotherm, derived from the surface coverage parameter, gives insight on the spontaneity of the adsorption reaction. The Flory-Huggins isotherm is presented by the relation:³²

where K_FH is the Flory-Huggins equilibrium constant (L mg^-1). The n_FH parameter represents the number of adsorbate ions occupying sorption sites. The equilibrium constant, K_FH, can be employed to calculate the Gibbs free energy following the relation:³³

The error function analysis depicts that this model suited the equilibrium data better than the Langmuir isotherm (Table 3). The calculated Gibbs free energy (AG) from the Flory-Huggins equilibrium constant (K_FH) was -6787.4 J mol^-1 at 298 K. The negative AG value implies that the adsorption reaction of SMX onto CBG is thermodynamically spontaneous.

3.3.5. Fowler-Guggenheim Isotherm

The Fowler-Guggenheim model takes into account the lateral interaction of the adsorbate species in the solid phase. The Fowler-Guggenheim model is defined as:³⁴

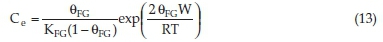
where K_FG is the Fowler-Guggenheim equilibrium constant (L mg^-1), 0 the fractional coverage, R the gas constant (kJ mol^-1 K^-1), T the temperature (K), and W represents the interaction energy between adsorbed molecules (kJ mol^-1).

The isotherm theorizes a linear variation of the energy of adsorption with adsorbate loading. On adsorbate interactions, when W is positive, the interaction between the adsorbates is attractive. Contrarily, negative W denote repulsive interaction between adsorbed moieties. However, in cases of no interaction between adsorbed molecules, thenW = 0.From Table 3, the calculated value of W was positive, indicating attractive interaction between the adsorbed SMX molecules. This corroborates the cooperative adsorption alluded to by the 1/n value of the Freundlich isotherm. The applicability of this model was less favourable from the error functions perspective.

3.3.6. Elovich Isotherm

The Elovich model isotherm³⁵ model presupposes that the binding sites increase exponentially with adsorption, a characteristic of multilayer adsorption. The Elovich isotherm equation is given as:

where K_E is the Elovich equilibrium constant (L mg^-1) and q_mE is the Elovich maximum adsorption capacity (mg g^-1).

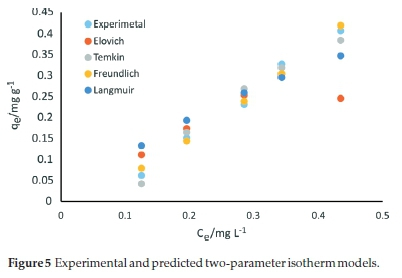
The Elovich isotherm constants, K_E, and q_mE, with the corresponding error function values for the adsorption of SMX onto the carbonized bagasse are presented in Table 3. Based on error analysis, the Elovich isotherm better-fitted the experimental data than Flory-Huggins and Langmuir equations. The calculated Elovich maximum adsorption capacity of CBG for adsorption of SMX was 105.6 mg g^-1. Conformity to the Elovich model implies multilayer adsorption and agrees with the conclusions from the Freundlich model. Therefore, for the approximation of the adsorption capacity, the Elovich model was suitable relative to the Langmuir isotherm equation. From the error functions analysis, the relevance of the tested adsorption isotherms to account for the experimental data was in the order Freundlich > Temkin > Elovich > Flory-Huggins > Fowler-Guggenheim > Langmuir model. Figure 5 shows the predictions of two-parameter isotherms relative to the experimental data.

 

 

3.4. Three-parameter Isotherm Modelling

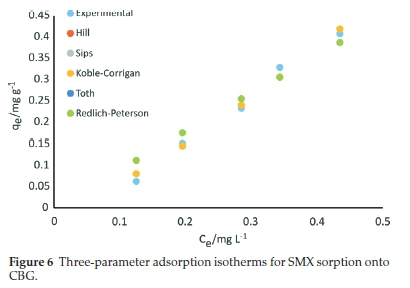
The equilibrium sorption data for SMX onto CBG was also fitted to five three-parameter isotherms, namely Hill, Sips, Koble-Corrigan, Toth, and Redlich-Peterson models and the calculated parameters and corresponding error functions values are summarized in Table 5 and the plots presented in Fig. 6..

 

 

3.4.1. Hill Isotherm

The Hill equation³⁶ theorizes the fixing of the adsorbates onto a homogeneous surface. The Hill isotherm model is given by the relation:

This model infers a cooperative adsorption mechanism. In this model, three scenarios are possible: n_H > 1, positive cooperativity in binding, n_H = 1, non-cooperative, n_H < 1, negative coopera-tivity in binding. In this study, the Hill isotherm afforded a high R² value (0.986) with favourable error function values and the calculated n_H value 1.34 >1 corresponds to positive cooperativity in binding. The cooperative adsorption is coherent with the observation from the Freundlich isotherm.

3.4.2. Sips Isotherm

The Sips isotherm³⁷ is an amalgam of the Freundlich and Langmuir isotherms and is applicable for heterogeneous systems where the adsorbed molecule can occupy more than one binding site. However, the model does not allow for adsor-bate-adsorbate synergy. The Sips isotherm equation is given by:

where q_ms,a_s and B_s are the isotherm constants. The constant B_s is the heterogeneity index. Generally, the greater the B_s value is, the more heterogeneous the system is said to be. Contrarily, values closest to unity imply a homogeneous adsorbent surface corresponding to the Langmuir equation.³⁸ The equilibrium data was suitably fitted to the Sips isotherm as attested to by the high coefficient of determination (R² = 0.986) and error function values. Notably, the B_s parameter (1.34) was above unity a testament of a heterogeneous system, and consistent with the Freundlich model. The fitting of this model was equivalent to the Hill isotherm. The Sips maximum adsorption capacity (128.8 mg g^-1) was comparable to the value predicted by the Elovich model.

3.4.3. Toth Isotherm

The Toth isotherm model³⁹ improves the fitness of the Langmuir isotherm to equilibrium data at both small and large amounts of adsorbed molecules. The Toth correlation is presented as:

The parameter z describes the system's heterogeneity and is independent of temperature. The degree of its deviation from unity is a measure of the degree of heterogeneity.⁴⁰ The non-linear regression parameters for the Toth isotherm are listed in Table 5. The parameter z, an indicator of heterogeneity, was 4.53 X 10^-6 far from unity. Since the degree of departure from unity depicts increased heterogeneity, the value obtained in the present work attests that the adsorption behaviour is heterogeneous in agreement with Sips and Freundlich isotherms. However, the model predicted an extremely low maximum adsorption capacity of 4.53 X 10^-6 mg g^-1 with a relatively lower R² value (0.945) than Hill and Sips isotherms and the high EABS, HYBRID and MPSD values, signifying a poor fitting.

3.4.4. Koble-Corrigan Isotherm

Akin to the Sips isotherm model, the Koble-Corrigan iso-therm⁴¹ amalgamates both Langmuir and Freundlich parameters and postulates heterogeneous sorption. The Koble-Corrigan equation is given as:

where A, B, and n_K are Koble-Corrigen isotherm constants.

In the present work, the Kolbe-Corrigan isotherm afforded a high coefficient of determination (R² = 0.986) with the parameter n_K value of 1.335 > 1. Hossain et al.⁴⁰interpreted less than unity values of n_K for biosorption of copper onto palm oil fruit shells to denote heterogeneous adsorption systems. Therefore, values of exponent 'n_K' (<1), unlike in the present work, suggest that the sorption surface is heterogeneous.⁴¹ However, a comparison of the Freundlich and the Langmuir model indicates that heterogeneous adsorption is the preferred mechanism for uptake of SMX ions onto CBG. Noteworthy, Saadi et al.⁴² reported that the Kolbe-Corrigan model is valid only when n_K>1. Therefore, the R² value, relatively lower error function values and n_K > 1 support the applicability of the Kolbe-Corrigan model though the conclusions from the model are debatable relative to Hill and Sips isotherms.

3.4.5. Redlich-Peterson Isotherm

The Redlich-Peterson model⁴³ integrates the parameters of the Langmuir and the Freundlich isotherms, and therefore the adsorption mechanism can be homogeneous as well as heterogeneous. The Redlich-Peterson isotherm equation is given as:

where K_R (L g^-1) and a_R (mg L^-1)^-g are the Redlich-Peterson constants, and the g (dimensionless) parameter takes values from 0 to 1. The parameter g ranges between 0 and 1 for heterogeneous sorption.⁴⁴ When g = 1, the equation is reduced to the Langmuir model. In the present work, the low R² value (0.945) and the error function values for Redlich-Peterson isotherm ascertain its inapplicability to account for the sorption of SMX onto CBG. The obtained parameter g value of zero (0) denotes that the adsorption system approached the Henry equation and postulates a heterogeneous adsorption system.⁴⁴ However, the error function values attest to the inapplicability of the model for SMX adsorption onto CBG relative to the other three-parameter models. From the coefficient of determination and error functions analysis, the tested three-parameter isotherms fitted the equilibrium data in the order Sips = Hill > Koble-Corrigan > Toth = Redlich-Peterson model. The equivalence of the models is shown by the overlap of data points.

3.5. Effect of pH

The effect of solution pH on adsorption of sulfamethoxazole (SMX) onto the CBG was investigated in solution pH ranging between 2 and 10 and the amount adsorbed (mg g^-1) as influenced by pH is depicted in Fig. 7.

 

 

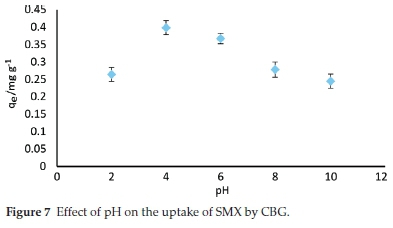
SMX adsorption was strongly affected by pH variation. The amount of SMX adsorbed at equilibrium decreased from 0.39 to 0.26 mg g^-1 when the pH rose from 4 to 10. This variation was accounted for by a comparison of the pH_pzc of the adsorbent (5.8) and the pK_a value of sulfamethoxazole (5.7).⁴⁵ The adsorbent surface is theorized to have an overall positive charge below the pH_pzc and negatively charged above this value (5.8). Therefore, in the pH range between 6 and 10, both the biochar surface and SMX molecules were negatively charged and the decreased adsorption is a result of coulombic repulsion. Similarly, at pH 2, both sorbate (SMX+) and adsorbent are positively charged and hence a significant reduction in amount adsorbed due to electrostatic repulsion. Furthermore, a change from neural (SMX⁰)to negatively charged ion (SMX^-) results to an increase in hydro-philicity⁴⁵ with a concomitant increase in solubility from approximately 281 mg L^-1atpH = 3.22 (298 K)toas high as17 900mgL^-1 at pH of 7.5.⁴⁶ Therefore, hydrophobic interactions between anionic SMX and the adsorbent become less significant at pH above 6. Similar findings have been highlighted by other researchers.⁴⁵ The maximum adsorption was realized at pH 4. which depicts that electrostatic attraction cannot account for the maximum adsorption of SMX onto CBZ. Lian el al.⁴⁵postulated that when the pK_a and pH_pzc are very close, as in the present study, then strong charge-assisted hydrogen bonds (-)CAHB are formed. Therefore, it is plausible that the adsorption mechanism of SMX onto CBG could be driven by (-)CAHB under the examined conditions.

3.6. Adsorption Thermodynamics

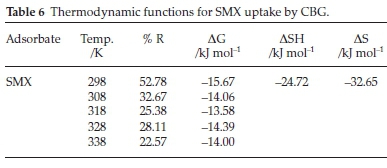
The adsorption energetics was investigated in the range 298-338 K. The thermodynamic functions, enthalpy change (AH), Gibb's free energy (AG), and entropy (AS) were determined using Equations 20 to 22 and the calculated parameters are presented in Table 6:

 

 

 

where K_c is the equilibrium constant (dimensionless), C_e is the SMX concentration in the aqueous phase at equilibrium (mg L^-1) and C_ads is the SMX concentration in the adsorbent at equilibrium (mg g^-1). R is the gas constant (8.314 J mol^-1 K^-1)andTisthe solution temperature (K).

The removal efficiency (% R), (Table 6), of SMX, diminished with increased solution temperature indicative of an exothermic reaction. This is corroborated by the negative and positive H and b_T obtained from Temkin isotherm, respectively. The decrease in adsorption could be due to increased solubility of the adsorbate and increase in hydrophilicity resulting in lower SMX attraction for the CBG sites.⁷ The negative G values denote the uptake of SMX by CBG is thermodynamically spontaneous and corroborates the prediction from the Flory-Huggins isotherm model. The AH value (24.70 kJ mol^-1), sufficiently below the 40 kJ mol^-1 linked with chemisorption mechanism,⁴⁷ attests that uptake of SMX onto CBG entails a physisorption mechanism, and is also supported by the adsorption energy parameter value (B_Tln(A_T)) calculated from the Temkin isotherm model and consistent with conformity to PFO kinetic model and the hypothesized (-)CAHB adsorption mechanism. The negative AS implies increased orderliness at the adsorbate-adsorbent interphase.

 

3.7. Effect of Adsorbent Dosage

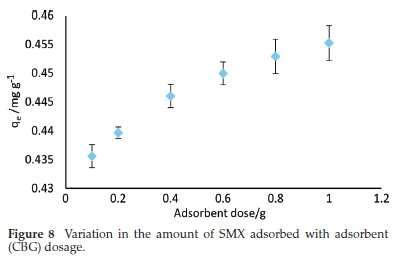
The effect of adsorbent dosage was evaluated from the range 0.1-1 g 50 mL^-1 solution at a constant SMX concentration of 1mgL^-1. As shown in Fig. 8, the amount of SMX adsorbed appreciated by the rise in CBG dosage. This is expected and is due to the increased number of binding sites with the rise in the mass of adsorbent.

 

 

3.8. Batch Adsorption Design

An adsorption isotherm is a relevant mathematical tool for predicting the blueprint of a batch or column adsorption regime. This enables a priori determination of the mass of CBG, m (g), necessary to remove sulfamethoxazole in the effluent of volume V (L), from a known initial amount C_i to an acceptable concentration C_e (mg L^-1).

Since the equilibrium data were best explained by the Sips Isotherm, equating Equation 1 and 16 and rearranging, gave Equation 24.

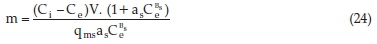
Rearranging Equation 2 gives rise to Equations 25 and 26.

Replacing Equations 25 and 26 into equation 24 we obtained Equation 27:

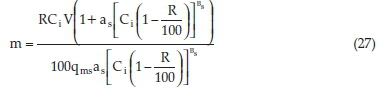
Equation 27 can be used to predict the mass m (g) of CBG necessary to realize any desired percentage removal (R) of SMX from water provided the effluent volume V (L) and SMX concentration, C_i (mg L^-1) are known. The equation holds except for 100 % removal and provided the adsorption is well described by the Sips model.

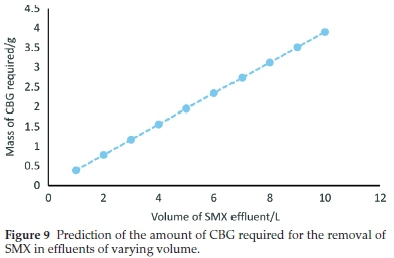
Figure 9 is a plot predicting the mass of CBG required for 99 % sequestration of SMX from effluents of different volumes. An initial concentration of 0.2 mg L^-1 was used. The revelation that that approximately 4 g of CBG is needed to oust 99 % SMX in a 10 L solution provides evidence that CBG is a low-cost and efficient adsorbent.

 

 

3.9. Performance Relative to Other Adsorbents

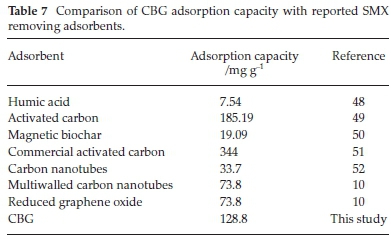
The theoretical maximum capacity of CBG for the uptake of SMX was examined against other reported adsorbents and the comparative performance is presented in Table 7. It is demonstrable that the performance of CBG is comparable to and better than reported adsorbents and the precursor material and preparation conditions for the adsorbent development make CBG an efficient and techno-economic adsorbent for SMX uptake in comparison to many adsorbents.

 

 

4. Conclusion

In this work, agricultural waste, sugarcane bagasse, was used as precursor biomass for the preparation of residue waste-derived biochar using a techno-economic pyrolysis process. The product (CBG) was tested for adsorption of sulfamethoxazole (SMX) from aqueous solution. CBG exhibited a high removal efficiency of 78 % within 300 min. The equilibrium data were tested using six two-parameter and five three-parameter nonlinear isotherm models and the best fitting model was determined using error functions analysis. The three-parameter isotherm models better fitted the experimental data than two-parameter isotherms. The maximum adsorption capacity was between 105.6 and 128.8 mg g^-1. Adsorption kinetics followed the PFO model while the thermodynamics data showed the adsorption reaction is spontaneous, exothermic, and physical. Chargeassisted hydrogen bonding (-)CAHB is hypothesized to be the likely adsorption mechanism of SMX onto CBG. Carbonized bagasse is a low-cost adsorbent suitable for the removal of organic contaminants from water.

 

Acknowledgement

The authors acknowledge the International Foundation for Science (IFS) for providing funding for this work. Grant number W/5587-1.

 

References

1 S.J. Kimosop, Z.M. Getenga, F. Orata, V.A. Okello and J.K. Cheruiyot, Residue levels and discharge loads of antibiotics in wastewater treatment plants (WWTPs), hospital lagoons, and rivers within Lake Victoria Basin, Kenya, Environ Monil Assess., 2016,188, 532. https://doi.org/10.1007/s10661-016-5534-6        [ Links ]

2 Y.A.J. Al-Hamadani, C.M. Park, L.N. Assi, K.H. Chu, S. Hoque, M. Jang, Y. Yoon and P. Ziehl, Sonocatalytic removal of ibuprofen and sulfamethoxazole in the presence of different fly ash sources, Ullrason. Sonochem., 2017, 39, 354-362.         [ Links ].

3 E. Ngumba, A. Gachanja and T. Tuhkanen, Occurrence of selected antibiotics and antiretroviral drugs in Nairobi river basin, Sci. Total Environ., 2016, 539, 206-213.         [ Links ]

4 Y. Zhang, S.U. Geißen and C. Gal, Sulfamethoxazole and diclofenac: removal in wastewater treatment plants and occurrence in water bodies, Chemosphere, 2008, 73, 1151-1161.         [ Links ]

5 W. Baran, E. Adamek, Z. Justyna and S. Andrzej, Effects of the presence of sulfonamides in the environment and their influence on human health, J. Hazard. Mater., 2011,196(30), 1-15.         [ Links ]

6 S. Teixeira, C. Delerue-Matos and L. Santos, Removal of sulfamethox-azole from solution by raw and chemically treated walnut shells, Environ. Sci. Pollut. Res., 2012,19, 3096-3106.         [ Links ]

7 V.O. Shikuku, R. Zanella, C.O. Kowenje, F. Donato, N. Bandeira and O.D. Prestes, Single and binary adsorption of sulphonamide antibiotics onto iron-modified clay: linear and nonlinear isotherms, kinetics, thermodynamics, and mechanistic studies, Appl. Water Sci., 2018,8,175. https://doi.org/10.1007/s13201-018-0825-4        [ Links ]

8 K. Rajendran and S. Sen, Adsorptive removal of carbamazepine using biosynthesized hematite nanoparticles. Environ. Nanotechnol. Monit. Manag., 2018, 9, 122-127.         [ Links ]

9 X. Guo, C. Yang, Z. Dang, Q. Zhang, Y. Li and Q. Meng, Sorption thermodynamics and kinetics properties of tylosin and sulfamethazine on goethite, Chem. Eng. J., 2013, 223, 59-67.         [ Links ]

10 F.F. Liu, J. Zhao, S. Wang and B. Xing, Adsorption of sulfonamides on reduced graphene oxides as affected by pH and dissolved organic matter, Environ. Pollut., 2016, 210, 85-93.         [ Links ]

11 M.B. Ahmed, J.L. Zhou, H.H. Ngo, W. Guo, A.H. Johir and K. Sornalingam, Single and competitive sorption properties and mechanism of functionalized biochar for removing sulfonamide antibiotics from water, Chem. Eng. J., 2017, 311, 348-358.         [ Links ]

12 M.B. Ahmed, J.L. Zhou, H.H. Ngo and W. Guo, Insight into biochar properties and its cost analysis, Biomass Bioenergy, 2016, 84, 76-86.         [ Links ]

13 F. Lian, B. Sun, Z. Song, L. Zhu, X. Qi and B. Xing, Physicochemical properties of herb-residue biochar and its sorption to ionizable antibiotic sulfamethoxazole, Chem. Eng. J., 2014, 248, 128-134.         [ Links ]

14 K.K. Shimabuku, J.P. Kearns, J.E. Martinez, L. Mahoney, R.S. Moreno-Vasquez and S. Summers, Biochar sorbents for sulfa-methoxazole removal from surface water, stormwater, and waste-water effluent, Water Res., 2016, 96, 236-245.         [ Links ]

15 E. Ng'eno, F. Orata, D.B. Lilechi, V.O. Shikuku and S. Kimosop, Adsorption of caffeine and ciprofloxacin onto pyrolytically derived water hyacinth biochar: isothermal, kinetics, and thermodynamics, J. Chem. Chem. Eng., 2016,10, 185-194.         [ Links ]

16 D. Mohan, H. Kumar, A. Sarswat, M. Alexandre-franco and C.U. Pittman, Cadmium and lead remediation using magnetic oak wood and oakbarkfast pyrolysis biochars, Chem. Eng. J., 2014,236,513-528. http://doi.org/10.1016/j.cej.2013.09.057        [ Links ]

17 H. Jin, C. Sergio, C. Zhizhou, G. Jun, X., Yueding and Z. Jianying, Biochar pyrolytically produced from municipal solid wastes for aqueous As(V) removal: adsorption property and its improvement with KOH activation, Bioresour. Technol, 2014,169, 622-629.         [ Links ]

18 Y.S. Ho, and G. McKay, Sorption of dye from aqueous solution by peat, Chem. Eng. J, 1998, 70, 115-124.         [ Links ]

19 Y.S. Ho, Review of second-order models for adsorption systems, J. Hazard. Mater., 2006, 136, 681-689.         [ Links ]

20 L. Zheng, Y. Yang, P. Meng and D. Peng, Absorption of cadmium (II) via sulfur-chelatingbased cellulose: characterization, isotherm models and their error analysis, Carbohydr. Polymers., 2019, 209, 38-50.         [ Links ]

21 Shikuku, V.O., C.O. Kowenje and F. Kengara, Errors in parameters estimation using linearized adsorption isotherms: sulfadimethoxine adsorption onto kaolinite, Clay. Chem. Sci. Inter., 2018, J. 23, 1-6.         [ Links ]

22 E. Ng'eno, VO. Shikuku, F. Orata, D.B. Lilechi and S. Kimosop, Caffeine and ciprofloxacin adsorption from water onto clinoptilolite: linear isotherms, kinetics, thermodynamics, and mechanistic studies, S. Afr. J. Chem., 2019, 72, 136-142.         [ Links ]

23 I. Langmuir, The constitution and fundamental properties of solids and liquids, J. Am. Chem. Soc., 1918, 38, 2221-2295.         [ Links ]

24 H.M.F. Freundlich, Über die adsorption in lösungen, Z. Phys. Chem., 1906, 57, 385^70.         [ Links ]

25 R.E. Treybal, Mass Transfer Operations, 3rd edn., McGraw-Hill, New York, NY, USA, 1981.         [ Links ]

26 M. To, Hui, C. Lin and G. McKay, Mechanistic study of atenolol, acebutolol and sulfamethoxazole adsorption on waste biomass derived activated carbon, J. Mol. Liq., 2017, 241, 386-398.         [ Links ]

27 T.A. Saleh, Isotherm, kinetic, and thermodynamics studies on Hg(II) adsorption from aqueous solution by silica-multiwall carbon nanotubes, Environ. Sci. Pollut. Res., 2015, 22, 16721-16731.         [ Links ]

28 M.I. Temkin and V. Pyzhev, Kinetics of ammonia synthesis on promoted iron catalyst, Acta Phys. Chim. USSR., 1940, 12, 327-356.         [ Links ]

29 H. Shahbeig, N. Bagheri and S.A. Ghorbanian, A. Hallajisani and S. Poorkarimi, A new adsorption isotherm model of aqueous solutions on granular activated carbon, World J. Modell. Simulation, 2013, 9(4), 243-254.         [ Links ]

30 D. Rahangdale and A. Kumar, Chitosan as a substrate for simultaneous surface imprinting of salicylic acid and cadmium, Carbohydr. Polymer., 2018, 202, 334-344.         [ Links ]

31 S.M. Miraboutalebi, S.K. Nikouzad, M. Peydayesh, N. Allahgholi, L. Vafajoo and G. McKay, Methylene blue adsorption via maize silk powder: kinetic, equilibrium, thermodynamic studies, and residual error analysis, Proc. Safety Environ. Prot., 2017, 106, 191-202.         [ Links ]

32 M. Horsfall and A.I. Spiff, Equilibrium sorption study of Al³⁺,Co²⁺, and Ag²+ in aqueous solutions by fluted pumpkin (Telfairia occidentalis Hook) waste biomass, Acta Chim. Slov., 2005, 52, 174-181.         [ Links ]

33 K. Vijayaraghavan, T.V.N. Padmesh, K. Palanivelu and M. Velan, Biosorption of nickel(II) ions onto Sargassum wightii: application of two-parameter and three-parameter isotherm models, J. Hazard. Mater. B., 2006, 133, 304-308        [ Links ]

34 R.H. Fowler and E.A. Guggenheim, Statistical Thermodynamics, Cambridge University Press, London, 1939, 431-450.         [ Links ]

35 S.Y. Elovich and O.G. Larinov, Theory of adsorption from solutions of non-electrolytes on solid (I) equation adsorption from solutions and the analysis of its simplest form, (II) verification of the equation of adsorption isotherm from solutions, Izv. Akad. Nauk. SSSR, Otd. Khim. Nauk., 1962, 2, 209-216.         [ Links ]

36 K.Y. Foo and B.H. Hameed, Review: Insights into the modeling of adsorption isotherm systems, Chem. Eng. J., 2010, 156, 2-10.         [ Links ]

37 R.J. Sips, On the structure of a catalyst surface, J. Chem. Phys., 1948,16, 490-495.         [ Links ]

38 D.D. Do, Adsorption Analysis: Equilibria and Kinetics, Imperial College Press, London, 1998.         [ Links ]

39 J. Toth, State equations of the solid-gas interface layer, Acta Chem. Acad. Hung., 1971, 69, 311-317.         [ Links ]

40 M.A. Hossain, H.H. Ngo, WS. Guo and TV Nguyen, Palm oil fruit shells as biosorbent for copper removal from water and wastewater: experiments and sorption models, Bioresour. Technol., 2012,113, 97-101.         [ Links ]

41 R.A. Koble and T.E. Corrigan, Sorption isotherms for pure hydrocarbons, Ind. Eng. Chem., 1952, 44, 383-387.         [ Links ]

42 R. Saadi, Z. Saadi, R. Fazaeli and N.E. Fard, Monolayer and multilayer adsorption isotherm models for sorption from aqueous media, Korean J. Chem. Eng., 2015, 32(5), 787-799.         [ Links ]

43 O. Redlich and D.L. Peterson, A useful adsorption isotherm, J. Phys. Chem., 1959, 63, 1024.         [ Links ]

44 S.J. Allen, Q. Gan, R. Matthews and P.A. Johnson, Comparison of optimized isotherm models for basic dye adsorption by kudzu, Bioresour. Technol., 2003, 88, 143-152.         [ Links ].

45 F. Lian, B. Sun, Z. Song, L. Zhu, X. Qi and B. Xing, Physicochemical properties of herb-residue biochar and its sorption to ionizable antibiotic sulfamethoxazole, Chem. Eng. J., 2014, 248, 128-134. DOI: 10.1016/j.cej.2014.03.021        [ Links ]

46 R. Dahlan, C. McDonald and VB. Sunderland, Solubilities and intrinsic dissolution rates of sulfamethoxazole and trimethoprim, J. Pharm. Pharmacol., 1987, 39, 246-251.         [ Links ]

47 V.O. Shikuku, F. Donato, C.O. Kowenje, R. Zanella and O.D. Prestes, A comparison of adsorption equilibrium, kinetics, and thermodynamics of aqueous phase clomazone between Faujasite X and a natural zeolite from Kenya, S. Afr. J. Chem., 2015, 68, 245-252.         [ Links ]

48 X. Liu, S. Lu, Y. Liu, W. Meng and B. Zheng, Adsorption of sulfa-methoxazole (SMZ) and ciprofloxacin (CIP) by humic acid (HA): characteristics and mechanism, RSC Adv., 2017, 7, 50449.         [ Links ]

49 E. Çaliçkan and G. Sinem, Adsorption characteristics of sulfamethox-azole and metronidazole on activated carbon, Separation Sci. Technol., 2010, 45(2), 244-255.         [ Links ]

50 F. Reguyal and A.K. Sarmah, Adsorption of sulfamethoxazole by magnetic biochar: effects of pH, ionic strength, natural organic matter and 17a-ethinylestradiol, Sci. Total Environ., 2018, 628-629, 722-730.         [ Links ]

51 X. Li, H. Yuan, X. Quan, S. Chen and S. You, Effective adsorption of sulfamethoxazole, bisphenol A and methyl orange on nanoporous carbon derived from metal-organic frameworks, J. Environ. Sci., 2018, 63, 250-259.         [ Links ]

52 F. Wang, W. Sun, W. Pan and N. Xu, Adsorption of sulfamethoxazole and 17ß-estradiol by carbon nanotubes/CoFe₂O₄ composites, Chem. Eng. J., 2015, 274, 17-29.         [ Links ]

 

 

Received 20 March 2020
Revised 9 June 2020
Accepted 17 June 2020

 

 

* To whom correspondence should be addressed. E-mail: vshikuku@kafuco.ac.ke